Keywords

1 A New Regional Supply Chain

Buffalo milk mozzarella is an appreciated typical Italian fresh cheese. Its protected designation of origin (D.O.P.) requires its production to occur in Campania, in Southern Italy, where specialized dairies are located. However, a very large fraction of Italian production of buffalo milk occurs in Lombardy, in the North of the country; moreover, Lombardy, the most populated Italian region, is also the largest national market for mozzarella. More details can be found in [3]. This geographically unbalanced scenario implies the transportation of significant North-to-South flows of milk and South-to-North flows of cheese. The cost has been estimated in 1200 Euros for each truck traveling forth and back. Moreover every other travel is done with an empty vehicle, because different types of vehicles are required to trasport milk and fresh cheese. This motivated a feasibility study to assess the economic viability of a regional supply chain for the production of buffalo milk mozzarella, not endowed with the D.O.P. certification but possibly more profitable than the current national supply chain.

2 Strategic Level: Location and Allocation

At a strategic level two scenari were considered: scenario A implies the construction of a new specialized dairy, to be optimally located and sized in order to support the whole regional supply chain; scenario B is based on the re-conversion of two existing dairies of given production capacity. For each scenario it was also required to study how milk transport operations should be organized to minimize the total transportation cost.

Scenario A: Locating and Sizing a New Dairy

The strategic problem of optimally locating a new specialized dairy was formulated as a weighted 1-median problem (see [5] for a comprehensive treatment of discrete location problems) on the road network of South-Lombardy: distances were weighted with the (known) average daily production of each of the twenty-eight buffalo farms involved.

The optimization concerned only milk transportation cost, i.e. the first echelon of the supply chain; the transportation cost of cheese to retailers, i.e. the second echelon, was not considered, because of the high variability in the spatial distribution of the demand and the heterogeneity of the destinations, including stores, supermarkets, restaurants and hotels.

Two additional requirements were stated: (1) the location of the new dairy had to be easily accessible to trucks, i.e. along some main road or highway; (2) it also had to be close to a city, in order to have a nearby set of potential customers large enough to make a local shop sustainable. Such a local shop is meant for selling fresh mozzarella with no final packaging and possibly additional products characterized by relatively small production volumes.

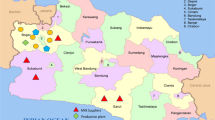
The optimal solution was computed on a weighted digraph obtained from digital maps of the road network of South Lombardy, with a software tool based on MapWinGIS [4]. To comply with the two additional constraints a GIS-based decision-support system was designed to compute the set of points for which the value of the objective function is within a user-defined small percentage of the optimum, as shown in Fig. 1.

Fig. 1
figure 1

Scenario A: quasi-optimal zones within 1% (green), 5% (orange) and 10% (yellow) from the optimum

Full size image

The optimal solution occurs along one of the main internal streets of Soncino, close to the intersection of the borders between the three provinces of Cremona, Brescia and Bergamo. This point is a few hundred meters from the ring road surrounding the town, which could be a perfectly suitable location satisfying both the above mentioned requirements (see Fig. 2).

Fig. 2
figure 2

Scenario A: the optimal location and the ring road just North of it

Full size image

In scenario A the sizing problem is trivial: the needed capacity should be at least equal to the total estimated production capacity of the twenty-eight buffalo farms of the supply chain (18,477 L of milk per day).

Scenario B: Demand Allocation

In scenario B the location and the capacity of two existing dairies is given (Acquanegra sul Chiese (MN), 20,000 L per day and Dorno (PV), 3000 L per day) and two corresponding clusters of buffalo farms must be defined in order to minimize transportation costs complying with capacity constraints. A generalized assignment problem instance arises (see [2] for a comprehensive survey on the problem). Owing to its small size, it could be solved with a spreadsheet add-in such as Microsoft Excel Solver. Its optimal solution is represented in Fig. 3.

Fig. 3
figure 3

Optimal allocation of farms (blue and red triangles) to dairies (black icons)

Full size image

All farms turn out to be allocated to the closest dairy with a single exception: Casirate d’Adda (the break item in the optimal solution of the linear relaxation) is 91 km far from Acquanegra sul Chiese and 76 km far from Dorno, but it is assigned to the former one. The closest dairy (Dorno) has enough residual capacity to accommodate about 75% of the milk production from Casirate d’Adda. However, the option of splitting the Casirate d’Adda supply, allowing for a fractional allocation, was discarded in favor of the more expensive integer allocation, because of three main reasons: (1) integer allocation implies lower administrative costs and simpler administrative procedures; (2) it allows for more reliable forward tracing, which is especially important in food supply chains; (3) the resulting solution is more robust, because no dairy is saturated and this is useful to absorb fluctuations of the daily milk production.

3 Tactical Level: Optimal Pick-Up Frequencies

For the whole set of suppliers in scenario A and for each farm cluster in scenario B one has to decide how to organize the visits of vehicles to pick-up milk and carry it to the dairies. We indicate with \(\mathcal {P}\) the set of farms to be visited.

Since milking occurs twice a day, the time slots considered in this problem correspond to half-days. For each time slot the forecasted milk production at each farm is known. An additional datum is the maximum amount s p of milk that can be stored at each farm \(p \in \mathcal {P}\). This amount is not larger than the total production of 7 time slots, because buffalo milk cannot be stored for more than three-and-a-half days. The available storage is further reduced by the production of the last time slot, because it is a good practice to leave fresh milk “resting” for about twelve hours before transporting it.

The possibility of storing milk at the farms allows not to visit every farm in every time slot, which would be very expensive from the viewpoint of transportation costs. Instead, one wants to define a cyclic schedule of visits that repeats every T time slots, where T is a user-defined parameter. We indicate with \(\mathcal {T}\) the set of time slots for each problem instance.

The mathematical model includes binary variables v pt, representing whether farm \(p \in \mathcal {P}\) is visited in time slot \(t \in \mathcal {T}\) or not, as well as continuous non-negative variables z pt and y pt, representing respectively the amounts of milk picked-up at farm \(p \in \mathcal {P}\) in time slot \(t \in \mathcal {T}\) and the amount of milk stored at farm \(p \in \mathcal {P}\) at the end of time slot \(t \in \mathcal {T}\). The integer linear programming model includes the dairy capacity constraint (a datum m indicates the capacity of the dairy in every time slot), the farms storage capacity constraint, the typical flow balance constraints y pt−1 + q p = z pt + y pt that link the stored amount y, the production q and picked-up amount z in each time slot for each farm, and constraints stating that pick-up operations can occur only when a farm is visited (i.e. z pt > 0 implies v pt = 1).

In principle the objective function of this problem should be the total travel cost, i.e. the total distance traveled in the T time slots of the planning horizon. This would generate a vehicle routing problem (actually, a periodic inventory-routing problem) which cannot be solved by general-purpose ILP solvers. Instead of implementing an ad hoc optimization algorithm, it was decided to minimize the total number of visits to the farms. Intuitevely, this is a good proxy for the solution that minimizes the total distance traveled, with the disadvantage that several solutions can exist implying the same total number of visits but different transportation costs.

The model is as follows:

$$\displaystyle \begin{aligned} \text{minimize } f = & \sum_{p \in \mathcal{P}} \sum_{t \in \mathcal{T}} v_{pt} & \\ \text{subject to } & \sum_{p \in \mathcal{P}} z_{pt} \leq m & \forall t \in \mathcal{T} \\ & y_{pt} = y_{pt-1} - z_{pt} + q_p & \forall p \in \mathcal{P}\ \forall t \in \mathcal{T}: t \neq 1 \\ & y_{p1} = y_{pT} - z_{p1} + q_p & \forall p \in \mathcal{P} \\ & y_{pt} \leq s_p & \forall p \in \mathcal{P}\ \forall t \in \mathcal{T} \\ & z_{pt} \leq v_{pt} s_p & \forall p \in \mathcal{P}\ \forall t \in \mathcal{T} \\ & z_{pt} \geq 0 & \forall p \in \mathcal{P}\ \forall t \in \mathcal{T} \\ & y_{pt} \geq 0 & \forall p \in \mathcal{P}\ \forall t \in \mathcal{T} \\ & v_{pt} \text{ binary} & \forall p \in \mathcal{P}\ \forall t \in \mathcal{T} \end{aligned} $$

The optimization was repeated for several values of T. It is worth noting that in order to allow farmers to easily plan the visits, it is not recommendable to use large values of T.

In spite of the simplified objective function, the resulting ILP model turned out to be too difficult for the Microsoft Excel Solver and also for the free solver glpsol, even for the smallest instance (Dorno dairy in scenario B, with only 7 allocated farms). Using ILOG CPLEX, on the contrary, it was possible to solve all instances of interest to optimality. Moreover, it is worth observing that even values of T are preferable to odd values, because their effect is that visits to each farm always occur in the morning or in the afternoon without annoying alternations.

The results reported here refer to the case where all farms are assumed to be equipped with sufficent capacity to store a 7 time slots production. Two different cases were studied, indicated by “constrained” and “unconstrained”. In the constrained case, the farm refrigerator is assumed to be completely emptied when a visit occurs, while the unconstrained case allows for partial pick-up. The unconstrained case is more difficult to implement in practice, because it requires separated refrigerators and an additional information to be communicated to the driver (i.e. the exact amount of milk to pick-up), which may be a source of errors. However the unconstrained case was considered as a benchmark to evaluate the costs of the constrained case. Tables 1, 2, and 3 report the results.

Table 1 Optimal visit frequencies (scenario A, Soncino dairy)
Full size table
Table 2 Optimal visit frequencies (scenario B, Acquanegra dairy)
Full size table
Table 3 Optimal visit frequencies (scenario B, Dorno dairy)
Full size table

The results show that the constraint does not yield any significant increase of the number of visits per time slot, with only a few exceptions of the smallest dairy (Dorno) for some values of T.

The average number of visits per slot decreases when T increases, because farms storage capacity is better and better exploited. When the time threshold of 7 slots is reached, the average number of visits per slot suddenly doubles. This effect would not be so concentrated on a specific value of T if the farm storage capacities were assumed to be different from one another.

4 Routing

The last step in this feasibility study was the evaluation and minimization of milk transportation costs. This would require to solve some instances of the capacitated vehicle routing problem (see [6] for a comprehensive survey) with some additional constraints. However, owing to budget and time limits, in this preliminary feasibility study it was not required to develop an exact solution algorithm (typically a branch-and-price or branch-and-cut-and-price algorithm), but rather to compute a reliable estimate of the transportation cost.

For this purpose, three assumptions were made. First, a single vehicle was assumed to be sufficient for each time slot; this is not restrictive, because the capacity of the available vehicles is larger than the amount of milk to be transported in every scenario and for every value of T. Second, no constraints were imposed on the maximum distance and the maximum duration for each vehicle route; this is also unlikely to be restrictive in a real situation, because farms are not far from one another. Third, it was assumed that routes were determined by the optimal farm-to-slot assignment computed in the previous phase of the study, where the number of visits had been minimized. This is the most restrictive assumption, because the composition of the farms subsets assigned to the same time slots does not take into account farm-to-farm distances; therefore, from the viewpoint of travel cost minimization such clusters are likely to be sub-optimal. This effect is mitigated by the decentralized position of the dairies in scenario B: this means that the total distance travelled depends more on the number of routes than on their composition.

Owing to these assumptions, it is possible to obtain an estimate of the total transportation costs by solving some instances of the asymmetric traveling salesman problem (see [1] for a comprehensive survey), one for each scenario, for each dairy, for each value of T and for each time slot. The size of these instances was between 2 and 29, including the dairy which is assumed to act as the vehicle depot. The results obtained with ILOG CPLEX for T up to 7 are reported in Table 4.

Table 4 Average distance [Km] travelled in each time slot for different values of T
Full size table

The reason why the constrained cost is sometimes lower than the unconstrained one is the third assumption mentioned above. This effect is possible when one estimates costs using clusters of farms that are not guaranteed to be optimal from the viewpoint of distance minimization.

5 Extensions and Conclusions

The aim of the preliminary study was to evaluate the feasibility and economic sustainability of a new regional supply chain. For this reason some assumptions and approximations were done to pursue a trade-off between reliability of estimates on one side and development time and cost on the other side.

Several extensions are possible from this starting point. A first possible extension consists of formulating and solving a vehicle routing problem, replacing the many instances of the asymmetric traveling salesman problem, in order to obtain more accurate estimates of the milk transportation cost. In such a vehicle routing prooblem one can allow for the use of two types of vehicles (with capacity 17,000 and 35,000 L). Another extension consists of using tighter (and more realistic) constraints on the available storage capacity at the farms. However this would change the results but not the structure of the mathematical models.

An important possible extension concerns the production and distribution of cheese. Taking into account the milk-to-cheese conversion factor (typically 25–28% for mozzarella), one should determine the optimal production mix of mozzarella and other types of cheese. For this purpose one should also consider seasonal effects both in production and consumption. On one side, the monthly production of milk is different along the year and it also depends on the buffalos reproduction cycle. On the other side, the market demand is not uniform along the year; in winter, demand for mozzarella is lower and demand for other types of cheese is higher than in summer. A critical decision is how to manage production surplus in winter, i.e. deciding whether to sell the surplus milk (for instance in the Southern Italy market) or to freeze it to meet demand peaks in summer.

Finally it should be pointed out that this feasiblity study has shown that a new regional supply chain of buffalo milk mozzarella in Lombardy would allow to transport every liter of milk for about 33 km in average, instead of the 700 km currently travelled to supply dairies in South Italy.