Keywords

1 Introduction

Reverse logistics aims at improving the exploitation of used products through recycling or re-manufacturing and leads to a reduction in environmental damage. Products may reverse direction in the supply chain for several motivations, such as manufacturing returns, product recalls, warranty or service returns, end-of-use returns, and end-of-life returns. Reverse logistics and, in particular, second-hand trading have received large interest for the opportunity of sustainable consumption, extending the life span of products, and reducing adverse environmental impacts due to the purchase of new goods. Recently, the increasing use of the Internet and trading platforms, such as eBay or Vinted, has completely changed the market conditions, see [1, 15]. In the U.S., the e-commerce sales have reached $876 billion in the first quarter of 2021, up 38% year-over-year. Moreover, the speculative buying of limited edition goods has become a real business. In fact, people may gain profit from selling high-uniqueness goods at a price much higher than the original one to potential consumers when the goods get scarce over time.

Due to several advantages, closed-loop supply chains (CLSCs) have been extensively studied in recent years. Many researchers have investigated the network structure of the CLSC, which includes competitive manufacturers, competitive retailers and consumer markets. For example, Nagurney and Toyasaki [4] develop a network model for supply chain decision-making with environmental criteria. In [5], the authors explore a reverse supply chain network model using variational inequality. In [10], Shen et al. examine the sale of second-hand products through an online platform on a supply chain consisting of contributors, one second-hand online platform, and one supplier. Different scenarios in terms of CLSC structure and block-chain use are considered. In [13], Wang et al. study the waste of electrical and electronic equipment and provide a variational inequality to model the CLSC network. In [16], the authors examine a CLSC network equilibrium problem in multiperiod planning horizons, with consideration to product lifetime and carbon emission constraints. By variational inequalities and complementary theory, the governing CLSC network equilibrium model is established. Other valuable contributions can be found in [3, 9, 11, 12, 14].

Motivated by all the above analysis, this paper establishes a CLSC network equilibrium model with online second-hand trading of high-uniqueness products. We consider a CLSC network consisting of manufacturers, retailers, demand markets, and one online platform, in which the consumers purchase new products and collect them. Then, collectors sell the goods to consumers through the online platform. By variational inequalities, the optimal behaviors of all the decision-makers are modeled, and, in turn, the governing CLSC network equilibrium model is given. The main contributions of this paper are: the modeling of the second-hand market in a reverse logistics setting, and the study of the horizontal competition among the members of the same tiers as well as the vertical one between adjacent tiers. We describe the forward and the reverse logistics, taking into account capacity constraints of manufacturers and retailers, as well as consumers’ risk-aversion to purchasing second-hand goods, and platform’s risk-aversion to transacting with collectors.

The paper is organized as follows. In Sect. 2, we develop the CLSC model by describing the manufacturers’ and the retailers’ competitive behavior, and the interactions with the demand markets and the online platform. We then provide a variational inequality formulation of the optimal behavior of decision-makers. In Sect. 3, we state that the governing equilibrium conditions of the CLSC network. We summarize our results and present our conclusions in Sect. 4.

2 The Closed-Loop Supply Chain Network

We consider a CLSC network consisting of multiple manufacturers, multiple retailers, and multiple demand markets, in which the consumers purchase new products and collect them. Collectors distribute the used goods through an online platform for the aim of gaining profit on the resale. The criterion of each player in the network is the total profit maximization.

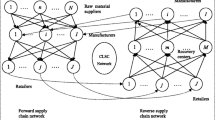
Let M be the set of manufacturers (we denote by m the typical manufacturer), R be the set of retailers (we denote by r the typical retailer), K be the set of demand markets (we denote by k the typical demand market) and we consider a single online platform like eBay, Marketplace by Facebook, Vinted etc…Abusing notation, without risk of confusion, we use the same symbols here to denote the sets M, R, K and their cardinalities. Furthermore, we introduce the set of collectors K c, with |K c|≤ K, that represents the set of consumers who decide to resell their collectibles. The network can be divided into two parts: the forward chain, formed by manufacturers, retailers and consumers, and the reverse chain, formed by collectors, the online platform and consumers. The collectors and the online platform make it possible to connect the forward and the reverse chains and form the closed-loop network. We consider two different types of items: the new ones denoted by index n = 1, …N and the used ones indicated by index u = 1…U. The model network can be represented as in Fig. 1. The solid lines represent the forward transactions and the dashed lines refer to the reverse ones.

Fig. 1
figure 1

The closed-loop supply chain network

Full size image

We first focus on the manufacturers. We then turn to the retailers, to the consumers, and, finally, to the platform. The complete equilibrium model is then constructed as a variational inequality.

2.1 The Optimal Behavior of the Manufacturers

Let \(x^n_{mr}\) be the quantity of new item n sold by manufacturer m to retailer r. We group all the n and r elements into the vector \(x_m\in \mathbb {R}^{NR}\), and then we group all the vectors (x m) for all m into the vector \(x^M\in \mathbb {R}^{NMR}\). We denote by \(x^{max}_m\) the production capacity of manufacturer m.

In the forward logistics, a manufacturer incurs production costs and transaction costs. In order to maximize his own profit, each manufacturer m must decide the quantity \(x^n_{mr}\) of new item n to be sold to retailer r. We associate with each manufacturer the production cost, c m, and assume that it can depend, in general, on the entire vector of production outputs, namely, c m = c m(x M). We denote by \(t_{mr}(x^n_{mr})\) the transaction cost from manufacturer m to retailer r. Moreover, we assume that c m(x M) and \(t_{mr}(x^n_{mr})\) are continuously differentiable and convex functions. Finally, we consider \(p^n_{mr} \) as the selling price of a new product. Given the above notation, each manufacturer m wishes to maximize the profit as follows:

$$\displaystyle \begin{aligned} & \max \sum_{n \in N}\sum_{r\in R}p^n_{mr}x^n_{mr}-c_{m}(x^M)-t_{mr}(x^n_{mr}){} \end{aligned} $$
(1)
$$\displaystyle \begin{aligned} &\sum_{n \in N}\sum_{r\in R} x^n_{mr}\leq x^{max}_{m}, {}\quad x^n_{mr}\geq 0, \forall n,r. \end{aligned} $$
(2)

The objective function (1) maximizes the profit, which equals sales revenue minus costs associated with production and transaction. The first constraint in (2) expresses the production capacity of manufacturer m. All the manufactures compete in a non-cooperative fashion, and each manufacturer seeks to maximize his profit given other manufacturers’ decisions. Thus, the optimality conditions of all the manufacturers can be described by the following variational inequality, see [2]:

$$\displaystyle \begin{aligned} & \sum_{n \in N}\sum_{m\in M}\sum_{r \in R}\Bigg(\frac{\partial c_{m}(x^{*M})}{\partial x_{mr}^n}+\frac{\partial t_{mr}(x^{*n}_{mr})}{\partial x_{mr}^n}-p^n_{mr}\Bigg)(x_{mr}^n-x_{mr}^{*n})\geq 0, \forall x^M\in S^M{}, \end{aligned} $$
(3)
$$\displaystyle \begin{aligned} &S^M=\Big\{x^M\in \mathbb{R}^{NMR}_+: \sum_{n \in N}\sum_{r\in R} x^n_{mr}\leq x^{max}_{m}, \forall m\in M\Big\}. \end{aligned} $$
(4)

2.2 The Optimal Behavior of Retailers

The retailers interact with manufacturers and consumers. Specifically, they decide the amount of products to order from the manufactures, so as to transact with the demand markets, while seeking to maximize their profit. The product shipment of new good n between retailer r and consumer k is denoted by \(x^n_{rk}\); the product shipments \(x^n_{rk}\) for all n and k are then grouped into the column vector \(x_r\in \mathbb {R}^{NK}\) and, further, into the vector \(x^R\in \mathbb {R}^{NRK}\).

Each retailer r has associated management cost c r, which may include, for example, the storage cost associated with the products in stock. For the sake of generality, and to enhance the modeling of competition, see [6], we allow the function to depend also on the amounts of the products held by other retailers, that is, c r = c r(x M). Let \(\hat {c}^n_{mr}(x^n_{mr})\), be the transportation cost from m for new items and let \(p^{n}_{rk}\) be the sale price associated with a new item. Moreover , retailers incur transaction costs \(t^n_{rk}(x^n_{rk})\), when selling new products to consumers. Finally, we assume that \(c_r (x^n_{mr})\), \(\hat {c}^n_{mr}(x^M)\), and \(t_{rk}(x^N_{rk})\) are continuously differentiable and convex functions.

Each retailer r seeks to maximize his profit function as follows:

$$\displaystyle \begin{aligned} &\max \sum_{n \in N}\Bigg (\sum_{k\in K}p^{n}_{rk}x^n_{rk} -\sum_{m \in M} \hat{c}^n_{mr}(x^n_{mr})-\sum_{k\in K}t^{n}_{rk}(x^n_{rk}) -\sum_{m\in M}p^{n}_{mr}x^n_{mr}\Bigg )-{c}_{r}(x^M){} \end{aligned} $$
(5)
$$\displaystyle \begin{aligned} & \sum_{n \in N}\sum_{k\in K}x^n_{rk}\leq \sum_{n \in N}\sum_{m\in M}x^n_{mr}{}, \quad x^n_{mr}\geq 0,\, x^n_{rk}\geq 0, \forall n,m,k. \end{aligned} $$
(6)

Objective function (5) expresses that the profit of the retailer is equal to sales revenues minus costs associated with the management, the transportation, the transaction and the payout to the manufacturers. The first constraint in (6) states that consumers cannot purchase more from a retailer than is held in stock. Since all the retailers compete in a non-cooperative fashion, the optimality conditions for all retailers can be expressed as the variational inequality:

$$\displaystyle \begin{aligned} & \sum_{n \in N}\sum_{r\in R}\sum_{k \in K}\Bigg(\frac{\partial t_{rk}(x^{*n}_{rk})}{\partial x_{rk}^n}-p^n_{rk}\Bigg)(x_{rk}^n-x_{rk}^{*r})\\& + \sum_{n \in N}\sum_{m \in M}\sum_{r\in R}\Bigg(p^n_{mr}+\frac{\partial c_{r}(x^{*n}_{mr})}{\partial x_{mr}^n}+\frac{\partial \hat{c}^n_{mr}(x^{*M})}{\partial x_{mr}^n}\Bigg)(x_{mr}^n-x_{mr}^{*r})\geq 0,\\ & \forall (x^R,x^M)\in S^{R}{}, \end{aligned} $$
(7)
$$\displaystyle \begin{aligned} &S^R=\Big\{(x^R,x^M)\in \mathbb{R}^{NRK+NMR}_+: \sum_{n \in N}\sum_{k\in K}x^n_{rk}\leq \sum_{n \in N}\sum_{m\in M}x^n_{mr},\forall r\in R\Big\}. \end{aligned} $$
(8)

2.3 The Optimal Behavior of the Consumers

The consumers at demand markets transact with the retailers as well as the online platform. Specifically, in the forward supply chain, consumers purchase new products; in the reverse supply chain, consumers act as collectors and sell their goods on the online platform, that are then purchased by consumers at demand markets. We analyze these situations separately.

2.3.1 The Consumers in the Forward Logistics

Let \(\hat {c}^n_ {rk}(x^n_{rk})\) be the transportation cost for new product n sold by retailer r to demand market k. Moreover, let \(d^n_k\) be the demand of new item n at demand market k and be \(p^{n}_k\) the price of new product n at demand market k. The equilibrium conditions for consumers at demand market k are (see [4,5,6,7,8]):

$$\displaystyle \begin{aligned} p^{*n}_{rk}+\hat{c}^n_{rk}(x^{*n}_{rk}) \begin{cases} = p^{*n}_k & \mbox{if }x^{*n}_{rk}> 0, \\ \geq p^{*n}_k & \mbox{if }x^{*n}_{rk}=0 , \end{cases}{}\quad \forall r,k,n. \end{aligned} $$
(9)
$$\displaystyle \begin{aligned} d^n_k(p^{*n}_k) \begin{cases} =\sum_{r\in R}x^{*n}_{rk} & \mbox{if }p^{*n}_k>0, \\ \leq \sum_{r\in R}x^{*n}_{rk} & \mbox{if }p^{*n}_k=0, \end{cases}{} \quad \forall k,n. \end{aligned} $$
(10)

Inequality (9) states that if the consumers at demand market k purchase the products from retailer r, then the price charged by the retailer for the product plus the transportation cost undertaken by the consumers does not exceed the price that the consumers are willing to pay. Equation (10) states that if the equilibrium price that the consumers are willing to pay for the new products at the demand market is positive, then the quantities purchased of new goods from the retailers will be exactly equal to the demand. These conditions correspond to the well-known spatial price equilibrium conditions, see [2].

2.3.2 The Consumers in the Reverse Logistics

In the reverse supply chain, some consumers resell collectible items to the demand market through the online platform. The product shipment of second-hand good u between collector k c and consumer k, using the platform, is denoted by \(x^{u}_{k_ck}\). The product shipments \(x^{u}_{k_ck}\), for all u and k, are then grouped into the column vector \(x_{k_c}\in \mathbb {R}^{UK}\) and, further, into the vector \(x^{U}\in \mathbb {R}^{UK^cK}\). We set \(Q_{k_c}\) as the amount of items in the collection of collector k c. Let \(p^u_{k_c}\) be the price charged by the collector k c for second-hand items. We note that selling on the online platform can give higher visibility to the products and, as a consequence, it can be more profitable, even if the platform retains a portion of the sale price. For instance, on eBay the transaction price amounts to the 10% of the selling price, indicated by the coefficient γ. Let \(c_{k_c}(x_{k_c})\) be the maintenance and restoring cost of the collector k c, depending on the amount of items that he resells on the online platform. Let \(\hat {c}^n_{rk_c}(x^R)\), be the transportation cost from r for new item n to collector k c. We assume that \(c_{k_c}(x_{k_c})\) and \(\hat {c}^n_{rk_c}(x^R)\) are continuously differentiable and convex functions. We denote by \(\mu _{k_c}\in (0, 1]\) the portion of second-hand goods that collector k c ∈ K c decides to sell on the platform.

Each collector k c ∈ K c seeks to maximize his profit function as follows:

$$\displaystyle \begin{aligned} & \max \sum_{u \in U}\sum_{k\in K}(1-\gamma)p_{k_c}^{*u}x_{k_ck}^u-c_{k_c}(x_{k_c})-\sum_{n\in N}\sum_{r\in R}\Big(p^{n}_{rk_c}x^n_{rk_c}-\hat{c}^n_{rk_c}(x^R)\Big) {} \end{aligned} $$
(11)
$$\displaystyle \begin{aligned} & \quad \sum_{u \in U}\sum_{k \in K}{x}^{u}_{k_ck}\leq \mu_{k_c} Q_{k_c}, \quad x^u_{k_ck}, x^n_{rk_c} \geq 0, \quad \forall n,u,r,k.{} \end{aligned} $$
(12)

Objective function (11) expresses that the profit of the collector is equal to sales revenues minus costs associated with restoring, purchasing and transportation. The first constraint in (12) states that the amount of products collector k c decides to sell should be less than or equal to the amount of collectibles in k c’s collection.

We now examine the transactions between the platform and the demand market k. Let \(\hat {c}^u_{k_ck}(x^U)\) be the transportation cost from collector k c to consumer k for used product u purchased on the platform. Furthermore, let \(d^u_k\) be the demand of second-hand items at demand market k, and \(\rho ^{u}_k\) be the willingness to pay second-hand items at demand market k. We group all these \(\rho ^{u}_k\) into a column vector \(\rho _{k}\in \mathbb {R}^{U}\), and then into the vector \(\rho ^{U}\in \mathbb {R}^{UK}\). We also consider a risk associated with purchasing second-hand items from the trading platform. Therefore, each consumer exhibits risk aversion that may be dependent on flows controlled by other demand markets. Hence, the risk aversion function can be expressed as the continuous function π k(x U) [8]. The equilibrium conditions for consumers at demand market k in the reverse supply chain are

$$\displaystyle \begin{aligned} p^{*u}_{k_c}+\hat{c}^u_{k_ck}({x}^{*U})+\pi_k({x}^{*U}) \begin{cases} = \rho^{*u}_k & \mbox{if }{x}^{*u}_{k_ck}> 0,\\ \geq \rho^{*u}_k & \mbox{if } {x}^{*u}_{k_ck}=0, \end{cases}{} \quad \forall k_c,u. \end{aligned} $$
(13)
$$\displaystyle \begin{aligned} d^u_k(\rho^{*U}) \begin{cases} ={x}^{*u}_{k_ck} & \mbox{if }\rho^{*u}_k>0,\\ \leq {x}^{*u}_{k_ck} & \mbox{if }\rho^{*u}_k=0, \end{cases}{} \quad \quad p^{*n}_{rk}-\rho^{*u}_k \begin{cases} <0 & \mbox{if }x^{*n}_{rk}=0, \\ \geq 0 & \mbox{if }x^{*n}_{rk}>0, \end{cases} \quad \forall r,k,u,n. \end{aligned} $$
(14)

Equality (13) states that if the consumers at demand market k purchase the product on the online platform, then the price charged by the collector k c for second-hand items plus the transportation cost plus the risk undertaken by the consumer is equal to the price that the consumer is willing to pay. The first condition in (14) states that if the equilibrium price the consumers at demand market k are willing to pay for the second-hand product is positive, then the amount purchased of second-hand product should exactly be equal to the demand of this second-hand item. The second condition in (14) means that the unitary price of a second-hand collectible is higher than the unitary price of a new collectible that is totally sold out.

2.3.3 The Consumers’ Equilibrium Conditions

Combining consumer behaviors in both forward and reverse supply chain, and assuming that the tranposrtation costs, the demand functions and the risk function are continuous, the equilibrium conditions for all the demand markets can be expressed as the following variational inequality, see [4,5,6,7,8]:

$$\displaystyle \begin{aligned} &\sum_{n \in N}\sum_{k \in K}\Bigg ( \sum_{r \in R}x_{rk}^n-d_k^{*n}(p_k^{*n}) \Bigg )(p_k^{n}-p_k^{*n})\\ &+\sum_{u \in U} \sum_{k_c\in K^c}\Bigg(\frac{\partial c_{k_c}(x_{k_c})}{\partial x^u_{k_ck}}+\gamma p_{k_c}^{*u}+\hat{c}^u(x_{k_c k}^{*U})+\pi_k(x^{*U})-\rho^{*u}_k\Bigg)(x^u_{k_ck}-x^{*u}_{k_ck})\\ &+ \sum_{u \in U}\sum_{k\in K}\Bigg(x^{*u}_{k_c k}-d_k^u(\rho^{*U})\Bigg)(\rho^{u }_k-\rho^{*u}_k)\\ & \!+\!\sum_{n \in N}\sum_{r\in R}\sum_{k\in K}\Bigg(p_{rk}^{*n}\!+\!\hat{c}_{rk}^n(x_{rk}^{*n})\!-\!p_k^{*n}+p^{*n}_{rk}\!-\!\sum_{u \in U}\rho^{*u}_k\!+\!\frac{\partial \hat{c}^n_{rk_c}(x^R)}{\partial x^n_{rk}} \Bigg)(x^n_{rk}-x^{*n}_{rk}),\\ & \!+\!\sum_{n\in N}\sum_{r\in R}p^{n}_{rk_c}(x^n_{rk_c} \!-\!x^{*n}_{rk_c} )\geq 0,\quad \forall (p^N,x^{UK},\rho^U,x^{U},x^R)\in S^K {}, \end{aligned} $$
(15)
$$\displaystyle \begin{aligned} &S^K\!=\!\Big\{(p^N,x^{UK},\rho^U,x^{U},x^R)\in \mathbb{R}^{KN\!+\!2UK\!+\!UK^cK+NRK}_+\!:\! \sum_{u \in U}\sum_{k \in K}{x}^{u}_{k_ck}\!\leq\! \mu _{k_c} Q_{kc}\Big\}. \end{aligned} $$

2.4 The Behavior of the Online Platform

Now, we present the behavior of the online platform as an intermediary that matches consumers and collectors. As an intermediary, the platform is involved in transactions both with the collectors, as well as with the consumers at the demand markets.

Collectors resell items on the platform and determine the unitary price \(p^{u}_k\) of second-hand goods. Let C u(x U) be the management costs of second-hand product u, including processing and advertisement, and let \(\hat {t}^u_k(x^u_{k})\) be the transaction cost function between the platform and demand market k, where \(x^u_k=\sum _{k_c}x^u_{k_ck}\). Since the platform has no decision-making power on the choice of products that will be sold, it takes the risk of owning false objects or with descriptions that do not correspond to the real conditions of the item. As a consequence, the intermediary may have risk associated with transacting with the various collectors and with the demand markets. Let π(x U) denote the risk function associated with online platform. We assume that C(x U), \(\hat {t}^u_k(x^u_{k})\) and π(x U) are continuously differentiable and convex. Let \(\mu _{k_c}\) the portion of second-hand goods that collector k c decides to sell on the platform, and satisfies \(\mu _{k_c}\in (0,1]\). We define Q u ∈ R U as the total amount of item u on the online platform. Each online platform makes his optimal decisions based on maximizing the following profit function:

$$\displaystyle \begin{aligned} & \max \sum_{u\in U}\Big ( \sum_{k_c\in K^c}\sum_{k\in K}\gamma p^{u}_{k_c}{x}^u_{k_ck}-C^u(x^U)-\sum_{k\in K}\hat{t}^u_k({x}^u_{k})-{\pi (x^U)}\Big ).{} \end{aligned} $$
(16)
$$\displaystyle \begin{aligned} &\sum_{k \in K}x^u_k\leq Q^u, \;\; {} \quad x^u_{k}, x^u_{k_ck}\geq 0, \; \forall u, \, \forall k. \end{aligned} $$
(17)

Objective function (16) expresses that the profit of the online platform is equal to a percentage of the profit of sale of the product minus the management, transaction costs and the risk. The first constraint in (17) states that the total amount of each second-hand item bought by all consumers k on platform should be less or equal than the availability of item u.

Under our assumptions, the optimality conditions for the online platform can be expressed as the variational inequality:

$$\displaystyle \begin{aligned} & \sum_{u\in U}\sum_{k_c \in K^c}\sum_{k \in K}\Bigg( \frac{\partial C^u(x^{*U})}{\partial x_{k_ck}^u}-\frac{\partial \pi ^u(x^{*U})}{\partial x_{k_ck}^u}-\gamma p^{*u}_k\Bigg)(x_{k_ck}^u-x_{k_ck}^{*u}) \end{aligned} $$
(18)
$$\displaystyle \begin{aligned} & +\sum_{u\in U}\sum_{k \in K}\Bigg(\frac{\partial\hat{t}^u_k(\bar{x}^u_k)}{\partial x_{k}^u}\Bigg)(x_{k}^u-x_{k}^{*u})\geq 0, \, \forall ({x}^U,x^{K^c}) \in S^P{} \end{aligned} $$
(19)
$$\displaystyle \begin{aligned} &S^P=\Big\{(x^{U},x^{K^c})\in \mathbb{R}^{UK^cK+UK}_+: \sum_{k \in K}x^u_k\leq Q^u, \forall u\in U {}\Big\}. \end{aligned} $$
(20)

3 The Equilibrium Conditions of the CLSC Network

In equilibrium state, the optimality conditions for all suppliers, manufacturers, retailers, demand markets and online platform must be satisfied simultaneously. We now define the CLSC network equilibrium and give an equivalent variational inequality formulation.

Definition 1

The CLSC network is at equilibrium if the forward and reverse flows between the tiers of the decision-makers coincide and the product flows and prices satisfy the sum of optimal conditions in (3), (7), (15), and (19).

Using standard arguments, it can be proved that the equilibrium conditions governing the CLSC network model with competition are equivalent to solve a single variational inequality problem. We can establish the following theorem:

Theorem 1

The equilibrium conditions governing the CLSC network model with competition are equivalent to solve a single variational inequality problem, given by the sum of problems (3), (7), (15), and (19).

The equilibrium conditions presented can be used by policy-makers to anticipate the effects of the second-hand business on the market. Second-hand economy is an increasingly important phenomenon because it is a sustainable way for manufacturers and retailers to operate, and also because it is a convenient system for users. In fact, it allows consumers to put a used or unwanted product back into the supply chain and gain money.

4 Conclusions

This paper presents an equilibrium model of a CLSC network consisting of manufacturers, retailers, demand markets, and one online platform, in which the consumers purchase new products and collect them. Then, the collectors sell the goods to consumers through the online platform. We take into consideration capacity constraints of manufacturers and retailers, as well as consumers’ risk-aversion to purchasing second-hand goods, and platform’s risk-aversion to transacting with collectors. We model the optimal behaviors of all the decision-makers as variational inequality problems and provide the governing CLSC network equilibrium conditions.

Our study can provide an analytical tool for investigating the market equilibrium when collectors engage in the second-hand business. We emphasize that adopting circular business models can be an effective system to extend the life span of products and to inspire sustainable consumption. The entire society will benefit from the lengthened use of available resources.

Future research can explore the equilibrium problem in multi-period planning horizons, and examine some random factors in the demand functions.