Finding Model Parameters

Abstract

Irrespective of the elegance or mathematical complexity of one’s modelling framework, it has little practical usefulness without proper parametrization. This observation is particularly pertinent in the credit-risk setting. Transition and default probabilities, factor correlations and loadings, systemic weights, default dependence, recovery dispersion, spread duration, and credit spreads all need to be estimated and specified to produce meaningful economic-capital estimates. This necessarily lengthy and detailed chapter (metaphorically) rolls up its sleeves and sequentially addresses, explains, and motivates our choices with respect to each of these key parameter families. Where possible and relevant, alternatives and implications are presented. Finally, during the discussion, the consequences of the generally accepted and centrally important through-the-cycle perspective are also explored.

If you have a procedure with ten parameters, you probably missed some.

(Alan Perlis)

We can loosely think of a firm-wide credit-risk economic-capital model as a complicated industrial system, such as a power plant, an air-traffic control system, or an interconnected assembly line. The operators of such systems typically find themselves—at least, conceptually—sitting in front of a large control panel with multiple switches, levers, and buttons.¹ Getting the system to run properly, for their current objective, requires setting everything to its proper place and level. Failure to align the controls correctly can lead to inefficiencies, defective results, or even disaster. In a modelling setting, unfortunately, there is no exciting control room. There are, however, invariably a number of important parameters to be determined. It is useful to imagine the parameter selection process as being roughly equivalent to adjusting the switches, levers, and buttons in an industrial process. There are many possible combinations and their specific constellation depends on the task at hand. Good choices require experience, reflection, and judgement. Transparency and constructive challenge also contribute importantly to this process.

The previous chapter identified a rich array of parameters associated with our large-scale industrial model. The principal objective of this chapter is to motivate our actual parameter choices. It is neither particular easy nor terribly relaxing to walk through a detailed explanation of such a complex system. The labyrinth of questions that need to be answered can easily lead us astray or obscure the thread of the discussion. Figure 3.1 attempts to mitigate this problem somewhat through the introduction of a parameter tree. It highlights five main categories of parameters: credit states, systemic factors, portfolio-level quantities, recovery rates, and credit migration. Each of the five divisions of Fig. 3.1 corresponds to one of the main sections of this chapter. These categories are further broken down into a number of sub-categories identifying the specific parameter questions to be answered. Overall, there more than a dozen avenues of parameter investigation to be covered. Figure 3.1 thus forms not only a rough outline of this chapter, but also a logical guide for navigating the complexity of our credit-risk economic capital control panel.

Fig. 3.1

A parameter tree: This schematic highlights five main classes of parameters and further illustrates the key questions associated with each grouping. This parameter tree forms a rough outline of this chapter—providing the main sections—and acts as a logical guide through the complexity of our credit-risk economic capital control panel.

Before jumping in and answering the various parameter questions raised in Fig. 3.1, it is useful to establish a few ground rules. The first rule, already highlighted in previous chapters, is that economic capital is intended to be a long-term, unconditional, or through-the-cycle estimate of asset riskiness. This indicates that we need to ensure a long-term perspective in our parameter selection. A second essential rule is that, wherever possible, we wish to select our parameters in an objective, defensible fashion. In other words, we need to rely on data. Data, however, brings its own set of challenges. We will not always be able to find the perfect dataset to precisely measure what we wish; as a small institution with limited history, NIB often finds itself faced with such challenges. This suggests the need to employ some form of logical proxy. Moreover, consistency of data for different parameters types, the choice of time horizons, and the relative weight on extreme observations are all tricky questions to be managed. We will not pretend to have resolved all of these questions perfectly, but will endeavour to be transparent about our choices.

A final rule, or perhaps guideline, is that a model owner or operator needs to be keenly aware of the sensitivity of model outputs to various parameter choices. This is exactly analogous to our industrial process. The proper setting for a lever is hard to determine absent knowledge of how its setting impacts one’s production process. Such analysis is a constant component of our internal computations and regular review of parameter choices. It will not, however, figure much in this chapter.² The reason is twofold. First of all, such an analysis inevitably brings one into the specific details of the portfolio: regional and industrial breakdowns and the impact on specific clients. Such information is naturally sensitive and, as such, cannot be shared in such a forum. The second, more practical, reason relates to the volume of material. This chapter is already extremely long and detailed—perhaps too much so—and adding analysis surrounding parameter sensitivity will only make matters worse. Let the reader be nonetheless assured that parameter sensitivity is an important internal theme and forms a central component of the parameter-selection process.

The mathematical structure of any model is deeply important, but it is the specific values of the individual parameters that really bring it to life. The remaining sections of this chapter will lean upon the structure introduced in Fig. 3.1 to describe and motivate our parametric choices. Necessarily very NIB-centric, the general themes and key questions apply very widely to a broad range of financial institutions.

1 Credit States

As is abundantly clear in the previous chapter, the default and migration risk estimates arising from the t-threshold model depend importantly on the obligor’s credit state. One can make a legitimate argument that this is the most important aspect of the credit-risk economic capital model. The corollary of this argument is the treatment of credit states—and their related properties—is the natural starting point for any discussion on parameterization.

1.1 Defining Credit Ratings

NIB has, for decades, made use of a 21-notch credit-rating scale.³ This is a fairly common situation among lending institutions; control over one’s internal rating scale is a very helpful tool in loan origination and management. For large institutions, it is also the source of rich internal firm-specific data on default, transition, and recovery outcomes. NIB—as are many other lending organizations—is unfortunately too small to enjoy such a situation. The consequence is a lack of sufficient internal credit-rating data and history to estimate firm-specific quantities. It is thus necessary to identify and use longer and broader external credit-state datasets for this purpose. A natural source for this data is the large credit-rating agencies: S&P, Moodys, or Fitch. We have taken the decision to generally rely upon S&P transition probabilities, but we also examine Moodys’ data for comparison purposes. One can certainly question the representativeness of this data for our specific application, but there are unfortunately not many legitimate alternatives. We will attempt to make adjustments for data representation as appropriate.

Both Moody’s and S&P also allocate 19 and 20 non-default credit ratings, respectively; each is described with a different alphanumeric identifier as shown in Table 3.1. Typically, we refer to the top-ten ratings—in either scale—as investment grade. The remaining lower groups are usually called speculative grade. The most obvious solution—for small- to medium-sized firms—would be to create a one-to-one mapping between one’s internal scale and the S&P and Moody’s categories; this would ultimately preclude managing different numbers of groupings. This is, however, a problem for NIB (and many other lending institutions), since the very lower end of the S&P and Moody’s scales are simply too far outside of our typical lending risk appetite.⁴ These categories are referred to as either “extremely speculative” or in “imminent risk of default.” This is simply not representative of our business mandate and practice. For this reason, everything below S&P’s B- and Moody’s B3 categories are lumped together into the final PD20 NIB credit rating. This makes the mapping rather more difficult. We need to link 20 (non-default) NIB categories into 17 (non-default) S&P and Moody’s credit notches.

Table 3.1 An internal credit scale: This table introduces the 21-notch NIB rating scale and maps it to the 18-notch S&P and Moody’s credit categories. Both Moody’s and S&P and have many additional speculative-grade groupings below the B3 and B- levels, respectively. These are, however, outside of NIB’s investment range and thus not explicitly considered. PD20 is thus a catch-all category for everything below the B3 and B-cut-offs.

Finding a sensible mapping between these two mismatched scales requires some thought. As an over-specified problem, a unique mapping solution naturally does not exist. Some external logic or justification is required to move forward.⁵ The first ten (investment-grade) categories are easy. They are simply matched on a one-to-one basis among the S&P, Moody’s and NIB scales. The hard part relates to the speculative grade. Our practical solution to this mapping problem involves sharing of a pair of S&P and Moody’s rating categories between three triplets of NIB groupings. This links six credit-rating agency groups into nine NIB categories; the three-notch mismatch is thus managed. The overlap occurs for rating triplets PD11-13, PD14-16, and PD17-19. The specific values are summarized in Table 3.1. As a final step, PD20 maps directly to the CCC and Caa S&P and Moody’s categories, respectively.

Colour and Commentary 25

(Credit Rating Scale and Mappings) : NIB’s internal 21-notch credit scale is not a modelling choice. It was designed, and has evolved over the years, to meet its institutional needs. This includes the creation of a common language around credit quality, the need to support the loan-origination process, and also to aid in risk-management activities. ^a Our modelling activities need to reflect this internal reality. Our position as a small lending institution nonetheless requires looking outwards for data. To do this, explicit decisions about the relationships between the internal scale and external ratings need to be established. This is a modelling question. The solution is a rather practical mapping between NIB’s 20 non-default notches and the first 17 non-default credit ratings for S&P and Moody’s. Its ultimate form, summarized in Table 3.1 , was designed to manage the notch mismatch and the nature of our internal rating scale. We will return to this decision frequently in the following parameter discussion as well as in subsequent chapters.

^aInternal rating scales are a common tool among lending institutions all over the world.

1.2 Transition Matrices

The previous credit-rating categorization has some direct implications. In particular, it implicitly assumes that the credit quality of its obligors can be roughly described by a small, discrete and finite set of q-states. From a mathematical modelling perspective, this strongly suggests the idea of a discrete-time, discrete-state Markov-chain process.⁶ While there are limits to how far we can push this idea—Chap. 7 will explore this question in much more detail—treating the collection of credit states as a Markov chain is a useful starting point. It immediately provides a number of helpful mathematical results. In particular, the central parametric object used to describe a Markov chain is the transition matrix. Denoted as $P\in \mathbb {R}^{q\times q}$, it provides a full, parsimonious characterization of the one-period movements from any given state to all other states (including default). Chapter 2 has already demonstrated the central role that the transition matrix plays in determining default and migration thresholds. The question we face now is how to defensibly determine the individual entries of P.

One might, very reasonably, argue for the use of multiple transition matrices differentiated by the type of credit obligor. There are legitimate reasons to expect that transition dynamics are not constant across substantially different business lines. A very large lending institution, for example, may employ a broad range of transition matrices for different purposes. In our current implementation, however, only two transition matrices are employed for all individual obligors; one for corporate borrowers and another for sovereign obligors. This allows for a slight differentiation in transition dynamics between these two classes of credit counterparty.⁷ With q × q individual entries, a transition matrix is already a fairly high-dimensional object. This discussion will focus principally on the corporate transition matrix; the same ideas, it should be stressed, apply equally in the sovereign setting.

Prior to the data analysis, we seek some clarity on what we expect to observe in a generic credit-migration transition matrix. Kreinin and Sidelnikova [31], a helpful source in this area, identify four properties of a regular credit-migration model.⁸ These include:

• 1. There exists a single absorbing, default state. In other words, once default occurs, it is permanent. While in real life there may be the possibility of workouts or negotiations, this is an extremely useful abstraction in a modelling setting.

• 2. There exists some $\tilde {t}$ such that $p_{qi}(\tilde {t})>0$ for all i = 1, …, q − 1. In words, this means that all states will, at some time horizon, possess a positive probability of default. Empirically, $\tilde {t}$ is somewhere between one to three or four years, even for AAA rated credit counterparts.

• 3. The $\det (P)>0$ and all of the eigenvalues of P are distinct. These are necessary conditions for the computation of the matrix logarithm of P, which is important if one wishes to compute a generator matrix to lengthen (or shorten) the time perspective.⁹

• 4. The matrix, P, is diagonally dominant. Since each entry, p _ij ∈ (0, 1), for all i, j = 1, .., q and each row sums to unity, this implies that the majority of the probability mass is assigned to a given entity remaining in their current credit state. Simply put, credit ratings are characterized by a relatively high degree of inertia.

These specific properties, for credit-risk analysis, are useful to keep in mind. An important consequence of the second point, and the existence of an absorbing default state is that,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \lim_{t\rightarrow\infty} P^t \equiv \begin{bmatrix} 0 & 0 &\displaystyle \cdots &\displaystyle 1\\ 0 & 0 &\displaystyle \cdots &\displaystyle 1\\ \vdots & \vdots &\displaystyle \ddots &\displaystyle \vdots\\ 0 & 0 &\displaystyle \cdots &\displaystyle 1\\ \end{bmatrix}. \end{array} \end{aligned} $$

(3.1)

That is, eventually everyone defaults.¹⁰ In practice, of course, this can take a very long time and, as a consequence, this property does not undermine the usefulness of the Markov chain for modelling credit-state transitions.

Discussing and analyzing actual transition matrices is a bit tricky given their significant dimension. Our generic transition matrix, $P\in \mathbb {R}^{21 \times 21}$, has 441 individual elements. This does not translate into 441 model parameters, but it is close. The absorbing default state makes the final row redundant reducing the total parameter count to 420. The final column, which includes the default probabilities, is specified separately. This is discussed in the next section. This still leaves a dizzying 400 transition probability parameters to be determined.

How do we go about informing these 400 parameters? Despite seeming like an insurmountable task, the answer is simple. These values are borrowed, and appropriately transformed, from rating agency estimates.¹¹ The principal twist is that some logic is required, as previously discussed, to map the low-dimensional rating agency data into NIB’s 21-notch scale. This important question, along with a number of other key points relating to default and transition properties, is relegated to Chap. 7.¹² In this parametric discussion, we will examine the basic statistical properties of these external transition matrices. In doing so, an effort will be made to verify, where appropriate, Kreinin and Sidelnikova [31]’s properties. We will also decide if there is any practical difference in employing S&P or Moody’s transition probabilities.

Such a large collection of numbers does not really lend itself to conventional analysis. In such situations, it consequently makes sense to make an attempt at dimension reduction. For each rating category, over a given period of time, there are only four logical things that can happen: an entity can downgrade, upgrade, move into default, or stay the same. While there is only way to default or stay the same, there are typically many ways to upgrade or downgrade. If we sum over all of these potential outcomes, and stick with the four categories, the result is a simpler viewpoint. Figure 3.2 illustrates these four possibilities for each of the pertinent 18 S&P and Moody’s credit ratings.

Fig. 3.2

A low-dimensional view: This figure breaks out the long-term S&P and Moody’s transition matrices into four categories: the probabilities of upgrade, downgrade, default, and staying put. This dramatically simplifies the matrices and permits a meaningful visual comparison.

Figure 3.2 illustrates a number of interesting facts. First, far and away the most probable outcome is staying put. This underscores our fourth property; each transition matrix is diagonally dominant. As an additional point, the probability of downgrade increases steadily as we move down the credit spectrum. Downgrade remains nonetheless substantially more probable than default until all but the lowest credit-quality categories. Indeed, the probability of default is not even visible until we reach the lower five rungs on the credit scale. Interestingly, the probability of upgrade tends down as credit quality decreases, but it appears to be generally more flat than for downgrades. The final, and perhaps most important, conclusion is that there does not appear to be any important qualitative differences between the S&P and Moody’s transition-probability estimates. This does not immediately imply that there are no differences, but suggests broad similarity at this level of analysis.

Figure 3.3 employs the notion of a heat map to further illustrate the long-term one-year, corporate S&P and Moody’s transition matrices. A heat map uses colours to represent the magnitude of the 400+  individual elements in both matrices; lighter colours indicate a high level of transition probability, whereas darker colours represent lower probabilities. The predominance of light colors across the diagonal of both heat maps underscores the strong degree of diagonal dominance in both estimates already highlighted in Fig. 3.2; indeed, most of the action is in the neighbourhood of the diagonal. Comparison of the right- and left-hand side graphics in Fig. 3.3 reveals that, visually at least, the two matrices seem to be quite similar. This is additional evidence suggesting that we need not be terribly concerned which of these two data sources is employed.

Fig. 3.3

The heat map: This figure illustrates a colour-based visualization of our high-dimensional transition matrices. It includes the long-term S&P and Moody’s estimates along our abbreviated 18-notch scale(s).

One final technical property needs to be considered. Figure 3.4 illustrates the q eigenvalues associated with our S&P and Moody’s transition matrices. All eigenvalues are comfortably positive, distinct, and less than or equal to unity. The eigenvalue structure of our two alternative transition-matrix estimates are quite similar. Moreover, the determinant of both matrices is a small positive number with condition numbers of less than 3.¹³ All of these attributes—consistent with Kreinin and Sidelnikova [31]’s third property—can be interpreted in many ways when combined with the theory of Markov chains. For our purposes, however, we may conclude that P is non-singular and can be used with both the matrix exponential and natural logarithm. These technical properties are not of immediate usefulness, but will prove very helpful in Chap. 7 when building forward-looking stress scenarios.

Fig. 3.4

Transition-probability eigenvalues: This figure illustrates the q eigenvalues associated with each of our S&P and Moody’s transition matrices. All eigenvalues are positive, distinct, and less than one. Moreover, the eigenvalue structure of our two estimates is quite similar.

Colour and Commentary 26

(The Transition Matrix) : Our t-threshold credit-risk economic capital model, as the name clearly indicates, requires the specification of a large number of default and migration thresholds . These are inferred from estimated transition probabilities, which are traditionally stored and organized in a transition matrix. A transition matrix is a wonderfully useful object, which has a number of important properties. The most central is the existence of a permanent absorbing default state that is accessible from all states. Despite all of its benefits, the transition matrix has one drawback: it includes a depressingly large number of parameters. With 20 (non-default) credit states, about 400 transition probabilities need to be determined. We, like (almost) all small lending institutions, simply do not have sufficient internal data to defensibly estimate these values. The solution is to look externally. Examination of comparable S&P and Moody’s transition matrices happily reveals that both sources provide results that are qualitatively very similar. This supports our decision to adopt—subject to an appropriate transformation to our internal scale—the long-term, through-the-cycle transition probabilities published by S&P.

1.3 Default Probabilities

Default probabilities are quietly embedded in the final column of our transition matrix. For credit-risk economic-capital they play a starring role; their determination of the default threshold is tantamount to describing each obligor’s distance to default. As a consequence, they merit special examination and attention. We have thus constructed a separate logical approach to their determination. This is an important distinction from the remaining transition probabilities, which are adopted (fairly) directly from external rating agency estimates.

Default is—at least, for investment-grade loans—a rather rare event. To this point, given their relatively small values, it is difficult for us to assess the default-probability assumptions embedded in our transition matrix. Indeed, they were hardly visible in Fig. 3.2. Figure 3.5 rectifies this situation with a close up of the S&P and Moody’s default probabilities. Unlike our previous analysis, these 18 credit notches have been projected onto the 20-step NIB scale using the mapping logic from Table 3.1.¹⁴ The right-hand graphic illustrates the raw values, which exhibit an exponentially increasing trend in default probabilities as we move down the credit spectrum. This is the classical form of default probabilities; each step out the credit-rating scale leads to a multiplicative increase in the likelihood of default.¹⁵

Fig. 3.5

Default probabilities: The raw values in the left-hand graphic illustrate the exponentially increasing trend in default probabilities as we move down the credit spectrum. The right-hand graphic performs a natural logarithmic transformation of these values; its linear form verifies the exponential observation. Internal NIB values are compared to the implied S&P and Moody’s estimates.

Exponential growth is tough to visualize. It is difficult, for example, to verify the magnitude and strict positivity of the default probabilities of strong credit ratings. The right-hand graphic thus performs a natural logarithmic transformation of the default probabilities. Since the natural logarithm is undefined for non-positive values, the highest two or three external rating default probabilities are assigned to identically zero. Incorporating this directly into our model would imply that, at a one-year horizon, default would be impossible for the stronger credits. This is a difficult point. Simply because default, over one-year horizon, has never been observed for such counterparties does not imply that it is impossible. Rare, certainly, but not impossible. Setting these values to zero, as a model parameter, is simply not a conservative choice. We resolve this issue by assigning small positive values to the first three default-probability classes.

How does this assignment occur? The data provides a helpful clue. If we divide each successive (non-zero) default probability by its adjacent value, we arrive at a constant ratio of roughly 1.5; in other words, the exponential growth factor is about 1.5. Extrapolating forwards and backwards using this trend yields the blue line in Fig. 3.5. This might seem a bit naive, but it actually yields values that are highly consistent with—and even slightly more conservative than–those produced by S&P and Moody’s. The only exception is the final category, which is termed PD20. This corresponds to S&P’s CCC and Moody’s Caa, which is basically an amalgamation of lowest rungs in their credit scale. It is simply not representative of our lending business. For this reason, the PD20 default-probability value has been capped at 0.2. This is an example of using modelling judgement and business knowledge to tailor the results to one’s specific circumstances.

Colour and Commentary 27

(Default Probabilities) : Not all transition probabilities—from an economic-capital perspective, at least—are created equally. Default probabilities, used to determine the distance to default, play a disproportionately important role in our risk computations. Their central importance motivates a deviation from broad-based adoption of external credit-rating agency estimates. The set of default probabilities is determined by exploiting the empirical exponential form. Each subsequent rating is simply assumed to be a fixed multiplicative proportion of the previous value. Some additional complexity occurs at the end points. External rating agencies’ estimates—due to lack of actual observations—imply zero (one-year) default probabilities for the highest credit-quality obligors. In the spirit of conservatism, we allocate small positive values—consistent with the multiplicative definition—to these rating classes. At the other end of the spectrum, the lowest rating category is simply not representative of the credit quality in our portfolio. Consequently, the 20th NIB default-probability estimate is capped at 0.2. The end product is a logically consistent, conservative, and firm-specific set of default-probability estimates.

2 Systemic Factors

Although the assumption of default independence would dramatically simplify our computations, it is inconsistent with economic reality. A modelling alternative is an absolute necessity. The introduction of systemic factors is the mechanism used to induce default (and migration) correlation among the credit obligors in our portfolio. While conceptually clear and rather elegant, it immediately raises a number of practical questions. What should be the number and composition of these factors? How do we inform their dependence structure? What is the relative importance of the individual factors for a given credit obligor. All of these important queries need to be answered before the model can be implemented. This section addresses each in turn.

2.1 Factor Choice

The systemic factors driving default correlation are—unlike many popular model implementations—assumed to be correlated. With orthogonal factors, it is possible to maintain a latent (or unobservable) form. This choice is unavailable in this setting. Since we ultimately need to estimate the cross correlations between these factors, it will be necessary to give them concrete identities. Our credit-risk economic-capital model thus includes a total of J = 24 systemic factors; these fall into industrial and regional (or geographic) categories. There are 11 industrial sectors and 13 geographic regions. The dependence structure between these individual factors is, as is often the case in practice, informed by analysis of equity index returns. This means that we require historical equity indices for each of our systemic factors; this constrains somewhat the choice.

Even within these constraints, there is a broad range of choice. Were you to place five people into a room and ask them to give their opinion on the correct set of systemic factors, you would likely get five, or more, opinions. The reason is simple; there is no one correct answer. On one hand, completeness argues for the largest possible factor set. Too many factors, however, will be difficult to manage. Judiciously managing the age-old trade-off between granularity and parsimony is not easy. It ultimately comes down to a consideration of the costs and benefits of including each systemic factor.

These specific sector systemic-factor choices are summarized in Table 3.2. Such an approach requires some kind of internal or external industrial taxonomy, which may, or may not, be specialized for one’s purposes.¹⁶ With one exception, our industrial classification is mapped to a rather high level. Paper and forest products, which can probably be best viewed as a sub-category of the material or industrial groupings, is further broken out due to its importance to the Nordic region. This is another clear example of tuning the level of model granularity required for the analysis of one’s specific problem.

Table 3.2 Industrial systemic factors: This table summarizes the industrial systemic factors employed in our credit-risk economic-capital model implementation.

Table 3.3 provides an visual overview of the set of 13 geographic systemic factors. A very broad or detailed partition along this dimension is possible, but the granularity is tailored to meet specific business needs. Roughly half of the regional systemic factors, as one would expect with our mandate-driven focus, fall into the Baltic and Nordic sectors. Europe is broken down into two main categories: Europe and new Europe. The latter category relates primarily to Eurozone ascension countries in central and eastern Europe. The remaining geographic factors split the globe into a handful of large, but typical, zones.

Table 3.3 Geographic systemic factors: This table summarizes the various systemic factors associated with geographic regions employed in our credit-risk model implementation. Shaded regions represent NIB member countries.

Colour and Commentary 28

(Number of Systemic Factors) : Selecting the proper set of systemic risk factors is not unlike putting together a list of invitees for a wedding. The longer the list, the greater the cost. Some people simply have to be there, some would be nice to have but are unnecessary, while others might actually cause problems. Finally, different people are likely to have diverging opinions. We have opted for 24 industrial and regional factors. This is a fairly large wedding, but it is hard to argue for a much smaller one. With one exception, the lowest level of granularity is used for the industrial classification. On the regional side, roughly one half of the factors relate to NIB member countries. The remaining geographic factors are important for liquidity investments on the treasury side of the business. While there is always scope for discussion and disagreement, from a business perspective, the majority of the selected systemic factors are necessary guests.

2.2 Systemic-Factor Correlations

Having determined the identity of our systemic factors, we move to the central question of systemic-factor dependence. These so-called asset correlations are sadly not observable quantities. Default data can be informative in this regard.¹⁷ We have elected to follow the well-accepted approach of informing asset correlation through a readily available proxy: equity prices. This is not a crazy idea. Equity prices, and more particularly returns, communicate information about the value of a firm. Cross correlations between movements in a given firm’s value and other firm-value movements provide some insight into the question at hand. Moreover, a broad range of firm level, geographic, and industry equity return data is available.

The logical reasonableness of the link between asset and equity data, as well as its ready availability, should not lure us into believing that equity data does not have its faults. Equities are bought and sold in markets; these markets may react to general macroeconomic trends, supply and demand, and investor sentiment in ways not entirely consistent with asset-value dynamics. The inherent market-based interlinkages between individual equities will tend to overstate the true dependence at the firm level. By precisely how much, of course, is rather difficult to state with any degree of accuracy.¹⁸ The granularity and dimensionality of the model construction, however, leaves us with no other obvious alternatives. It is nonetheless important to be frank and transparent about the quality of equity data as a proxy. In short, it is useful, available, and logically sensible, but far from perfect.

Risk-factor correlations are thus proxied by equity returns; these returns are, practically, computed as logarithmic differences of equity indices. Armed with a matrix of equity returns, $X\in \mathbb {R}^{\tau \times J}$, where τ represents the number of collected equity return time periods, we may immediately write $S=\mathrm {cov}(X)\in \mathbb {R}^{J\times J}$. Technically, it is straightforward to decompose our covariance matrix, S, as follows:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} S = V \Omega V^T, \end{array} \end{aligned} $$

(3.2)

where $V\in \mathbb {R}^{J\times J}$ is a diagonal matrix collecting the individual volatility terms associated with each systemic factor and $\Omega \in \mathbb {R}^{J\times J}$ is a positive-definite, symmetric correlation matrix. τ, for this analysis, is set to 240 months or 20 years of index data.

Analogous to the transition-matrix setting, it is not particularly informative to examine large-scale tables with literally hundreds of pairwise correlation estimates. Figure 3.6 attempts to gain visual insight into this question through another application—in the left-hand graphic—of a heat map. The lighter the shading of the colour in Fig. 3.6, the closer the correlation is to unity. This explains the light yellow—or almost white—stripe across the diagonal. The right-hand graphic examines the distribution of all (roughly 300) distinct off-diagonal elements.¹⁹ Overall, the smallest pairwise correlation between two systemic factors is roughly 0.15, with the largest exceeding 0.90. The average lies between 0.5 and 0.6. This supports the general conclusion that there is a strong degree of positive correlation between the selected systemic factors.

Fig. 3.6

(Linear) Systemic correlations: This figure attempts to graphically illustrate the roughly 300 distinct pairwise estimated product-moment (or Pearson) correlation-coefficient outcomes associated with our system of J = 24 industrial and geographic systemic factors. The left-hand side provides a heat map of the correlation matrix, while the right-hand side focuses on the cross section.

This is hardly a surprising observation. All variables are equity indices, which have structural similarities due to typical co-movements of equity markets. The high concentration in the Nordic sector, with strong regional interdependencies, further complicates matters. Many institutions would gather together all Nordic and Baltic factors under the umbrella of a single European risk factor. NIB does not have this luxury. The granularity in this region can hardly be avoided if we desire to distinguish between member country contributions to economic capital—its centrality to our mission makes it a modelling necessity. Nevertheless, this is a highly positively correlated collection of random financial-market variables. It will be important to recall this fact when we turn to the question of systemic-factor loadings.

The next step involves examining the factor volatilities. Figure 3.7 illustrates the elements of our diagonal volatility matrix; each can be allocated to an individual equity return series. The average annualized return volatility is approximately 19%, which appears reasonable for equities. Consumer staples, health care and utilities—as one might expect—appear to have the most stable returns with volatility in the 10–15% range. On the upper end of the volatility scale, exceeding 20%, are paper-and-forest products and IT. Generally, deviations of the regional indices from the overall average level are relatively modest. The exception is Iceland with annualized equity return volatility of approximately 45%, which is approaching three times the average. This is certainly influenced by the relative small size of the Icelandic economy, its large financial sector, and Iceland’s macroeconomic challenges in the period following the 2008 financial crisis.

Fig. 3.7

Factor volatilities: This figure illustrates the annualized-percentage factor (i.e., equity index return) volatility of each of the J = 24 industrial and geographic systemic factors. This information is only pertinent if we employ the covariance matrix rather than the correlation matrix for describing the systemic-risk factor dependence.

A legitimate question, which will be addressed in the following sections, is whether or not we have any interest in the volatility of these systemic risk factors. Equity return data is a convenient and sensible proxy for our systemic risk factors. In principle, however, this proxy seeks to inform the dependence between these factors, not their overall level of uncertainty. Volatility is centrally important in market-risk computations, but the threshold-model approach actually involves normalizing away these volatilities.

Outfitted with 20 years of monthly equity index data for 24 logically sensible geographical and industrial systemic-risk factors, a number of practical decisions still need to be taken. Indeed, one could summarize these decisions in the form of three, important, and interrelated questions:

• 1. Should we employ the covariance or correlation matrices to model the dependence structure of our systemic risk-factor system?

• 2. If we opt to use correlation, should we use the classical, product-moment Pearson correlation coefficient or the rank-based, Spearman measure?

• 3. Should we employ our full 20-year dataset or some sub-period?

While these are all pertinent questions that need answering, let us begin with the first question. This is more of a mathematical choice and, once answered, we may turn our attention of the latter two more empirical decisions.

2.2.1 Which Matrix?

Should we employ a covariance or a correlation matrix? This might, to the reader, appear to be a rather odd question.²⁰ In principle, if managed properly, it should not really matter. Equation 3.2 illustrates, rather clearly, that the same information is found in both matrices. The only difference is scaling; covariances are adjusted, in a quadratic manner, for the factor volatility. The correlation matrix summarizes raw correlation values.

What would be the benefit of using covariances rather correlations? There does not appear to be any concrete advantage. The factor volatilities play, in the credit-risk economic-capital calculation, absolutely no role. Indeed, their presence requires an additional adjustment. That is, when using the covariance matrix, we must take extra pains to exclude these elements through their inclusion in the normalization constant. It is the correlation between these common systemic factors that bleeds through to our latent creditworthiness index, ΔX, and ultimately, induces default and migration correlations among our individual risk owners. At best, the factor volatilities are a distraction, while at worst, they might possibly have some unforeseen scaling impact on our latent creditworthiness indices. As a consequence, we may as well eliminate them at the outset.

Use of the covariance matrix may also confuse the interpretation of the factor-loading parameters. One would conceptually prefer that, in the final implementation, the factor loadings are not quietly being modified by the factor volatilities. Overall, the difference is not dramatic, but anything that simplifies our understanding of the model and the interpretation of model parameters—without undermining the basic requirements of the model—is difficult to argue against. For this reason, we have definitively elected to use the correlation matrix as the fundamental measure of systemic risk-factor dependence.

2.2.2 Which Correlation Measure?

The classical notion of correlation, often referred to as the product-moment definition, is typically called Pearson correlation.²¹ It basically compares, for a set of observations associated with two random variables, how each pair of joint outcomes deviates from their respective means. The classic construction, for two arbitrary random variables X and Y , is described by the following familiar (and already employed) expression

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \rho = \frac{\mathbb{E}\left(\bigg(X-\mathbb{E}(X)\bigg)\bigg(Y-\mathbb{E}(Y)\bigg)\right)}{\sqrt{\mathrm{var}(X)\mathrm{var}(Y)}}. \end{array} \end{aligned} $$

(3.3)

An alternative approach, termed rank correlation, approaches the computation in an alternative manner. The so-called Spearman’s rank correlation is defined as

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} r = \frac{\mathbb{E}\left(\bigg(r(X)-\mathbb{E}(r(X))\bigg)\bigg(r(Y)-\mathbb{E}(r(Y))\bigg)\right)}{\sqrt{\mathrm{var}(r(X))\mathrm{var}(r(Y))}}, \end{array} \end{aligned} $$

(3.4)

where r(⋅) denotes the rank outcome of random variable.²² Instead of comparing the distance of each observation from its mean, it compares the rank of each observation to the mean rank. It is thus basically an order-statistic version of the correlation coefficient.²³ Otherwise, Eqs. 3.3 and 3.4 are structurally identical.

Spearman’s coefficient is popular due to its lower degree of sensitivity to outliers; broadly speaking, it has many parallels, in this regard, to the median. For relatively well-behaved random variables, there is only a modest amount of difference between the two measures. Indeed, for bivariate Gaussian random variates, the relationship between Spearman’s r and Pearson’s ρ is given as,²⁴

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} r = \frac{6}{\pi}\arcsin\left(\frac{\rho}{2}\right), \end{array} \end{aligned} $$

(3.6)

which directly implies that

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \rho = 2\sin\left(\frac{r\pi}{6}\right). \end{array} \end{aligned} $$

(3.7)

This may appear to be a complicated relationship, but practically, over the domain of the coefficients, [−1, 1], there is not much difference. Figure 3.8 provides a graphical perspective on Eq. 3.7. While they do not match perfectly, the differences are minute; consequently, imposition of Spearman’s rank correlation—in a Gaussian setting—will imply an extremely similar level of correlation along the typical Pearson definition. The point of this discussion is to indicate that the decision to use rank or product-moment correlation, in a Gaussian setting, is more a logical than an empirical choice. In a non-Gaussian setting, however, differences can be more important. It becomes particularly pertinent—as is common in financial-market data—in the presence of large, and potentially, distorting outlier observations.

Fig. 3.8

Comparing Pearson’s ρ to Spearman’s r: The preceding figure examines, across the range of − 1 to 1, the link between two notions of correlation for bivariate Gaussian data: Pearson’s ρ and Spearman’s r. While they do not match perfectly, the differences are minute; consequently, imposition of Spearman’s rank correlation—in a Gaussian setting—will imply a rather similar level of correlation relative to the typical Pearson definition. In non-Gaussian settings, the differences can be more important.

Figure 3.9 provides two heat maps comparing the roughly 300 pairwise linear and rank correlation coefficients across our 24 separate systemic risk variables. While there is little in the way of qualitative difference between the two measures, due to their lower sensitivity to outliers, the rank correlation coefficients are slightly lower than their linear compatriots. The rank correlation coefficients have distinctly, albeit not dramatically, more darker colour in their heat map. Both figures are computed using 20 years of monthly equity return data; this leads to a total of 240 observations for each pairwise correlation estimate. The first twenty years of the twenty-first century have not been, from a financial perspective at least, particularly calm. Equity markets have experienced a number of rather extreme events during this period. The rank correlation will capture these extremes, but in a less dramatic way, given the relative stability of the rank of return relative to its level. This stability property is rather appealing.

Fig. 3.9

Competing heat maps: The preceding heat maps compare the roughly 300 pairwise linear and rank correlation coefficients across our 24 separate systemic risk variables. There is little in the way of qualitative difference between the two measures, but due to their lower sensitivity to outliers, the rank correlation coefficients are slightly lower than their linear compatriots.

We wish these crisis periods to have an impact on the final results, but not to potentially dominate them. To judge this question, however, we need a bit more information than is found in Fig. 3.9. Figure 3.10 accordingly attempts to help by examining the cross section of off-diagonal elements of Ω. The centres of these two cross-section correlation-coefficient distribution are rather close: in the linear case it is 0.57 and 0.52 in the rank setting. The range of correlation values are qualitatively quite similar, spanning the values of about 0.1 to 0.9. There is, however, a slight difference. The cross section of rank correlation coefficients appears to be somewhat more symmetric than with the linear estimates. Both sets of values lean somewhat towards the upside of the unit interval, but the rank correlation graphic is less extreme.²⁵ This is, in fact, exactly how the rank correlation is advertised.

Fig. 3.10

Competing cross sections: This figure illustrates, again for linear and rank dependence measures, the cross section of pairwise correlation coefficients. On average, the rank correlation is about 0.05 less than the linear metric. Visually, however, relatively little separates these two estimators.

There does not appear to be an unequivocally correct choice. The product-moment definition of correlation allows the extremes to exert more influence on the final results; as a risk manager, this has some value, because crisis episodes receive a larger weight. The rank correlation approach—like its sister measure, the median—attempts to generate a more balanced view of dependence. The lower impact of data outliers—typically, in this case, stemming from crisis outcomes—implies slightly lower and more symmetric correlation estimates. We seek, in our economic-capital estimates, to construct a long-term, unconditional estimate of risk consumption.²⁶ With this in mind, given the preceding conclusions, we have a preference for the rank correlation.

There are also more technical arguments. Both correlation matrices, as previously indicated, exhibit a significant number of individual correlation coefficient entries exceeding 0.75. Such a highly correlated system is often referred to as multicollinear.²⁷ If we were using this system to estimate a set of statistical parameters, this could potentially pose serious problems. Although this is not our specific application of Ω, even a slight dampening of the high level of correlations implies a greater numerical distinction between our J = 24 individual systemic risk factors. Many models, after all, impose orthogonality on their systemic state variables to avoid such issues. On this dimension, therefore, we also have a slight preference for the rank-correlation measure.

Colour and Commentary 29

(Flavour of Correlation) : Correlation refers to the interdependence between a pair of random variables. There are a variety of ways that it might be practically measured. Two well-known alternatives are the product-moment and rank correlation coefficients. Although they attempt to address the same question, they approach the problem from different angles. Since we find ourselves in the business of computing a large number of pairwise systemic-factor correlations, this distinction is quite relevant for us. On the basis of lower sensitivity to extreme events, greater cross-sectional symmetry, and a modest dampening of the highly collinear nature of our systemic risk-factor system, we have opted to employ the rank-correlation measure to estimate systemic-factor correlations. In the current analysis, the difference is relatively small. Moreover, nothing suggests that these two measures will deviate dramatically in the future. Our choice is thus based upon the perceived conceptual superiority of the rank-correlation measure.

2.2.3 What Time Period?

There are two time-related extremes to be considered in the measurement of risk: long-term unconditional and short-term conditional. A virtual infinity of possible alternatives exists for a spectrum between these two endpoints. Following basic regulatory principles, an economic-capital model is a long-term, unconditional, through-the-cycle risk estimator. This implies that a relatively lengthy time period should be employed for the estimation of our systemic risk-factor correlations. While helpful to understand this choice, it does not entirely answer our question. We have managed to source 20 years of monthly equity time-series data for each of our J = 24 systemic risk factors. Should we use it all, or should we employ some subset of this data? A 10-, 15-, or 20-year period would still be consistent, at least in principle, with through-the-cycle estimation.

Figure 3.11 illustrates, one final time, two rank correlation heat maps for our J = 24 systemic risk factors. The only distinction between the two heat maps is that they are estimated using varying time periods. The 10-year values are based on the months from January 2010 to December 2019, while the 20-year period utilizes the 240 monthly observations from January 2000 to December 2019. On a superficial level, the colour patterns in the two heat maps look highly similar. The 20-year estimates, however, look to be, on average, a bit lighter. This implies higher levels of correlation, which is not terribly surprising, given that the longer period incorporates the most severe parts of the great financial crisis. There is general agreement that financial-variable correlations tend to trend higher—thereby reducing the value of diversification—during periods of turmoil.²⁸

Fig. 3.11

Time-indexed heat maps: These heat maps compare the roughly 300 pairwise rank correlation coefficients—over the last 10 and 20 years working backwards from December 2019—across our 24 separate systemic risk variables. The most recent 10-year period appears structurally similar, but exhibits significantly lower levels of correlation than the associated 20-year time horizon.

Figure 3.12 illustrates, again using only the rank dependence measure, the cross section of pairwise (rank) correlation coefficients over our 10- and 20-year periods, respectively. Average correlation, as we’ve seen before, is roughly 0.52 over the full 20-year period. It falls to 0.46 when examining only the last 10 years. We further observe that both the location and dispersion of the two cross sections appear to differ; the most recent 10-year period exhibits generally lower levels of systemic-risk factor dependence.

Fig. 3.12

Time-indexed cross sections: This figure illustrates, again using the rank dependence measure, the cross section of pairwise correlation coefficients over the 10- and 20-year periods working backwards from December 2019, respectively. Both the location and dispersion the two cross sections appear to differ; the last 10-year period exhibits generally lower levels of systemic-risk factor dependence.

Few logical arguments speak for the preference of the 20-year period, relative to the shorter 10-year time span, other than conservatism. Either time interval fulfils the basic requirements of a through-the-cycle risk estimator. A 20-year period could, of course, be considered more appropriate for a long-term unconditional correlation estimate. More importantly, the full 20-year period includes a broader range of equity return outcomes—including the great financial crisis—and consequently generates slightly more conservative estimates. For this reason, the decision is to use the full 20-year period and, over time, simply continue to add to the existing dataset. Each year, this decision on the overall span of data is revisited to ensure both representativeness and consistency with our economic-capital objectives.

Colour and Commentary 30

(Length of Parameter-Estimation Horizon) : When estimating parameters for a long-term through-the-cycle perspective, we would theoretically prefer the longest possible collection of historical time series. Such a dataset is likely to permit an average of the greatest possible number of observed business cycles. There are two catches. First, pulling together such a dataset can be both difficult and expensive. Second, even if you succeed, there are dangers in going far back in time. Too far into the past and—due to structural changes in economic relationships—the data may not be representative of current conditions. This forces the analyst into an awkward dance: the through-the-cycle requires lengthy data history, but not too long. Our approach is, where available, to start with a roughly 20-year time horizon. We then work with this data and carefully examine various sub-periods to understand the implications of different choices. Endeavouring to find conservative and defensible parameters, an appropriate horizon is ultimately selected.

2.3 Distinguishing Systemic Weights and Factor Loadings

Systemic-factor weights and loading parameters, while related, are asking two slightly different questions. The systemic weight attempts to answer the following query:

How important is the overall systemic component, in the determination of the creditworthiness index, relative to the idiosyncratic dimension?

The systemic weight is, following from this point, simply a number between zero and one. These are the parameter values, {α ₁, …, α _I}, introduced in Chap. 2. A value of zero, for a given credit obligor, suggests that only idiosyncratic risk matters for determination of its migration and default risk outcomes. Were this to apply to all credit counterparties, we would, in essence, have an independent-default model. On the other hand, a systemic weight of unity places all of the importance on the systemic factor. Gordy [18]’s asymptotic single-risk factor model is an example of an approach that implies the presence of only systemic risk.²⁹ A defensible position, of course, lies somewhere in between these two extremes.

Factor loadings focus on a different, but again related, dimension. They seek to answer the following question:

How important is each of the J individual systemic risk factors—again, for the calculation of the creditworthiness index—to a given credit obligor?

Factor loadings, for a given counterparty, are thus not, as in the systemic-weight case, a single value, but rather a vector in $\mathbb {R}^{J}$. Let’s continue to refer to each of these vectors as $\beta _i\in \mathbb {R}^{1\times J}$ for the ith credit counterpart; this allows us to consistently write the entire matrix of factor loadings as,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \beta = \begin{bmatrix} \beta_1 \\ \beta_2 \\ \vdots \\ \beta_I \end{bmatrix}\in\mathbb{R}^{I\times J}. \end{array} \end{aligned} $$

(3.8)

Such a constellation of parameters, for each i = 1, …, I, implies a potentially very rich mathematical structure. With J = 24 and I ≈ 600, our β factor loading matrix contains almost 15,000 individual entries. Such flexibility can offer benefits, but it may also dramatically complicate matters.

The structure of each β _i essentially creates a linear combination of our J risk factors to act as the systemic contribution for that obligor. Let’s consider a few extreme cases, since they might provide a bit of insight. Imagine that each β _i was constant—however, one might desire to define it—across all counterparties. The consequence would be, in fact, a single-factor model. We could easily, in this case, simply replace our J factors with a single linear combination of these variables. Each pair of obligors in the model would thus have a common level of factor-, asset-, and default correlation. Such an approach would, of course, undermine the whole idea of introducing a collection of J systemic variables.

At the opposite end of the spectrum, one could assign distinctly different non-zero values to each of the roughly 15,000 elements in β. The implication—setting aside the practical difficulties of such an undertaking for the moment—is that each obligor’s systemic contribution would be a unique linear combination of our J systemic variables. Given two obligors, i and j, the vectors β _i and β _j would play a central role in determining their level of default correlation. Indeed, this latter point holds in a general sense.

Once again, an appropriate response to this challenge certainly lies somewhere between these two extreme ends of the spectrum. The actual estimation of the factor loadings and systemic weights should also be informed, in principle, by empirical data. A significant distinction between the factor loadings and systemic weights is that the former possesses dramatically greater dimensionality. The specific data that one employs and, perhaps equally importantly, how the structure of these parameters are organized are important questions. The following sections outline our choices, and the related thought processes, in both of these related areas.

2.4 Systemic-Factor Loadings

Let us begin with the factor loadings; these values are—algebraically speaking—closer to the actual systemic factor. Determination of our factor loadings will, as a consequence, turn out to be rather important in the specification of the systemic weights. As indicated, each β _i vector determines the relative weight of the individual systemic factors in the creditworthiness of the ith distinct credit obligor. Some procedure is required to determine the magnitude of each β _ij parameter for i = 1, …, I and j = 1, …, J.

2.4.1 Some Key Principles

When beginning any modelling effort, it is almost invariably useful to give some thought to one’s desired conceptual structure. In this case, there is a potentially enormous number of parameters involved, which will create problems of dimensionality and, more practically, statistical identification. Some direction would be helpful. A bit of reflection reveals a few logical principles that we might wish to impose upon this problem:

• 1. Obligors with the same sectoral and geographical profiles should share the same loadings onto the systemic factors. If this did not hold, it would be very difficult, or even impossible, to interpret and communicate the results.³⁰

• 2. A given obligor should load only onto those sectoral and geographical factors to which it is directly exposed. The correlation matrix, Ω, describes the dependence structure of the underlying equity return factors. As a consequence, the interaction between the factors is already captured. If an obligor then proceeds to load onto all factors, untangling the dependence relationships would become rather messy. This principle can thus inform sensible parameter restrictions.

• 3. Factor loadings should be both positive and restricted to the unit interval. There is no mathematical or statistical justification for this principle; it stems solely from a desire to enhance our ability to interpret and communicate these choices.

• 4. A minimal number of systemic factors should be targeted; this is the principal of model parsimony. Not only does this facilitate implementation—in terms of dimensionality and computational complexity—but it also minimizes problems associated with collinearity.

• 5. To the extent possible, the factor loadings should be informed by empirical data. Since asset returns are not, strictly speaking, observable, it is necessary to identify a sensible proxy. Moreover, the previous principles may restrict the goodness of fit to this proxy data. Nonetheless, this would form an important anchor for the estimates.

While each of these principles make logical sense, nothing suggests that all can be simultaneously achieved. It may be the case, for example, that some of these principles are mutually exclusive.

2.4.2 A Loading Estimation Approach

The structure of the threshold model provides clear insights into a possible estimation procedure for the factor loadings. In particular, for a given obligor i, we have that

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \beta_i \Delta z & =&\displaystyle \sum_{j=1}^J \beta_{ij} \Delta z_j, \end{array} \end{aligned} $$

(3.9)

where $\Delta z\in \mathbb {R}^{J\times 1}$. The right-hand side of Eq. 3.9 clearly illustrates the fact that each column of the β _i row vector is a linear weight upon the systemic factors. Imagine that we could identify K individual equities with similar properties. That is, stemming from the same geographic region, operating in the same region, and possessing similar overall size. Given T return observations of the kth equity—corresponding to the equivalent time periods for our systemic factors—we could construct the following equation:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} r_{kt} = \sum_{j=1}^J \beta_{ijk} \Delta z_{jt} + \epsilon_{kt}, \end{array} \end{aligned} $$

(3.10)

for t = 1, …, τ and k = 1, …, K and where r _kt is the t-period return of the kth equity in our collection. This is, of course, an ordinary least squares (OLS) problem.³¹ In this setting, the β’s simply reduce to regression coefficients. Further inspection of Eq. 3.10 reveals a certain logic; the return of the kth equity is written as a linear combination of the set of systemic factors plus an idiosyncratic component. This is rather close to what we seek. Again, this amounts to using equity behaviour to estimate asset returns.

Equation 3.10, while logically promising, is not without problems. First of all, there are K equities in each category. The natural consequence is thus K × J individual factor-loading estimates. One could presumably solve this problem by taking an average—basically integrating out the K dimension—of the individual $\hat {\beta }_{ijk}$ parameters over each j in J.

The second problem, however, is dimensionality. Use of Eq. 3.10 implies a separate weight on each of the J systemic risk factors. Such a complex structure is not easy to interpret. The larger number of parameters also raises issues of parameter robustness. Estimating J = 24 separate parameters with perhaps 10 or 20 years of monthly data is certainly possible, but the sheer number of regression coefficients, the high degree of collinearity between the systemic-risk explanatory variables, and the necessity of averaging estimates collectively represent significant estimation challenges. Computing standard errors is not easy is such a setting and, more importantly, they are unlikely to be entirely trustworthy.

A third problem, making matters even worse, is the fact that nothing in the OLS framework hinders individual β _ij values from taking negative values further complicating clarification. Some additional normalization is possible to force positivity, of course, but this only adds to the overall complexity and adds an ad hoc, and difficult-to-justify, element to the estimation procedure.

There are, therefore, at least three separate problems: averaging, dimensionality, and non-positivity. Some of these problems can be mitigated with clever tricks, but the point is that estimating factor-loading coefficients—even with strong simplifying assumptions—is fraught with practical headaches. The results are neither particularly robust nor satisfying. We will, in a few short sections, find ourselves in a similar situation with regard to the systemic weights. In this case the complexity and dimensionality is unavoidable, which argues for maximal simplicity.

2.4.3 A Simplifying Assumption

These sensible reasons to strongly restrict systemic-factor loadings lead to the fairly reasonable question: should we even formally estimate these parameters? One might simply load—for these non public-sector cases—equally onto each obligor’s geographic and industrial systemic factors. The consequence of this legitimate reflection is the following extremely straightforward set of factor-loading coefficients:

• only a credit entity’s geographic and industrial factor loadings are non-zero;

• each non-zero factor loading is set to 0.5; and

• the only exception is a weight of unity on a public-sector counterpart’s geographic loading.

The consequence is a sparse β-matrix entirely populated with non-estimated parameters.³² This approach allows us to fulfil four of our five previously highlighted principles. It controls the number of parameters, creates consistency, ensures positivity, and dramatically aids interpretability. The only shortcoming is that the parameter values are not informed by empirical data. This would appear to be the price to be paid for the attainment of the other points.

There is another constructive way to think about this important simplifying assumption. The systemic risk-factor correlation matrix, Ω, possesses a certain dependence structure. The choice of factor loadings further combines our systemic factors to establish some additional variation of obligor-level correlations. There are, however, many possible combinations of factor-loading parameters that achieve basically the same set of results. In a statistical setting, such a situation is referred to as overidentification.³³ To simplify this fancy term, we can imagine a situation of trying to solve two equations in three unknowns. The problem is not it cannot be solved, but rather the existence of an infinity of possible solutions. Resolving such a situation typically requires restricting it somewhat through the imposition of some kind of constraint.³⁴ The current set of non-estimated factor loadings can thus be thought of as a collection of constraints, or over-identifying restrictions, used to permit a sensible model specification.

Colour and Commentary 31

(Factor-Loading Choices) : Having established a set of five key principles for the specification of factor-loading parameters, a number of potential estimation options are found wanting. They require averaging, lead to relatively high degrees of dimensionality, and pose difficulties for statistical inference. Dimension reduction and normalization solve some of these problems, but this leads to relatively small degrees of (economic) variation between individual obligors. Ultimately, therefore, we have decided to employ a simple set of rules for the specification of the factor-loading parameters. This choice fulfils all of our principles, save one: the desire to empirically estimating our factor-loading values. This choice was not taken lightly and can, conceptually, be viewed as a set of overidentifying restrictions upon the usage of our collection of systemic risk factors.

2.4.4 Normalization

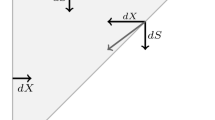
Introduction of correlated systemic factors, without some adjustment, will distort the variance structure of our collection of latent creditworthiness state variables. Unit variance of these threshold state variables is necessary for the straightforward determination of default and migration events. A small correction is consequently necessary to preserve this important property of each systemic random observation. Mathematically, the task is relatively simple. For the ith risk obligor, the contribution of the systemic component—abstracting, for now, from the systemic-weight parameter—is given as,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mathrm{B}_i = \frac{\beta_i}{\sqrt{\beta_i\Omega\beta_i^T}}, \end{array} \end{aligned} $$

(3.11)

where $\beta _i\in \mathbb {R}^{1\times J}$ is the ith row of the $\beta \in \mathbb {R}^{I\times J}$ matrix.³⁵

The definition in Eq. 3.11 was already introduced in Chap. 2. Equipped with our factor correlations and loading choices, it is interesting to examine the magnitude of these normalization constants (i.e., the denominator of Eq. 3.11). Figure 3.13 displays the range of these values—for an arbitrary date in 2020—used to ensure that the systemic component has unit variance. The impact is rather a gentle. The span of adjustment factors ranges from roughly 0.75 to one; the average value is approximately 0.95. Normalization thus represents a small, but essential, adjustment to maintain the integrity of the model’s threshold structure.

Fig. 3.13

Normalization constants: Since the introduction of factor loadings distorts the variance of the systemic risk factors, it is necessary to perform a normalization to preserve unit variance. This graphic provides an illustration of the resulting normalization constants.

2.5 Systemic Weights

We were able to avoid some complexity in the specification of the factor loadings; we are not quite as lucky in the case of system weights. A methodology is required to approximate the systemic-weight parameters associated with each group of credit counterparties sharing common characteristics. Consider, similar to the previous setting, a collection of N credit entities from the same region with roughly the same total amount of assets (i.e., firm size) and the same industry classification. Let us begin with a proposition. Imagine that the following identity holds:

(3.13)

What does this mean? First, we are assuming that each the N individual obligors in this sub-category have a common systemic weight, α _N. The proposition holds that a reasonable estimator for α _N is the average correlation between these N assets. There are, of course, N ² possible pairwise combinations of these N entities. If we subtract the N diagonal elements, this yields N(N − 1) combinations. Only half of these elements, of course, are unique. We need only examine the lower off-diagonal elements, which explains the conditions on the double sum and the $\frac {1}{2}$ in the denominator of the constant.

Under what conditions is Eq. 3.13 true? This requires a bit of tedious algebra and a few observations. First, the expected value of each ΔX _n and ΔX _m is, by construction, equal to zero for all n, m = 1, …, N. Second, the idiosyncratic factors, { Δw _n;n = 1, …, N} are independent of all of the systemic factors; the expectation of the product of any idiosyncratic and systemic factor will thus vanish. Finally, we recall that only two factor loadings, as highlighted in previous discussion, are non-zero. These final happy facts eliminate many terms from our development.

Let’s begin with the correlation term in the double sum of our identity from Eq. 3.13 and see how it might be simplified. Working from first principles, we have

(3.14)

where I _k and G _k denote the industrial and geographic loading from the kth equity series, respectively. We now have a clearer idea of the condition required to establish our identity in Eq. 3.13. If the expectation equates to unity, then the identity holds. In this case, the double sum yields the same value as the denominator in the constant preceding the sum. These terms cancel one another out establishing equality between the left- and right-hand sides indicating that our proposition holds.

Under what conditions does the expectation in Eq. 3.14 reduce to one? It turns out that the collection of N equity series needs to share the same industrial and geographic factors (and factor loadings). In other words, the factor correlations among the N members of our dataset must be identical. Practically, this means that $\mathrm {B}_{I_{m}}=\mathrm {B}_{I_{n}}$ and $\mathrm {B}_{G_{m}}=\mathrm {B}_{G_{n}}$.³⁶ In this case, we have that

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathrm{corr}\left(\Delta X_n,\Delta X_m\right) & =&\displaystyle \mathbb{E}\left(\bigg( \mathrm{B}_{I_{n}}\Delta z_{{I}_{n}} + \mathrm{B}_{G_{n}}\Delta z_{{G}_{n}} \bigg)^2\right),{}\\ & =&\displaystyle \mathrm{var}\bigg(\mathrm{B}_{I_{n}}\Delta z_{{I}_{n}} + \mathrm{B}_{G_{n}}\Delta z_{{G}_{n}} \bigg),\\ & =&\displaystyle \mathrm{var}\bigg(\mathrm{B}_n\Delta z \bigg),\\ & =&\displaystyle 1, \end{array} \end{aligned} $$

(3.15)

by construction from Eq. 3.12. Naturally, this choice of estimation is applied under the assumption that the model actually holds.

The consequence of this development is that if we organize our estimation categories into a grid with each square sharing a common industrial and geographic systemic factor, then Eq. 3.13 will provide a reasonable estimate of the equity-based systemic weight. In a more general sense, it would appear that as long as the granularity of the systemic-weight estimation matches that of the systemic factor structure, this estimator will work. The analysis thus strongly suggests the use of a regional-sectoral grid to inform the various systemic-weight parameters.

Geographical and industrial identities are sensible and desirable categorizations for systemic weights. They are not, however, the only dimensions that we would like to consider. There is, for example, a reasonable amount of empirical evidence suggesting that systemic importance is also a function of firm size.³⁷ Adding a size dimension to the determination of systemic weights is possible, but it transforms a region-industry grid into a cube including region, industry and firm size.

Figure 3.14 provides a schematic view of this systemic-weight cube. It clearly nests the industrial sector and geographical region grid introduced in the derivation of the systemic-weight estimator. With 11 sectors and 13 regions, this yields 143 individual systemic weights. For each firm-size dimension, therefore, it is necessary to add an additional 143 parameters. Each additional firm-size category must thus be selected judiciously. Not only would too many firm-size groups violate the principle of model parsimony, but would also create a significant data burden. As a consequence, we have opted to employ only three firm size groups:

Small: :

total assets size in the interval of EUR (0, 1] billion;

Fig. 3.14

A cube of systemic weights: To include the notion of firm size and respect the estimation method introduced in Eq. 3.13, we have elected to create a cube of systemic-weight parameters.

Medium: :

total firm assets from EUR (1, 10] billion; and

Large: :

total firm assets is excess of EUR 10 billion.

One can clearly dispute the size of the thresholds separating these three categories, but it is hard to disagree that this represents a minimal characterization of the firm-size dimension. Any smaller than three size categories and this dimension would best be ignored; a larger set of groups, on the other hand, would only magnify existing issues surrounding data parsimony and sufficiency.

Although this cube format provides a sensible decomposition of the main factors required to inform systemic weights and offers a convenient representation—along these three dimensions—it is not without a few challenges. The following sections detail the measures taken to address them.

2.5.1 A Systemic-Weight Dataset

There is no way around it: estimation of systemic weights requires a significant amount of data. With 11 industries, 13 regions, and 3 firm-size categories, a set of K = 11 × 13 × 3 = 429 cube sub-categories sharing common characteristics is required. If we hope to have 15–30 equity time series in each sub-category—to ensure a reasonably robust estimate of its average equity return cross correlations—this would necessitate roughly 6000 to 12,000 individual equity time series.

While the actual parameters are determined annually based on an extensive internal analysis, we will use a sample dataset to illustrate the key elements of the estimation procedure.³⁸ Our starting point is a collection of 20,000 individual, 120-month, equity index time series across various industries, regions, and firm sizes.³⁹ At first glance, this would appear to fall approximately within our (overall) desired dataset size. This is only true, of course, if the underlying equity time series are uniformly distributed across our 429 cube entries. The first order of business, therefore, is to closely examine our dataset to understand how it covers our three cube dimensions.

Table 3.4 takes the first step in exploring our dataset.⁴⁰ It examines, from a marginal perspective, the total number of equity series within each region, industry, and firm-size classification. Our hope of a uniform distribution along our key dimensions does not appear to be fulfilled. Along the regional front, Developed Asia and North America dominate the equity series; they account for roughly 40% of the total. Some important regions for NIB—such as the Baltics and Iceland—are only very lightly represented. With only two equity series, for example, we have virtually no information for Iceland. Indeed, both the Nordic and Baltic regions—as one might expect by virtue of their size—exhibit only a modest amount of data. Given the central importance of these member countries to our mandate, and the need to have granularity for these regions within the economic capital model, it will be necessary to adapt to these data deficiencies.

Table 3.4 Equity series by dimension: The underlying tables illustrate—along the region, industry, and size dimensions—the marginal distributions of equity series. Some geographic regions, such as Iceland and the Baltics, are quite thin. The coverage of industrial sectors, with the possible exception of paper, is rather better.

The industrial and size dimensions look to have, in general, a rather broader range of equity series. Financials and industrials are, by a sizable margin, the largest categories accounting for almost one half of all series. The paper industry looks somewhat thin, but appears to be in better shape than the worst regional categories. Finally, the size decomposition is not exactly split into equally sized groups, but there are substantial numbers of series observations in each group.

While the marginal perspective is a useful starting point, it does not tell the full story. Table 3.5 illustrates the first of three pairwise joint perspectives. It shows the number of equities found within a two-dimensional grid of geographic and industry categories. Again, we see our roughly 20,000 time series in a manner that helps us understand how uniformly distributed they are along our dimensions of interest. 15 grid entries, or about 10% of the total, are empty. More than half of these, of course, stem from the Icelandic region. Numerous individual grid points have hundreds of observations. About one third of the grid entries, conversely, has five or less equity series. It is possible to construct an estimate in this cases, but it will not necessarily be the strongest signal of equity return correlations in this sub-sector.

Table 3.5 Sector-region grid: The underlying table illustrates the number of equities found within a grid based on geographic and industry categories.

Since we are considering a cube, there are two other possible two-dimensional viewpoints to be examined: region versus size and sector versus size. Table 3.6 outlines the equity counts for these perspectives. Once again, the regional aspect is the most problematic. Slicing each region into three size categories does not, of course, help out the situation in Iceland and the Baltics. Denmark, Finland, and Norway also exhibit a rather small number of individual series within the largest size category. The sector-size breakdown is somewhat less problematic; again, the paper industry has relatively few equity series. From each of our three two-dimensional perspectives, the number of equity series is far from equally spread among our three dimensions. This is less a data quality issue and more a feature of the regional, sectoral, and size distributions of listed equities.

Table 3.6 Region and sector-size grid: The underlying tables illustrate the number of equities found within a two-dimensional grid based on firm size versus geographic and industry categories. The Baltics, Iceland, and the paper industry remain problematic in terms of numbers of equity series.

With 20,000 total series and 429 entries, a uniform distribution would place about 45 equity series in each individual cube entry. Our preliminary analysis has made it clear that this will not occur. Figure 3.15 thus attempts to examine how far we are from this ideal. It provides a visualization of the number of equity series associated with each of the 429 individual cube elements. Colours—using a familiar traffic-light scheme—are used to organize entries into three categories. Red, the most problematic, represents zero equity series associated with a given entry. Yellow, which suggests that an estimate is possible although perhaps not terribly robust, is applied for cases of 2 to 5 equity series. Finally, the colour green indicates the presence of more than 5 equity series; this is a desired outcome. The results are as expected. While we observe substantial amounts of green and yellow, the number of problematic red dots clearly increases as we move from small to large firm size. It is consequently difficult to imagine that each of our cube points will be equally well informed by our dataset.

Fig. 3.15

A cube perspective: The preceding figure attempts to provide a useful visualization of the number of equity series associated with each of the 429 individual cube elements. Colours are used to organize entries into three categories: red for no series, yellow for 2 to 5 series, and green for more than 5 equity series. The number of red dots clearly increases as we move from small to large firm size.

This does not mean that our estimation procedure is doomed to failure. Five equity series does not imply only five correlation coefficients, but rather yields $\frac {5\cdot (5-1)}{2}=10$ pairwise estimates. This is not an incredibly rich amount of data, but it should provide a reasonable first-order estimate. It does, however, still suggest that a clear and defensible strategy is required to identify those entries with missing data. The overall dataset is not small and useful inferences can be drawn from neighbouring cube entries with similar properties. In the coming discussion, we’ll outline our approach towards addressing this problem.

Colour and Commentary 32

(Systemic-Weight Choice and Data) : Our systemic weight parametrization takes the form of a three-dimensional cube of systemic-weight coefficients. With 11 sectors, 13 regions, and 3 size categories, however, this choice implies a daunting 429 values to be estimated. A systemic-weight estimator can be constructed from the average cross correlation coefficients of firms with the same industrial, geographic, and firm-size classifications. The correlation between historical equity returns of individual firms is employed for the approximation of these parameters. To do this correctly, a non-trivial amount of data is required. A dataset with 20,000 monthly equity return series, over a ten-year period, has been sourced to outline the various aspects of the estimation process. Although the data is far from uniformly distributed across our three dimensions, it provides significant cross-correlation information. A clear strategy is nonetheless required to manage those cube entries with little or no data.

2.5.2 Estimating Correlations

Logistically, the job before us is rather simple. We need only compute a correlation coefficient for each of the pairs of equity series allocated to each entry in our cube definition. These collections of estimates for each grid point then need to be aggregated somehow to a single estimate representing our associated systemic weight. As is often the case in practice, there are a few complications. Four methodological questions arise:

• 1. What measure of correlation is to be employed?

• 2. How should we aggregate the pairwise correlation estimates for each cube entry?

• 3. How are we to manage cube entries without any data?

• 4. Should any constraints or logical relationships be imposed on the cube structure?

As always, when taking these decisions, we endeavour to be consistent with previous solutions. In the area of missing data, it makes sense to impose the smallest possible non-empirical footprint on the parameters. This implies leveraging the existing dataset, to the extent possible, to inform our cube entries absent equity series data. This is a fine line to successfully walk. The general approach is to reflect carefully, take a judicious choice, and then provide full transparency about the process.⁴¹

The first question—which correlation coefficient to use—can be conceptually difficult. Having wrestled with this point in the determination of the systemic correlation matrix, we have elected to use the rank (i.e., Spearman) correlation across the K equity series in each cube point. The underlying argument of less sensitivity to outliers applies equally well in this context. It is further strengthened by a general desire to take consistent choices across the various elements of the economic-capital model.

The second question would appear to be directly answered by Eq. 3.13. It clearly suggests that we average our individual pairwise correlation estimates. Use of rank correlation, which belongs to the family of order statistics, is justified on the basis of the reduced impact of outliers. Use of the median, rather than the mean, would further insulate our estimates of pairwise correlation coefficients for each cube entry against outliers. This would appear to be particularly important given the relatively sparse amount of data associated with many of our cube points. For this reason, we use the median for cube-entry aggregation.

How do we handle missing data entries? The cube is essentially three slices of a sector-region grid, each indexed to one of the size categories. A missing data point is essentially an empty grid entry. The other median correlation entries occurring within the missing data-point’s grid are the most natural source of information to approximate the missing entry. Often in such problems, from a mathematical perspective, one would approximate the missing point with a two dimensional plane estimated using surrounding non-empty points. In this setting, this is not a particularly sensible strategy. The adjacent cells could be from quite different regions and industries. Only the parallel adjacent cells, relating to the same industry or region, are logically informative. The likelihood of similarities, in terms of cross correlation, would appear to be highest along the industrial rather than the geographic dimension.⁴² We’ve also seen that our industrial equity series are more equally distributed along the sector aspect. Missing data entries are, therefore, replaced using the (non-empty) industry median systemic-weight grid estimates for the same size category.

The fourth, and final, practical question is the most difficult, the most heuristic, and has the greatest potential for criticism. Relying entirely on the previous computational logic may still provide unreasonable results. Such unreasonableness may manifest itself in different ways. Regulatory guidance, for example, suggests that systemic weights should fall into the range of [0.12, 0.24]. It is entirely possible, however, for a given estimate to fall below the lower bound of this interval. Another example relates to the size dimension. Nothing in the current estimate approach ensures, as one would expect, that the medium-size systemic weight—for a given region and sector—exceeds the small-size estimate. Economically, we expect systemic weights to be a monotonically increasing function of firm size. Some, hopefully sensible, manipulation is required should we desire to ensure this idea is incorporated into our final cube estimate.

To this end, we impose the following additional constraints onto our individual systemic-cube entries:

• a minimum systemic weight of 0.12, which is the bottom of the regulatory requirement;

• a maximum value of 0.40, which also represents the systemic weight applied to all public-sector entities; and

• a monotonic relationship between systemic weight and firm size.

The final point suggests that the systemic weight cannot decrease—for a given industrial sector and geographic region—as the firm size increases. The first two elements are relatively easy to implement, while the final aspect will require a bit of justification.

Before getting to these key points, let us first examine the first-order systemic-weight approximations. These do not yet include an application of the minimum and maximum values, but they do handle the missing data with industry medians. They also impose a very simple, and logical, monotonicity constraint. As we move along the size dimension—for fixed sector and region—the systemic weight estimate must be greater than, or equal, to the value from the previous size grouping.

Table 3.7 illustrates, along our first two-dimensional sector-region grid, the raw median rank correlation estimates. Despite the wall of numbers, it does provide a useful perspective. The overall median value is 0.17 with a minimum value of 0.01 and a maximum of 0.76. The median values, across each region and sector slice, are not terribly far from the regulatory interval of [0.12, 0.24]. The highest systemic weights appear to occur in Finland, Sweden, Norway, and the Baltics. Africa and Middle East and Emerging Asia are at the lower end of the regional spectrum. Along the sector aspect, financials, paper, and energy exhibit higher systemic weights, while telecommunications, health care, and utilities receive lower estimates.

Table 3.7 Sector-region correlations: The underlying table outlines the median pairwise (rank) cross correlations for each of the equity series along the sector and region dimensions. Missing data points are replaced with industry medians and a weak monotonicity constraint is imposed. Red, yellow, and green shading indicate below, within, and above regulatory guidance, respectively.

Table 3.8 provides similar median rank correlation coefficients for the remaining two-dimensional grids: region- and sector-size combinations. The first interesting point is the relationship—be it by region or sector—between systemic weight and firm size. There is a fairly convincing increasing trend in systemic weights as we increase firm size. It holds in aggregate and, with one exception, at each regional and sectoral level. One might argue that this is an artifact of our monotonicity constraint. This was only imposed in a limited set of cases. Our analysis, while hardly a solid academic finding, does provide some comfort that inclusion of the firm-size dimension is a sensible choice.

Table 3.8 Region and sector-size correlations: The underlying tables provides raw median rank-correlation estimates—similar to Table 3.7—along the region-size and sector-size dimensions; the colour scheme is also the same.

The range of values in Table 3.8 are qualitatively similar to those found in Table 3.7. The vast majority of the systemic-weight estimates are also entirely consistent with regulatory guidance. Finland, Sweden, and the Baltics also exhibit higher levels of systemic weights, when we examine the size dimension. On the industry side, the paper, energy and IT sectors continue to exhibit higher levels of systemic weight. Not everything completely matches up, since it is entirely possible to view different dependence structures as we organize our data along varying dimensions.⁴³

Having examined all of the possible two-dimensional views of our systemic-weight estimates, we may now turn our attention to the cube values. Using the same basic approach outlined previously—without yet imposing upper or lower bounds on the results—Table 3.9 provides a number of summary statistics. These are computed across the region-sector grids, each holding the size dimension constant, and also at the overall level. The mean and median figures appear to be generally consistent with the two-dimensional analysis. In particular, the minimum and maximum values remain quite extreme. Moreover, the percentage of values outside of our predefined limits is significantly higher than in the two-dimensional settings.

Table 3.9 Raw-cube summary statistics: The adjacent table houses a broad range of summary statistics related to our raw systemic-weight cube estimates in aggregate and along the size dimension.

What is driving this small number of extreme results? Only a small fraction of the 215 two-dimensional estimates fall outside of our limits, whereas about one fifth does in the cube setting. The situation appears to be magnified when moving from the grid to cube perspectives. This stems from the decrease in entry sample sizes associated with moving to a cube. As we have fewer equity series to inform a given cube entry, there is an increased possibility of a small number of fairly extreme pairwise correlation estimates dominating the outcome.

Setting bounds, in this context, would thus appear to be a reasonable solution. Presumably, the lower bound, by virtue of its increased conservatism, would not expose us to undue amounts of criticism. The upper bound, however, is another matter. It could, at worst, be seen as a non-conservative action. There are at least three compelling reasons to envisage placing a cap on our systemic weight estimates. The first is a structural question. Systemic weights ultimately play a critical role in the correlation of the underlying model default events; indeed, this is the entire point of the introduction of systemic risk factors. Many systemic-weight estimation procedures, therefore, use default incidence data among various rating classes, to inform these parameters.⁴⁴ The results associated with such default-based estimation approaches, relative to the use of equity data, typically generate significantly lower systemic-weight values. The reason is a global, persistent level of cross correlation between general equity prices and returns.⁴⁵ When using equity data as a proxy, the consequence is an upward bias in our systemic-weight estimates. Although the magnitude of this bias is difficult to determine, it does argue for eliminating some of the more extreme upside estimates.

The second point relates to a category of credit counterparty that has not yet been discussed: public-sector entities. Such credit obligors do not, unfortunately, possess a public-listed stock and, as such, we may not use equity price returns as a proxy. There are relatively few good alternatives. One could try to infer public-sector correlations from bond or credit-default-swap (CDS) spreads. Both ideas, while containing some information on inter-entity correlations, raise many technical challenges. Moreover, many public-sector exposures have neither liquid bond issues nor listed CDS contracts.⁴⁶ This would then suggest using sovereign proxies; thereby creating an awkward situation of layering multiple data sources. The solution is a logical, and conservative, simplification. All public-sector entities—irrespective of region, sector, or size—are allocated a systemic-weight equal to the upper bound on our systemic cube.

Is this a good decision? There are sensible reasons to expect a high level of systemic weight for public-sector entities. Their revenues are highly related to tax receipts, whereas their expenditures are significantly linked to various social programs. Both items are macroeconomically procyclical, presumably creating important common systemic linkages. To avoid a potential error-prone and uninformative estimation approach, placing all public-sector obligors into the highest systemic-weight group is a clean solution. It does, of course, strongly argue for the establishment of a reasonable upper limit.

The third and final point has already been addressed. As we chop up our 20,000 equity series into 429 distinct sub-buckets, the average behaviour appears to be fairly reasonable. There are, however, a minority of fairly extreme outcomes that appear to be driven by issues associated with small sample sizes. Regulatory guidance caps systemic weights at 0.24. The data, and economic logic, would appear to suggest that a practical estimate could exceed this level. We have, not completely arbitrarily but also not completely defensibly, placed our upper bound at slightly above $1\frac {1}{2}$ times the regulatory upper bound.

Colour and Commentary 33

(An Upper Bound on Systemic Weights) : Arbitrarily setting a key model parameter can be a controversial undertaking. Done correctly, it can help one’s model implementation. Done poorly, it can almost be considered a criminal act. In all cases, however, it needs to be done in a transparent and defensible manner. The application of an upper bound on systemic weights exhibits this element of arbitrariness. Three main reasons argue for this choice. First, there is a general tendency of equity based systemic-weight estimates—relative to default correlation-based techniques—to be structurally higher. Conservatism is a fine objective, but anything in excess can be a problem. Second, due to difficulties in finding good proxy data and their strong systemic linkages, all public-sector entities are assigned systemic weights at the upper bound. This practice argues for a reasonable maximum level of systemic weight. Finally, we need to be symmetrical in our logic. If we are comfortable with a lower bound for reasons of conservatism, then a (reasonable) upper bound should not be overly difficult to digest.

2.5.3 Imposing Strict Monotonicity

The final step in the specification of the systemic-weight cube relates to monotonicity constraints. Thus far, only a weakly monotonic relationship has been imposed along the size dimension. That is, as we move from small- to large-sized firms, the systemic weight must be greater than or equal to the previous entry. This implies that, practically, for some region-sectors pairs, the systemic weight may be flat along the size dimension. In principle, we would prefer a strictly monotonous relationship. This means that a large firm’s systemic weight, for each combination of region and sector, would always be greater than for a smaller one.

For about one quarter of the 143 distinct region-sector pairs, upward steps along the size dimension are not strictly monotonous. Our desired strict monotonicity is imposed using a simple heuristic method. We first compute the slope among those region-sector pairs with increasing systemic weights along the size dimension. This mean slope is subsequently imposed along each of the flat aspects; caution, of course, is taken to ensure that the upper bound remains respected.⁴⁷ Although definitely ad hoc, the rationale behind this adjustment is related to logical consistency and conservatism. Systemic weights do generally increase in a strictly monotonic manner, ceteris paribus, as we increase firm size. When this does not occur naturally, it appears defensible to (gently) force this condition.

Table 3.10 describes the results of this process. It begins by illustrating, for each fixed sector-region pair, the mean systemic weight parameter. These outcomes are utilized to construct a scaling factor. The systemic-weight of a medium-sized firm, for a given pair of regions and sectors, should be 43% greater than the small-sized equivalent; this rises to more than 80% from small to large firms. The final average results are presented. On average, the adjustment is small, because it only impacts a small subset of the entries. Although the change is modest in aggregate, this adjustment nonetheless ensures an important logical consistency to the model. Its limited size, upon consideration, is actually a feature. It implies that only modest adjustment is required to the empirical estimates.

Table 3.10 Size-slope adjustment summary: The underlying table describes, for each fixed sector-region pair, the average systemic weight parameter. Values are provided before and after the adjustment along with the scaling factor employed. On average, the adjustment is small, but it adds logical consistency and conservatism to the model.

Figure 3.16 provides a visualization of this heuristic operation. The left-hand graphic illustrates the initial, unadjusted, situation. A small number of flat size-dimension slopes can be identified. The right-hand graphic repeats the analysis after the adjustment; with a few exceptions around the upper limit, all firm-size slopes along fixed sector-region pairs have a strict increasing monotonic form. At the same time, we observe that the overall impact is relatively modest and the majority of cube entries remains untouched.

Fig. 3.16

Size-slope adjustment: These graphics illustrate, for each fixed sector-region pair, the systemic-weight slope along the size aspect. A before-and-after perspective is provided to help understand the impact of the heuristic adjustment used to impose strict monotonicity over this dimension.

2.5.4 A Final Look

Specification of systemic weights is a critical aspect of a credit-risk economic-capital model. The relative importance of the common systemic component is a key driver of default correlations and, ultimately, the form of the credit-loss distribution. With 11 regional and 13 sectoral systemic state variables, the process is a particular challenge. Following regulatory guidance to further introduce the notion of firm size does not make the task any easier. A desire for modelling accuracy nevertheless makes us reluctant to forego this (size) aspect of the model.

A principal objective in the systemic-weight estimation process is to allow the data to inform, to the extent possible, the final results. Any heuristic adjustments should, in principle, minimally impact the outcomes. Although our degree of success in this venture is an open question, four main interventions were imposed. The first is that missing data points—identified for a fixed firm size along the sector-region grid—are replaced with the median industry outcome. The second and third are systemic-weight constraints. A minimum systemic weight of 0.12—the lower bound of the regulatory interval—is imposed in conjunction with an upper bound of 0.4. The former, by virtue of its conservatism, is uncontroversial. The latter, which is defended by a range of arguments, provides fuel for debate. The final adjustment is the imposition of strict monotonicity—for each sector-region pair—along the size dimension. This final choice also introduces additional prudence into the systemic-weight parametrization.

Figure 3.17 provides a last view on the final set of cube systemic-weight estimates. Similar to Fig. 3.15, it permits a full visualization of our 429 cube elements. Once again, colours are used to organize the entries. Light blue indicates values falling into the regulatory range, regular blue describes estimates from 0.24 to 0.34, while dark blue describes estimates exceeding 0.34. The general trend involves dots getting darker as we move up the size dimension. Nevertheless, consistent with our previous analysis, a significant number of the individual systemic-weight estimates falls into the interval, [0.12, 0.34].

Fig. 3.17

Cube values: This figure, similar to Fig. 3.15, permits visualization of our final 429 cube elements. Once again, colours are used to organize the entries. Light blue indicates values falling into the regulatory range, regular blue describes estimates from 0.24 to 0.34, while dark blue describes estimates exceeding 0.34. The general trend involves dots getting darker as we move up the size dimension.

3 A Portfolio Perspective

The previous section highlights the statistical estimation of a range of parameters relating to the systemic risk factors: correlations, loadings, and weights. The details of this process are central to understanding the role of default and migration dependence in any credit-risk economic capital model. Looking at parameters in isolation, however, rarely provides deep insight into their overall impact. Two notions, in particular, can help in this regard: systemic proportions and a deeper examination of default correlation. Both require a portfolio perspective and, in the following sections, will be investigated.

3.1 Systemic Proportions

The α coefficients, as already highlighted in detail, specify the relative weight on the systemic and idiosyncratic weights. The systemic-weight coefficients themselves are not true weights. α _i and $\sqrt {1-\alpha _i^2}$, while fairly close, cannot be interpreted as the weight on the systemic and idiosyncratic components, respectively. They have, instead, been constructed to ensure the unit variance of the creditworthiness index. To provide a clean description of the true weights on our two principal risk dimensions, we introduce the idea of systemic proportions. It involves a simple, even trivial, adjustment. The systemic proportion is simply,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mbox{Systemic proportion}_i = \frac{\alpha_i}{\alpha_i + \sqrt{1-\alpha_i^2}}, \end{array} \end{aligned} $$

(3.16)

while, it follows naturally, that the idiosyncratic proportion is

$$\displaystyle \begin{aligned} \mbox{Idiosyncratic proportion}_i = \bigg(1- \mbox{Systemic proportion}_i\bigg) = \frac{\sqrt{1-\alpha_i^2}}{\alpha_i + \sqrt{1-\alpha_i^2}},\end{aligned} $$

(3.17)

for i = 1, …, I. By construction, of course, these two proportions sum to unity. Neither of these quantities has any direct model-specific application, but they can help us understand the relative importance of the idiosyncratic and systemic components in the threshold model.

Figure 3.18 provides histograms summarizing the observed distribution of these systemic and idiosyncratic proportions for an arbitrary date in 2020; these values naturally depend on the confluence of firm size, region, and industry within the underlying portfolio. The average systemic proportion is roughly 0.4 with values ranging from as low as 0.3 and up to 0.45. There is a significant amount of probability at the upper end of this range. This clustering is related to the imposition of an upper bound on the systemic weight and the assignment of all public-sector entities—an important part of our portfolio, as is the case with most international financial institutions—to this maximum value.

Fig. 3.18

Component proportions: This figure illustrates the distribution of idiosyncratic and systemic proportions associated with our portfolio for an arbitrary date in 2020. Although these proportions are a slight variation on the actual systemic weights—adjusted to be interpreted as true weights—they provide interesting insight into the relative importance of these two key risk dimensions.

The idiosyncratic proportions are, by their very definition, the mirror image of the systemic proportions. The average value is roughly 0.60, with a significant amount of probability mass in the neighbourhood of 0.55, which naturally corresponds to the clump of systemic proportions in the region of 0.45. Values range from around 0.55 to slightly more than 0.7. We can approximately conclude that common systemic factors drive roughly 40% of the risk, with the remainder described by specific, idiosyncratic elements. This is, as a point of comparison, significantly more conservative than the regulatory guidance. Use of the lower bound, $\alpha _i^2=0.12$, leads to a split of roughly 0.3 to 0.7 for the systemic and idiosyncratic components, respectively. This rises to about 0.35 to 0.65 if we use the regulatory upper bound, $\alpha _i^2=0.24$.⁴⁸

Figure 3.19 takes the analysis a step further by illustrating the systemic and idiosyncratic proportions by default-probability class and firm size. To anchor our perspective, the roughly 40% mean systemic proportion is provided. PD classes one through five appear to be slightly above this average, while the classes 7 to 12 are somewhat below.⁴⁹ A gradual increase in systemic proportion is evident when moving from small to large firms; medium and large firms, however, do not manifest any (material) visual difference.

Fig. 3.19

Weighting perspectives: This figure breaks out the average idiosyncratic and systemic weights by rating category and firm size; the weights were adjusted to sum to one to ease the interpretation. Again, we see that on average about 40% the weight is allocated to the idiosyncratic factor. This ratio is not, however, constant across the PD-class and firm-size dimensions.

Figure 3.20 extends the view from Fig. 3.19 to include the systemic and idiosyncratic proportions by region and sector. The majority of regions does not visually deviate from the overall average. New Europe and Africa and Middle East are somewhat higher than the mean, whereas Iceland and Developed Asia are somewhat below this level. IT, public-sector entities, and financials exhibit higher than average systemic proportions; this is sensible, since these firms exhibit strong macroeconomic linkages. Health care, utilities, and telecommunication firms, conversely, exhibit a higher weight on the idiosyncratic dimension. Again, this appears reasonable, since such firms often operate in controlled, regulated environments reducing the role of systemic factors.

Fig. 3.20

More weighting perspectives: This figure, building on Fig. 3.19, breaks out the average idiosyncratic and systemic proportions by region and industrial sectors. Differences in systemic proportions are visible, but individual values do not appear to vary dramatically from the mean values.

Colour and Commentary 34

(Systemic-Weight Reasonableness) : With even a modest number of systemic-risk factors, it is hard to definitively opine on the magnitude of the systemic weights in one’s credit-risk model. Regulatory guidance places the $\alpha _i^2$ values in the interval, [0.12, 0.24] with higher credit-quality firms tending towards the upper end. This argues for systemic proportions in the range of 0.3 to 0.35. On average, in this case, about two thirds of default and migration events are driven by systemic factors. The remainder thus stems from idiosyncratic elements. Our systemic-weight parametrization moves this average value up to approximately 0.4. On the surface, therefore, one may conclude that a conservative approach to internal modelling has been taken. ^a On the systemic-weight dimension, at least, a compelling argument can be made for the prudence of the systemic parameters.

^aWhile this was the intention, the reasonableness of this choice also needs to be considered with other modelling alternatives—such as inclusion or exclusion of migration effects and the form of copula function. Conservatism is best assessed through joint examination of the entire set of modelling decisions.

In the following section, we will turn our attention towards understanding how these systemic-weight choices impact the central driver of credit-risk interdependence; the notion of default correlation. The mathematical chain from systemic correlations to systemic weights to default correlations is not particularly direct, but it merits careful examination. It is, after all, the nucleus of the threshold model.

3.2 Factor-, Asset-, and Default-Correlation

Correlations, as we’ve seen in the context of a threshold model, come in a variety of flavours. Factor correlation refers to the pairwise dependence between the loaded systemic-risk factors associated with two credit obligors. Asset correlation addresses—also for an arbitrarily selected pair of credit counterparts—the interdependence between latent creditworthiness index variables. The final, and perhaps most interesting quantity, is the pairwise correlation between underlying default events; we call this default correlation. Each of these three elements provides an alternative perspective into our model’s interactions between any two obligors.

Our objective in this section is to examine, to the best of our ability, the various definitions of correlation at the portfolio level. This will require re-organizing some of our previous definitions. Let us begin by repeating the generic definition of the ith obligor’s creditworthiness index,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \Delta X_i & =&\displaystyle \sqrt{\frac{\nu}{W}}\left(\alpha_i \mathrm{B}_i \Delta z + \sqrt{1-\alpha_i^2}\epsilon_i \right). \end{array} \end{aligned} $$

(3.18)

This expression illustrates all of the characters within our threshold-model implementation: systemic and idiosyncratic elements, factors loadings, systemic weights, systemic-factor correlations, and the mixing variable employed to induce a multivariate t distribution. In Chap. 2, we demonstrated that $\Delta X_i \sim \mathcal {T}_{\nu }\left (0,\frac {\nu }{\nu -2}\right )$.

The systemic-risk factor correlation between any two obligors, n and m, is a function of its systemic factor loadings and the common systemic-risk factor outcomes. The covariance between these two quantities is,

(3.19)

where the last step follows from the previously established fact that var(B_i Δz) = 1 for all i = 1, …, I. The factor correlation is thus a rather complicated cocktail of systemic-factor loadings and correlations.⁵⁰

The asset correlation, as derived in the previous chapter, has a fairly elegant form. It is written as α _n ρ _nm α _m. Given the dimensionality of our systemic factors, most of the complexity is embedded in the factor correlation term, ρ _nm. The pair of systemic weights works together to complete the picture. If there is a high degree of factor correlation and both systemic weights are large, then the asset correlation will be correspondingly high. A few simple examples can help build some intuition. Imagine that the factor correlation is 0.75 and both credit obligors share systemic weights at the upper bound of $\alpha _i^2 = 0.4$. The asset correlation would then become,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mbox{Case 1}_{\mbox{Asset correlation}} & =&\displaystyle \alpha_n \rho_{nm} \alpha_m,\\ & =&\displaystyle \sqrt{0.4}\cdot 0.75 \cdot \sqrt{0.4} = 0.30. \end{array} \end{aligned} $$

(3.21)

If only one of the obligors is at the lower bound of 0.12, then we observe,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mbox{Case 2}_{\mbox{Asset correlation}} & =&\displaystyle \sqrt{0.4}\cdot 0.75 \cdot \sqrt{0.12} \approx 0.16, \end{array} \end{aligned} $$

(3.22)

which amounts to a twofold decrease in overall asset correlation between these two credit counterparts. Following this to the lower limit, when both parties have systemic weights at the lower bound, then

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mbox{Case 3}_{\mbox{Asset correlation}} = \sqrt{0.12} \cdot 0.75 \cdot \sqrt{0.12} \approx 0.09. \end{array} \end{aligned} $$

(3.23)

Naturally, this is scaled upwards and downwards by the factor correlation, but these simple examples illustrate the critical role of the systemic weights in the determination of asset correlations.⁵¹

The final object of interest is the default correlation. This quantity, also derived in the previous chapter, has the following model-independent form,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \rho\left(\mathbb{I}_{\mathcal{D}_{n}},\mathbb{I}_{\mathcal{D}_{m}}\right) & =&\displaystyle \frac{\mathbb{P}\left(\mathcal{D}_{n}\cap\mathcal{D}_{m}\right) - p_n p_m}{\sqrt{p_n p_m(1-p_n)(1-p_m)}}. \end{array} \end{aligned} $$

(3.24)

Given the t-copula implementation, the joint distribution of ΔX _n and ΔX _m follows a bivariate-t form. This helps us evaluate the tricky quantity $\mathbb {P}\left (\mathcal {D}_{n}\cap \mathcal {D}_{m}\right )$.⁵² Specifically, from the previous chapter, it has the following generic form,

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathbb{P}\left(\mathcal{D}_{n}\cap\mathcal{D}_{m}\right) & =&\displaystyle \mathbb{P}\bigg(\Delta X_n\leq \Phi^{-1}(p_n), \Delta X_m \leq \Phi^{-1}(p_m)\bigg),{}\\ & =&\displaystyle F_{\mathcal{T}_{\nu}}\left(F_{\mathcal{T}_{\nu}}^{-1}(p_n),F_{\mathcal{T}_{\nu}}^{-1}(p_m); \alpha_n\rho_{nm}\alpha_m\right). \end{array} \end{aligned} $$

(3.25)

The final expression for default correlation, within the credit-risk model is thus

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \rho\left(\mathbb{I}_{\mathcal{D}_{n}},\mathbb{I}_{\mathcal{D}_{m}}\right) & =&\displaystyle \frac{F_{\mathcal{T}_{\nu}}\left(F_{\mathcal{T}_{\nu}}^{-1}(p_n),F_{\mathcal{T}_{\nu}}^{-1}(p_m); \alpha_n\rho_{nm}\alpha_m\right) - p_n p_m}{\sqrt{p_n(1-p_n)}\sqrt{p_m(1-p_m)}}. \end{array} \end{aligned} $$

(3.26)

This expression is readily computed with the use of numerical integration.⁵³

The preceding ingredients are everything that is needed to compute factor, asset, and default correlations for each pair of credit obligors. There is, however, a problem. With 500+  obligors, this amounts to approximately 140,000 distinct pairs of counterparties to examine. Even for the hardest-working and most committed quantitative analyst, this is a tad too much to visually wade through and digest. What is required is some conceptual organization. Table 3.11 lessens the burden somewhat by introducing a logical partition of our collection of credit counterparties using the model structure; this amounts to public-sector status, industrial sector, geographical region, and firm size. These divisions were, of course, not selected by random. They relate to the differences in the key drivers of our correlation quantities: systemic weights and loadings.⁵⁴

Table 3.11 Cross-correlation cases: We can identify 14 logical distinct cross-correlation cases—along the public-sector, industry, regional, and size dimensions—to analyze the degree of factor, asset, and default correlation embedded in the current model parameters.

Let’s work through the basic logic of our partition:

• In the first two cases, both entities are in the public sector. In this case, the industry designation and firm size do not matter. There are two cases: the counterparts share the same geographic region or they do not.

• In the second setting, only one of the obligors falls in the public sector. Since only one member of the pair has an industry identity, they can only differ along the regional and firm size dimensions. This amounts to four possible cases.

• The final part is perhaps the most interesting. Both counterparties are in the corporate sector implying potential differentiation along the industrial, regional, and firm-size categories. The consequence is eight distinct cases.

The result is a reduction of 140,000 correlation pairs into 14 logical cases.⁵⁵ While losing a significant amount of information, hopefully we gain a bit of perspective.

Each group is mutually exclusive and covers all possible outcomes; that is, no obligor pair can fall into more than one group. Equally importantly, each sub-group exhibits a link to the lending business. It is interesting and sensible, for example, to consider the set of public-sector obligor pairs falling into the same geographic region. Similarly, we care about the nature of default correlation between two non-public-sector entities in the same industry, but stemming from different geographic regions. Practically, we would expect to observe a greater degree of factor correlation associated with obligors sharing a greater number of characteristics. Two obligors in the same industry and region should, in principle, be more correlated than two entities dissimilar along these dimensions. This analysis can, hopefully, shed some light onto the economic reasonableness of these empirically driven parameter estimates. We can thus think of this as a kind of parameter sanity check.

Despite our logical breakdown, there remains a substantial amount of heterogeneity within each of our sub-groups. Even if they fall into the same industry, region, and asset-size category, they can potentially have very different default probabilities, exposure, and loss-given default settings. This means that they may exhibit significant correlation, but impact the overall portfolio risk in quite distinct ways. This does not negate this analysis, but it is useful in understanding and interpreting the results.

Table 3.12 provides a daunting number of correlated-related figures organized by our previously defined cases using our portfolio on an arbitrary date during 2020. With so many numbers, it is useful to examine the extremes. In particular,

• Cases 1, 3, and 7 represent situations of correspondence along the public-sector dimension, but literally no overlap among the other three categories. These cases, logically at least, have the lowest amount of agreement in terms of correlation outcomes. We will refer to these as low-agreement cases.

  Table 3.12 Correlation analysis: The underlying table describes the number and percent of obligor pairs falling into each logical class along with their respective average factor-, asset-, and default-correlation values.

• Cases 2, 6, and 14, in contrast, after public-sector correspondence, involve the greatest degree of overlap among our three categories. Conceptually, we would expect them to exhibit the highest amount of agreement in terms of cross-correlation coefficients. Let’s call these high-agreement cases.

With only 14 cases, were the portfolio to be uniformly distributed along our key dimensions, we would expect about 7% of the pairs in each case. Interestingly, our three low-agreement cases represent about half of the total number of obligor pairs. This is significantly above what one would expect under uniformity. If we add in case 5—where the only level of dimensional agreement is firm size—this rises to about 70%. The high-agreement cases appear to be relatively less frequently occurring; all together they amount to about 10% of the individual counterparty pairs. This does suggest, at least along these dimensions, a reassuringly low level of concentration.

Factor correlation is, across all 14 cases, quite high. The lowest average value is about 0.7. Indeed, our low-agreement cases—as we had suspected—exhibit the lowest levels of factor correlation. On the other hand, Cases 2, 6, and 14 show the highest levels of factor correlation with levels approaching unity. Cases 2 and 14, by construction, load onto the same factors in the same way and, as such, have perfect factor correlation. At the factor correlation level, therefore, the trend in factor correlations is as expected. The overall factor-correlation levels remain quite high due to significant positive correlation among our systemic risk factors stemming from the use of equity returns in their parametrization.

The asset-correlation coefficients, which work from the factor correlation and add the systemic weights, tell a similar story. Cases 1, 3, and 7—we could also add case 5 to this group—possess lower asset-correlation values relative to the others. The average asset-correlation coefficient for these cases appears to be between 0.2 and 0.25. The high agreement group displays values in excess of 0.32. Again, we observe consistent, and expected, behaviour among our logical cases. Asset correlation levels are also, if somewhat differentiated among cases, generally quite high.

Moving to default correlation, the same trend persists, albeit at significantly lower levels. Default correlation coefficients in a threshold setting, even in the most aggressively parametrized situations, rarely exceed about 0.05. The average level, across all obligor pairs, is roughly 0.02. The low-agreement cases all display average default-correlation coefficients south of this figure. The high-agreement cases, however, each exhibit values almost twice the overall average.

Colour and Commentary 35

(A Parametric Sanity Check) : Parameter selection is a tricky business and any tools that can help us assess the consistency of our choices are very welcome. Sorting out factor, asset, and default correlation, for example, is not trivial. Each quantity is a complicated combination of factor correlation, factor-loading, and systemic-weight model parameters. Moreover, with even a modest number of credit obligors, there are many possible pairwise interactions. One can, in our specific case, organize the (intimidatingly large) number of obligor pairs into 14 logical cases along the type-of-entity, industry, geographic-region, and firm-size dimensions. This helps to organize our thinking and formulate expectations regarding the level of correlation within the model. Counterparties with stronger agreement along these dimensions should reveal higher degrees of default dependence. To test this proposition, we compute the average levels of factor, asset, and default correlation across each of these logical cases. At all levels, the various correlation coefficients appear to be consistent with our presuppositions; greater agreement among our predefined key dimensions appears to lead to a higher degree of model dependence. This analysis, which basically amounts to something of a sanity check on the model calibration, helps us to conceptualize and judge the reasonableness of the current parameters.

3.3 Tail Dependence

Equation 3.18 describes the latent creditworthiness state variable associated with each of the individual obligors in our portfolio. Quietly, in the background, sits a difficult to manage parameter, ν. This is the degrees-of-freedom parameter of the chi-squared (mixing) random variable used to generate marginal and joint t distributions for our state-variable system. The strategic business rationale for this specific implementation of threshold model is the inclusion of non-zero tail dependence. In this respect, the t-copula model is a significant conceptual improvement over the Gaussian version.

To actually use the model, of course, one needs to select a value for ν. This is easier said than done. Bluhm et al. [6], in their excellent text on credit risk, state that:

We do not know about an established standard calibration methodology for fitting t-copulas to a credit portfolio.

Neither do we. This is, therefore, a challenge faced by any user of the t-threshold model. Central to the problem is the fundamental notion of tail dependence. Since it relates to the joint incidence of extreme outcomes, data is understandably very scarce. As a consequence, this parameter is determined by a combination of expert judgement and trial and error.

What we do know is that ν should not be a very large value—say 100 to 300—because this practically amounts to a Gaussian copula model with its attendant shortcomings. On the other hand, a very low value of ν—below, for example, about 30 or 40—is really quite aggressive. The current parameter value has been set to 70. It is certainly easy to throw rocks at this choice.⁵⁶ Why not 65 or 75? Or 50 or 90? There is no good objective rationale that can be used to defend this decision. It amounts to walking a fine line between being sufficiently or overly conservative. Ultimately, it is about model judgement and risk-management needs. It is, in our view, logically preferable to incorporate positive tail dependence into our model—and live with a hard-to-calibrate parameter—than not to have it at all.

4 Recovery Rates

Recovery, as discussed in Chap. 2, is assumed to be a stochastic quantity. For each default outcome, a simultaneous random variable is drawn from a distribution to determine the amount recovered. Naturally, this raises two important questions: how is the recovery aspect distributed and is it somehow related to the default element? Both questions are, from an empirical perspective, a bit difficult to answer. Default is a generally rare event making estimation of default probabilities a challenging problem; recovery is an outcome conditional on default. Thus, we are trying to estimate the distribution of an outcome conditional on another rather rare event. Availability and richness of data is thus the principal problem in this area.

To handle these problems, three main assumptions are typically made:

• 1. the recovery rate, which varies among obligors, is assumed to be function of numerous elements of counterparty’s current general creditworthiness;

• 2. the recovery process is assumed to be independent of the default mechanics; and

• 3. the stochastic element of recovery is described by the beta distribution.

All three of these assumptions can be relaxed and other choices are, of course, possible. These common assumptions, however, represent reasonable choices in the face of limited data.

A key follow-up question is how does one specify the stochastic dynamics of the recovery elements. Moreover, once a specific choice is made, how is the parametrization performed? This can, in principle, be as complex as one desires. These objects, for example, could be treated as multivariate stochastic processes; that is, they could possess randomness across both the cross-sectional and time dimensions. This would, not to mention the challenges of parameter estimation, likely be overkill. Instead, recovery values are typically drawn from a convenient time-invariant distribution.

The Beta Distribution

To operationalize this general notion, it is necessary to specify the distribution of each individual recovery variable, $\mathcal {R}_{i}$; in our case, the beta distribution. Let us first consider this decision generically; afterwards, we can specialize it to our needs and desires. Consider the following random variable,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} X \sim \mbox{Beta}(a,b), \end{array} \end{aligned} $$

(3.27)

where a and b are parameters in $\mathbb {R}_+$.⁵⁷ In words, X is beta distributed. The density of X is summarized as,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} f_X(x) = \frac{1}{\beta(a,b)}x^{a-1}(1-x)^{b-1}, \end{array} \end{aligned} $$

(3.28)

for x ∈ (0, 1). That is, the support of X is the unit interval.⁵⁸ β(a, b) denotes the so-called beta function, which is described as,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \beta(a,b) = \int_0^1 t^{a-1} (1-t)^{b-1} dt, \end{array} \end{aligned} $$

(3.29)

which bears a strong resemblance to the form of the beta density. The beta function is also closely related to the gamma function. In particular,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \beta(a,b) = \frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}. \end{array} \end{aligned} $$

(3.30)

The gamma function, which can be seen as a continuous analogue of the discrete factorial function, is written as⁵⁹

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \Gamma(t) = \int_{\infty}^{\infty} x^{t-1} e^{-x} dx. \end{array} \end{aligned} $$

(3.31)

The beta distribution, given its finite support, is often used in statistics and engineering to model proportions. Interestingly, if one sets a = b = 1, then the beta distribution collapses to a continuous uniform distribution.⁶⁰ Moreover, it can easily be constructed from the generation of gamma random variates.⁶¹ Finally, the mean of a beta-distributed random variable, X, with parameters a and b is,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mathbb{E}(X) & =&\displaystyle \frac{a}{a+b}, \end{array} \end{aligned} $$

(3.32)

while its variance is,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mathrm{var}(X) & =&\displaystyle \frac{ab}{\left(a+b\right)^2(a+b+1)}. \end{array} \end{aligned} $$

(3.33)

So much for the mathematical background on the beta distribution. The key question is: how precisely is this choice utilized in a default credit-risk model? It basically comes down to parameter choice. In principle, one could expect to have slightly different parameters for each region, industry, or business line. As one would expect, however, a number of simplifying assumptions are imposed. Each individual credit obligor is assigned to a loss-given-default value following from an internal framework. We then transform this loss-given-default value into an recovery amount.

To simulate recoveries, which is our ultimate goal, we need to establish a link between the moments furnished by internal assignment and the model parameters. This is basically a calibration exercise. We denote M _i and V _i as the mean and variance conditions associated with the ith credit obligor.⁶² M _i is directly informed by the policy; the choice of V _i, however, is less obvious. A common value might be assigned to all individual credit obligors. We could also use this parameter to target specific characteristics of the recovery distribution. In the forthcoming analysis, we will explore the implications of both choices. For the time being, let’s just think of it as a generic value.

We thus view M _i and V _i as economically motivated moment conditions for the recovery variable. The idea is to determine how we might transform these values into beta-distribution shape parameters, a _i and b _i, for employment in our model. Using the definitions provided in Eqs. 3.32 and 3.33, we construct a system of (non-linear) equations. The first expression equates the first moments

$$\displaystyle \begin{aligned} \begin{array}{rcl} M_i & =&\displaystyle \frac{a_i}{a_i+b_i},{}\\ M_i(a_i+b_i) & =&\displaystyle a_i,\\ a_i & =&\displaystyle \frac{b_i M_i}{1-M_i}. \end{array} \end{aligned} $$

(3.34)

The second piece, equating the variance terms, is a bit more complex

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} V_i & =&\displaystyle \frac{a_ib_i}{(a_i+b_i)^2(a_i+b_i+1)}. \end{array} \end{aligned} $$

(3.35)

If we substitute Eq. 3.34 into 3.35, a tiresome calculation reveals

(3.36)

Now plugging this quantity back into Eq. 3.34, we recover the required value of a _i as,

(3.37)

We thus have a concrete link between the beta-distribution parameters and the provided moment conditions. This is, in fact, a closed-form application of the method-of-moments estimation technique.⁶³

While technically correct, this result is not terribly intuitive. If, however, we introduce the term,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \xi_i = \frac{M_i(1-M_i) - V_i}{V_i}, \end{array} \end{aligned} $$

(3.38)

then we can rewrite our recovery model parameter choices as,

$$\displaystyle \begin{aligned} \begin{array}{rcl} a_i & =&\displaystyle M_i\xi_i,{}\\ b_i & =&\displaystyle (1-M_i)\xi_i. \end{array} \end{aligned} $$

(3.39)

We can interpret ξ _i in Eq. 3.38 as the normalized distance between the provided value and the variance of a Bernoulli trial with parameter, M _i. This is not a coincidence since the beta distribution approaches the Bernoulli distribution as the shape parameters, a _i and b _i, approach zero. This would be precisely the case, as is clear from Eq. 3.38, should we set M _i(1 − M _i) = V _i. That is, this is the variance of a Bernoulli trial, with parameter, M _i. In this situation, which is the point, both a _i and b _i reduce to zero.

One way to see that these are equivalent conditions is to re-examine the definition of the beta distribution’s variance from Eq. 3.35,

(3.40)

As long as the sum of the two parameters a _i and b _i remains greater than zero, then the denominator of Eq. 3.40 exceeds unity. This, by extension, ensures that V _i < M _i(1 − M _i).

The Bernoulli trial limiting case is, however, practically rather unsatisfactory. It is conceptually equivalent to flipping a coin. The outcome is binary; heads with probability M _i and tails with 1 − M _i. Instead of heads and tails, however, we have values 0 and 1. That is, the probability of the full recovery of a claim is M _i; the corollary is that our recovery takes the value of zero (i.e., we lose the entire exposure) with probability 1 − M _i. This is probably not a reasonable recovery model, but it is interesting that it is embedded in the structure of the beta-distribution approach.⁶⁴ If we avoid this unrealistic extreme case, then the beta distribution will permit the recovery of any claim to, in principle, take any value in the unit interval.

Fixed Recovery Volatility

The uncertainty surrounding the mean recovery rate—referred to previously as $\sqrt {V_i}$—is not obviously determined. We have, in the past, experimented with the assignment of a value of $\sqrt {V_i}\equiv 0.25$ to all counterparties. Why might one do this? The simple, and perhaps not very satisfying, answer is that one lacks sufficient information to empirically differentiate between individual obligors. Small to medium institutions will generally have a correspondingly modest—and typically uninformative, default and loss-given-default—data history.

Using the method-of-moments estimator derived in Eqs. 3.38 and 3.39, Fig. 3.21 summarizes the associated beta-distribution parameters utilized to generate beta-distributed random variates arising from the blanket assumption of $\sqrt {V_i}\equiv 0.25$. Since each a _i and b _i parameter is a function of both moment conditions, we cannot speak of a mapping between the beta parameters and assumed moments.⁶⁵ The a _i values take an average value of roughly 1.3; observed values range from close to zero to about 1.75. The b _i values, conversely, exhibit a mean value of about 0.7; again, observations range from 0 to almost 2. The a _i outcomes are clustered around the mean, while the b _i’s appear to have a multimodal form with probability mass around 0.25, 1, and 1.75.

Fig. 3.21

Fixed V _i Beta-distribution parameters: Using a method-of-moments approach, this figure illustrates the mapping of M _i choices and fixed V _i ≡ 0.25 into a collection of the beta distribution’s two shape parameters, a _i and b _i.

How does the beta distribution take these two shape parameters and determine the relative probabilities of an outcome? Since the standard beta distribution is restricted to the unit interval, we seek to understand how probability mass is spread over this region. Figure 3.22 helps us answer this question by plotting a broad range of beta densities. The first uses the mean shape parameters—in particular, a = 1.3 and b = 0.7—to describe the average density associated with a fixed choice recovery volatility. This outcome, summarized by the red line, places a significant amount of probability mass around unity and gradually falls down towards zero; in this case, the mean appears to lie between 0.65 and 0.7. The blue line repeats this analysis, but uses financial exposures to find a weighted set of beta parameters.⁶⁶ There is very little difference, although the weight on higher recoveries falls slightly with a modest impact on the mean outcome. The final high-level point of comparison is the uniform density, where all values in [0, 1] are equally likely.

Fig. 3.22

Fixed V _i beta densities: The preceding figure plots the entire range of beta densities associated with the (indirectly) assumed shape parameters. For reference, the beta densities associated with the simple-mean and exposure-weighted mean shape parameters are also provided. On average, a higher probability of large recovery is assumed.

In addition to these three high-level comparative densities, every single observed pair of a and b shape parameters are used to display the entire range of employed densities. A broad range of shapes are evident. Some look flat, others have the standard upward-sloping shape found in the average density, a few bell-shaped densities can be identified, others exhibit a u-shaped form, while another group looks to be downward sloping.⁶⁷ There is a fairly rich range of assumed beta densities. Empirically, there is some evidence that actual recovery rates are actually bimodal; this implies that there is a disproportionately high probability of quite large or quite small recoveries.⁶⁸ This is a rather stark deviation between this empirical finding and the constant recovery-variance assumptions illustrated in Fig. 3.22.

Colour and Commentary 36

(Fixed Recovery Volatility) : Determination of recovery volatility is hard. One might quite reasonably opt to make a common assessment of recovery uncertainty for all one’s credit obligors. Although not terribly defensible, it has the benefit of simplicity. The resulting beta densities are helpful in assessing this choice. While a range of beta densities is observed with varying forms, the average result places a relatively high degree of probability mass on high-recovery outcomes. Empirical evidence suggests that actual recovery rates are actually bimodal; the consequence is a disproportionately high probability of quite large or quite small recoveries. This would appear to be something of a shortcoming of the constant recovery volatility assumption. To resolve this, we need to identify an approach permitting the introduction of recovery bimodality. The consequence, of course, will be more extreme recovery and loss-given-default outcomes with a commensurate increase in one’s associated economic-capital estimates.

Bimodal Recovery

The method-of-moments technique provides a useful link between the desired recovery moments and these shape parameters. The mean of this distribution (i.e., M _i) should be clearly provided by one’s loss-given-default framework, but its variance (i.e., V _i) may not be known. While this feels problematic, it represents something of an opportunity. We might treat the V _i value as a free parameter. It could be selected to obtain desired distributional characteristics; such as, quite pertinent in our situation, bimodality.

A bimodal beta distribution is consistent with a so-called U-shaped density function. That is, there is a preponderance of probability mass at the lower and upper—or extreme—ends of the distribution’s support. Practically, this means that, irrespective of the mean, large or small recoveries are relatively more probable. It turns out that there is a convenient condition ensuring that a beta density has a U-shaped form: both the a and b parameters must be less than 1. The imposition of a bi-model recovery distribution thus reduces to something like the following optimization problem:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \min_{a_i(M_i,V_i),b_i(M_i,V_i)} & &\displaystyle V_i,{}\\ \mbox{subject to:}& &\displaystyle \\ a_i(M_i,V_i),b_i(M_i,V_i) & \in &\displaystyle (0,1),\\ \frac{a_i(M_i,V_i)}{a_i(M_i,V_i)+b_i(M_i,V_i)} & =&\displaystyle M_i,\\ V_i & >&\displaystyle 0. \end{array} \end{aligned} $$

(3.41)

In words, therefore, we seek the smallest variance value that would lead to a U-shaped beta density. Inspection of Eq. 3.41 suggests that it is not much of an optimization problem. Indeed, there exists a (hopefully, non-empty) set of possible V _i values that respect our three constraints. This set is defined—in what basically amounts to a simple manipulation of Eq. 3.41—as follows:

(3.42)

Any member of this set—that is, $V_i\in \mathcal {V}_i$—will respect one’s internal loss-given-default framework, provide a U-shaped or bimodal beta distribution, and involve a mathematically legitimate choice for the second moment of the recovery distribution.

Figure 3.23 provides a graphical visualization of this set for an arbitrarily selected credit obligor; it is, however, quite representative of the general problem faced by obligors. The red-shaded area in Fig. 3.23 represents the confluence of a _i, b _i, and $\sqrt {V_i}$ values that preserve the mean, provide positive variance, and permit a U-shaped beta density function. Permissible values of $\sqrt {V_i}$, in this case, appear to range from about 0.25 to roughly 0.4.

Fig. 3.23

Visualizing $\mathcal {V}_i$: For the ith arbitrarily selected credit obligor, this figure provides a visualization of the set $\mathcal {V}_i$ defined in Eq. 3.42. The red-shaded area represents the confluence of a _i, b _i, and $\sqrt {V_i}$ values that preserve the mean, provide positive variance, and permit a U-shaped beta density function.

A bit of effort can help us identify the boundaries of the set defined in Eq. 3.42. This means working with the U-shaped condition constraints to understand what they imply for the possible values of V _i. Let’s start with the a _i parameter. It has to be strictly less than unity, which implies, from our previous definitions, that

$$\displaystyle \begin{aligned} \begin{array}{rcl} a(M_i,V_i) & <&\displaystyle 1,{}\\ M_i\xi_i & <&\displaystyle 1,\\ M_i\left(\frac{M_i(1-M_i)-V_i}{V_i} \right) & <&\displaystyle 1,\\ \frac{M_i(1-M_i)}{V_i} & <&\displaystyle \frac{1}{M_i}+1,\\ V_i & >&\displaystyle \frac{M_i^2(1-M_i)}{1+M_i}. \end{array} \end{aligned} $$

(3.43)

This suggests a lower bound on V _i, based on the specification of a, which depends entirely on the mean recovery value. A corresponding upper bound can be derived from the second constraint condition as follows,

$$\displaystyle \begin{aligned} \begin{array}{rcl} a(M_i,V_i) & >&\displaystyle 0,{}\\ M_i\left(\frac{M_i(1-M_i)-V_i}{V_i} \right) & >&\displaystyle 0,\\ \frac{M_i(1-M_i)}{V_i} & >&\displaystyle 1,\\ V_i & <&\displaystyle M_i(1-M_i). \end{array} \end{aligned} $$

(3.44)

Combining these two values together, and applying the square-root operator to return to volatility space, the a _i-parameter bounds on the V _i parameter are defined by the following open interval

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \sqrt{V_i} \in \left(\sqrt{\frac{M_i^2(1-M_i)}{1+M_i}},\sqrt{M_i(1-M_i)}\right). \end{array} \end{aligned} $$

(3.45)

Interestingly, the (unattainable) upper bound is the volatility of a Bernoulli trial with parameter, M _i.

We also may similarly compute a similar set of b-parameter induced bounds. The lower bound is given as,

$$\displaystyle \begin{aligned} \begin{array}{rcl} b(M_i,V_i) & <&\displaystyle 1,{}\\ (1-M_i)\xi_i & <&\displaystyle 1,\\ (1-M_i)\left(\frac{M_i(1-M_i)-V_i}{V_i} \right) & <&\displaystyle 1,\\ \frac{M_i(1-M_i)}{V_i} & <&\displaystyle \frac{1}{1-M_i}+1,\\ V_i & >&\displaystyle \frac{M_i(1-M_i)^2}{2-M_i}, \end{array} \end{aligned} $$

(3.46)

while the upper bound is,

$$\displaystyle \begin{aligned} \begin{array}{rcl} b(M_i,V_i) & >&\displaystyle 0,{}\\ (1-M_i)\left(\frac{M_i(1-M_i)-V_i}{V_i} \right) & >&\displaystyle 0,\\ \frac{M_i(1-M_i)}{V_i} & >&\displaystyle 1,\\ V_i & <&\displaystyle M_i(1-M_i). \end{array} \end{aligned} $$

(3.47)

Combining, these two values together yields a second interval

$$\displaystyle \begin{aligned} \begin{array}{rcl} \sqrt{V_i} \in \left(\sqrt{\frac{M_i(1-M_i)^2}{2-M_i}},\sqrt{M_i(1-M_i)}\right).{} \end{array} \end{aligned} $$

(3.48)

The Bernoulli-trial variance upper bound is common between both the a _i and b _i calculations. Overall, since both a _i and b _i constraints need to be jointly respected, the final set of parameter-induced bounds, in terms of M _i, are

$$\displaystyle \begin{aligned} \sqrt{V_i} \in \left(\max\left(\sqrt{\frac{M_i(1-M_i)^2}{2-M_i}},\sqrt{\frac{M_i^2(1-M_i)}{1+M_i}}\right),\sqrt{M_i(1-M_i)}\right) \equiv \left(\underline{V_i},\overline{V_i}\right). \end{aligned} $$

(3.49)

The left-hand graphic in Fig. 3.24 examines the practical upper and lower bounds on $\sqrt {V_i}$ for the full range of mean recovery values, M _i, over the unit interval. The broadest range of possible V _i values occurs when M _i = 0.5. As M _i moves to its lower and upper extremes, the set of permissible values shrinks asymptotically to zero.⁶⁹

Fig. 3.24

Identifying V _i: Respecting our constraints, explicit upper and lower bounds, for a given level of M _i, can be traced out. We seek to avoid being too close to the upper bound, which approaches the Bernoulli-trial case, so we select one quarter of the distance between the lower and upper bounds. The final results are presented in the right-hand graphic.

The previous bound derivations are tedious, but provide some useful insight into the problem. As we move towards the upper bound, our beta-distribution structure tends towards a Bernoulli trial with parameter, M _i. This coin-flip approach pushes the a _i and b _i shape parameters, as previously seen, towards zero. This is the ultimate bimodal distribution; full or zero recovery.⁷⁰ While it makes logical sense that our investigation would take us towards this approach, we prefer to avoid its extreme nature. Instead, we opt for neither extreme, but exhibit a bias for the lower end. Our selected recovery volatility for the ith credit obligor is thus defined as,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \sqrt{V_i} = \sqrt{\underline{V_i} + 0.25\cdot\bigg(\overline{V_i} - \underline{V_i}\bigg)}. \end{array} \end{aligned} $$

(3.50)

There is nothing particularly special about the choice of 0.25. It was intended to represent a compromise between the extremes with a preference for slightly more distance from the Bernoulli-trial case. One could, of course, argue for a value of 0.5. Ultimately, the impact on the final parameter values and, by extension, the economic-capital results is rather modest.

The right-hand graphic in Fig. 3.24 illustrates the range of $\sqrt {V_i}$ associated with Eq. 3.50. There is not a dramatic difference in the average outcome—of about 0.3—and the common legacy setting of 0.25. With the exception of an outlier or two, the computed values lie comfortably from about 0.2 to 0.35 with peaks in probability mass around 0.3 and 0.35, respectively.

The shape parameters associated with the approach highlighted in Eq. 3.50 are presented in Fig. 3.25. No individual a _i or b _i value exceeds one or falls below zero. The mean a _i parameter is roughly 0.6, which compares to the fixed-V _i average outcome of 1.3. The b _i parameters exhibit an average of about 0.3, which is less than half of what was observed in the constant-recovery-volatility approach. The bottom line is that the imposition of U-shaped density constraints on our method-of-moments estimator leads to fairly important changes in the associated beta-distribution shape-parameter estimates.

Fig. 3.25

Revised beta-distribution parameters: Using the modified method-of-moments approach from Eq. 3.50, this figure illustrates the mapping of M _i and V _i choices into a collection of the beta distribution’s two shape parameters, a _i and b _i.

Figure 3.26 completes the picture. It provides—analogous to Fig. 3.22 for the constant-recovery-volatility case—an illustration of the entire population of beta densities associated with our U-shaped constrained method-of-moments estimator. The results are visually quite striking. Not only do the mean and exposure-weighted mean densities demonstrate a U-shaped form, every single beta density exhibits the desired bimodal structure. This was accomplished while preserving the mean recovery rate and generating recovery volatility estimates that are generally consistent with the constant $\sqrt {V_i}$ approach. This clearly exemplifies the ability of our constraint set to achieve our targeted beta-density outcomes.

Fig. 3.26

Revised beta densities: This figure plots the entire range of beta densities associated with the (indirectly) assumed shape parameters. For reference, the beta densities associated with the simple-mean and exposure-weighted mean shape parameters are also provided. On average, this approach implies a relatively higher probability of extreme—large loss or recovery—outcomes, which is consistent with empirical evidence surrounding recoveries.

Colour and Commentary 37

(Bimodal Recovery) : Empirical evidence—see, for example, Chen and Wang [ 11 ]—suggests that the recovery rate distribution is bimodal. In plain English, this means there is a disproportionately high probability of extreme (i.e., high or low) outcomes. Practically, the bimodal property enhances model conservatism by increasing the global probability of extremely low levels of default recovery. Bimodal beta densities are mathematically attainable through restriction of the shape (a _i and b _i ) parameters to the unit interval. Incorporating these constraints into the method-of-moments estimator, and using the recovery volatility as a free parameter, permit imposition of a bimodal form. Under this approach, the mean recovery rate is preserved, all beta densities are bimodal, and reasonable recovery volatility estimates are generated. Beyond a desire to meet an empirical stylized fact, however, this is not an economically motivated parametrization; it is a mathematical trick to induce bimodality. The main alternative, a constant and common recovery volatility parameter, provides no logical competition. Absent another clear justification for the choice of recovery volatility, this parameter-estimation technique would thus appear to be a judicious choice.

5 Credit Migration

Incorporation of credit migration into the credit-risk economic capital model necessitates a number of parametric ingredients. The central quantity, the transition matrix, has already been identified and examined in detail. Two additional variables are necessary. The first is a description of the spread implications of moving from one credit state to another. The second requirement is some notion of the sensitivity of individual loan prices to changes in their discount rate. This section will explore how one might estimate both of these important modelling inputs.

5.1 Spread Duration

Let us begin with the easier quantity: the current sensitivity or modified spread-duration assumption. Spread duration is readily available for instruments traded in active secondary markets, but it rather less obviously computed for untraded loans. We thus employ the cash-flow weighted average maturity as a spread-duration proxy for each of our loan obligors. This involves an embedded assumption, which requires some explanation. To help understand our choice, let’s return to first principles. The value of a fixed-income security at time t with yield y and N remaining cash-flows is simply,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} V(y) = \sum_{i=1}^{N} \frac{c_{t_{i}}}{(1+y)^{t_{i}-t}}, \end{array} \end{aligned} $$

(3.51)

where each $c_{t_{i}}$ represents an individual cash-flow. In other words, the value is merely the sum of the discounted individual cash-flows. The yield, y, is the common discount rate for all individual cash-flows that provides the observed valuation.

Equation 3.51 is silent on the credit spread, which complicates computation of spread duration. It is thankfully possible to decompose—for a given underlying tenor—any fixed-income security’s yield into two logical parts: the risk-free yield and its associated credit spread. More concretely, we write:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} y = \hat{y} + s, \end{array} \end{aligned} $$

(3.52)

where $\hat {y}$ and s denote the risk-free yield and credit spread, respectively.⁷¹ This permits us to rewrite the pricing, or valuation, function of an arbitrary loan as,

(3.53)

The advantage of this formulation is that it directly includes the credit (or lending) spread.⁷²

The modified spread-duration is defined as the normalized first derivative of our loan-price relation with respect to the credit spread, s. It is written as,

(3.54)

where the absolute-value operator is introduced because, in practice, we typically treat this as a positive quantity and introduce the negative sign as required by the context. The product of Eq. 3.54 and a given spread perturbation provides an approximation of the percentage return change in one’s loan value. This explains its usefulness for the credit-migration computation.⁷³

While Eq. 3.54 provides a direct, practical description for the first-order, linear, credit-spread sensitivity of a loan, it is not easy for us to employ. For a given loan, it may be difficult to clearly identify the specific credit spread and risk-free rates, which makes the determination of y a rather noisy and uncertain affair. A set of cash-flow forecasts are, however, available for every individual loan based on forward interest rates and actual loan margins. This permits a simple proxy representation of Eq. 3.54. It is conceptually similar and has the following form:

(3.55)

This proxy is simply the cash-flow weighted average tenor. We can see, of course, that our proxy stems from setting y = 0; in this case, Eqs. 3.54 and 3.55 coincide exactly. For any non-negative yield, however, the modified spread duration will be inferior to this weighted average cash-flow proxy. The magnitude of this difference is, in the ongoing low-yield environment, likely to be rather small. One useful characteristic of this proxy choice is that it forms a conservative spread-duration estimator for any (non-negative) loan yield.

Some NIB loan contracts have an interesting, and important, feature that has practical implications for the spread-duration calculations. In particular, various individual loans possess what is contractually referred to as a negotiation date. This future date, typically occurring a few years after disbursement, but a number of years before final maturity, offers both parties an opportunity to revisit the details of the loan. The consequence may involve re-pricing, repayment, or ultimately no change. It basically offers a potential loan reset; as such, it makes sense to consider this negotiation date as the effective maturity date of the loan for spread-duration purposes.

Practically, the presence of a pre-maturity negotiation feature makes very little difference to our sensitivity formula. If, for our generic loan, we define the number of cash-flows associated with the negotiation date as $\tilde {N}\leq N$, then

$$\displaystyle \begin{aligned} \begin{array}{rcl} D_m & =&\displaystyle \frac{1}{V(y)(1+y)}\sum_{i=1}^{\tilde{N}} \frac{(t_i-t) c_{t_{i}}}{(1+y)^{t_{i}-t}},{}\\ & \approx&\displaystyle \left(\sum_{i=1}^{\tilde{N}} c_{t_{i}}\right)^{-1} \sum_{i=1}^{\tilde{N}} (t_i-t) c_{t_{i}}. \end{array} \end{aligned} $$

(3.56)

The structure of the spread-duration approximation is unchanged, it is merely truncated when the negotiation date is inferior to the true maturity date. For those loans without such a feature in their contract—where $N=\tilde {N}$—then no difference in the spread-duration measure is observed.

Colour and Commentary 38

(Spread Duration) : The estimation of credit migration requires, for each individual loan obligation, an estimate of its sensitivity to credit-spread movements. In other words, we require spread-duration estimates. A proxy for modified spread duration is employed that assumes a zero overall yield level. The linear nature of this assumption and the consequent overestimate of sensitivity for any non-negative yield imply that this is a relatively conservative estimator. One additional, firm-specific, adjustment is involved. Many loans involve a negotiation date—typically occurring several years prior to final maturity—that provides both parties the opportunity, in the event of material changes to their position, to revise the contractual details. When such a feature is present, a revised cash-flow stream to this intermediate date is employed. ^a Ultimately, the computation of spread duration is a simple, but data-intensive affair.

^aMore generally, any lending entity engaged in such calculations will need to take into account any important firm-specific contractual details.

5.2 Credit Spreads

Logically, one could imagine the specification of a separate loan-spread value for each credit class and loan. This would quickly become practically unmanageable. Instead, the typical approach is to specify a generic credit-spread level for each of one’s credit categories. Were a loan to migrate from one credit class to another, it would experience an associated change in its category specific credit-spread level with a corresponding valuation effect.

There is a broad range of sources one might use to inform credit spreads: internal lending spreads, observed corporate bond prices, the credit-default swap (CDS) market, and even model-based implied values. Each offers advantages and disadvantages and, unfortunately, there is no one dominant data source. Bond-market information is a useful benchmark for comparative purposes, but these values are computed in an overly broad-based manner. That is, the range of entities within a credit-rating class used to estimate generic bond spreads are surprisingly heterogeneous and not necessarily representative of firm-specific business exposure. For this reason, we argue that internal lending spreads are the most sensible source for determination of credit spreads.

Data alone will not resolve the problem. We also require a theoretical, and economically motivated, approach towards the description of credit spreads. This turns out to a surprisingly deep question. To make progress, one must touch upon a variety of areas: bond pricing, corporate finance, credit-risk models, probability theory, and statistics. The following sections, accepting this challenge, offer a simplified, workable implementation for use in our economic-capital framework.

5.2.1 The Theory

The hazard rate is a central character in the modelling of credit spreads. Loosely speaking, it can be thought of as the default probability over a (very) short time period. Bolstered with this concept, the credit spread of the ith entity—following from Hull and White [23]—can be profitably described by the following identity,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} h_i \approx \frac{\mathbb{S}_i(t,T)}{1-\gamma_i}, \end{array} \end{aligned} $$

(3.57)

where h _i denotes the hazard rate, $\mathbb {S}_i(t,T)$ is the credit spread for the time interval (t, T) and γ _i is the loss-given-default. This expression also plays a central role in fitting hazard-rate functions for the valuation of loan and other credit-risky portfolios.⁷⁴ It also highlights an important, but intuitive, notion: the credit spread depends on one’s assessment of the firm’s creditworthiness and, in the event of default, recovery assumptions.

Equation 3.57 is the key character for an empirical estimation of credit spreads—and indeed it will prove useful in latter discussion for verification purposes—but we seek a theoretical approach. Merton [35] remains, to this day, the seminal theoretical work in the area of credit-risk modelling. It forms the foundation of the entire branch of structural credit-risk models. The key idea is that a default occurs when the value of the firm’s asset dip below their liabilities. Framed in a continuous-time mathematical setting, this logical idea permits derivation of a host of useful relationships for computation of credit-risk-related prices and risk measures. We will lean on it heavily in the following development.

The Merton [35] approach begins by defining the intertemporal dynamics of an arbitrary firm’s assets on the probability space $(\Omega ,\mathcal {F},\mathbb {P})$ as

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \frac{dA_t}{A_t} = \mu dt + \sigma dW_t, \end{array} \end{aligned} $$

(3.58)

where A _t denotes the asset value, while μ and σ represent the expected asset return and volatility, respectively. $\{W_t,\mathcal {F}_t\}$ is a standard, scalar Wiener process on $(\Omega ,\mathcal {F},\mathbb {P})$.⁷⁵ Operationalizing this key idea leads to the second ingredient in our recipe: the default condition. Practically, the default event over (t, T] is written as,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \left\{A_T\leq K\right\}, \end{array} \end{aligned} $$

(3.59)

where K represents the firm’s liabilities. Practically, and this is Merton [35]’s central insight, it occurs when the value of a firm’s assets fall below its liabilities. Succinctly put, default is triggered when equity is exhausted.⁷⁶

With a gratuitous amount of mathematics and some patience, one can describe the probability of default in this structure, over the time interval (t, T], as

(3.60)

where Φ denotes the cumulative distribution function of the standard univariate Gaussian probability law.⁷⁷ The fairly unwieldy ratio in Eq. 3.60—which we have called δ _t(μ)—is a quite famous output from the Merton [35] framework. δ _t is the so-called distance to default. This quantity plays an important role in industrial credit-analytic methodologies.⁷⁸ As the name suggests, distance-to-default is a standardized measure of how far away a firm is from default. It seems quite natural that it would show up in a default-probability definition. Mechanically, the larger the distance to default, the lower the probability of default. It depends, again quite intuitively, on the current value of firm assets (i.e., A _t), the length of the time horizon under consideration (i.e., T − t), the size of the liabilities (K), and the risk and return characteristics of the firm’s assets (i.e., μ and σ).

One of the challenges of using Eq. 3.60 is that determination of asset returns and volatilities can be practically quite challenging. This is because firm assets are not—outside infrequent balance-sheet disclosures—observed with any regularity. Resolving this problem involves turning to firm equity values, which, in contrast to their asset equivalents, are readily and frequently observable. This brings us into the realm of asset pricing and necessitates moving to a new probability measure. More specifically, we need to use the equivalent martingale measure, $\mathbb {Q}$, induced with the choice of money market account as the numeraire asset; this is often termed the risk-neutral measure. This takes us off onto another mathematical foray, but with some persistence we may actually write the risk-neutral default probability as,

(3.61)

where r represents the risk-free interest rate.⁷⁹ Under the $\mathbb {Q}$ measure, by construction, all assets return the risk-free rate. This is a core idea behind risk-neutrality.

What has all this provided? In Eqs. 3.60 and 3.61, we have two alternative default-probability definitions that apply under two different probability measures. Their forms are essentially identical, up to the expected asset returns. Beyond their obvious utility as default-probability estimates, Eqs. 3.60 and 3.61 provide the first step towards a more general credit-spread definition. This begins with understanding that the risk-neutral default probability is also closely related to the credit spread. Both are involved in pricing activities and both depend on the firm’s basic creditworthiness. With a bit of basic algebraic manipulation, we can simplify the risk-neutral default probability in Eq. 3.61 to help us with our objective of creating a sensible credit-spread estimator.

Reorganizing Eq. 3.60, we can identify the following relationship

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} -\ln\left(\frac{A_t}{K}\right) = \Phi^{-1}\bigg(p(t,T)\bigg)\sigma\sqrt{T-t}+ \left(\mu-\frac{\sigma^2}{2}\right)(T-t). \end{array} \end{aligned} $$

(3.62)

If we insert this expression into Eq. 3.61, we may write the risk-neutral default probability as a function of the physical probability of default. The result is,

(3.63)

This is quite elegant. If μ = r, then the two default probability definitions coincide. Since in the face of risk aversion, μ > r, we find ourselves in a situation where risk-neutral default probabilities are systemically greater than physical default likelihoods. A crucial factor in Eq. 3.63 is the $\frac {\mu -r}{\sigma }$ term, which is broadly known as the Sharpe ratio.⁸⁰ The difference between these two default quantities thus basically boils down to a risk-adjusted return ratio.⁸¹

Although this result depends upon the underlying assumption of asset returns, it does have a fairly general applicability. Bluhm et al. [6], who explore this idea in detail, also offer a variety of options to expand and motivate Eq. 3.63. Most of them are related, in one way or another, to the well-known Capital Asset Pricing Model (or CAPM) introduced decades ago by Treynor [43], Sharpe [39, 40] and Lintner [32]. For our purposes, we will examine this in a rather more blunt fashion. In particular, we rewrite Eq. 3.63 as,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} q(t,T) & =&\displaystyle \Phi\left(\Phi^{-1}\bigg(p(t,T)\bigg)+ \lambda \sqrt{T-t}\right), \end{array} \end{aligned} $$

(3.64)

where $\lambda \in \mathbb {R}_+$. This step involves basically rolling the μ, r, and σ values into a single parameter. Capturing each individual quantity in an accurate manner is not a trivial undertaking; a single-parameter approach, as we’ll see soon, turns out to be practical for calibrating credit spreads.

The consequence of the previous development is an economically motivated description of the relationship between physical and risk-neutral default probabilities. Arriving at Eq. 3.64 has touched upon a variety of foundational contributions to the finance literature: Merton [35]’s structural-default model, Black and Scholes [5]’s option-pricing formula, Sharpe [41]’s famous ratio, the market price of risk formulation found the short-rate model literature launched by Vasicek [44], and the omnipresent CAPM model. The next step is to link this definition more closely to the credit spread.

5.2.2 Pricing Credit Risky Instruments

Asset-pricing, in its most formal sense, entails the evaluation of the discounted expected cash-flows associated with a given financial instrument. In a no-arbitrage pricing—see, for example, Harrison and Kreps [20] and Harrison and Pliska [21]—this expectation must be evaluated with respect to the equivalent martingale measure, $\mathbb {Q}$. This may seem to be an excessive amount of financial-economic machinery, but it is important to ensure that the foundations of our proposed method are solid.

Our credit-spread proposal is best understood, in this specific context, using a zero-coupon bond. In the absence of credit risk, one need only discount the one unit of currency pay-off back to the present time. In the presence of a possible firm default, an adjustment is necessary. Let’s denote the cash-flow profile of this instrument as C(t, T). Following from Duffie and Singleton [14, Chapter 5], this can be succinctly described as,

(3.65)

where

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mathbb{I}_{A_T\leq K} = \left\{ \begin{array}{r@{\;:\;}l} 1 & \mbox{Default (i.e., }A_T\leq K\mbox{)} \\ 0 & \mbox{Survival (i.e., }A_T> K\mbox{)}\\ \end{array} \right., \end{array} \end{aligned} $$

(3.66)

and r is the instantaneous short-term interest rate. To simplify things somewhat, we will assume that r is deterministic. As previously discussed, the price of the cash-flows in Eq. 3.65 is simply the expectation under $\mathbb {Q}$. The result is,

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathbb{E}^{\mathbb{Q}}_t\bigg(C(t,T)\bigg) = \hat{P}(t,T) & =&\displaystyle \mathbb{E}^{\mathbb{Q}}_t\left(e^{-\int_{t}^T r du} - \gamma \cdot \mathbb{I}_{A_T\leq K} \cdot e^{-\int_{t}^T r du}\right),{}\qquad \\ & =&\displaystyle e^{-r(T-t)} - \gamma \cdot \mathbb{Q}(A_T\leq K) \cdot e^{-r(T-t)},\\ & =&\displaystyle e^{-r(T-t)}\bigg(1-\gamma \cdot q(t,T)\bigg). \end{array} \end{aligned} $$

(3.67)

If we are willing to assume the reasonableness of the structural Merton [35] model, then we could introduce the definition of q(t, T) from Eqs. 3.61 or 3.64. Using the latter version, we can write the price of a zero-coupon bond as,

(3.68)

This is progress. We have represented the price of an, admittedly simple, credit-risky fixed-income security as a function of its tenor, physical default probability, and loss-given-default values. This is not the typical pricing relationship, but it is both consistent with first principles and well suited to our specific purposes. All that is missing is an explicit connection to the credit spread.

The price of a zero-coupon bond can always be represented as,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \hat{P}(t,T) & =&\displaystyle e^{-y(T-t)}, \end{array} \end{aligned} $$

(3.69)

where y is essentially an unknown that is used to solve for the price. y, of course, is generally termed the bond yield. A common, and powerful, decomposition of the bond yield is,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} y \approx r + \mathbb{S}, \end{array} \end{aligned} $$

(3.70)

where r and $\mathbb {S}$ denote the risk-free rate and credit spread, respectively.⁸² Quite simply, the yield of any fixed-income security can be allocated into two portions: the risk-free, time-value-of-money component and an adjustment for potential default.⁸³

With this decomposition, we are only a few steps from our destination. Combining Eqs. 3.68 to 3.70 and simplifying, we have

(3.71)

The consequence is a defensible expression for the credit spread as a direct function of bond tenor, loss-given-default, physical default probability, and a risk-related tuning parameter, λ. The first three quantities—for a given instrument—can be directly estimated. The tuning parameter, however, needs to be calibrated to current—or average—market conditions.

Equation 3.71 may look somewhat messy; one might worry that it is not completely intuitive. A quick sanity check can help. Let’s set γ = 1 and return to the first line of Eq. 3.71. A bit of manipulation reveals,

(3.72)

where S(t, T) and $\hat {\delta }(t,T)$ are the survival and risky discount functions over (t, T], respectively. Here we see the classical construction of the credit-risky discount curve. We can take comfort that this relationship—only a step or two from our formulation—lies at the heart of modern loan and corporate-bond valuation methodologies.

5.2.3 The Credit-Spread Model

Equation 3.71 offers a succinct, economically plausible analytic link between the credit spread and our key economic-capital model variables: physical default probabilities and loss-given-default values. This functional form offers a path to enhancing the generality and robustness of a firm’s credit-spread estimates. It is not, however, without a few drawbacks. As always, the principal drawbacks of any mathematical model are found in the assumptions. Establishment of Eq. 3.71 involved the following key choices:

• 1. a log-normal distributional assumption (i.e., geometric Brownian-motion dynamics) for the firm’s asset prices;

• 2. use of a simplified zero-coupon bond structure for its construction;

• 3. collapsing the entire market-price of risk, or Sharpe ratio, structure into a single parameter; and

• 4. assumption of a constant risk-free interest rate.

All of these assumptions, with patience and hard work, could potentially be relaxed. The cost, however, would be incremental complexity. We actually desire to move in the opposite direction; that is, introduce more simplicity.

The credit-spread estimates within our credit-risk economic capital model are, by construction, independent of tenor. The principal reason is to manage conceptual and computational complexity. It also helps to keep the results reasonable intuitive and easier to communicate with various stakeholders. For this reason, we propose effectively eliminating the time dimension by setting T − t = 1. We furthermore select a common loss-given-default parameter for all issuers. Let’s call this $\hat {\gamma }$. This permits us to immediately simplify Eq. 3.71 to

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mathbb{S}_i(\hat{\gamma},p_i,\lambda) & =&\displaystyle -\ln\bigg(1-\hat{\gamma} \cdot \Phi\bigg(\Phi^{-1}(p_i)+ \lambda \bigg)\bigg), \end{array} \end{aligned} $$

(3.73)

for the ith credit-spread observations. As a practical matter, we set $\hat {\gamma }=0.45$. This value is close to the historical portfolio average, reasonably conservative, and consistent with regulatory guidance.⁸⁴

The next point is that a single market price of risk parameter, λ, is not sufficiently flexible to fit either the observed internal margin or bond-market data. It can fit either the investment grade or speculative grade credit spreads, but not both. As a consequence, we have elected to make λ a function of the rating class to permit sufficient flexibility to accurately fit the observed data. This can, of course, be accomplished in a number of ways. The simplest would be to assign a separate parameter to each of our 20 distinct notches. Such an approach raises two issues. First, it gives rise to a large number of parameters. Second, it does not constrain the interaction between the credit-rating-related λ values in any way. Economically, for example, we would anticipate reasonably smooth risk-preference movements across the credit scale.

Our solution is to construct the following non-linear market price of risk function:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \lambda(p_i) = \varsigma_0 + \varsigma_1 p_i + \varsigma_2 p_i^2. \end{array} \end{aligned} $$

(3.74)

Other choices are certainly possible, but this form is parsimonious and provides a reasonable degree of smoothness. The non-linearity does not play a central role, but appears to add a bit of additional flexibility to the overall fit.

Equation 3.74 permits us to restate our credit-spread representation in its final form as

(3.75)

for i = 1, …, K internal credit-margin observations in our dataset. If we use $\mathbb {S}_i$ to denote the ith observed credit-margin value, then our three ς parameters can be estimated by solving the following optimization problem:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \min_{\varsigma_0,\varsigma_1,\varsigma_2} \sum_{i=1}^K \bigg(\mathbb{S}_i - \mathbb{S}_i\bigg(\hat{\gamma},p_i,\varsigma_0,\varsigma_1,\varsigma_2\bigg)\bigg)^2. \end{array} \end{aligned} $$

(3.76)

The least-squares or $\mathcal {L}_2$ objective function was selected for its mathematical advantages.

As a final practical (and technical) matter, the problem can be solved in the raw form presented in Eq. 3.76 or the squared differences can be weighted by the position sizes. The discrepancy between the two approaches is not particularly large, but we adopt the weighted estimator to lend a bit more importance to the larger disbursements. This necessitates a small change to the optimization problem in Eq. 3.76. To accommodate this, we denote $\vec {\mathbb {S}}\in \mathbb {R}^{K\times 1}$ as the column vector of observed and estimated spread deviations as

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \vec{\mathbb{S}} = \begin{bmatrix} \mathbb{S}_1 - \mathbb{S}_1\bigg(\hat{\gamma},p_1,\varsigma_0,\varsigma_1,\varsigma_2\bigg)\\ \mathbb{S}_2 - \mathbb{S}_2\bigg(\hat{\gamma},p_2,\varsigma_0,\varsigma_1,\varsigma_2\bigg)\\ \vdots \\ \mathbb{S}_K - \mathbb{S}_K\bigg(\hat{\gamma},p_K,\varsigma_0,\varsigma_1,\varsigma_2\bigg)\\ \end{bmatrix} \end{array} \end{aligned} $$

(3.77)

and introduce $W\in \mathbb {R}^{K\times K}$ as a diagonal matrix of loan exposures with the following form:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} W = \begin{bmatrix} c_1 & 0 &\displaystyle \cdots &\displaystyle 0\\ 0 & c_2 &\displaystyle \cdots &\displaystyle 0\\ \vdots & \vdots &\displaystyle \ddots &\displaystyle \vdots\\ 0 & 0 &\displaystyle \cdots &\displaystyle c_K \end{bmatrix}, \end{array} \end{aligned} $$

(3.78)

where c _i represents the exposure of the ith lending position. Using these two components, our revised optimization problem becomes:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \min_{\varsigma_0,\varsigma_1,\varsigma_2} \vec{\mathbb{S}}^T W \vec{\mathbb{S}}. \end{array} \end{aligned} $$

(3.79)

The only difference with this latter representation—beyond the introduction of matrix notation—is that smaller loans play a slightly less important role in the final estimates than their larger equivalents.

5.2.4 Credit-Spread Estimation

The credit spread incorporates four key elements: the nature of the default event, an assessment of the entity’s default probability, the magnitude of loss given default, and an approximation of general risk preferences. Our methodology incorporates all four pieces. First, it leans on the structural default definition that colours much of modern financial literature and practical applications. Non-coincidentally, it also sits at the heart of our economic-capital framework. Second, it employs the same default probabilities found in the final column of our transition matrix. Third, it makes a generic assumption for the loss-given-default of all counterparties.⁸⁵ Finally, the actual credit-spread calibration occurs through the risk-preference parameters.

It is rather difficult, given the high sensitivity of internal credit spread data, to provide any significant degree of transparency regarding the actual parameter-selection process. As a consequence, we will focus principally on the final results. A few global comments are, however, entirely possible. First of all, consistent with the long-term through-the-cycle approach, the internal margin dataset spans the last two decades. A second point is that, in accordance with lending mandate and policies, it is rather skewed towards the investment and high-quality speculative grades. Since credit-risk estimates are necessary for the entire range of credit-rating classes, this precludes a simply curve-fitting approach to the problem.⁸⁶ This underscores the value of an economically motivated approach.

Figure 3.27 provides the resulting credit spreads associated our approach. The credit spread increases in a monotonic fashion from roughly 40 basis points at the highest level of credit quality to approximately 10% at the lower end of the scale. Reassuringly, broad-based bond-spread averages—collected over the same period as the internal spread data—are qualitatively similar to the final results.

Fig. 3.27

Credit-spread estimates: This graphic illustrates the estimated credit spreads, organized by credit-risk rating, stemming from the previously described methodology. Corporate bond spreads, where available, are included for comparison purposes.

Circling back to Eq. 3.57, an additional sanity check on our spread estimates is also possible. Following our characterization of the hazard rate in Eq. 3.57—also offered by Hull et al. [24]—a quick, but meaningful, approximation of the risk-neutral probability is given as

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathcal{Q}_i & =&\displaystyle \mathbb{Q}(\tau\leq T),{}\\ & \approx&\displaystyle 1-\mathbb{Q}(\tau>T),\\ & \approx&\displaystyle 1-e^{-h_i}, \end{array} \end{aligned} $$

(3.80)

where, in this example, T − t = 1 and τ denotes the default event. Taking this a step further, actual and risk-neutral default probabilities are linked—see, for example, Jarrow [25] for more detail—by the following identity:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mathcal{Q}_i = \vartheta_i \mathcal{P}_i, \end{array} \end{aligned} $$

(3.81)

where 𝜗 _i > 0 is yet another representation of the risk premium. Less accurate (and formal) than the Sharpe ratio structure found in Eq. 3.63, it nonetheless captures the distance between the physical and risk-neutral default probabilities. This (model-independent) form is often used in empirical academic studies. Equation 3.81 further suggests that if we compute the physical and risk-neutral probabilities, their ratio will provide some insight into the level of the risk premium (i.e., $\vartheta _i = \frac {\mathcal {Q}_i}{\mathcal {P}_i}$).

All we need are the risk-neutral default probabilities. Incorporating our estimated spreads into Eq. 3.80 provides the solution. Embedded, quite naturally, in our economically motivated credit-spread methodology are both flavours of default probability. From Eq. 3.57, we have that

(3.82)

for i = 1, …, q. This provides all of the necessary ingredients to calculate the inferred risk premium.

Figure 3.28 summarizes the results. The left-hand graphic explicitly compares the physical—extracted from the final column of our transition matrix—and the implied risk-neutral default probabilities. In all cases, the risk-neutral values dominate the physical default probabilities; the magnitude of the dominance, however, decreases as we move out the credit spectrum. The right-hand figure displays the ratio of these two default probabilities—in this manner, we may infer the risk premium. The average value—across all credit classes—is approximately 17 units. At the short end, however, it approaches 100 and it falls to less than 2 for credit category 20.

Fig. 3.28

A point of comparison: This figure examines the implied risk-neutral default probabilities and inferred risk premia associated with the estimated internal-margin-based credit-spreads. The results are broadly consistent with empirical evidence in this area.

A number of empirical studies examine this relationship. Heynerickx et al. [22] is a good example. This work performs a rather involved study using a broad range of credit classes and tenors over the period from 2004–2014. Referring to the risk premium as the coverage ratio, they present a similar pattern to that found in Fig. 3.28. Over the entire period, for example, risk premia range from more than 200 for AAA issuers to roughly 2 for CCC entities.⁸⁷ In the post-crisis period, however, the general levels are somewhat lower, although the basic shape remains consistent. In this framework, the general form of our results appears to be consistent with this (and other) empirical work.

Colour and Commentary 39

(Credit-Spread Estimation) : Estimation of long-term, through-the-cycle, unconditional credit spread levels is, under any circumstances, a serious undertaking. Closely linked to macroeconomic conditions and the vagaries of financial markets, credit spreads are observably volatile over time. Broad-based credit indices, observed bonds spreads, and credit-default swap contracts can provide insight into credit spread levels. The specificity of one’s lending activities and pricing policies nonetheless renders it difficult to make direct use of these values. We present an economically motivated approach that uses one’s history of internal lending margins. While the actual implementation is relatively straightforward, the underpinnings of the model take us on a whirlwind tour of central theoretical finance results over the last four or five decades. An interesting, and useful, sanity check on the final results involves direct comparison of the physical default probabilities from our transition matrix with the risk-neutral equivalents implied by our credit-spread estimates. In this regard, the final results appear to be broadly consistent with extant empirical evidence.

6 Wrapping Up

This long and detailed chapter focuses on the specific choices one needs to take in determining the parametric structure of a large-scale credit-risk economic capital model. There is no shortage of moving parts. Table 3.13 tries to help manage all of this complexity by summarizing the key decisions; these are the main settings of our control panel.

Table 3.13 Parametric fact sheet: The underlying table provides, at a glance, a summary of the key methodological choices associated with our credit-risk economic-capital model.

When combined with Chap. 2, a fairly complete and practical credit-risk model view should be emerging. The remaining missing point—before we can turn our attention to a collection of interesting and helpful applications—relates to the actual implementation. With some models, such questions are not terribly interesting; many possible approaches are possible and can be considered broadly equivalent. In this case, the combination of simulation methods with even a moderately sized portfolio imply the need to think hard about questions of model implementation. Industrial economic capital, along with many related applications, is required on a daily basis to properly manage our portfolios; as a consequence, computational speed matters. One also needs a plan to organize and build the factory performing these ongoing calculations.