Sublabel-Accurate Multilabeling Meets Product Label Spaces

Abstract

Functional lifting methods are a promising approach to determine optimal or near-optimal solutions to difficult nonconvex variational problems. Yet, they come with increased memory demands, limiting their practicability. To overcome this drawback, this paper presents a combination of two approaches designed to make liftings more scalable, namely product-space relaxations and sublabel-accurate discretizations. Our main contribution is a simple way to solve the resulting semi-infinite optimization problem with a sampling strategy. We show that despite its simplicity, our approach significantly outperforms baseline methods, in the sense that it finds solutions with lower energies given the same amount of memory. We demonstrate our empirical findings on the nonconvex optical flow and manifold-valued denoising problems.

1 Introduction

Many tasks in imaging and low-level computer vision can be transparently modeled as a variational problem. In practice, the resulting energy functionals are often nonconvex, for example due to data terms based on image-matching costs or manifold-valued constraints. The goal of this work is to develop a convex optimization approach to total variation-regularized problems of the form

$$\begin{aligned} \inf _{ u : \varOmega \rightarrow \varGamma } ~ \int _{\varOmega } c(x, u_1(x), \ldots , u_k(x)) \, \mathrm {d}x + \sum _{i=1}^k \lambda _i \text {TV}(u_i). \end{aligned}$$

(1)

Here, $\varGamma = \{ (\gamma _1, \ldots , \gamma _k) \in \mathbf {R}^N : \gamma _i \in \varGamma _i, i=1\ldots k \}$ is based on compact, embedded manifolds $\varGamma _i \subset \mathbf {R}^{N_i}$ with $N = N_1 + \ldots + N_k$. Throughout this paper we only consider imaging applications and pick $\varOmega \subset \mathbf {R}^2$ to be a rectangular image domain. The cost function $c : \varOmega \times \varGamma \rightarrow \mathbf {R}_{\ge 0}$ in (1) can be a general nonconvex function. Notably, we only assume that we can evaluate the cost function c(x, u(x)) but no gradient information or projection operators are available. This allows us to consider degenerate costs that are out of reach for gradient-based approaches.

As a regularization term in (1) we consider a simple separable total variation regularization $\text {TV}(u_i)$ on the individual components $u_i : \varOmega \rightarrow \mathbf {R}^{N_i}$ weighted by a tunable hyper-parameter $\lambda _i > 0$. The total variation (TV) encourages a spatially smooth but edge-preserving solution. It is defined as

$$\begin{aligned} \text {TV}(u_i) := \sup _{\begin{array}{c} p : \varOmega \rightarrow \mathbf {R}^{N_i \times 2}\\ \Vert p(x) \Vert _* \le 1 \end{array}} \int _{\varOmega } \langle {{\,\mathrm{Div}\,}}_x p(x), u_i(x) \rangle \, \mathrm {d}x = \int _{\varOmega } \Vert \nabla u_i(x) \Vert \, \mathrm {d}x, \end{aligned}$$

(2)

where the last equality holds for sufficiently smooth $u_i$. We denote by $\nabla u_i(x) \in \mathbf {R}^{N_i \times 2}$ the Jacobian matrix in the Euclidean sense and by $\Vert \cdot \Vert _*$ the dual norm. Since our focus is on the data cost c, we consider only this separable TV case.

Problems of the form (1) find applications in low-level vision and signal processing. An example is the optical flow estimation between two RGB images $I_1, I_2 : \varOmega \rightarrow \mathbf {R}^3$, where $\varGamma _1 = \varGamma _2 = [a, b] \subset \mathbf {R}$ are intervals and the cost function is given by $c(x, u_1(x), u_2(x)) = | I_1(x + (u_1(x), u_2(x))) - I_2(x) |$. In many applications, $\varGamma _i$ is a curved manifold, see [24, 37]. Examples include $\varGamma _i = \mathbb {S}^2$ in the case of normal field processing [24], $\text {SO}(3)$ in the case of motion estimation [16] or the circle $\mathbb {S}^1$ for processing of cyclic data [11, 33].

As one often wishes to estimate multiple quantities in a joint fashion, one naturally arrives at the product space formulation as considered in (1). A popular approach to address such joint optimization problems are expectation maximization procedures [12] or block-coordinate descent and alternating direction-type methods [6], where one estimates a single quantity while holding the other ones fixed. Sometimes, such approaches depend on a good initialization and can be prone to getting stuck in bad local minima. Our goal is to devise a convex relaxation of Problem (1) that can be directly solved to global optimality with standard proximal methods (possibly implemented on GPUs) such as the primal dual algorithm [29]. To achieve this, we offer the following contributions:

• To tackle relaxations of (1) in a memory-efficient manner, we propose a sublabel-accurate implementation of the product-space lifting [15]. This implementation is enabled by building on ideas from [26], which views sublabel-accurate multilabeling as a finite-element discretization.

• Our main contribution presented in Sect. 4 is a simple way to implement the resulting optimization problem with a sampling strategy. Unlike previous liftings [25, 26, 36], our approach does not require epigraphical projections and can therefore be applied in a black-box fashion to any cost c(x, u(x)).

• We show that our sublabel-accurate implementation attains a lower energy than the product-space lifting [15] on optical flow estimation and manifold-valued denoising problems.

The following Sect. 2 is aimed to provide an introduction to relaxation methods for (1) while also reviewing existing works and our contributions relative to them. We present the relaxation for (1) and its discretization in Sect. 3. In Sect. 4, we show how to implement the discretized relaxation with the proposed sampling strategy. Section 5 presents numerical results on optical flow and manifold-valued denoising and our conclusions are drawn in Sect. 6.

2 Related Work: Convex Relaxation Methods

Let us first consider a simplified version of problem (1) where $\varOmega$ consists only of a single point, i.e., the nonconvex minimization of one data term:

$$\begin{aligned} \min _{\gamma \in \varGamma } ~ c(\gamma _1, \ldots , \gamma _k). \end{aligned}$$

(3)

A well-known approach to the global optimization of (3) is a lifting or stochastic relaxation procedure, which has been considered in diverse fields such as polynomial optimization [19], continuous Markov random fields [3, 13, 28], variational methods [30], and black-box optimization [5, 27, 32]. The idea is to relax the search space in (3) from $\gamma \in \varGamma$ to probability distributions¹ $\mathbf {u}\in \mathcal {P}(\varGamma )$ and solve

$$\begin{aligned} \min _{\mathbf {u}\in \mathcal {P}(\varGamma )} \int _{\varGamma } c(\gamma _1, \ldots , \gamma _k) \, \mathrm {d}\mathbf {u}(\gamma _1, \ldots , \gamma _k). \end{aligned}$$

(4)

Due to linearity of the integral wrt. $\mathbf {u}$ and convexity of the relaxed search space, this is a convex problem for any c. Moreover, the minimizers of (4) concentrate at the optima of c and can hence be identified with solutions to (3). If $\varGamma$ is a continuum, this problem is infinite-dimensional and therefore challenging.

Discrete/Traditional Multilabeling. In the context of Markov random fields [17, 18] and multilabel optimization [9, 21, 22, 39] one typically discretizes $\varGamma$ into a finite set of points (called the labels) $\varGamma = \{ \mathbf {v}_1, \ldots , \mathbf {v}_{\ell } \}$. This turns (4) into a finite-dimensional linear program $\min _{\mathbf {u}\in \varDelta ^\ell }\,\langle c', \mathbf {u} \rangle$ where $c' \in \mathbf {R}^\ell$ denotes the label cost and $\varDelta ^\ell \subset \mathbf {R}^\ell$ is the $(\ell -1)$-dimensional unit simplex.. If we evaluate the cost at the labels, this program upper bounds the continuous problem (3), since instead of all possible solutions, one considers a restricted subset determined by the labels. Since the solution will be attained at one of the labels, typically a fine meshing is needed. Similar to black-box and zero-order optimization methods, this strategy suffers from the curse of dimensionality. When each $\varGamma _i$ is discretized into $\ell$ labels, the overall number is $\ell ^k$ which quickly becomes intractable since many labels are required for a smooth solution. Additionally, for pairwise or regularizing terms, often a large number of dual constraints has to be implemented. In that context, the work [23] considers a constraint pruning strategy as an offline-preprocessing.

Sublabel-Accurate Multilabeling. The discrete-continuous MRF [13, 38, 40] and lifting methods [20, 25, 26] attempt to find a more label-efficient convex formulation. These approaches can be understood through duality [13, 26]. Applied to (3), the idea is to replace the cost $c : \varGamma \rightarrow \mathbf {R}$ with a dual variable $\mathbf {q}: \varGamma \rightarrow \mathbf {R}$:

$$\begin{aligned} \min _{\mathbf {u}\in \mathcal {P}(\varGamma )} \sup _{\mathbf {q}: \varGamma \rightarrow \mathbf {R}} ~ \int _{\varGamma } \mathbf {q}(\gamma _1, \ldots , \gamma _k) \, \mathrm {d}\mathbf {u}(\gamma _1, \ldots , \gamma _k), \, \text {s.t.} ~\mathbf {q}(\gamma ) \le c(\gamma ) ~\forall \gamma \in \varGamma . \end{aligned}$$

(5)

The inner supremum in the formulation (5) maximizes the lower-bound $\mathbf {q}$ and if the dual variable is sufficiently expressive, this problem is equivalent to (4).

Approximating $\mathbf {q}$, for example with piecewise linear functions on $\varGamma$, one arrives at a lower-bound to the nonconvex problem (3). It has been observed in a recent series of works [20, 25, 26, 36, 40] that piecewise linear dual variables can lead to smooth solutions even when $\mathbf {q}$ (and therefore also $\mathbf {u}$) is defined on a rather coarse mesh. As remarked in [13, 20, 25], for an affine dual variable this strategy corresponds to minimizing the convex envelope of the cost, $\min _{\gamma \in \varGamma } c^{**}(\gamma )$, where $c^{**}$ denotes the Fenchel biconjugate of c.

The implementation of the constraints in (5) can be challenging even in the case of piecewise-linear $\mathbf {q}$. This is partly due to the fact that the problem (5) is a semi-infinite optimization problem [4], i.e., an optimization problem with infinitely many constraints. The works [25, 40] implement the constraints via projections onto the epigraph of the (restricted) conjugate function of the cost within a proximal optimization framework. Such projections are only available in closed form for some choices of c and expensive to compute if the dimension is larger than one [20]. This limits the applicability in a “plug-and-play” fashion.

Product-Space Liftings. The product-space lifting approach [15] attempts to overcome the aforementioned exponential memory requirements of labeling methods in an orthogonal way to the sublabel-based methods. The main idea is to exploit the product-space structure in (1) and optimize over k marginal distributions of the probability measure $\mathbf {u}\in \mathcal {P}(\varGamma )$, which we denote by $\mathbf {u}_i \in \mathcal {P}(\varGamma _i)$. Applying [15] to the single data term (3) one arrives at the following relaxation:

$$\begin{aligned} \min _{ \{ \mathbf {u}_i \in \mathcal {P}(\varGamma _i) \} } \sup _{ \{ \mathbf {q}_i : \varGamma _i \rightarrow \mathbf {R}\}} \sum _{i=1}^k \int _{\varGamma _i} \mathbf {q}_i(\gamma ) \, \mathrm {d}\mathbf {u}_i(\gamma ) ~ \text { s.t. } \sum _{i=1}^k \mathbf {q}_i(\gamma ) \le c(\gamma ) ~ \forall \gamma \in \varGamma . \end{aligned}$$

(6)

Since one only has to discretize the individual $\varGamma _i$ this substantially reduces the memory requirements from $\mathcal {O}(\ell ^N)$ to $\mathcal {O}(\sum _{i=1}^k \ell ^{N_i})$. While at first glance it seems that the curse of dimensionality is lifted, the difficulties are moved to the dual, where we still have a large (or even infinite) number of constraints. A global implementation of the constraints with Lagrange multipliers as proposed in [15] again leads to the same exponential dependancy on the dimension.

As a side note, readers familiar with optimal transport may notice that the supremum in (6) is a multi-marginal transportation problem [8, 35] with transportation cost c. This view is mentioned in [1] where relaxations of form (6) are analyzed under submodularity assumptions.

In summary, the sublabel-accurate lifting methods, discrete-continuous MRFs [25, 40] and product-space liftings [15] all share a common difficulty: implementation of an exponential or even infinite number of constraints on the dual variables.

Summary of Contribution. Our main contribution is a simple way to implement the dual constraints in an online fashion with a random sampling strategy which we present in Sect. 4. This allows a black-box implementation, which only requires an evaluation of the cost c and no epigraphical projection operations as in [25, 40]. Moreover, the sampling approach allows us to propose and implement a sublabel-accurate variant of the product-space relaxation [15] which we describe in the following section.

3 Product-Space Relaxation

Our starting point is the convex relaxation of (1) presented in [15, 34]. In these works, $\varGamma _i \subset \mathbf {R}$ is chosen to be an interval. Following [36] we consider a generalization to manifolds $\varGamma _i \subset \mathbf {R}^{N_i}$ which leads us to the following relaxation:

$$\begin{aligned} \min _{ \{ \mathbf {u}_i : \varOmega \rightarrow \mathcal {P}(\varGamma _i) \} }&\sup _{ \begin{array}{c} \{ \mathbf {q}_i : \varOmega \times \varGamma _i \rightarrow \mathbf {R}\} \\ \{ \mathbf {p}_i : \varOmega \times \varGamma _i \rightarrow \mathbf {R}^2 \} \end{array} } \sum _{i=1}^k \int _{\varOmega } \int _{\varGamma _i} \mathbf {q}_i(x, \gamma _i) - {{\,\mathrm{Div}\,}}_x \mathbf {p}_i(x, \gamma _i) \, \, \mathrm {d}\mathbf {u}_{i}^x(\gamma ) \, \mathrm {d}x, \end{aligned}$$

(7)

$$\begin{aligned} \text {s.t. } ~~&\Vert P_{T_{\gamma _i}}\nabla _{\gamma _i} \mathbf {p}_i(x, \gamma _i) \Vert _* \le \lambda _i, \text { for all } 1\le i \le k, ~ (x, \gamma _i) \in \varOmega \times \varGamma _i, \end{aligned}$$

(8)

$$\begin{aligned}&\sum _{i=1}^k \mathbf {q}_i(x, \gamma _i) \le c(x, \gamma ), \text { for all } (x, \gamma ) \in \varOmega \times \varGamma . \end{aligned}$$

(9)

This cost function appears similar to (6) explained in the previous section, but with two differences. First, we now have marginal distributions $\mathbf {u}_i(x)$ for every $x \in \varOmega$ since we do not consider only a single data term anymore. The notation $\, \mathrm {d}\mathbf {u}_i^x$ in (7) denotes the integration against the probability measure $\mathbf {u}_i(x) \in \mathcal {P}(\varGamma _i)$. The variables $\mathbf {q}_i$ play the same role as in (6) and lower-bound the cost under constraint (9). The second difference is the introduction of additional dual variables $\mathbf {p}_i$ and the term $-{{\,\mathrm{Div}\,}}_x \mathbf {p}_i$ in (7). Together with the constraint (8), this can be shown to implement the total variation regularization [24, 36]. Following [36], the derivative $\nabla _{\gamma _i} \mathbf {p}_i(x, \gamma _i)$ in (8) denotes the $(N_i \times 2)$-dimensional Jacobian considered in the Euclidean sense and $P_{T_{\gamma _i}}$ the projection onto the tangent space of $\varGamma _i$ at the point $\gamma _i$. Next, we describe a finite-element discretization of (7).

3.1 Finite-Element Discretization

We approximate the infinite-dimensional problem (7) by restricting $\mathbf {u}_i$, $\mathbf {p}_i$ and $\mathbf {q}_i$ to be piecewise functions on a discrete meshing of $\varOmega \times \varGamma _i$. The considered discretization is a standard finite-element approach and largely follows [36]. Unlike the forward-differences considered in [36] we use lowest-order Raviart-Thomas elements (see, e.g., [7, Section 5]) in $\varOmega$, which are specifically tailored towards the considered total variation regularization.

Discrete Mesh. We approximate each $d_i$-dimensional manifold $\varGamma _i \subset \mathbf {R}^{N_i}$ with a simplicial manifold $\varGamma _i^h$, given by the union of a collection of $d_i$-dimensional simplices $\mathcal {T}_{i}$. We denote the number of vertices (“labels”) in the triangulation of $\varGamma _i$ as $\ell _i$. The set of labels is denoted by $\mathcal {L}_i = \{ \mathbf {v}_{i,1}, \ldots , \mathbf {v}_{i,\ell _i} \}$. As assumed, $\varOmega \subset \mathbf {R}^2$ is a rectangle which we split into a set of faces $\mathcal {F}$ of edge-length $h_x$ with edge set $\mathcal {E}$. The number of faces and edges are denoted by $F = |\mathcal {F}|$, $E = |\mathcal {E}|$.

Data Term and the $\mathbf {u}_i$, $\mathbf {q}_i$ Variables. We assume the cost $c : \varOmega \times \varGamma \rightarrow \mathbf {R}_{\ge 0}$ is constant in $x \in \varOmega$ on each face and denote its value as $c(x(f), \gamma )$ for $f \in \mathcal {F}$, where $x(f) \in \varOmega$ denotes the midpoint of the face f. Similarly, we also assume the variables $\mathbf {u}_i$ and $\mathbf {q}_i$ to be constant in $x \in \varOmega$ on each face but continuous piecewise linear functions in $\gamma _i$. They are represented by coefficient functions $\mathbf {u}_i^h, \mathbf {q}_i^h \in \mathbf {R}^{F \cdot \ell _i}$, i.e., we specify the values on the labels and linearly interpolate inbetween. This is done by the interpolation operator $\mathbf {W}_{i, f, \gamma _i} : \mathbf {R}^{F \cdot \ell _i} \rightarrow \mathbf {R}$ which given an index $1 \le i \le k$, face f, and (continuous) label position $\gamma _i \in \varGamma _i$ computes the function value: $\mathbf {W}_{i, f, \gamma _i} \mathbf {u}_i^h = \mathbf {u}_i(x(f), \gamma _i)$. Note that after discretization, $\mathbf {u}_i$ is only defined on $\varGamma _i^h$ but we can uniquely associate to each $\gamma _i \in \varGamma _i^h$ a point on $\varGamma _i$.

Divergence and $\mathbf {p}_i$ variables. Our variable $\mathbf {p}_i$ is represented by coefficients $\mathbf {p}_i^h \in \mathbf {R}^{E \cdot \ell _i}$ which live on the edges in $\varOmega$ and the labels in $\varGamma _i$. The vector $\mathbf {p}_i(x, \gamma _i) \in \mathbf {R}^2$ is obtained by linearly interpolating the coefficients on the vertical and horizontal edges of the face and using the interpolated coefficients to evaluate the piecewise-linear function on $\varGamma _i^h$. Under this approximation, the discrete divergence ${{\,\mathrm{Div}\,}}_x^h : \mathbf {R}^{E \cdot \ell _i} \rightarrow \mathbf {R}^{F \cdot \ell _i}$ is given by $({{\,\mathrm{Div}\,}}_x^h \mathbf {p}_i^h)(f) = \left( \mathbf {p}_i^h(e_r) + \mathbf {p}_i^h(e_t) - \mathbf {p}_i^h(e_l) - \mathbf {p}_i^h(e_b) \right) / h_x$ where $e_r, e_t, e_l, e_b$ are the right, top, left and bottom edges of f, respectively.

Total Variation Constraint. Computing the operator $P_{T_{\gamma _i}} \nabla _{\gamma _i}$ is largely inspired by [36, Section 2.2]. It is implemented by a linear map $\mathbf {D}_{i, f, \alpha , t} : \mathbf {R}^{E \cdot \ell _i} \rightarrow \mathbf {R}^{d_i \times 2}$. Here, $f \in \mathcal {F}$ and $\alpha \in [0,1]^2$ correspond to a point $x \in \varOmega$ while $t \in \mathcal {T}_i$ is the simplex containing the point corresponding to $\gamma _i \in \varGamma _i$. First, the operator computes coefficients in $\mathbf {R}^{\ell _i}$ of two piecewise-linear functions on the manifold by linearly interpolating the values on the edges based on the face index $f \in \mathcal {F}$ and $\alpha \in [0,1]^2$. For each function, the derivative in simplex $t \in \mathcal {T}_i$ on the triangulated manifold is given by the gradient of an affine extension. Projecting the resulting vector into the $d_i$-dimensional tangent space for both functions leads to a $d_i \times 2$-matrix which approximates $P_{T_{\gamma _i}} \nabla _{\gamma _i} \mathbf {p}_i(x, \gamma _i)$.

Final Discretized Problem. Plugging our discretized $\mathbf {u}_i$, $\mathbf {q}_i$, $\mathbf {p}_i$ into (7), we arrive at the following finite-dimensional optimization problem:

$$\begin{aligned} \min _{\{\mathbf {u}_i^h \in \mathbf {R}^{F \cdot \ell _i} \}}&\max _{\begin{array}{c} \{\mathbf {p}_i^h \in \mathbf {R}^{E \cdot \ell _i} \},\\ \{\mathbf {q}_i^h \in \mathbf {R}^{F \cdot \ell _i} \} \end{array}} h_x^2 \cdot \sum _{i=1}^k \langle \mathbf {u}_i^h, \mathbf {q}_i^h - {{\,\mathrm{Div}\,}}_x^h \mathbf {p}_i^h \rangle + \sum _{f \in \mathcal {F}} \mathbf {i}\{\mathbf {u}_i^h(f) \in \varDelta ^{\ell _i}\}, \end{aligned}$$

(10)

$$\begin{aligned} \text {s.t. } ~~&\Vert \mathbf {D}_{i, f, \alpha , t} \mathbf {p}_i^h \Vert _* \le \lambda _i, ~ \forall 1 \le i \le k, f \in \mathcal {F}, \alpha \in \{ 0, 1 \}^2, t \in \mathcal {T}_i, ~ \end{aligned}$$

(11)

$$\begin{aligned}&\sum _{i=1}^k \mathbf {W}_{i, f, \gamma _i}\mathbf {q}_i^h \le c \left( x(f), \gamma \right) , ~ \forall f \in \mathcal {F}, \gamma \in \varGamma , \end{aligned}$$

(12)

where $\mathbf {i}\{\cdot \}$ is the indicator function. In our applications, we found it sufficient to enforce the constraint (11) at the corners of each face which corresponds to choosing $\alpha \in \{ 0, 1 \}^2$. Apart from the infinitely many constraints in (12), this is a finite-dimensional convex-concave saddle-point problem.

3.2 Solution Recovery

Before presenting in the next section our proposed way to implement the constraints (12), we briefly discuss how a primal solution $\{ \mathbf {u}_i^h \}$ of the above problem is turned into an approximate solution to (1). To that end, we follow [24, 36] and compute the Riemannian center of mass via an iteration $\tau =1,\dots ,T$:

$$\begin{aligned} V^\tau _{j} = \log _{u_i^\tau }(\mathbf {v}_{i,j}), ~~ v^\tau = \sum _{j=1}^{\ell _i} ~ \mathbf {u}_i^h(f, j) V^\tau _j, ~~ u_i^{\tau +1} = \exp _{u_i^\tau }(v^\tau ). \end{aligned}$$

(13)

Here, $u_i^0 \in \varGamma _i$ is initialized by the label with the highest probability according to $\mathbf {u}_i^h(f, \cdot )$. $\log _{u_i^\tau }$ and $\exp _{u_i^\tau }$ denote the logarithmic and exponential mapping between $\varGamma _i^h$ and it’s tangent space at $u_i^\tau \in \varGamma _i$, which are both available in closed-form for the manifolds we consider here. In our case $T=20$ was enough to reach convergence. For flat manifolds, $T=1$ is enough, as both mappings boil down to the identity and (13) computes a weighted Euclidean mean.

In general, there is no theory which shows that $u^T(x)=(u_1^T(x), \ldots , u_k^T(x))$ from (13) is a global minimizer of (1). Tightness of the relaxation in the special case $k = 1$ and $\varGamma \subset \mathbf {R}$ is shown in [31]. For higher dimensional $\varGamma$, the tightness of related relaxations is ongoing research; see [14] for results on the Dirichlet energy. By computing a-posteriori optimality gaps, solutions of (7) were shown to be typically near the global optimum of the problem (1); see, e.g., [15].

4 Implementation of the Constraints

Though the optimization variables in (10) are finite-dimensional, the energy is still difficult to optimize because of the infinite constraints in (12).

Before we present our approach, let us first describe what we refer to as the baseline method in the rest of this paper. For the baseline approach, we consider the direct solution of (10) where we implemented the constraints only at the label/discretization points $\mathcal {L}_1 \times \ldots \times \mathcal {L}_k$ via Lagrange multipliers. This strategy is also employed by the (global variant) of the product-space approach [15].

We aim for a framework that allows for solving a better approximation of (12) than the above baseline while being of similar memory complexity. To achieve this, our algorithm alternates the following two steps in an iterative way.

1) Sampling. Based on the current solution we prune previously considered but feasible constraints and sample a new subset of the infinite constraints in (12). From all current sampled constraints, we consider the most violated constraints for each face, add one sample at the current solution and discard the rest.

2) Solving the subsampled problem. Considering the current finite subset of constraints, we solve problem (10) using a primal-dual algorithm.

These two phases are performed alternatingly, with the aim to eventually approach the solution of the continuous problem (10). The details of our constraint sampling strategy are shown in Algorithm 1. For each face in $\mathcal {F}$, the algorithm generates a finite set of “sublabels” $\mathcal {S}_f \subset \varGamma$ at which we implement the constraints (12). In the following, we provide the motivation behind each line in the algorithm.

Random Uniform Sampling (Line 1). To have a global view of the cost function, we consider a uniform sampling on the label space $\varGamma$. The parameter $n > 0$ determines the number of the samples for each face.

Local Perturbation Around the Mean (Line 2). Besides the global information, we apply local perturbation around the current solution u. In case the current solution is close to the optimal one, this strategy allows us to refine it with these samples. The parameter $\delta > 0$ determines the size of the local neighbourhood. In experiments, we always used a Gaussian perturbation with $\delta =0.1$.

Pruning Strategy (Lines 3–4). Most samples from previous iterations are discarded because the corresponding constraints are already satisfied. We prune all current feasible constraints as in [4]. Similarly, the two random sampling strategies (Lines 1 and 2) might return some samples for which the constraints are already fulfilled. Therefore, we only consider the samples with violated constraints and pick the r most violated from them. This pruning strategy is essential for a memory efficient implementation as shown later.

Sampling at u (Line 5). Finally, we add one sample which is exactly at the current solution $u \in \varGamma$ to have at least one guaranteed sample per face.

Overall Algorithm. After implementing the constraints at the finite set determined by Algorithm 1, we apply a primal-dual method [10] with diagonal preconditioning [29] to solve (10). Both constraints (11) and (12) are implemented using Lagrange multipliers. Based on the obtained solution, a new set of samples is determined.

This scheme is alternated for a fixed number of outer iterations $N_{it}$ and we have summarized the overall algorithm in Algorithm 2. While we do not prove convergence of the overall algorithm, convergence results for related procedures exist; see, e.g., [4, Theorem 2.4].

Finally, let us note that a single outer iteration of Algorithm 2 with large number of $M_{it}$ corresponds to the baseline method.

5 Numerical Validation

Our approach and the baseline are implemented in PyTorch. Code for reproducing the following experiments can be found here: https://github.com/zhenzhangye/sublabel_meets_product_space. Note that a specialized implementation as in [15] will allow the method to scale by factor $10-100\times$.

Fig. 1.

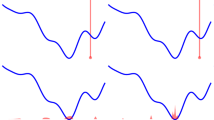
Illustration of sampling strategies. (a) Two samples (red dots) are considered leading to the shown optimal dual variable $\mathbf {q}$ after running primal-dual iterations. (b) The two samples are pruned because the constraints are feasible. Several random samples are proposed (gray dots) and only one of them is picked (red dot). (c) One more sample on $u^{it}$ is added and the $\mathbf {q}$ is refined. (Color figure online)

Table 1. Ablation study indicating the effect of individual lines in Algorithm 1. Numbers in parentheses indicate the standard deviation across 20 runs.

Fig. 2.

Comparison between the baseline and our approach on a $64\times 64$ image, degraded with Gaussian and salt-and-papper noise. Our approach finds lower energies in fewer iterations and time, which implements the constraints only at the label points.

Fig. 3.

We compute the optical flow on Grove3 [2] using our method and our baseline for a varying amount of labels. Given an equal number of labels/memory, our sampling strategy performs favorably to an implementation of the constraints at the labels.

5.1 Illustration of Our Sampling Idea

To illustrate the effect of the sampling strategies, we consider the minimization of a single nonconvex data term. The cost c and the corresponding dual variable $\mathbf {q}$ are plotted in Fig. 1. As shown in (a), the primal-dual method can obtain the optimal $\mathbf {q}^h$ for the sampled subproblem only. Our sampling strategy can provide necessary samples and prune the feasible ones as, cp. (b). These few but necessary samples lead the $\mathbf {q}^h$ to achieve global optimality, cp. (c). If one more iteration is performed, the sampling at $u^{it}$ can stabilize the optimal $\mathbf {q}$.

5.2 Ablation Study

Next, we study the effect of each line in Algorithm 1. We evaluate our method on the truncated quadratic energy $c(x, u(x)) = \min \{(u(x) - f(x))^2, \nu \}$. where $f : \varOmega \rightarrow \mathbf {R}$ is the input data. For this specific experiment, the parameters are chosen as $\nu =0.025$, $\lambda =0.25$, $N_{it}=10$, $M_{it}=200$, $n=10$ and $r=1$. To reduce the effect of randomness, we run each algorithm 20 times and report mean and standard deviation of the final energy for different number of labels in Table 1.

Adding uniform sampling and picking the most violated constraint per face already decreases the final energy significantly, i.e. Line 1 and Line 4 of Algorithm 1. We also consider local exploration around the current solution, cf. Line 2, which helps to find better energies at the expense of higher memory requirements.

To circumvent that, we introduce our pruning strategy in Line 3 of Algorithm 1. However, the energy deteriorates dramatically because some faces could end up having no samples after pruning. Therefore, keeping the current solution as a sample (Line 5) per face prevents the energy from degrading.

Including all the sampling strategies, the proposed method can achieve the best energy and run-time, at comparable memory usage to the baseline method. We further illustrate the comparison on the number of iterations and time between the baseline and our proposed method in Fig. 2. Due to the replacement on the samples, we have a peak right after each sampling phase. The energy however converges immediately, leading to an overall decreasing trend.

Fig. 4.

Denoising of an image in HSV color space ($\varGamma _1 = \mathbb {S}^1$) using our method and the baseline. Since our approach implements the constraints adaptively inbetween the labels it reaches a lower energy with less label bias.

5.3 Optical Flow

Given two input images $I_1$, $I_2$, we compute the optical flow $u : \varOmega \rightarrow \mathbf {R}^2$. The label space $\varGamma = [a,b]^2$ in our case is chosen as $a=-2.5$ and $b=7.5$. We use a simple $\ell _2$-norm for the data term, i.e. $c(x, u(x)) = ||I_2(x) - I_1(x+u(x))||$ and set the regularization weight as $\lambda =0.04$. The baseline approach runs for 50K iterations, while we set $N_{it}=50$ and $M_{it}=1000$ for a fair comparison. Additionally, we choose $n=20$ and $r=1$ in Algorithm 1.

The results are shown in Fig. 3. Our method outperforms the baseline approach regarding energy under the same number of labels and requires the same amount of memory. We can achieve lower energy with about half number of labels.

5.4 Denoising in HSV Color Space

In our final application, we evaluate on a manifold-valued denoising problem in HSV color space. The hue component of this space is a circle, i.e., $\varGamma _1 =\mathbb {S}^1$, $\varGamma _2, \varGamma _3 = [0,1]$. The data term of this experiment is a truncated quadratic distance, where for the hue component the distance is taken on the circle $\mathbb {S}^1$.

Both the baseline and our method are implemented with 7 labels. 30K iterations are performed on the baseline and $N_{it}=100$ outer iterations for our method with 300 inner primal-dual steps are used to get an equal number of total iterations. Other parameters are chosen as $\lambda =0.015$, $n=30$ and $r=5$. As shown in Fig. 4, our method can achieve a lower energy than the baseline. Qualitatively, since our method implements the constraints not only at the labels but also inbetween, there is less bias compared to the baseline.

6 Conclusion

In this paper we made functional lifting methods more scalable by combining two advances, namely product-space relaxations [15] and sublabel-accurate discretizations [26, 36]. This combination is enabled by adapting a cutting-plane method from semi-infinite programming [4]. This allows an implementation of sublabel-accurate methods without difficult epigraphical projections.

Moreover, our approach makes sublabel-accurate functional-lifting methods applicable to any cost function in a simple black-box fashion. In experiments, we demonstrate the effectiveness of the approach over a baseline based on the product-space relaxation [15] and provided a proof-of-concept experiment showcasing the method in the manifold-valued setting.