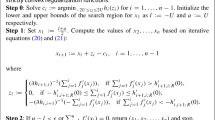Total Cyclic Variation and Generalizations

Abstract

We introduce a general framework for regularization of signals with values in a cyclic structure, such as angles, phases or hue values. These include the total cyclic variation ${TV_{{S}^{1}}}$, as well as cyclic versions of quadratic regularization, Huber-TV and Mumford-Shah regularity. The key idea is to introduce a convex relaxation of the original non-convex optimization problem. The method handles the periodicity of values in a simple way, is invariant to cyclical shifts and has a number of other useful properties such as lower-semicontinuity. The framework allows general, possibly non-convex data terms. Experimental results are superior to those obtained without special care about wrapping interval end points. Moreover, we propose an equivalent formulation of the total cyclic variation which can be minimized with the same time and memory efficiency as the standard total variation. We show that discretized versions of these regularizers amount to NP-hard optimization problems. Nevertheless, the proposed framework provides optimal or near-optimal solutions in most practical applications.

1 Introduction

1.1 Total Variation and Cyclic Structures

Total variation (TV) has been widely recognized as an effective and efficient means to regularize variational problems. The main advantage of TV is that it is able to preserve sharp discontinuities in the data while still providing a smoothing effect. Secondly, TV is convex and thus relatively easy to handle in minimization problems. Thirdly, due to the coarea formula the total variation applied to the characteristic function of a set coincides with a measure of its boundary making it well suited for various geometric optimization problems. TV has been applied to a great variety of image analysis problems, such as denoising [25], segmentation [15, 17], superresolution [16], inpainting [3], multi-view reconstruction [14] and optical flow [6, 26]. All these examples assume that the range of the function u, which is to be regularized, is a space of linear structure, e.g. ℝⁿ for some n≥1.

In many interesting image and signal processing applications, however, the range of signals is the unit circle S ¹, or equivalently the space of planar orientations. Here, the function values representing e.g. angles, phases or hue values are periodic in nature. Important application areas where cyclical data arises naturally include interference microscopy, synthetic aperture radar (SAR) satellite imagery [8], or the analysis of imagery from time of flight cameras. In SAR image processing, one aims at reconstructing the object of interest, e.g. the ground elevation from the difference of phases between two phase image measurements. Similarly, time-of-flight cameras capture distance measurements of the scene, but only for distances up to the wavelength of the employed light. Distances above this limit are cyclically wrapped into the first basic interval. In all these applications, since the measurements are typically rather noisy, denoising of the cyclical signals is an integral part.

A straightforward attempt to realize a notion of total variation for functions with cyclical range is to simply represent the circle S ¹ as [0,1) and then to apply the usual TV seminorm. However, this approach leads to artifacts due to neglecting the value wrapping at the boundary of [0,1). Jumps from 0 to 1, or to values near 1, will be penalized with a substantial contribution to the energy whereas there is actually no jump at all with respect to the S ¹ structure. This generally leads to oversmoothing, important image structures may get lost when applied to segmentation, and artificial structures may appear. Moreover, TV is dependent on the specific representation of S ¹ as [0,1), i.e. the penalization is different depending on which point of S ¹ is taken to be 0. Specifically, cyclic shifts of input data will not result in the corresponding cyclic shift of the output.

1.2 Prior Work

The notion of total variation for functions $u:\varOmega\to{\mathcal{Y}}$ defined on manifold domains Ω and with values in general manifolds ${\mathcal{Y}}$ has been studied by Giaquinta and Mucci [11, 12] using the theory of cartesian currents. They rigorously define the space ${BV}(\varOmega;{\mathcal{Y}})$ and provide a number of theoretical insights, proving several properties of functions with bounded total variation such as lower-semicontinuity and structure theorems. This extends the previous work [9] by Giaquinta et al. which handles specifically the case ${\mathcal{Y}}={{S}^{1}}$ and, among others, shows existence of minimizers of certain energies in the space of functions with bounded total cyclic variation. Although these papers provide a notion of total cyclic variation ${TV_{{S}^{1}}}$, they differ from our approach in several fundamental ways.

First, the above approach uses an embedding of the manifold S ¹ into ℝ² to define BV(Ω;S ¹) and ${TV_{{S}^{1}}}$. This means that one works entirely with functions ${\widehat{u}}:\varOmega\to{\mathbb{R}}^{2}$ satisfying |u(x)|=1 for a.e. x∈Ω. The theory is formulated entirely in terms of cartesian currents, which are specific continuous linear maps on differential forms and represent generalized graphs of functions of bounded variation. It is not clear how to transfer the theoretical properties of ${TV_{{S}^{1}}}$ to the corresponding statements in the setting of functions u:Ω→S ¹, and even whether these properties still hold. In contrast, in the present paper we work directly with functions u:Ω→S ¹, respectively u:Ω→ℝ. We present proofs of the theoretical properties for this setting and refer to the related results in [9, 11, 12] for cartesian currents where appropriate. Most of our results do not have equivalent formulations in [9, 11, 12], since they only make sense when working directly with u:Ω→ℝ, i.e. without the embedding. For instance, this is the case for our main theoretical contribution, the novel convex representation of ${TV_{{S}^{1}}}$ in Theorem 1. We believe that our derivations may be more accessible to the computer vision community because they do not rely on advanced mathematical concepts like k-forms and k-currents.

Second, and most importantly, for the approach of Giaquinta et al. it is not clear how to derive an algorithm to practically compute the minimizers of energies with cyclic regularizers. Neither of these works have performed any numerical validations or experiments. In contrast, our method leads to a convex formulation of the energy minimization problem and can be easily employed to compute the solutions numerically.

Finally, our approach also extends to more general regularizers such as Huber-TV, and even to non-convex regularizers such as the piecewise smooth Mumford-Shah model for regularizing signals with cyclic values.

To the best of our knowledge, the derivation, analysis and numerical implementation of regularizers for cyclic signals (with a direct definition on these signals without embedding the values into ℝ²) has not been addressed systematically in the literature. Moreover, it turns out that this is by no means straightforward.

1.3 Contributions

In this paper we introduce and mathematically characterize regularizers for functions with values in a cyclical range. Specifically we make the following contributions:

• We introduce a novel kind of total variation, ${TV_{{S}^{1}}}$, for functions u:Ω→S ¹ with cyclic or periodic values. The regularizer resembles closely the usual total variation and provides an elegant solution to handle the wrap-around of values. We show that ${TV_{{S}^{1}}}$ can be defined for all measurable functions u:Ω→ℝ by means of a dual representation.

• From the theoretical viewpoint we show that ${TV_{{S}^{1}}}$ has a number interesting and desired mathematical properties such as invariance to cyclic shifts and isometries as well as lower-semicontinuity.

• Beyond the total cyclic variation ${TV_{{S}^{1}}}$, our framework also allows more general regularizers for S ¹-valued functions. This includes regularizers such as Huber-TV and the quadratic penalizer as well as more advanced ones like truncated linear and the full Mumford-Shah regularizer. We show how to incorporate the S ¹ structure into these regularizers, so that changes of the representation of the data will have no effect on the regularization.

• We prove the existence of minimizers for general ${TV_{{S}^{1}}}$ regularized functionals. This result requires an especially tailored argument since functions u with ${TV_{{S}^{1}}}(u)<\infty$ are not necessarily elements of BV(Ω). We show that ${TV_{{S}^{1}}}$ optimization is in general NP-hard and also propose an adaptive binarization method to obtain solutions closer to the global optimum.

• Furthermore, we give an equivalent reformulation of the constraint sets which enables one to minimize ${TV_{{S}^{1}}}$ regularized energies with the same time and memory efficiency as the standard total variation. Finally, several experiments illustrate the applications of the S ¹ framework. Comparing to usual regularizers for functions with linear values like TV, the proposed framework gives rise to visually superior and more natural results.

A preliminary version of this work was presented at a conference [28]. In comparison to [28] the present work has a number of novelties:

• We eliminate the range constraint u:Ω→[0,1) in the definition of ${TV_{{S}^{1}}}$ and work entirely with functions u:Ω→ℝ. This gives rise to more intuitive formulations and reveals novel properties of ${TV_{{S}^{1}}}$. For instance, the cyclic shift property is reduced to a more fundamental representation invariance property.

• We extend the S ¹ framework to more general regularizers, such as Huber-TV and Mumford-Shah.

• The mathematical properties of ${TV_{{S}^{1}}}$ are extended, for instance we prove the existence of minimizers for ${TV_{{S}^{1}}}$ regularized problems.

• We provide new experiments—phase denoising and cyclical smoothing—further demonstrating the advantages of cyclic regularizers.

The paper is organized as follows. First, in Sect. 2 we introduce the notion of the total cyclic variation ${TV_{{S}^{1}}}$ for functions exhibiting certain regularity, for instance u∈SBV. Motivated by the non-convexity of ${TV_{{S}^{1}}}$, we prove in Sect. 3 a convex formulation in terms of the graph function 1 _u of u based on the functional lifting theory. In Sect. 4 we show a number of mathematical properties of ${TV_{{S}^{1}}}$. Subsequently, Sect. 5 applies the framework to general optimization problems where an energy involving a data term and ${TV_{{S}^{1}}}$ as the regularizer is to be minimized. Section 6 introduces more general regularizers for S ¹-valued functions. Finally, we present experimental results in Sect. 7 and give a conclusion in Sect. 8.

2 Definition of ${TV_{{S}^{1}}}$

In this section we give a definition of the total cyclic variation ${TV_{{S}^{1}}}$. This first definition can be seen as an intuitive and natural way of introducing ${TV_{{S}^{1}}}$, and can be formulated only for functions exhibiting certain regularity. We will extend this definition in later sections.

2.1 Preliminaries

Let Ω⊂ℝ^m be a bounded open set, m≥1. Let

$$ {{S}^1}=\bigl\{x\in{\mathbb{R}}^2 \big||x|=1\bigr\} $$

(1)

be the unit circle. Since there is a one-to-one correspondence between S ¹ and the unit interval Γ:=[0,1), any function u:Ω→S ¹ can be conveniently represented as a function u:Ω→Γ. This representation proves to be both convenient and useful for theoretical treatment of ${TV_{{S}^{1}}}$. More generally, we give a definition of ${TV_{{S}^{1}}}$ for functions u:Ω→ℝ, without restricting the range of u to Γ. This means that at each point x∈Ω one is free to choose different representatives in ℝ modulo 1 of the value u(x).

As one easily checks, the distance function on S ¹ transfers to the distance function $d_{{S}^{1}}$ on ℝ given by $d_{{S}^{1}}(a,b)=\min(|a-b|,1-|a-b| )$ for a,b∈Γ. For general a,b∈ℝ, we can easily show the representation in the lemma below. For fixed b this gives a “saw-tooth” shaped curve in a (Fig. 1).

Fig. 1

In contrast to the linear distance (dashed), the cyclic distance $d_{{S}^{1}}$ (solid) accounts for the periodicity of S ¹

Lemma 1

Let x,y∈ℝ. Then

$$ d_{{S}^1}(x,y) = \min_{k\in{\mathbb{Z}}} |y-x-k|. $$

(2)

Proof

Observe that $d_{{S}^{1}}(x,y)=d_{{S}^{1}}(0,y-x)$ and the right hand side of (2) are 1-periodic in y−x. Since both coincide with min(y−x,1−(y−x)) for y−x∈Γ the equation follows. □

For functions u∈L ¹(Ω) the total variation of u is defined by

$$ TV(u) = \int_\varOmega|Du| := \sup_{|\varphi|\leq1} \int_\varOmega u \operatorname{div}\varphi\,dx $$

(3)

where the supremum is taken over all $\varphi\in{C_{c}^{\infty}(\varOmega; {{\mathbb{R}}^{m}})}$ with |φ(x)|≤1 for all x. The space of functions of bounded variation, i.e. where TV(u)<∞, is denoted by BV(Ω).

If u∈BV(Ω), we denote by S _u its “essential” jump set. This is where one cannot unambiguously define u(x), but rather two values u ⁺(x)>u ⁻(x) and a normal vector ν _u (x), indicating the direction of the jump and pointing from the u ⁻ to the u ⁺ side.

One says that u∈SBV(Ω), the special functions of bounded variation, if the distributional gradient can be decomposed as $Du=\nabla u \,dx+(u^{+}-u^{-})\nu_{u} d \mathcal{H}^{{m}-1}|{S_{u}}$ into a smooth part and a jump part. The former is the absolutely continuous part of Du, the corresponding density function ∇u:Ω→ℝ^m is called the approximate gradient of u [2, Definition 3.70]. The latter is the jump height u ⁺−u ⁻ multiplied with the Hausdorff (m−1)-dimensional measure restricted to the jump set S _u (Fig. 2). A general function u∈BV(Ω) may in addition have a “Cantor” part, an uncountable accumulation of infinitesimal jumps. We refer to [2] for a comprehensive introduction to functions of bounded variation.

Fig. 2

Graph of a function u∈SBV(Ω). The jump set S _u consists here of two points, the second jump being just a wrap-around and not an actual jump in S ¹ sense. The function 1 _u is defined as 1 in the shaded area under the graph and 0 otherwise

2.2 Definition of ${TV_{{S}^{1}}}$ for SBV Functions

We first define ${TV_{{S}^{1}}}$ for functions u∈SBV, as this space allows to handle the smooth part and the jump part of the gradient in an explicit way. A more general definition for all measurable functions u:Ω→ℝ will be given in Sect. 3.3 based on a dual formulation.

Definition 1

(${TV_{{S}^{1}}}$ for SBV Functions)

For u∈SBV(Ω) we define the total cyclic variation as

$$ {TV_{{S}^1}}(u)= \int_{\varOmega\setminus{S_u}} |\nabla u| \,dx +\int_{S_u}d_{{S}^1}\bigl(u^-,u^+\bigr) {d \mathcal{H}^{{m}-1}}. $$

(4)

A straightforward generalization is the weighted ${TV_{{S}^{1}}}$ where the contribution to ${TV_{{S}^{1}}}$ at each point x∈Ω is weighted by a function g:Ω→ℝ_>0:

$$ \begin{aligned}[b] {TV_{{S}^1}^g}(u)&= \int_{\varOmega\setminus{S_u}}g\:|\nabla u| \,dx \\ &\quad + \int_{S_u}g d_{{S}^1}\bigl(u^-,u^+ \bigr) {d\mathcal{H}^{{m}-1}}. \end{aligned} $$

(5)

This can be used to enable spatially adaptive regularizations. Writing |u ⁻−u ⁺| instead of $d_{{S}^{1}}(u^{-},u^{+})$ in (4) would give just the usual TV seminorm. Thus, in the region where u is smooth ${TV_{{S}^{1}}}$ behaves just like TV, whereas at jumps it explicitly handles the S ¹ structure by taking the cyclic distance $d_{{S}^{1}}$ instead of the linear one.

Note that ${TV_{{S}^{1}}}$ is not convex on the vector space SBV(Ω) because of the nonconvex distance $d_{{S}^{1}}$:

Proposition 1

${TV_{{S}^{1}}}$ is not convex on SBV(Ω).

Proof

For any A⊂Ω with a rectifiable nonzero perimeter, $\operatorname{Per}_{\varOmega}(A):={TV}(\chi_{A})>0$, define u ₁,u ₂∈SBV(Ω) by u ₁:=0, u ₂:=χ _A . Then ${TV_{{S}^{1}}}(u_{1})={TV_{{S}^{1}}}(u_{2})=0$ but ${TV_{{S}^{1}}}(\frac{u_{1}+u_{2}}{2})=\frac{1}{2}\operatorname {Per}_{\varOmega}(A)>0$. □

In the next section, we will introduce a convex representation for efficiently minimizing functionals involving ${TV_{{S}^{1}}}$. As a consequence, this will also allow us to extend the definition of ${TV_{{S}^{1}}}$ to all measurable functions u:Ω→ℝ.

3 Convex Representation of ${TV_{{S}^{1}}}$

The convexification of ${TV_{{S}^{1}}}$ is based on the general framework of functional lifting.

3.1 Functional Lifting

In a series of papers [1, 20–23] it was shown that for functionals of the form

$$ \begin{aligned}[b] {E}(u) &= \int_{\varOmega\setminus{S_u}} h\bigl(x,u(x),\nabla u(x)\bigr) \,dx \\ &\quad+ \int_{S_u}d\bigl(x,u^-(x),u^+(x)\bigr) {d \mathcal{H}^{{m}-1}}(x) \end{aligned} $$

(6)

a tight convex relaxation can be found using the method of cartesian currents [10] and that this relaxation can be employed to minimize these functionals. The idea is to restate E(u) in terms of the graph function 1 _u of u, see Figs. 2 and 3:

$$ 1_u:{\varOmega\times{\mathbb{R}}}\to{\mathbb{R}}, \quad 1_u(x,t) = \begin{cases} 1 &\text{if}\ t<u(x),\\ 0 &\text{else}. \end{cases} $$

(7)

Fig. 3

The graph function 1 _u :Ω×Γ→{0,1} of a function u∈SBV(Ω). The function 1 _u has the value 1 under the graph of u, and 0 otherwise

Although the functional E(u) is in general highly nonconvex, it turns out that in case where h:Ω×ℝ×ℝ^m→ℝ is convex in its third argument (i.e. in the gradient ∇u) it can be recast as a convex function of 1 _u [1, Lemma 3.7]:

Lemma 2

For v∈BV(Ω×ℝ) define

$$ {\mathcal{E}}(v)= \sup_{\varphi} \int_{\varOmega \times{\mathbb {R}}} \varphi Dv $$

(8)

where the supremum is taken over all vector fields φ=(φ ^x,φ ^t):Ω×ℝ↦ℝ^m×ℝ satisfying

(9)

for all x∈Ω and t,t′∈ℝ. Then, for all u∈SBV(Ω),

$$ {\mathcal{E}}(1_u)\leq{E}(u). $$

(10)

Moreover, equality holds in (10) for a given u if and only if there is a vector field φ∈K with certain properties, see [1, Lemma 3.7]. Here, h ^∗(x,t,q):=sup _p p⋅q−h(x,t,p) is the Legendre-Fenchel conjugate of h(x,t,p) with respect to p. For a detailed introduction to convex analysis we refer to [24]. Dv denotes the distributional gradient of v.

The main advantage of formulation (10) is that ${\mathcal{E}}$ in (8) is convex in v=1 _u . This can be used to efficiently find minimizers of E as was done e.g. in [21], see also Sect. 5. In our case ${E}={TV_{{S}^{1}}}$, we have h(x,t,p)=|p| and $d(x,t,t')=d_{{S}^{1}}(t,t')$, comparing (4) with (6). Application of the above Lemma 2 leads to the following convex representation of ${TV_{{S}^{1}}}$.

Proposition 2

For u∈SBV(Ω),

$$ {TV_{{S}^1}}(u) = \sup_{\varphi^x\in K} \int _{\varOmega\times{\mathbb {R}}}\varphi^x\cdot\nabla_x1_u $$

(11)

with the constraint set

(12)

We write ∇ _x 1 _u for the distributional gradient D _x 1 _u with respect to the spatial variable x, and later also $\operatorname{div}_{x}\varphi^{x}$ for the spatial divergence of φ ^x and $\operatorname{div}\varphi=\operatorname{div}_{x}\varphi ^{x}+\partial_{t}\varphi^{t}$ for the spatio-temporal divergence of φ=(φ ^x,φ ^t). Since equality (11) is fundamental for our discussion, for the convenience of the reader we present here a direct proof without referring to Lemma 2. This also has the advantage that one sees how the constraints (12) on φ naturally arise. Lemma 2 will be used later when we deal with more general regularizers for S ¹-valued functions.

Proof of Proposition 2

Let u∈SBV(Ω). For a general vector field φ:Ω×ℝ→ℝ^m×ℝ, φ=(φ ^x,φ ^t) with φ ^t≡0, Lemma 2.8 of [1] states that

where u, u ^±, ∇u and ν _u are all evaluated at x. Here, ν _u is the normal vector indicating the jump direction of u as described in Sect. 2.1. Comparing the corresponding parts, this expression is less than or equal to

if

(13)

for a.e. x∈Ω∖S _u , respectively for ${\mathcal{H}^{{m}-1}}$-a.e. x∈S _u . Demanding these constraints for all possible vectors p∈ℝ^m instead of ∇u and all t,t′ instead of u and u ^±, we arrive at the constraints

$$ \bigl|\varphi^x(x,t)\bigr|\leq1,\qquad \biggl|\int _{t}^{t'}\varphi^x(x,s) \,ds \biggr|\leq d_{{S}^1}\bigl(t,t'\bigr) $$

(14)

for all x∈Ω, t,t′∈ℝ, which are exactly the ones in (12). Inequalities (13) are certainly fulfilled given (14). This proves (11) at least with ≥ instead of equality.

To show equality, we must construct a vector field φ ^x satisfying (14) such that equalities hold in (13). We first define φ ^x(x,t) for t∈Γ=[0,1) only, and then extend this definition to all t∈ℝ by 1-periodicity. For x∈Ω∖S _u set

$$\varphi^x(x,t):=\frac{\nabla u}{|\nabla u|} \bigl(1-2\bigl((t-u) \ \mathrm{mod}\ 1\bigr) \bigr) $$

if ∇u≠0, and φ ^x(x,t):=0 otherwise. Note that the approximate gradient ∇u:Ω→ℝ^m is by definition always a function and not only a measure (Sect. 2.1). For x∈S _u , let h:=(u ⁺−u ⁻) mod 1, so that h∈Γ, and set

if h>0, and φ ^x(x,t):=0 otherwise. Let us first verify the equalities in (13). The first one for x∈Ω∖S _u is immediate. For the second one for x∈S _u , observe that $\int_{u^{-}}^{u^{-}+1}\varphi^{x}(x,s) \,ds=0$ and thus $\int_{u^{-}+k}^{u^{-}+k+1}\varphi^{x}(x,s) \,ds=0$ for any k∈ℤ due to 1-periodicity of φ ^x. Therefore, the integral in (13) reduces to

$$\int_{u^-}^{u^+}\varphi^x(x,s) \,ds = \int _{u^-}^{u^-+h}\varphi^x(x,s) \,ds $$

with h as defined above. This can be easily evaluated to $d_{{S}^{1}}(0,h)=d_{{S}^{1}}(u^{-},u^{+})$ times ν _u (x), giving the second equality in (13).

Next, we must verify the constraints (14). The first one is obviously fulfilled for x∈Ω∖S _u , and also for x∈S _u due to $d_{{S}^{1}}(0,h)\leq h$ and $d_{{S}^{1}} (0,h)\leq1-h$. The second constraint can be verified directly for all t,t′, but is most easily seen to hold using the equivalent formulation in Proposition 3 below: The integral of φ ^x over the interval [u,u+1) for x∈Ω∖S _u , respectively over [u ⁻,u ⁻+1) for x∈S _u is zero. Since φ is 1-periodic by construction, also the integrals over Γ are zero by Lemma 3 below. Thus, φ ^x satisfies the conditions of Proposition 3, so that also the second constraint of (14) is fulfilled. □

3.2 From Quadratic to Linear Complexity

The integral constraint in the definition (12) of K, using this formulation, must be satisfied for all pairs t<t′. In practice, the space of cyclical values Γ needs to be discretized at n levels $\frac{0}{n},\ldots,\frac{n-1}{n}$ for some n≥1. In the discretization, this means that the number of constraints in (12) grows quadratically with the number of levels. Enforcing them quickly becomes unfeasible with respect to both runtime and memory consumption even for a moderate number of levels. Surprisingly, for the special metric $d=d_{{S}^{1}}$ there is an equivalent formulation of this constraint which leads to a much more efficient implementation.

One of the main contributions of this paper is to show that one can efficiently minimize functionals involving the ${TV_{{S}^{1}}}$ regularizer. This is based on the following proposition which states that one can replace the integral constraint by a much simpler equivalent formulation:

Proposition 3

(Constraint Equivalence)

(15)

(16)

(17)

(18)

Proof

Direction “⇒”: From (15) we have

$$\biggl|\int_{t}^{t'}\varphi^x(x,s) \,ds \biggr| \leq d_{{S}^1}\bigl(t,t'\bigr)\leq t'-t. $$

Dividing both sides by t′−t for t<t′ and letting t,t′→t ₀ for some t ₀∈Γ we obtain (17). Furthermore, setting t=t ₀ and t′=t ₀+1 for a fixed t ₀ yields

$$\biggl|\int_{t_0}^{t_0+1}\varphi^x(x,s) \,ds \biggr| \leq d_{{S}^1}(t_0,t_0+1)=0 $$

and therefore $\int_{t_{0}}^{t_{0}+1}\varphi^{x}(x,s) \,ds=0$. Specifically, t ₀=0 yields (18). Defining $f(t):=\int_{0}^{t}\varphi^{x}(x,s) \,ds$, this means that f(t+1)=f(t) for all t, i.e. f is 1-periodic. Since φ ^x(x,t)=f′(t), (16) follows.

Direction “⇐”: Let t,t′∈ℝ. Since φ ^x(x,⋅) is 1-periodic, from (18) we easily get that also

$$\int_{t}^{t+k}\varphi^x(s) \,ds=0 $$

for all integers k, using Lemma 3 below. Also, by 1-periodicity (17) holds more general for all t∈ℝ. Therefore,

$$\begin{aligned}[t] \biggl|\int_{t}^{t'} \varphi^x(s) \,ds \biggr| &= \biggl|\int_{t}^{t'} \varphi^x(s) \,ds - \int_{t}^{t+k} \varphi^x(s) \,ds \biggr| \\ &= \biggl|\int_{t+k}^{t'}\varphi^x(s) \,ds \biggr| \leq\int_{t+k}^{t'}\bigl|\varphi^x(s)\bigr| \,ds \\ &\leq\int_{t+k}^{t'}1\,ds =|t'-t-k| \end{aligned} $$

for k with t+k≤t′ and in the same way also for k with t+k≥t′. Combining these estimates for every k, we arrive at (15) using the representation of $d_{{S}^{1}}$ in Lemma 1. □

Effectively, this reduces the memory and time complexity of enforcing the constraint from quadratic to just linear. This way, from the implementation side the regularization of general data terms with ${TV_{{S}^{1}}}$ becomes just as inexpensive as the usual TV regularization [22], where the number of constraints also grows linearly with the number of levels. In the proof, we have used the following simple fact about integrals of periodic functions:

Lemma 3

Let p:ℝ→ℝ be 1-periodic. Then, for any a,b∈ℝ,

(19)

Proof

By the periodicity of p we obtain for all a∈ℝ

$$\begin{aligned}[t] \int_a^{a+1}p(s) \,ds &= \int_a^1p(s) \,ds + \int_1^{a+1}p(s) \,ds \\ &= \int_a^1p(s) \,ds + \int_0^{a}p(s+1) \,ds \\ &= \int_a^1p(s) \,ds + \int_0^{a}p(s) \,ds = \int_0^1p(s) \,ds, \end{aligned} $$

from which the statement follows. □

3.3 Dual Representation of ${TV_{{S}^{1}}}$ and Definition for All Measurable Functions

In the representation (11), the vector fields φ ^x over which the supremum is taken are not required to be smooth or continuous. However, having only smooth φ can be useful for applications. In fact, one can show that one can restrict the supremum to vector fields φ ^x which are smooth in x and t, and have compact support with respect to the x variable (compact support in the t variable is not required). Since the proof of this is quite technical, we only give the main lines here. Basically, if u is smooth outside the jump set S _u , i.e. u∈C ^∞(Ω∖S _u ), then a smooth vector field φ ^x with (14) and equalities in (13) can be constructed, so that the supremum is attained for this φ ^x. For general u∈SBV, using partitions of unity one can construct smooth vector fields φ ^x such that the integrals of φ ^x∇ _x 1 _u are arbitrarily close to ${TV_{{S}^{1}}}(u)$.

Starting from representation 2 of ${TV_{{S}^{1}}}$ and considering only smooth φ ^x we can employ integration by parts to obtain the following useful dual formulation of ${TV_{{S}^{1}}}$ which does not require to know the jump set S _u explicitly:

Theorem 1

(Dual Representation)

For every u∈SBV(Ω) it holds

$$ {TV_{{S}^1}}(u) = \sup_{\varphi^x\in K}\int _{\varOmega}\int_0^{u(x)}\operatorname {div}_x \varphi^x(x,s) \,ds \,dx $$

(20)

with

$$ \begin{aligned}[b] K= \biggl\{ &\varphi^x \in{C_c^\infty\bigl(\varOmega; C^\infty\bigl({\mathbb {R}};{{\mathbb{R}}^{m}}\bigr)\bigr)} \bigg| \\ &\varphi^x(x,\cdot)\ \text{1-\textit{periodic}}, \ \bigl|\varphi^x(x,t)\bigr|\leq1, \\ &\int_\varGamma\varphi^x(x,s) \,ds=0 \ \forall x\in\varOmega,\ t\in\varGamma\biggr\}. \end{aligned} $$

(21)

Proof

Follows directly from representation 2 by integration by parts and utilizing the efficient constraint reformulation in Proposition 3 (and substituting φ ^x by −φ ^x). □

The lower bound 0 of the inner integral in (20) can be replaced by any other constant, leaving the overall integral value unchanged. For the weighted variant ${TV_{{S}^{1}}^{g}}$ the constraint |φ ^x(x,t)|≤1 must be replaced by |φ ^x(x,t)|≤g(x).

Note that the expression (20) is well defined for all measurable u:Ω→ℝ. Indeed, since φ ^x(x,⋅) is 1-periodic with ∫ _Γ φ ^x(x,s) ds=0, for each x∈Ω we can replace the upper integration bound u(x) in (20) by a value from Γ=[0,1). Hence, the overall integral is finite and well defined for each φ∈K.

Definition 2

(${TV_{{S}^{1}}}$ for Measurable Functions)

We define ${TV_{{S}^{1}}}(u)$ for every measurable u:Ω→ℝ by (20).

The representation in Theorem 1 is amazingly similar to the dual representation (3) of the usual total variation for scalar valued function. In fact, the integral in (20) reduces directly to (3) assuming that φ(x,t) only depends on x. Therefore, our definition of ${TV_{{S}^{1}}}$ can be seen as a natural notion of total variation for S ¹-valued functions.

We remark that the dual formulation of ${TV_{{S}^{1}}}$ requires the introduction of an additional dimension to the problem corresponding to the range space of u. On one hand this means additional memory requirements (after discretization). But on the other hand this allows one to easily couple and minimize ${TV_{{S}^{1}}}$ with arbitrary, possibly nonconvex data terms, as will be done in Sect. 5.

4 Properties of ${TV_{{S}^{1}}}$

We will now investigate some mathematical properties of ${TV_{{S}^{1}}}$. First of all, ${TV_{{S}^{1}}}$ has the desired property that, whenever u attains two different values a,b∈ℝ, the value change is penalized by the $d_{{S}^{1}}$ distance of a and b multiplied with the length of the interface:

Proposition 4

(Consistency with $d_{{S}^{1}}$)

With fixed a,b∈ℝ and A⊂Ω, let $u=a\chi_{A}+b\chi_{\bar{A}}$. Then

$$ {TV_{{S}^1}}(u) = d_{{S}^1}(a,b) \operatorname{Per}_\varOmega(A) $$

(22)

where $\operatorname{Per}_{\varOmega}(A)={TV}(\chi_{A})$ is the perimeter of A in Ω.

Proof

By Theorem 1,

(23)

The last integral is zero since φ is zero on the boundary. For each φ∈K, the function $p(x):=\int_{b}^{a}\varphi(x,s) \,ds$ in the first integral belongs to ${C_{c}^{\infty}(\varOmega; {{\mathbb{R}}^{m}})}$ and it holds $|p(x)|\leq d_{{S}^{1}}(a,b)$ using Proposition 3. Conversely, any $p\in{C_{c}^{\infty}(\varOmega; {{\mathbb{R}}^{m}})}$ bounded like this can be represented by a φ∈K, e.g. set φ(x,t):=p(x)w _a,b (t) for any 1-periodic function w∈C ^∞(ℝ) satisfying $\int_{b}^{a}w(s) \,ds=d_{{S}^{1}}(a,b)$ and |w _a,b (t)|≤1. This means that in (23) we can instead take the supremum over all $p\in{C_{c}^{\infty}(\varOmega; {{\mathbb{R}}^{m}})}$ with $|p|\leq d_{{S}^{1}}(a,b)$. This results in the definition of just the usual total variation and we obtain

 □

Thus, ${TV_{{S}^{1}}}$ as defined above is indeed the total cyclic variation of u. As a corollary we obtain that ${TV_{{S}^{1}}}(u)$ is zero for any constant u:Ω→ℝ.

Since the values in S ¹ are periodic in nature one expects that ${TV_{{S}^{1}}}(u)$ does not change if the values of u are cyclically shifted everywhere by the same amount. This is indeed the case as stated in the following proposition. This means that ${TV_{{S}^{1}}}$ is independent of a concrete representation of S ¹ as the unit interval Γ=[0,1), respectively as the line ℝ, i.e. it does not matter which point of S ¹ is taken to be 0. This property is not shared by TV regularization (Fig. 10). For α∈ℝ we define the shift operator T _α :Γ→Γ by T _α (t)=t+α mod 1.

Proposition 5

(Cyclic Shift Invariance)

For every u:Ω→Γ and α∈ℝ it holds

$$ {TV_{{S}^1}}(T_\alpha\circ u)={TV_{{S}^1}}(u). $$

(24)

Note that the cyclic shift T _α is a usual shift followed by a change of representation modulo 1. Since ${TV_{{S}^{1}}}$ is clearly invariant under usual shifts, i.e. ${TV_{{S}^{1}}}(u+\alpha)={TV_{{S}^{1}}}(u)$ which follows immediately from the general definition (20), the statement follows from the more fundamental Proposition 6, stated below.

Proposition 6

(Representation Invariance)

For a u:Ω→ℝ and an integer function k:Ω→ℤ define u _k (x):=u(x)+k(x). Then

$$ {TV_{{S}^1}}(u_k)={TV_{{S}^1}}(u). $$

(25)

Proof

By Theorem 1,

$${TV_{{S}^1}}(u_k) = \sup_{\varphi^x\in K} \int _\varOmega\int_0^{u_k(x)} \operatorname{div}_x\varphi^x(x,s) \,ds \,dx. $$

Writing $a(s):=\operatorname{div}_{x}\varphi^{x}(x,s)$ for brevity, the inner integral is

$$\begin{aligned}[t] \int_0^{u_k(x)} a(s) \,ds &= \int_0^{u(x)+k(x)}a(s) \,ds \\ &= \int_{k(x)}^{u(x )+k(x)}a(s) \,ds + \int _0^{k(x)}a(s) \,ds \\ &= \int_{0}^{u(x)}a\bigl(s+k(x)\bigr) \,ds + \int _0^{k(x)}a(s) \,ds. \end{aligned} $$

Since φ ^x(x,⋅) is 1-periodic with $\int_{0}^{1}\varphi ^{x}(x,s) \,ds=0$ and the operator $\operatorname{div}_{x}$ is linear, also $(\operatorname{div}_{x}\varphi^{x})(x,\cdot)$ is 1-periodic with $\int_{0}^{1}\operatorname{div}_{x}\varphi^{x}(x,s) \,ds=0$. Therefore, the above equality gives

$$\int_\varOmega\int_0^{u_k(x)} \operatorname{div}_x\varphi^x \,ds \,dx = \int _\varOmega\int_{0}^{u(x)} \operatorname{div}_x\varphi^x \,ds \,dx. $$

Taking the supremum over φ ^x∈K on both sides yields the required identity. □

This means that ${TV_{{S}^{1}}}$ is independent of the ℝ-representation of the S ¹-value u(x) at each point x∈Ω. We can safely choose any other representation u(x)+k(x) at every x∈Ω without altering the value of ${TV_{{S}^{1}}}(u)$. On the other hand, the usual TV of course does depend on the representation.

A useful geometrical property of ${TV_{{S}^{1}}}$ is that it is invariant with respect to rigid transformations of the domain Ω:

Proposition 7

(Rigid Transformation Invariance)

Let Ω′⊂ℝ^m and A:Ω′→Ω be an isometry. Then for any u:Ω→ℝ,

$$ {TV_{{S}^1}}(u\circ A)={TV_{{S}^1}}(u). $$

(26)

Proof

Follows from representation (20) by the integral transformation formula and the invariance of the set K in (21) with respect to linear isometries. □

In Sect. 5 we will address the existence of minimizers for general ${TV_{{S}^{1}}}$ regularized problems. The proof relies on the following important lower-semicontinuity property of ${TV_{{S}^{1}}}$.

Proposition 8

(Lower-Semicontinuity)

${TV_{{S}^{1}}}$ is lower-semicontinuous with respect to pointwise a.e. convergence in the $d_{{S}^{1}}$ metric, i.e. it holds

$$ {TV_{{S}^1}}(u)\leq\liminf_{n\to\infty}{TV_{{S}^1}}(u_n) $$

(27)

for all sequences u _n :Ω→ℝ, n≥1, and functions u:Ω→ℝ with $d_{{S}^{1}}(u_{n}(x),u(x))\to0$ for a.e. x∈Ω.

Proof

Let u _n ,u:Ω→ℝ with u _n (x)→u(x) pointwise a.e. in Ω in the $d_{{S}^{1}}$ metric, i.e. $d_{{S}^{1}}(u_{n}(x),u(x))\to0$ for a.e. x∈Ω. For every φ∈K and v:Ω→ℝ define

$$ {F}_\varphi(v):=\int_{\varOmega}\int_0^{v(x)} \operatorname{div}_x \varphi^x(x,s) \,ds \,dx. $$

(28)

By representation in Theorem 1 it holds

$$ {TV_{{S}^1}}(v)= \sup_{\varphi\in K}{F}_\varphi(v) \quad\text{for all}\ v:\varOmega \to \mathbb{R}, $$

(29)

and for instance

$$ {F}_\varphi(v) \leq{TV_{{S}^1}}(v)\quad\text{for all}\ v:\varOmega\to\mathbb{R}\ \mbox{and}\ \varphi\in K. $$

(30)

For each fixed φ∈K and n≥1 we have the estimate

with $C_{\varphi}:={\|\operatorname{div}_{x}\varphi^{x}\| }_{L^{\infty}(\varOmega\times \varGamma)}$ for every k:Ω→ℤ. We have used $\int_{\varGamma}\operatorname{div}_{x}\varphi^{x}(x,s) \,ds=0$ and the 1-periodicity of $\operatorname{div}_{x}\varphi(x,\cdot)$ together with Lemma 3 for the second equality. For each x∈Ω we can choose a k(x)∈ℤ such that $|u_{n}(x)-u(x)-k(x)|=d_{{S}^{1}}(u_{n}(x),u(x))$ due to Lemma 1. Choosing this specific function k:Ω→ℤ in the above inequality, we obtain for all φ∈K and n≥1

$$ \bigl|{F}_\varphi(u_n)-{F}_\varphi (u)\bigr| \leq C_\varphi\int_{\varOmega}d_{{S}^1} \bigl(u_n(x),u(x)\bigr) \,dx. $$

(31)

By assumption, the integrand on the right hand side tends to 0 pointwise a.e. in Ω and is obviously bounded by 1, with 1∈L ¹(Ω). Thus, Lebesgue’s convergence theorem yields that the right hand side of (31) tends to zero for n→∞, so that

$$ {F}_\varphi(u)= \lim_{n\to\infty} {F}_\varphi(u_n). $$

(32)

Therefore, by (30) we also have

$$ {F}_\varphi(u)= \liminf_{n\to\infty}{F}_\varphi(u_n)\leq \liminf_{n\to\infty}{TV_{{S}^1}}(u_n). $$

(33)

Taking the supremum over all φ in (33), and using (29), we finally get

$${TV_{{S}^1}}(u)=\sup_{\varphi\in K}F_\varphi(u)\leq \liminf_{n\to \infty }{TV_{{S}^1}}(u_n), $$

i.e. the lower-semicontinuity of ${TV_{{S}^{1}}}$. □

Giaquinta et al. proved several weak lower-semicontinuity results in [11, Sect. 6] for the ℝ²-embedding formulation of ${TV_{{S}^{1}}}$ using cartesian currents.

5 Regularization with ${TV_{{S}^{1}}}$

The introduction of the regularizer ${TV_{{S}^{1}}}$ is of course motivated by optimization problems, namely the ones where the S ¹ structure must be taken into account.

5.1 Optimization Problem and Existence of Minimizers

We consider an arbitrary, possibly nonconvex pointwise data term ∫ _Ω ϱ(x,u(x)) dx and apply ${TV_{{S}^{1}}}$ regularization to obtain the overall optimization problem

$$ \inf_{u:\varOmega\to{\mathbb{R}}} {E}(u),\quad {E}(u)=\int _\varOmega\varrho\bigl(x,u(x)\bigr) \,dx +\lambda {TV_{{S}^1}}(u). $$

(34)

The weight λ>0 allows to choose the influence of the regularizer. Since we work with functions u:Ω→S ¹, represented by u:Ω→ℝ, it is natural to assume that ϱ is representation invariant, i.e. that ϱ(x,⋅) is 1-periodic. To make sure that the problem (34) has a minimizer we also assume that ϱ(x,⋅) is lower-semicontinuous with respect to $d_{{S}^{1}}$ convergence, i.e.

$$ \varrho(x,t)\leq\liminf_{n\to\infty}\varrho(x,t_n) \quad \text{whenever}\ d_{{S}^1}(t_n,t)\to0 $$

(35)

for each fixed x∈Ω and t∈ℝ. To ensure lower semicontinuity of the data term energy, we further assume a lower bound ϱ(x,t)≥g(x) for all x∈Ω, t∈ℝ with some g∈L ¹(Ω). For example, this is automatically satisfied if the data term is nonnegative, as will be the case in all of our considered applications.

First of all, the next theorem ensures the existence of minimizers of (34). The proof of this result requires an argument especially tailored for the S ¹ case, since functions u with ${TV_{{S}^{1}}}(u)<\infty$ need not necessarily lie in BV(Ω). As a simple example consider any function u:Ω→{0,1} on Ω=(0,1) which jumps infinitely often between 0 and 1, so that ${TV_{{S}^{1}}}(u)=0$ and TV(u)=∞. Note that the theorem establishes existence of functions u:Ω→ℝ instead of u:Ω→[0,1), in accordance with the extended Definition 2 of ${TV_{{S}^{1}}}$.

Theorem 2

(Solvability)

Problem (34) admits a minimizer u:Ω→ℝ (with ${TV_{{S}^{1}}}(u)<\infty$).

Proof

Consider a minimizing sequence (u _n ) _n , so that

$$ \int_\varOmega\varrho\bigl(x,u_n(x)\bigr) \,dx + \lambda{TV_{{S}^1}}(u_n) \stackrel{n\to\infty}{ \longrightarrow} {E}^\ast $$

(36)

with E ^∗ being the optimal infimum value in (34). First, this gives the uniform bound ${TV_{{S}^{1}}}(u_{n})\leq C$ for all n with some C>0. Consider the embedding e:ℝ→ℝ² of the circle S ¹, respectively line ℝ into ℝ² as in Lemma 4 below. By this lemma the functions e∘u _n :Ω→ℝ² are elements of BV(Ω;ℝ²) with ${TV}({{\mathrm {e}}\circ u_{n}})\leq{TV_{{S}^{1}}}(u_{n})\leq C$ for all n. Thus, the sequence (e∘u _n ) _n is uniformly bounded in BV(Ω;ℝ²) (the L ¹ norm is trivially bounded since $|{{\mathrm{e}}\circ u_{n}(x)}|=\frac {1}{2\pi}$ for all x and n). By the weak^∗ compactness of BV(Ω;ℝ²) there exists a subsequence, again denoted by e∘u _n , weak^∗ converging to some v:Ω→ℝ². For instance, e∘u _n →v in L ¹(Ω;ℝ²).

Therefore, also e∘u _n →v pointwise a.e. in Ω for a subsequence. Since $|{{\mathrm{e}}\circ u_{n}}(x)|=\frac{1}{2\pi}$ for all x and n, this gives that also $|v(x)|=\frac{1}{2\pi}$ a.e. in Ω. This allows us to define a function u:Ω→ℝ with e∘u(x)=v(x) a.e. in Ω. The convergence (e∘u _n )(x)→v(x)=(e∘u)(x) directly gives u _n (x)→u(x) a.e. in the $d_{{S}^{1}}$ metric, i.e. $d_{{S}^{1}}(u_{n}(x),\allowbreak u(x))\to0$. By the lower-semicontinuity property 8 of ${TV_{{S}^{1}}}$ it follows that

$${TV_{{S}^1}}(u)\leq\liminf_{n\to\infty} {TV_{{S}^1}}(u_n). $$

Also, by the lower-semicontinuity and the lower bound of the data term ϱ we can apply Fatou’s lemma to get

$$\int_\varOmega\varrho\bigl(x,u(x)\bigr) \,dx\leq \liminf_{n\to\infty}\int_\varOmega\varrho\bigl(x,u_n(x) \bigr) \,dx. $$

Combining these two estimates we get

i.e. u:Ω→ℝ minimizes E and ${TV_{{S}^{1}}}(u)<\infty$. □

Existence of Dirichlet minimizers for the corresponding formulation of energy (34) in the setting of cartesian currents was proven in [9, Sect. 5, Theorem 1].

In the proof we have used the following embedding result.

Lemma 4

Define an embedding map of the circle S ¹, respectively the line ℝ, into ℝ² by

$$ {\mathrm{e}}:{\mathbb{R}}\to{\mathbb{R}}^2,\quad{\mathrm{e}}(t):= \frac{1}{2\pi}\binom{\cos2\pi t}{\sin2\pi t}. $$

(37)

Then each u:Ω→ℝ with ${TV_{{S}^{1}}}(u)<\infty$ defines a function e∘u:Ω→ℝ² with e∘u∈BV(Ω;ℝ²) and the following inequality holds:

$$ {TV}({{\mathrm{e}}\circ u}) \leq{TV_{{S}^1}}(u). $$

(38)

Proof

Recall that the total variation for vectorial functions v∈L ¹(Ω;ℝ²) is defined similarly as in the scalar case (3) by

$$TV(v) := \sup_{|\varphi|\leq1} \int_\varOmega v_1(x) \operatorname{div}_x \varphi_1(x)+v_2(x) \operatorname{div}_x \varphi_2(x) \,dx $$

where the supremum is taken over all $\varphi\in{C_{c}^{\infty}(\varOmega; {{\mathbb{R}}^{m}})}^{2}$ with $\sqrt{\varphi_{1}(x)^{2}+\varphi_{2}(x)^{2}}\leq1$ for all x. Consider specifically v:=e∘u and an arbitrary fixed $\varphi\in {C_{c}^{\infty}(\varOmega; {{\mathbb{R}}^{m}})}^{2}$. Define a p:Ω×ℝ→ℝ^m by

$$p(x,t):=-\varphi_1(x)\sin2\pi t + \varphi_2(x)\cos2\pi t $$

for all x∈Ω and t∈ℝ. Then one easily checks that p∈K with the set K in (21). Furthermore, by simple integration

The constant $\frac{1}{2\pi}$ in this expression can be eliminated, since φ ₁ is zero on the boundary of Ω. We obtain

By the representation (20) of ${TV_{{S}^{1}}}$, the right hand side is bounded by ${TV_{{S}^{1}}}(u)$ independently of p and thus of φ. Taking the supremum over all φ we get the required inequality (38). □

5.2 Lifted Optimization Problem and Relaxation

The question is now how to efficiently solve the problem (34). For the implementation, it is convenient to work with specific unique representatives of the cyclic values u(x) for each x. We choose Γ=[0,1) as the basic interval, i.e. consider u:Ω→Γ as the solution candidates.

First, using representation (20) the problem (34) can be rewritten as the saddle-point problem

$$ \inf_{u}\sup_{\varphi\in K}\int_{\varOmega\times \varGamma}-1_u \operatorname{div}\varphi\,ds \,dx $$

(39)

with the set K given by

$$ \begin{aligned}[b] K= \biggl\{&\varphi= \bigl(\varphi^x,\varphi^t\bigr)\in{C_c^\infty \bigl(\varOmega; C^\infty\bigl(\varGamma;{{\mathbb{R}}^{m}}\times{ \mathbb{R}}\bigr)\bigr)} \bigg| \\ &\varphi^t(x,t)\geq-\varrho(x,t), \bigl|\varphi^x(x,t)\bigr|\leq\lambda, \\ &\int_\varGamma\varphi^x(x,s) \,ds=0 \ \forall x\in\varOmega,\ t\in\varGamma\biggr\}. \end{aligned} $$

(40)

The dual variables φ=(φ ^x,φ ^t) in the set K now also have a “vertical” component φ ^t in addition to φ ^x to handle the data term ϱ. The constraint set (40) can be derived exactly as in Sect. 3, using the equivalent constraint reformulation of Proposition 3. Alternatively, one could derive the constraints from the general Lemma 2. As opposed to (21) the 1-periodicity is not required in (40) because we consider φ only on the basic set Γ=[0,1). Note that we have incorporated the weight λ of ${TV_{{S}^{1}}}$ in (34) into the set K. For the weighted variant ${TV_{{S}^{1}}^{g}}$, the second constraint in K must be replaced by |φ ^x(x,t)|≤λg(x).

The idea to find a solution u of (39) is to optimize directly in terms of graph functions 1 _u instead of u. Note that although the expression (39) is convex in 1 _u , the set of solutions {1 _u ∣u:Ω→Γ} is not convex. The reason is that the graph functions 1 _u :Ω×Γ→{0,1} have binary range. Therefore, to overcome this difficulty we set v=1 _u and relax the problem (39) to

$$ \inf_{v\in C}{\mathcal{E}}(v),\quad{ \mathcal{E}}(v)=\sup_{\varphi \in K}\int_{\varOmega\times\varGamma}-v \operatorname{div}\varphi\,ds \,dx $$

(41)

with the convex set

(42)

This set is the convex hull of the valid binary graph functions. In other words, we extend the set of possible solutions 1 _u to also allow relaxed “graph functions” with possible intermediate values in [0,1].

Note that the condition in C on the monotonicity of v(x,⋅) is actually not necessary. In fact, since φ ^t can be chosen arbitrarily large in (40), the supremum in (41) will be finite only if ∂ _t v≤0, i.e. if v(x,⋅) is non-increasing.

5.3 Efficient Primal-Dual Minimization

We discretize the two-dimensional image domain Ω into a {0,…,W−1}×{0,…,H−1} pixel grid, with W≥1 pixels horizontally and H≥1 pixels vertically. Dimensions other than m=2 can be handled in the same way. The discretized image domain is again denoted by Ω. We also discretize the range space Γ=[0,1) of u into n≥1 levels $\frac{0}{n},\ldots,\frac{n-1}{n}$. This is needed since the relaxed problem (41) is defined on the space Ω×Γ. The discretized variables v and φ, and the data term ϱ are represented by their node values $v(x,\frac{i}{n})=v_{i}(x)\in{\mathbb{R}}$, $\varphi^{x}(x,\frac{i}{n})=n \varphi^{x}_{i}(x)\in{{\mathbb{R}}^{m}}$, $\varphi^{t}(x,\frac{i}{n})=\varphi^{t}_{i}(x)\in{\mathbb{R}}$ and $\varrho(x,\frac{i}{n})=\varrho_{i}(x)\in{\mathbb{R}}$ at the pixels x∈Ω for every 0≤i<n. The factor n for φ ^x is chosen to simplify the resulting discretized energy.

The discretized version of (41) becomes

$$ \inf_{v\in C^d}\sup_{\varphi\in K^d} \sum _{x\in\varOmega}\sum_{i=0}^{n-1} \varphi^x_i(x)\nabla v_i(x)+ \varphi^t_i(x)\partial_t^+v_i(x) $$

(43)

with

$$ C^d = \bigl\{ (v_i)_{0\leq i<n}:\varOmega \to[0,1] \big| v_0(x)=1\ \forall x\in\varOmega\bigr\} $$

(44)

and

$$ \begin{aligned}[b] K^d = \Biggl\{& \bigl( \varphi^x_i,\varphi^t_i \bigr)_{0\leq i<n}:\varOmega\to{{\mathbb{R}}^{m}}\times{\mathbb{R}} \Bigg| \\ & \varphi^t_i(x)\geq-\varrho_i(x), \ \big|\varphi^x_i(x)\big|\leq\frac{\lambda}{n}, \\ & \sum_{j=0}^{n-1} \varphi^x_j(x)=0 \ \forall0\leq i<n, x\in\varOmega \Biggr\}. \end{aligned} $$

(45)

The discretization C ^d of the set C in (42) does not include the monotonicity constraint since it is already implied through the supremum over φ ^t as described at end of the last section. The slightly altered constraint $|\varphi^{x}|\leq\frac{\lambda}{n}$ in (45) instead of |φ ^x|≤λ in (40) arises as a consequence of discretizing the integral ∫ _Γ and the derivative ∂ _t .

We use forward differences with Neumann boundary conditions for the spatial gradient ∇. For example, $\partial_{x_{1}}f_{x_{1},x_{2}}=f_{x_{1}+1,x_{2}}-f_{x_{1},x_{2}}$ if x ₁<W−1 and 0 if x ₁=W−1 and define the divergence by $\operatorname{div}:=-\nabla^{T}$, the negative adjoint operator, in order for a discrete form of partial integration to hold. For the t-derivative $\partial_{t}^{+}$ we use forward differences with zero boundary condition: $\partial_{t}^{+}f_{t}=f_{t+1}-f_{t}$ if t<n−1 and −f _t if t=n−1. This is done to implicitly have v _n (x)=0. The negative adjoint t-derivative $\partial_{t}^{-}=-(\partial_{t}^{+})^{T}$ is then given by backward differences: $\partial_{t}^{-}f_{t}=f_{t}-f_{t-1}$ if t>0 and f _t if t=0.

The optimization problem (43) is a classical saddle-point problem. We solve it by the general algorithm of [21] which is especially devised for this kind of problems. This is a fast primal-dual algorithm which consists essentially in a gradient descent in v and a gradient ascent in φ, with an orthogonal reprojection onto the sets C ^d and K ^d. Since K ^d includes the non-local constraint $\sum_{j=0}^{n-1}\varphi^{x}_{j}=0$ there is no simple formula for the projection. Therefore, instead of a direct projection we implement this sum constraint by Lagrange multipliers. For this, we add the term

$$ \inf_{q:\varOmega\to{{\mathbb{R}}^{m}}}\sum _{x\in\varOmega} - q(x)\cdot\sum_{j=0}^{n-1} \varphi^x_j(x) $$

(46)

to the energy (43). The overall optimization problem becomes

(47)

with no constraints on the Lagrange multiplier q:Ω→ℝ^m, the set C ^d as in (44) and the set $K^{d}_{0}$, which is K ^d in (45) without the integral constraint:

$$ K^d_0 = \biggl\{ \varphi\bigg|\varphi^t_i(x) \geq-\varrho_i(x),\ \big|\varphi^x_i(x)\big|\leq \frac{\lambda}{n}\ \forall i,x \biggr\}. $$

(48)

The equations for minimization of (47) can now be obtained in a straightforward way from the general algorithm in [21] and are listed in Fig. 4. In the algorithm, we denote by π _M the euclidean projection onto M. Beside τ=σ=1 one is also free to choose any other time steps τ,σ>0 with τσ≤1. We use [19] to set the time steps automatically.

Fig. 4

Primal-dual algorithm for the ${TV_{{S}^{1}}}$ regularized optimization problem (34), with the discrete formulation (47)

Note that due to Proposition 3 we can substantially reduce the amount of memory required to implement the ${TV_{{S}^{1}}}$ regularization by an order of magnitude. For illustration, for a 256×256 image and n=64 levels discretization for the range set Γ, the original set (12) having quadratically many constraints requires 1232 MB memory overall, while the set (21) with linearly many constraints requires only 97 MB. In fact, for (21) only one constraints needs to be dualized as an additional energy term (46), introducing new variables q(x), x∈Ω.

5.4 Optimality of Solutions

In practice, the computed relaxed graph function solution v:Ω×Γ→[0,1] may actually not be binary at some points x∈Ω, so that v(x,⋅) is some decreasing function different from a step function. For the optimization problem with the usual TV regularizer instead of ${TV_{{S}^{1}}}$ in (34) it is known [22] that a simple thresholding of the relaxed solution v e.g. at level $\frac{1}{2}$,

$$ u(x):=\sup_{t\in\varGamma:\ v(x,t)\geq\frac{1}{2}}t, $$

(49)

produces an optimal solution u of (34). In our ${TV_{{S}^{1}}}$ case there is a striking difference: The discretized problem is NP-hard!

Proposition 9

(Discrete ${TV_{{S}^{1}}}$ is NP-Hard)

For a discrete range Γ with n≥3 levels, where n=3z for some z∈ℤ, the optimization problem (34) is NP-hard.

Proof

The range Γ is discretized into n equally spaced angles $\alpha_{i}=\frac{i}{n}$, i=0,…,n−1. Since n=3z with some z∈ℤ, the set of angles contains the subset $\mathcal{M}=\{0,\frac {1}{3},\frac{2}{3}\}$. Choosing the data term ϱ _i (x)=∞ for every i with $\alpha_{i}\not\in\mathcal{M}$ ensures that any candidate solution with finite energy will be a function $u:\varOmega\to\mathcal{M}$, i.e. only these three angles will be present. As the distance $d_{{S}^{1}}$ is the same for any pair of these three angles, by Proposition 4, ${TV_{{S}^{1}}}$ then is nothing but a Potts regularizer on three labels. The latter problem is known to be NP hard [5] as the multiway cut problem [13] can be reduced to it. □

Of course, the discretization step is necessary in order to practically compute a solution. In light of the above result, in general we cannot expect exact solutions to (34). Nevertheless, we still can use the thresholding formula (49) to obtain an approximate solution. Furthermore, an energy bound holds which gives an a posteriori energy estimate of the quality of the obtained solution:

$$ \bigl|{E}(u)-{E}\bigl(u^\ast\bigr)\bigr |\leq \bigl|{ \mathcal{E}}(1_u)-{\mathcal{E}}(v)\bigr|. $$

(50)

Here u ^∗ is the unknown optimal solution to (34), v the relaxed solution of (41) and u an approximate solution to (34) obtained by some binarization method from v, e.g. by (49). The bound follows from the simple observation that

$$ {\mathcal{E}}(v) \leq{\mathcal{E}}(1_{u^\ast}) = {E}\bigl(u^\ast \bigr) \leq{E}(u) = {\mathcal{E}}(1_u), $$

(51)

where the inequalities hold because v is optimal for ${\mathcal{E}}$ and u ^∗ is optimal for E. In all our experiments the deviation from the optimal solution was less than 5 % energy-wise. This is an overestimation of the true deviation obtained with regard to formula (50) by comparing ${\mathcal{E}}(1_{u})$ to ${\mathcal{E}}(v)$.

5.5 Primal Energy Computation

The primal energy ${\mathcal{E}}(v)$ for each candidate solution v∈C ^d can be computed by evaluating the supremum in (43) or, equivalently, the supremum in (47) and the infimum over the Lagrange multiplier q:

$$ \begin{aligned}[b] {\mathcal{E}}(v)&=\sum_{x\in\varOmega} \sum_{i=0}^{n-1}-\varrho_i(x) \partial_t^+ v_i(x) \\ &\quad + \frac{\lambda}{n}\sum_{x\in\varOmega} \min_{q\in{{\mathbb{R}}^{m}}}\sum_{i=0}^{n-1} \bigl|\nabla v_i(x)-q \bigr|. \end{aligned} $$

(52)

A value q∈ℝ^m minimizing

$$ {\|z\|}:=\min_{q\in{{\mathbb{R}}^{m}}}\sum _{i=0}^{n-1}|z_i-q| $$

(53)

for a collection of vectors z=(z ₀,…,z _n−1)∈(ℝ^m)ⁿ is known as the “geometric median” of z. It can be computed e.g. using the iterative algorithm in [18].

5.6 Improved Binarization Method

The binary solution u obtained by the simple thresholding method (49) may produce undesirable artifacts in some cases as seen in the left image of Fig. 5. We propose an improved binarization method, which chooses the “best” binarized solution with respect to the actually used regularizer ${TV_{{S}^{1}}}$. For a fixed point x∈Ω let v(x)=(v ₀(x),…,v _n−1(x)) be the vector v(x,⋅) computed by the algorithm. We compare v(x) with all possible n candidate binary graph functions $f^{i}=(f^{i}_{0},\ldots,f^{i}_{n-1})$, 0≤i<n, with $f^{i}_{j}:=\chi_{j\leq i}$. For all x∈Ω we assign

$$ u(x):=\frac{i(x)}{n},\quad \text{where}\ i(x):=\mathop{\mathrm{arg\, min}}_{ 0\leq i<n} \bigl\|v(x)-f^i\bigr\| $$

(54)

with the seminorm ∥⋅∥ in (53). Since here we only deal with scalar values $z_{j}:=v_{j}(x)-f^{i}_{j}$, the “geometric median” q realizing the minimum in (53) is easily seen to be the usual median of the numbers z ₀,…,z _n−1. It can thus be computed by simply sorting these numbers. In practice, we observed that this binarization removes the artifacts of the simple method (49), see Fig. 5.

Fig. 5

Improved binarization of the relaxed solution, here for the inpainting problem from Sect. 7.3. While simple binarization by thresholding the relaxed graph function (left) may lead to artifacts (center), the proposed adaptive method (right) picks a binary value closest with respect to a distance derived from the regularizer ${TV_{{S}^{1}}}$ itself

6 General Regularizers for S ¹-Valued Functions

Recall that our formulation of the total cyclic variation ${TV_{{S}^{1}}}$ is, in essence, based on the functional lifting framework of Sect. 3.1, choosing special penalizations for the smooth and the jump part of u. We have explicitly accounted for the S ¹ structure by setting the jump penalization to zero if u jumps by 1 or some other integer value. Following this idea, we can also devise convex representations for more general functionals for S ¹-valued functions.

Consider a general functional of the form (10). In order for it to be well defined for functions u:Ω→S ¹ with cyclical range S ¹, which are represented by functions u:Ω→ℝ, the functions h and d must naturally satisfy the following compatibility conditions:

(55)

(56)

This is because we want the values u(x)+k to actually represent one and the same point on S ¹ independently of k∈ℤ. In other words, we demand E(u) to be representation invariant in the sense of Proposition 6.

By functional lifting, a convex representation of E in terms of 1 _u is given by (8) with the constraints (9) on φ. Just as in the proof of Proposition 3, we can show that (56) implies that φ(x,⋅) is necessarily 1-periodic and that ∫ _Γ φ ^x(x,s) ds=0.

The supremum over φ may not be attained for general E. Then, functional lifting yields a convex relaxation of E in terms of 1 _u . We also assume that we have smooth vector fields, so that we can employ integration by parts. Summarizing, a convex relaxation of E(u) for u∈SBV(Ω) is given by

$$ \begin{aligned}[b] {{E}}_{\mathrm{conv}}(u)&:=\sum _{\varphi\in K}\int_\varOmega-1_u \operatorname{div} \varphi\,ds \,dx \\ &\quad= \sup_{\varphi\in K}\int_\varOmega\int_0^{u(x)}- \operatorname{div}\varphi(x,s) \,ds \,dx \end{aligned} $$

(57)

with the constraint set

(58)

Note that the inequality constraints are required only for t,t′∈Γ=[0,1). Assuming the compatibility conditions (55) and (56) we can prove a similar representation invariance property of the convex relaxation E _conv as in Proposition 6. This means that the convex relaxation E _conv of E can indeed be viewed as a functional defined for functions u:Ω→S ¹, independently of their representation as u:Ω→ℝ.

Proposition 10

(Representation Invariance)

Let u:Ω→ℝ and let k:Ω→ℤ be some integer function. Define u _k (x):=u(x)+k(x). Then E _conv(u _k )=E _conv(u).

Proof

By (57),

$$\begin{aligned}[t] {{E}}_{\mathrm{conv}}(u) &= \sup_{\varphi\in K} \int _\varOmega\int_{0}^{u_k(x)} \bigl( \operatorname{div}_x\varphi^x+\partial_t \varphi^t \bigr) \,ds \,dx \\ &= \sup_{\varphi\in K} \int_\varOmega\int_{0}^{u(x)+k(x)} \bigl(\operatorname{div}_x\varphi^x+\partial_t \varphi^t \bigr) \,ds \,dx. \end{aligned} $$

Just as in the proof of Proposition 6, the integral over $\operatorname{div}_{x}\varphi^{x}$ can be written as

$$\int_\varOmega\int_{0}^{u(x)+k(x)} \operatorname{div}_x\varphi^x \,ds \,dx = \int _\varOmega\int_{0}^{u(x)} \operatorname{div}_x\varphi^x \,ds \,dx. $$

On the other hand, for the inner integral over ∂ _t φ ^t we can write

$$\begin{aligned}[t] \int_{0}^{u(x)+k(x)} \partial_t\varphi^t \,ds &= \varphi^t \bigl(u(x)+k(x) \bigr)-\varphi^t(0) \\ &= \varphi^t \bigl(u(x) \bigr)-\varphi^t(0) = \int _{0}^{u(x)}\partial_t \varphi^t \,ds \end{aligned} $$

since φ ^t(x,⋅) is 1-periodic. Together, this combines to

Taking the supremum over φ∈K on both sides we obtain the required identity. □

In the next sections we give some notable examples of regularizers R for S ¹-valued functions, which have already been successfully applied in the case of functions with linear range. In each case, we give the constraints on the duals φ for the convex relaxation of the overall energy ∫ _Ω ϱ(x,u(x)) dx+R(u).

6.1 Huber S ¹-Regularization

Regularization with the usual TV is known to produce piecewise constant solutions, an effect known as staircasing. Experiments show that this is also the case for ${TV_{{S}^{1}}}$. A simple remedy is to use quadratic penalization for small values of ∇u and linear penalization otherwise. For this, one penalizes the gradients ∇u (in the region Ω∖S _u where u is smooth) by the Huber function

$$ h_\varepsilon(p) := \begin{cases} \frac{|p|^2}{2\varepsilon} &\text{if}\ |p|\leq\varepsilon, \\ |p|-\frac{\varepsilon}{2} &\text{else} \end{cases} $$

(59)

for some small ε>0, which smooths out the kink at the origin. The regularizer is then

$$ R(u)=\lambda\int_{\varOmega\setminus {S_u}}h_\varepsilon( \nabla u) \,dx +\lambda\int_{{S_u}}d_{{S}^1}\bigl(u^-,u^+ \bigr) {d\mathcal{H}^{{m}-1}}. $$

(60)

The corresponding convex set K for linear structures was computed in [22]. Adding the vanishing integral constraint, the constraints (58) become

(61)

6.2 Quadratic S ¹-Regularization

In the case of vector space valued functions, application of the quadratic regularizer produces a smoothing of the image, which is roughly equivalent to smoothing with a Gaussian kernel. Our framework enables one to define such a smoothing operation also for S ¹-valued functions in a natural way. We consider the regularizer

$$ R(u)=\alpha\int_{\varOmega}|\nabla u|^2 \,dx + \int _{S_u}\delta_{d_{{S}^1}(u^-,u^+)=0} {d\mathcal{H}^{{m}-1}} $$

(62)

with parameter α>0 where the indicator function δ _t is defined as zero if t=0 and as ∞ otherwise. It can be seen as the limiting case of the Huber regularization (60), defining λ depending on ε by λ _ε :=α⋅2ε and letting ε→∞. Then λ _ε h _ε (∇u)→α|∇u|² in the smooth part, and in the jump part the jumps are penalized more and more, so that in the limit they become prohibited unless $d_{{S}^{1}}(u^{-},u^{+})=0$, i.e. if u ⁻ and u ⁺ actually represent one and the same value in S ¹.

The relaxation is derived from (61) by means of this limiting process giving the constraints

(63)

6.3 Truncated Linear S ¹-Regularization

If two values u ₁,u ₂ are “too” distinct, it is often useful to penalize just the fact that the values are different, by a constant c independent of u ₁,u ₂. For small differences one can still use e.g. the $d_{{S}^{1}}$ distance as in the case of ${TV_{{S}^{1}}}$. This leads to the truncated linear penalizer

$$ \begin{aligned}[b] R(u)&=\lambda\int_{\varOmega\setminus{S_u}}|\nabla u| \,dx \\ &\quad+ \int_{{S_u}} \min\bigl(\nu, \lambda d_{{S}^1} \bigl(u^-,u^+\bigr) \bigr) {d\mathcal{H}^{{m}-1}} \end{aligned} $$

(64)

with parameters λ,ν>0. A relaxation is given by (41) with the constraints

(65)

In order for the truncation in the jump part to have any effect, the truncation parameter ν must of course be chosen smaller than $\frac{1}{2}\lambda$, where $\frac{1}{2}$ is the maximal value achievable by $d_{{S}^{1}}$.

6.4 Mumford-Shah S ¹-Regularization

We can even obtain the full Mumford-Shah regularizer for cyclic structures:

$$ R(u)=\alpha\int_{\varOmega\setminus{S_u}}|\nabla u|^2 \,dx + \nu\int _{{S_u}}\chi_{d_{{S}^1}(u^-,u^+)\neq0} {d\mathcal{H}^{{m}-1}} $$

(66)

with parameters α,ν>0. The last integral over the jump part penalizes the overall length of the interface S _u , but it considers only the interface points where $d_{{S}^{1}}(u^{-},u^{+})\neq0$, i.e. if there is really a jump in the S ¹ sense. Minimization of the Mumford-Shah functional produces piecewise smooth approximations of input signals f:Ω→ℝ, choosing for example $\varrho(x,u(x)):=d_{{S}^{1}}(u(x),f(x))^{2}$.

For the case of functions with linear range, in [21] Pock et al. introduced an algorithm for the minimization of this functional based on the method of functional lifting. A relaxation for functions u:Ω→S ¹ is given by (41) with the constraints

(67)

6.5 Implementation

The quadratic and Huber-TV penalization can be implemented in exactly the same way as in the case of ${TV_{{S}^{1}}}$. The only difference is the projection of dual variables φ onto the corresponding constraint sets K in (58). For the quadratic penalizer one has to project onto a parabola, and for Huber-TV onto a sideways truncated parabola, see [22] for more details.

The situation is different for the truncated linear and the Mumford-Shah penalizer since there are quadratically many non-local constraints $|\int_{t}^{t'}\varphi^{x}(x,s) ds|\leq\nu$, respectively in the discrete setting

$$ \biggl|\sum_{i<z\leq j} \varphi^x_z(x)\biggr|\leq\nu\quad\forall0\leq i<j<n. $$

(68)

Since each constraint involves many φ’s at once, we use a different scheme than in Sect. 5.3. First, we introduce auxiliary variables p _i :Ω→ℝ^m for 0≤i<n through $\partial_{t}^{-}p_{i}=\varphi^{x}_{i}$ and add the corresponding Lagrange multiplier terms

$$ \inf_{\mu_i:\varOmega\to{{\mathbb{R}}^{m}}}\sum_{x\in\varOmega}\sum _{i=0}^{n-1}\mu_i \bigl( \partial_t^-p_i-\sigma^x_i \bigr) $$

(69)

to the energy (43) to enforce these equalities. Second, by this the constraints on φ ^x translate to the simpler ones |p _j −p _i |≤ν for 0≤i<j<n, x∈Ω. We now use the observation that

$$ \delta_{|d|\leq\nu}=\sup_{a\in{{\mathbb{R}}^{m}}}a\,d-\nu|a| \quad\forall d\in{{ \mathbb{R}}^{m}} $$

(70)

to enforce them (the indicator function δ _|d|≤ν is 0 if the constraint |d|≤ν is fulfilled and ∞ otherwise), adding the terms

$$ \inf_{a_{ij}:\varOmega\to{{\mathbb {R}}^{m}}}\sum_{x\in\varOmega} \sum_{0\leq i<j<n}-a_{ij}(p_j-p_i)+ \nu|a_{ij}| $$

(71)

to the energy. Finally, in terms of p the S ¹-constraint ∑_0≤j<n φ _j (x)=0 translates into simply p _n−1(x)=0.

We use the extension [7] of the primal-dual algorithm [21], since the proximal operators are not simply projections this time. As there are far more primal than dual variables due to quadratically many a _ij ’s in (71), we suggest to use the version of the algorithm in [7] where the “bar”-copies are introduced for the duals rather than for the primals.

7 Experiments

In this section we present several experiments demonstrating the use of ${TV_{{S}^{1}}}$ and other cyclic regularizers for various imaging problems. We evaluate the ${TV_{{S}^{1}}}$ results by comparing them with TV regularization, since no regularizers for S ¹-valued functions have yet been investigated and ${TV_{{S}^{1}}}$ is supposed to behave like TV in regions where u is smooth.

With a parallel CUDA implementation on NVIDIA GTX 480 a typical runtime for 256×256 images using 64 levels for Γ is about 10 seconds for ${TV_{{S}^{1}}}$. TV [22] requires about 5 seconds. For illustration, the ${TV_{{S}^{1}}}$ runtime without using our efficient formulation in Proposition 3 is about 12 minutes for 64 levels, and still about 2 minutes for 32 levels. The latter are also the runtimes for the more advanced regularizers such as truncated linear and Mumford-Shah from Sect. 6, since we use the same implementation scheme in Sect. 6.5 for the non-local integral constraints in (58) and in (15). We used n=32 levels for Γ in all our experiments.

7.1 The ${TV_{{S}^{1}}}$-L ² Model

The analogon of the famous ROF denoising model of Rudin, Osher and Fatemi [25] for the cyclic case is

$$ \inf_u\int_\varOmega d_{{S}^1}\bigl(u(x),f(x)\bigr)^2 \,dx + \lambda {TV_{{S}^1}}(u). $$

(72)

We apply this to a one dimensional example in Fig. 6. The signal f consisting of a monotonous and a constant part has been degraded by adding 10 % Gaussian noise producing numerous wrap-arounds. The results show that only ${TV_{{S}^{1}}}$ is able to reconstruct the signal. Thus cyclic wrap-arounds are handled correctly by ${TV_{{S}^{1}}}$. In contrast, for TV there is no choice of λ leading to a reconstruction without heavy fluctuations or large displacements. This example clearly demonstrates the advantage of ${TV_{{S}^{1}}}$ over noncyclic regularizers.

Fig. 6

Denoising of angle values. ${TV_{{S}^{1}}}$ (right) reconstructs the monotonous and the constant signal part correctly despite the strong noise (Gaussian 10 %). TV (center) falsely penalizes wrap-arounds driving the values towards the middle to reduce jump height. The reconstruction lacks monotonicity and is falsely equal to 1 in the constant part to avoid the jump from 1 to 0.05 in the middle

7.2 Cyclical Smoothing

A frequently encountered task in image processing is to produce a slightly smoothed version of a noisy signal. For functions with a linear range this can be easily accomplished by the standard convolution with a smoothing kernel. However, this simple approach is not applicable for functions with cyclic values. The reason is that the smoothing also occurs across jumps of length 1 which do not constitute real jumps in the S ¹ sense but only a change of representation.

In contrast, as can be seen in Fig. 7 the proposed quadratic S ¹-penalizer from Sect. 6.2 indeed provides a smoothing effect of cyclical signals while preserving jumps of length 1.

Fig. 7

Smoothing of angle values. The proposed quadratic penalizer (right) for S ¹ structures in Sect. 6.2 correctly recognizes wrap-arounds of cyclic values and produces a smoothed signal which naturally resembles the original noisy one (left). In contrast, the usual quadratic penalizer (center) for functions with linear range does not allow any value jumps at all. The resulting smoothed signal (with the cyclic data term as in (72)) tends to stick either at value 0 or 1 in the presence of wrap-arounds, and forfeits essential signal details

7.3 Inpainting

Figure 8 shows an inpainting experiment for the periodic hue values of the HSV color space. Values 0/9,…,8/9 are circularly arranged starting from the top left red region with value 0 and ending with the top right magenta region with value 8/9. We use model (72) with λ=1 and the weighted variant of the data term $\varrho(x,t)=g(x) d_{{S}^{1}} (t,f(x))^{2}$, setting g(x)=0 for points x within the inpainting circle area and g(x)=∞ otherwise.

Fig. 8

Inpainting of periodic hue values. While total variation regularization (center) does not handle wrap-arounds correctly (shrinking the interface with the highest value jump, here from magenta to red) the proposed ${TV_{{S}^{1}}}$ formulation (right) is designed to provide an optimal solution for cyclic structures at no additional cost (Color figure online)

As Fig. 8 shows, ${TV_{{S}^{1}}}$ produces the expected symmetric result, as opposed to TV. Thus, the image prior for cyclic values in regions with no available data is more natural with ${TV_{{S}^{1}}}$ than with TV.

7.4 Phase Denoising

Synthetic aperture radars (SAR) [8] capture terrain elevations by means of interferometry. A satellite sends out radio waves of certain wavelength and records the echoed waves going back from earth surface, producing a complex valued image. Two such images taken from different view points or at different times are combined to a phase differences image of the respective complex numbers at each point. The phase differences Δϕ∈[0,1) are essentially proportional to the wrapped unknown ground height H,

$$ \Delta\phi=c (H\ \mathrm{mod}\ 1) $$

(73)

with some factor c>0. Phase unwrapping techniques aim to reconstruct H from Δϕ. As the phase images Δϕ are noisy, a denoising preprocessing step is typically required. Because the phases are cyclic, our framework of S ¹ regularizers applies naturally here.

Figure 9 shows phase denoising using ${TV_{{S}^{1}}^{g}}$ on the image “longs” from the publicly available data from [8].¹ We added 10 % Gaussian noise to this simulated clean phase image, wrapping the noisy values outside of [0,1) back to this interval. We use the model (72) with λ=0.1 and apply the weighted variant ${TV_{{S}^{1}}^{g}}$ in (5). The weight g is set to the “correlation” which is available as part of the data. This is an image with (0,1] values which are inversely proportional to the local standard deviation of Δϕ in a small window.

Fig. 9

Denoising of cyclic phase images from synthetic aperture radar (SAR). The phase measurements objects of interest (left), e.g. terrain elevation, are typically rather noisy. Proposed regularizers such as ${TV_{{S}^{1}}}$ provide a natural method to obtain a denoised result (right). Top row shows the representatives of the phases from Γ=[0,1) and the bottom row the same phases using continuous hue coloring

7.5 Atom Lattice Orientations

Many material properties such as deformation behavior can be deduced knowing the structures at atomic scale. In particular one is interested in the segmentation of grains, i.e. regions with homogeneous orientation of the atom lattice. To this end, when smooth transitions between neighboring regions are allowed Boerdgen et al. [4] used TV regularization with a nonconvex data term.

Since orientations are cyclic, the total cyclic variation ${TV_{{S}^{1}}}$ is a more natural regularizer for this problem. Figure 10 shows a comparison of segmentations using ${TV_{{S}^{1}}}$ and TV, applied to an image obtained by the phase field crystal simulation model [27]. This experiment shows the solution behavior if one uses different representations of the orientation space S ¹ as [0,1). The two solutions with ${TV_{{S}^{1}}}$ are essentially identical due to the cyclic shift invariance in Proposition 5. On the contrary, with TV they may differ and important structures may not be recognized in the segmentation. For example, in Fig. 10 the upper right red area of (c) is missing in (d).

Fig. 10

Segmentation of regions with homogeneous atom lattice orientation, coloring different orientations by different hues. This example demonstrates the cyclic shift invariance of ${TV_{{S}^{1}}}$ in Proposition 5. The results in (e) for the original data term ϱ(x,t) and in (f) for the cyclically shifted one, ϱ(x,t−0.5 mod 1), are nearly indistinguishable using ${TV_{{S}^{1}}}$ (coloring in (f) is shifted accordingly for comparison). In contrast, using TV the solution may be different for different zero orientations (c–d) (Color figure online)

8 Conclusion

We have introduced a novel kind of total variation, ${TV_{{S}^{1}}}$, for cyclic structures as well as cyclic versions of other more general regularizers such as Huber-TV and Mumford-Shah. The regularizer ${TV_{{S}^{1}}}$ penalizes the value jumps with the S ¹ distance instead of linearly. A convex formulation is obtained through a recent theory for general functionals using functional lifting. We show that ${TV_{{S}^{1}}}$ has a number of useful mathematical properties such as invariance to cyclic shifts and lower-semicontinuity. The framework allows to couple the ${TV_{{S}^{1}}}$ regularizer with arbitrary data terms, subject only to natural conditions. We show existence of minimizers and provide an equivalent formulation which allows to solve the optimization problem as efficiently as the usual total variation. Experiments on a variety of imaging problems show the clear advantage of cyclic regularizers in the correct handling of value wrap-arounds as opposed to noncyclic ones such as TV.