Abstract
When defining a security notion, one typically specifies what dishonest parties cannot achieve. For example, communication is confidential if a third party cannot learn anything about the messages being transmitted, and it is authentic if a third party cannot impersonate the real (honest) sender. For certain applications, however, security crucially relies on giving dishonest parties certain capabilities. As an example, in Designated Verifier Signature (DVS) schemes, one captures that only the designated verifier can be convinced of the authenticity of a message by guaranteeing that any dishonest party can forge signatures which look indistinguishable (to a third party) from original ones created by the sender.
However, composable frameworks cannot typically model such guarantees as they are only designed to bound what a dishonest party can do. In this paper we show how to model such guarantees—that dishonest parties must have some capability—in the Constructive Cryptography framework (Maurer and Renner, ICS 2011). More concretely, we give the first composable security definitions for Multi-Designated Verifier Signature (MDVS) schemes—a generalization of DVS schemes.
The ideal world is defined as the intersection of two worlds. The first captures authenticity in the usual way. The second provides the guarantee that a dishonest party can forge signatures. By taking the intersection we have an ideal world with the desired properties.
We also compare our composable definitions to existing security notions for MDVS schemes from the literature. We find that only recently, 23 years after the introduction of MDVS schemes, sufficiently strong security notions were introduced capturing the security of MDVS schemes (Damgård et al., TCC 2020). As we prove, however, these notions are still strictly stronger than necessary.
C. Portmann—Work done while author was at ETH Zürich, Switzerland.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
1.1 Composable Security
In a nutshell, composable security frameworks define security by designing an ideal world and proving that the real world is indistinguishable [2, 5, 8, 12, 20, 22, 23, 26]. Typically, one first designs an ideal functionality, which corresponds to the functionality one wishes to achieve. For example, if one wants confidential communication from Alice to Bob, then the ideal functionality allows Alice to input messages, Bob to read messages, and guarantees that Eve can only learn the length of the messages input by Alice. Eve could additionally be given extra capabilities that do not violate confidentiality, e.g. inputting messages. A simulator is then connected to this ideal functionality, covering the idealized inputs and outputs available to dishonest parties and providing “real” inputs and outputs to the environment (that should be indistinguishable from those of the real world). Let \(\mathbf {S}\) denote an ideal functionality, and \(\mathsf {sim}^{}\mathbf {S}\) the ideal world consisting of \(\mathbf {S}\) with some simulator \(\mathsf {sim}^{}\) attached. Since any (efficient) simulator \(\mathsf {sim}^{}\in \varOmega \) is acceptable, one can alternatively view the ideal world as the set of all possible acceptable ideal worlds:
A security proof then shows that the real world \(\boldsymbol{\mathcal {R}}\) (also modeled as a set) is a subset of the ideal world \(\boldsymbol{\mathcal {S}}\). Since \(\mathsf {sim}^{}\) covers the dishonest parties’ interfaces of \(\mathbf {S}\), it can only further limit the capabilities of dishonest parties. For example, an ideal functionality for confidentiality might allow a third party to change Alice’s message, but if this is not possible in the real world, the simulator can disallow the environment to use that capability. This structure of the ideal world makes it impossible for traditional composable frameworks to provide guarantees about a dishonest party’s capabilities, because these might be blocked by the simulator.
Some prior works using the Constructive Cryptography (CC) framework [14, 23] have noted that the ideal world does not have to be structured as in Eq. (1.1). In particular, the simulator does not have to necessarily cover all dishonest parties’ interfaces (or might not be present at all). This relaxed view of the ideal world allows one to define composable security notions capturing the security of schemes whose security could not be modeled by traditional composable frameworks. In this work we crucially exploit this to give the first composable security notions for Multi-Designated Verifier Signature schemes. We refer the interested reader to [3] to see how to model Digital Signature Schemes (DSS) in CC, and to [14] for an extended introduction to CC, in which some of the novel techniques used here were first applied.
1.2 MDVS Schemes
Designated Verifier Signature (DVS) schemes are a variant of DSS that allow a signer to sign messages towards a specific receiver, chosen (or designated) by the signer [9, 11, 13, 16,17,18,19, 27,28,29,30, 32]. The goal of these schemes is to establish an authentic communication channel, say from a sender Alice to a receiver Bob, where the authenticity property is exclusive to the receiver Bob designated by Alice, i.e. Bob and only Bob can tell whether Alice actually sent some message authentically. In Multi-Designated Verifier Signature (MDVS) schemes [9, 11, 13, 16, 32], multiple receivers may be designated verifiers for the same message, e.g. Alice signs a message so that both Bob and Charlie can verify that Alice generated the signature, but a third party Eve would not be convinced that Alice signed it. This should hold even if a verifier is dishonest, say Bob, and provides his secret keys to Eve. MDVS schemes achieve this by guaranteeing that Bob could forge signatures that would look indistinguishable to Eve from Alice’s signatures—but Charlie could distinguish the two using his secret key, thus authenticity with respect to the designated verifiers is not violated.
MDVS schemes have numerous applications: from secure messaging (and in particular secure group messaging for the multi-verifier case) [11], to online auctions wherein all bidders place their binding-bids in a non-interactive way, and the highest bidder wins. In the case of online auctions a bidder Bob would then sign its bid to both the auctioneer Charlie and his bank Blockobank, and if Bob wins Charlie would then sign a document stating Bob is the winner of the auction; the winner could also be kept anonymous by having Charlie signing such document only with respect to Bob, its bank Blockobank and any other official entity needed to confirm Bob’s ownership of the auctioned item.
While composable security notions for DSS are well understood [1, 3, 5, 6], the literature on (M)DVS schemes provides only a series of different game-based security definitions—which we discuss in detail in Sect. 5—capturing a variety of properties that an MDVS scheme could possess. By defining the ideal world for an MDVS scheme in this work, we can compare the resulting composable definition to the game-based ones and determine which security properties are needed. It turns out that crucial properties for the security of MDVS schemes like consistency—all (honest) designated verifiers will either accept or reject the same signature—and security against any subset of dishonest verifiers were only introduced very recently [11].
1.3 Contributions
Providing Guarantees to Dishonest Parties. To capture that a dishonest party is guaranteed to have some capability, we introduce a new type of ideal world specification, which we sketch in this section. The first step consists in defining a set of ideal functionalities (called resources or resource specification in CC [22, 23]) that have the required property. For example, in the case of MDVS schemes, we want a dishonest receiver to be able to generate a valid signature. This corresponds to a channel in which both Alice (the honest sender) and Bob (the dishonest receiver) may insert messages. Thus anyone reading from that channel would not know if the message is from Alice or Bob. Let \(\widehat{\boldsymbol{\mathcal {X}}}\) denote such a set. The ideal worlds we are interested in are those in which a dishonest receiver could achieve this property if they run an (explicit) forging algorithm \(\pi \). Thus, the ideal world of interest is defined as
where \(\pi \mathbf {X}\) denotes a resource \(\mathbf {X}\) with the algorithm \(\pi \) being run at the dishonest receivers’ interface of \(\mathbf {X}\).
Similar techniques could be used to model ideal worlds for ring signatures [4, 27] or coercibility [22, 31].
Composable Security Notions for MDVS Schemes. We then use the technique described above to define composable security for MDVS schemes. For example, if one considers a fixed honest sender and a fixed set of designated verifiers (some of which may be dishonest), then an MDVS scheme is expected to achieve authenticity with respect to the honest verifiers, but this authenticity should be exclusive to them, meaning that any dishonest player should be able to generate a signature that would fool a third party Eve. Authenticity is captured in the usual way (see, e.g. [3]), as in Eq. (1.1), i.e. we define an authentic channel \(\mathbf {A}\) from Alice to the honest verifiers, and the ideal world is given by a set
The exclusiveness of the authenticity is defined with a (set of) ideal world(s) as in Eq. (1.2). Both properties are then achieved by taking the intersection of the two, namely by proving that for the real world \(\boldsymbol{\mathcal {R}}\) we have
Comparison With Existing Notions for MDVS. Now that the composable security notion is defined, we compare it to the game-based definitions from the literature. It turns out that only the most recent definitions from [11] are sufficient to achieve composable security.
More precisely, we prove reductions and a separation between our composable security definition and the games of [11]. Our statements imply the following:
-
any MDVS scheme which is Correct, Consistent, Unforgeable and Off-The-Record (according to [11]) can be used to construct the ideal world for MDVS;
-
there is an MDVS scheme which satisfies the composable definition, but which is not Off-The-Record (as defined in [11]).
1.4 Structure of This Paper
In Sect. 2 we start by introducing the concepts from CC [14, 20, 22, 23] that are needed to understand the framework. We also define repositories which are the resources we use in this work for communication between parties jointly running a protocol (see also [3]). In Sect. 3 we consider a setting in which the sender and designated receivers are fixed and publicly known. This allows us to define the ideal worlds and the corresponding composable security definition in a simpler setting. Also for simplicity, we only require that dishonest delegated verifiers have the ability to forge signatures, not third parties. We then prove that the security games from [11] are sufficient to imply composable security. In Sect. 4 we model the more general setting where the sender and designated receivers can be arbitrarily chosen. As before, we model composable security and prove that the security games from [11] are sufficient to achieve composable security in this setting as well. But we also prove a seperation between the Off-The-Record game from [11] and the composable security defintion, showing that this game is stronger than necessary. Note that in this section any dishonest party should be able to forge signatures, not only the dishonest designated verifiers. Finally, in Sect. 5 we discuss the literature related to MDVS schemes and some of the issues in previous security definitions.
2 Constructive Cryptography
The Constructive Cryptography (CC) framework [20, 22] views cryptography as a resource theory: protocols construct new resources from existing (assumed) ones. For example, a CCA-secure encryption scheme constructs a confidential channel given a public key infrastructure and an insecure channel on which the ciphertext is sent [10]. The notion of resource construction is inherently composable: if a protocol \(\pi _1\) constructs \(\boldsymbol{\mathcal {R}}\) from \(\boldsymbol{\mathcal {S}}\) and \(\pi _2\) constructs \(\boldsymbol{\mathcal {T}}\) from \(\boldsymbol{\mathcal {S}}\), then running both protocols will construct \(\boldsymbol{\mathcal {T}}\) given that one initially has access to \(\boldsymbol{\mathcal {R}}\).Footnote 1
In this section we first review the building blocks of CC in Sect. 2.1. We explain how security is defined in Sect. 2.2. Then in Sect. 2.3 we model a specific type of resources, namely repositories, which is an abstract model of communication. Throughout the rest of the paper, for any set of parties \(\mathcal {S}\), we denote by \({\mathcal {S}}^{H}\) the partition of \(\mathcal {S}\) containing all honest parties, and \(\overline{{\mathcal {S}}^{H}}\) the partition containing all dishonest parties, such that \(\mathcal {S} = {\mathcal {S}}^{H}\ \uplus \ \overline{{\mathcal {S}}^{H}}\). The set of all parties is denoted \(\mathcal {P}\).
2.1 Resource Specifications, Converters, and Distinguishers
Resource. A resource is an interactive system shared by all parties, e.g. a channel or a key resource—and is akin to an ideal functionality in UC [5]. Each party can provide inputs and receive outputs from the resource. We use the term interface to denote specific subsets of the inputs and outputs, in particular, all the inputs and outputs available to a specific party are assigned to that party’s interface. For example, an insecure channel \(\mathbf {INS}\) allows all parties to input messages at their interface and read the contents of the channel. A confidential channel resource \(\mathbf {CONF}\) shared between a sender Alice, a receiver Bob and an eavesdropper Eve allows Alice to input messages at her interface; it allows Eve to insert her own messages and it allows her to duplicate Alice’s messages, but not to read themFootnote 2; and it allows Bob to receive at his interface any of the messages inserted by Alice or Eve. As another example, an authenticated channel from Bob to Alice (\(\mathbf {AUT}\)) allows Bob to send messages through the channel and allows Alice and Eve to read messages from the channel.
Formally, a resource is a random system [24, 25], i.e. it is uniquely defined by a sequence of conditional probability distributions. For simplicity, however, we usually describe resources by pseudo-code.
If multiple resources \(\{\mathbf {R}_i\}_{i=1}^n\) are simultaneously accessible, we write  , or alternatively
, or alternatively  , for the new resource obtained by the parallel composition of all \(\mathbf {R}_i\), i.e. \(\mathbf {R}\) is a resource that provides each party with access to the (sub)resources \(\mathbf {R}_i\).
, for the new resource obtained by the parallel composition of all \(\mathbf {R}_i\), i.e. \(\mathbf {R}\) is a resource that provides each party with access to the (sub)resources \(\mathbf {R}_i\).
Converter. A converter is an interactive system executed either locally by a single party or cooperatively by multiple parties. Its inputs and outputs are partitioned into an inside interface and an outside interface. The inside interface connects to (those parties’ interfaces of) the available resources, resulting in a new resource. For instance, connecting a converter \(\alpha \) to Alice’s interface \(A\) of a resource \(\mathbf {R}\) results in a new resource, which we denote by \(\alpha ^{A}\mathbf {R}\). The outside interface of the converter \(\alpha \) is now the new \(A\)-interface of \(\alpha ^{A}\mathbf {R}\). Thus, a converter may be seen as a map between resources. Note that converters applied at different interfaces commute, i.e. \(\beta ^{B}\alpha ^{A}\mathbf {R} = \alpha ^{A} \beta ^{B}\mathbf {R}\).
A protocol is given by a tuple of converters \(\pi = \left( {\pi _{P_i}}\right) _{P_i \in {\mathcal {P}}^{H}}\), one for each (honest) party \(P_i \in {\mathcal {P}}^{H}\). Simulators are also given by converters. For any set \(\mathcal {S}\) will often write \(\pi ^{\mathcal {S}}\mathbf {R}\) for \(\left( {\pi _{P_i}}\right) _{P_i \in \mathcal {S}}\mathbf {R}\). We also often drop the interface superscript and write just \(\pi \mathbf {R}\) when it is clear from the context to which interfaces \(\pi \) connects.
For example, suppose Alice and Bob share an insecure channel \(\mathbf {INS}\) and a single use authenticated channel from Bob to Alice \(\mathbf {AUT}\) and suppose that Alice runs a converter \(\mathsf {enc}\) and Bob runs a converter \(\mathsf {dec}\), and that these converters behave as follows: First, converter \(\mathsf {dec}\) generates a public-secret key-pair (\(\mathtt {pk}\), \(\mathtt {sk}\)) for Bob and sends \(\mathtt {pk}\) over the single-use authenticated channel \(\mathbf {AUT}\) to Alice. Each time a message m is input at the outside interface of \(\mathsf {enc}\), the converter uses Bob’s public key \(\mathtt {pk}\)—which it received from \(\mathbf {AUT}\)—to compute a ciphertext \(c = {{ Enc}}_{\mathtt {pk}}\left( {m}\right) \); it then sends this ciphertext over the insecure channel to Bob (via the inside interface of \(\mathsf {enc}\) connected to \(\mathbf {INS}\)). Each time Bob’s decryption converter \(\mathsf {dec}\) receives a ciphertext c from the \(\mathbf {INS}\) channel, it uses Bob’s secret key \(\mathtt {sk}\) to decrypt c, obtaining a message \(m = {{ Dec}}_{\mathtt {sk}}\left( {c}\right) \), and if m is a valid plaintext, the converter then outputs m to Bob (via the outside interface of the converter). The real world of such a system is given by

Specification. Often one is not interested in a unique resource, but in a set of resources with common properties. For example, the confidential channel described above allows Eve to insert messages of her own. Yet, if she did not have this ability, the resulting channel would still be a confidential one. We call such a set a resource specification (or simply also a resource), and denote it with a bold calligraphic letter, e.g. a specification of confidential channels could be defined as
where \(\varOmega \) is a set of converters (the simulators) that are applied at Eve’s interface.Footnote 3
Parallel composition of specifications \(\boldsymbol{\mathcal {R}}\) and \(\boldsymbol{\mathcal {S}}\), and composition of a converter \(\alpha \) and a specification \(\boldsymbol{\mathcal {R}}\) follow by applying the operations elementwise to the resources \(\mathbf {R} \in \boldsymbol{\mathcal {R}}\) and \(\mathbf {S} \in \boldsymbol{\mathcal {S}}\).
Distinguisher. To measure the distance between two resources we use the standard notion of a distinguisher, an interactive system \(\mathbf {D}\) which interacts with a resource at all its interfaces, and outputs a bit 0 or 1. The distinguishing advantage for distinguisher \(\mathbf {D}\) is defined as

where \(\mathbf {D} {\mathbf {R}}\) and \(\mathbf {D} {\mathbf {S}}\) are the random variables over the output of \(\mathbf {D}\) when it interacts with \(\mathbf {R}\) and \(\mathbf {S}\), respectively.
Relaxation. Typically one proves that the ability to distinguish between two resources is bounded by some function of the distinguisher, e.g. for any \(\mathbf {D}\),

where \(\varepsilon (\mathbf {D})\) might be the probability that \(\mathbf {D}\) can win a game or solve some finite instance of a problem believed to be hard.Footnote 4
This distance measure then naturally defines another type of specification, namely an \(\varepsilon \)-ball: for a resource specification \(\boldsymbol{\mathcal {R}}\), the \(\varepsilon \)-ball around \(\boldsymbol{\mathcal {R}}\) is given by

If one chooses a function \(\varepsilon \left( {\mathbf {D}}\right) \) which is small for a certain class of distinguishers \(\mathbf {D}\)—e.g. \(\varepsilon \left( {\mathbf {D}}\right) \) is small for all \(\mathbf {D}\) that cannot be used to solve (a finite instance of) a problem believed to be hard, as described in Footnote 4—but potentially large for other \(\mathbf {D}\), then we have a specification of resources that are indistinguishable (to the distinguishers in the chosen class) from (one of) those in \(\boldsymbol{\mathcal {R}}\).
Remark 1
(Finite vs. Asymptotic security statements). In this paper, rather than making asymptotic security statements (where one considers the limit \(k \rightarrow \infty \) for security parameter k) we make a security statement for each possible \(k \in \mathbb {N}\). Specifications, resources, converters and distinguishers are then defined for a fixed security parameter k. If needed, one can obtain the corresponding asymptotic statements by defining sequences of resources, converters and distinguishers and then making a statement about the limit behavior of these sequences when \(k \rightarrow \infty \).
2.2 Composable Security
We now have all the elements needed to define a cryptographic construction.
Definition 1
(Cryptographic Construction [14, 23]). Let \({\boldsymbol{\mathcal {R}}}\) and \({\boldsymbol{\mathcal {S}}}\) be two resource specifications, and \(\pi \) be a protocol for \({\boldsymbol{\mathcal {R}}}\). We say that \(\pi \) constructs \(\boldsymbol{\mathcal {S}}\) from \(\boldsymbol{\mathcal {R}}\) if
For example, in the case of constructing the confidential channel described above, the real world is the singleton set with the element given in Eq. (2.1), and the ideal world is given by an \(\varepsilon \)-ball around the set of confidential channels given in Eq. (2.2), i.e. to prove security one would need to show that

Equation (2.5) is equivalent to the more traditional notation of requiring the existence of a simulator \(\mathsf {sim}\) such that for all \(\mathbf {D}\),

But the formulation in Definition 1 is more general and allows other types of ideal worlds to be defined than the specification obtained by appending a simulator at Eve’s interface of the ideal resource and taking an \(\varepsilon \)-ball.
Remark 2
(Asymptotic Construction). As pointed out in Remark 1, specifications, resources, converters and distinguishers are defined for a fixed security parameter k. The specifications and converters in Definition 1 are then to be interpreted as being defined for a concrete security parameter k, and Eq. (2.4) is to be understood as a statement about a fixed k, i.e.
For simplicity we omit the security parameter whenever it is clear from the context, and thus will simply write as in Eq. (2.4). If one wishes to make an asymptotic security statement then one defines efficient families  ,
,  ,
,  and shows that Eq. (2.6) holds asymptotically in k, meaning that there is a family
and shows that Eq. (2.6) holds asymptotically in k, meaning that there is a family  of \(\varepsilon \)-balls such that \(\pi _k \boldsymbol{\mathcal {R}}_k \subseteq \left( {\boldsymbol{\mathcal {S}}_k}^{\varepsilon _k}\right) \), and for any efficient family of distinguishers
of \(\varepsilon \)-balls such that \(\pi _k \boldsymbol{\mathcal {R}}_k \subseteq \left( {\boldsymbol{\mathcal {S}}_k}^{\varepsilon _k}\right) \), and for any efficient family of distinguishers  , the function \({\overrightarrow{\varepsilon }}({\overrightarrow{\mathbf {D}})}: \mathbb {N}\rightarrow \mathbb {R}\) defined as \({\overrightarrow{\varepsilon }}({\overrightarrow{\mathbf {D}})}({k}) := \varepsilon _k({\mathbf {D}_k})\) is negligible.
, the function \({\overrightarrow{\varepsilon }}({\overrightarrow{\mathbf {D}})}: \mathbb {N}\rightarrow \mathbb {R}\) defined as \({\overrightarrow{\varepsilon }}({\overrightarrow{\mathbf {D}})}({k}) := \varepsilon _k({\mathbf {D}_k})\) is negligible.
Remark 3
(Modeling different sets of (dis)honest parties). When one is interested in making security statements for different sets of (dis)honest parties it is not sufficient to make a single statement as in Definition 1. Instead, one makes a statement for each relevant set of (dis)honest parties. For example, let \(\pi \) be the protocol defining a converter \(\pi _i\) for each party \(P_i \in \mathcal {P}\). For every relevant subset of honest parties \({\mathcal {P}}^{H} \subseteq \mathcal {P}\), letting \(\boldsymbol{\mathcal {R}}^{{\mathcal {P}}^{H}}\) and \(\boldsymbol{\mathcal {S}}^{{\mathcal {P}}^{H}}\) denote, respectively, the available resources’ specifications—the real world—and the desired resources’ specifications—the ideal world—one needs to prove that
where \(\pi ^{{\mathcal {P}}^{H}} \boldsymbol{\mathcal {R}}^{{\mathcal {P}}^{H}}\) denotes the attachment of each converter \(\pi _i\)—run by honest party \(P_i \in {\mathcal {P}}^{H}\) as ascribed by the protocol \(\pi \)—to \(\boldsymbol{\mathcal {R}}^{{\mathcal {P}}^{H}}\). In this paper, although we will make statements of this format, i.e. modeling different sets of (dis)honest parties, we will drop the superscript \({\mathcal {P}}^{H}\) from the notation of the converters and specifications, whenever clear from the context.
2.3 Access Restricted Repositories
We formalize communication between different parties as having access to a repository resource. More specifically, a repository consists of a set of registers and a single buffer containing register identifiers; a register is a pair \(\mathtt {reg} = \left( {\mathtt {id},m}\right) \), which includes the register’s identifier \(\mathtt {id}\) (uniquely identifying the register among all repositories), and a message \(m \in \mathcal {M}\) (where \(\mathcal {M}\) is the message space of the repositoryFootnote 5). Access rights to a repository are divided in three classes: write access allows a party to add messages to a repository, read access allows a party to read all the messages in a repository, and copy access allows a party to make duplicates of messages already existing in the repository (without necessarily being able to read the messages).Footnote 6 Let \(\mathcal {P}\) be the set of all parties, and let \(\mathcal {W} \subseteq \mathcal {P}\), \(\mathcal {R} \subseteq \mathcal {P}\) and \(\mathcal {C} \subseteq \mathcal {P}\) denote the parties with write, read and copy access to a repository \(\mathbf {rep}\), respectively. We will write \({^{\mathcal {C}}}{\mathbf {rep}}_{\mathcal {R}}^{\mathcal {W}}\) whenever it is needed to make the access permissions explicit. Though we may drop them and only write \(\mathbf {rep}\) whenever clear from the context. For example, in the three party setting with sender Alice, receiver Bob and dishonest Eve, i.e. \(\mathcal {P} = \{A,B,E\}\), the insecure channel mentioned in Sect. 2.1—which allows all parties to read and write—is given by \({^{}}{\mathbf {INS}}_{\mathcal {P}}^{\mathcal {P}}\);Footnote 7 an authentic channel from Alice to Bob is given by \({^{\{E\}}}{\mathbf {AUT}}_{\{B,E\}}^{\{A\}}\); for fixed-length message spaces, the confidential channel mentioned in Sect. 2.1 is given by \({^{\{E\}}}{\mathbf {CONF}}_{\{B\}}^{\{A,E\}}\). The exact semantics of such an (atomic) repository are defined in Algorithm 1.

Parties will typically have access to many repositories simultaneously, e.g. an authentic repository from Alice to Bob and one from Alice to Charlie. One could model this as providing all these (atomic) repositories in parallel to the players, i.e.

However, this would mean that to check for incoming messages, a party would need to check every possible atomic repository \(\mathbf {rep}_i\), which could be inefficient if the number of atomic repositories is very high. Instead, we define a new resource \(\mathbf {REP}\) which is identical to a parallel composition of the atomic repositories, except that it allows parties to efficiently check for incoming messages (rather than requiring parties to poll each atomic repository \(\mathbf {rep_i}\) they have access to). Abusing notation, we denote such a resource as in Eq. (2.7), namely

The new resource \(\mathbf {REP}\) allows every party with read or copy access to issue a single ReadBuffer operation that returns a list of pairs, each pair containing a register’s identifier and a label identifying the atomic repository in which the register was written. In addition, it provides single ReadRegister and CopyRegister operations which return the contents of the register with the given \(\mathtt {id}\) and copy the register with the given \(\mathtt {id}\), respectively. Write operations for \(\mathbf {REP}\) additionally have to specify the atomic repository for which the operation is meant. The exact semantics of \(\mathbf {REP}\) are defined in Algorithm 2.

3 Modeling MDVS with Fixed Sender and Receivers
One can find multiple definitions of Multi-Designated Verifier Signature (MDVS) schemes in the literature [9, 11, 16, 32]. In this paper, we define an MDVS \(\varPi \) as a 5-tuple \(\varPi = \left( {{{ Setup}},{{ G}}_{S},{{ G}}_{V},{{ Sign}},{{ Vfy}}}\right) \) of Probabilistic Polynomial Time algorithms (PPTs), following [17]. \({{ Setup}}\) takes the security parameter as input, and produces public parameters (\(\mathtt {pp}\)) and a master secret key \((\mathtt {msk}\)),
These are then used by \({{ G}}_{S}\) and \({{ G}}_{V}\) to generate pairs of public and secret keys for the signers and verifiers, respectively,
Finally, the signing algorithm \({{ Sign}}\) requires the signer’s secret key and the public keys of all the verifiers, and the verifying algorithm \({{ Vfy}}\) requires the signer’s public key, the secret key of whoever is verifying and the public keys of all verifiers. For example suppose that party A is signing a message m for a set of verifiers \(\mathcal {V}\) and that \(B \in \mathcal {V}\) verifies the signature, then

where \(b = 1\) if the verification succeeds and \(b = 0\) otherwise.
In this section we consider a fixed sender A, a fixed set of receivers  and one eavesdropper E that is neither sender nor receiver, and is always dishonest. The set of parties is then given by
and one eavesdropper E that is neither sender nor receiver, and is always dishonest. The set of parties is then given by  . Furthermore, we assume that sender A always designates \(\mathcal {R}\) as the set of designated receivers for the messages it sends. This means in particular that if all receivers are honest then E always learns when A sends a message (as no other party can send messages).
. Furthermore, we assume that sender A always designates \(\mathcal {R}\) as the set of designated receivers for the messages it sends. This means in particular that if all receivers are honest then E always learns when A sends a message (as no other party can send messages).
3.1 Real-World
To communicate, each party in \(\mathcal {P}\) has access to an insecure repository \(\mathbf {INS}:= \mathbf {INS}_k\) (for a fixed security parameter k) to which everyone can read from and write to (recall Sect. 2.3). In addition, parties also have access to a Key Generation Authority (\(\mathbf {KGA}\)), which generates and stores the parties’ key pairs.Footnote 8 For a fixed security parameter k, the \(\mathbf {KGA}:= \mathbf {KGA}_k\) resource runs the \({{ Setup}}\) algorithm giving it the (implicit) parameter k, and then generates and stores all key pairs for the sender A and each receiver in \(\mathcal {R}\), using \({{ G}}_S\) and \({{ G}}_V\), respectively. Every honest party can then query their own public-secret key pair, the public parameters and everyone’s public key at their own interface. Dishonest parties can additionally query the public-secret key pairs of any other dishonest party. The semantics of the \(\mathbf {KGA}\) resource is defined in Algorithm 3.Footnote 9

The sender A runs a converter \(\mathsf {Snd}\) (locally) and each receiver \(B_j \in \mathcal {R}\) runs a converter \(\mathsf {Rcv}\) (also locally). This means sender A can send messages by simply running its converter \(\mathsf {Snd}\), and each receiver can receive messages by simply running its converter \(\mathsf {Rcv}\).
The \(\mathsf {Snd}\) converter connects to \(\mathbf {INS}\) and \(\mathbf {KGA}\) at its inner interface, and has an outer interface that is identical to the interface of a repository for a party who is a writer, i.e. it provides a procedure Write which takes as input a label \(\langle {A_i}\rightarrow {\mathcal {V}}\rangle \) defining the sender \(A_i\) and set of receivers \(\mathcal {V}\) and a message \(m \in \mathcal {M}\) to be signed. \(\mathsf {Snd}\) then gets the necessary keys and public parameters from \(\mathbf {KGA}\), signs the input message m using the algorithm \({{ Sign}}\), which outputs some signature \(\sigma \in \mathcal {S}\), and then writes \(\left( {m,\sigma ,\left( {A_i,\mathcal {V}}\right) }\right) \) into the insecure repository \(\mathbf {INS}\). For simplicity, since in this section the label is always \(\langle {A}\rightarrow {\mathcal {R}}\rangle \) it is simply omitted. In addition, rather than making the \(\mathsf {Snd}\) converter always write \(\left( {m,\sigma ,({A,\mathcal {R}})}\right) \) tuples into \(\mathbf {INS}\), we omit \(\left( {A,\mathcal {R}}\right) \) and simply write \(\left( {m,\sigma }\right) \) pairs instead. The exact (simplified) semantics for converter \(\mathsf {Snd}\) is given in Algorithm 4.

Similarly to \(\mathsf {Snd}\), the \(\mathsf {Rcv}\) converter connects to \(\mathbf {KGA}\) and \(\mathbf {INS}\) at its inner interfaces and provides the same outer interface as a repository for a party with read access, i.e. it gives access to two read operations, namely ReadBuffer and ReadRegister. The behavior of \(\mathsf {Rcv}\) for each such read operation is specified by means of a procedure with the same name (i.e. a ReadBuffer and a ReadRegister procedure). The ReadBuffer procedure first reads all tuples \(\left( {m,\sigma ,\left( {A_i,\mathcal {V}}\right) }\right) \) written into \(\mathbf {INS}\)—by issuing a ReadBuffer operation to \(\mathbf {INS}\) followed by a series of ReadRegister operations, one for each \(\mathtt {id}\) returned by the first operation—and for each tuple satisfying \(A_i = A\) and \(\mathcal {V} = \mathcal {R}\), the converter verifies whether \(\sigma \) is a valid signature on m with respect to sender A and set of receivers \(\mathcal {R}\). To this end, the \(\mathsf {Rcv}\) converter first fetches all the public parameters and keys needed from \(\mathbf {KGA}\), and then checks if \(\sigma \) is a valid signature on m with respect to the public keys of the sender A and of each receiver in \(\mathcal {R}\) using the Vfy algorithm defined by the underlying MDVS scheme \(\varPi \). The converter then outputs a list of pairs—one for each register stored in \(\mathbf {INS}\) containing a valid message-signature pair according to Vfy and with respect to A and \(\mathcal {R}\)—where each pair contains a register’s \(\mathtt {id}\) and a label \(\langle {A}\rightarrow {\mathcal {R}}\rangle \). Since in this section the label is always the same, we simply omit it. The ReadRegister procedure of the \(\mathsf {Rcv}\) converter receives as input the \(\mathtt {id}\) of the register to be read; if the register contains a valid tuple (in the same sense as above) the procedure then outputs the message contained in the register. The exact (simplified) semantics for the \(\mathsf {Rcv}\) converter is given in Algorithm 5.

In the case where the sender and all receivers are honest—i.e.  with \({\mathcal {R}}^{H} = \mathcal {R}\)—the real world specification is given by
with \({\mathcal {R}}^{H} = \mathcal {R}\)—the real world specification is given by

where \(\mathsf {Rcv}^{{\mathcal {R}}^{H}} = \mathsf {Rcv}^{B_1} \cdots \mathsf {Rcv}^{B_n}\) denotes all receiver converters run at the interfaces of \(B_j \in {\mathcal {R}}^{H}\). This is illustrated in Fig. 1. As explained in Remark 3 in Sect. 2.2, if a party P is dishonest, then we simply remove their converter from Eq. (3.1) to get the corresponding real world.
3.2 Ideal-Worlds
Whether the sender is honest or dishonest completely changes the guarantees one wishes to give, and thus completely changes the ideal world. So we divide this in two subsections, the first models a dishonest sender and the second an honest sender. Recall that the third-party E is always dishonest.
Dishonest Sender. In case of a dishonest sender the only property the construction must capture is consistency, namely that all honest receivers in \(\mathcal {R}^H\) get the same messages (for any \(\mathcal {R}^H \ne \emptyset \)). This means that even if all dishonest parties collude, including the sender A, the dishonest receivers \(\overline{\mathcal {R}^H}\) and the third-party E, they are unable to generate confusion within the honest senders as to whether some message is authentic or not: either every receiver \(B_j \in \mathcal {R}^H\) accepts a message as authentic or none does. A repository to which all honest receivers have read access captures this guarantee. Since dishonest parties may share secret keys with each other, any of them may have either read or write access. The repository we want to construct is then

where we have used \(\mathbf {\langle {A}\rightarrow {\mathcal {R}}\rangle }\) as label to denote the repository. By considering a set of converters \(\varOmega \)Footnote 10 that could be run jointly at the dishonest parties’ interfaces, one can then define the ideal world specification \(\boldsymbol{\mathcal {C}}^{\mathrm {Fix}}_{\varOmega }\) capturing consistency as

Illustration of the real world system specified by Eq. (3.1) for the case where
 , with
, with
 .
.
Finally, we also want the ideal world to contain systems that are indistinguishable from the perfect ones defined above, so we put an \(\varepsilon \)-ball around the ideal resource.Footnote 11 The ideal world is then
Honest Sender. In the case of an honest sender, there are two properties that we expect from an MDVS scheme. The first is that the (honest) designated receivers can verify the authenticity of the message as coming from the actual sender A. The second is that this authenticity is exclusive to the designated receivers,Footnote 12 i.e. a third party E cannot be convinced that any message was sent by A, even if dishonest receivers leak all their secret keys to E.Footnote 13 To this end, MDVS schemes need to be such that every possible set of dishonest receivers can (cooperatively) come up with forged signatures that are indistinguishable from the real ones generated by A to the third-party E (who has access to the dishonest receivers’ secret keys). Note, on the other hand, that honest designated receivers are not “fooled” by signatures forged by dishonest (designated) receivers; authenticity guarantees that honest designated receivers can verify whether it was really A signing a message or otherwise.
Authenticity is straightforward to capture: it essentially corresponds to a repository where only the sender can write, but everyone else can read. The only twist is that dishonest parties might be able to duplicate messages written by the sender A [3].Footnote 14 So the repository we wish to be constructed is given by

As for consistency, by considering a set of converters \(\varOmega \) that could be run jointly at the dishonest parties’ interfaces, one can then define the ideal world specification \(\boldsymbol{\mathcal {A}}^{\mathrm {Fix}}_{\varOmega }\) capturing authenticity as

Here too, we extend the ideal world to also contain systems that are indistinguishable from those in Eq. (3.3) by adding a \(\varepsilon \)-ball around the specification. The final ideal specification is thus
Figure 2 illustrates the ideal world systems from the \(\boldsymbol{\mathcal {A}}^{\mathrm {Fix}}_{\varOmega }\) specification.
Illustration of an ideal world system from the \(\boldsymbol{\mathcal {A}}^{\mathrm {Fix}}_{\varOmega }\) specification (Eq. (3.3)) for the case where
 , with
, with
 .
.
Finally, the notion of exclusiveness of authenticity is captured in a world where there exists an (explicit) behavior \(\pi \) for the dishonest receivers that allows them to generate signatures that look just like fresh signatures to any third party E. This means that running \(\pi \) would result in a repository in which both the honest sender A and all the dishonest receivers in \(\overline{{\mathcal {R}}^{H}}\) can write and E can read, namelyFootnote 15

As usual, we extend the specification by attaching a converter \(\mathsf {sim}^{}\) at the dishonest parties’ interfaces. However, \(\mathsf {sim}^{}\) is not allowed to block or cover the write ability at the interfaces of the parties in \(\overline{\mathcal {R}^H}\), because we wish to guarantee that a dishonest receiver can write to the repository.Footnote 16 The specification providing the guarantee that E cannot distinguish real signatures (created by A) from fake ones (forged by the dishonest designated receivers) is given by

Figure 3 illustrates an ideal world system from \(\widehat{\boldsymbol{\mathcal {X}}}^{\mathrm {Fix}}_{\varOmega }\). As stated above, there must exist a converter \(\pi \) that the dishonest receivers \(\overline{{\mathcal {R}}^{H}}\) can run jointly to achieve a resource in the specification from Eq. (3.5). Since dishonest receivers could have run (and can run) \(\pi \), a third party E cannot tell if the message was sent by them or by the honest sender A even when given access to the keys of all dishonest receivers (notice that E, being one of the dishonest parties, can query the \(\mathbf {KGA}\) to obtain the secret keys of any dishonest receiver). Putting things together, the ideal world is defined as

where \(\bot ^{{\mathcal {R}}^{H}}\) blocks the interfaces of all honest receivers \(\mathcal {R}^H\).Footnote 17 Figure 4 illustrates a possible real world system in the \(\boldsymbol{\mathcal {X}}^{\mathrm {Fix}}_{\varOmega ,\pi }\) specification with a converter \(\bot ^{{\mathcal {R}}^{H}}\) blocking the interface of the (only) honest receiver \(B_1\), and protocol \(\pi ^{\overline{{\mathcal {R}}^{H}}}\) attached to the interfaces of the dishonest receivers (i.e. \(B_2\) and \(B_3\)). Again, we put an \(\varepsilon \)-ball around Eq. (3.6), and define the ideal specification for the exclusiveness of authenticity to be
Illustration of an ideal world system from the \(\widehat{\boldsymbol{\mathcal {X}}}^{\mathrm {Fix}}_{\varOmega }\) specification (Eq. (3.5)) for the case where
 , with
, with
 .
.
Illustration of a possible real world system in the \(\boldsymbol{\mathcal {X}}^{\mathrm {Fix}}_{\varOmega ,\pi }\) specification (Eq. (3.6)) for the case where
 , with
, with
 blocks \(B_1\)’s interface; signature forgery protocol \(\pi ^{\overline{{\mathcal {R}}^{H}}}\) is attached to the interfaces of \(B_2\) and \(B_3\).
blocks \(B_1\)’s interface; signature forgery protocol \(\pi ^{\overline{{\mathcal {R}}^{H}}}\) is attached to the interfaces of \(B_2\) and \(B_3\).
Putting things together, the ideal world specification for the case of an honest sender is then given by
3.3 Reduction to Game-Based Security
We now compare our composable notions against the existing game-based security notions from the literature. The definitions of these game-based security notions can be found in the full version of this paper, together with full proofs of all the theorems below [21].
The first theorem shows that in the case of a dishonest sender, the advantage in distinguishing the real and ideal systems is upper bounded by the advantage in winning the consistency game.
Theorem 1
When the sender \(\mathcal {A}\) is dishonest, i.e. \({\mathcal {P}}^{H} = {\mathcal {R}}^{H}\), we find an explicit reduction system \(\mathbf {C}\) and an explicit simulator \(\mathsf {sim}^{}\) such that for any
 :
:

where for any distinguisher \(\mathbf {D}\),
 is the advantage of \(\mathbf {D}' = \mathbf {DC}\) (the distinguisher resulting from composing \(\mathbf {D}\) and \(\mathbf {C}\)) in winning the Consistency game (see [21, Definition 3]).
is the advantage of \(\mathbf {D}' = \mathbf {DC}\) (the distinguisher resulting from composing \(\mathbf {D}\) and \(\mathbf {C}\)) in winning the Consistency game (see [21, Definition 3]).
A proof of Theorem 1 is provided in the full version [21].
The second theorem shows that in the case of an honest sender, the advantage in distinguishing the real world from the ideal world for authenticity is upper bounded by the advantage in winning the unforgeability game and the correctness game.
Theorem 2
When the sender is honest, i.e. for
 , we find explicit reduction systems \({\mathbf {C}}'\) and \(\mathbf {C}\) and an explicit simulator \(\mathsf {sim}^{}\) such that for any
, we find explicit reduction systems \({\mathbf {C}}'\) and \(\mathbf {C}\) and an explicit simulator \(\mathsf {sim}^{}\) such that for any
 :
:

where for any distinguisher \(\mathbf {D}\),
 is the advantage of \(\mathbf {D}' = \mathbf {DC}\) (the distinguisher resulting from composing \(\mathbf {D}\) and \(\mathbf {C}\)) in winning the Unforgeability game (see [21, Definition 4]), and
is the advantage of \(\mathbf {D}' = \mathbf {DC}\) (the distinguisher resulting from composing \(\mathbf {D}\) and \(\mathbf {C}\)) in winning the Unforgeability game (see [21, Definition 4]), and
 is the advantage of \(\mathbf {D}'' = \mathbf {DC}'\) in winning the Correctness game (see [21, Definition 2])
is the advantage of \(\mathbf {D}'' = \mathbf {DC}'\) in winning the Correctness game (see [21, Definition 2])
A proof of Theorem 2 is provided in the full version [21].
In the third theorem we show that in the case of an honest sender, the advantage in distinguishing the real world from the ideal world for the exclusiveness of authenticity is bounded by the advantage in winning the Off-The-Record game.
Theorem 3
When the sender is honest, i.e. for
 , and for any signature forgery algorithm Forge suitable for the Off-The-Record security notion (see [21, Definition 5]), we find an explicit reduction system \(\mathbf {C}\) and an explicit simulator \(\mathsf {sim}^{}\) such that for any
, and for any signature forgery algorithm Forge suitable for the Off-The-Record security notion (see [21, Definition 5]), we find an explicit reduction system \(\mathbf {C}\) and an explicit simulator \(\mathsf {sim}^{}\) such that for any
 :
:

where \(\pi ^{{{ Forge}}}\) is the converter running the Forge algorithm (see Algorithm 6), and for any distinguisher \(\mathbf {D}\),
 is the advantage of \(\mathbf {D}' = \mathbf {DC}\) (the distinguisher resulting from composing \(\mathbf {D}\) and \(\mathbf {C}\)) in winning the Off-The-Record game with respect to the signature forgery algorithm Forge (see [21, Definition 5]).
is the advantage of \(\mathbf {D}' = \mathbf {DC}\) (the distinguisher resulting from composing \(\mathbf {D}\) and \(\mathbf {C}\)) in winning the Off-The-Record game with respect to the signature forgery algorithm Forge (see [21, Definition 5]).

4 Modeling MDVS for Arbitrary Parties
In this section we model the security of MDVS schemes in the presence of multiple possible senders and multiple sets of receivers, which corresponds to a generalization of the models given in Sect. 3. Throughout this section, we denote by \(\mathcal {S}\) the set of senders, and by \({\mathcal {S}}^{H}\) and \(\overline{{\mathcal {S}}^{H}}\) the partitions of \(\mathcal {S}\) corresponding to honest and dishonest senders. As before, \(\mathcal {R}\), \({\mathcal {R}}^{H}\) and \(\overline{{\mathcal {R}}^{H}}\) correspond to the set of all receivers, honest and dishonest receivers, respectively. Furthermore, we assume that \({\mathcal {R}}^{H}\), \(\overline{{\mathcal {R}}^{H}}\), \({\mathcal {S}}^{H}\) and \(\overline{{\mathcal {S}}^{H}}\) are all non-empty sets.
4.1 Real-World
The real world specification for this security model is similar to the one given in Sect. 3.1 for the fixed sender and fixed set of receivers case. However, in Sect. 3 we made a few simplifications in the description of converters \(\mathsf {Snd}\) and \(\mathsf {Rcv}\) namely, the fixed sender and a fixed set of receiver are hard-coded in the converters. In this section, the converters \(\mathsf {Snd^{\mathrm {Arb}}}\) and \(\mathsf {Rcv^{\mathrm {Arb}}}\) (see Algorithm 7 and Algorithm 8, respectively) allow the sender to specify the set of receivers for each message they send, and the \(\mathsf {Rcv^{\mathrm {Arb}}}\) converters explicitly output the sender and the set of designated receivers. Moreover, the \(\mathsf {Snd^{\mathrm {Arb}}}\) converter now attaches to each message-signature pair also the sender and set of receivers meant for that message-signature pair; the \(\mathsf {Rcv^{\mathrm {Arb}}}\) converter then relies on this information to validate the authenticity of messages meant for the corresponding receiver. Apart from this, the real-world specification is as before: the \(\mathsf {Snd^{\mathrm {Arb}}}\) and \(\mathsf {Rcv^{\mathrm {Arb}}}\) converters connect to the \(\mathbf {KGA}\) and to an insecure repository \(\mathbf {INS}\), and behave otherwise similarly to the \(\mathsf {Snd}\) and \(\mathsf {Rcv}\) converters. Since we assumed that \({\mathcal {S}}^{H}\) and \({\mathcal {R}}^{H}\) are non-empty sets, the real-world specification is then defined by

as illustrated in Fig. 5.


Illustration of the real world system specified by Eq. (4.1) for the case where
 and
and
 , with
, with
 and
and
 .
.
4.2 Ideal-Worlds
As aforementioned in Sect. 3.2, the guarantees given by the ideal world when a sender is honest are completely different from the ones when it is dishonest. However, since now we have both honest and dishonest senders at the same time, the ideal-world specification modeling the security of MDVS schemes consists of the intersection of only two (relaxed) specifications, one capturing the consistency and authenticity together \(\boldsymbol{\mathcal {\left( {CA}\right) }}^{\mathrm {Arb}}_{\varOmega }\),Footnote 18 and one capturing the exclusiveness of authenticity \(\boldsymbol{\mathcal {X}}^{\mathrm {Arb}}_{{\varOmega }',\pi }\). The ideal world is then

One key difference between the model we now introduce and the one from Sect. 3 is that we may have dishonest parties (other than Eve) that are neither sender nor designated receivers in this section, and we require exclusiveness of authenticity to hold with respect to them as well. So it is not sufficient that (any non-empty subset of) dishonest verifiers who have a secret verification key can forge signatures, parties with no secret verification key should also be able to forge.Footnote 19
Consistency and Authenticity. As just mentioned, \(\boldsymbol{\mathcal {\left( {CA}\right) }}^{\mathrm {Arb}}_{\varOmega }\) models consistency and authenticity. More concretely, for dishonest senders \(A_i \in \overline{{\mathcal {S}}^{H}}\), \(\boldsymbol{\mathcal {\left( {CA}\right) }}^{\mathrm {Arb}}_{\varOmega }\) includes the repository

which captures consistency, since all honest receivers have access to the same messages. And for honest senders \(A_i \in {\mathcal {S}}^{H}\), \(\boldsymbol{\mathcal {\left( {CA}\right) }}^{\mathrm {Arb}}_{\varOmega }\) includes the repository

which captures authenticity, since only \(A_i\) can write. As before, a simulator \(\mathsf {sim}^{}\) is added at the interfaces of the dishonest parties, hence

Figure 6 illustrates the ideal world systems from the \(\boldsymbol{\mathcal {\left( {CA}\right) }}^{\mathrm {Arb}}_{\varOmega }\) specification.
Illustration of the ideal world system specified by Eq. (4.3) for the case where
 ,
,
 , with
, with
 and
and
 .
.
Exclusiveness of Authenticity. To model exclusiveness of authenticity, for honest senders \(A_i \in {\mathcal {S}}^{H}\), we define a resource containing a repository where \(A_i\) and all dishonest parties (except Eve) can write and Eve can read, i.e.

This means that Eve does not know if the messages she sees are from Alice or another dishonest party—even those that are not designated verifiers can input messages.
In the arbitrary party setting, we also need to deal with the case of dishonest senders. Since we cannot exclude that by submitting forged signatures and seeing whether they are accepted, dishonest parties might learn something about the honest receivers’ secret keys, we also include repositories where a dishonest party (Eve) can write and honest verifiers read,Footnote 20 namely

Like in the previous section, we want to guarantee that the ability of dishonest parties to write in the repositories for honest senders is preserved, so the simulator only covers Eve’s interface.Footnote 21 We thus get a resource specification,

As previously, our ideal world consists of all resources that when the interfaces of the honest designated verifiers on repositories with honest senders are covered and when the dishonest parties (excluding Eve) collude to run a forging protocol \(\pi \) result in a resource contained in \(\widehat{\boldsymbol{\mathcal {X}}}^{\mathrm {Arb}}_{\varOmega }\), i.e. the ideal-world specification \(\boldsymbol{\mathcal {X}}^{\mathrm {Arb}}_{\varOmega ,\pi }\) is defined as

where \(\bot _{\mathrm {Arb}}\) is the converter specified in Algorithm 9 which does not allow the receiver to verify the authenticity of messages input into any repository \(\langle {A_i}\rightarrow {\mathcal {V}}\rangle \) with an honest sender (i.e. for which \(A_i \in {\mathcal {S}}^{H}\)).Footnote 22

4.3 Reduction to Game-Based Security
We now compare our composable notions for arbitrary parties to the existing game-based security notions from the literature. Again, the definitions of these game-based security notions can be found in the full version of this paper, together with full proofs of all the theorems [21].
The first theorem in this section shows that that advantage in distinguishing the real world from the ideal world for authenticity and consistency is upper bounded by the advantage in winning the consistency, unforgeability and correctness games.
Theorem 4
Consider a setting where \({\mathcal {R}}^{H}\), \(\overline{{\mathcal {R}}^{H}}\), \({\mathcal {S}}^{H}\) and \(\overline{{\mathcal {S}}^{H}}\) are all non-empty. We find an explicit reduction system \({\mathbf {C}}'\), an explicit simulator \(\mathsf {sim}^{}\) and explicit reduction systems \({\mathbf {C}}\), \({\mathbf {C}}_{\text {Cons}}\) and \({\mathbf {C}}_{\text {Unforg}}\) such that, for any


where for any distinguisher \(\mathbf {D}\),
 ,
,
 , and
, and
 are, respectively, the advantages of \(\mathbf {D}'=\mathbf {D}\mathbf {C}{\mathbf {C}}_{\text {Cons}}\) (the distinguisher resulting from composing \(\mathbf {D}\), \(\mathbf {C}\) and \(\mathbf {C}_{\text {Cons}}\)) in winning the Consistency game (see [21, Definition 3]), of \(\mathbf {D}''=\mathbf {D}\mathbf {C}{\mathbf {C}}_{\text {Unforg}}\) in winning the Unforgeability game (see [21, Definition 4]) and of \(\mathbf {D}'''={{\mathbf {D}}{\mathbf {C}}'}\) in winning the Correctness game (see [21, Definition 2])
are, respectively, the advantages of \(\mathbf {D}'=\mathbf {D}\mathbf {C}{\mathbf {C}}_{\text {Cons}}\) (the distinguisher resulting from composing \(\mathbf {D}\), \(\mathbf {C}\) and \(\mathbf {C}_{\text {Cons}}\)) in winning the Consistency game (see [21, Definition 3]), of \(\mathbf {D}''=\mathbf {D}\mathbf {C}{\mathbf {C}}_{\text {Unforg}}\) in winning the Unforgeability game (see [21, Definition 4]) and of \(\mathbf {D}'''={{\mathbf {D}}{\mathbf {C}}'}\) in winning the Correctness game (see [21, Definition 2])
A proof of Theorem 4 is provided in the full version [21].
In the second theorem we show that the advantage in distinguishing the real world from the ideal world for the exclusiveness of authenticity is bounded by the advantage in winning the Off-The-Record and Consistency games.
Theorem 5
Consider a setting where \({\mathcal {R}}^{H}\), \(\overline{{\mathcal {R}}^{H}}\), \({\mathcal {S}}^{H}\) and \(\overline{{\mathcal {S}}^{H}}\) are all non-empty. For any signature forgery algorithm Forge suitable for the Off-The-Record security notion we find explicit reduction systems \(\mathbf {C}\) and \({\mathbf {C}}'\), and an explicit simulator \(\mathsf {sim}^{}\) such that for any
 :
:

where \(\pi ^{{{ Forge}}}\) is the converter running the Forge algorithm (see Algorithm 10), and for any for any distinguisher \(\mathbf {D}\),
 and
and
 are, respectively, the advantage of \(\mathbf {D}'=\mathbf {D}\mathbf {C}\) (the distinguisher resulting from composing \(\mathbf {D}\) and \(\mathbf {C}\)) in winning the Off-The-Record game with respect to forgery algorithm Forge (see [21, Definition 5]), and the advantage of \(\mathbf {D}''=\mathbf {D}{\mathbf {C}}'\) in winning the Consistency game (see [21, Definition 3]).
are, respectively, the advantage of \(\mathbf {D}'=\mathbf {D}\mathbf {C}\) (the distinguisher resulting from composing \(\mathbf {D}\) and \(\mathbf {C}\)) in winning the Off-The-Record game with respect to forgery algorithm Forge (see [21, Definition 5]), and the advantage of \(\mathbf {D}''=\mathbf {D}{\mathbf {C}}'\) in winning the Consistency game (see [21, Definition 3]).

A proof of Theorem 5 is provided in the full version [21].
Asymptotic Composable Security of MDVS. Analogously to Remark 2, for a security notion \(\mathsf {X}\),
 denotes a function defined as
denotes a function defined as  . We say that a scheme satisfies \(\mathsf {X}\) asymptotically if
. We say that a scheme satisfies \(\mathsf {X}\) asymptotically if
 is negligible on the security parameter k.
is negligible on the security parameter k.
In the following, let \(\varPi = \left( {{{ Setup}},{{ G}}_{S},{{ G}}_{V},{{ Sign}},{{ Vfy}}}\right) \) be an MDVS scheme. The following corollaries, Corollary 1 and Corollary 2, follow from Theorem 4 and Theorem 5, respectively. These results state that any MDVS scheme \(\varPi \) that is asymptotically secure—according to asymptotic versions of [21, Definition 2], [21, Definition 3], [21, Definition 4], and [21, Definition 5]— and which is used as specified in Sect. 4.1 asymptotically constructs, from a real world specification \(\boldsymbol{\mathcal {R}}\), the ideal world specification defined in Eq. 4.2 (see Remark 2). Note that, since we are making asymptotic construction statements, \({\varOmega }\) and \({\varOmega }'\) are both classes of efficient simulators (say non-uniform probabilistic polynomial time), and for any efficient family of distinguishers \(\overrightarrow{\mathbf {D}}\), \({\overrightarrow{\varepsilon }}\) and \({\overrightarrow{\varepsilon }'}\) are both negligible functions (on the security parameter).
Corollary 1
Consider a setting where \({\mathcal {R}}^{H}\), \(\overline{{\mathcal {R}}^{H}}\), \({\mathcal {S}}^{H}\) and \(\overline{{\mathcal {S}}^{H}}\) are all non-empty. If \(\varPi \) is asymptotically Correct (see [21, Definition 2]), Consistent (see [21, Definition 3]) and Unforgeable (see [21, Definition 4]), then \(\boldsymbol{\mathcal {R}}\) asymptotically constructs \(\boldsymbol{\mathcal {\left( {CA}\right) }}^{\mathrm {Arb}}\).
Corollary 2
Consider a setting where \({\mathcal {R}}^{H}\), \(\overline{{\mathcal {R}}^{H}}\), \({\mathcal {S}}^{H}\) and \(\overline{{\mathcal {S}}^{H}}\) are all non-empty. If \(\varPi \) is asymptotically Off-The-Record (see [21, Definition 5]) and Consistent (see [21, Definition 3]), then \(\boldsymbol{\mathcal {R}}\) asymptotically constructs \(\boldsymbol{\mathcal {X}}^{\mathrm {Arb}}_{\pi ^{{{ Forge}}}}\), where \(\pi ^{{{ Forge}}}\) is the converter defined in Algorithm 10, running an algorithm Forge with respect to which \(\varPi \) is asymptotically Off-The-Record (i.e. no non-uniform probabilistic polynomial time adversary \(\overrightarrow{\mathbf {A}}\) can win the Off-The-Record game of \(\varPi \) with respect to algorithm Forge with non-negligible advantage).
4.4 Separation from Existing Game-Based Security Notions
The game-based security notion from [11] capturing the Off-The-Record security property of MDVS schemes (see [21, Definition 5]) is unnecessarily strong as for some MDVS schemes it allows the adversary to verify the validity of the challenge signatures, and thus allows it to trivially win the game. As hinted by our composable security notions, the main goal of the Off-The-Record security notion is capturing that a third party cannot tell whether a given signature is a valid one generated by the signer, or a forged one generated by dishonest receivers. The ability of a third party to generate signature replays—which might only be valid if the original signatures were already valid—does not violate any of the security properties that MDVS schemes intend to guarantee, and as such should not help in winning the corresponding security game. However, it does help in winning the Off-The-Record game from [11], meaning that this notion (i.e. the one from [11]) is unnecessarily strong.
Theorem 6
Let
 . Consider any MDVS scheme \(\varPi \), and let \(\varepsilon _{\varPi \text {-}4}\) and \(\varepsilon _{\varPi \text {-}5}\) denote the \(\varepsilon \)-balls (see Eq. (2.3)) given by, respectively, Theorem 4 and Theorem 5 for settings where \({\mathcal {R}}^{H}\), \(\overline{{\mathcal {R}}^{H}}\), \({\mathcal {S}}^{H}\) and \(\overline{{\mathcal {S}}^{H}}\) are all non-empty sets. Then there is a modified MDVS scheme \({\varPi }'\) that is also secure as in each of these two theorems and for essentially the same \(\varepsilon \)-balls as \(\varPi \), but such that for any suitable algorithm Forge for the Off-The-Record security notion (see [21, Definition 5]) there is an explicit and efficient adversary \(\mathbf {A}\) such that
. Consider any MDVS scheme \(\varPi \), and let \(\varepsilon _{\varPi \text {-}4}\) and \(\varepsilon _{\varPi \text {-}5}\) denote the \(\varepsilon \)-balls (see Eq. (2.3)) given by, respectively, Theorem 4 and Theorem 5 for settings where \({\mathcal {R}}^{H}\), \(\overline{{\mathcal {R}}^{H}}\), \({\mathcal {S}}^{H}\) and \(\overline{{\mathcal {S}}^{H}}\) are all non-empty sets. Then there is a modified MDVS scheme \({\varPi }'\) that is also secure as in each of these two theorems and for essentially the same \(\varepsilon \)-balls as \(\varPi \), but such that for any suitable algorithm Forge for the Off-The-Record security notion (see [21, Definition 5]) there is an explicit and efficient adversary \(\mathbf {A}\) such that

where
 denotes the advantage of \(\mathbf {A}\) in winning the Off-The-Record game for \({\varPi }'\) with respect to the signature forgery algorithm Forge(see [21, Definition 5]), \(\delta _{\text {corr}}\) is the probability that a single honestly generated signature does not verify correctly and \(\delta _{\text {auth}}\) is the probability that a single forged signature is considered valid by the signature verification algorithm.
denotes the advantage of \(\mathbf {A}\) in winning the Off-The-Record game for \({\varPi }'\) with respect to the signature forgery algorithm Forge(see [21, Definition 5]), \(\delta _{\text {corr}}\) is the probability that a single honestly generated signature does not verify correctly and \(\delta _{\text {auth}}\) is the probability that a single forged signature is considered valid by the signature verification algorithm.
5 Further Related Work
In [13], Jakobsson, Sako, and Impagliazzo introduce DVS and MDVS schemes and give two property-based security notions for the single designated verifier case. Their weaker notion is intended to capture essentially the same as our weaker exclusiveness of authenticity notion—if all receivers are honest, Eve learns that Alice is the one sending messages—whereas their stronger notion is intended to capture our stronger notion—even if all receivers are honest, Eve cannot tell if Alice sent any message. Unfortunately, the signature unforgeability notion considered—equivalent to Existential Unforgeability under No-Message Attacks (EUF-NMA)—is known to be too weak to allow for authentic communication.Footnote 23 Furthermore, the security notion capturing the exclusiveness of authenticity which is implicitly considered for the case of multiple receivers is also too weak, and in particular is not sufficient to achieve neither of our composable notions. This is so since simulating signatures requires secret information from every designated verifier, and thus if at least one of the verifiers is honest, doing so is not feasible.
In [29], Steinfeld, Bull, Wang and Pieprzyk introduce Universal Designated Verifier Signatures, wherein a signer can generate publicly verifiable signatures which can then be transformed into designated verifier ones (possibly by a distinct party not possessing the secret signing key). Although the security notions capturing the exclusiveness of authenticity property introduced in that paper are weak—in that they only meet the weaker notion we introduce in this paper—the proposed schemes meet our stronger notion for this property (for the single receiver case). On the other hand, the unforgeability notion considered in the paper is too weak: it does not suffice to achieve even our weaker composable security notion. Unfortunately, numerous subsequent works have considered the same unforgeability notion [16,17,18,19, 30, 32].
In [15], Krawczyk and Rabin introduce Chameleon signature schemes, which work by first using a chameleon hash function to hash a message and then using a normal signature scheme to sign the resulting hash. Chameleon hash functions are public key schemes which are collision-resistant for anyone not possessing the secret key, but which allow for efficient collision finding given the secret key. The intended use of these schemes is to provide the same guarantees as DVS schemes: a designated receiver first generates its chameleon hash function, and sends the corresponding public key to the signer; the signer then sends a signature on the message under the hash function provided by the receiver, which it can verify. Since the receiver knows the secret key of the chameleon hash function it sent to the signer, no one other than the receiver gets convinced that the signer signed any particular message. However, these schemes do not allow to achieve the exclusiveness of authenticity that our stronger composable notion captures: anyone with the public keys of the signer and of the chameleon hash function can verify whether a certain signature is a valid one (for some message), which implies that no third-party can feasibly forge signatures that are indistinguishable from real ones (or otherwise the signature scheme used by the signer is not unforgeable). Moreover, they also do not achieve our weaker notion, as dishonest receivers can only forge signatures once the signer signed a message.
In [27], Rivest, Shamir and Tauman mention that two party ring signatures are DVS schemes. Indeed, one can obtain a DVS scheme meeting our weaker composable notion for the case of a single receiver B by taking a ring signature scheme and using it to produce signatures for a ring composed by the signer A and by the intended (designated) receiver of that message, B.Footnote 24 But notice that, similarly to the case of Chameleon signature schemes, public keys are enough to verify signatures, implying that the DVS schemes yielded by ring signatures can really only achieve our weaker security notion—where if both A and B are honest, E learns A is the signer. Furthermore, since any ring member can locally sign messages that are valid with respect to the entire ring, which is incompatible with the stronger authenticity requirement of MDVS schemes, ring signatures may only be used as DVS schemes for the case of a single receiver. Unfortunately, this went unnoticed in various prior works [9, 16, 18], which gave constructions of MDVS schemes based on ring signature schemes.
One could think that perhaps, to achieve our stronger notion for exclusiveness of authenticity—where a third party is not convinced that the signer signed some message even when all the designated receivers (and the signer) are honest—it suffices to guarantee that the validity of a signature can only be efficiently determined with the secret key given as input [28]. However, this is not the case. Consider for example, the case where the sender and the designated receivers share the signing key \(\mathtt {dsk}\) of some (traditional) Digital Signature Scheme (DSS) (with the corresponding verification key \(\mathtt {dvk}\) being publicly known), and where the MDVS signature \(\sigma _m\) for each message m also includes a signature \({\sigma _m}'\) under \(\mathtt {dsk}\) on m. Then, while to verify the validity of an MDVS signature \(\sigma _m\) one may need the secret verification key for the MDVS scheme, by verifying the corresponding \({\sigma _m}'\) using \(\mathtt {dvk}\) signature a third party already gets convinced, in the case where the sender and all the designated receivers are honest, that the really signer signed m. This same reasoning also explains why, in general, MAC schemes cannot be used per se as DVS schemes (in the stronger sense, captured by our stronger composable notion) for the two party case: it may not be feasible to simulate MAC schemes which look just like real ones.
Notes
- 1.
- 2.
More precisely, the \(\mathbf {CONF}\) channel only allows Eve to read the length of messages.
- 3.
The definition of the set \(\varOmega \) may depend on the context, e.g. whether one is interested in bounded run time, bounded memory, and whether one is making finite or asymptotic statements.
- 4.
Formally, one first finds an (efficient) reduction \(\chi \) which constructs a solver \(\mathbf {S} = \chi (\mathbf {D})\) from any distinguisher \(\mathbf {D}\). Then one bounds the distance
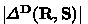 with a function of the probability that \(\chi (\mathbf {D})\) succeeds is solving some problem, i.e., \(\varepsilon (\mathbf {D}) := f(\Pr [\chi (\mathbf {D}) \text { succeeds}])\) for an f that does not significantly alter the probability of success. Thus for any \(\mathbf {D}\) that cannot be used to solve the problem,
with a function of the probability that \(\chi (\mathbf {D})\) succeeds is solving some problem, i.e., \(\varepsilon (\mathbf {D}) := f(\Pr [\chi (\mathbf {D}) \text { succeeds}])\) for an f that does not significantly alter the probability of success. Thus for any \(\mathbf {D}\) that cannot be used to solve the problem,  must be small.
must be small. - 5.
In analogy to Remark 1 we consider that a repository defined for security parameter k has message space \(\mathcal {M}_k\); for a family of repositories one then considers a corresponding family of message spaces
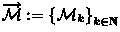 . Since most statements are made for a fixed parameter k, we usually omit k from the notation, writing \(\mathcal {M}\) instead.
. Since most statements are made for a fixed parameter k, we usually omit k from the notation, writing \(\mathcal {M}\) instead. - 6.
Copy access is used to capture the capability that dishonest parties have for copying or resending (modifications of) whatever they see; modeling this capability is crucial for some of the security proofs.
- 7.
Since all parties can read and write, copying capabilities are redundant.
- 8.
- 9.
Algorithm 3 defines the behavior of \(\mathbf {KGA}\) in the case of multiple senders, which will only be used in Sect. 4.
- 10.
We do not define \(\varOmega \) at this point, since in a finite setting there is no “good” and “bad” system (efficient or inefficient, negligible or non-negligible). Instead, in the theorem statement for a security proof we explicitly give the set \(\varOmega \) which is used, as the meaningfulness of the theorem will depend on the choice of this set.
- 11.
Like for \(\varOmega \) (see Footnote 10) we do not define acceptable \(\varepsilon \) here, but in a theorem statement for a security proof we explicitly give the one used.
- 12.
A third important property is correctness, but in our setting dishonest parties cannot delete the messages of honest parties, so correctness follows from authenticity and does not need to be considered separately.
- 13.
If all receivers are honest only A can send messages, and so in this case E just knows that A must be the one sending messages.
- 14.
They can do this either by creating a copy of a valid message-signature pair or by sending the same message but with a different signature.
- 15.
As one might note, the repository in Eq. (3.4) does not allow the honest designated receivers \({\mathcal {R}}^{H}\) to read. The reason for this is that the security statement does not concern them, so we remove them from the security statement. In fact, due to authenticity the honest designated receivers could distinguish signatures written by Alice or forged by the dishonest receivers.
- 16.
Traditional composable security frameworks require the simulator to cover all dishonest interfaces making it impossible to model Eq. (3.5).
- 17.
Note that the ideal specification in Eq. (3.6) does not follow the ideal-functionality-simulator paradigm, making it impossible to (directly) model the same thing in traditional composable frameworks.
- 18.
As noted in Sect. 3, in our setting correctness follows from authenticity, so it does not need to be considered separately.
- 19.
This could have been modeled in Sect. 3 by adding a second Eve, but we omitted it for simplicity.
- 20.
Messages signed by a party with no knowledge of the signer’s secret key will likely be recognized as forgeries, so we only need to consider the case where the sender is dishonest and the keys are shared. Furthermore, the distinguisher could in principle use any party’s interface to submit these messages, but since it simplifies the presentation to only have the simulator at Eve’s interface we only include Eve in the parties with write abilities.
- 21.
Traditional composable security frameworks require the simulator to cover all dishonest interfaces making it impossible to model Eq. (4.4).
- 22.
Note that the ideal specification in Eq. (4.5) does not follow the ideal-functionality-simulator paradigm, making it impossible to (directly) model the same thing in traditional composable frameworks.
- 23.
- 24.
As one might note, the resulting DVS scheme can only meet our weaker composable notion if the underlying ring signature scheme meets the stronger Anonymity against Attribution Attacks [4, Definition 4].
References
Backes, M., Hofheinz, D.: How to break and repair a universally composable signature functionality. In: Zhang, K., Zheng, Y. (eds.) ISC 2004. LNCS, vol. 3225, pp. 61–72. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30144-8_6
Backes, M., Pfitzmann, B., Waidner, M.: The reactive simulatability (RSIM) framework for asynchronous systems. Cryptology ePrint Archive, Report 2004/082 (2004). https://eprint.iacr.org/2004/082
Badertscher, C., Maurer, U., Tackmann, B.: On composable security for digital signatures. In: Abdalla, M., Dahab, R. (eds.) PKC 2018, Part I. LNCS, vol. 10769, pp. 494–523. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_17
Bender, A., Katz, J., Morselli, R.: Ring signatures: stronger definitions, and constructions without random oracles. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 60–79. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_4
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: 42nd FOCS, pp. 136–145. IEEE Computer Society Press, October 2001. https://doi.org/10.1109/SFCS.2001.959888
Canetti, R.: Universally composable signatures, certification and authentication. Cryptology ePrint Archive, Report 2003/239 (2003). https://eprint.iacr.org/2003/239
Canetti, R.: Universally composable signature, certification, and authentication. In: 17th IEEE Computer Security Foundations Workshop (CSFW-17 2004), 28–30 June 2004, Pacific Grove, CA, USA, p. 219. IEEE Computer Society (2004). https://doi.org/10.1109/CSFW.2004.24. http://doi.ieeecomputersociety.org/10.1109/CSFW.2004.24
Canetti, R., Dodis, Y., Pass, R., Walfish, S.: Universally composable security with global setup. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 61–85. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_4
Chow, S.S.M.: Multi-designated verifiers signatures revisited. Int. J. Netw. Secur. 7(3), 348–357 (2008). http://ijns.jalaxy.com.tw/contents/ijns-v7-n3/ijns-2008-v7-n3-p348-357.pdf
Coretti, S., Maurer, U., Tackmann, B.: Constructing confidential channels from authenticated channels—public-key encryption revisited. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part I. LNCS, vol. 8269, pp. 134–153. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42033-7_8
Damgård, I., Haagh, H., Mercer, R., Nitulescu, A., Orlandi, C., Yakoubov, S.: Stronger security and constructions of multi-designated verifier signatures. In: Pass, R., Pietrzak, K. (eds.) TCC 2020, Part II. LNCS, vol. 12551, pp. 229–260. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64378-2_9
Hofheinz, D., Shoup, V.: GNUC: a new universal composability framework. J. Cryptol. 28(3), 423–508 (2013). https://doi.org/10.1007/s00145-013-9160-y
Jakobsson, M., Sako, K., Impagliazzo, R.: Designated verifier proofs and their applications. In: Maurer, U. (ed.) EUROCRYPT 1996. LNCS, vol. 1070, pp. 143–154. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68339-9_13
Jost, D., Maurer, U.: Overcoming impossibility results in composable security using interval-wise guarantees. In: Micciancio, D., Ristenpart, T. (eds.) CRYPTO 2020, Part I. LNCS, vol. 12170, pp. 33–62. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-56784-2_2
Krawczyk, H., Rabin, T.: Chameleon signatures. In: NDSS 2000. The Internet Society, February 2000
Laguillaumie, F., Vergnaud, D.: Multi-designated verifiers signatures. In: Lopez, J., Qing, S., Okamoto, E. (eds.) ICICS 2004. LNCS, vol. 3269, pp. 495–507. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30191-2_38
Laguillaumie, F., Vergnaud, D.: Designated verifier signatures: anonymity and efficient construction from any bilinear map. In: Blundo, C., Cimato, S. (eds.) SCN 2004. LNCS, vol. 3352, pp. 105–119. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30598-9_8
Li, Y., Susilo, W., Mu, Y., Pei, D.: Designated verifier signature: definition, framework and new constructions. In: Indulska, J., Ma, J., Yang, L.T., Ungerer, T., Cao, J. (eds.) UIC 2007. LNCS, vol. 4611, pp. 1191–1200. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73549-6_116
Lipmaa, H., Wang, G., Bao, F.: Designated verifier signature schemes: attacks, new security notions and a new construction. In: Caires, L., Italiano, G.F., Monteiro, L., Palamidessi, C., Yung, M. (eds.) ICALP 2005. LNCS, vol. 3580, pp. 459–471. Springer, Heidelberg (2005). https://doi.org/10.1007/11523468_38
Maurer, U.: Constructive cryptography – a new paradigm for security definitions and proofs. In: Mödersheim, S., Palamidessi, C. (eds.) TOSCA 2011. LNCS, vol. 6993, pp. 33–56. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-27375-9_3
Maurer, U., Portmann, C., Rito, G.: Giving an adversary guarantees (or: how to model designated verifier signatures in a composable framework). Cryptology ePrint Archive, Report 2021/1185 (2021). https://eprint.iacr.org/2021/1185
Maurer, U., Renner, R.: Abstract cryptography. In: Chazelle, B. (ed.) ICS 2011, pp. 1–21. Tsinghua University Press, January 2011
Maurer, U., Renner, R.: From indifferentiability to constructive cryptography (and back). In: Hirt, M., Smith, A. (eds.) TCC 2016, Part I. LNCS, vol. 9985, pp. 3–24. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53641-4_1
Maurer, U.: Indistinguishability of random systems. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 110–132. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_8
Maurer, U., Pietrzak, K., Renner, R.: Indistinguishability amplification. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 130–149. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_8
Pfitzmann, B., Waidner, M.: A model for asynchronous reactive systems and its application to secure message transmission. In: 2001 IEEE Symposium on Security and Privacy, pp. 184–200. IEEE Computer Society Press, May 2001. https://doi.org/10.1109/SECPRI.2001.924298
Rivest, R.L., Shamir, A., Tauman, Y.: How to leak a secret. In: Boyd, C. (ed.) ASIACRYPT 2001. LNCS, vol. 2248, pp. 552–565. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45682-1_32
Saeednia, S., Kremer, S., Markowitch, O.: An efficient strong designated verifier signature scheme. In: Lim, J.-I., Lee, D.-H. (eds.) ICISC 2003. LNCS, vol. 2971, pp. 40–54. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24691-6_4
Steinfeld, R., Bull, L., Wang, H., Pieprzyk, J.: Universal designated-verifier signatures. In: Laih, C.-S. (ed.) ASIACRYPT 2003. LNCS, vol. 2894, pp. 523–542. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-40061-5_33
Steinfeld, R., Wang, H., Pieprzyk, J.: Efficient extension of standard Schnorr/RSA signatures into universal designated-verifier signatures. In: Bao, F., Deng, R., Zhou, J. (eds.) PKC 2004. LNCS, vol. 2947, pp. 86–100. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24632-9_7
Unruh, D., Müller-Quade, J.: Universally composable incoercibility. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 411–428. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_22
Zhang, Y., Au, M.H., Yang, G., Susilo, W.: (Strong) multi-designated verifiers signatures secure against rogue key attack. In: Xu, L., Bertino, E., Mu, Y. (eds.) NSS 2012. LNCS, vol. 7645, pp. 334–347. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34601-9_25
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 International Association for Cryptologic Research
About this paper
Cite this paper
Maurer, U., Portmann, C., Rito, G. (2021). Giving an Adversary Guarantees (Or: How to Model Designated Verifier Signatures in a Composable Framework). In: Tibouchi, M., Wang, H. (eds) Advances in Cryptology – ASIACRYPT 2021. ASIACRYPT 2021. Lecture Notes in Computer Science(), vol 13092. Springer, Cham. https://doi.org/10.1007/978-3-030-92078-4_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-92078-4_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-92077-7
Online ISBN: 978-3-030-92078-4
eBook Packages: Computer ScienceComputer Science (R0)











 with a function of the probability that
with a function of the probability that  must be small.
must be small. . Since most statements are made for a fixed parameter k, we usually omit k from the notation, writing
. Since most statements are made for a fixed parameter k, we usually omit k from the notation, writing