Persistent Homology: A Topological Tool for Higher-Interaction Systems

Abstract

The aim of this chapter is to give a handy but thorough introduction to persistent homology and its applications. The chapter’s path is made by the following steps. First, we deal with the constructions from data to simplicial complexes according to the kind of data: filtrations of data, point clouds, networks, and topological spaces. For each construction, we underline the possible dependence on a fixed scale parameter. Secondly, we introduce the necessary algebraic structures capturing topological informations out of a simplicial complex at a fixed scale, namely the simplicial homology groups and the Hodge Laplacian operator. The so-obtained linear structures are then integrated into the multiscale framework of persistent homology where the entire persistence information is encoded in algebraic terms and the most advantageous persistence summaries available in the literature are discussed. Finally, we introduce the necessary metrics in order to state properties of stability of the introduced multiscale summaries under perturbations of input data. At the end, we give an overview of applications of persistent homology as well as a review of the existing tools in the broader area of Topological Data Analysis (TDA).

3.1 Introduction

Persistent homology is an emerging tool to identify robust topological features underlying the higher-order structure of (high-dimensional) data and complex dynamical systems (such as brain dynamics, molecular folding, distributed sensing). In the broader sense, persistence aims to associate meaningful mathematical objects to filtrations of data, point clouds, networks, topological spaces, simplicial complexes etc. Here, a filtration is a sequence of spaces, point clouds, networks, etc. together with maps connecting them. Very often these maps, if not always, will be inclusions and the sequence will results from filtering on similarities, or weights, in a way akin to hierarchical clustering. More specifically, we will be interested in considering filtrations of simplicial complexes, higher dimensional tetrahedral foams, combinatorial topological spaces naturally associated to the input data. Attached to simplicial complexes there are the homology groups that represent the lack of k-connectivity: the zeroth group measures usual connectivity, the first one the lack of tiles, e.g. three cliques, the second one the lack of four cliques and so on. The objects counted by the homology groups are voids as dis-junctions, cycles, empty boxes and so on. The homology groups corresponding to the stages of the filtration at the relevant scales, are connected via linear mappings induced by the filtration’s maps (by so called functoriality). Persistence studies the entanglement of these information into a single object called the persistence module, which is a linear space endowed with a structure of graded module encoding births and deaths of the voids along the filtration.

The main feature characterizing the persistence approach is to associate a data filtration with a unique well defined algebraic summary, computable by using linear algebra tools, whose behaviour represent in a principled way the topological properties of the data at the various scales in a single summary. This differentiate in an unequivocal way persistence from its germane, clustering. Indeed, while clustering analyze the behaviour of data with respect to e.g. some similarity by representing the process of aggregating data at the various scales but implicitly forces to choose a significative scale where to stop the process, persistence formalize and compress the information of the aggregation process itself. Furthermore, when persistence is applied to the higher degrees homologies it deals with information that no longer can be seen as a mere representation of the connectivity properties of the data along their characteristic scales.

In this chapter, we review the main notions in persistent homology according to the persistence pipeline. In Sect. 3.2, we address the main constructions to obtain a simplicial complex, or a filtration of simplicial complexes, according to the kind of input data. In Sect. 3.3, we introduce the notion of simplicial homology and its relation to the Hodge Laplacian as a way to deal with topological features of a simplicial complex, into linear algebraic terms. In Sect. 3.4, the multiscale approach of persistent homology is introduced and its main summaries are reviewed. Stability properties of metrics to compare changes in the data filtration to changes in the persistence summaries are reviewed in Sect. 3.5. In Sect. 3.6, we review some applications of persistent homology and provide the necessary references for tools implementing the persistence pipeline in practice.

Notations

• $\Sigma$ Simplicial Complex (finite and $\emptyset \not \in \Sigma$)

• $\sigma , \tau , \rho$ simplices

• $\mathbb {F}, \mathbb {R}, \mathbb {Z}, \mathbb {Z}_2$ an arbitrary field, real numbers, integers, $\mathbb {Z}/2\mathbb {Z}$

• $(v_0, \dots , v_q)$ q-simplex (simplex of dimension q)

• $[v_0, \dots , v_q]$ oriented q-simplex

• $\Sigma _q$ the set of the q-simplices of $\Sigma$

• $\Sigma _{(q)}$ the q-skeleton of $\Sigma$ (i.e. the set of the p-simplices of $\Sigma$ with $p\le q$)

• $C_q(\Sigma ;\mathbb {F})$ (short $C_q$ or $C_q(\Sigma )$) group of q-chains of $\Sigma$ with coefficients in $\mathbb {F}$

• $\mathscr {C}_q$ canonical basis of $C_q(\Sigma ;\mathbb {F})$

• $\partial _q: C_q(\Sigma ;\mathbb {F}) \rightarrow C_{q-1}(\Sigma ;\mathbb {F})$ boundary map

• $\delta ^q: C^{q}(\Sigma ;\mathbb {F}) \rightarrow C^{q+1}(\Sigma ;\mathbb {F})$ co-boundary map

• $D_q$ matrix representing the map $\partial _q: C_q(\Sigma ;\mathbb {F}) \rightarrow C_{q-1}(\Sigma ;\mathbb {F})$ with respect to the basis $\mathscr {C}_q$, $\mathscr {C}_{q-1}$

• $B_q(\Sigma ;\mathbb {F})$ (short $B_q$ or $B_q(\Sigma )$) q-boundaries of $\Sigma$ with coefficients in $\mathbb {F}$

• $Z_q(\Sigma ;\mathbb {F})$ (short $Z_q$ or $Z_q(\Sigma )$) q-cycles of $\Sigma$ with coefficients in $\mathbb {F}$

• $H_q(X;\mathbb {F})$ (short $H_q$ or $H_q(\Sigma )$) $q^{th}$ homology group of $\Sigma$ with coefficients in $\mathbb {F}$

• $\beta _q(\Sigma ;\mathbb {F})$ (short $\beta _q$ or $\beta _q(\Sigma )$) $q^{th}$ Betti number of $\Sigma$ with coefficients in $\mathbb {F}$

• $\ker (f)$ kernel of f

• ${{\,\mathrm{im}\,}}(f)$ image of f

• $\dim (\Sigma )$ dimension of $\Sigma$

• $\mathcal {H}_q$ Laplacian kernel

• $\varphi : \emptyset \subseteq \Sigma ^0 \subseteq \Sigma ^1 \subseteq \dots \Sigma ^m:=\Sigma$ filtration of $\Sigma$

• $C^i_q$ short for $C_q(\Sigma ^i ;\mathbb {F})$

• $H^i_q$ short for $H_q(\Sigma ^i ;\mathbb {F})$

• $H_q(\varphi ):=\bigoplus _i H_q(\Sigma ^i; \mathbb {F})$ the $q^{th}$ persistence module of $\varphi$

• $(a,b), (a, +\infty )$ persistence pairs

3.2 From Data to Simplicial Structures

In this section, we review and discuss the main constructions to obtain the main higher-order representation in the persistence pipeline, namely a simplicial complex associated to the original input datum [49]. We begin with Sect. 3.2.1 introducing simplicial complexes. We proceed further in Sect. 3.2.2 by introducing general constructions for simplicial complexes. In particular, we focus on the Nerve and the Flag complexes. Then, we review specific constructions according to the kind of the given data. We discuss point cloud data, graph and complex networks, partially ordered sets, and functions. A summary of the discussed methods according to the kind of input datum is depicted in Table 3.1.

Table 3.1 A summary of the possible simplicial complex construction (columns) introduced in this section according to the input data (rows)

3.2.1 Simplicial Complexes

Simplicial complexes are a classical mathematical tool for representing discrete shapes [78]. The elementary building blocks which form a simplicial are called simplices.

A simplex $\sigma$ of dimension q (also addressed as q-simplex) is the convex hull of $q+1$ affinely independent points in the Euclidean space. Practically speaking, a 0-simplex is just a point, a 1-simplex an edge, a 2-simplex a triangle, a 3-simplex a tetrahedron, and so on. Given a q-simplex $\sigma$, any simplex $\tau$ which is the convex hull of a non-empty subset of the points generating $\sigma$ is called a face of $\sigma$. Conversely, $\sigma$ is called a coface of $\tau$.

A (finite) simplicial complex $\Sigma$ is a finite set of simplices such that:

• each face of a simplex in $\Sigma$ belongs to $\Sigma$;

• each non-empty intersection of any two simplices in $\Sigma$ is a face of both.

Worth to be noticed that formally there is no obstruction in considering the empty simplex as included in any simplicial complex $\Sigma$. Its inclusion is typically allowed in theoretical frameworks and it will lead to the definitions of augmented chain complexes and of reduced homology. For the sake of simplicity, in this chapter we will only consider simplicial complexes not including the empty simplex.

Fig. 3.1

A (geometric) simplicial complex $\Sigma$ (on the left). The collection of simplices of the various dimensions $\Sigma$ consists of (on the right)

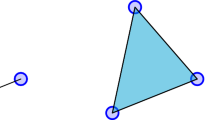
The two above claimed conditions are visually depicted in Fig. 3.1. In particular, we highlight the fact that once a simplex (such as the tetrahedron ABCD) belongs to a simplicial complex $\Sigma$, then all its faces (vertices, edges, and triangle in the depicted case) also belong to $\Sigma$. Moreover, in accordance with the second condition, notice that given any two simplices of the depicted simplicial complex $\Sigma$ their intersection is empty or another simplex of $\Sigma$ which is face of both.

By definition, a simplicial complex is a collection of simplices lying in an Euclidean space $\mathbb {R}^d$ of a certain dimension d. In order to adopt the notion of simplicial complex to a larger variety of datasets, it is useful to introduce a more general definition of simplicial complexes which do not necessarily need for a geometric realization. An abstract simplicial complex $\Sigma$ on a finite set V is a collection of non-empty subsets of V, called simplices, with the property of being closed under inclusion (see Fig. 3.2 for an example). More explicitly, if $\sigma$ is a simplex which belongs to $\Sigma$ and $\tau$ is a non-empty subset of V such that $\tau \subset \sigma$, then $\tau$ belongs to $\Sigma$. Given a simplicial complex $\Sigma$, the elements of V are called vertices of $\Sigma$ and a simplex $\sigma \in \Sigma$ is called a q-simplex (equivalently, a simplex of dimension q) if it consists of $q+1$ vertices.

Given a simplicial complex or an abstract simplicial complex $\Sigma$, the maximum of the dimensions of its simplices is called the dimension of $\Sigma$ and denoted as $\dim (\Sigma )$. Moreover, we will denoted by $\Sigma _q$ the set of the q-simplices of $\Sigma$ and by $\Sigma _{(q)}$ the q-skeleton of $\Sigma$ (i.e. the set of the p-simplices of $\Sigma$ with $p\le q$).

In spite of the different definitions, the two presented notions of simplicial complexes are strictly related. In fact, given a simplicial complex $\Sigma$, one can associate to it an abstract simplicial complex $\Sigma '$ defined as the collection of the simplices of $\Sigma$. Vice versa, given an abstract simplicial complex $\Sigma$, it always possible to retrieve a simplicial complex $\Sigma '$ whose associated abstract simplicial complex coincides with $\Sigma$ [78]. The simplicial complexes $\Sigma$ and $\Sigma '$ depicted in Figs. 3.1 and 3.2 , respectively, represent an example of this correspondence. $\Sigma '$ is the abstract simplicial complex associated to $\Sigma$, while $\Sigma$ is a geometric realization of $\Sigma '$.

Fig. 3.2

An abstract simplicial complex $\Sigma '$ on $V=\{A, B, C, D, E \}$. $\Sigma '$ is the abstract simplicial complex associated to the geometric simplicial complex $\Sigma$ depicted in Fig. 3.1

In the following, in the few cases in which we would like to distinguish between simplicial complexes and abstract simplicial complexes, we will adopt the term “geometric” simplicial complex to refer to the former. Differently, we will simply use the term “simplicial complex” to address both the structures.

3.2.2 Nerve Complexes, Flag Complexes, and Other Constructions of Simplicial Complexes

As already mentioned, Topological Data Analysis aims at describing and characterizing data in terms of their shape. In order to satisfy this assumption, the first required step in the persistence pipeline concerns associating to the input dataset a simplicial complex that will provide the data with a suitable topological structure needed for the next steps of the topological-based analysis.

The kinds of datasets eligible for this process of “translation” into a simplicial complex are various and heterogeneous and cover a vast majority of the datasets which a researcher could face in its work.

For the sake of simplicity, in this document we will focus mainly on point clouds embedded in an Euclidean space, (weighted) graphs or complex networks, functions, and sets endowed with a relation of partial order among its elements. In spite of this, most of the presented constructions can be generalized/adapted to the case of a finite collection of elements endowed with a notion of proximity enabling to cover a wide plethora of datasets. More properly, with the term “proximity” we mean a semi-metric, i.e. a distance not necessarily satisfying the triangle inequality.

Two common tools adopted in this step assigning a simplicial complex to an arbitrary dataset are the Nerve complex and the Flag complex.

Nerve complex

Let us consider a finite collection S of sets in $\mathbb {R}^n$. The Nerve complex Nrv(S) of S is the abstract simplicial complex generated by the non-empty common intersections among the sets of S [49]. More precisely,

$$\begin{aligned} Nrv(S):=\big \{ \sigma \subseteq S \, | \, \bigcap _{s \in \sigma } s \ne \emptyset \big \}. \end{aligned}$$

(3.1)

Fig. 3.3

A cover S (a) and its Nerve complex Nrv(S) (b)

As depicted in Fig. 3.3, intuitively the Nerve complex produces a simplicial complex whose vertices are in correspondence with the sets of S, whose edges represents the non-empty intersections among two sets in S, whose triangles the non-empty intersections among three sets in S, and so on. One of the most desirable properties of this construction relies on its capability of “preserving the shape” of the input collection of sets. In fact, (a simplified version of the) Nerve theorem ensures that, if all the sets in S are convex sets of $\mathbb {R}^n$, then the Nerve complex of S and the union of the sets in S are homotopy equivalent. Intuitively, this represents a theoretical guarantee ensuring us that the proposed construction respect the shape of the data and, specifically, its homology.

Flag complex

Given a (undirected) graph $G=(V,E)$, its Flag complex Flag(G) is the abstract simplicial complex having as simplices all the subsets $\sigma$ of vertices of G such that, for any two vertices u, v in $\sigma$, (u, v) is an edge of the graph G (see Fig. 3.4 for an example).

Fig. 3.4

A (undirected) graph G (a) and its Flag complex Flag(G) (b)

In other words, Flag(G) consists of all the cliques of the graph G. For this reason, it is also called clique complex. Intuitively, the Flag complex of a graph G captures the connectivity among the vertices of G: two connected vertices are turned into an edge of the simplicial complex, three fully-connected vertices into a triangle, and so on.

Each of the next subsections will focus on a specific kind of dataset showing how the introduced tools can be applied in order to transform the input data into a simplicial complex. Let us notice how, in most of the cases, the described constructions will not produce a single simplicial complex but a collection of simplicial complexes $\Sigma ^a$ depending on a parameter a such that, if $a\le b$, then $\Sigma ^a \subseteq \Sigma ^b$.

3.2.2.1 Point Clouds

Let us consider a finite set of points V in $\mathbb {R}^n$ and let us investigate several different techniques to associate to it a simplicial complex. Table 3.2 highlights some properties of the methods to be introduced in this section: the simplicial complex might be a purely combinatorial object (abstract) or embedded in some space (geometric); the maximum dimension reached by the simplices in the complex might be dependent on the original point cloud dimension or not; and the construction might be dependent on a fixed parameter or not. The last property is particularly relevant when the parameter is left free to vary. This multi-scale framework will be treated in Sect. 3.4.

Table 3.2 A summary of the properties of simplicial complexes obtained from point cloud data embedded in $\mathbb {R}^n$

Delaunay triangulations

One of the most traditional ways to build a simplicial complex from a point cloud is the so called Delaunay triangulation [37]. This construction, originally described for sets of points in $\mathbb {R}^2$ but generalizable to arbitrary dimensions, aims at producing a triangulation of the convex hull of V (i.e. the smallest convex set containing V) free of long and skinny triangles. More properly, a Delaunay triangulation Del(V) of V is a triangulation of the convex hull of V such that the circumcircle of any triangle does not contain any point of V in its interior. A Delaunay triangulation of V can be achieved by computing the Nerve complex of the Voronoi regions of the points in V, where the Voronoi region $R_V(u)$ of a vertex u of V is the set of all points in $\mathbb {R}^n$ whose Euclidean distance to u is not greater than their distance to the any other vertex v of V. More formally,

$$\begin{aligned} R_V(u):=\{x\in \mathbb {R}^n \, | \, \forall \, v \in V, d(x,u)\le d(x,v)\}, \end{aligned}$$

(3.2)

where d is the Euclidean distance.

Figure 3.5 depicts an example of Delaunay triangulation. Specifically, Fig. 3.5b shows a Delaunay triangulation of the point cloud V represented in Fig. 3.5a.

Fig. 3.5

A point cloud V in $\mathbb {R}^2$ (a) and its Delaunay triangulation Del(V) (b). In (b), the Voronoi regions in which $\mathbb {R}^2$ is subdivided are delimited by dotted lines

The points in $V\subseteq \mathbb {R}^n$ will be said in general position if no $n+2$ points lie on a common $(n-1)$-dimensional sphere. E.g., for $n=2$, the points of V are in general position if and only if no four or more points are co-circular. The hypothesis that the points in V are in general position enables to ensure that the Delaunay triangulation of V is unique and its realization as the Nerve complex of the Voronoi regions of the vertices of V produces not simply an abstract simplicial complex but a geometric simplicial complex embedded in $\mathbb {R}^n$.

Čech complexes

Given a point cloud V in $\mathbb {R}^n$ and fixed a scalar parameter $\epsilon >0$, the Čech complex $\check{C}ech_\epsilon (V)$ associated with V and $\epsilon$ is the abstract simplicial complex defined as:

$$\begin{aligned} \check{C}ech_\epsilon (V):=\big \{\sigma \subseteq V \,|\, \sigma \ne \emptyset \text { and } \bigcap _{v \in \sigma } B(v, \epsilon /2)\ne \emptyset \big \}, \end{aligned}$$

(3.3)

where $B(v, \epsilon /2)$ is the closed ball of radius $\epsilon /2$ centered in v (see Fig. 3.6a for an example) [36, 49].

One can notice that the above definition arises from the idea of replacing each vertex of V with a ball of radius $\epsilon /2$ and then taking the Nerve complex associated to this collection of balls. While considering the Čech complex of a point cloud V is one of the most natural way in order to associate a simplicial complex to V, its computation is definitely a time consuming procedure. For this reason, several “approximated” versions of the Čech complex have been proposed in the literature.

Vietoris-Rips complexes

A first approximated version of the Čech complex is represented by the Vietoris-Rips complex [49, 102]. Fixed a scalar parameter $\epsilon >0$, the Vietoris-Rips (VR) complex $VR_\epsilon (V)$ associated with V and $\epsilon$ is the abstract simplicial complex defined as:

$$\begin{aligned} VR_\epsilon (V):=\{\sigma \subseteq V \,|\, \sigma \ne \emptyset , \text { and } \forall \, u, v \in \sigma , d(u, v)\le \epsilon \}, \end{aligned}$$

(3.4)

where d is the Euclidean distance (see Fig. 3.6b for an example).

Fig. 3.6

The Čech complex $\check{C}ech_\epsilon (V)$ (a) and the Vietoris-Rips complex $VR_\epsilon (V)$ (b) associated with the point cloud V depicted in Fig. 3.5a and $\epsilon$. The depicted closed balls are of radius $\epsilon /2$

By definition, it easy to notice that the Vietoris-Rips complex $VR_\epsilon (V)$ coincides with the Flag complex of the 1-skeleton of the Čech complex $\check{C}ech_\epsilon (V)$. Moreover, the fact that the Vietoris-Rips complex represents an approximation of the Čech complex is ensured by the property claiming that for any $\epsilon >0$,

$$\begin{aligned} VR_{\frac{\sqrt{2}}{2} \epsilon }(V)\subseteq \check{C}ech_{\epsilon }(V) \subseteq VR_\epsilon (V). \end{aligned}$$

(3.5)

Alpha-shapes

The previously described constructions present several pros and cons. Delaunay triangulations produce geometrical simplicial complexes embedded in the same Euclidean space in which the input point cloud lies but, as a drawback, the obtained complex, being a triangulation of a convex hull, is quite trivial from a topological point of view (in fact, it has the same homology of a space consisting of a single point). On the contrary, Čech and Vietoris-Rips complexes better preserve the shape of the input dataset but they produce abstract simplicial complexes of arbitrarily high dimension. The idea behind alpha-shapes is to define a new strategy which could satisfies the positive aspects achieved by the previously described constructions and, at the same time, avoid to have their drawbacks [35, 40]. Given a point cloud V in $\mathbb {R}^n$ and fixed a scalar parameter $\epsilon >0$, this can simply achieved by defining the alpha-shape $Alpha_\epsilon (V)$ associated with V and $\epsilon$ as the Nerve complex generated by the regions obtained as the intersections between the closed balls of radius $\epsilon /2$ centered in the points of V and the Voronoi regions of the points in V. More precisely,

$$\begin{aligned} Alpha_\epsilon (V):=\big \{\sigma \subseteq V \,|\, \sigma \ne \emptyset \text { and } \bigcap _{v \in \sigma } A(v, \epsilon /2)\ne \emptyset \big \}, \end{aligned}$$

(3.6)

where $A(v, \epsilon /2)$ is defined as $B(v, \epsilon /2) \cap R_V(v)$ (see Fig. 3.7a for an example). So, since by definition $A(v, \epsilon /2)\subseteq B(v, \epsilon /2)$, we have that for any $\epsilon >0$,

$$\begin{aligned} Alpha_\epsilon (V) \subseteq \check{C}ech_{\epsilon }(V). \end{aligned}$$

(3.7)

Witness complexes

When dealing with point clouds consisting of a huge number of elements, the previously introduced constructions (even if sometimes still tractable) require a considerable amount of computational resources. Witness complexes aim at fixing this potential issue by constructing a simplicial complex still well representing the “shape” of the point cloud V in input but having a vertex sets of cardinality equal to just a fraction of V [30]. While a detailed definition of this class of complexes is out of the scope of this chapter, we can intuitively describe the witness complex of V as follows. In a nutshell, a witness complex is built by choosing a set of “landmark” points from V and then constructing a simplicial complex by using the remaining (non-landmark) data points as witnesses to the existence of edges or simplices spanned by combinations of landmark points (see Fig. 3.7b for an example). Analogously to the previous constructions, the definition of the witness complex associated with a point cloud V depends on a scalar parameter $\epsilon >0$.

Fig. 3.7

The alpha-shape $Alpha_\epsilon (V)$ (a) and the witness complex (b) associated with the point cloud V depicted in Fig. 3.5a and $\epsilon$. The depicted closed balls in (a) are of radius $\epsilon /2$

3.2.2.2 Graphs and Complex Networks

Given a complex network represented as a graph $G=(V, E)$ a natural way to associate with it a simplicial complex is by considering its Flag complex Flag(G) [102]. If (as it is common is several application domains) the edges of graph G are weighted by a function $w: E\rightarrow \mathbb {R}$, fixed a scalar parameter $\epsilon >0$, let us denote as $G_\epsilon =(V_\epsilon , E_\epsilon , w_\epsilon :E_\epsilon \rightarrow \mathbb {R})$, the subgraph of G such that:

• its vertex set $V_\epsilon$ coincides with V;

• its set of edges $E_\epsilon$ consists of the edges of G having weight lower or equal than $\epsilon$;

• its weight function $w_\epsilon$ is the restriction of w to the edge set $E_\epsilon$.

Combining this definition with the notion of Flag complex, one can define the Flag complex associated with G and $\epsilon$ as the Flag complex $Flag(G_\epsilon )$ of $G_\epsilon$.

3.2.2.3 Functions

Given a simplicial complex $\Sigma$ a function $f: \Sigma \rightarrow \mathbb {R}$ is called a filtering function if, whenever $\sigma$ is a face of $\tau$ with $\sigma , \tau \in \Sigma$, then $f(\sigma )\le f(\tau )$. Given a filtering function, it is possible to associate with f a collection of simplicial subcomplexes of $\Sigma$ depending on a parameter $r\in \mathbb {R}$. Specifically, choosing a scalar value $r\in \mathbb {R}$, the sublevel set of f with respect to r is defined as

$$\begin{aligned} \Sigma ^r:=f^{-1}\big ( (-\infty ,r] \big ). \end{aligned}$$

(3.8)

In several applicative scenarios, the function f could be defined on a domain which is not a simplicial complex. In spite of this, in most of the cases this does not represents a serious obstruction since one can often reconduct the situation to the previously described case. For instance, if the domain of f is a point cloud V, one can:

• construct from V a simplicial complex $\Sigma$ by adopting one of the techniques described in Subsect. 3.2.2.1;

• extend f to $\Sigma$ by defining, for any $\sigma \in \Sigma$,

  $$\begin{aligned} f(\sigma ):=\max \{ f(v) \, |\, v \text { is a vertex of } \sigma \}. \end{aligned}$$

  (3.9)

3.2.2.4 Partially-Ordered Sets

Order complexes

A partially-ordered set, usually called a poset, $(S, \le )$ is a set S endowed with a partial order $\le$ defined among its elements. Given a (finite) poset $(S, \le )$, the order complex $\Sigma (S, \le )$ associated to it is the abstract simplicial complex on S whose vertex set coincides with S and whose simplices are the finite chains of $(S, \le )$, i.e. the finite totally-ordered subsets of S [73, 82].

Fig. 3.8

The order complexes associated to [2] $=\{0, 1, 2\}$ (a) and to $\{(0,1),(1,0),(1,1)\}$ (b). The considered partial orders $\le$ are the standard ordering of natural numbers in the first case, while its component-wise extension in the second one

For example, let us consider the subset $[n] \subseteq \mathbb {N}$ consisting of the first $n+1$ natural numbers, i.e. $[n]=\{0, 1, 2, \dots , n\}$. By considering the standard ordering $\le$ on natural numbers, $([n], \le )$ is a totally-ordered set (in particular, a poset). As depicted in Fig. 3.8a for the case $n=2$, the order complex associated to $([n], \le )$ consists of a n-simplex and all its faces.

Differently, let us consider the subset $S:=\{(0,1),(1,0),(1,1)\} \subseteq \mathbb {N}^2$ and endow it with the partial order $\le$ defined by: $(x, y)\le (x', y')$ if and only if $x\le x'$ and $y\le y'$. Then, as depicted in Fig. 3.8b, the order complex associated to $(S, \le )$ consists of two 1-simplices connected by a vertex (corresponding to the point (1, 1)). Please notice that the edge connecting (0, 1) and (1, 0) is missing since the two points are not comparable with respect to the considered partial order.

3.3 From Simplicial Structure to Linear Algebra

In the previous section, we described how to endow data with a shape through the combinatorial and topological notion of a simplicial complex. In this section, we introduce the notion of simplicial homology and its relation to the Hodge Laplacian as a way to capture topological features coming from a simplicial complex into linear algebraic terms. The notions introduced in this section have to be seen as preliminary ones to persistent homology, that is the core multiscale notion of this chapter introduced in Sect. 3.4. Differently from persistent homology, a simplicial homology group and a Hodge Laplacian refer to a single scale parameter characterizing the shape we have associated to our data, and provides the building blocks for the multiscale approach of persistent homology.

3.3.1 Simplicial Homology

Homology is a mathematical tool able to describe a shape in terms of its holes [78]. In order to define the homology of a simplicial complex $\Sigma$, we need to move from the combinatorial notion of a simplicial complex to the algebraic structures of chain groups.

Let $\sigma$ be a q-simplex spanned by the vertices $v_0, v_1, \dots , v_q$. Two orderings of the vertices of $\sigma$ are defined equivalent if they differ by an even permutation. If $q>0$, the orderings of the vertices of $\sigma$ fall into two equivalence classes called orientations of $\sigma$. A pair consisting of a simplex and an orientation of it will be called oriented simplex. We will adopt the symbol $[v_0, v_1, \dots , v_q]$ to denote the oriented simplex generated by $v_0, v_1, \dots , v_q$ and the equivalence class of the specific ordering $(v_0, v_1, \dots , v_q)$. When clear from the context, we will simply use $\sigma$ to denote either a simplex or an oriented simplex.

Given a simplicial complex $\Sigma$ and a field $\mathbb {F}$, we define the $q^{th}$ chain group $C_q(\Sigma ;\mathbb {F})$ of $\Sigma$ as the vector space over $\mathbb {F}$ generated by the oriented q-simplices of $\Sigma$ and where $- \sigma$ coincides with the simplex $\sigma$ endowed with the opposite orientation. An element of $C_q(\Sigma ;\mathbb {F})$ is called q-chain and it is a finite linear combination $\sum _i \lambda _i \sigma _i$ with coefficients in $\mathbb {F}$ of oriented q-simplices. Once an orientation for each simplex of $\Sigma _q$ is fixed, a canonical basis $\mathscr {C}_q$ of $C_q(\Sigma ;\mathbb {F})$ is determined. Properly, $\mathscr {C}_q$ consists of the q-chains corresponding to the oriented q-simplices of $\Sigma$. In the following when it will not cause any ambiguity, we will often write $C_q(\Sigma )$ or simply $C_q$ for in place of $C_q(\Sigma ; \mathbb {F})$. For the sake of readability, an analogous simplification will be adopted to all the other notations presented in the following.

Chain groups of a simplicial complex $\Sigma$ are connected by linear maps $\partial _q:C_q(\Sigma ;\mathbb {F}) \rightarrow C_{q-1}(\Sigma ;\mathbb {F})$ called boundary operators. Given an element of the basis $\mathscr {C}_q$ corresponding to the oriented q-simplex $\sigma =[v_0, v_1, \dots , v_q]$ of $\Sigma$, $\partial _q(\sigma )$ is defined as:

$$\begin{aligned} \partial _q(\sigma ):=\sum _{i=0}^q (-1)^i [v_0, \dots , \hat{v}_i, \dots , v_q], \end{aligned}$$

(3.10)

where $\hat{v}_i$ means that vertex $v_i$ is not present (see Fig. 3.9 for an example).

Fig. 3.9

Examples of boundaries and cycles of a simplicial complex $\Sigma$. The yellow edges represent the boundary of the triangle $\sigma$. All the highlighted collections of edges represent 1-cycles. The yellow and the purple cycles are also 1-boundaries while the red and the light blue ones are not. Moreover, the red and the light blue cycles are homologous, i.e. they are two representatives of the same homology class (the triangular hole they both include)

The boundary $\partial _q$ is extended to each q-chain of $\Sigma$ by linearity. In the following, we will denote by $D_q$ the matrix representing the map $\partial _q: C_q(\Sigma ;\mathbb {F}) \rightarrow C_{q-1}(\Sigma ;\mathbb {F})$ with respect to the basis $\mathscr {C}_q$, $\mathscr {C}_{q-1}$.

We denote as $Z_q(\Sigma ; \mathbb {F}):=\ker \partial _q$ the $\mathbb {F}$-vector space of the q-cycles of $\Sigma$ and as $B_q(\Sigma ; \mathbb {F}):={{\,\mathrm{im}\,}}\partial _{q+1}$ the $\mathbb {F}$-vector space of the k-boundaries of $\Sigma$. Examples of boundaries and cycles are depicted in Fig. 3.9.

It is immediate to check that, for any q, $\partial _{q}\partial _{q+1}=0$ or, equivalently, that $B_q(\Sigma ) \subseteq Z_q(\Sigma )$. This fact ensures that the quotient

$$\begin{aligned} H_q(\Sigma ; \mathbb {F}):=\frac{Z_q(\Sigma ; \mathbb {F})}{B_q(\Sigma ; \mathbb {F})} \end{aligned}$$

(3.11)

is a well-defined vector space over $\mathbb {F}$. The space $H_q(\Sigma ; \mathbb {F})$ will be called the $k^{th}$ homology group of $\Sigma$ with coefficients in $\mathbb {F}$.

By definition of $H_q(\Sigma ; \mathbb {F})$, q-cycles of $\Sigma$ are partitioned in equivalence classes called homology classes. Two q-cycles are said homologous if they belong to the same homology class (see Fig. 3.9 for an example). Given a q-cycle c its homology class (i.e. the collection of all the q-cycles homologous to c) will be denoted by [c].

The dimension of $H_q(\Sigma ; \mathbb {F})$ as $\mathbb {F}$-vector space is called the $k^{th}$Betti number of $\Sigma$ and denoted by $\beta _q(\Sigma ; \mathbb {F})$.

Intuitively, homology spots the “holes” of a simplicial complex $\Sigma$. In fact, a non-null element of $H_q(\Sigma )$ is an equivalence class of homologous cycles that are not the boundary of any $(q+1)$-chain of $\Sigma$. The number $\beta _q$ of such classes represents, in dimension 0, the number of connected components of $\Sigma$, in dimension 1, the number of its tunnels and its loops, in dimension 2, the number of voids or cavities, and so on.

3.3.2 Hodge Decomposition

In this section, the ground ring of coefficients will be the field of real numbers $\mathbb {R}$ unless otherwise stated. We fix an arbitrary finite simplicial complex $\Sigma$, and we set $C_q:=C_q(\Sigma ; \mathbb {R})$ so that $\partial _q: C_{q} \rightarrow C_{q-1}$ will stand for the boundary operator for any $q=0, \dots ,\dim (\Sigma )$. Furthermore, we set $H_q:=H_q(\Sigma ; \mathbb {R})$. We will work in a simplified setting, adopting for the entire section the canonical basis $\mathscr {C}_q$ of $C_q(\Sigma ;\mathbb {F})$ for $C_q$ i.e. the one in bijection with (equivalence classes of oriented) $q-$dimensional simplices and this will allow us to identify $\partial _q$ with its matrix $D_q$ w.r.t. the bases $\mathscr {C}_q$ and $\mathscr {C}_{q-1}$,

$$\begin{aligned} D_q:= M_{\partial _q}^{\mathscr {C}_q,\mathscr {C}_{q-1}}. \end{aligned}$$

(3.12)

The Hodge q-Laplacian, that is also called q-th Combinatorial Laplacian, can be defined both in terms of cohomology, coboundaries and adjoint, as it has been proposed in the previous chapter, than as follows in terms of homology, boundary maps and their matrices

$$\begin{aligned} \mathcal {L}_q:=\partial ^{^{*}}_q\partial _q^{^{ }}+\partial _{q+1}^{^{ }}\partial _{q+1}^{^{*}}, \end{aligned}$$

(3.13)

where $\partial _q^{^{*}}$ denotes the adjoint of $\partial _q$ w.r.t some inner product defined on the chains groups. We fix the standard inner (scalar) product on $C_q$ which makes $\mathscr {C}_q$ an orthonormal basis so that the matrix of $\partial _q^{^{*}}$ with respect to $\mathscr {C}_{q-1},\, \mathscr {C}_{q}$ is $D_q^{^{T}}$ the transposed of $D_q$. We write

$$\begin{aligned} L_q:=D_q^{^{T}}D_q^{^{ }}+D_{q+1}^{^{ }}D^{^{T}}_{q+1}. \end{aligned}$$

(3.14)

We will now study some properties of the Laplacians by taking advantage of this formulation and following [68].

The fundamental theorem of topology states that $D_{q+1}D_q=0$ for all $q\ge 0.$ Therefore, it makes sense to study the Laplacians as follows.

Definition 3.1

Let $A\in \mathbb {R}^{m\times n}$ and $B\in \mathbb {R}^{n\times p}$ be two real matrices such that $AB=\mathbf {0}\in \mathbb {R}^{n\times n}$, then

$$\begin{aligned} {{\,\mathrm{im}\,}}(B) \subseteq \ker (A) \end{aligned}$$

(3.15)

and we set

$$\begin{aligned} H_{A,B}:=\ker (A)/{{\,\mathrm{im}\,}}(B), \end{aligned}$$

(3.16)

for the homology group with respect to A and B.

Accordingly, their Hodge Laplacian is

$$\begin{aligned} L_{A,B}:= A^{T}\!\!A+BB^{T}. \end{aligned}$$

(3.17)

Note that $L_{A,B}^T=L_{A,B}^{^{ }}$.

Theorem 3.1

Let A and B be as above. Then, the following hold

• 1. $H_{A,B}\cong \ker (L_{A,B})$;

• 2. $\ker (L_{A,B})=\ker (A)\cap \ker (B^T)$;

• 3. ${{\,\mathrm{im}\,}}(L_{A,B})={{\,\mathrm{im}\,}}(A^T)\oplus {{\,\mathrm{im}\,}}(B)$;

• 4. (Hodge Decomposition) There is an orthogonal direct sum decomposition

  

  (3.18)

• 5. Hodge Decomposition versus Fredholm Alternative

  

  (3.19)

Proof

See [68].

Now, by substituting $A=\partial _{q}$ and $B=\partial _{q+1}$ in Theorem 3.1 we obtain the classical result on Hodge decomposition.

Theorem 3.2

Let $\partial _q$, $\partial _{q+1}$ and $L_q$ be as above. Then, the following hold

• 1. $H_{q}\cong \ker (L_{q})$;

• 2. $\ker (L_{q})=\ker (D_q^{})\cap \ker (D_{q+1}^T)$;

• 3. ${{\,\mathrm{im}\,}}(L_{q})={{\,\mathrm{im}\,}}(D_{q}^T)\oplus {{\,\mathrm{im}\,}}(D_{q+1})$;

• 4. (Hodge Decomposition) There is an orthogonal direct sum decomposition

  

  (3.20)

• 5. Hodge Decomposition versus Fredholm Alternative

  

  (3.21)

We will present some interesting applications of the Hodge decomposition in Sect. 3.6.

3.4 Multiscale Topology a.k.a. Persistent Homology

As described in Sect. 3.3, shapes can be associated with homology groups capturing topological features. Instead, the idea of persistent homology [16, 39] is to deal with, not simply the homology group at a specific scale, but rather the homology groups of filtrations of shapes, that is shapes at multiple scales. This section aims at introducing persistent homology along with the most known persistent homology summaries. Theoretical comparisons among such summaries are provided. The same notions will be extensively used in Sect. 3.5 to discuss stability results for persistence.

3.4.1 Persistent Homology

As described in Sect. 3.2.1, given a dataset there are multiple ways in order to assign to it the structure of a simplicial complex and, therefore, to study the “shape” of the original dataset by computing the homology of the associated complex. Certainly, in most of cases, the presented construction strategies depend on the choice of a scalar parameter $\epsilon$ while the considered dataset gives us no clue as to which $\epsilon$ is preferable. In spite of this, fixing a construction strategy and varying the value $\epsilon$ produces a collection $\varphi$ of encapsulated simplicial complexes to be studied in a multiscale framework. Since our simplicial complexes are always finite, we can restrict to consider finite collections of encapsulated simplicial complexes were indexes take integer values only.

A filtration of $\Sigma$ is a finite sequence of subcomplexes $\varphi :=\{\Sigma ^a\, |\, 0\le a \le m\}$ of $\Sigma$ such that $\emptyset =\Sigma ^0 \subseteq \Sigma ^1 \subseteq \dots \subseteq \Sigma ^m=\Sigma$. We refer to $\Sigma ^a$ as the step a in the filtration $\varphi$. In Fig. 3.11, we see a filtration obtained from a set V of 7 points by constructing the VR-complex $VR_\epsilon$(V) for 7 selected values of parameter $\epsilon$ (see Sect. 3.2.2.1).

Let $C_q^a$ be the short notation for $C_q(\Sigma ^a;\mathbb {F})$ introduced in Sect. 3.3.1. Consider an inclusion $\Sigma ^a\subseteq \Sigma ^b$. Then, we get induced a map $f_q^{a,b}:C_q^a \longrightarrow C_q^b$ defined over each q-simplex $\sigma$ of the basis of $C_q^a$ by $f_q(\sigma )=\sigma$ and then extended linearly. The linear map $f_q^{a,b}$ is a q-chain map since it satisfies

$$\begin{aligned} f_q(\partial _q \sigma ) = \partial _qf_q(\sigma ). \end{aligned}$$

(3.22)

This implies obviously the homology functoriality. Indeed, Equation (3.22) ensures that $f_q$ preserves q-cycles and q-boundaries. Hence, the homology construction can be applied not simply to all filtration steps in $\varphi$ to obtain a collection of vector spaces $H_q(\Sigma ^a;\mathbb {F})$, shortly indicated by $H_q^a$, but also to all inclusion maps to get maps $i_q^{a,b}:H_q^a\longrightarrow H_q^b$ at homology level defined by

$$\begin{aligned} i_q^{a,b}([c]) = [f^{a,b}_q(c)], \quad \text {for any }k\text {-cycle } c. \end{aligned}$$

(3.23)

More generally, the homology functoriality holds due to the inclusion $\Sigma ^a\subseteq \Sigma ^b$ being a simplicial map. That is, a map $s:\Sigma \longrightarrow \Sigma '$ satisfying

$$\begin{aligned} \text {for all } \sigma , \tau \in \Sigma , \quad \sigma \subset \tau \quad \Rightarrow \quad s(\sigma ) \subset s(\tau ). \end{aligned}$$

Thus, given a filtration $\varphi = \{\Sigma ^a\, |\, 0\le a \le m\}$, we can define the following. For $a, b \in \{0, \dots , m\}$ such that $a\le b$, the (a, b)-persistent q-homology group $H_q^{a,b}(\Sigma )$ is

$$\begin{aligned} H_q^{a,b}(\varphi ):={{\,\mathrm{im}\,}}(i_q^{a, b}). \end{aligned}$$

(3.24)

Since homology captures cycles in a shape by factoring out the boundary cycles, persistent homology [16, 39] captures whether cycles that are non-boundary elements in a certain step of the filtration and will turn into boundaries in some subsequent step. The persistence, along a filtration, of a cycle gives quantitative information about the relevance of the cycle itself for the shape.

3.4.2 Representing: from Persistence to Topological Summaries

The purpose of this section is that of introducing the most relevant ways of representing the persistent homology information. Our main focus is on the information encoded by each descriptor. Thus, we begin by exposing the algebraic correspondence that provides a complete and standard way of encoding the whole persistent homology information. We review some equivalent descriptors such as persistence diagrams [38], barcodes, and persistent Betti numbers [44, 94]. We will go through the diverse summaries by following the guiding example in Fig. 3.11. Afterwards, we move to other summaries encoding the persistent homology information in a more structured way. Statistical approaches require desciptor spaces being suitable not simply for measurements (covered in Sect. 3.5) but where collections of descriptors can be summed up, weighted and averaged. We close this part by reviewing some proposals in statistical and learning direction to encode the persistent homology information, namely persistence landscapes [13], persistence images [1] and other kernel representations. A comparison of persistent homology summaries over the same example is contained Fig. 3.10.

Fig. 3.10

A Vietoris-Rips filtration for increasing values of the parameter $\varepsilon$ (top). From left to right the persistence diagram, persistence landscapes, persistence surface, and persistence image, for homology degree 0 (middle) and 1 (bottom)

In order to deal with the totality of the persistence information is common to consider the following definition.

Given a filtration $\varphi = \{\Sigma ^a\, |\, 0\le a \le m\}$, the $q^{th}$-persistence module $H_q(\varphi )$ is the collection of the groups $H_q^a$, with $0\le a\le m$, connected by the linear maps $i_q^{a,b}$, with $0\le a\le b \le m$.

As explained in [16], a $q^{th}$-persistence module $H_q(\varphi )$ can be thought of as a finitely generated graded $\mathbb {F}[x]$-module $M=\bigoplus _{a\in \mathbb {N}} H_q^a$ where, each $H_q^a$ is taken as the set of homogeneous elements of grade a, and the action $x^{b-a} h$ over an element h of grade a is defined by $i_{q}^{a,b}(h)$. Hence, $x^{b-a} h$ belongs to $H_q^b$ for all $h\in H_q^a$, that is the graded module definition is met.

Theorem 3.3

(Structure Theorem) Any finitely generated graded $\mathbb {F}[x]$-module can be decomposed as a finite direct sum of finitely generated $\mathbb {F}[x]$-modules as follows

$$\begin{aligned} M\cong \bigoplus _{i=1}^\alpha x^{a_i}\mathbb {F}[x] \oplus \bigoplus _{j=1}^\beta \left( \left( x^{b_j}\mathbb {F}[x]\right) / \left( x^{c_j-b_j} \mathbb {F}[x] \right) \right) , \end{aligned}$$

(3.25)

where $a_i, b_i, c_i\in \mathbb {N}$ with $b_i<c_i$, and, for any $n\in \mathbb {N}$, $x^{n}\mathbb {F}[x]$ is the ideal generated by $x^n$ inside $\mathbb {F}[x]$. Furthermore, the decomposition is unique up to reordering of the summands.

Fig. 3.11

A filtration with the corresponding persistence pairs and barcode. All bars starting at 0 represent homological classes of degree 0. At the bottom, only one bar corresponds to the life-span of a cycle

The summands entailing only one parameter $a'_i$ capture the generators of M appearing at grade $a'_i$, whereas the other summands capture generators appearing at grade $a_j$ and disappearing at grade $b_j$. The former kind of summands form what is called the free part of the module decomposition, the latter kind form the torsion part.

By applying the Structure Theorem to the graded $\mathbb {F}[x]$-module $\bigoplus _{a\in \mathbb {N}} H_q^a$ associated with the $q^{th}$-persistence module $H_q(\varphi )$, we can encode, up to isomorphisms, the entire information of persistent homology by means of pairs of two kinds. Each summand in the free part provides us with a pair $(a,\infty )$, representing the persistence of a single homology class appearing at step a and never vanishing along the filtration. Each summand in the torsion part provides us with a pair (a, b), for a single class appearing at step a and vanishing at step b. The example in Fig. 3.11 has only the pair $(0,\infty )$ for the homology degree 0 which never vanishes. All the other persistence pairs in the example vanishes.

Tame persistence module

In order to obtain persistence modules from a filtering function as introduced in Sect. 3.2.2.3 and in view of Sect. 3.5 on the stability of persistence summaries, we generalize the persistence module definition to indexes in the set of real numbers $\mathbb {R}$ totally ordered under the standard order relation $\le$.

An $\mathbb {R}$-persistence module [23] $\mathscr {F}$ with coefficients in $\mathbb {F}$ and real indexes consists of a collection $\{F^a\}_{a\in \mathbb {R}}$ of $\mathbb {F}$-vector spaces along with a collection $\{f^{a,b}\}_{a\le b \in \mathbb {R}}$ of linear maps such that

$$\begin{aligned} \begin{aligned} \forall a\le b\le c \in A,\qquad&f^{a,c}=f^{b,c}\circ f^{a,b} \\ \forall a\in A,\qquad&f^{a,a}=\text {id}_{F^a}. \end{aligned} \end{aligned}$$

(3.26)

An $\mathbb {R}$-persistence module $\mathscr {F}$ is said to be tame if and only if,

$$\begin{aligned} \forall a\in A,\qquad&\dim _\mathbb {F}F^a<+\infty \nonumber \\ f^{a,b} \qquad&\text { is an isomorphism,}\\&\text {except for a finite number of index pairs} (a, b). \nonumber \end{aligned}$$

(3.27)

The notion of an $\mathbb {R}$-persistence module generalizes the one with finite natural indexes introduced at the beginning of this section. Indeed as an example, the $q^{th}$-persistence module $H_q(\varphi )$ of a filtration $\varphi = \{\Sigma ^a\, |\, 0\le i\le m, a\in \mathbb {N}\}$ with $m\in \mathbb {N}$ can be made into an $\mathbb {R}$-persistence module. First, we extend the indexes to the integers $\mathbb {Z}$. The collection of groups $\{H^i\}$ is extended by setting $H^i=0$ if $i<0$, and $H^i=H^m$ if $i>m$. The collection of linear maps $\{f^{i,j}\}$ is extended by setting $f^{i,i+1}=0$ if $i+1<0$, and $f^{i,i+1}$ the identity map if $i>m$. Then, all possible compositions define $f^{i,j}$ for general indexes $i\le j$. The extension to indexes in $\mathbb {R}$ is obtained by setting, for all real numbers $a\le b$, $H^a = H^i$ with the integer i such that $i\le a <i+1$, $H^b = H^j$ with the integer j such that $j\le b <j+1$, and $f^{a,b}=f^{i,j}$. Moreover, it is obvious to check that the obtained $\mathbb {R}$-persistence module is tame.

This extension allows us to consider relevant examples of tame $\mathbb {R}$-persistence modules such as the one obtained via sublevel sets of a filtering function introduced in Sect. 3.2.2.3, or the ones obtained via filtrations from point clouds, as the one in Fig. 3.11, introduced in Sect. 3.2.2.1, or the ones from graph data introduced in Sect. 3.2.2.2.

Persistence diagrams

Fix the notation $\bar{\mathbb {R}}= (\mathbb {R}\cup \{\infty \})$ and $\bar{\mathbb {N}}= (\mathbb {N}\cup \{\infty \})$. Consider a tame $\mathbb {R}$-persistence module $\mathscr {F}$. The finite multi-set of points obtained from the Structure Theorem applied to $\mathscr {F}$ defines the persistence diagram [38] as

(3.28)

The elements belonging to the persistence diagram are called persistence pairs. By the Structure Theorem, the persistence diagram is a complete invariant for a persistence module. The persistence diagram of the filtration in Fig. 3.11 consists of the pairs depicted in column on the left. Notice that the pair (0, 0.35) appears with multiplicity 2.

An invariant for a persistence module equivalent to the persistence diagram is the barcode. The barcode $\text {Bar}(\mathscr {F})$ is the finite collection $\{(b_i,d_i)\}_{i\in I}$ of points $(b_i,d_i)$ varying in the support of $\text {PD}(\mathscr {F})$ counted $\text {PD}(\mathscr {F})(b,d)$ times. The barcode of the filtration in Fig. 3.11 consists of the bars of different length according to the persistence of the corresponding homology class as the value of the parameter $\epsilon$ varies.

As treated in [23], the tameness condition ensures that $\mathscr {F}$ admits a representation as a finitely generated module by a suitable reindexing. Hence, the definition in Equation (3.28) applies. The tameness condition ensures that a sequence of nested discretizations of $\mathscr {F}$ converges to a unique persistence diagram with respect to a similarity notion between persistence modules called the interleaving distance which will be introduced in Sect. 3.5.

Persistent Betti numbers

Given a tame persistence module $\mathscr {F}=(\{F^a\},\{f^{a,b}\})$ with coefficients in $\mathbb {F}$ and indexes in $(\mathbb {R},\le )$, we define the persistent Betti numbers [44] of $\mathscr {F}$ as the function $\beta : \mathbb {R}\times \bar{\mathbb {R}}\rightarrow \mathbb {N}$ defined by

$$\begin{aligned} \beta (a,b):={\left\{ \begin{array}{ll} \dim f^{a,b}(F^a) &{} \text { if } a\le b \\ 0 &{} \text { if } a > b. \end{array}\right. } \end{aligned}$$

(3.29)

Equivalently, given the barcode $\text {Bar}(\mathscr {F})=\{ (b_i,d_i) \}_{0\le i\le N}$, we obtain the same function by defining

$$\begin{aligned} \beta (a,b)=\#\{ 0\le i\le N \ |\ \text {s.t. } b_i\le a \le b \le d_i \}. \end{aligned}$$

(3.30)

The Representation Theorem in [21] , or the Triangle Lemma in [27], guarantees that knowing $\beta$ is equivalent to knowing the persistence diagram. For a given homology degree, the value at (a, b) of the persistent Betti numbers of the filtration can be easily read off from Fig. 3.11 by counting the number of bars of full length in the $\epsilon$ range from a to b.

Persistence landscapes

A limitation of a persistence diagram in encoding the persistence information is that the mean of multiple persistence diagrams as functions might be ambiguous. To overcome this, persistence landscapes are introduced in [13].

The persistence landscape of $\mathscr {F}$ is the function $\lambda :\mathbb {N}\times \mathbb {R}\rightarrow \bar{\mathbb {R}}$ such that

$$\begin{aligned} \lambda (k,t) := \sup \{ m\ge 0 \ |\ \beta (t-m,t+m)\ge k \}. \end{aligned}$$

(3.31)

Notice that the transformation $t=\frac{a+b}{2}$, $m=\frac{b-a}{2}$ sends the diagonal of the persistence diagram domain to the horizontal axis as we can see by comparing persistence diagrams and landscapes in Fig. 3.12.

The persistence landscapes are invertible in the sense that the persistent diagram can be recovered from the persistence landscapes. Indeed, persistent Betti numbers $\beta (a,b)$ at a point (a, b) can be recovered. Consider the set of integers $I_{(a,b)}=\{ k \ |\ \text {s.t. } \text {supp}\lambda (k,\cdot )\supseteq [a,b] \}$. It follows that $\beta (a,b)= \sum _{k\in I_{(a,b)}} \lambda (k,\frac{a+b}{2})$. The definition of the function $\lambda$ can be extended to the domain $\mathbb {R}^2$ by setting $\lambda (\lceil x\rceil , t)$. The mean $\bar{\lambda }$ of $\lambda ^1, \dots , \lambda ^n$ persistence landscapes is defined by

$$\begin{aligned} \bar{\lambda }(x,t):= \frac{1}{n} \sum _{i=1}^n \lambda ^i(x,t). \end{aligned}$$

(3.32)

Fig. 3.12

Persistence diagrams and landscapes for the first homology degree of a sampling of 100 points over a torus (top) and a sphere (bottom)

Persistence images

Recently, a very powerful summary for persistence has been introduced, called persistence images [1]. Actually, their representation approximizes the information in a persistence diagram and a persistence image is not invertible in the sense of persistence landscapes.

Nonetheless, the key strength point is that persistence images represent persistence as a finite dimensional vector in $\mathbb {R}^n$. The finite dimensional representation makes persistence images a favorable way for integrating persistence into deep neural architectures thus opening the way for an interplay between deep learning and TDA (see Sect. 3.6).

A persistence diagram D is transformed into a persistence surface $\rho _D:\mathbb {R}^2\rightarrow \mathbb {R}$

$$\begin{aligned} \rho _D(x) := \sum _{y\in T(D)} \omega (y) k_{G}(x,y), \end{aligned}$$

(3.33)

where T(D) is the set of birth-persistence pairs obtained from D by applying $(a,b)\mapsto (a,b-a)$, the weight function $\omega :\mathbb {R}^2\rightarrow \mathbb {R}$ is zero on the horizontal axis and step-wise differentiable, the function $k_G$ is the Gaussian kernel defined by $k_G(x,y)=\exp {-\frac{\Vert x-y \Vert ^2}{2\sigma ^2}}$, for some parameter $\sigma$.

The persistence image $I(\rho _D)$ of D is obtained from $\rho _D$ by subdividing its domain into n pixels P by means of a regular grid and by computing the integral of $\rho _D$ over each P. In Fig. 3.13, we see an example with the birth-persistence diagram T(D) and the corresponding persistence image obtained by discretization.

Fig. 3.13

Birth-persistence diagrams and persistence images for the first homology degree of a sampling of 100 points over a torus (top) and a sphere (bottom)

Homological scaffolds

Homological scaffolds are effective and compact summaries of the homological features of weighted networks capable of simultaneously make their homological properties amenable to networks theoretical methods [87].

Given a complex network represented as a weighted graph $G=(V, E, w: E \rightarrow \mathbb {R})$, let B be a collection of representative cycles of the 1-dimensional homological classes occurring during the filtration $\varphi$ of Flag complexes associated to G. Given an edge e of G, it is possible to associate to it a weight $\omega (e)$ defined as it follows:

$$\begin{aligned} \omega (e):=\sum _{g \in B, e \in g} \omega _g, \end{aligned}$$

(3.34)

where $\omega _g$ is a weight value associated to the homological class of g. Based on the weight $\omega$, the homological scaffold of the network G is defined as the weighted graph $G'=(V',E', \omega : E' \rightarrow \mathbb {R}_{>0})$ where:

• $V':=V$;

• $E'$ consists of the edges e of E for which $\omega (e)>0$.

The scaffold is called persistence homological scaffold by defining $\omega _g$ as the life-span $\pi _g$ of g, while it is called frequency homological scaffold by setting, for any cycle g, $\omega _g:=1$.

Despite their proven applicative capabilities, (persistence and frequency) homological scaffolds theoretically depend on the choice of representative cycles. In order to address this potential issue and thanks to the recent advances in the computation of minimal homology bases [32], a quasi-canonical version of the scaffold, called minimal, has been introduced in [48].

Formally, given a complex network $G=(V, E, w: E \rightarrow \mathbb {R})$, let us consider the minimal homology basis $B^\epsilon$ of $H_1(Flag(G_\epsilon ))$ (i.e. a collection of representative cycles of minimal total length whose classes form a basis of $H_1(Flag(G_\epsilon ))$). Moreover, let us define $B^*$ as $\bigsqcup _{\epsilon } B^\epsilon$. Similarly to the frequency homological scaffold, the minimal homological scaffold of G is defined as the weighted graph $G'=(V',E', \omega : E' \rightarrow \mathbb {R}_{>0})$ where:

• $V':=V$;

• $\omega (e):=\sum _{g \in B^*, e \in g} 1$ (i.e. the number of cycles in $B^*$ containing e);

• $E'$ consists of the edges e of E for which $\omega (e)>0$.

Fig. 3.14

At the top, filtration with minimal 1-homology generators (loops) highlighted. Below, the associated minimal scaffold. Image available under courtesy of the authors of [48]

In Fig. 3.14, an example of the minimal scaffold consisting of minimal 1-homology generators appeared along the filtration is depicted.

3.4.2.1 Representing the Topological Information Through Kernels

Topological information and, specifically, persistence diagrams are effective data discriminants. On the other hand, interfacing persistence diagrams directly with statistics and Machine Learning poses technical difficulties, because the space of persistence diagrams is not endowed with a structure of an inner product or, more properly, of a Hilbert space structure. This lack prevents that lengths, angles, and means of persistence diagrams can be defined as well as that kernel-based learning methods such as kernel PCA and support vector machines for classification [92] can be adopted.

Given an input space X, a kernel for X is a map $k: X \times X \rightarrow \mathbb {R}$ such that there exist a Hilbert space H and a map $\phi : X \rightarrow H$, called feature map for which, for any $x,y \in X$, $k(x,y) = \langle \phi (x), \phi (y)\rangle$. Equivalently, k is a kernel if the following diagram commutes:

(3.35)

Recall that a Hilbert space H is a complete metric space with respect to the distance induced by the inner product $\langle \, \cdot \,, \, \cdot \,\rangle$. A widely adopted assumption for an inner product $\langle \, \cdot \,, \, \cdot \,\rangle$ is the request of being positive semi-definite. In such a case, a kernel will be called reproducing kernel.

Worth to be mentioned that the definition a kernel k does not require the explicit knowledge of its feature map $\phi$ but just a theoretical guarantee of its existence. Results as the theorems of Moore-Aronszajn and of Mercer characterize the conditions under which a function $k: X \times X \rightarrow \mathbb {R}$ can serve as a kernel [59]. For instance, Moore-Aronszajn’s theorem claims that any finite function $k: X \times X \rightarrow \mathbb {R}$ is a reproducing kernel as long as it is finite, symmetric, and positive semi-definite.

The idea of defining a kernel for the space X of persistence diagrams has been introduced in the late nineties in [33, 43] but it has been widely adopted just in the last few years. In the framework of persistence-based kernels, the feature map is usually explicitly provided and the chosen Hilbert space is typically the $L^2(\mathbb {R}^2)$ space of the square-integrable functions. In the following, we will list and briefly discuss the main features of all (to the best of our knowledge) persistence-based kernels introduced in the literature.

Roughly, we can classify them into three groups: persistence landscapes [13]; Gaussian kernels [1, 61, 92]; sliced Wasserstein kernels [19].

Persistence landscapes as kernels

Persistence landscapes, introduced in [13] and previously described in Sect. 3.4.2, allow for representing any persistence diagram as a square-integrable function. Even if not previously mentioned, the procedure assigning a $L^2$ function $\lambda (D)$ to a persistence diagram D can be considered as a feature map from the space of the persistence diagrams to $L^2(\mathbb {R}^2)$. According with this perspective, a kernel k based on persistence landscapes can be plainly defined as

$$\begin{aligned} k(D,D')= \Vert \lambda (D)-\lambda (D') \Vert _{L^2}, \end{aligned}$$

(3.36)

where D and $D'$ are two persistence diagrams.

Gaussian kernels

The second class of persistence-based kernels is defined thanks to the explicit introduction of a feature map $\phi$. In [92] and in [61], a similar approach is adopted. Focusing on [92], let denote as $\Omega$ the region $\{x=(x_1,x_2)\in \mathbb {R}^2 \,|\, x_2 \ge x_1\}\subseteq \mathbb {R}^2$ above the diagonal and as $\delta _x$ the Dirac delta centered at the point x. The feature map $\phi$ will be defined on a given persistence diagram D, as the solution $u: \Omega \times \mathbb {R}_{\ge 0} \rightarrow \mathbb {R}$ of the partial differential equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta _x u = \frac{\partial u}{\partial t} &{} \text {in } \Omega \times \mathbb {R}_{\ge 0} \\ u = 0 &{} \text {on } fr(\Omega ) \times \mathbb {R}_{\ge 0} \\ u = \sum _{y \in D} \delta _y &{} \text {in } \Omega \times \{0\}. \end{array}\right. } \end{aligned}$$

(3.37)

A solution of the above equation is achieved by posing

$$\begin{aligned} \phi _\sigma ^D(x):= \frac{1}{4\pi \sigma }\sum _{y\in D} \left( e^{\left( -\frac{{\Vert x-y \Vert }^2}{4\sigma } \right) } - e^{\left( -\frac{{\Vert x-y' \Vert }^2}{4\sigma } \right) } \right) , \end{aligned}$$

(3.38)

with $y'=(b,a)$ if $y=(a,b)$.

So, we obtain the following explicit expression for the associated kernel

$$\begin{aligned} k(D, D')= \frac{1}{8\pi \sigma }\sum _{y\in D, z\in D'} \left( e^{\left( -\frac{{\Vert y-z \Vert }^2}{8\sigma } \right) } - e^{\left( -\frac{{\Vert y-z' \Vert }^2}{8\sigma } \right) } \right) . \end{aligned}$$

(3.39)

Intuitively, given a persistence diagram D, the above described procedure returns an $L^2$ function $\phi (D)$ having a Gaussian peak centered at each point of the considered diagram D. Moreover, in order to obtain a stable kernel, the height of each peak is set as proportional to the distance of the corresponding point (a, b) from the diagonal of the first quadrant of $\mathbb {R}^2$.

Even if still based on Gaussian peaks, a different approach has been adopted in [1]. As previously mentioned, persistence images enable to convey the persistent homology information through a vector. This is achieved by: (i) transforming any persistence diagram D into a surface $\rho _D$ obtained by centering at each point of D a suitably weighted Gaussian peak; (ii) discretizing $\rho _D$ by decomposing the domain into a regular grid of pixels; (iii) representing the obtained result through a heat map $I(\rho _D)$. Among other advantages, such a vectorization process promptly provides a notion of kernel. In fact, given two persistence diagrams D and $D'$, one can define their kernel simply as the inner product of their associated vectors $I(\rho _D)$ and $I(\rho _{D'})$:

$$\begin{aligned} k(D,D') := \langle I(\rho _D), I(\rho _{D'}) \rangle . \end{aligned}$$

(3.40)

Sliced Wasserstein kernel

In various contexts, a standard way to construct a kernel is to exponentiate the negative of an Euclidean distance. In [19], the authors aim at adopting a similar approach in order to define a kernel between persistence diagrams. According with this idea, given two persistence diagrams D and $D'$ a kernel can be defined as:

$$\begin{aligned} k(D, D'):= e^{\left( -\frac{f(D,D')}{2\sigma ^2} \right) }. \end{aligned}$$

(3.41)

An important theorem in [8] (Theorem 3.2.2, page 74) ensures that the above formula defines a valid positive definite kernel for any $\sigma > 0$ if and only if f is negative semi-definite. Unfortunately, none of the already introduced distances between persistence diagrams can serve as f since does not satisfy the property of negative semi-definiteness. In order to overcome this limitation, a new distance $d_{SW}$, called sliced Wasserstein distance, has been introduced in [19]. Sliced Wasserstein distance represents an approximation of $1^{st}$-Wasserstein distance and, thanks to the fact of being provably negative semi-definite, it can be chosen as f in Eq. (3.41) in order to define a valid positive definite kernel of persistence diagrams.

3.5 Comparing Multiscale Summaries: Distances and Stability

Stability is a concept rooted in celestial mechanics and, thereafter, in the study of dynamical systems. Loosely speaking, a quantity related to the system is stable if small perturbations will result in relatively small changes of it. In this spirit stability has been studied also in the area of persistence. Namely, several results have been obtained about the behaviour of the topological summaries presented in the previous sections with respect to perturbations of the input data. In particular, this has been addressed by comparing suitable set distances variations, as for example the Gromov-Hausdorff distance, with the corresponding modifications of their e.g. persistence diagrams and the other summaries. This section is devoted to introduce and elucidate this topic and the main results on it.

3.5.1 Distances on Data

In this section, we collect the definitions of the dissimilarity measures applying to input data within the persistence pipeline (see Sect. 3.2). The first one is the natural pseudo-distance [62] and it applies to continuous functions used to filter a domain by sublevel sets. In the case of continuous functions over the same domain, the natural pseudo-distance is usually replaced by the actual distance defined by the $L_\infty$-norm.

The second distance to be introduced is the Gromov-Hausdorff [24] distance which applies to finite metric spaces such as the point clouds discussed in Sect. 3.2.2.1.

Natural pseudo-distance

A topological space X is called triangulable [78] if there exists a (finite) simplicial complex homemorphic to X. A continuous function $f:X\longrightarrow \mathbb {R}$ is called tame if and only if it induces a filtration on X via sublevel sets of the form $X^a=f^{-1}((-\infty ,a])$ (see Sect. 3.2.2.3) such that each $X^a$ has finite dimensional homology. Notice that the tameness condition on functions implies the tameness condition for the $\mathbb {R}$-persistence module obtained through sublevel sets discussed in Sect. 3.4.2. A pair (X, f) consisting of a triangulable space X and a tame function is called a size pair.

Let (X, f) be a size pair. The natural pseudo-distance [62] between two pairs (X, f), (Y, g) is defined by

(3.42)

where ${{\,\mathrm{Hom}\,}}(X,Y)$ is the set of all homeomorphisms from X to Y.

In the case $Y=X$, it is preferable to consider the $L_\infty$ -norm inducing an actual distance function between f and g instead of their natural pseudo-distance. Indeed, if there exists an homeomorphism h such that $f=g\circ h$, then even though their $L_\infty$-norm is in general non-trivial.

Gromov-Hausdorff distance

A finite metric space is a pair $(X,d_X)$ consisting of a finite set X and a metric function $d_X:X\times X\longrightarrow \mathbb {R}$. For example, we can think of X endowed with the metric function inherited from some embedding into a finite dimensional Euclidean space. A correspondence r between X and Y is a subset of $X\times Y$ such that the canonical projection from the Cartesian product $\pi _X:X\times Y\longrightarrow X$ and $\pi _Y:X\times Y\longrightarrow Y$ are both surjective. The set of all correspondences between X and Y will be denoted by $X\rightleftharpoons Y$. A correspondence generalizes a bijection between two sets with different cardinalities.

Once we have a correspondence $r\in X\rightleftharpoons Y$ between the underlying sets, we can define its distorsion as

$$\begin{aligned} {{\,\mathrm{Dis}\,}}(r):= \sup \{ | d_X(x,y) - d_Y(x',y')| \ | \ (x,y),(x',y')\in r \}. \end{aligned}$$

(3.43)

The Gromov-Hausdorff distance [47] between two finite metric spaces $(X,d_X)$, $(Y,d_Y)$ is defined as

(3.44)

3.5.2 Distances on Persistence Summaries

In this section, we collect the definitions of the dissimilarity measures applying to persistent homology summaries (see Sect. 3.4.2).

We first review the interleaving distance [23] applying to $\mathbb {R}$-persistence modules. Afterwards, we review the p-landscape distance [13] applying in the same way to both $\mathbb {R}$-persistence modules and persistence diagrams. Later, we review the distances on persistence diagrams: the matching/bottleneck distance [27, 62], the $p^{th}$-Wasserstein distance [28], and the Hausdorff distance [27].

We close this section by stating the Isometry Theorem [14, 65] for relating the interleaving distance and the introduced distances on diagrams.

Interleaving distance

Let $\mathscr {F}$, $\mathscr {G}$ be $\mathbb {R}$-persistence modules as in Eq. (3.26) and $\epsilon >0$. We say that $\mathscr {F}$ and $\mathscr {G}$ are $\epsilon$-interleaved if and only if there exists a family $\{ \Phi ^a: F^a \longrightarrow G^{a+\epsilon } \}_{a\in \mathbb {R}}$ and a family $\{ \Psi ^a: G^a \longrightarrow F^{a+\epsilon } \}_{a\in \mathbb {R}}$ such that the following diagrams commute

(3.45)

The interleaving distance between real-indexed persistence modules is defined by

(3.46)

Distance on persistence landscapes

Let $\lambda$, $\lambda '$ be the persistence landscapes associated to two persistence modules $\mathscr {F}$, $\mathscr {F}'$, respectively. Fix p a real number $p\ge 1$ or $p=\infty$. Then, the p -landscape distance is defined by means of the $L_p$-norm as follows

$$\begin{aligned} \Lambda _p(\mathscr {F},\mathscr {F}'):=\Vert \lambda - \lambda '\Vert _p. \end{aligned}$$

(3.47)

In the same way, if $\lambda$, $\lambda '$ are the persistence landscapes associated to two persistence diagrams D, $D'$ we define $\Lambda _p(D,D'):=\Vert \lambda - \lambda '\Vert _p$.

Distances on persistence diagrams

Let $D_1$ and $D_2$ be persistence diagrams as defined in Eq. (3.28). Some pseudo-metrics require the notion of a matching between persistence diagrams. A matching between $D_1$ and $D_2$ is simply a bijection between the underlying sets. Notice that the persistence diagrams are not finite metric spaces like those in Eq. (3.44). Despite there might be points with finite multiplicity in different number within two persistence diagrams, such a cardinality discrepancy is overcome by matching points to the diagonal when needed. The bottleneck distance [27] (also called matching distance [62]) is defined as

(3.48)

where the $\Vert \Vert _\infty$-norm is always taken for points as part of $\mathbb {R}^2$.

The bottleneck distance can be seen as part of a family of pseudo-metrics. For any integer $1\le p\le +\infty$, the $p^{th}$ -Wasserstein distance [28] is defined as

(3.49)

The Hausdorff distance [27] does not require a bijection between the underlying sets and it is defined as

(3.50)

Let (X, f), (Y, g) be two pairs consisting of a triangulable topological space and a continuous real-valued function on it. Suppose f and g are both tame functions, meaning that the respective $\mathbb {R}$-persistence modules $\mathscr {F}$ and $\mathscr {G}$ obtained by sublevel sets are tame in the sense of Equation (3.27). Let $D_f$, $D_g$ be the persistence diagrams associated to the sublevel set filtrations induced by f and g, respectively. It follows that the following relations among persistence pseudo-metrics hold:

(3.51)

(3.52)

By Eq. (3.51), we get that, on persistence diagrams, a stability result with respect to the bottleneck distance implies the corresponding stability with respect to the Hausdorff distance. Equation (3.52) is usually referred to as the Isometry Theorem [14, 65].

3.5.3 Stability Results

In this section, we collect the main results concerning the stability with respect to the dissimilarity measures introduced in Sect. 3.5.1 and Sects. 3.5.2.

We begin by stating Theorem 3.4 and Theorem 3.5 for the stability in terms of bottleneck distance of persistence diagrams and natural pseudo-distance of size pairs [29]. We proceed further with Theorem 3.6 and Theorem 3.7 for extending to persistence landscapes the stability results just stated [13]. Afterwards, we state Theorem 3.8 for the stability of the bottleneck distance of persistence diagrams with respect to the Gromov-Hausdorff distance of finite metric spaces [28]. We conclude this part with a focus on the stability of the persistence-based kernels which have been introduced in Sect. 3.4.2.1.

Theorem 3.4

Let (X, f), (Y, g) be two pairs consisting of a triangulable topological space and a tame function on it. Let $D_f$, $D_g$ be the persistence diagrams associated to the sublevel set filtrations induced by f and g, respectively. Then, it holds that

In the case of $X=Y$, the stronger result with respect to the $L_\infty$-norm applies [29].

Theorem 3.5

Let (X, f), (X, g) be two pairs consisting of a triangulable topological space and a tame function on it. Let $D_f$, $D_g$ be the persistence diagrams associated to the sublevel set filtrations induced by f and g, respectively. Then, it holds that

Notice that, by Eq. (3.52), the two stability results apply also to the interleaving distance between the corresponding persistence modules. That is usually referred to as algebraic stability theorem [23]. Moreover, recently the stability result has been sharpened and generalized to interval decomposable persistence modules and block decomposable $\mathbb {R}^n$-persistence modules [12]. The former ones apply to modified persistence frameworks: zig-zag persistence [76] and Reeb graphs (a survey in [10]). The latter ones apply to the the case of persistence generalized to filtrations determined by multiparameters [17] instead of a single one.

In the case of persistence landscapes, the stability is stated by the following and proved in [13].

Theorem 3.6

Let (X, f), (X, g) be two pairs consisting of a triangulable topological space and a function on it. Let $\mathscr {F}$, $\mathscr {G}$ be the two persistence modules associated to the sublevel set filtrations induced by f and g, respectively. Then, it holds that

$$\begin{aligned} \Lambda _\infty (\mathscr {F},\mathscr {G}) \le \Vert f - g \Vert _\infty . \end{aligned}$$

In the same way, the stability of persistence landscapes with respect to the $p^{th}$-Wasserstein distance of persistence diagrams is also proven [13].

Theorem 3.7

Let $D_1$, $D_2$ be two persistence diagrams. Fix p a real number $p\ge 1$ or $p=\infty$. Then, it holds that

In the case of filtrations built on top of a finite metric space such as those introduced in Sect. 3.2.1, the following result holds [24].

Theorem 3.8

Let $(X,d_X)$, $(Y,d_Y)$ be two finite metric spaces. Let , be the persistence diagrams associated to the Vietoris-Rips complex constructions over $(X,d_X)$, $(Y,d_Y)$, respectively. Then, it holds that

By applying Formula (3.5), the result can be extended to the Čech construction.

Stability of persistence-based kernels

Analogously to the the previously discussed topological summaries, it is crucial that also for the information conveyed by a persistence-based kernel to be stable. Given a (pseudo) distance $d: X \times X \rightarrow \mathbb {R}$ of a space X, a kernel k for X is called stable with respect to d if there exists a constant $C>0$ such that, for any $x,y\in X$,

$$\begin{aligned} \Vert \phi (x) - \phi (y) \Vert _H\le C \cdot d(x,y), \end{aligned}$$

(3.53)

where $\Vert \, \cdot \, \Vert _H$ is the norm induced by the inner product of H.

All the described persistence-based kernels satisfy some stability result. We refer to the papers in which each kernel is introduced for the details about the specific stability properties they satisfy. As an example, we report here the stability results satisfied by the scale-space kernel. Stability of scale-space kernel with respect to $1^{st}$-Wasserstein distance of persistence diagrams

(3.54)

3.6 Applications

In this section, we review applications of Topological Data Analysis (TDA) exploiting the persistent homology pipeline. Our purpose is not to provide a comprehensive list. Surveys on the topic may be found in [25, 84]. Instead, we aim at showing how TDA general properties are exploited and adapted to specific application fields. Generally speaking, TDA is well-appreciated since it:

• summarizes multiscale information according to the relevance of homology classes along the scale range on data;

• captures higher-order relations among data entities;

• captures mesoscale information on complex data since homology mediates between local properties (holes) inserted in global contexts (homologous holes are not necessarily close each other);

• captures coarse information;

• captures robust information.

The reader interested in computational aspects of the persistence pipeline is referred to the standard algorithm for persistence introduced in [16]. A list of softwares implementing several persistent homology algorithms comprises: PHAT [6] which is written in C++ and Python along with its distributed version DIPHA [5], the tool Ripser [4], and the more recent tool GIOTTO [98]. A persistence tool specifically designed for complex networks is jHoles [11]. The reader interested in a comprehensive comparison of algorithms and tools for persistent homology is referred to the roadmap work in [81].

Libraries for performing general TDA computations are available in C++ and Python through the Gudhi library [72] along with its R software interface [42]. A previous C++ library for persistent homology is Dionysus [77]. A comprehensive tool-kit for TDA not limited to the persistence pipeline is available at [85] in C++ and Python.

In the following part, we focus on the fields of complex networks, neuroscience, and biology where the contribution of TDA is well recognized. We proceed by presenting two specific scopes where the q-Hodge Laplacian (see Sect. 3.3.2) finds applications. In the final part, we present a collection of other applications to be easily accessible by domain experts.

Complex networks and social science

Most of applications in complex networks exploits the ability of TDA of capturing higher-order relations among data entities. Graphs and weighted graphs naturally encode the pairwise relation of complex networks. The simplicial complex constructions introduced in Sect. 3.2.2.2 allow to endow a (weighted) graph with a (filtered) higher-order structure.

Some applications are focused on translations of graph concepts into simplicial complex terms. In [9], the percolation is extended from graph to simplicial complexes. In [54], the clique complex is introduced. This allows for a persistence multiscale summary of higher-order structures [93] to track community cliques. This leads the authors to introducing a new non-local measure which is proven to be complementary to standard centrality and comparison measures. A classification of network models which integrates topological information is proposed in [97].

Some applications in the field of complex networks exploit the ability of persistence in capturing mesoscale information. For instance, in [89] authors apply persistence to detect new non-local structures. In [88], a new and robust filtration is introduced which is proven to be richer than both metrical and clique filtrations.

Due to the formalization into (weighted) graph terms, applications to Social Science exploit a framework similar to that of complex networks. In [2], topology is used to detect a correlation between socio-economic indicators and spatial structures in the city environment. In [99], topology is combined to non-linear dimensional reduction to provide new contagion maps. In [20], authors apply the degree 0 and 1 persistence to analyze collaboration networks and differentiate them from the random case. In [95], persistence is applied for selecting features out of the high-dimensional point clouds of clients connected by weighted interaction links.

Neuroscience

The multiscale summaries provided by TDA have shown relevant impact on the study of structural and functional brain connectivity. The brain connectivity is often represented by a connectivity matrix based on physical adjacency or correlation measures between brain regions. This can be easily turned into weighted graph terms thus allowing for the application of TDA and, specifically, the persistence pipeline.

TDA supports the exploration and visualization purposes especially by means of the Mapper graph [96]. The Mapper graph is a topological signature alternative to persistence. The signature captures the adjacency of connected components with respect to scalar function level sets. The Mapper signature is exploited in [83] to show coherence of topological information on structural and functional brain aspects.

Coming back to the persistence pipeline, we first focus on structural aspects. In [75], authors investigate the dynamics of the Kuramoto model in the case of higher-order relations. In [7], graph filtrations are exploited to study tree-like structures of brain arteries to find correlations between age and sex higher than previously obtained without higher-order structures.

As for the functional aspects, in [46] the clique complex construction is used to derive the critical role of the hippocampal circuits in shaping the geometrical structure of correlations in the brain of rats. In [87], the scaffold persistence summary is exploited to discriminate between healthy and psycoactive patients. The function brain connectivity is also studied under fMRI data (Functional Magnetic Resonance Images) in [70] to introduce a new topology-based measure based on the scaffold summary. In [101], vineyards, that is continuous families of persistence diagrams, are used to classify between resting and gaming subjects to obtain more robust results compared to Principal Component Analysis.

Brain functionalities other than the connectivity are also investigated under data represented by functions. Image data of cortical surfaces are classified in [26] according to persistence summaries. Most applications are focused on EEG signals treated in several works. In [100] denoising of signals is performed by means of persistence landscape summaries. The original signal and the transformed one are found to share topological properties. The independence from scales and translations of topological features is exploited over the frequent space after Fourier transform to isolate the signal. In [52, 53], EEG signals are treated for finding evidences of correlations between head positioning and hypnotizability of patients. In [15], authors propose feature selection to separate signals of able-bodied from amputee subjects.

Biology

The field of biology is experimenting a growing interest towards topological data analysis. A first motivation relies on the high number of features known to be involved in many biological studies. This is the case of the work in [90] where TDA is integrated into feature selection to detect subgroups of features based on similarity measures.

A second case is that of gene sequences. The gene sequence evolutions can be represented by treelike structures where points are gene sequences. As stated in [22], treelike structures accurately reflect vertical evolution (mutations over generations) but not horizontal evolution (genomic mixture between individuals). Tree structures capture vertical evolution. They consist of a single connected component without loops. Hence, homology in degree 0 might be associated to vertical evolution, whereas higher-order homological features might be associated with horizontal evolution. Higher-order homological features are captured by starting from the same initial gene sequences and considering the Vietoris-Rips complex with respect to some distance measuring genetic dissimilarity. These assumptions are applied in [41] to characterize and study antibiotic resistance. Another gene sequence application is in the scope of pattern recognition. TDA is applied to finding patterns within gene expressions [31] with no periodicity assumption, unlike, for instance, in the case of those retrieved by the Fourier transform.

A third case of relevant interest is the study of proteins. Protein data are particularly suited for geometrical representations, that is graphs or point clouds embedded in some metric space. Most persistent loops are found to appear in correspondence of active protein sites [56]. For instance, DNA can be modeled by weighted graph structures where vertexes are atoms, edges are bonds and weights represent biological properties. In [74], the attitude of persistence of capturing mesoscale features is used to reveal local functional properties, where local is not a priori determined but retrieved. Weights are locally associated to persistence features within the generalized framework of weighted persistent homology. Moreover, in [45], protein compressibiity is related to the protein geometric structure. The simplicial model involved is that of $\alpha$-shapes. A correlation between the topological measure and the experimentally-determined compressibility of most proteins is found.

HodgeRank

In [68], the Hodge decomposition has been successfully applied in the setting of statistical ranking. The main problem discussed in [68] is that of determining a global ranking from a dataset comprising a number of alternatives ranked by a number of voters. This is a relevant problem which sprung form several fields and it is of paramount relevance for, e.g., online global platform as Netflix, Amazon, Google, Ebay, etc.

Besides deducing a global ranking from the data, whenever possible, the authors also showed a way to analyze the obstructions not permitting a statistically meaningful global ranking. Their methods, collectively called HodgeRank, analyze pairwise rankings represented as edge flows on a graph using combinatorial Hodge theory also to provide a mean to determine a global ranking that also comes with a certificate of reliability for its validity. Alternatives are $V=\{1, \ldots , m\}$ and voters $\Lambda =\{1, \ldots , n\}$ For each voter $\alpha \in \Lambda$ ranking matrix

$$ Y^{\alpha } \in \mathbb {R}^{n \times n}, \quad Y_{i j}^{\alpha }=-Y_{j i}^{\alpha } $$

Weight function $w: \Lambda \times V \times V \rightarrow [0, \infty )$

$$ w_{i j}^{\alpha }=\left\{ \begin{array}{l} 1 \text{ if } \alpha \text{ compared } (i, j) \\ 0 \text{ otherwise } \end{array}\right. $$

are provided. Let $\Sigma$ be the clique complex whose one skeleton is the graph $G:=(V, E)$ with vertices the alternatives and adjacency matrix $(w_{i,j})$ i.e. edge are between compared alternatives. Hodge theory then provides an orthogonal decomposition of the assigned pairwise comparison flow into three components: a gradient flow that is globally acyclic, a harmonic flow that is locally acyclic but globally cyclic, and a curl flow that is locally cyclic. Namely

$$ Y=Y^{(g)}+{Y}^{(h)}+{Y}^{(c)} $$

from

Usually, in this two dimensional case the components of the decomposition have traditional name caming for physics, that is: the elements of ${{\,\mathrm{im}\,}}(D_1^T)$ are the gradient flows; the elements of $\ker (L_1)$ are the harmonic flows; the elements of ${{\,\mathrm{im}\,}}(D_2)$ are the curl flows. The gradient flows component induces a global ranking of the alternatives and this can be computed via a linear least squares problem. Furthermore, the $l-2$-norm of the least squares residual, provides a measure of the validity of the global ranking induced by the gradient flow component. If the residual is small, then the gradient flow accounts for most of the variation in the given data and, therefore, the global ranking obtained from it is expected to be a majority consensus. Viceversa, if the residual is large, then the data manifest cyclic inconsistencies and no reasonable global ranking is expected to exist. The curl flow and harmonic flow components of an edge flow quantify respectively the local and global cyclic inconsistencies. Inconsistencies of a local nature will cause a dominant curl flow component, while a dominant harmonic flow component reflects a global nature of the inconsistencies. If in addition the harmonic flow component is small, then most of the inconsistencies happen locally and this could be read as the global ranking is sound on a coarse scale (infra-cluster ranking) but not on a finer scale (intra-cluster ranking).

Communication networks

In [3] the authors used the Hodge decomposition to analyze signals residing over a simplicial complex. Although they focused on signals defined over the edges of a complex of order two, i.e. including triangles, their findings and tools can be directly translated to analyze signals defined over higher order structures. What would be missing in the higher order cases would be concepts as solenoidal or irrotational behaviors. A signal over over a simplicial complex $\Sigma$ is a family of functions $s^k:\Sigma _k\rightarrow \mathbb {R}$, with $k=0,\dots ,\dim {\Sigma }$. By using the decomposition (4) and (5) in Theorem 3.2 one can orthogonally decompose $s^k$ as

$$ s^k =D_k^Ts^{k-1}+s^k_H+D_{k+1}s^{k+1} $$

where $L_k(s^k_H)=0$ i.e. it is an harmonic. Taking advantage of this representation the authors were able to prove that the Lovàsz extension of the triple-wise coupling function gives rise to a measure of the curl of edge signals along triangles. They also proposed a method to infer the structure of a second order simplicial complex from flow data and we showed that in applications over real wireless traffic data, the proposed approach can significantly outperform methods based only on graph representations. Furthermore, they analyze discrete vector fields and showed an application to the recovery of the RNA velocity field to predict the evolution of living cells. In such a case, using the eigenvectors of the first combinatorial Laplacian have been able to highlight irrational and solenoidal behaviors that would have been difficult to highlight using only the eigenvectors of the zeroth one.

TDA applied to other fields

The number fields where TDA has found or is gaining success is experimenting an impressive grow.

In particular, thanks to the translation into vector representations and the statistically significant improvements in representing persistent homology (Sect. 3.4.2.1), the last few years have seen the flourishing of the interplay between TDA and Machine Learning. To this scope, the survey [51] on TDA and deep learning provides an interesting discussion on contributions of TDA in Machine learning as well as the converse.

Finally, we close this section by providing a not exhaustive list of applications which can possibly be of interest to field experts. The list entails: physics [34, 57, 58, 86], medicine [7, 63, 67, 80], chemistry [64], image analysis [18], shape study [60], object recognition [66], fractal geometry [71], quantum computing [69], machine monitoring [55], automated productivity [50], data analysis in biomechanics [91], and material science [79].