10.1 Introduction

Synchronization is an ubiquitous phenomenon in natural and engineered systems. It corresponds to the emergence of a collective behavior wherein the system components eventually adjust themselves into a common evolution in time. [1, 2] Various studies have shed light on the intimate relations between the topology of a networked system, its synchronizability, and the properties of the synchronized states. In particular, synchronous behaviors have been observed and characterized in small-world  [3], weighted [4], multilayer [5], and adaptive networks [6, 7]. Outside complete synchronization, moreover, other types of synchronization have been revealed to emerge in networked systems, including remote synchronization [8, 9], cluster states [10] and synchronization of group of nodes [11], chimera [12, 13], Bellerophon states [14, 15], and Benjamin-Feir instabilities [16,17,18]. Finally, the transition to synchronization has been shown to be either smooth and reversible, or abrupt and irreversible (as in the case of explosive synchronization, resembling a first-order like phase transition [19]).

While attempts of extending to \(p-\)uniform hypergraphs the analysis of complete synchronization of dynamical systems have been recently made [20], most studies of systems interplaying through higher order interactions in simplicial complexes have focused on the case of the Kuramoto model [21, 22]. This is, in fact, a specific model, wherein each unit of the ensemble \(i=1, \ldots , N\) is a phase oscillator and is characterized by the evolution of its real valued phase \(\theta _i(t) \in [0,2\pi ]\). The model has been studied in all different sorts of network topologies with possible applications to biological and social systems [2, 21], and recently extensions of it have been proposed that include higher-order interactions. Namely, it has been shown that the Kuramoto model may exhibit abrupt desynchronization when three-body interactions among all the oscillators are added to [23], or completely replace [24], the all-to-all pairwise interactions of the original model. Similar results have been obtained with a non-symmetric variation of the Kuramoto model in which the microscopic details of the interactions among the phase oscillators are described in the form of a simplicial complex [25]. A different approach has been proposed by Millán et al., who have formulated a higher-order Kuramoto model in which the oscillators are placed not on the nodes but on higher-order simplices, such as links, triangles, and so on, of a simplicial complex [26].

In Chap. 9, an extension of the Kuramoto model to interactions of any order, which is still analytically tractable because all the oscillators have identical frequencies, has been discussed [27]. In this chapter, we move from the analysis of a specific model to the study of the most general ensemble of, yet identical, dynamical systems, organized on the nodes of a simplicial complex of any order, and interacting via any coupling functions. In such a general context, we show that complete synchronization in systems of identical units exists as an invariant solution, as far as the coupling functions cancel out. Furthermore, we give the necessary condition for it to be observed as a stable state and then we show that such condition can be written in terms of a Master Stability Function, a method initially developed in Ref. [28] for pairwise coupled systems, and later extended in many ways to complex networks [29] and to time-varying interactions [30,31,32,33]. Therefore, the framework discussed here is valid for a large number of situations, and, as so, it is applicable to a very wide range of experimental and/or practical circumstances. We will show, indeed, that all the theoretical predictions that our method entitles us to make are fully verified in simulations of synthetic and real-words networked systems.

10.2 Networks and Higher-Order Structures

A network is a collection of nodes and of edges connecting pairs of nodes. Mathematically, it is represented by a graph \(\mathcal {G} =(\mathcal {V},\mathcal {E})\), which consists of a set \(\mathcal {V}\) with \(N=|\mathcal {V}|\) elements called vertices (or nodes), and a set \(\mathcal {E}\) whose K elements, called edges or links, are pairs of nodes (i, j) (\(i,j=1,2,\ldots ,N\) and \(i \ne j\)). As graphs explicitly refer to pairwise interactions, networks have been very successful in capturing the properties of coupled dynamical systems in all such cases in which the interactions can be expressed (or approximated) as a sum of two-body terms [34]. Conversely, their limits emerge when it comes to model higher-order interactions. In fact, the presence of a triangle of three nodes i, j, k in a network, e.g. the presence of the three links (i, j), (i, k), (j, k) in the corresponding graph, is not able to capture the difference between a three-body interaction of the three individuals, from the sum of three pairwise interactions. Notice that these are two completely different situations, with completely different social mechanisms and dynamics at work [35].

Fig. 10.1
figure 1

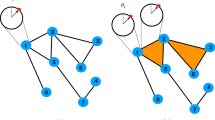
From networks to simplicial complexes. a Simplices of different orders d: the node \(d=0\), the edge \(d=1\), the triangle \(d=2\), the tetrahedron \(d=3\). b A network only consists of \(0-\) and \(1-\)simplices. c A simplicial complex consists of simplices of any order \(d=0,1,\ldots ,D\) (in this case \(D=3\))

Full size image

Simplicial complexes are instead the proper mathematical structures for describing high order interactions. A simplicial complex is an aggregate of simplices, objects that generalize links and can in general be of different dimension. A d-simplex, or simplex of dimension d, \(\sigma \) is, in its simplest definition, a collection of \(d+1\) nodes. In this way, a 0-simplex is a node, a 1-simplex is a link, a 2-simplex (i, j, k) is a two-dimensional object made by three nodes, usually called a (full) triangle, a 3-simplex is a tetrahedron, i.e. a three-dimensional object and so on (Fig. 10.1a). It is now possible to differentiate between a three-body interaction, and three bodies in pairwise interactions: the first case will be represented by a complete triangle, a two-dimensional simplex, while the second case will consist of three one-dimensional objects. Hence, in the following of this chapter, simplices of dimension d will be used to describe the structure of \((d+1)\)-body interactions. Finally, a simplicial complex \(\mathcal {S}\) on a given set of nodes \(\mathcal {V}\), with \(|\mathcal {V}|=N\), is a collection of M simplices, \({\mathcal {S}} = \{ \sigma _1, \sigma _2, \ldots , \sigma _M \}\), with the extra requirement that, for any simplex \(\sigma \in \mathcal {S}\), all the simplices \(\sigma '\) with \(\sigma ' \subset \sigma \), i.e. all the simplices built from subsets of \(\sigma \), are also contained in \(\mathcal {S}\). Due to this requirement, simplicial complexes are a very particular type of hypergraphs [36]. Simplicial complexes have shown to be appropriate in the context of social systems [35, 37, 38] and, as we will see in the next Section, they will turn very useful to study coupled dynamical systems. In the following, we will indicate as \(M_d\), \(d=1,2,\ldots D\) the number of d-simplices present in \(\mathcal {S}\) (where D, the order of the simplicial complex, is the dimension of the largest simplex in \(\mathcal {S}\)), and we have the constraint \(\sum _{d=1}^D M_d = M\). Note that a network is a particular case of a simplicial complex with \(D=1\) (Fig. 10.1b), whereas for \(D>1\) a truly higher-order structure is obtained (Fig. 10.1c).

As a mathematical representation of simplicial complexes, we will use here a formalism which generalises directly the concept of adjacency matrix for a network. For each dimension d, we can define the \(\underbrace{N\times N \times \dots \times N}_{d+1}\) adjacency tensor \(\mathrm {A}^{(d)}\), whose entry \(a^{(d)}_{i_1,\dots ,i_{d+1}}\) is equal to 1 if the d-simplex \((i_1,\dots ,i_{d+1})\) belongs to the simplicial complex \({\mathcal {S}}\), and is 0 otherwise [39]. Notice that each tensor is symmetric with respect to its \(d+1\) indices, which means that the value of a given entry \(a^{(d)}_{i_1,\dots ,i_{d+1}}\) is equal to the value of the entries corresponding to any permutation of the indices.

With the definition above, \(\mathrm {A}^{(1)}\) coincides with the standard adjacency matrix \(\mathrm {A}\), while the \(N \times N \times N\) adjacency tensor \(\mathrm {A}^{(2)}\) characterizes two-dimensional objects: one has \(a_{ijk}^{(2)}=1\) if the three nodes i, j, k form a full triangle, and otherwise \(a_{ijk}^{(2)}=0\). As a conclusion, it is possible to map completely the connectivity structure of a simplicial complex \(\mathcal {S}\) into the entire set of D adjacency tensors \(\mathrm {A}^{(d)}\), \(d=1,2,\ldots D\).

A node i of a simplicial complex \(\mathcal {S}\) cannot be, therefore, characterized only by giving its degree \(k_i = \sum _{j=1}^N a^{(1)}_{ij}\), but one needs instead to account for the number of simplices of any dimension, incident in i. It is therefore extremely useful to define the generalized d-degree, \(k_i^{(d)}\), of a node i as:

$$\begin{aligned} k_i^{(d)} = \frac{1}{d!}\sum _{i_1=1}^N \sum _{i_2=1}^N \ldots \sum _{i_d=1}^N a^{(d)}_{i,i_1,i_2,\ldots ,i_d}, \end{aligned}$$
(10.1)

with \(d=1,2,\ldots ,D\) so that \(k_i^{(1)}\) coincides with the standard degree of node i, \(k_i^{(2)}\) counts the number of triangles (2-simplices) to which i participates:

$$\begin{aligned} k_i^{(2)}= \frac{1}{2} \sum _{j=1}^N \sum _{k=1}^N a_{ijk}^{(2)} \end{aligned}$$
(10.2)

\(k_i^{(3)}\) the number of tetrahedrons, and so on.

Analogously, we can also define the generalized d-degree \(k^{(d)}_{ij}\) of a link (i, j) as the number of d-simplices to which link (i, j) is part of. We can write its expression in terms of the adjacency tensor \(\mathrm {A}^{(d)}\) of dimension d, with \(d=1,2,\ldots ,D\), as[39]:

$$\begin{aligned} k_{ij}^{(d)} = \frac{1}{(d-1)!}\sum _{i_1=1}^N \sum _{i_2=1}^N \ldots \sum _{i_{d-1}=1}^N a^{(d)}_{i,j,i_1,i_2,\ldots ,i_{d-1}}, \end{aligned}$$
(10.3)

so that \(k_{ij}^{(1)}=a_{ij}^{ (1)}\), while \(k_{ij}^{(2)}\) counts the number of triangles (2-simplices) to which (i, j) participates:

$$\begin{aligned} k_{ij}^{(2)}= \sum _{k=1}^N a_{ijk}^{(2)}, \end{aligned}$$
(10.4)

and so on.

Finally, we introduce here a generalized Laplacian describing the case of systems with high-order interactions. The generalized Laplacian of order d, with \(d=1,2,\ldots , D\), is a matrix \( \mathcal {L}^{(d)}\) whose elements are defined as:

$$\begin{aligned} \mathcal {L}^{(d)}_{ij} = {\left\{ \begin{array}{ll} 0 &{} \quad \text {for} \ i \ne j \ \ \ \text {and} \ \ \ a^{(1)}_{ij}=0 \\ -{(d-1)!}k_{ij}^{(d)} &{} \quad \text { for } i \ne j \ \ \ \text {and} \ \ \ a^{(1)}_{ij}=1 \\ d! \ k^{(d)}_i &{} \quad \text { for } i = j, \end{array}\right. } \end{aligned}$$
(10.5)

where \(k^{(d)}_{ij}\) is the generalized d-degree of the link (i, j), and \(k^{(d)}_{i}\) is the generalized d-degree of node i. Replacing (10.1) and (10.3) in (10.5), in the case \(D=2\), we get an equivalent expression for the generalized Laplacian:

$$\begin{aligned} \mathcal {L}^{(2)}_{ij} = {\left\{ \begin{array}{ll} - \sum _k a^{(2)}_{ijk} &{} \quad \text { for } i \ne j \\ - \sum _{\ell \ne i} \mathcal {L}^{(2)}_{i \ell } &{} \quad \text { for } i = j, \end{array}\right. } \end{aligned}$$
(10.6)

Notice that \(\mathcal {L}^{(1)}\) recovers exactly the classical Laplacian matrix. This definition of generalized Laplacian will turn useful in the following sections.

10.3 Dynamical Systems with Higher-Order Interactions

The object of our study is the most general simplicial complex of N coupled dynamical systems, such that the nodes are subject not only to pairwise interactions, but also to three-body interactions, four-body interactions and so on. We write the equations of motion governing the dynamics of our D-dimensional simplicial complex as follows

$$\begin{aligned} \begin{array}{lll} \dot{\mathbf {x}}_i &{} = &{} \mathbf {f}(\mathbf {x}_i ) + \sigma _{1}\sum \limits _{j_1=1}^{N} a_{ij_1}^{(1)} \, \mathbf {g}^{(1)}(\mathbf {x}_i, \mathbf {x}_{j_1}) + \sigma _{2} \sum \limits _{j_1=1}^N \sum \limits _{j_2=1}^N a_{ij_{1}j_{2}}^{(2)} \, \mathbf {g}^{(2)}(\mathbf {x}_i, \mathbf {x}_{j_1}, \mathbf {x}_{j_2})+\ldots \\ &{} &{} + \sigma _{D} \sum \limits _{j_1=1}^N \ldots \sum \limits _{j_D=1}^N a_{ij_1 \ldots j_D}^{(D)} \, \mathbf {g}^{(D)}(\mathbf {x}_i, \mathbf {x}_{j_1}, \ldots , \mathbf {x}_{j_D}), \end{array} \end{aligned}$$
(10.7)

where \(\mathbf {x}_i(t)\) is the m-dimensional vector state describing the dynamics of unit i, \(\sigma _{1},\ldots , \sigma _{D}\) are real valued parameters describing coupling strengths, \(\mathbf {f}: \mathbb {R}^m \longrightarrow \mathbb {R}^m\) describes the local dynamics (which is assumed identical for all units), while \(\mathbf {g}^{(d)}: \mathbb {R}^{(d+1)\times m} \longrightarrow \mathbb {R}^m\) (\(d=1,\ldots ,D\)) are synchronization non-invasive functions (i.e. \(\mathbf {g}^{(d)}(\mathbf {x}, \mathbf {x}, \ldots , \mathbf {x}) \equiv 0 \ \forall d\)) ruling the interaction forms at different orders. Furthermore, for \(d=1,\ldots ,D\), \(a_{ij_1\ldots j_d}^{(d)}\) are the entries of the adjacency tensor \(\mathrm {A}^{(d)}\). This is the most general type of system we can consider, as there are no further specific restrictions on both the adjacency tensors of the simplicial complex and the functions \(\mathbf {f}\) and \(\mathbf {g}^{(d)}\).

For the sake of clarity in what follows we illustrate our study for the case of \(D=2\) and then summarize the steps needed to generalize the results to any order D. Let us then consider the following set of coupled differential equations

$$\begin{aligned} \begin{array}{lll} \dot{\mathbf {x}}_i= & {} \mathbf {f}(\mathbf {x}_i ) + \sigma _{1}\sum \limits _{j=1}^{N} a_{ij}^{(1)} \, \mathbf {g}^{(1)}(\mathbf {x}_i, \mathbf {x}_j) + \sigma _{2} \sum \limits _{j=1}^N \sum \limits _{k=1}^N a_{ijk}^{(2)} \, \mathbf {g}^{(2)}(\mathbf {x}_i, \mathbf {x}_j, \mathbf {x}_k), \end{array} \end{aligned}$$
(10.8)

where \(\sigma _{1}\) and \(\sigma _{2}\) are the coupling strengths associated to two- and three-body interactions.

Notice that existence and invariance of the synchronized solution \(\mathbf {x}^s(t) = \mathbf {x}_1(t) = \cdots = \mathbf {x}_N(t) \) are warranted by the non-invasiveness of the coupling functions.

10.4 Linear Stability Analysis

Here we study the stability of the synchronous solution via linearization around the synchronous state \(\mathbf {x}^s\). Let us then consider considers small perturbations around the synchronous state \(\mathbf {x}^s\), i.e., \(\delta \mathbf {x}_i = \mathbf {x}_i - \mathbf {x}^s\), and write the dynamics of these variables as follows

$$\begin{aligned} \begin{array}{lll} \dot{ \delta \mathbf {x}}_i &{} = &{} J \mathbf {f}(\mathbf {x}^s) \delta \mathbf {x}_i + \sigma _{1} \sum \limits _{j=1}^{N} a^{(1)}_{ij} \, \biggl [ \frac{\partial \mathbf {g}^{(1)}( \mathbf {x}_i, \mathbf {x}_j)}{\partial \mathbf {x}_i } \bigg |_{(\mathbf {x}^s, \mathbf {x}^s) } \delta \mathbf {x}_i + \frac{\partial \mathbf {g}^{(1)}( \mathbf {x}_i, \mathbf {x}_j) }{\partial \mathbf {x}_j } \bigg |_{(\mathbf {x}^s, \mathbf {x}^s) } \delta \mathbf {x}_j \biggr ] \\ &{} &{} + \sigma _{2} \sum \limits _{j=1}^N \sum \limits _{k=1}^N a_{ijk}^{(2)} \, \biggl [ \frac{\partial \mathbf {g}^{(2)}( \mathbf {x}_i, \mathbf {x}_j, \mathbf {x}_k)}{\partial \mathbf {x}_i } \bigg |_{(\mathbf {x}^s,\mathbf {x}^s, \mathbf {x}^s) } \delta \mathbf {x}_i + \frac{\partial \mathbf {g}^{(2)}( \mathbf {x}_i, \mathbf {x}_j, \mathbf {x}_k)}{\partial \mathbf {x}_j } \bigg |_{(\mathbf {x}^s,\mathbf {x}^s, \mathbf {x}^s) } \delta \mathbf {x}_j \\ &{} &{} +\frac{\partial \mathbf {g}^{(2)}( \mathbf {x}_i, \mathbf {x}_j, \mathbf {x}_k) }{\partial \mathbf {x}_k } \bigg |_{(\mathbf {x}^s,\mathbf {x}^s, \mathbf {x}^s) } \delta \mathbf {x}_k \biggr ], \end{array} \end{aligned}$$
(10.9)

where \(J \mathbf {f}(\mathbf {x}^s) \) denotes the \(m\times m\) Jacobian matrix of the function \(\mathbf {f}\), evaluated at the synchronous state \(\mathbf {x}^s\).

Now, let us make our first, very important, conceptual step, noticing that all coupling functions are synchronization non-invasive, i.e. \(\mathbf {g}^{(1)}(\mathbf {x}, \mathbf {x}) \equiv 0\) and \(\mathbf {g}^{(2)}(\mathbf {x}, \mathbf {x},\mathbf {x}) \equiv 0\). As their value is then constant (equal to zero) at the synchronization manifold, it immediately follows that their total derivative vanishes as well, which implies on its turn that

$$\begin{aligned} \begin{array}{l} \frac{\partial \mathbf {g}^{(1)}( \mathbf {x}_i, \mathbf {x}_j)}{\partial \mathbf {x}_i } \bigg |_{(\mathbf {x}^s, \mathbf {x}^s) } + \frac{\partial \mathbf {g}^{(1)}( \mathbf {x}_i, \mathbf {x}_j) }{\partial \mathbf {x}_j } \bigg |_{(\mathbf {x}^s, \mathbf {x}^s) } = 0, \\ \frac{\partial \mathbf {g}^{(2)}( \mathbf {x}_i, \mathbf {x}_j, \mathbf {x}_k)}{\partial \mathbf {x}_i } \bigg |_{(\mathbf {x}^s,\mathbf {x}^s, \mathbf {x}^s) } + \frac{\partial \mathbf {g}^{(2)}( \mathbf {x}_i, \mathbf {x}_j, \mathbf {x}_k)}{\partial \mathbf {x}_j } \bigg |_{(\mathbf {x}^s,\mathbf {x}^s, \mathbf {x}^s) } + \frac{\partial \mathbf {g}^{(2)}( \mathbf {x}_i, \mathbf {x}_j, \mathbf {x}_k) }{\partial \mathbf {x}_k } \bigg |_{(\mathbf {x}^s,\mathbf {x}^s, \mathbf {x}^s) } = 0. \end{array} \end{aligned}$$
(10.10)

Then, one can factor out the terms \(\frac{\partial \mathbf {g}^{(1)}( \mathbf {x}_i, \mathbf {x}_j)}{\partial \mathbf {x}_i } \bigg |_{(\mathbf {x}^s, \mathbf {x}^s) } \delta \mathbf {x}_i\) and \(\frac{\partial \mathbf {g}^{(2)}( \mathbf {x}_i, \mathbf {x}_j, \mathbf {x}_k)}{\partial \mathbf {x}_i } \bigg |_{(\mathbf {x}^s,\mathbf {x}^s, \mathbf {x}^s) } \delta \mathbf {x}_i\) in the summations (both of them, indeed, do not depend on the indices of the summations). Furthermore, one has that \(\sum _{j=1}^{N} a^{(1)}_{ij}=k_i^{(1)}\) and \(\sum _{j=1}^N \sum _{k=1}^N a_{ijk}^{(2)}=2 k_i^{(2)}\). Plugging back the resulting terms inside the summations, and using Eq. (10.10), one eventually obtains

$$\begin{aligned} \begin{array}{lll} \dot{ \delta \mathbf {x}}_i &{} = &{} J \mathbf {f}(\mathbf {x}^s) \delta \mathbf {x}_i - \sigma _{1} \sum \limits _{j=1}^{N} \mathcal {L}^{(1)}_{ij} \, J \mathbf {g}^{(1)}( \mathbf {x}^s,\mathbf {x}^s) \delta \mathbf {x}_j \\ &{} &{} - \sigma _{2} \sum \limits _{j=1}^N \sum \limits _{k=1}^N \tau _{ijk} \, \biggl [ J_1 \mathbf {g}^{(2)} (\mathbf {x}^s,\mathbf {x}^s, \mathbf {x}^s) \delta \mathbf {x}_j + J_2 \mathbf {g}^{(2)} (\mathbf {x}^s, \mathbf {x}^s, \mathbf {x}^s) \delta \mathbf {x}_k \biggr ] , \end{array} \end{aligned}$$
(10.11)

where we introduced a tensor \(\mathrm {T}\) whose elements are \(\tau _{ijk}=2 k_i^{(2)} \delta _{ijk} - a_{ijk}^{(2)}\) for \(i,j,k=1, \ldots , N\), and simplified the notation as

$$\begin{aligned} \begin{array}{l} J \mathbf {g}^{(1)} (\mathbf {x}^s,\mathbf {x}^s) = \frac{\partial \mathbf {g}^{(1)}( \mathbf {x}_i, \mathbf {x}_j)}{\partial \mathbf {x}_j } \bigg |_{(\mathbf {x}^s,\mathbf {x}^s)} , \\ J_1 \mathbf {g}^{(2)} (\mathbf {x}^s, \mathbf {x}^s, \mathbf {x}^s)= \frac{\partial \mathbf {g}^{(2)}(\mathbf {x}_i, \mathbf {x}_j, \mathbf {x}_k)}{\partial \mathbf {x}_j } \bigg |_{(\mathbf {x}^s, \mathbf {x}^s, \mathbf {x}^s) }, \\ J_2 \mathbf {g}^{(2)} (\mathbf {x}^s, \mathbf {x}^s, \mathbf {x}^s)= \frac{\partial \mathbf {g}^{(2)}(\mathbf {x}_i, \mathbf {x}_j, \mathbf {x}_k)}{\partial \mathbf {x}_k } \bigg |_{(\mathbf {x}^s, \mathbf {x}^s, \mathbf {x}^s) }. \end{array} \end{aligned}$$
(10.12)

Already at this stage, it is fundamental to remark that our approach even extends the validity of the classical Master Stability Function theory [the case \(\sigma _2=0\) in Eq. (10.11)], in that we do not require a diffusive functional form for the interplay among the network nodes, and therefore we are actually encompassing a much broader class of coupling functions. For instance, our approach allows the formal treatment of the Kuramoto model [21], where \(m=1\), each network unit i is identified by the instantaneous phase \(\theta _i\) of an oscillator, and the coupling between nodes i and j is given by the function \(\sin {(\theta _j-\theta _i)}\), which is not diffusive.

Let us now make our second, conceptual, step, which will allow us to greatly simplify the last term on the right hand side of Eq.(10.11). Such a term refers to three-body interactions, and we now show how to map it into a single summation involving the generalized Laplacian matrix. This is done by remarking that the two Jacobian matrices \(J_1 \mathbf {g}^{(2)} (\mathbf {x}^s, \mathbf {x}^s, \mathbf {x}^s)\) and \(J_2 \mathbf {g}^{(2)} (\mathbf {x}^s, \mathbf {x}^s, \mathbf {x}^s)\) are both independent on k and j. Accordingly, Eq.(10.11) becomes

$$\begin{aligned} \begin{array}{lll} \dot{ \delta \mathbf {x}}_i &{} = &{} J \mathbf {f}(\mathbf {x}^s) \delta \mathbf {x}_i - \sigma _{1} \sum \limits _{j=1}^{N} \mathcal {L}^{(1)}_{ij} \, J \mathbf {g}^{(1)}( \mathbf {x}^s, \mathbf {x}^s) \delta \mathbf {x}_j \\ &{} &{} - \sigma _{2} \biggl [ \sum \limits _{j=1}^N J_1 \mathbf {g}^{(2)} (\mathbf {x}^s,\mathbf {x}^s, \mathbf {x}^s) \delta \mathbf {x}_j \sum \limits _{k=1}^N \tau _{ijk} + \sum \limits _{k=1}^N J_2 \mathbf {g}^{(2)} (\mathbf {x}^s,\mathbf {x}^s, \mathbf {x}^s) \delta \mathbf {x}_k \sum \limits _{j=1}^N \tau _{ijk} \biggr ]. \end{array} \end{aligned}$$
(10.13)

Then, using the symmetric property of \( \mathrm {T}\), namely \( \sum _k \tau _{ijk}= \sum _k \tau _{ikj} \), we obtain

$$\begin{aligned} \begin{array}{lll} \dot{ \delta \mathbf {x}}_i &{} = &{} J \mathbf {f}(\mathbf {x}^s) \delta \mathbf {x}_i - \sigma _{1} \sum \limits _{j=1}^{N} \mathcal {L}^{(1)}_{ij} \, J \mathbf {g}^{(1)}( \mathbf {x}^s, \mathbf {x}^s) \delta \mathbf {x}_j \\ &{} &{} - \sigma _{2} \sum \limits _{j=1}^N \mathcal {L}^{(2)}_{ij} \biggl [ J_1 \mathbf {g}^{(2)} (\mathbf {x}^s,\mathbf {x}^s, \mathbf {x}^s) + J_2 \mathbf {g}^{(2)} (\mathbf {x}^s,\mathbf {x}^s, \mathbf {x}^s) \biggr ] \delta \mathbf {x}_j. \end{array} \end{aligned}$$
(10.14)

Equations (10.14) can be rewritten in block form by introducing the stack vector \(\delta \mathbf {x}=[\delta \mathbf {x}_1^T,\delta \mathbf {x}_2^T,\ldots ,\delta \mathbf {x}_N^T]^T\) and denoting by \(\mathrm {JF}= J \mathbf {f}(\mathbf {x}^s)\), \( \mathrm {JG}^{(1)} = J \mathbf {g}^{(1)}( \mathbf {x}^s, \mathbf {x}^s)\) and \( \mathrm {JG}^{(2)} = J_1 \mathbf {g}^{(2)} (\mathbf {x}^s,\mathbf {x}^s, \mathbf {x}^s) + J_2 \mathbf {g}^{(2)} (\mathbf {x}^s,\mathbf {x}^s, \mathbf {x}^s) \). One obtains

$$\begin{aligned} \dot{ \delta \mathbf {x}} = \left[ \mathrm {I}_N \otimes \mathrm {JF} - \sigma _1 \mathcal {L}^{(1)} \otimes \mathrm {JG}^{(1)} - \sigma _2 \mathcal {L}^{(2)} \otimes \mathrm {JG}^{(2)} \right] \delta \mathbf {x}. \end{aligned}$$
(10.15)

The third, and final, conceptual step is to remark that all generalized Laplacians \(\mathcal {L}^{(d)}\) are symmetric real-valued zero-row-sum matrices. Therefore: (i) they are all diagonalizable; (ii) for each one of them the set of eigenvalues is made of real non-negative numbers, and the corresponding set of eigenvectors constitutes a orthonormal basis of \(\mathbb {R}^N\); (iii) they all share, as the smallest of their eigenvalues, \(\lambda _1 \equiv 0\), whose associated eigenvector \(\frac{1}{\sqrt{N}} \ (1,1,1,\ldots ,1)^T\) is aligned along the synchronization manifold; (iv) as in general they do not commute, the sets of eigenvectors corresponding to all others of their eigenvalues are different from one another, and yet any perturbation to the synchronization manifold (which, by definition, lies in the tangent space) can be expanded as linear combination of one whatever of such eigenvector sets (the relevant consequence is that one can arbitrarily select any of the generalized Laplacians as the reference for the choice of the basis of the transverse space, and all other eigenvector sets will map to such a basis by means of unitary matrix transformations).

We are then fully entitled to take, as reference basis, the one constituted by the eigenvectors of the classic Laplacian \(\mathcal {L}^{(1)}\) (\(\mathrm {V}=[\mathbf {v}_1,\mathbf {v}_2,\ldots ,\mathbf {v}_N]\)), and consider new variables \(\mathbf {\delta \eta }=(\mathrm {V}^{-1}\otimes \mathrm {I}_m)\mathbf {\delta x}\). We get

$$\begin{aligned} \dot{ \delta \mathbf {\eta }} = \left[ \mathrm {I}_N \otimes \mathrm {JF} - \sigma _1 \mathrm {\Lambda }^{(1)} \otimes \mathrm {JG}^{(1)} - \sigma _2 \tilde{\mathcal {L}}^{(2)} \otimes \mathrm {JG}^{(2)} \right] \delta \mathbf {\eta }. \end{aligned}$$
(10.16)

where we have used the fact that \(\mathrm {V}^{-1}\mathcal {L}^{(1)}\mathrm {V}=\text {diag}(\lambda _1,\lambda _2,\ldots ,\lambda _N)=\mathrm {\Lambda }^{(1)}\), where \(0=\lambda _1<\lambda _2\le \ldots \lambda _N\) are the eigenvalues of \(\mathcal {L}^{(1)}\), and we have indicated with \(\tilde{\mathcal {L}}^{(2)}=\mathrm {V}^{-1}\mathcal {L}^{(2)}\mathrm {V}\) the transformed generalized Laplacian of order 2.

As \(\mathcal {L}^{(2)}\) is zero-row sum (i.e. \(\mathcal {L}^{(2)}\mathbf {v}_1=0\)), Eqs. (10.16) may be rewritten as

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\mathbf {\eta }}_1 &{} = \mathrm {JF}\mathbf {\eta }_1\\ \dot{ \mathbf {\eta }_i} &{} = (\mathrm {JF}-\sigma _1 \lambda _i \mathrm {JG}^{(1)} ) \mathbf {\eta }_i - \sigma _2 \sum \limits _{j=2}^N \tilde{\mathcal {L}}^{(2)}_{ij}\mathrm {JG}^{(2)} \mathbf {\eta }_j, \end{array}\right. } \end{aligned}$$
(10.17)

that is, the dynamics of the linearized system is decoupled into two parts: the dynamics of \(\mathbf {\eta }_1\) accounting for the motion along the synchronous manifold, and that of all other variables \(\mathbf {\eta }_i\) (with \(i=2,\ldots ,N\), representing the different modes transverse to the synchronization manifold) which are coupled each other by means of the coefficients \(\tilde{\mathcal {L}}^{(2)}_{ij}\) (all of them being known quantities) given by transforming \(\mathcal {L}^{(2)}\) with the matrix that diagonalizes \(\mathcal {L}^{(1)}\). The problem of stability is then reduced to: (i) simulating a single, uncoupled, nonlinear system; (ii) using the obtained trajectory to feed up the elements of the Jacobians \(\mathrm {JG}^{(1)}\) and \(\mathrm {JG}^{(2)}\); (iii) simulating the dynamics of a system of \(N-1\) coupled linear equations, and tracking the behavior of the norm \(\sqrt{\sum _{i=2}^N \sum _{j=1}^m (\eta _i^{(j)})^2}\) for the calculation of the maximum Lyapunov exponent (being \(\mathbf {\eta }_{i} \equiv (\eta _i^{(1)}, \eta _i^{(2)}, \ldots ,\eta _i^{(m)})\)).

Stability of the synchronous solution requires, as a necessary condition, that the maximum among the Lyapunov exponents associated to all transverse modes is negative. Therefore, this quantity provides a generalized Master Stability Function, \(\Lambda _{\max }\), which, given the node dynamics and the coupling functions, is in general function of the topology of the two body interactions, the topology of the three body interactions, and the two coupling strengths \(\sigma _1\) and \(\sigma _2\), i.e., \(\Lambda _{\max }=\Lambda _{\max }(\sigma _1,\sigma _2,\mathcal {L}^{(1)},\mathcal {L}^{(2)})\).

Notice that, in full analogy with the classical MSF approach, also in the case of simplicial complexes one is, therefore, able to separate the motion along the synchronization manifold and that transverse to it. And it is such a crucial separation that ultimately enables the study of stability of the synchronous manifold, retaining the general applicability of the original approach. In the case of simplical complexes, the higher complexity in the structure of the interactions yields a formalism requiring the analysis of a set of coupled differential equations, rather than of a single parametric variational equation (as in the case of network synchronization). In other words, in the fully general case the set of equations describing the motion transverse to the synchronous manifold cannot be further decomposed into independent, decoupled modes, as it happens in the network case; however, the analysis of stability still requires the computation of a single quantity, i.e., the maximum Lyapunov exponent, which has to be performed on such a set of coupled, linear equations. Hence, while in the classical MSF on networks, once fixed the node dynamics and coupling function, one obtains \(\Lambda _{\max }=\Lambda _{\max }(\sigma ,\mathrm {L})\), which can be further simplified introducing \(\alpha \) parametrizing the product of the coupling coefficient and the nonzero eigenvalues of \(\mathrm {L}\), i.e., \(\Lambda _{\max }=\Lambda _{\max }(\alpha )\), for simplicial complexes, once fixed the node dynamics and the coupling functions, one obtains \(\Lambda _{\max }=\Lambda _{\max }(\sigma _1,\sigma _2,\mathcal {L}^{(1)},\mathcal {L}^{(2)})\). Note, however, that there are still special cases where such an expression can be simplified up to even recover cases where it is formally identical to that of the classical MSF, as we will show explicitly later on in Sec. 10.5.

In analogy with the classification scheme adopted for synchronization in complex networks (Chap. 5 in Ref. [40]), one immediately realizes that, once the local dynamics of each node (i.e. the function \(\mathbf {f}\)), the various coupling functions \(\mathbf {g}^{(1,2)}\), and the structure of the simplicial complex (i.e. \(\mathcal {L}^{(1)}\) and \(\mathcal {L}^{(2)}\)) are specified, all possible cases can be divided in three different classes:

  1. 1.

    class I problems, where \(\Lambda _{\max }\) is positive in all the half plane \((\sigma _1 \ge 0,\sigma _2 \ge 0)\), and therefore synchronization is never stable;

  2. 2.

    class II problems, for which \(\Lambda _{\max }\) is negative within a unbounded area of the half plane and

  3. 3.

    class III problems, for which the area of the half plane in which \(\Lambda _{\max }\) is negative is instead bounded, and therefore additional instabilities of the synchronous motion may occur at larger values of the coupling strengths.

We conclude this section by showing how the approach described above can be extended to simplicial complexes of any order D. Indeed, each term on the right hand side of Eq. (10.7) can be manipulated following exactly the same steps described above. Defining \( \mathrm {JG}^{(d)} = J_1 \mathbf {g}^{(d)} (\mathbf {x}^s,\ldots , \mathbf {x}^s) + J_2 \mathbf {g}^{(d)} (\mathbf {x}^s,\ldots , \mathbf {x}^s) + \cdots + J_d \mathbf {g}^{(d)} (\mathbf {x}^s,\ldots , \mathbf {x}^s)\), Eq. (10.15) becomes

$$\begin{aligned} \begin{array}{lll} \dot{ \delta \mathbf {x}}= & {} \biggl [ \mathrm {I}_N \otimes \mathrm {JF} - \sigma _1 \mathcal {L}^{(1)} \otimes \mathrm {JG}^{(1)} - \sigma _2 \mathcal {L}^{(2)} \otimes \mathrm {JG}^{(2)} - \ldots - \sigma _D \mathcal {L}^{(D)} \otimes \mathrm {JG}^{(D)} \biggr ] \delta \mathbf {x}. \end{array} \end{aligned}$$
(10.18)

Once again, one can select the eigenvector set which diagonalizes \(\mathcal {L}^{(1)}\), and to introduce the new variables \(\mathbf {\delta \eta }=(\mathrm {V}^{-1}\otimes \mathrm {I}_m)\mathbf {\delta x}\). Following the same steps which led us to write Eqs. (10.17), one then obtains

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{\mathbf {\eta }}_1 &{} = &{} \mathrm {JF}\mathbf {\eta }_1,\\ \dot{\mathbf {\eta }_i} &{} = &{} (\mathrm {JF}-\sigma _1 \lambda _i \mathrm {JG}^{(1)} ) \mathbf {\eta }_i - \sigma _2 \sum \limits _{j=2}^N \tilde{\mathcal {L}}^{(2)}_{ij}\mathrm {JG}^{(2)} \mathbf {\eta }_j - \ldots - \sigma _D \sum \limits _{j=2}^N \tilde{\mathcal {L}}^{(D)}_{ij}\mathrm {JG}^{(D)} \mathbf {\eta }_j , \end{array} \right. \end{aligned}$$
(10.19)

where the coefficients \(\tilde{\mathcal {L}}^{(d)}_{ij}\) result from transforming \(\mathcal {L}^{(d)}\) with the matrix that diagonalizes \(\mathcal {L}^{(1)}\). As a result, one has the same reduction of the problem to a single, uncoupled, nonlinear system, plus a system of \(N-1\) coupled linear equations, from which the maximum Lyapunov exponent \(\Lambda _{\max }{=}\Lambda _{\max }(\sigma _1,\sigma _2,\ldots , \sigma _D,\mathcal {L}^{(1)},\mathcal {L}^{(2)}, \ldots , \mathcal {L}^{(D)})\) can be extracted and monitored (for each simplicial complex) in the D-dimensional hyper-space of the coupling strength parameters.

10.5 Master Stability Functions

The problem can be greatly simplified in a few special cases in which either the connectivity of the system (i.e. the structure of the simplicial complex), or the coupling functions, allow for a further reduction of complexity. For the sake of illustration, we start considering first the case of \(D=2\), and, then, the extension to any possible order D.

The first special case is the all-to-all coupling, for which every pair of two nodes is connected by a link and every triple of nodes is connected by a 2-simplex, namely all the possible two and three-body interactions are active. In this case, the classical Laplacian matrix is

$$\begin{aligned} \mathcal {L}_{ij}^{(1)} = {\left\{ \begin{array}{ll} -1 &{} \quad \text { for } i \ne j \\ N-1 &{} \quad \text { for } i = j. \end{array}\right. } \end{aligned}$$
(10.20)

Then, it is easy to rewrite \(\mathcal {L}^{(2)}\). First, the off diagonal terms \(-\mathcal {L}^{(2)}_{ij}\) (\(i \ne j\)) represent the number of triangles formed by the link (i, j) which, in the present case, is simply equal to \(N-2\). Second, the terms of the main diagonal \(\mathcal {L}^{(2)}_{ii}\) indicates the number of triangles having the node i as a vertex, which is

$$\begin{aligned} k^{(2)}_{i} = \left( {\begin{array}{c}N-1\\ 2\end{array}}\right) = \frac{(N-1)(N-2)}{2}. \end{aligned}$$
(10.21)

Consequently, one has that

$$\begin{aligned} \mathcal {L}^{(2)} = (N-2) \; \mathcal {L}^{(1)}. \end{aligned}$$
(10.22)

For the linearized dynamics, one gets

$$\begin{aligned} \dot{ \delta \mathbf {x}}_i = \mathrm {JF} \delta \mathbf {x}_i - \sum _{j=1}^{N} \mathcal {L}_{ij}^{(1)} \, \left[ \sigma _{1}\, \mathrm {JG}^{(1)} + \sigma _{2}\,(N-2)\, \mathrm {JG}^{(2)} \right] \delta \mathbf {x}_j. \end{aligned}$$
(10.23)

By expanding the perturbation vector \(\delta \mathbf {x}\) on the othornormal basis formed by the eigenvectors of the classical Laplacian matrix \(\mathcal {L}^{(1)}\), and after noticing that in the all-to-all configuration \(\lambda _{2} = \dots \lambda _{N} = N\), for each \(\mathbf {\eta }_{i}\) (with \(i \in \left\{ 2,\dots ,N\right\} \)) one has

$$\begin{aligned} \dot{\mathbf {\eta }}_i=[\mathrm {JF}-\sigma _1 N \, \mathrm {JG}^{(1)} -\sigma _2 N(N-2)\,\mathrm {JG}^{(2)}]\mathbf {\eta }_i . \end{aligned}$$
(10.24)

In other words, in the all-to-all case, the variables \(\mathbf {\eta }_{i}\) come out to be all uncoupled to each other, so that the MSF uniquely depends on \(\sigma _1\), \(\sigma _2\) and N, i.e., \(\Lambda _{\max }=\Lambda _{\max }(\sigma _1,\sigma _2,N)\).

In the more general case of a D-dimensional simplicial complex, it is easy to write the generalized Laplacian of order d as a function of the classical Laplacian matrix. In fact, the number of d-simplices having node i as a vertex and the number of d-simplices formed by the link (i, j) are respectively

$$\begin{aligned} k^{(d)}_{i} = \left( {\begin{array}{c}N-1\\ d\end{array}}\right) = \frac{(N-1)(N-2)\dots (N-d)}{d!} \end{aligned}$$
(10.25)

and

$$\begin{aligned} k^{(d)}_{ij} = \left( {\begin{array}{c}N-2\\ d-1\end{array}}\right) = \frac{(N-2)\dots (N-d)}{(d-1)!}. \end{aligned}$$
(10.26)

Given the definition of the generalized Laplacian in Eq. (10.5), we find that

$$\begin{aligned} \begin{array}{lll} \mathcal {L}^{(d)}= & {} (N-d) \; \mathcal {L}^{(d-1)} = (N-2)(N-3)\dots (N-d)\mathcal {L}^{(1)}. \end{array} \end{aligned}$$
(10.27)

Once again, one can derive a parametric equation analogous to Eq. (10.24), with the MSF (once fixed both the node dynamics and the coupling functions) which solely depends on the coupling coefficients and the number of nodes, i.e. \(\Lambda _{\max }=\Lambda _{\max }(\sigma _1,\sigma _2,\dots ,\sigma _D,N)\)

$$\begin{aligned} \begin{array}{lll} \dot{\mathbf {\eta }}_i= & {} [\mathrm {JF}-\sigma _1 N \, \mathrm {JG}^{(1)} - \dots -\sigma _D N(N-2)\dots (N-D)\,\mathrm {JG}^{(D)}]\mathbf {\eta }_i . \end{array} \end{aligned}$$
(10.28)

Another interesting case is that of generalized diffusion interactions with natural coupling functions. This amounts to consider diffusive coupling functions, given by

$$\begin{aligned} \begin{array}{ll} \mathbf {g}^{(1)}(\mathbf {x}_i, \mathbf {x}_j) &{}= \mathbf {h}^{(1)}( \mathbf {x}_j) - \mathbf {h}^{(1)}(\mathbf {x}_i), \\ \mathbf {g}^{(2)}(\mathbf {x}_i, \mathbf {x}_j, \mathbf {x}_k) &{}= \mathbf {h}^{(2)}( \mathbf {x}_j, \mathbf {x}_k) - \mathbf {h}^{(2)}(\mathbf {x}_i, \mathbf {x}_i), \end{array} \end{aligned}$$
(10.29)

where \(\mathbf {h}^{(1)}: \mathbb {R}^{m} \longrightarrow \mathbb {R}^m\) and \(\mathbf {h}^{(2)}: \mathbb {R}^{2m} \longrightarrow \mathbb {R}^m\). In addition, a condition of natural coupling is considered

$$\begin{aligned} \mathbf {h}^{(2)}(\mathbf {x},\mathbf {x}) = \mathbf {h}^{(1)}(\mathbf {x}). \end{aligned}$$
(10.30)

Equation (10.30) expresses, indeed, the fact that the coupling to node i from two-body and three-body interactions is essentially similar, in that a three-body interaction where two nodes are on the same state is equivalent to a two-body interaction. Here, the MSF assumes a particularly convenient form, as it can be written as a function of a single parameter.

The consequence of Eq. (10.30) is that \(J_1 \mathbf {h}^{(2)} (\mathbf {x}^s, \mathbf {x}^s) + J_2 \mathbf {h}^{(2)} (\mathbf {x}^s, \mathbf {x}^s) {=} J \mathbf {h}^{(1)}(\mathbf {x}^s)\). Therefore, one has

$$\begin{aligned} \begin{array}{lll} \dot{ \delta \mathbf {x}}_i= & {} J \mathbf {f}(\mathbf {x}^s) \delta \mathbf {x}_i - \sum \limits _{j=1}^N \left[ \sigma _{1} \mathcal {L}_{ij}^{(1)} + \sigma _{2} \mathcal {L}_{ij}^{(2)} \right] \, J \mathbf {h}^{(1)}( \mathbf {x}^s) \delta \mathbf {x}_j. \end{array} \end{aligned}$$
(10.31)

Alternatively, one can consider the zero-row-sum, symmetric, effective matrix \(\mathcal {M}\), given by

$$\begin{aligned} \mathcal {M} = \mathcal {L}^{(1)} + r \mathcal {L}^{(2)}, \qquad r = \frac{\sigma _2}{\sigma _1}. \end{aligned}$$
(10.32)

The eigenvalues of \(\mathcal {M}\) depend on the ratio r of the coupling coefficients, and one has that

$$\begin{aligned} \dot{ \delta \mathbf {x}}_i = J \mathbf {f}(\mathbf {x}^s) \delta \mathbf {x}_i - \sigma _{1} \sum _{j=1}^{N} \mathcal {M}_{ij} \, J \mathbf {h}^{(1)}( \mathbf {x}^s) \delta \mathbf {x}_j. \end{aligned}$$
(10.33)

Equation (10.33) allows to establish a formal full analogy between the case of a simplicial complex and that of a network with weights given by the coefficients of the effective matrix \(\mathcal {M}\). In this case, by diagonalizing the effective matrix \(\mathcal {M}\), the transverse modes can be fully decoupled and a single-parameter MSF can be defined, starting from the following m-dimensional linear parametric variational equation

$$\begin{aligned} \dot{\mathbf {\eta }} = \left[ J \mathbf {f}(\mathbf {x}^s) - \alpha J \mathbf {h}^{(1)}(\mathbf {x}^s) \right] {\mathbf {\eta }} \end{aligned}$$
(10.34)

from which the maximum Lyapunov exponent is calculated: \(\Lambda _{\max }=\Lambda _{\max }(\alpha )\) with \(\alpha =\lambda (\sigma _1\mathcal {L}^{(1)}+\sigma _2\mathcal {L}^{(2)})\) or \(\alpha =\sigma _1\lambda (\mathcal {L}^{(1)}+r\mathcal {L}^{(2)})=\sigma _1\lambda (\mathcal {M})\). The situation is therefore conceptually equivalent to that of synchronization in complex networks, with the effective matrix \(\mathcal {M}\) playing the same role of the classical Laplacian: given the dynamical system \(\mathbf {f}\), the coupling functions \(\mathbf {h}^{(1)}\) and \(\mathbf {h}^{(2)}\), and the structure of connection of the simplicial complex (i.e. \( \mathcal {L}^{(1)}\) and \(\mathcal {L}^{(2)}\)) one can define three possible classes of problems: 1) class I problems, for which the curve \(\Lambda _{\max }=\Lambda _{\max }(\alpha )\) does not intercept the abscissa and it is always positive. In this case synchronization is always forbidden, no matter which simplicial complex is used for connecting the dynamical systems; 2) class II problems, for which the curve \(\Lambda _{\max }=\Lambda _{\max }(\alpha )\) intercepts the abscissa only once at \(\alpha _c\), and for which, therefore, the synchronization threshold is given by the self consistent equation \(\sigma _1^{c}= \alpha _c/ \lambda _2 [\mathcal {M}(\sigma _1^{c},\sigma _2^{c})]\), i.e. it scales with the inverse of the second smallest eigenvalue of the effective matrix; 3) class III problems, for which the curve \(\Lambda _{\max }=\Lambda _{\max }(\alpha )\) intercepts the abscissa twice at \(\alpha _1\) and \(\alpha _2 >\alpha _1\). In this case, synchronization can be observed only if the entire eigenvalue spectrum of the effective matrix is such that \(\sigma _1 \lambda _2(\mathcal {M}) > \alpha _1\) and, at the same time, \(\sigma _1 \lambda _N(\mathcal {M}) < \alpha _2\). In this case, the ratio \({\lambda _2(\mathcal {M})}/{\lambda _N(\mathcal {M}})\) can be considered as a proxy measure of synchronizability of the simplicial complex, in that the closer is such a parameter to unity (the more compact is the spectrum of eigenvalues of \(\mathcal {M}\)) the larger can be the range of coupling strengths for which the two above synchronization conditions can be satisfied.

We have so far considered the case of \(D=2\). In the fully general scenario, the condition for natural coupling is given by

$$\begin{aligned} \mathbf {h}^{(D)}(\mathbf {x},\ldots ,\mathbf {x}) = \ldots =\mathbf {h}^{(2)}(\mathbf {x},\mathbf {x}) =\mathbf {h}^{(1)}(\mathbf {x}). \end{aligned}$$
(10.35)

The equation for the MSF is formally analogous to Eq. (10.34), where now \(\alpha =\sigma _1\lambda _2(\mathcal {M}^{(D)})\) parametrizes the eigenvalues of the effective matrix of order D

$$\begin{aligned} \mathcal {M}^{(D)} = \mathcal {L}^{(1)} + \frac{\sigma _2}{\sigma _1}\mathcal {L}^{(2)}+\ldots +\frac{\sigma _D}{\sigma _1}\mathcal {L}^{(D)}. \end{aligned}$$
(10.36)

10.6 Numerical Results

In this section we show some numerical results confirming the validity of the proposed approach. In particular, we focus on a paradigmatic example of three-dimensional (\(\mathbf {x}=(x,y,z)^T \in \mathbb {R}^3\)) chaotic systems, i.e., the Rössler oscillator [41], and consider the case of natural coupling with \(D=3\).

In this case, as discussed in Sec. 10.5, in full analogy with what occurs for networks, the MSF is a function of a single parameter, i.e., \(\Lambda _{\max }=\Lambda _{\max }(\alpha )\) with \(\alpha =\lambda (\sigma _1\mathcal {L}^{(1)}+\sigma _2\mathcal {L}^{(2)}+\sigma _3\mathcal {L}^{(3)})\). This enables the study of synchronization stability into two steps, one pertaining only to the node dynamics and coupling functions, providing \(\Lambda _{\max }=\Lambda _{\max }(\alpha )\), and a second step, where the condition \(\Lambda _{\max }(\alpha )<0\) is checked at the points \(\alpha =\{\sigma _1\lambda _2(\mathcal {M}),\ldots ,\sigma _1\lambda _N(\mathcal {M})\}\).

Here, we have calculated the MSF for the Rössler oscillator with several choices of the coupling functionsFootnote 1:

$$\begin{aligned} \mathbf {h}^{(1)}(\mathbf {x}_j)&=[x_j^3,0,0]^T, \mathbf {h}^{(2)}(\mathbf {x}_j,\mathbf {x}_k)=[x_j^2x_k,0,0]^T,\mathbf {h}^{(3)}(\mathbf {x}_j,\mathbf {x}_k,\mathbf {x}_h)\\&=[x_jx_kx_h,0,0]^T;\mathbf {h}^{(1)}(\mathbf {x}_j)=[0,x_j^3,0]^T,\mathbf {h}^{(2)}(\mathbf {x}_j,\mathbf {x}_k)\\&=[0,x_j^2x_k,0]^T, \mathbf {h}^{(3)}(\mathbf {x}_j,\mathbf {x}_k,\mathbf {x}_h)=[0,x_jx_kx_h,0]^T;\mathbf {h}^{(1)}(\mathbf {x}_j)\\&=[0,0,x_j^3]^T,\mathbf {h}^{(2)}(\mathbf {x}_j,\mathbf {x}_k)=[0,0,x_j^2x_k]^T,\mathbf {h}^{(3)}(\mathbf {x}_j,\mathbf {x}_k,\mathbf {x}_h)\\&=[0,0,x_jx_kx_h]^T; \mathbf {h}^{(1)}(\mathbf {x}_j)=[y_j^3,0,0]^T,\mathbf {h}^{(2)}(\mathbf {x}_j,\mathbf {x}_k)\\&=[y_j^2y_k,0,0]^T,\mathbf {h}^{(3)}(\mathbf {x}_j,\mathbf {x}_k,\mathbf {x}_h)=[y_jy_ky_h,0,0]^T\ldots \, \text {and}\, \mathbf {h}^{(1)}(\mathbf {x}_j)\\&=[0,0,z_j^3]^T, \mathbf {h}^{(2)}(\mathbf {x}_j,\mathbf {x}_k) =[0,0,z_j^2z_k]^T, \mathbf {h}^{(3)}(\mathbf {x}_j,\mathbf {x}_k,\mathbf {x}_h)\\&=[0,0,z_jz_kz_h]^T. \end{aligned}$$

As an example, when the coupling functions are fixed as \(\mathbf {h}^{(1)}(\mathbf {x}_j)=[x_j^3,0,0]^T\), \(\mathbf {h}^{(2)}(\mathbf {x}_j,\mathbf {x}_k)=[x_j^2x_k,0,0]^T\), and \(\mathbf {h}^{(3)}(\mathbf {x}_j,\mathbf {x}_k,\mathbf {x}_h)=[x_jx_kx_h,0,0]^T\), the equations governing the simplicial complex of Rössler systems read

$$\begin{aligned} \begin{array}{lll} \dot{x}_{i} &{} = &{} -y_{i} -z_{i} +\sigma _1\sum \limits _{j=1}^N a_{ij}^{(1)}(x_j^3-x_i^3)\\ &{} &{} +\sigma _2\sum \limits _{j=1}^N\sum \limits _{k=1}^N a_{ijk}^{(2)}(x_j^2x_k-x_i^3)+\sigma _3\sum \limits _{j=1}^N\sum \limits _{k=1}^N\sum \limits _{h=1}^N a_{ijkh}^{(3)}(x_jx_kx_h-x_i^3),\\ \dot{y}_{i} &{} = &{} x_{i} + a y_{i}, \\ \dot{z}_{i} &{} = &{} b + z_{i} (x_{i} -c),\\ \end{array} \end{aligned}$$
(10.37)

where \(i=1,\ldots ,N\), and the parameters have been fixed so that the resulting dynamics is chaotic, i.e., \(a=b=0.2\), \(c=9\).

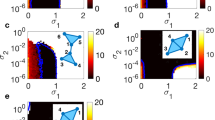
It is interesting to note that the MSFs characterizing simplicial complexes of Rössler oscillators (Fig. 10.2) exhibit a variety of behaviors that actually encompass all possible classes of MSF. In particular, we find one class III example (Fig. 10.2a), one class II example (Fig. 10.2e), while all remaining cases do correspond to class I.

Fig. 10.2
figure 2

Synchronization in simplicial complexes of Rössler oscillators, in the case of natural coupling, is characterized by a master stability function \(\Lambda _{\max }(\alpha )\), here obtained for several coupling functions. On the top of each panel, the expression used for \(\mathbf {h}^{(3)}\) is reported

Full size image
Fig. 10.3
figure 3

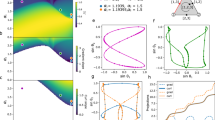
Synchronization in the simplicial complex of Rössler oscillators of Fig. 10.1c. a Contour plot of the time averaged (over an observation time \(T=500\)) synchronization error E in the plane (\(\sigma _1\), \(\sigma _2\)) for \(\sigma _3=0.1\). The red continuous line is the theoretical prediction of the synchronization thresholds obtained from Eq. (10.34). b Synchronization region as predicted from Eq. (10.34) at different values of the coupling strength \(\sigma _3\)

Full size image

Let us now consider the simplicial complex with \(N=10\) nodes represented in Fig. 10.1c and simulate Eqs. (10.37) on top of this structure. Let us first fix \(\sigma _3=0.1\) and integrateFootnote 2 Eqs. (10.37) for different values of \(\sigma _1\) and \(\sigma _2\). For each configurations of the coupling parameters, the state of the system is monitored by the average synchronization error defined as \(E=\langle \left( \frac{1}{N(N-1)}\sum \limits _{i,j=1}^N \Vert \mathbf {x_j}-\mathbf {x_i}\Vert ^2\right) ^{\frac{1}{2}}\rangle _{T}\), where T is a sufficiently large window of time where the synchronization error is averaged, after discarding the transient. As it is shown in Fig. 10.3a, which illustrates \(E(\sigma _1,\sigma _2)\) along with the theoretical predictions provided by the MSF, the numerical simulations are in very good agreement with the theoretical predictions for the synchronization thresholds. This is an example of a class III system, with a synchronization region that is bounded. In particular, it is interesting to note that synchronization is impossible to achieve for very small values of \(\sigma _1\), suggesting that in this structure interactions through links are essential for synchronization. To study the role of four-bodies interaction we have then varied \(\sigma _3\) and illustrated the predictions of the MSF obtained from Eq. (10.34) in Fig. 10.3b. We observe that, due to the fact that configuration under analysis is class III, increasing \(\sigma _3\) actually decreases the area of the synchronization region, in particular, lowering the threshold (for both \(\sigma _1\) and \(\sigma _2\)) from synchronization to desynchronization.

10.7 Conclusions

In a complex system consisting of many coupled dynamical units, collective behaviors are shaped by the functional form and by the architecture of the interactions. To account for the most general type of interactions, we have here leveraged the mathematical formalism of simplicial complexes to formulate a general model that include many-body interactions of arbitrary order among dynamical systems of arbitrary nature. Assuming the non-invasiveness of the coupling functions, we have shown that is possible to derive necessary conditions for stable synchronous regime in a simplicial complex. Remarkably, these conditions depend on generalized Laplacian matrices that map the effects of high-order interactions. For specific types of structures (e.g., all-to-all interactions) and couplings (that we named natural couplings), this approach ultimately provides a Master Stability Function, which formalizes the interplay between the dynamics of the single units and the topology of the simplicial complex.

The generality of the introduced framework and of the assumptions considered make it applicable in a wide range of scenarios, so that we expect that our method could be used to produce a-priori predictions on the emergence of synchronization in many diverse theoretical and practical cases. In particular, our study only focused on the regime of synchronization where all the units follow the same trajectory. However, many other different forms of synchronization exist, including cluster synchronization, chimera and Bellerophon states, remote synchronization, and so on. It would be particularly intriguing to investigate the emergence of such states, or even of novel ones, in structures that do not include exclusively pairwise couplings, but also incorporate other, types of higher-order interaction mechanisms, such as the simplicial complexes considered here.