Randomized Component Based Secure Secret Reconstruction in Insecure Networks

Abstract

In Shamir (t, n) secret sharing scheme, the secret can be recovered by any t or more than t shareholders. However, in insecure networks, if the number of participants is greater than t, a participant who does not own a valid share can also recover the secret by collecting components from other honest shareholders. Harn proposed the first secure secret reconstruction scheme, which used linear combination of shares to solve this problem, but this scheme is vulnerable to linear subspace attack. Miao used randomized component to disrupt the linear relationship and protect the share from being exposed. However, it can also be attacked by lattice. In this paper, we propose two randomized component based secure secret reconstruction schemes in insecure networks. The first scheme uses a random element whose distribution range at least equals to the share to protect the secrecy of share. Furthermore, the scheme is ideal and perfect. The second scheme is an improved scheme using bivariate polynomial, which is not only used for share and randomized component generation, but for secure channel construction. We don’t need to establish the secure channel for each pairwise shareholders in advance. s-box transmission breaks the linear relationship among randomized components and guarantee the perfect secrecy of our scheme.

Supported by National Key R&D Program of China 2018YFB0803405.

1 Introduction

(t, n) secret sharing (SS) was first introduced respectively by Shamir [22] and Blakley [4] in 1979. It is mainly divided into share distribution and secret reconstruction these two parts. In distribution phase, a mutually trusted dealer divides the secret s into n shares and distributes them to n shareholders through secure channel. Then threshold t or more than t shareholders cooperate in the secret reconstruction to reconstruct the secret, while less than t shareholders cannot get any information about the secret. Different from Shamir scheme of recovering secret using interpolation polynomials, Bloom [3] also proposed a secret sharing scheme using Chinese Remainder Theorem (CRT) in 1983. Then many secret sharing schemes (i.e. [5, 6, 10, 20, 24]) based on Chinese Remainder Theorem were proposed.

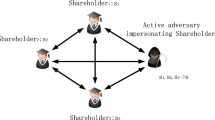
Shamir (t, n) secret sharing scheme can realize that any t or more than t shareholders can recover the secret. However, when the communication among shareholders is in an insecure network, it may lead to some threats. We show the two models of active attack and passive attack in Fig. 1.

Fig. 1.

Model of attacks in insecure networks.

• (a) Active attack: If the number of participants is larger than t, there may exist an active attack adversary who does not own a valid share participating in secret reconstruction and releasing his components last. In this case, he can recover the secret or forge a legal share by collecting enough components from other honest shareholders.

• (b) Passive attack: Since all components are sent in insecure networks, even a passive attack adversary who does not participate in the secret reconstruction directly, he can eavesdrop all components sent in secret reconstruction and recover the secret himself.

1.1 Related Work

One potential method against passive attack is establishing secure channels for each pair of shareholders. Many proposed secret sharing schemes are based on the assumption that secure channels have been established in advance. Then in order to resist active attack, Chor [7] proposed verifiable secret sharing (VSS) to verify other participants’ shares before secret reconstruction. In a VSS scheme, each shareholder verifies the authenticity of received shares rather than uses them to recover the secret directly. There are also many research papers (i.e. [2, 8, 15, 21, 25]) based on VSS. However, VSS scheme requires more calculation processes. Furthermore, the adversary still gets valid shares from honest shareholders even though his illegal behaviour can be detected.

Harn [9] proposed secure secret reconstruction (SSR) using linear combination of shares to protect the privacy of shares and prevent the adversary from obtaining secret by releasing his share last. Then more schemes based on secure secret reconstruction were proposed. Xiao [27] modified the scheme [9] by changing the degree of polynomial. Harn [12] proposed an asynchronously rational secret sharing scheme to solve the problem, in which a dishonest shareholder can release a fake share at last to make the correct secret recoverable only by himself when shares are released asynchronously. Using bivariate polynomial, Hsu [14] proposed a secure secret reconstruction scheme which can verify all shares at once; Meng [18] proposed a threshold changeable secret sharing, which can increase the threshold of the scheme to the exact number of the participants. Then Harn [13] proposed a secure secret reconstruction scheme which claimed to be information theoretical secure. He [11] also proposed a dynamic threshold secret sharing scheme using bivariate polynomial, which can make the threshold equal to the exact number of participants.

However, a participant who does not own a valid share can also forge a legal share in secure secret reconstruction schemes [9, 11] by using linear subspace cryptanalysis [1, 16]. Since the schemes [12,13,14, 18, 27] employ the same idea as scheme [9] to protect the share, all these schemes can be attacked by subspace linear attack. Ahmadian [1] found that $t+k-1$ valid released components are sufficient to forge any number of components in scheme [9]. Then Jamshidpour [16] found that no matter how large the threshold is, any $t+1$ released components can recover the secret and forge a legal share in scheme [11]. Xia [26] also analyzed the linear subspace attack in schemes [9, 11] and introduced a game-based model that can be used to formally analyze secret sharing schemes.

The main drawback in Harn scheme [9] is that $t+k-1$ components expand a linear subspace of components. That is, an adversary can forge a legal share if he knows $t+k-1$ linearly independent components. In order to prevent this attack, Miao [19] proposed a randomized component based secure secret sharing scheme. Compared to scheme [9], this scheme uses random integers to break the linear relationship among components. Furthermore, each shareholder only needs to own one share. Based on Miao scheme, Meng [17] also proposed a novel threshold changeable secret sharing scheme. However, as the distribution range of random integers in Miao scheme is smaller than share, it leads to short vectors consisting these random integers. The scheme is vulnerable to lattice attack.

1.2 Our Contribution

Based on the idea of randomized component in Miao scheme [19], we propose two secure secret reconstruction schemes in insecure networks, one is based on Chinese Remainder Theorem for polynomial and the other is based on bivariate polynomial. We add random element in our schemes to break the relationship among components. Then different from Miao scheme, the distribution range of our random element is no less than that of shares. As a result, both schemes can well protect the secrecy of shares and resist lattice attack.

We summarize contributions as follows:

• A (t, n) secure secret reconstruction scheme based on Chinese Remainder Theorem for polynomial is proposed. Using a novel randomized polynomial whose distribution range is no less than that of shares, the scheme can prevent the participant who does not own a valid share from recovering the secret and forging a legal share. This scheme can resist both the linear subspace attack and lattice attack. Furthermore, it is perfect and ideal.

• A (t, n) secure secret reconstruction scheme based on bivariate polynomial is proposed, in which bivariate polynomial is used to generate shares, secure channel key and randomized components. Shareholders don’t need to establish secure channels in advance. s-boxes are used during the generation of randomized components to enable the scheme to be resistant to both linear subspace and lattice attack.

1.3 Organization

The rest of this paper is organized as follows. Section 2 introduces some preliminaries and analyzes the problems of secure secret reconstruction schemes [9, 19]. Section 3 introduces the model and security goals. In Sect. 4, a basic SSR scheme based on CRT for polynomial is proposed. In Sect. 5, an improved SSR scheme using bivariate polynomial is also proposed. Section 6 describes our schemes’ properties and compares our schemes with other SSR schemes. Conclusion is included in Sect. 7.

2 Preliminaries

Some definitions are introduced in this section. Then description of Asmuth-Bloom (t, n) secret sharing and secure secret reconstruction schemes [9, 19] are also given.

Definition 1

Information entropy

Suppose X is a discrete-time discrete valued random variable with a sample space SP. Let $H( \cdot )$ be the information entropy function, then the entropy of X is denoted as:

$$\begin{aligned} H(X) = E( - {\log _2}P(X)) = \sum \limits _{x \in SP} { - P(x){{\log }_2}P(x)}, \end{aligned}$$

where E is the expectation operator and $P( \cdot )$ is the probability distribution function of X.

Definition 2

Perfect secrecy [23]

For any distribution on plaintext space M and the corresponding distribution on ciphertext space C, the condition of perfect secrecy for an encryption scheme $\varPi = (Gen,Enc,Dec)$ is that

$$\begin{aligned} \Pr (M = m|C = c) = \Pr (M = m), \end{aligned}$$

where m is a plaintext and c is a ciphertext.

Perfect Secrecy Necessary Condition: If an encryption scheme with message space M and key space K satisfies perfect secrecy, then $|K| \ge |M|$. From the view of information entropy, a perfect secrecy scheme satisfies $H(K) \ge H(M)$.

Definition 3

Perfect secret sharing scheme

Let P be a set of participants, $\varGamma$ be an access structure on P and S be the set of secrets. A perfect secret sharing scheme $PS(\varGamma ,S)$ satisfies:

• 1. any qualified subset can reconstruct the secret: ${\forall _{X \in \varGamma }}H(S|X) = 0;$

• 2. any non-qualified subset has no information on secret: ${\forall _{X \notin \varGamma }}H(S|X) = H(S).$

Definition 4

Information Rate

Information rate is the size ratio of secret to share. Let s be the secret and $S = \{ {s_1},{s_2}, \ldots {s_n}\}$ be the share set, then the information rate is

$$\begin{aligned} \rho = \frac{{{{\log }_2}|s|}}{{{{\max }_{{s_i} \in S}}({{\log }_2}|{s_i}|)}}. \end{aligned}$$

Ideal Secret Sharing Scheme: If a perfect scheme has the information rate 1, it’s an ideal scheme.

2.1 Asmuth-Bloom (t, n) SS Scheme

Asmuth-Bloom (t, n) SS Scheme is a secret sharing scheme based on Chinese Remainder Theorem (CRT). First, dealer selects a large prime p and a secret $s < p$. Then dealer selects n pairwise coprime integers ${m_1},{m_2}, \ldots {m_n}$ satisfying:

• 1. ${m_1}< {m_2}< \ldots < {m_n}$;

• 2. $\gcd ({m_i},p) = 1,1 \le i \le n$ and $\gcd ({m_i},{m_j}) = 1,1 \le j \le n,j \ne i$;

• 3. ${m_1}{m_2} \ldots {m_t} > p{m_{n - t + 2}}{m_{n - t + 3}} \ldots {m_n}$.

• Share Generation. Let $m = {m_1}{m_2} \ldots {m_t}$, then dealer selects a random integer r in $[0,\frac{m}{p} - 1]$ and calculates $s' = s + rp$. Each shareholder’s share is ${s_i} = s'\bmod {m_i}(i = 1,2, \ldots ,n)$, where ${m_i}$ is the public identity of shareholder ${U_i}$.

• Secret Reconstruction. If $h(h \ge t)$ shareholders try to recover the secret, the following system of congruence equations can be obtained:

  $$\left\{ {\begin{array}{*{20}{l}} {s' = {s_1} \bmod {m_1}}\\ {s' = {s_2} \bmod {m_2}}\\ \cdots \\ {s' = {s_h} \bmod {m_h}} \end{array}} \right. .$$

  According to the Chinese Remainder Theorem, because of ${m_1}{m_2} \ldots {m_h} \ge m$, the system has a unique solution $s'$ and the secret $s = s'\bmod p$.

2.2 Harn (t, n) Secure Secret Reconstruction Scheme

In order to prevent the participant who does not own a valid share from recovering the secret, Harn proposed a (t, n) secure secret reconstruction scheme. Shareholders need to compute a linear combination of multiple shares as Lagrange component. Then on the basis of this scheme, Harn also modified it to a secure multi-secret sharing scheme with h shares. The following is a detailed description of Harn (t, n) secure multi-secret sharing scheme with h shares.

• Share Generation. To reconstruct h secrets ${s_i}(i = 1,2, \ldots ,h)$ for n shareholders, dealer selects k random polynomials ${f_l}(x)(l = 1,2, \ldots ,k)$ of degree $t-1$, where $kt > h(n + 1) - 2$ and $k > (h - 1)(n - t + 2)$. Dealer sends k shares ${f_l}({x_r})$ to each shareholder ${U_r}$ secretly, where $x_r$ is the public identity of $U_r$.

  Then dealer finds public integers ${w_l}$, $d{}_{i,l}$ in GF(p) for each secret ${s_i}$, such that: ${s_i} = \sum \limits _{i = 1}^k {{d_{i,l}}{f_l}({w_l})} (l = 1,2, \ldots ,k)$, where ${w_i} \ne {w_j}$, ${w_i} \notin \{ {x_1},{x_2}, \ldots {x_n}\}$.

• Secret Reconstruction. If $h(h \ge t)$ shareholders try to reconstruct the secret ${s_i}$, each participant ${U_r}$ computes

  $$\begin{aligned} {c_r} = \sum \limits _{i = 1}^k {{d_{i,l}}{f_l}({x_r})\prod \limits _{v = 1,v \ne r}^h {\frac{{{w_l} - {x_v}}}{{{x_r} - {x_v}}}} } \bmod p \end{aligned}$$

  and sends it to other participants. Then the secret ${s_i} = \sum \limits _{r = 1}^h {{c_r}} \bmod p$.

• Vulnerable to Linear Subspace Attack. Linear subspace attack is an algebraic-based analysis for linear released components. If the released components are modelled as a linear system with a structured matrix, adversary can use the rank property to mount attacks through rank analysis.

  The main drawback in Harn scheme is that it is not sufficient only to hide the polynomials’ coefficients for information protection. Since the Lagrange components are generated by the linear combination of the shares, all released components are in a linear subspace of dimension of $t+k-1$. Consequently, a non-shareholder is able to forge a new component after collecting up to $t+k-1$ components by using linear subspace attack.

2.3 Miao Randomized Component Based (t, n) SSR Scheme

Miao proposed an improved randomized component based SSR scheme to break the linear relationship among components. Suppose that there are n shareholders $U{\,\mathrm { = }\,}\{ {U_1},{U_2}, \ldots ,{U_n}\}$ and each shareholder ${U_i}$ has a public identity ${x_i}$.

• Share Generation. Dealer selects two large primes p, q satisfying $p > q + n{q^2}$. He also selects a polynomial over ${F_p}$: $f(x) = {a_0} + {a_1}x + \ldots {a_{t - 1}}{x^{t - 1}}\bmod p$, where ${a_0} \in {F_q}$, ${a_i} \in {F_p},i = 1,2, \ldots t - 1$, ${a_{t - 1}} \ne 0$. The secret $s = {a_0}$. Then dealer sends the share ${s_i} = f({x_i})\bmod p$ to each shareholder ${U_i}$ secretly.

• Randomized Component Computation. If $h(h \ge t)$ shareholders try to recover the secret, each participant ${P_i}$ randomly selects ${r_i}{ \in _R}{F_q}$ and constructs the randomized components:

  $$\begin{aligned} R{C_i} = (f({x_i})\prod \limits _{v = 1,v \ne i}^m {\frac{{ - {x_v}}}{{{x_i} - {x_v}}} + {r_i}q}) \bmod p. \end{aligned}$$

• Secret Reconstruction. Then each participant releases $R{C_i}(1 \le i \le h)$ and the secret can be recovered by $s = (\sum \limits _{i = 1}^h {R{C_i} \bmod p} ) \bmod q$.

• Vulnerable to Lattice Attack. Lattice attack is used to analyze a series of adding short vectors linear components such as $\{ {f_1} + {v_1},{f_2} + {v_2}, \ldots ,{f_n} + {v_n}\}$, where ${f_1},{f_2}, \ldots {f_n}$ are linear related and ${v_1},{v_2}, \ldots {v_n}$ are short vectors added to ${f_i}(i = 1,2, \ldots n)$. The adversary can find these short vectors by constructing lattice base and using LLL reduction algorithm.

  In Miao scheme, ${RC_i}$ can be regarded as the encryption of $f({x_i})$ with ${r_i}$ as the encryption key. Since $f({x_i})$ is uniformly distributed over ${F_p}$ and ${r_i}$ is uniformly distributed over ${F_q}$, $q < p$, then $|K| < |M|$. From the view of perfect secrecy, ${r_i}$ cannot protect the secrecy of $f({x_i})$. When adversary collects multiple randomized components, he constructs lattice base and each ${r_i}$ consisting short vectors can be found by LLL reduction algorithm. Then the adversary obtains share $f({x_i})$ from ${RC_i}$ and recover the secret.

In order to specifically show the relationship among these related work in Sect. 2, we summarize them in Fig. 2.

Fig. 2.

Summary of related work.

3 Scheme Model and Security Goals

This section presents the model and security goals of our secure secret reconstruction schemes in insecure networks.

3.1 Scheme Model

Our proposed secure secret reconstruction schemes adopt the same model as Harn [9], which includes three types of entities: dealer, shareholder and adversary.

• Dealer: Dealer is trusted by all shareholders. He sets up parameters and distributes shares to shareholders.

• Shareholder: A shareholder receives valid share from the dealer. Then he uses share to generate the component and sends it to other shareholders through secure channel. Only t or more than t shareholders can recover the secret, while less than t shareholders cannot get any information about the secret.

• Adversary: In our scheme, adversary is divided into two types:

  • Inside adversary: Less than threshold t legal shareholders use their shares and conspire to recover the secret.

  • Outside adversary: A participant who does not own a valid share participates in secret reconstruction and tries to recover the secret or forge a legal share by collecting components from honest shareholders.

  The two models of adversary are shown in Fig. 3.

Fig. 3.

Model of adversary.

3.2 Security Goals

Generally, in order to achieve the security of secure secret sharing scheme, we need to ensure that only t or more than t honest shareholders can recover the secret. In insecure networks, shareholders cannot identify other participants and the components sent among shareholders may be captured by outside adversary. As a result, we need to thwart both the inside shareholder conspiracy attack and the outside adversary attack. The security goals of our model are as follows:

• Resist attack from inside adversary: Only t or more than t shareholders can recover the secret, while less than t shareholders cannot.

• Resist attack from outside adversary: If a participant who does not own a valid share collects components from other honest participants, he cannot recover the secret. Even using linear subspace attack and lattice attack, he cannot get any information about the share and secret.

4 Basic Proposed SSR Scheme

4.1 Scheme

First, we propose a (t, n) randomized component based secure secret reconstruction scheme in insecure networks, which is an improvement of Miao scheme [19]. Different from Miao scheme, the random element in our scheme can cover up the information of share and resist lattice attack. Furthermore, this scheme is perfect and ideal.

The scheme is divided into three parts, including initialization, share generation and secret reconstruction.

• Initialization: Assume that there are n shareholders $U = \{ {U_1},{U_2},...,{U_n}\}$ and a trusted dealer.

  • Step 1: Dealer randomly chooses a large prime p and threshold t publicly. The secret s(x) is a polynomial of degree $d-1$ over ${F_p}$.

  • Step 2: Dealer selects ${m_0}(x)$ and n public monic and irreducible polynomials of degree d over $F_p$ as each shareholder’s identity: ${m_i}(x)(i = 1,2, \ldots ,n)$.

• Share Generation: In order to distribute shares for shareholders to recover the secret s(x):

  • Step 1: Dealer constructs polynomials $F(x) = s(x) + k(x) \cdot {m_0}(x)$, where k(x) is a random polynomial over $F_p$ and $\deg (k(x)) = (t - 1)d - 1$.

  • Step 2: Dealer computes and distributes the share ${s_i}(x) = F(x) \bmod {m_i}(x)$ for each shareholder ${U_i}$.

• Secret Reconstruction: Suppose that there are $h(h \ge t)$ shareholders trying to recover the secret.

  • Step 1: Before secret reconstruction, each participant ${P_i}(1 \le i \le h)$ randomly selects a polynomial ${r_i}(x)$, which is uniformly distributed over $F_p$ and satisfies $d-1 \le \deg ({r_i}(x)) \le (h - 1)d - 1$.

  • Step 2: Randomized component ${RC_i}$ is computed by each participant as

    $$\begin{aligned} R{C_i}(x) = ({s_i}(x) \cdot {c_i}(x) + {r_i}(x) \cdot {m_0}(x))\bmod M(x), \end{aligned}$$

    where ${c_i}(x) = {M_i}(x){M'_i}(x)$, ${M_i}(x) = \frac{{M(x)}}{{{m_i}(x)}}$, $M(x) = \prod \limits _{i = 1}^h {{m_i}} (x)$ and ${M_i}(x){M'_i}(x) = 1\bmod {m_i}(x)$.

  • Step 3: Each participant ${P_i}$ sends ${RC_i}(x)$ to other $h-1$ participants through secure channel. After receiving $h-1$ components, the secret can be computed by $s(x) = (\sum \limits _{i = 1}^h {R{C_i}(x) \bmod M(x)} )\bmod {m_0}(x)$.

4.2 Correctness Analysis

Suppose that there are $h(h \ge t)$ shareholders trying to recover the secret.

Lemma 1

The sum of all the adding random polynomials equals to 0, in other words, $\sum \limits _{i = 1}^h {{r_i(x)} \cdot {m_0}(x)} \bmod M(x)\bmod {m_0}(x) = 0$.

Proof

Since $\deg ({r_i(x)}) \le (h - 1)d - 1$, $M(x) = \prod \limits _{i = 1}^h {{m_i}(x)}$ and $\deg ({m_i}(x)) = d$, for $i = 0,1, \ldots ,n$, then we have $\deg ({r_i}(x) \cdot {m_0}(x)) \le hd - 1 < \deg (M(x))$. Therefore, $\sum \limits _{i = 1}^h {{r_i(x)} \cdot {m_0}(x)} \bmod M(x)\bmod {m_0}(x) = 0$.

Theorem 1

The secret s(x) can be recovered by $h(h \ge t)$ shareholders.

Proof

On account of Lemma 1, we have:

$$\begin{aligned} \nonumber&\sum \limits _{i = 1}^h {R{C_i}(x)\,\bmod \,M(x)} \,\bmod \,{m_0}(x) \\ \nonumber&= (\sum \limits _{i = 1}^h {{s_i}(x) \cdot {c_i}(x)} + \sum \limits _{i = 1}^h {{r_i}(x) \cdot {m_0}(x)} )\,\bmod \,M(x)\,\bmod \,{m_0}(x) \\&= \sum \limits _{i = 1}^h {({s_i}(x) \cdot {c_i}(x))} \,\bmod \,M(x)\,\bmod \,{m_0}(x) \end{aligned}$$

(1a)

$$\begin{aligned}&= F(x)\,\bmod \,{m_0}(x) = s(x). \end{aligned}$$

(1b)

Since ${s_i}(x) = F(x)\bmod {m_i}(x)$ and ${c_i}(x) = {M_i}(x){M'_i}(x)$, step (1a) is equivalent to step (1b) on the basis of Chinese Remainder Theorem. Therefore, $h(h \ge t)$ shareholders can recover the secret by $s(x) = \sum \limits _{i = 1}^h {{RC_i}(x)\bmod M(x)} \bmod {m_0}(x)$.

4.3 Security Analysis

Lemma 2

The distributed share ${s_i}(x)$ is uniformly distributed over ${F_p}$.

Proof

A map $\sigma$ from $F_p[x]$ to its quotient ring $F_p[x]/\langle m_i(x) \rangle$ can be constructed:

$$\begin{aligned} \begin{aligned} \sigma :F_p[x]&\rightarrow F_p[x]/\langle m_i(x) \rangle ,\quad F(x)&\mapsto {s_i}(x) \equiv F(x)\bmod {m_i}(x). \end{aligned} \end{aligned}$$

(2)

Then given $F(x),G(x)\in F_p[x]$, the above Eq. (2) satisfies:

$$\begin{aligned} \nonumber \begin{aligned} \sigma (F(x)+G(x)) =&\left( {F(x) + G(x)} \right) \bmod {m_i}(x) \\ =&\left( {F(x)\bmod {m_i}(x)} \right) + \left( {G(x)\bmod {m_i}(x)} \right) \\ =&\, \sigma (F(x)) + \sigma (G(x)). \end{aligned} \end{aligned}$$

Therefore, $\sigma$ is a group homomorphism. For any $s_i(x)\in F_p[x]/\langle m_i(x) \rangle$, there exists $F(x)\in F_p[x]$ such that $\sigma (F(x)) = s_i(x)$. Thus, $\sigma$ is an epimorphism. As a result, if F(x) is uniformly distributed over ${F_p}$, then the distributed share ${s_i}(x) = F(x)\bmod {m_i}(x)$ is also uniformly distributed over ${F_p}$.

Theorem 2

The proposed scheme can resist attack from inside adversary. In detail, the secret s(x) cannot be recovered by less than t legal shareholders.

Proof

We consider the worst case of $t-1$ shareholders with valid shares trying to recover the secret illegally. Any $t-1$ inside adversaries can generate $t-1$ congruence equations based on modular of d degree, which can only recover a unique polynomial $F'(x)$ of degree not higher than $d(t-1)-1$. They need to use this polynomial $F'(x)$ to recover the secret $s(x) = F(x)\bmod {m_0}(x)$.

However, $F'(x)$ satisfies $F'(x) = F(x)\bmod \prod \limits _{i = 1}^{t - 1} {{m_i}(x)}$. They have $F(x) = F'(x) + k(x) \cdot \prod \limits _{i = 1}^{t - 1} {{m_i}(x)}$, where $\deg (k(x)) = d - 1$. From the view of information entropy, let H(s) represents the information entropy of the secret and $H(s|\{ {s_1},{s_2}, \ldots ,{s_{t - 1}}\}$ represents the information entropy of knowing $t-1$ shareholders’ shares to recover the secret. Since both k(x) and s(x) are polynomials of degree $d-1$ over ${F_p}$, then $H(s) = H(s|\{ {s_1},{s_2}, \ldots ,{s_{t - 1}}\} ) = d{\log _2}p$. Thus, $t-1$ inside adversaries cannot get any information about the secret.

Lemma 3

Given a randomized component ${RC_i}(x)$, it is impossible to derive the share ${s_i}(x)$.

Proof

The randomized component $R{C_i}(x) = {s_i}(x) \cdot {c_i}(x) + {r_i}(x) \cdot {m_0}(x)$, where ${r_i}(x)$ is randomly selected over ${F_p}$ by shareholder. According to Lemma 2, ${s_i}(x)$ is uniformly distributed over ${F_p}$ and $\deg ({s_i}(x)) = d - 1$, the probability of inferring ${s_i}(x)$ directly is ${d^p}$. Then since $\deg ({r_i}(x)) \ge d - 1$, the probability of deriving ${s_i}(x)$ from ${RC_i}$ by inferring ${r_i}(x)$ at least equals to ${d^p}$. Thus, given a randomized component ${RC_i}(x)$, it is impossible to derive the share ${s_i}(x)$.

Theorem 3

The proposed scheme can resist attack from outside adversary. In detail, when $h(h \ge t)$ participants try to recover the secret, a participant who does not own a valid share cannot get any information about secret and share by collecting $h-1$ randomized components from other honest participants.

Proof

Suppose adversary is the hth participant who releases his component last, he can collect $h-1$ randomized components from other participants.

• 1. First, we prove the outside adversary cannot get any information about the secret. The secret $s(x) = (\sum \limits _{i = 1}^{h - 1} {R{C_i}(x)} + R{C_h}(x))\,\bmod \,M(x)\,\bmod \,{m_0}(x)$, where $R{C_h}(x) = {s_h}(x) \cdot {c_h}(x) + {r_h}(x) \cdot {m_0}(x)$. If the outside adversary wants to compute $R{C_h}(x)$, he needs to know the share ${s_h}(x)$. Both s(x) and ${s_h}(x)$ are unknown polynomials of $d-1$ degree over ${F_p}$ in x. From the view of information entropy, let H(s) represents the information entropy of the secret and $H(s|\{ R{C_1},R{C_2}, \ldots R{C_{h - 1}}\} )$ represents the information entropy of knowing $h-1$ shareholders’ randomized components to recover the secret. $H(s) = H(s|\{ R{C_1},R{C_2}, \ldots R{C_{h - 1}}\} ) = d{\log _2}p$, then outside adversary cannot get any information about the secret by collecting $h-1$ randomized components from other honest participants.

• 2. Next, we prove the outside adversary cannot get any information about the share. On account of Lemma 3, it is impossible for outside adversary to derive the original share ${s_i}$ from the randomized component ${RC_i}$.

  Then we discuss whether the outside adversary can obtain the share through linear subspace attack and lattice attack. Since ${r_i}(x)$ is randomly selected and separated from F(x), adversary cannot find any relationship among randomized components by linear subspace cryptanalysis. In randomized component ${RC_i}(x)$, ${r_i}(x)$ can be regarded as the key K to protect the message ${s_i}(x)$. The degree of ${r_i}(x)$ is at least $d-1$, which satisfies $\deg ({r_i}(x)) \ge \deg ({s_i}(x)) = d - 1$ and guarantee $\left| K \right| \ge \left| M \right|$. Our scheme satisfies perfect secrecy and can resist both linear subspace attack and lattice attack.

5 Improved Bivariate Polynomial Based SSR Scheme

5.1 Scheme

This scheme is an improved randomized component based secure secret reconstruction scheme using bivariate polynomial, which can generate both the share and the randomized component. Furthermore, we don’t need to establish the secure channel for each pairwise shareholders in advance. Each shareholder owns two shares, where the additional share is used for secure channel key generation.

The second scheme is divided into six parts, including initialization, share generation, calculation of pairwise key, establishment of secure channel, calculation of randomized component and secret reconstruction.

Here we use ${\deg _x}(F(x,y))$ to represent the degree of bivariate polynomial F(x, y) in x and use ${\deg _y}(F(x,y))$ to represent the degree of F(x, y) in y.

• Initialization: Assume that there are n shareholders $U = \{ {U_1},{U_2},...,{U_n}\}$ and a trusted dealer.

  • Step 1: Dealer randomly chooses a large prime p, a integer d, the threshold t and makes them public.

  • Step 2: Dealer selects ${a_{i,j}} \in {Z_p} (1 \le i,j \le dt - 1)$ and construct a matrix A as:

    $$\begin{aligned} \nonumber A = \left[ {\begin{array}{*{20}{c}} {{a_{0,0}}}&{}{{a_{0,1}}}&{} \ldots &{}{{a_{0,dt - 1}}}\\ {{a_{1,0}}}&{}{{a_{1,1}}}&{} \ldots &{}{{a_{1,dt - 1}}}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {{a_{dt - 1,0}}}&{}{{a_{dt - 1,1}}}&{} \ldots &{}{{a_{dt - 1,dt - 1}}} \end{array}} \right] . \end{aligned}$$

    Then the bivariate polynomial F(x, y) with degree $dt-1$ can be constructed as: $F(x,y) = \left[ {\begin{array}{*{20}{c}} {{x^0}}&{{x^1}}&\ldots&{{x^{dt - 1}}} \end{array}} \right] \cdot A \cdot {\left[ {\begin{array}{*{20}{c}} {{y^0}}&{{y^1}}&\ldots&{{y^{dt - 1}}} \end{array}} \right] ^T}\bmod p$.

  • Step 3: Dealer chooses public polynomials ${m_0}(x)$ and ${m_0}(y)$ of degree d over ${F_p}$ and public non-linear mapping s1-box and s2-box: ${F_p} \rightarrow {F_p}$. The secret

    $$\begin{aligned} s(x,y) = F(x,y) \bmod {m_0}(x) \bmod {m_0}(y). \end{aligned}$$

• Share Generation:

  • Step 1: Shareholders pick coprime polynomials ${m_i}(x)(1 \le i \le n)$ of degree d over ${F_p}$ as their public identity.

  • Step 2: Dealer computes and distributes two shares ${s_{i,1}}(x,y) = F(x,y) \bmod {m_i}(x)$ and ${s_{i,2}}(x,y) = {F}(x,y)\bmod {m_i}(y)$ for each shareholder ${U_i}(1 \le i \le n)$ secretly. ${m_i}(y)$ is the polynomial which uses variable y to replace the variable x in ${m_i}(x)$.

• Calculation of Pairwise Key: We use function sgn to describe the relationship of shareholder’s identity.

  $${\mathrm{sgn}}({m_i}(x) - {m_j}(x)) = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {1;}&{\begin{array}{*{20}{c}} {if}&{}{{m_i}(x) > {m_j}(x)} \end{array}} \end{array}}\\ {\begin{array}{*{20}{c}} { - 1;}&{}{\begin{array}{*{20}{c}} {if}&{}{{m_i}(x) < {m_j}(x)} \end{array}} \end{array}} \end{array}} \right. .$$

  Shareholder ${U_i}$ computes the pairwise key ${k_{i,j}}(x,y)$ with ${U_j}$ as follows:

  $$\begin{aligned} {k_{i,j}}(x,y) = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{s_{i,1}}(x,y)\bmod {m_j}(y);}&{\begin{array}{*{20}{c}} {if}&{}{{\mathrm{sgn}}({m_i}(x) - {m_j}(x)) = 1} \end{array}} \end{array}}\\ {\begin{array}{*{20}{c}} {{s_{i,2}}(x,y)\bmod {m_j}(x);}&{}{\begin{array}{*{20}{c}} {if}&{}{{\mathrm{sgn}}({m_i}(x) - {m_j}(x)) = - 1} \end{array}} \end{array}} \end{array}} \right. . \end{aligned}$$

  (3)

  We describe ${k_{i,j}}(x,y)$ as: ${k_{i,j}}(x,y) = \left[ {\begin{array}{*{20}{c}} {{x^0}}&{{x^1}}&\ldots&{{x^{d - 1}}} \end{array}} \right] \cdot E \cdot {\left[ {\begin{array}{*{20}{c}} {{y^0}}&{{y^1}}&\ldots&{{y^{d - 1}}} \end{array}} \right] ^T},$ where E is the coefficient matrix of ${k_{i,j}}(x,y)$:

  $$E = \left[ {\begin{array}{*{20}{c}} {{e_{0,0}}}&{}{{e_{0,1}}}&{} \ldots &{}{{e_{0,d - 1}}}\\ {{e_{1,0}}}&{}{{e_{1,1}}}&{} \ldots &{}{{e_{1,d - 1}}}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {{e_{d - 1,0}}}&{}{{e_{d - 1,1}}}&{} \ldots &{}{{e_{d - 1,d - 1}}} \end{array}} \right] .$$

• Establishment of Secure Channel: Before secret reconstruction, each pair of participants establish secure channels with each other.

  • Step 1: To generate the secure channel key with participant ${P_j}$, participant ${P_i}$ calculates ${k'_{i,j}} = \sum \limits _{i = 0,j = 0}^{d - 1} {{e_{i,j}}} \bmod p$, where ${e_{i,j}}(0 \le i,j \le d - 1)$ are parameters of coefficient matrix E in ${k_{i,j}}(x,y)$.

  • Step 2: Participant ${P_i}$ inputs ${k'_{i,j}}$ into $s_1$-box and generates the pairwise secure channel key ${s_1}({k'_{i,j}})$ with $P_j$.

• Calculation of Randomized Component: Assume that there are $h(h \ge t)$ shareholders trying to recover the secret.

  • Step 1: First, participant ${P_i}(1 \le i \le h)$ computes a new share for secret reconstruction ${s_i}(x,y) = {s_{i,1}}(x,y)\bmod {m_0}(y)$ and generates the component ${g_i}(x,y) = {s_i}(x,y){M_i}(x){M'_i}(x)$, where $M(x) = \prod \limits _{i = 1}^h {{m_i}(x)}$, ${M_i}(x) = \frac{{M(x)}}{{{m_i}(x)}}$ and ${M_i}(x){M'_i}(x) = 1\bmod {m_i}(x)$.

  • Step 2: Participant ${P_i}$ transforms each coefficient in Eq. (3) through $s_2$-box to gets ${s_2}({k_{i,j}}(x,y)$. Then he generates

    $$\begin{aligned} {k_i}(x,y) = \sum \limits _{j = 1,j \ne i}^h {\left( {{\mathrm{sgn}}({m_i}(x) - {m_j}(x)) \cdot {s_2}({k_{i,j}}(x,y))} \right) }. \end{aligned}$$

  • Step 3: Each randomized component ${RC_i}(x,y) = {g_i}(x,y) + {k_i}(x,y)$ is calculated and sent to other participants through previously established secure channel.

• Secret Reconstruction: After receiving $h-1$ randomized components from other participants, the secret $s(x,y) = \sum \limits _{i = 1}^h {R{C_i}(x,y)} \bmod M(x)\bmod {m_0}(x)$.

5.2 Correctness Analysis

Suppose that there are $h(h \ge t)$ shareholders trying to recover the secret.

Lemma 4

Each pair of shareholders can generate the same pairwise key. Specifically, shareholder $U_i$ and $U_j$ can generate ${k_{i,j}}(x,y) = {k_{j,i}}(x,y)$.

Proof

Assume that ${m_i}(x) > {m_j}(x)$, then ${\mathop {\mathrm {sgn}}} ({m_i}(x) - {m_j}(x)) = 1$. We have

$$\begin{aligned} {k_{i,j}}(x,y) = F(x,y)\bmod {m_i}(x) \bmod {m_j}(y); \end{aligned}$$

(4)

$$\begin{aligned} {k_{j,i}}(x,y) = F(x,y)\bmod {m_j}(x) \bmod {m_i}(y), \end{aligned}$$

(5)

where ${m_i(x)}$, $m_j(x)$ are polynomials only in x and $m_i(y)$, ${m_j(y)}$ are polynomials only in y. Since the order of modular operation of polynomials based on different variables does not affect the result of computation, Eq. (4) equals to Eq. (5). For any pairwise shareholders $U_i$ and $U_j$, we have ${k_{i,j}}(x,y) = {k_{j,i}}(x,y)$. Therefore, each pair of shareholders can generate the same pairwise key.

Lemma 5

The sum of adding random polynomials equals to 0, in other words, $\sum \limits _{i = 1}^h {{k_i}(x,y)} = 0$.

Proof

According to Lemma 4, for any pairwise shareholders $U_i$ and $U_j$, we have ${k_{i,j}}(x,y) = {k_{j,i}}(x,y)$ and ${s_2}({k_{i,j}}(x,y)) = {s_2}({k_{j,i}}(x,y))$. Thus,

$$\begin{aligned} \nonumber&{{\mathrm{sgn}}({m_i}(x) - {m_j}(x)) \cdot {s_2}\left( {{k_{i,j}}(x,y)} \right) + {\mathrm{sgn}}({m_j}(x) - {m_i}(x)) \cdot {s_2}\left( {{k_{j,i}}(x,y)} \right) } \\&= {\left( {{\mathrm{sgn}}({m_i}(x) - {m_j}(x)) + {\mathrm{sgn}}({m_j}(x) - {m_i}(x))} \right) \cdot {s_2}\left( {{k_{i,j}}(x,y)} \right) } \end{aligned}$$

(6a)

$$\begin{aligned}&= 0, \end{aligned}$$

(6b)

where step (6a) equals to step (6b) due to for any pairwise shareholders ${U_i}$ and ${U_j}$: ${\mathrm{sgn}}({m_i}(x) - {m_j}(x)) + {\mathrm{sgn}}({m_j}(x) - {m_i}(x)) = 1 + \left( { - 1} \right) = 0$.

For any pairwise shareholders $U_i$ and $U_j$, there is:

$$\begin{aligned} \sum \limits _{i = 1}^h {{k_i}(x,y)} = \sum \limits _{i = 1}^h {\sum \limits _{j = 1,j \ne i}^h {\left( {{\mathrm{sgn}}({m_i}(x) - {m_j}(x)) \cdot {s_2}({k_{i,j}}(x,y))} \right) } } = 0. \end{aligned}$$

Therefore, the sum of adding random polynomials equals to 0.

Theorem 4

The secret s(x, y) can be recovered by $h(h \ge t)$ shareholders.

Proof

According to Lemma 5, we have

$$\begin{aligned} \nonumber&\sum \limits _{i = 1}^h {R{C_i}(x,y)} \bmod M(x) \bmod {m_0}(x) \\ \nonumber&= (\sum \limits _{i = 1}^h {{g_i}(x,y)} + \sum \limits _{i = 1}^h {{k_i}(x,y)} ) \bmod M(x) \bmod {m_0}(x) \\ \nonumber&= \sum \limits _{i = 1}^h {{g_i}(x,y)} \bmod M(x) \bmod {m_0}(x) \\&= \sum \limits _{i = 1}^h {{s_i}(x,y){M_i}(x){{M'}_i}(x)} \bmod M(x) \bmod {m_0}(x) \end{aligned}$$

(7a)

$$\begin{aligned}&= F(x,y)\bmod {m_0}(x)\bmod {m_0}(y) = s(x,y). \end{aligned}$$

(7b)

Since ${s_i}(x,y) = F(x,y){} \,\bmod \,{} {m_i}(x)\,\bmod \,{m_0}(y)$, step (7a) is equivalent to step (7b) on the basis of Chinese Remainder Theorem. Therefore, $h(h \ge t)$ shareholders can recover the secret by $s(x) = \sum \limits _{i = 1}^h {R{C_i}(x,y)} \bmod M(x) \bmod {m_0}(x)$.

5.3 Security Analysis

Lemma 6

The distributed shares ${s_{i,1}}(x)$, ${s_{i,2}}(x)$ and share for secret reconstruction ${s_i}(x)$ are uniformly distributed over ${F_p}$.

Proof

Since for any bivariate polynomial $F(x,y)\in F_p[x,y]$, there exists unique $s_{i,1}(x,y)\in F_p[x,y]/\langle m_i(x) \rangle$ such that ${s_{i,1}}(x,y) \equiv f(x,y)\bmod {m_i}(x)$. A map $\sigma$ from $F_p[x,y]$ to its quotient ring $F_p[x,y]/\langle m_i(x) \rangle$ can be constructed as follows:

$$\begin{aligned} \begin{aligned} \sigma :F_p[x,y]&\rightarrow F_p[x,y]/\langle m_i(x) \rangle \\ F(x,y)&\mapsto {s_{i,1}}(x,y) \equiv F(x,y)\bmod {m_i}(x). \end{aligned} \end{aligned}$$

(8)

Given $F(x,y),G(x,y)\in F_p[x,y]$, Eq. (8) satisfies

$$\begin{aligned} \nonumber \begin{aligned} \sigma (F(x,y)+G(x,y)) =&\left( F(x,y) + G(x,y) \right) \bmod {m_i}(x) \\ =&\left( F(x,y)\bmod {m_i}(x) \right) + \left( G(x,y)\bmod {m_i}(x) \right) \\ =&\, \sigma (F(x,y)) + \sigma (G(x,y)). \end{aligned} \end{aligned}$$

Thus, $\sigma$ is a group homomorphism. For any $s_{i,1}(x,y)\in F_p[x,y]/\langle m_i(x) \rangle$, there exists $F(x,y)\in F_p[x,y]$ such that $\sigma (F(x,y)) = s_{i,1}(x,y)$. $\sigma$ is an epimorphism. As a result, if F(x, y) is uniformly distributed over ${F_p}$, then ${s_{i,1}}(x,y) = F(x,y)\bmod {m_i}(x)$ is also uniformly distributed over ${F_p}$. Similarly, we also have ${s_{i,2}}(x,y) = F(x,y)\bmod {m_i}(y)$ and ${s_i}(x,y) = {s_{i,1}}(x,y)\bmod {m_0}(y)$ uniformly distributed over ${F_p}$.

Theorem 5

The proposed scheme can resist attack from inside adversary. In detail, the secret s(x, y) cannot be recovered by less than t legal shareholders.

Proof

We consider the worst case of $t-1$ shareholders trying to recover the secret illegally. Any $t-1$ inside adversaries can generate $t-1$ congruence equations based on modular of d degree in x, which can only recover a unique bivariate polynomial $F'(x,y)$ with ${\deg _x}(F'(x,y)) \ge d(t - 1) - 1$. We use $\theta (x,y)$ to represent $F(x,y) \bmod {m_0}(y)$ and $\omega (x,y)$ to represent $F'(x,y)\,\bmod \,{m_0}(y)$. Inside adversaries need to use $\omega (x,y)$ to recover the secret $s(x,y) = \theta (x,y)\bmod \,{m_0}(x)$.

However, $\omega (x,y)$ satisfies $\omega (x,y) = \theta (x,y)\,\bmod \,\prod \limits _{i = 1}^{t - 1} {{m_i}(x)}$. Then they have $\theta (x,y) = \omega (x,y) + k(x,y) \cdot \prod \limits _{i = 1}^{t - 1} {{m_i}(x)}$, where ${\deg _x}(k(x,y)) = {\deg _y}(k(x,y)) = d - 1$. From the view of information entropy, let H(s) represents the information entropy of the secret and $H(s|\{ {s_1},{s_2}, \ldots ,{s_{t - 1}}\}$ represents the information entropy of knowing $t-1$ shareholders’ shares to recover the secret. Since ${\deg _x}(k(x,y)) = {\deg _x}(s(x,y)) = d - 1$ and ${\deg _y}(k(x,y)) = {\deg _y}(s(x,y)) = d - 1$, then $H(s) = H(s|\{ {s_1},{s_2}, \ldots ,{s_{t - 1}}\} ) = d{\log _2}2p$. Thus, $t-1$ inside adversaries cannot get any information about the secret.

Lemma 7

Given a randomized component ${RC_i}(x,y)$, it is impossible to derive the share ${s_i}(x,y)$.

Proof

The randomized component ${RC_i}(x,y) = {g_i}(x,y) + {k_i}(x,y)$, where ${g_i}(x,y) = {s_i}(x,y){M_i}(x){M'_i}(x)$ and ${k_i}(x,y)$ is generated by s2-box transmission. s2-box breaks the linear relationship between ${s_i}(x,y)$ and ${k_i}(x,y)$ and makes the transformed bivariate polynomial ${k_i}(x,y)$ distributed uniformly over ${F_p}$.

On account of Lemma 6, the share ${s_i}(x,y)$ is uniformly distributed over ${F_p}$ and ${\deg _x}({s_i}(x,y)) = {\deg _y}({s_i}(x,y)) = d - 1$, the probability of inferring ${s_i}(x,y)$ is ${d^{2p}}$. Since ${\deg _x}({k_i}(x,y)) = {\deg _y}({k_i}(x,y)) = d - 1$, the probability of deriving ${s_i}(x,y)$ from ${RC_i}(x,y)$ by inferring ${k_i}(x,y)$ also equals to ${d^{2p}}$. Thus, given a randomized component ${RC_i}(x,y)$, it is impossible to derive the share ${s_i}(x,y)$.

Theorem 6

The proposed scheme can resist attack from outside adversary. In detail, when $h(h \ge t)$ participants try to recover the secret, a participant who does not own a valid share cannot get any information about secret and share by collecting $h-1$ randomized components from other honest participants.

Proof

Suppose that the adversary is the hth participant who releases his component last, he can collect $h-1$ randomized component from other participants.

• 1. First, we prove the outside adversary cannot get any information about the secret. After collecting $h-1$ randomized components, the secret $s(x,y) = (\sum \limits _{i = 1}^{h - 1} {R{C_i}(x,y)} + R{C_h}(x,y))\bmod \,M(x)\,\bmod \,{m_0}(x)$, where ${\deg _x}(s(x,y)) = {\deg _y}(s(x,y)) = d - 1$. However, each participant uses ${k_i}(x,y)$ to cover up the original component and ${RC_h}(x,y) = {g_h}(x,y) + {k_h}(x,y)$, where ${RC_h}(x,y)$ is generated by ${s_{h,1}}(x,y)$ and ${s_{h,2}}(x,y)$. If the outside adversary want to recover the secret, he has to use these two shares to calculate ${RC_h}(x,y)$ and eliminate other participants’ disrupted information added. The shares are generated by ${s_{h,1}}(x,y) = F(x,y)\bmod {m_h}(x)$ and ${s_{h,2}}(x,y) = F(x,y)\bmod {m_h}(y)$, where both the degree of shares in x and y at least equals to the secret s(x, y). From the view of information entropy, let H(s) represents the information entropy of the secret and $H(s|\{ R{C_1},R{C_2}, \ldots R{C_{h - 1}}\} )$ represents the information entropy of knowing $h-1$ shareholders’ randomized components to recover the secret, then there is $H(s) = H(s|\{ R{C_1},R{C_2}, \ldots R{C_{h - 1}}\} ) = d{\log _2}2p$. As a result, the adversary cannot get any information about the secret by collecting $h-1$ randomized components.

• 2. Next, we prove the outside adversary cannot get any information about the share. On account of Lemma 7, it is impossible for outside adversary to derive the original share ${s_i}(x,y)$ from the randomized component ${RC_i}(x,y)$.

  Then we discuss whether the outside adversary can obtain the share through linear subspace attack and lattice attack. s-boxes are used to disrupt the linear relationship among randomized components. In randomized component ${RC_i}(x,y)$, ${k_i}(x,y)$ can be regarded as the key K to protect the message ${s_i}(x,y)$. Both ${k_i}(x,y)$ and ${s_i}(x,y)$ are polynomials of degree $d-1$ in x and y over ${F_p}$, which can guarantee $|K| = |M|$. Our scheme satisfies perfect secrecy and can resist linear subspace attack and lattice attack.

Theorem 7

Our proposed scheme can resist passive attack with each pair of shareholders generating the same secure channel key.

Proof

On account of Lemma 4, for any pairwise shareholders $U_i$ and $U_j$ with ${m_i}(x) > {m_j}(x)$, we have ${k_{i,j}}(x,y) = {k_{j,i}}(x,y)$. Since ${k'_{i,j}} = \sum \limits _{i = 0,j = 0}^{d - 1} {{e_{i,j}}} {} \,\bmod \,{} p$, where ${e_{i,j}}(0 \le i,j \le d - 1)$ are parameters of coefficient matrix E in ${k'_{i,j}}(x,y)$, then ${k'_{i,j}} = {k'_{j,i}}$ and ${s_1}({k'_{j,i}}) = {s_1}({k'_{i,j}})$. As a result, each pair of shareholders can generate the same secure channel key.

If a passive adversary want to compute the key ${s_1}({k'_{j,i}})$, he needs to know at least one of the shares ${s_{i,1}}(x,y)$. Since ${\deg _x}({s_{i,1}}(x,y)) = {\deg _x}(s(x,y))$ and ${\deg _y}({s_{i,1}}(x,y)) > {\deg _y}(s(x,y))$, the probability of guessing key is larger than guessing the secret. Our proposed scheme can resist passive attack.

6 Properties and Comparisons

We analyze the properties of our schemes in three aspects: active attack, passive attack and information rate. The active attack can be divided into inside adversary attack and outside adversary attack these two parts. Linear subspace attack and lattice attack are two attack strategies of outside adversary.

6.1 Properties

Our first secure secret reconstruction scheme can resist both the inside and outside adversary attack in insecure networks. The random element ${r_i}(x)$ added in the component can prevent the outside adversary from obtaining the secret and share by collecting randomized components from other honest participants. Since ${r_i}(x)$ is randomly selected, there is no linear relationship among randomized components. As a result, our first scheme can resist linear subspace attack. In addition, the degree of ${r_i}(x)$ at least equals to the share, which can guarantee perfect secrecy and prevent lattice attack. This scheme is based on the assumption that the secure channel is well established to resist passive attack.

The second secure secret reconstruction scheme uses bivariate polynomial, which can generate both the share and randomized component. This scheme can also prevent the inside and outside adversary from recovering secret illegally. Particularly, it establishes the secure channel for each pairwise shareholders before secret reconstruction and can resist passive attack in insecure networks. Each shareholder owns two shares, where the additional share is used for pairwise key and randomized component generation. s-boxes are used to disrupt the linear relationship and resist linear subspace attack. Then, because both share for secret reconstruction and random element are bivariate polynomials with the same degree in x and y, this scheme can protect the share in perfect secrecy and resist lattice attack.

Next, we analyze our schemes’ information rate according to Definition 4 and show their properties in Table 1.

Table 1. Properties of our schemes.

In the first scheme, both the secret and share are polynomials with degree $d-1$ over ${F_p}$. The information rate of our first scheme can be computed as:

$$\begin{aligned} \rho = \frac{{{{\log }_2}|s|}}{{{{\max }_{{s_i} \in S}}({{\log }_2}|{s_i}|)}} = \frac{{{{\log }_2}{p^d}}}{{{{\log }_2}{p^d}}} = 1. \end{aligned}$$

In the second scheme, the secret is a bivariate polynomial with degree $d-1$ in both x and y over ${F_p}$. Each shareholder owns two shares, where ${\deg _x}({s_{i,1}}(x,y)) = {\deg _y}({s_{i,2}}(x,y)) = d - 1$ and ${\deg _y}({s_{i,1}}(x,y)) = {\deg _x}({s_{i,2}}(x,y)) = dt - 1$. The information rate of our second scheme can be computed as:

$$\begin{aligned} \rho = \frac{{{{\log }_2}|s|}}{{{{\max }_{{s_i} \in S}}({{\log }_2}|{s_i}|)}} = \frac{{{{\log }_2}{p^{{d^2}}}}}{{{{\log }_2}{p^{{d^2}t}}}} = \frac{1}{t}. \end{aligned}$$

The information rate of our first scheme is 1, while the second scheme is $\frac{1}{t}$. Thus, our first scheme is perfect and ideal. The lower information rate in the second scheme is the price of establishing secure channel and generating randomized component effectively by distributing more information to each shareholder.

6.2 Comparisons

We compare our schemes with other secure secret reconstruction schemes [9, 11, 17,18,19] and the result is shown in Table 2.

Since information rate is the size ratio of secret to share, which can denote the efficiency of a shareholder sharing a secret, we mainly use information rate to describe the scheme performance bellow. For a secure secret sharing scheme, the information rate is generally not more than 1. The higher information rate is, the more efficiently the scheme works.

Table 2. Comparison of different SSR schemes.

From the table, we know that scheme [17, 19] and our schemes can resist linear subspace attack, but scheme [19] is vulnerable to lattice attack. Only scheme [11] and our scheme 2 don’t need to establish secure channel in advance and can resist passive attack in insecure networks. The information rate of scheme [9] and our first scheme is 1. Although the information rate of our second scheme is $\frac{1}{t}$, it can resist all attacks we analyzed in insecure networks.

7 Conclusion

In this paper, we first point two common attacks: active and passive attack on secret sharing in insecure networks. Then we introduce secure secret reconstruction scheme, which can prevent the participant who does not own a valid share from obtaining the secret and share by collecting other participants’ components. We also analyze the possible attacks on Harn and Miao proposed SSR scheme. Using linear subspace cryptanalysis, adversary can obtain the secret by analyzing the relationship among sending components. Due to the adding randomized integer cannot protect the share in an information theoretically secure manner, Miao scheme is vulnerable to lattice attack.

In order to solve these problems, we describe the model and security goals of our secure secret reconstruction scheme in insecure networks. Based on the same idea of randomized component in Miao scheme, we propose two novel secure secret reconstruction schemes. The first scheme is based on Chinese Remainder Theorem for polynomial. The adding random element in this scheme breaks the relationship among components and can protect the secrecy of share. Furthermore, this scheme is perfect and ideal. Then we also propose an improved secure secret reconstruction scheme based on bivariate polynomial. The bivariate polynomial is used for share and randomized component generation. Specifically, this scheme can resist passive attack and establish the secure channel for each pairwise shareholders in advance. Each shareholder owns two shares, where the additional share can generate the secure channel key and randomized component. s-boxes disrupt the linear relationship and randomized component can enable our scheme to satisfy perfect secrecy. Both of our schemes are resistance to linear subspace attack and lattice attack. The inside and outside adversary in insecure networks cannot get any information about the secret and share in our two schemes.