Abstract
\(\omega \)-regular energy games are two-player \(\omega \)-regular games augmented with a requirement to avoid the exhaustion of a finite resource, e.g., battery or disk space. \(\omega \)-regular energy games can be reduced to \(\omega \)-regular games by encoding the energy level into the state space. As this approach blows up the state space, it performs poorly. Moreover, it is highly affected by the chosen energy bound denoting the resource’s capacity. In this work, we present an alternative approach for solving \(\omega \)-regular energy games, with two main advantages. First, our approach is efficient: it avoids the encoding of the energy level within the state space, and its performance is independent of the engineer’s choice of the energy bound. Second, our approach is defined at the logic level, not at the algorithmic level, and thus allows solving \(\omega \)-regular energy games by seamless reuse of existing symbolic fixed-point algorithms for ordinary \(\omega \)-regular games. We base our work on the introduction of energy \(\mu \)-calculus, a multi-valued extension of game \(\mu \)-calculus. We have implemented our ideas and evaluated them. The empirical evaluation provides evidence for the efficiency of our work.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Energy games model a requirement to avoid the exhaustion of an initially available resource, e.g., disk space or battery capacity, and they have been studied extensively in the context of verification and synthesis, e.g., [11, 19,20,21]. They are formalized as weighted two-player turn-based games with the quantitative objective to keep the energy level, the accumulated sum of an initial credit and weights of transitions traversed thus far, non-negative in each prefix of a play. As such, they induce a decision problem that checks for the existence of a finite initial credit sufficient for winning, and an optimization problem for the minimum initial credit. They may be viewed as safety games with an additional quantitative objective. Nevertheless, they have also been generalized to \(\omega \)-regular games with energy objectives [20, 21], which are the focus of our work.
The work [11] has introduced an upper bound c that specifies the maximal energy level allowed to be accumulated throughout a play. Intuitively, c denotes the capacity of the relevant resource. Given such finite bound c, \(\omega \)-regular energy games can be reduced to ordinary \(\omega \)-regular games via a naive encoding: one may introduce new system variables that encode the energy level, and add the requirement that these variables always represent a non-negative value. A major problem with this naive encoding approach is that it blows up the state space by a factor of c, even when it is not necessary. For illustration, assume the engineer sets an upper bound c, but the tightest bound sufficient for winning is \(c_0<c\). The naive encoding will still consider \(\log (c)\) additional Boolean variables, although it is not required. Note that this scenario is realistic as it is difficult to estimate the tightest energy bound sufficient for winning.
In this work, we present an alternative approach for solving \(\omega \) -regular energy games, with two main advantages. First, our approach is efficient: it avoids the encoding of the energy level within the state space, and its performance is independent of the engineer’s choice of the capacity bound c . Second, our approach is defined at the logic level, not at the algorithmic level, and thus allows to solve \(\omega \) -regular energy games by seamless reuse of existing symbolic fixed-point algorithms for ordinary \(\omega \) -regular games.
Specifically, we introduce energy \(\mu \)-calculus, a multi-valued extension of game \(\mu \)-calculus, \(\mu \)-calculus over symbolic game structures [10, 23, 35]. Game \(\mu \)-calculus extends propositional logic with modal operators and least and greatest fixed-point operators. For every \(\omega \)-regular condition \(\varphi \), there exists a game \(\mu \)-calculus formula that defines a symbolic fixed-point algorithm for computing the set of states that win \(\varphi \) [4].
Importantly, the standard game \(\mu \)-calculus and our new energy \(\mu \)-calculus share the same syntax, but they differ in their semantics. While a game \(\mu \)-calculus formula characterizes a set of states, an energy \(\mu \)-calculus formula, interpreted with an energy bound \(c\in \mathbb N\), returns a function that maps states to \(\{0,\dots ,c\}\cup \{+\infty \}\). Intuitively, whereas a game \(\mu \)-calculus formula computes the set of winning states, an energy \(\mu \)-calculus formula computes a function that maps a state s to the minimal initial credit with which the system can win from s, while keeping the energy level non-negative, and further maps s to \(+\infty \) if no such initial credit exists.
Remark 1
Although we focus on bounded energy games, our approach can be used to solve \(\omega \)-regular energy games with no bound on the accumulated energy level (i.e., \(c=+\infty \)). In the technical report [7], we show that every \(\omega \)-regular energy game admits a sufficient finite bound \(c_f\in \mathbb N\) that can be calculated from the game parameters. That is, a bound \(c_f\) for which, if the system can win from state s with a bound \(c=+\infty \), then it can also win with the bound \(c = c_f\), and with the same initial credit. This fact is independent of the use of energy \(\mu \)-calculus.
We have implemented and integrated both methods, naive encoding and energy \(\mu \)-calculus, into Spectra, a specification language and GR(1) synthesis environment [1, 39]. GR(1) [10] is a popular assume-guarantee winning condition that, roughly speaking, expresses the schematic requirement: “if assertions \(a_1,\dots ,a_m\) hold infinitely often, then assertions \(g_1,\dots ,g_n\) must hold infinitely often as well”. As GR(1) subsumes other important \(\omega \)-regular winning conditions, specifically safety, reachability, Büchi, and generalized Büchi [29], our implementation allows us to empirically evaluate the efficiency of our approach over different \(\omega \)-regular energy games. Our implementation of naive encoding employs the standard Binary Decision Diagram [16] (BDD) based solver of Spectra. The efficient implementation of energy \(\mu \)-calculus employs Algebraic Decision Diagrams (ADDs) [8, 27]. While BDDs symbolically represent assertions and thus sets of states, ADDs extend BDDs to symbolically represent functions that map states to values (in our case, to energy levels). Both are implemented in the CUDD library [45].
The remainder of the paper is organized as follows. In Sect. 2 we present an example. In Sect. 3 we provide notations and relevant background. In Sect. 4 we present the semantics of energy \(\mu \)-calculus and our main theorem. In Sect. 5 we present an empirical evaluation of our approach. Related work is discussed in Sect. 6 and Sect. 7 concludes. Proofs for all claims and extended discussions appear in a technical report [7].
2 An Illustrative Example
To demonstrate the differences between our approach and naive encoding, we consider an energy augmented variant of the obstacle evasion specification, a popular benchmark from the literature inspired by robotic mission planning [22, 28, 40]. Consider a single cell sized robot (the system) and a \(2\times 2\) cells sized obstacle (the environment), both moving on a \(10\times 10\) grid. The robot is smaller and more agile; it moves twice upon each step of the obstacle. The obstacle chases the robot (always tries to get closer to it), and the robot must evade the obstacle so that collision will never occur.
Importantly, in our energy augmented variant, the robot has a c-capacity battery. A charger placed in cell (1, 1) can charge the battery by m energy units, and each move of the robot consumes k energy units. Thus, in addition to satisfying the different winning conditions we list below, the robot should behave such that its battery is never empty, i.e., it keeps its energy non-negative at all times. See an illustration in Fig. 1, and an excerpt of a Spectra specification in Listing 1. The full specification is available from [2].
The above defines legal transitions for the players and thus defines a game structure and a safety game. That is, a game in which as long as the environment takes valid transitions, the system must take valid transitions as well. Hence, the winning condition for a safety game is merely (1)  . We further consider the following \(\omega \)-regular winning conditions that we formulate in Linear Temporal Logic [43] (LTL).
. We further consider the following \(\omega \)-regular winning conditions that we formulate in Linear Temporal Logic [43] (LTL).
-
(2)
 , where a is the assertion: the robot is at cell (10, 10). In words, the robot must visit cell (10, 10).
, where a is the assertion: the robot is at cell (10, 10). In words, the robot must visit cell (10, 10). -
(3)
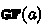 where a is the assertion: the robot is at cell (10, 10). In words, the robot must visit cell (10, 10) infinitely often.
where a is the assertion: the robot is at cell (10, 10). In words, the robot must visit cell (10, 10) infinitely often. -
(4)
 where \(a_i\) is the assertion: the robot is at the i-th corner. In words, the robot must visit all grid corners infinitely often.
where \(a_i\) is the assertion: the robot is at the i-th corner. In words, the robot must visit all grid corners infinitely often. -
(5)
 where b is the assertion: the obstacle is at most 4 cells away from the robot, and each \(a_i\) is the assertion: the robot is at the i-th corner. In words, if, infinitely often, the obstacle is close to the robot (4 cells or less), then the robot must visit all corners infinitely often.
where b is the assertion: the obstacle is at most 4 cells away from the robot, and each \(a_i\) is the assertion: the robot is at the i-th corner. In words, if, infinitely often, the obstacle is close to the robot (4 cells or less), then the robot must visit all corners infinitely often.

Formulas (1)–(5) are instances of safety, reachability, Büchi, generalized Büchi [29], and GR(1) [10] winning conditions, respectively, all of which are examples of \(\omega \)-regular winning conditions.
Recall that we seek an efficient technique for solving \(\omega \)-regular energy games that enables the reuse of existing algorithms. We turn to discuss how our approach addresses these two goals, using the energy-augmented obstacle evasion problem.
Efficiency of Energy \(\boldsymbol{\mu }\)-Calculus. In contrast to naive encoding, the algorithm that an energy \(\mu \)-calculus formula prescribes considers only the intermediate energy values revealed during the computation. In particular, this implies that we avoid the encoding of the energy levels within the state space. For illustration, with energy \(\mu \)-calculus, each of the energy-augmented obstacle evasion specifications employs a total of 17 variables, excluding reachability (winning condition (2)) that employs 18 variables (all specifications are available from [2]). However, the naive encoding approach adds \(\lceil \log c\rceil \) variables to the specification, on top of these 17–18 variables. Note that with our approach, the number of variables is not dependent on the chosen bound c.
Furthermore, the described feature reduces the size of the data structures the solver employs. For illustration, assume that when solving the reachability game, some fixed-point iteration of the algorithm constructs an ADD that maps a state s to the energy value e. This means that, so far, the algorithm discovered that e energy units are sufficient for reaching cell (10, 10) from s (ensuing iterations might improve this value). The corresponding iteration of a naive-encoding-based solver will create a BDD that accepts all valuations \((s,e')\), \(e'\ge e\). Hence, naive encoding creates rather large BDDs that depend on the energy bound, which is costly. In contrast, the size of the ADD we use depends on the size of the range of the function it represents, i.e., we only consider the actual energy values revealed during the computation.

Reuse of Existing Algorithms. In Sect. 4, we will prove that if a game \(\mu \)-calculus formula \(\psi \) solves games with an \(\omega \)-regular winning condition \(\varphi \), then when interpreted according to the energy \(\mu \)-calculus semantics, \(\psi \) computes a function that solves the minimum credit problem for the energy augmented game. That is, a function that maps a state s to the minimal initial credit with which the system wins from s.
To demonstrate this property, consider the Büchi condition  (winning condition (3) above). The following game \(\mu \)-calculus formula solves Büchi games with target states a:
(winning condition (3) above). The following game \(\mu \)-calculus formula solves Büchi games with target states a:

That is,  computes the set of all states from which the system can enforce infinitely many visits of the robot to cell (10, 10).
computes the set of all states from which the system can enforce infinitely many visits of the robot to cell (10, 10).
Relying on our main theorem, we replace each occurrence of the modal operator
 in Eq. 1 with the new operator
in Eq. 1 with the new operator
 , and obtain the following energy \(\mu \)-calculus formula that solves Büchi-energy games with target states a:
, and obtain the following energy \(\mu \)-calculus formula that solves Büchi-energy games with target states a:

That is, Eq. 2 defines the energy function that maps each state to the minimal initial credit sufficient for the system to reach cell (10, 10) infinitely often, while keeping the energy level non-negative.
Most importantly, the above formulas induce algorithms. Algorithm 1 is a symbolic fixed-point algorithm that implements Eq. 1 according to the game \(\mu \)-calculus’ semantics following [10]. Likewise, Algorithm 2 is a symbolic fixed-point algorithm that implements Eq. 2 according to the energy \(\mu \)-calculus’ semantics. We see that energy \(\mu \)-calculus allows the seamless reuse of existing game \(\mu \)-calculus formulas and thus automatically transforms the fixed-point algorithms they prescribe into algorithms that take also the energy constraints into account. Indeed, our implementation, in Spectra, takes advantage of this seamless reuse. We use the same template code for both implementations.
3 Preliminaries
We provide relevant and concise definitions that are sufficient for the readability of the paper. Extended discussions and further definitions that are needed for the proof of our main theorem are given in the technical report [7].
For a set of Boolean variables \(\mathcal V\), a state \(s\in 2^\mathcal V\), is a truth assignment to \(\mathcal V\), an assertion \(\phi \) is a propositional formula over \(\mathcal V\), \(s\models \phi \) denotes that s satisfies \(\phi \), and \(\mathcal V'\) denotes the set \(\{v'\mid v\in \mathcal V\}\) of primed variables. We denote by \(p(s)\in 2^\mathcal {V'}\) the primed version of the state \(s\in {2^\mathcal {V}}\), obtained by replacing each \(v\in {s}\) with \(v'\in \mathcal {V}'\). For \(\mathcal V=\bigcup _{i=1}^k\mathcal V_i\) and truth assignments \(s_i\in 2^{\mathcal V_i}\), we use \((s_1,\ldots ,s_k)\) as an abbreviation for \(s_1\cup {\ldots }\cup {s_k}\). Thus, we may replace expressions, e.g., \(s\in 2^\mathcal V\), \(s\models \varphi \), p(s), and f(s) with \((s_1,\dots s_k)\in 2^\mathcal V\), \((s_1,\dots ,s_k)\models \varphi \), \(p(s_1,\dots ,s_k)\), and \(f(s_1,\dots ,s_k)\), respectively. We denote by \(s|_{\mathcal {Z}}\) the projection of \(s\in {2^{\mathcal {V}}}\) to \(\mathcal {Z}\subseteq {\mathcal {V}}\), i.e., \(s|_{\mathcal {Z}}:= s \cap \mathcal {Z}\).
Games, Game Structures, and Strategies. We consider an infinite game played between an environment player (\( env \)) and a system player (\( sys \)) on a finite weighted directed graph as they move along its transitions. In each round of the game, the environment plays first by choosing a valid input, and the system plays second by choosing a valid output. Each such step consumes or reclaims energy, according to the weight function. The goal of the system is to satisfy the winning condition while keeping the energy level non-negative, regardless of the actions of the environment.
Formally, an energy game is symbolically represented by a weighted game structure (WGS) \(G^w\), that extends a game structure (GS) G [10, 42] with a weight function \(w^s\). It consists of the following components:
-
\(\mathcal {V} = \{v_1, \ldots , v_n\}\): A finite set of Boolean variables.
-
\(\mathcal {X}\subseteq {\mathcal {V}}\): A set of input variables controlled by the environment player (\( env \)).
-
\(\mathcal {Y}={\mathcal {V}\setminus {\mathcal {X}}}\): A set of output variables controlled by the system player (\( sys \)).
-
\(\rho ^e\): An assertion over \(\mathcal {V}\cup \mathcal {X'}\) that defines the environment’s transitions. The environment uses \(\rho ^e\) to relate a state over \(\mathcal {V}\) to possible next inputs over \(\mathcal X'\).
-
\(\rho ^s\): An assertion over \(\mathcal {V}\cup \mathcal V' = \mathcal {V}\cup \mathcal {X'}\cup \mathcal {Y'}\) that defines the system’s transitions. The system uses \(\rho ^s\) to relate a state over \(\mathcal {V}\) and an input over \(\mathcal {X}'\) to possible next outputs over \(\mathcal Y'\).
-
\(\varphi \): The \(\omega \)-regular winning condition of the system.
-
\(w^s\): a partial weight function, symbolically represented as pairs of the form \((\rho ,a)\) where \(\rho \) is an assertion over \(\mathcal V\cup \mathcal V'\), and \(a\in \mathbb {Z}\).
A state t is a successor of s if \((s, p(t)) \models \rho ^e \wedge \rho ^s\). The rounds of a game on \(G^w\) form a sequence of states \(\sigma =s_0s_1\ldots \) called a play, which satisfies the following conditions: (1) Consecution: for each \(i\ge 0\), \(s_{i+1}\) is a successor of \(s_i\). (2) Maximality: if \(\sigma \) is finite, then either it ends with a deadlock for the environment: \(\sigma =s_0\ldots s_k\), and there is no input value \(s_{\mathcal {X}}\in {2^\mathcal {X}}\) such that \((s_k, p(s_{\mathcal {X}}))\models {\rho ^e}\), or it ends with a deadlock for the system: \(\sigma =s_0\ldots s_k s_{\mathcal {X}}\) where \(s_{\mathcal {X}}\in {2^\mathcal {X}}\), \((s_k, p(s_{\mathcal {X}}))\models \rho ^e\), and there is no output \(s_{\mathcal {Y}}\in {2^\mathcal {Y}}\) such that \((s_k, p(s_{\mathcal {X}}), p(s_{\mathcal {Y}}))\models {\rho ^s}\). A play \(\sigma \) wins w.r.t. \(\varphi \) if it ends in an environment deadlock, or it is infinite and satisfies \(\varphi \).
A strategy for the system player is a function \(g_{{\scriptstyle sys }}: (2^\mathcal {V})^{+}\times 2^{\mathcal {X}}\rightarrow 2^{\mathcal {Y}}\). Roughly speaking, the system employs a strategy \(g_{{\scriptstyle sys }}\) to repeatedly choose outputs given the sequence of states traversed so far, and a new input. A strategy \(g_{\scriptstyle sys }\) wins from state s w.r.t. energy bound c if for any play \(\sigma \) from s, consistent with the strategy, (1) \(\sigma \) wins for the system w.r.t. \(\varphi \) and (2) the energy level remains non-negative during the play, given that whenever it exceeds the upper bound c, it is truncated to c. For a WGS, \(G^w\), we denote by \(W^c_{\scriptstyle sys }\) the set of all states s such that there exists a strategy \(g_{\scriptstyle sys }\) that wins from s. We omit c and write \(W_{\scriptstyle sys }\) in case of a GS G.
Game \(\boldsymbol{\mu }\)-Calculus over Game Structures. We consider the logic of the game \(\mu \)-calculus over GSs [10] below.
Definition 1
(game \(\mu \)-calculus: syntax). Let \(\mathcal {V}\) be a set of Boolean variables, and let \( Var = \{X, Y, \ldots \}\) be a set of relational variables. The formulas of game \(\mu \)-calculus (in positive form) are built as follows:

where \(v\in \mathcal {V}\), \(X\in Var \), and \(\mu \) and \(\nu \) denote the least and greatest fixed-point operators, respectively.
We denote by \(\mathcal {L}_{\mu }\) the set of all formulas generated by the grammar of Definition 1. We further denote by \({\mathcal {L}_{\mu }^{{\scriptstyle sys }}}\) (resp. \({\mathcal {L}_{\mu }^{{\scriptstyle env }}}\)) the subset of \(\mathcal {L}_{\mu }\) that consists of all formulas in which the modal operator
 (resp.
(resp.
 ) does not occur. We will refer to \({\mathcal {L}_{\mu }^{{\scriptstyle sys }}}\) (resp. \({\mathcal {L}_{\mu }^{{\scriptstyle env }}}\)) formulas as \( sys \text {-}\mu \) (resp. \( env \text {-}\mu \)) formulas.
) does not occur. We will refer to \({\mathcal {L}_{\mu }^{{\scriptstyle sys }}}\) (resp. \({\mathcal {L}_{\mu }^{{\scriptstyle env }}}\)) formulas as \( sys \text {-}\mu \) (resp. \( env \text {-}\mu \)) formulas.
Given a game structure \(G = \langle \mathcal {V}, \mathcal {X}, \mathcal {Y}, \rho ^e,\rho ^s, \varphi \rangle \) and a valuation \(\mathcal {E}: Var \rightarrow (2^{\mathcal {V}} \rightarrow \{0,1\})\), the semantics of a game \(\mu \)-calculus formula \(\psi \) with variables from \(\mathcal V\), \([\![\psi ]\!]^{G}_{\mathcal {E}}\),Footnote 1 is a subset of \(2^\mathcal V\). Intuitively,
 (resp.
(resp.
 ) is the set of states from which the system (resp. environment) can force reaching a state in \(\psi \)’s semantics in a single step. \(\mu \) and \(\nu \) are the least and greatest fixed-points, respectively. For a complete definition of the game \(\mu \)-calculus semantics see, e.g., [10].
) is the set of states from which the system (resp. environment) can force reaching a state in \(\psi \)’s semantics in a single step. \(\mu \) and \(\nu \) are the least and greatest fixed-points, respectively. For a complete definition of the game \(\mu \)-calculus semantics see, e.g., [10].
We say that a (closed) game \(\mu \)-calculus formula \(\psi \) matches an \(\omega \)-regular winning condition \(\varphi \), if for every GS \(G= \langle \mathcal {V},\mathcal {X}, \mathcal {Y}, \rho ^e,\rho ^s, \varphi \rangle \), \([\![{\psi }]\!]^{G}=W_{\scriptstyle sys }\). That is, \(\psi \) computes the set of states from which the system has a winning strategy. De Alfaro et al. [4] have shown that every \(\omega \)-regular condition \(\varphi \) has a matching formula \(\psi \in \mathcal {L}_{\mu }^{{\scriptstyle sys }}\).
BDDs and ADDs. A Binary Decision Diagram (BDD) [16] is a DAG representation of an assertion. The non-leaves nodes of a BDD are labeled with variable names, and its edges and leaves are labeled with  . A BDD B represents an assertion \(\rho \) if B’s accepting branches (i.e. branches that end with a
. A BDD B represents an assertion \(\rho \) if B’s accepting branches (i.e. branches that end with a  -labeled leaf) correspond to the satisfying assignments of \(\rho \). BDDs allow applying Boolean operators over assertions efficiently, and further satisfaction queries [17].
-labeled leaf) correspond to the satisfying assignments of \(\rho \). BDDs allow applying Boolean operators over assertions efficiently, and further satisfaction queries [17].
An Algebraic Decision Diagram (ADD) [8, 27] is a DAG representation of a function that maps states to values. ADDs differ from BDDs in that their leaves are labeled with values from some domain (\(\mathbb Z\), in our case).
Our implementation of energy \(\mu \)-calculus relies on the use of ADDs.
4 Energy \(\mu \)-Calculus over Weighted Game Structures
We are now ready to introduce energy \(\mu \)-calculus, the underlying novel logic behind our efficient solution for \(\omega \)-regular energy games. Energy \(\mu \)-calculus is a multi-valued extension of the modal game \(\mu \)-calculus over GSs [10, 23]. We define its syntax and semantics, interpreted w.r.t. a finite upper bound c, and prove our main theorem: if \(\psi \) matches an \(\omega \)-regular condition \(\varphi \), then with the energy \(\mu \)-calculus semantics, \(\psi \) solves energy \(\varphi \)-games.
Syntax of an Energy \(\boldsymbol{\mu }\)-Calculus Formula. Let \(\mathcal {L}_{e\mu }\) denote the set of formulas generated by the following grammar:
Definition 2
(Energy \(\mu \)-calculus: syntax). Let \(\mathcal {V}\) be a set of Boolean variables, and let \( Var = \{X, Y, \ldots \}\) be a set of relational variables. The syntax of energy \(\mu \)-calculus (in positive form) is as follows:

where \(v \in \mathcal V\) and \(X \in Var \).
We denote by \({\mathcal {L}_{e\mu }^{{\scriptstyle sys }}}\) (resp. \({\mathcal {L}_{e\mu }^{{\scriptstyle env }}}\)) the subset of \(\mathcal {L}_{e\mu }\) that consists of all formulas in which
 (resp.
(resp.
 ) does not occur. Further, let
) does not occur. Further, let  denote the energy \(\mu \)-calculus formula obtained from \(\psi \in \mathcal {L}_{\mu }\) by replacing all occurrences of
denote the energy \(\mu \)-calculus formula obtained from \(\psi \in \mathcal {L}_{\mu }\) by replacing all occurrences of
 and
and
 with
with
 and
and
 , respectively. Here, we focus on \({\mathcal {L}_{e\mu }^{{\scriptstyle sys }}}\) formulas as those solve energy \(\omega \)-regular games for the system.Footnote 2
, respectively. Here, we focus on \({\mathcal {L}_{e\mu }^{{\scriptstyle sys }}}\) formulas as those solve energy \(\omega \)-regular games for the system.Footnote 2
\(\boldsymbol{{\mathcal {L}_{e\mu }^{{\scriptstyle sys }}}}\) Semantics Overview. We now define the semantics of a formula  .
.  is valuated w.r.t. a WGS \(G^{w} = \langle \mathcal {V},\mathcal {X}, \mathcal {Y}, \rho ^e,\rho ^s, \varphi , w^s\rangle \), and a finite upper bound \(c \in \mathbb {N}\). We write \(G^w(c)\) as a shorthand for the pair \(\langle G^w,c \rangle \). The semantics
is valuated w.r.t. a WGS \(G^{w} = \langle \mathcal {V},\mathcal {X}, \mathcal {Y}, \rho ^e,\rho ^s, \varphi , w^s\rangle \), and a finite upper bound \(c \in \mathbb {N}\). We write \(G^w(c)\) as a shorthand for the pair \(\langle G^w,c \rangle \). The semantics  is an energy function that maps states of \(G^w\) to initial amounts of credit.Footnote 3 Hence, the range of the function
is an energy function that maps states of \(G^w\) to initial amounts of credit.Footnote 3 Hence, the range of the function  is the set of energy credits \( E(c) := [0,c] \cup \{+\infty \}\), and thus
is the set of energy credits \( E(c) := [0,c] \cup \{+\infty \}\), and thus  is an element of the set of energy functions \( EF(c) := E(c) ^{2^{\mathcal {V}}}\).
is an element of the set of energy functions \( EF(c) := E(c) ^{2^{\mathcal {V}}}\).
To define the semantics  in a precise manner, we need to define the semantics of the meet \(\wedge \) and join \(\vee \) operators, and of the energy controllable predecessor operator
in a precise manner, we need to define the semantics of the meet \(\wedge \) and join \(\vee \) operators, and of the energy controllable predecessor operator
 . We start with the meet and join operators.
. We start with the meet and join operators.
Meet \(\boldsymbol{\wedge }\) and join \(\boldsymbol{\vee }\) Semantics. The semantics of these operators is induced by a partial ordering of EF(c), the set of energy functions, and a linear ordering of the set of c-bounded energy credits \(E(c)=[0,c]\cup \{+\infty \}\). For \(x,y\in E(c)\), we write \(x\preceq y\) if \(y\le x\) (equivalently, \(y=\min \{x,y\}\)). Although seemingly unnatural, this design choice is not only technically justified (as we shall explain later), but also intuitive, considering our purposes, due to the next reasoning.
We study sufficient initial credits from the system’s perspective. Hence, the \(\le \)-smaller element y is preferable to the \(\le \)-larger element x, and thus y is declared to be \(\preceq \)-larger. In particular, \(+\infty \) is the \(\preceq \)-minimal (worst) element from the system’s perspective, as it indicates that no initial credit is sufficient for winning. In summary, \(x\preceq y\) if y is better (i.e. smaller) than x.
The ordering of E(c) transfers to EF(c). We say that \(f\preceq g\) if for every state s, \(f(s)\preceq g(s)\) (iff \(f(s)\ge g(s)\)). As for E(c), this definition matches the intuition that g is better than f if it maps each state to a \(\le \)-smaller credit. In particular, the minimal (worst) element is the function that maps each state to \(+\infty \), denoted \(f_{+\infty }\). This function indicates that the system cannot win from any state, regardless of its initial credit. Likewise, the maximal element is the function \(f_0\) defined by \(\forall s\in 2^\mathcal V(f_0(s)=0)\). Now, the meet \(\wedge \) (resp. join \(\vee \)) of two functions f and g is the maximal (resp. minimal) function that is \(\preceq \)-smaller (resp. \(\preceq \)-larger) than f and g:
To avoid confusion, we clarify that \(\max \) and \(\min \) always relate to the natural ordering \(\le \). For example, \(\max \{1,4\}=4\). We shall use the notations \(\max _{\preceq }\) and \(\min _{\preceq }\) to denote maximal and minimal elements w.r.t. the \(\preceq \)-ordering.
Energy Controllable Predecessor Semantics. We turn to discuss the semantics of the energy controllable predecessor operator
 . Recall that we aim to use \({\mathcal {L}_{e\mu }^{{\scriptstyle sys }}}\) formulas to compute the minimal initial credits with which the system can win w.r.t. the given \(\omega \)-regular winning condition. Hence, given an energy function f,
. Recall that we aim to use \({\mathcal {L}_{e\mu }^{{\scriptstyle sys }}}\) formulas to compute the minimal initial credits with which the system can win w.r.t. the given \(\omega \)-regular winning condition. Hence, given an energy function f,
 is the energy function that maps each state s to the minimal credit with which the system can force reaching a state t, in a single step, with energy level at least f(t). To define
is the energy function that maps each state s to the minimal credit with which the system can force reaching a state t, in a single step, with energy level at least f(t). To define
 properly, first, we analyze the next restricted case. We consider a single possible transition (s, t), and ask: if (s, t) is the ensuing step of the play, what credit is sufficient for the system to take this step and end with energy level at least \(e=f(t)\)? We denote this value by \(\textsf {EC}_c(s,t,e)\), and note that it depends on the weight function \(w^s\), and on the transition relations \(\rho ^e\) and \(\rho ^s\), as follows:
properly, first, we analyze the next restricted case. We consider a single possible transition (s, t), and ask: if (s, t) is the ensuing step of the play, what credit is sufficient for the system to take this step and end with energy level at least \(e=f(t)\)? We denote this value by \(\textsf {EC}_c(s,t,e)\), and note that it depends on the weight function \(w^s\), and on the transition relations \(\rho ^e\) and \(\rho ^s\), as follows:
-
If \((s,p(t|_\mathcal X))\not \models \rho ^e\), the step (s, t) is losing for the environment. Hence, all credits are sufficient and thus \(\textsf {EC}_c( s,t,e)=0\) in this case.
-
If \((s,p(t))\models \rho ^e \wedge \lnot \rho ^s\), the step (s, t) is losing for the system. Hence, all credits are insufficient and thus \(\textsf {EC}_c( s,t,e)=+\infty \) in this case.
-
If \(e=+\infty \), then no finite credit is sufficient. Hence, \(\textsf {EC}_c( s,t,e)=+\infty \) in this case.
-
If \(c+w^s(s,p(t))<e\), then no c-bounded credit is sufficient to achieve energy level at least e. Hence, \(\textsf {EC}_c(s,t,e)=+\infty \) in this case as well.
-
In any other case, any initial credit larger than \(e{-}w^s(s,p(t))\) is sufficient. Hence, in any case not listed above, \(\textsf {EC}_c(s,t,e)=\max \{0,e{-}w^s(s,p(t))\}\).
The above single-step analysis enables us to define
 properly. For a state s, we consider all possible inputs. For each input \(t_\mathcal X\in 2^\mathcal X\), we find the best possible output \(t_\mathcal Y\in 2^\mathcal Y\), i.e. the output that minimizes \(\textsf {EC}_c(s,t=(t_\mathcal X,t_\mathcal Y),f(t))\). Then, intuitively, we define
properly. For a state s, we consider all possible inputs. For each input \(t_\mathcal X\in 2^\mathcal X\), we find the best possible output \(t_\mathcal Y\in 2^\mathcal Y\), i.e. the output that minimizes \(\textsf {EC}_c(s,t=(t_\mathcal X,t_\mathcal Y),f(t))\). Then, intuitively, we define
 to be the value obtained by the best output for the worst input, as we formally define below.
to be the value obtained by the best output for the worst input, as we formally define below.
Definition 3
(Energy controllable predecessor operator). For all WGSs \(\langle G, w^s\rangle \), upper bounds \(c\in \mathbb {N}\), energy functions \(f\in EF(c) \), and states \(s \in 2^{\mathcal {V}}\),
where \(\textsf {EC}_c:2^\mathcal {V}\times 2^\mathcal {V}\times { E(c) }\rightarrow { E(c) }\) and for all \(s,t \in 2^{\mathcal {V}}\), and \(e \in E(c) \),
Example 1
Consider the game structure depicted in Fig. 2, in which the environment player controls variable x and the system controls variable y. Take \(c=10\) and \(g\in EF(c)\) such thatFootnote 4
What is \( ECpre_{{\scriptstyle sys }} (g)(!x,y)\)?
There are two possible inputs, x and !x. For the input x we have:
-
\(\textsf {EC}_c((!x,y),(x,y),g(x,y)=+\infty )=+\infty \).
-
\(\textsf {EC}_c((!x,y),(x,!y),g(x,!y)=1)=4\).
And for the input !x:
-
\(\textsf {EC}_c((!x,y),(!x,y),g(!x,y)=+\infty )=+\infty \).
-
\(\textsf {EC}_c((!x,y),(!x,!y),g(!x,!y)=0)=1\).
Therefore,
The value 4 is obtained as follows: the environment provides the input x, and thus the system can choose between \(+\infty \) and 4. The system chooses the preferable energy amount 4, and correspondingly outputs !y. Consequently, \( ECpre_{{\scriptstyle sys }} (g)(!x,y)=\textsf {EC}_c((!x,y),(x,!y),g(x,!y)=1)=4\).
Semantics of a  formula. We are finally ready to define the semantics of \({\mathcal {L}_{e\mu }^{{\scriptstyle sys }}}\) formulas.
formula. We are finally ready to define the semantics of \({\mathcal {L}_{e\mu }^{{\scriptstyle sys }}}\) formulas.
Definition 4
(\({\mathcal {L}_{e\mu }^{{\scriptstyle sys }}}\): semantics). The semantics  of
of  w.r.t. a WGS \(G^{w} = \langle \mathcal {V},\mathcal {X}, \mathcal {Y}, \rho ^e,\rho ^s, \varphi , w^s\rangle \), a finite upper bound \(c \in \mathbb {N}\), and a valuation \(\mathcal {D}: Var \rightarrow EF(c) \) over \( EF(c) \), is inductively defined as follows:Footnote 5
w.r.t. a WGS \(G^{w} = \langle \mathcal {V},\mathcal {X}, \mathcal {Y}, \rho ^e,\rho ^s, \varphi , w^s\rangle \), a finite upper bound \(c \in \mathbb {N}\), and a valuation \(\mathcal {D}: Var \rightarrow EF(c) \) over \( EF(c) \), is inductively defined as follows:Footnote 5
-
For \(~v\in \mathcal {V}\), \([\![{v}]\!]^{{G^{w}(c)}}_{\mathcal {D}}=f_v\) and \([\![{\lnot v}]\!]^{{G^{w}(c)}}_{\mathcal {D}}=f_{\lnot v}\) where
\(f_v(s) = {\left\{ \begin{array}{ll} 0, &{} \text { if } s\vDash {v} \\ +\infty , &{} \text { if } s\nvDash {v} \end{array}\right. }\) ; \(f_{\lnot v}(s) = {\left\{ \begin{array}{ll} +\infty , &{} \text { if } s\vDash {v} \\ 0, &{} \text { if } s\nvDash {v} \end{array}\right. }\).
-
For \(~X\in { Var }\), \([\![{X}]\!]^{{G^{w}(c)}}_{\mathcal {D}} = \mathcal {D}(X)\).
-
 .
. -
 .
. -
 .
. -
 , where \(~{\scriptscriptstyle \left\{ \begin{array}{l} h_0=f_{+\infty }\\ h_0=f_{0} \end{array}\right\} }~\),
, where \(~{\scriptscriptstyle \left\{ \begin{array}{l} h_0=f_{+\infty }\\ h_0=f_{0} \end{array}\right\} }~\),  , and \(\mathcal {D}[X\mapsto h_i]\) denotes the valuation that is like \(\mathcal {D}\) except that it maps X to \(h_i\).
, and \(\mathcal {D}[X\mapsto h_i]\) denotes the valuation that is like \(\mathcal {D}\) except that it maps X to \(h_i\).
Note that the semantics is well-defined, as greatest and least fixed-points of  exist. This fact holds since \({\mathcal {L}_{e\mu }^{{\scriptstyle sys }}}\) formulas are monotone: if \(f\preceq g\), then
exist. This fact holds since \({\mathcal {L}_{e\mu }^{{\scriptstyle sys }}}\) formulas are monotone: if \(f\preceq g\), then  .
.
As we mentioned earlier, we order E(c) and EF(c) by \(\preceq \) (rather than by the seemingly more natural ordering \(f\le g \Leftrightarrow \forall s\in 2^\mathcal V(f(s)\le g(s))\)) due to a technical reason. This design choice maintains correspondence between the values of \(\psi \in {\mathcal {L}_{\mu }^{{\scriptstyle sys }}}\) and  . Importantly, it keeps the classification of \(\mu \) and \(\nu \) formulas as liveness and safety properties [12]. For illustration, for \(p \in \mathcal {V}\), consider the \(\mu \)-formula
. Importantly, it keeps the classification of \(\mu \) and \(\nu \) formulas as liveness and safety properties [12]. For illustration, for \(p \in \mathcal {V}\), consider the \(\mu \)-formula
 that matches the p-states reachability winning condition [29]. If we had chosen to use \(\le \) instead of \(\preceq \), we would have needed to take the \(\nu \)-formula
that matches the p-states reachability winning condition [29]. If we had chosen to use \(\le \) instead of \(\preceq \), we would have needed to take the \(\nu \)-formula
 to solve energy augmented p-states reachability whereas, unnaturally, the formula
to solve energy augmented p-states reachability whereas, unnaturally, the formula
 would match the p-states safety winning condition [29]. The ordering \(\preceq \) enables our main result:
would match the p-states safety winning condition [29]. The ordering \(\preceq \) enables our main result:
Theorem 1
(\({\mathcal {L}_{e\mu }^{{\scriptstyle sys }}}\): correctness). Let \(\psi _{\varphi }\in {\mathcal {L}_{\mu }^{{\scriptstyle sys }}}\) be a closed formula that matches the \(\omega \)-regular winning condition \(\varphi \) of the WGS, \(G^{w} = (G, w^s)\). Then, for all states \(s\in {2^{\mathcal {V}}}\): (1) if  then
then  is the minimum initial credit for which the system wins from s w.r.t. c in \(G^{w}\); (2) otherwise, s does not win for the system w.r.t. c.
is the minimum initial credit for which the system wins from s w.r.t. c in \(G^{w}\); (2) otherwise, s does not win for the system w.r.t. c.
Note that Theorem 1 solves the decision problem (\(s\in W_{\scriptstyle sys }^c\) iff  ), and the minimum credit problem (return
), and the minimum credit problem (return  ).
).
Complexity. A straightforward implementation of  gives an algorithm to solve the decision and minimum credit problems in \(O((|2^\mathcal V|(c+1))^q)\) symbolic steps, where q is the largest number of nested fixed-point operators in the energy \(\mu \)-calculus formula \(\psi _\varphi \). Nevertheless, using the techniques proposed in [14] and [24] for faster computation of fixed-points, we can reduce this time complexity into \(O((|2^\mathcal V|(c+1))^{\lfloor d/2 \rfloor +1})\) symbolic steps, where d is the alternation depth of \(\psi _\varphi \).Footnote 6 Although this worst-case time complexity is equal to the time complexity of the naive encoding approach, the evaluation we present in Sect. 5 shows that energy \(\mu \)-calculus performs significantly better.
gives an algorithm to solve the decision and minimum credit problems in \(O((|2^\mathcal V|(c+1))^q)\) symbolic steps, where q is the largest number of nested fixed-point operators in the energy \(\mu \)-calculus formula \(\psi _\varphi \). Nevertheless, using the techniques proposed in [14] and [24] for faster computation of fixed-points, we can reduce this time complexity into \(O((|2^\mathcal V|(c+1))^{\lfloor d/2 \rfloor +1})\) symbolic steps, where d is the alternation depth of \(\psi _\varphi \).Footnote 6 Although this worst-case time complexity is equal to the time complexity of the naive encoding approach, the evaluation we present in Sect. 5 shows that energy \(\mu \)-calculus performs significantly better.
We conclude this section with an example for a valuation of an \({\mathcal {L}_{e\mu }^{{\scriptstyle sys }}}\)-formula.
Example 2
Consider again the game structure depicted in Fig. 2. The environment player controls variable x, and the system controls variable y. For illustration, from state (x, y), the environment can provide both possible inputs, x and !x. The system has no legal response for x (and thus it leads to a system-deadlock), but for the input !x, it can respond with y, which consumes 1 “energy units”, but not with !y.
Consider the reachability winning condition with target \(!x\wedge !y\). The game \(\mu \)-calculus formula that matches our winning condition is
 . We set an energy bound \(c=10\), and following Theorem 1 compute
. We set an energy bound \(c=10\), and following Theorem 1 compute
 . The fixed-point valuation is presented in the following table.
. The fixed-point valuation is presented in the following table.

The computation reaches a fixed-point after three iterations, and thus \(g_3\) maps each state to the minimal initial credit sufficient for the system to force reaching (!x, !y). Note that the energy bound \(c=4\) is a sufficient bound and that \(W_{\scriptstyle sys }^4=W_{\scriptstyle sys }^{10}\). Yet, importantly, the unnecessarily high energy bound we chose, \(c=10\), does not cause an overhead, and we did not perform additional redundant computations.
5 Evaluation
To evaluate our approach for solving \(\omega \)-regular energy games, we implemented it in the Spectra specification language and GR(1) synthesis environment [1, 39], while modeling energy functions via ADDs, using the CUDD package [45].Footnote 7
Adding support for energy \(\mu \)-calculus in Spectra allowed us to evaluate our approach over different types of \(\omega \)-regular winning conditions, since the GR(1) winning condition supported by Spectra subsumes safety, reachability, Büchi, and generalized Büchi. For illustration, GR(1) games are solved by the game \(\mu \)-calculus formula
 . A Büchi winning condition is a restricted GR(1) condition that merely requires: “\(g_1\) holds infinitely often”. Thus, with \(m=0\) and \(n=1\), the GR(1) game \(\mu \)-calculus formula is contracted into
. A Büchi winning condition is a restricted GR(1) condition that merely requires: “\(g_1\) holds infinitely often”. Thus, with \(m=0\) and \(n=1\), the GR(1) game \(\mu \)-calculus formula is contracted into
 , the game \(\mu \)-calculus formula that matches the Büchi condition (recall Eq. 1).
, the game \(\mu \)-calculus formula that matches the Büchi condition (recall Eq. 1).
We consider the following research questions:
-
RQ1. Is our approach better than naive encoding in terms of performance?
-
RQ2. Is the performance of our approach affected by the chosen energy bound?
Below we describe the experiments we performed to address RQ1 and RQ2. All relevant materials and means to reproduce the experiments are available in [2].
Corpus. Our corpus for the experiments includes two families of specifications. First, we created specifications based on the energy augmented obstacle evasion problem we described in Sect. 2. Recall that each movement of the robot consumes k energy units and a charger in cell (1, 1) charges the robot by m units. For each of the winning conditions from Sect. 2, safety, reachability, Büchi, generalized Büchi, and GR(1), and each energy bound \(c=10^2,\cdots ,10^6\), we created 30 realizable specifications by randomly choosing values for the parameters k and m. As c gets larger, we considered more possible values for k and m and thus created specifications with larger weights.
Second, we created energy-augmented specifications based on the arbiter problem from SYNTCOMP20.Footnote 8 The basic arbiter (the system) grants requests from 10 different clients (the environment). It can grant only a single request at each turn, and a request remains pending until it is granted.
On top of the basic specification, we impose the following energy weights. \( client _0\) is a preferable client. Hence, we penalize the arbiter by c energy units for the bad event: postponing a request by \( client _0\). Furthermore, we penalize the arbiter by k energy units for the bad event: postponing a request by \( client _i\), \(i>0\). Finally, we reward the arbiter by m energy units for the good event: granting a request from any client. See an excerpt of the Spectra specification in Listing 2. The full specification is available from [2].

We remark that our arbiter specification demonstrates a usage of energy that may seem different than the intuitive energy consumption and accumulation demonstrated in our obstacle evasion example. Here we use energy to synthesize a controller that must balance bad behaviors (that are perhaps unpreventable) with good behaviors. Otherwise, the controller will run out of “energy”.
In addition to the basic safety arbiter specification (i.e., winning condition (1)  ), we consider the following instances of reachability, Büchi, generalized Büchi, and GR(1).
), we consider the following instances of reachability, Büchi, generalized Büchi, and GR(1).
-
(2)
 where a is: only \( client _0\) requests have been granted for 10 consecutive steps.
where a is: only \( client _0\) requests have been granted for 10 consecutive steps. -
(3)
 where a is: \( client _0\) does not request, or its request is granted.
where a is: \( client _0\) does not request, or its request is granted. -
(4)
 where \(a_i\) is: \( client _i\) does not request, or its request is granted.
where \(a_i\) is: \( client _i\) does not request, or its request is granted. -
(5)
 where b is: \( client _0\) does not request, and each \(a_i\) is the assertion: \( client _i\) does not request, or its request is granted.
where b is: \( client _0\) does not request, and each \(a_i\) is the assertion: \( client _i\) does not request, or its request is granted.
As in the obstacle evasion specifications, for each winning condition and energy bound \(c=10^2,\dots ,10^6\), we created 30 realizable arbiter specifications by randomly choosing values for the parameters k and m. Again, as c gets larger, we considered more possible values for k and m and thus created specifications with larger weights.
Overall, our corpus includes 750 energy obstacle evasion specifications and 750 energy arbiter specifications.
Experiment Setup and Results. For each \(\omega \)-regular winning condition (safety, reachability, Büchi, generalized Büchi, GR(1)) and for each energy bound (\(c=10^2,\dots ,10^6\)), we applied Spectra realizability check over the corresponding 30 specifications with each of the two methods, naive encoding (NE) and energy \(\mu \)-calculus (E\(\mu \)C). We used a timeout of 10 min. We performed all experiments on a rather ordinary laptop with Intel i7-9750H processor, 32GB RAM, running windows 10, using a single processor.
Table 1 reports the median running times we obtained (in sec.). Columns titled NE present naive encoding results, and columns titled E\(\mu \)C present energy \(\mu \)-calculus results. For example, for the 30 obstacle evasion specifications with Büchi winning condition and energy bound \(c=10^5\), the median running time of a realizability check is 213.1 s with naive encoding, and only 16.6 s with energy \(\mu \)-calculus. Correspondingly, the cell on row ‘Obstacle Evasion/ ’, column ‘\(10^5\)/NE’ reads 213.1, and on row ‘Obstacle Evasion/
’, column ‘\(10^5\)/NE’ reads 213.1, and on row ‘Obstacle Evasion/ ’, column ‘\(10^5\)/E\(\mu \)C’ reads 16.6.
’, column ‘\(10^5\)/E\(\mu \)C’ reads 16.6.
To compute the median values, we assigned timeout executions with a distinguished maximal value. Cells that read ‘timeout’ indicate that the distinguished maximal value is the median value, i.e., at least 15/30 executions failed to return within 10 min.
Observations. To answer RQ1, we see that our approach outperforms naive encoding by far. In all experiments, our approach presents better results than naive encoding, sometimes by several orders of magnitude.
To answer RQ2, we see that with energy \(\mu \)-calculus, the increase in the energy bound had no effect on the performance of the realizability check. In contrast, with naive encoding, when increasing the bound, the realizability check is dramatically affected and quickly becomes infeasible.
Overall, while the naive encoding method reached the 10 min timeout for 365 (of the 1500) specifications, energy \(\mu \)-calculus reached the timeout with only one of these 1500 specifications.
6 Related Work
Energy games were introduced in [19] and solved in [11, 13, 19]. To tackle \(\omega \)-regular energy games, Chatterjee and Doyen studied energy parity games [20]. Of these, only [11] considers also a finite bound over the accumulated energy level, and none provides an implementation or an evaluation. Interestingly, essentially, the algorithms of [11, 13, 19] can be seen as a special case of our results, limited to safety games (i.e., applying the energy \(\mu \)-calculus formula
 .
.
Multi-valued and quantitative extensions of the \(\mu \)-calculus logic exist in the literature (e.g. [3, 15, 26, 30, 31]). Some extensions were introduced to solve generalizations of \(\omega \)-regular games: probabilistic concurrent \(\omega \)-regular games [6], and imperfect information \(\omega \)-regular games [44]. Surprisingly, perhaps, none of these extensions subsumes energy \(\mu \)-calculus. Some do not consider edge-weights [15, 30, 31]. Moreover, rather than addition of weights, the approach in [3] employs the max operator, and the approach in [26] employs weight multiplication.
ADDs have been used for the analysis of probabilistic models (e.g., [5, 9, 32, 36, 37]). ADDs have also been studied in the context of game solving: an ADD-based parity solver is described in [18] and is implemented and evaluated in [33]; an ADD-based, symbolic fixed-point algorithm for (safety-only) energy games appears in [38].
7 Conclusion
We presented efficient means to solve \(\omega \)-regular energy games, which relies on energy \(\mu \)-calculus, a novel multi-valued extension of the modal game \(\mu \)-calculus. Our technique avoids the encoding of the energy level within the state space, and allows the reuse of existing algorithms that solve \(\omega \)-regular winning conditions.
We have implemented our technique in the Spectra specification language and synthesis environment. The experiments we presented provided evidence showing that energy \(\mu \)-calculus is an efficient and scalable technique for solving energy games.
Future Work. Game \(\mu \)-calculus has not only been used to compute the sets of the winning states, but also to synthesize winning strategies; see, e.g., [10, 34]. Thus, in addition to solving the decision and the minimum credit problems, we believe that energy \(\mu \)-calculus can augment game \(\mu \)-calculus-based strategy synthesis with energy. That is, as future work, we consider how finite memory winning strategies may be extracted from the intermediate energy functions of the fixed-point iterations.
Notes
- 1.
If all of the relational variables in \(\psi \) are bound by fixed-point operators, i.e., \(\psi \) is a closed formula, we may omit \(\mathcal {E}\) from the semantic brackets.
- 2.
For a discussion of \({\mathcal {L}_{e\mu }^{{\scriptstyle env }}}\) we refer the reader to [7].
- 3.
Assuming at this stage, for simplicity, that
 has no free variables.
has no free variables. - 4.
Standardly, we use !x to denote that we assign the value
 to x. Hence, as an example, (!x, y) formally represents the state \(\{y\}\).
to x. Hence, as an example, (!x, y) formally represents the state \(\{y\}\). - 5.
We may drop the valuation \(\mathcal {D}\) from the semantic brackets for closed formulas.
- 6.
- 7.
Our implementation, just like the standard realizability check of Spectra, uses the direct \(O((|2^\mathcal V|(c+1))^q)\) time algorithm, rather than the \(O((|2^\mathcal V|(c+1))^{\lfloor d/2 \rfloor +1})\) approach. Note that a recent evaluation shows that, in practice, the later induces only a minor improvement, and can even be harmful for some instances [25].
- 8.
2020 reactive synthesis competition http://www.syntcomp.org.
References
Spectra Website. http://smlab.cs.tau.ac.il/syntech/spectra/
Supporting Materials Website. http://smlab.cs.tau.ac.il/syntech/energyefficient/
de Alfaro, L., Faella, M., Stoelinga, M.: Linear and branching system metrics. IEEE Trans. Softw. Eng. 35(2), 258–273 (2009). https://doi.org/10.1109/TSE.2008.106
de Alfaro, L., Henzinger, T.A., Majumdar, R.: From verification to control: dynamic programs for omega-regular objectives. In: 16th Annual IEEE Symposium on Logic in Computer Science, Boston, Massachusetts, USA, 16–19 June 2001, Proceedings, pp. 279–290. IEEE Computer Society (2001). https://doi.org/10.1109/LICS.2001.932504
de Alfaro, L., Kwiatkowska, M.Z., Norman, G., Parker, D., Segala, R.: Symbolic model checking of probabilistic processes using mtbdds and the kronecker representation. In: Tools and Algorithms for Construction and Analysis of Systems, 6th International Conference, TACAS 2000, Held as Part of the European Joint Conferences on the Theory and Practice of Software, ETAPS 2000, Berlin, Germany, 25 March–2 April 2000, Proceedings, pp. 395–410 (2000). https://doi.org/10.1007/3-540-46419-0_27
de Alfaro, L., Majumdar, R.: Quantitative solution of omega-regular games. J. Comput. Syst. Sci. 68(2), 374–397 (2004). https://doi.org/10.1016/j.jcss.2003.07.009
Amram, G., Maoz, S., Pistiner, O., Ringert, J.O.: Energy mu-calculus: symbolic fixed-point algorithms for omega-regular energy games. CoRR abs/2005.00641 (2020). https://arxiv.org/abs/2005.00641
Bahar, R.I., et al.: Algebraic decision diagrams and their applications. Formal Methods Syst. Des. 10(2/3), 171–206 (1997). https://doi.org/10.1023/A:1008699807402
Baier, C., Clarke, E.M., Hartonas-Garmhausen, V., Kwiatkowska, M.Z., Ryan, M.: Symbolic model checking for probabilistic processes. In: Automata, Languages and Programming, 24th International Colloquium, ICALP 1997, Bologna, Italy, 7–11 July 1997, Proceedings, pp. 430–440 (1997). https://doi.org/10.1007/3-540-63165-8_199
Bloem, R., Jobstmann, B., Piterman, N., Pnueli, A., Sa’ar, Y.: Synthesis of Reactive(1) Designs. J. Comput. Syst. Sci. 78(3), 911–938 (2012). https://doi.org/10.1016/j.jcss.2011.08.007
Bouyer, P., Fahrenberg, U., Larsen, K.G., Markey, N., Srba, J.: Infinite runs in weighted timed automata with energy constraints. In: Cassez, F., Jard, C. (eds.) FORMATS 2008. LNCS, vol. 5215, pp. 33–47. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85778-5_4
Bradfield, J., Stirling, C.: 12 modal mu-calculi. In: Patrick Blackburn, J.V.B., Wolter, F. (eds.) Handbook of Modal Logic, Studies in Logic and Practical Reasoning, vol. 3, pp. 721–756. Elsevier (2007). http://www.sciencedirect.com/science/article/pii/S1570246407800152
Brim, L., Chaloupka, J., Doyen, L., Gentilini, R., Raskin, J.: Faster algorithms for mean-payoff games. Formal Methods Syst. Des. 38(2), 97–118 (2011). https://doi.org/10.1007/s10703-010-0105-x
Browne, A., Clarke, E.M., Jha, S., Long, D.E., Marrero, W.R.: An improved algorithm for the evaluation of fixpoint expressions. Theor. Comput. Sci. 178(1–2), 237–255 (1997). https://doi.org/10.1016/S0304-3975(96)00228-9
Bruns, G., Godefroid, P.: Model checking with multi-valued logics. In: Díaz, J., Karhumäki, J., Lepistö, A., Sannella, D. (eds.) ICALP 2004. LNCS, vol. 3142, pp. 281–293. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-27836-8_26
Bryant, R.E.: Graph-based algorithms for boolean function manipulation. IEEE Trans. Comput. 35(8), 677–691 (1986). https://doi.org/10.1109/TC.1986.1676819
Bryant, R.E.: Symbolic boolean manipulation with ordered binary-decision diagrams. ACM Comput. Surv. 24(3), 293–318 (1992). https://doi.org/10.1145/136035.136043
Bustan, D., Kupferman, O., Vardi, M.Y.: A measured collapse of the modal \(\rm \mu \)-calculus alternation hierarchy. In: STACS 2004, 21st Annual Symposium on Theoretical Aspects of Computer Science, Montpellier, France, 25–27 March 2004, Proceedings, pp. 522–533 (2004). https://doi.org/10.1007/978-3-540-24749-4_46
Chakrabarti, A., de Alfaro, L., Henzinger, T.A., Stoelinga, M.: Resource interfaces. In: Alur, R., Lee, I. (eds.) EMSOFT 2003. LNCS, vol. 2855, pp. 117–133. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45212-6_9
Chatterjee, K., Doyen, L.: Energy parity games. Theor. Comput. Sci. 458, 49–60 (2012). https://doi.org/10.1016/j.tcs.2012.07.038
Chatterjee, K., Randour, M., Raskin, J.: Strategy synthesis for multi-dimensional quantitative objectives. Acta Inf. 51(3–4), 129–163 (2014). https://doi.org/10.1007/s00236-013-0182-6
Ehlers, R., Raman, V.: Slugs: extensible GR(1) synthesis. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9780, pp. 333–339. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41540-6_18
Emerson, E.A., Jutla, C.S.: Tree automata, mu-calculus and determinacy (extended abstract). In: 32nd Annual Symposium on Foundations of Computer Science, San Juan, Puerto Rico, 1–4 October 1991, pp. 368–377. IEEE Computer Society (1991). https://doi.org/10.1109/SFCS.1991.185392
Emerson, E.A., Lei, C.: Efficient model checking in fragments of the propositional mu-calculus (extended abstract). In: Proceedings of the Symposium on Logic in Computer Science (LICS 1986), Cambridge, Massachusetts, USA, 16–18 June 1986, pp. 267–278. IEEE Computer Society (1986). http://dblp2.uni-trier.de/rec/bib/conf/lics/EmersonL86
Firman, E., Maoz, S., Ringert, J.O.: Performance heuristics for GR(1) synthesis and related algorithms. Acta Informatica 57(1–2), 37–79 (2020). https://doi.org/10.1007/s00236-019-00351-9
Fischer, D., Grädel, E., Kaiser, Ł: Model checking games for the quantitative \(\mu \)-calculus. Theory Comput. Syst. 47(3), 696–719 (2010). https://doi.org/10.1007/s00224-009-9201-y
Fujita, M., McGeer, P.C., Yang, J.C.: Multi-terminal binary decision diagrams: an efficient data structure for matrix representation. Formal Methods Syst. Des. 10(2/3), 149–169 (1997). https://doi.org/10.1023/A:1008647823331
Galceran, E., Carreras, M.: A survey on coverage path planning for robotics. Robotics Auton. Syst. 61(12), 1258–1276 (2013). https://doi.org/10.1016/j.robot.2013.09.004
Grädel, E., Thomas, W., Wilke, T. (eds.): Automata Logics, and Infinite Games. LNCS, vol. 2500. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-36387-4
Grumberg, O., Lange, M., Leucker, M., Shoham, S.: Don’t know in the \({\mu }\)-calculus. In: Cousot, R. (ed.) VMCAI 2005. LNCS, vol. 3385, pp. 233–249. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30579-8_16
Grumberg, O., Lange, M., Leucker, M., Shoham, S.: When not losing is better than winning: abstraction and refinement for the full \(\mu \)-calculus. Inf. Comput. 205(8), 1130–1148 (2007). https://doi.org/10.1016/j.ic.2006.10.009
Hermanns, H., Kwiatkowska, M.Z., Norman, G., Parker, D., Siegle, M.: On the use of MTBDDs for performability analysis and verification of stochastic systems. J. Log. Algebr. Program. 56(1–2), 23–67 (2003). https://doi.org/10.1016/S1567-8326(02)00066-8
Jurdziński, M.: Small progress measures for solving parity games. In: Reichel, H., Tison, S. (eds.) STACS 2000. LNCS, vol. 1770, pp. 290–301. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-46541-3_24
Könighofer, R., Hofferek, G., Bloem, R.: Debugging formal specifications: a practical approach using model-based diagnosis and counterstrategies. STTT 15(5–6), 563–583 (2013). https://doi.org/10.1007/s10009-011-0221-y
Kozen, D.: Results on the propositional \(\mu \)-calculus. In: Proceedings of the 9th Colloquium on Automata, Languages and Programming, pp. 348–359. Springer, London (1982). http://dl.acm.org/citation.cfm?id=646236.682866
Kwiatkowska, M.Z., Norman, G., Parker, D.: Probabilistic symbolic model checking with PRISM: a hybrid approach. STTT 6(2), 128–142 (2004). https://doi.org/10.1007/s10009-004-0140-2
Kwiatkowska, M., Norman, G., Parker, D.: PRISM 4.0: verification of probabilistic real-time systems. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 585–591. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_47
Maoz, S., Pistiner, O., Ringert, J.O.: Symbolic BDD and ADD algorithms for energy games. In: Piskac, R., Dimitrova, R. (eds.) Proceedings Fifth Workshop on Synthesis, SYNT@CAV 2016, Toronto, Canada, 17–18 July 2016. EPTCS, vol. 229, pp. 35–54 (2016). https://doi.org/10.4204/EPTCS.229.5
Maoz, S., Ringert, J.O.: Spectra: a specification language for reactive systems. Softw. Syst. Model. (2021). http://springerlink.bibliotecabuap.elogim.com/article/10.1007/s10270-021-00868-z
Neider, D., Topcu, U.: An automaton learning approach to solving safety games over infinite graphs. In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 204–221. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49674-9_12
Niwiński, D.: On fixed-point clones. In: Kott, L. (ed.) ICALP 1986. LNCS, vol. 226, pp. 464–473. Springer, Heidelberg (1986). https://doi.org/10.1007/3-540-16761-7_96
Piterman, N., Pnueli, A., Sa’ar, Y.: Synthesis of reactive(1) designs. In: Emerson, E.A., Namjoshi, K.S. (eds.) VMCAI 2006. LNCS, vol. 3855, pp. 364–380. Springer, Heidelberg (2005). https://doi.org/10.1007/11609773_24
Pnueli, A.: The temporal logic of programs. In: 18th Annual Symposium on Foundations of Computer Science, Providence, Rhode Island, USA, 31 October–1 November 1977, pp. 46–57. IEEE Computer Society (1977). https://doi.org/10.1109/SFCS.1977.32
Raskin, J., Chatterjee, K., Doyen, L., Henzinger, T.A.: Algorithms for omega-regular games with imperfect information. Logical Methods Comput. Sci. 3(3) (2007). https://doi.org/10.2168/LMCS-3(3:4)2007
Somenzi, F.: CUDD: CU Decision Diagram Package Release 3.0.0 (2015). http://vlsi.colorado.edu/~fabio/CUDD/cudd.pdf
Acknowledgments
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 638049, SYNTECH).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Amram, G., Maoz, S., Pistiner, O., Ringert, J.O. (2021). Efficient Algorithms for Omega-Regular Energy Games. In: Huisman, M., Păsăreanu, C., Zhan, N. (eds) Formal Methods. FM 2021. Lecture Notes in Computer Science(), vol 13047. Springer, Cham. https://doi.org/10.1007/978-3-030-90870-6_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-90870-6_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-90869-0
Online ISBN: 978-3-030-90870-6
eBook Packages: Computer ScienceComputer Science (R0)






 , where a is the assertion: the robot is at cell (10, 10). In words, the robot must visit cell (10, 10).
, where a is the assertion: the robot is at cell (10, 10). In words, the robot must visit cell (10, 10).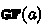 where a is the assertion: the robot is at cell (10, 10). In words, the robot must visit cell (10, 10) infinitely often.
where a is the assertion: the robot is at cell (10, 10). In words, the robot must visit cell (10, 10) infinitely often. where
where  where b is the assertion: the obstacle is at most 4 cells away from the robot, and each
where b is the assertion: the obstacle is at most 4 cells away from the robot, and each  .
. .
. .
. , where
, where  , and
, and 
 ), and the system controls variable y (
), and the system controls variable y (
 ). Edge-weights appear in parentheses. (Color figure online)
). Edge-weights appear in parentheses. (Color figure online) where a is: only
where a is: only  where a is:
where a is:  where
where  where b is:
where b is:  has no free variables.
has no free variables. to x. Hence, as an example, (!x, y) formally represents the state
to x. Hence, as an example, (!x, y) formally represents the state