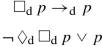Abstract
We consider the issue of the square of opposition for two modal extensions of the discussive logic D 2. To this aim we recall some basic information on discussive logic, but also mention some facts concerning the mentioned extensions of D 2. Our idea is to extend the discussive language with modalities, which although are considered in the context of the discussive logic, but are used only auxiliarily and are absent from its object language.
The authors of this work benefited from support provided by the Polish National Science Centre (NCN), grant number 2016/23/B/HS1/00344
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Discussive logic
- Modal logic
- Discussive modal logic
- Jaśkowski
- Extensions of the discussive logic
- The square of opposition
Mathematics Subject Classification (2000)
1 Introduction
Jaśkowski proposed a logical calculus that could be applied to inconsistent systems but would not result in their overfilling. Jaśkowski expressed his calculus with the use of the modal logic S5, so, via standard facts, in classical (quantifier) logic (see [2, p. 55]). The aim was to obtain a system that would not be overfilled, that is, would not lead in general to the set of all expressions when applied to inconsistent set of premisses. Additionally, two requirements were stipulated as regards the resulting calculus, that it ‘(2) would be rich enough to enable practical inference, (3) would have an intuitive justification’ [2, p. 38]. When proposing his solution, he used a model of discussion. During a discussion inconsistent opinions can be formulated, but participants of this discussion as well as external observers are not inclined to deduce every sentence from the set of statements presented in the discussion. Hence, in the model, two types of point of view are considered: internal ones of particular participants of the discussion and an external one of some observers.
Jaśkowski proposed to express some interactions that are taking place between participants, in particular, he proposed connectives of the so-called discussive conjunction and discussive implication (as well as definable discussive equivalence) that were used to represent some interactions that can take place during a discussion. From the point of view of a given debater, the statements of other participants of the discussion have to be differentiated from the debater’s own statements. The former is marked by the possibility operator—‘ ’. The justification for the use of the modal operator is that from debater’s point of view, the statements of others do not have to be true. The possibility operator can be treated according to Jaśkowski as saying [2, p. 43]:
’. The justification for the use of the modal operator is that from debater’s point of view, the statements of others do not have to be true. The possibility operator can be treated according to Jaśkowski as saying [2, p. 43]:
‘in accordance with the opinion of one of the participants in the discourse’.
Next to modalities corresponding to debater’s evaluations of statements made by other debaters, in his definition, Jaśkowski also includes a point of view of an external observer. This way of considering other statements is also expressed by possibility operator. It can be seen as expressing the fact that from the point of view of the ‘impartial arbiter’ (see [1, p. 149], English version) all opinions presented during the discussion are only possible. So ([1, p. 149], English version),
“if a thesis is recorded in a discursive system, its intuitive sense ought to be interpreted so as if it were preceded by the symbol Pos”.
Hence, the modal possibility operator is applied in the definition of D
2 on two levels, but none of these two uses is explicitly saved in the resulting language of the logic D
2. So, although D
2 is connected with a modal logic—the logic S5, D
2 has got neither  nor
nor  in its language. One can consider an extension of D
2 with the help of modal operators of
in its language. One can consider an extension of D
2 with the help of modal operators of  —possibility and
—possibility and  —necessity (see [6]). The obtained logics is denoted as mD
2. Similarly as the logic D
2, mD
2 is defined by translations referring to the modal logic S5. Semantic conditions for
—necessity (see [6]). The obtained logics is denoted as mD
2. Similarly as the logic D
2, mD
2 is defined by translations referring to the modal logic S5. Semantic conditions for  and
and  are standard. However, the resulting modal logic as a whole behaves rather in a non-standard way. In the present paper we consider the issue of the square of opposition for this logic. As a result of the given analysis, we consider also a modified version of this extension, where in the discussive model we allow an influence of some general community. For this aim we consider additional modalities.
are standard. However, the resulting modal logic as a whole behaves rather in a non-standard way. In the present paper we consider the issue of the square of opposition for this logic. As a result of the given analysis, we consider also a modified version of this extension, where in the discussive model we allow an influence of some general community. For this aim we consider additional modalities.
2 Basic Notions and Facts
2.1 Standard Modal Formulas
Modal formulas are formed standardly from propositional variables: ‘p’, ‘q’, ‘p
0’, ‘p
1’, ‘p
2’, …; truth-value operators: ‘\( \mathop {\neg }\)’, ‘ ’, ‘
’, ‘ ’, ‘
’, ‘ ’, and ‘
’, and ‘ ’ (connectives of negation, disjunction, conjunction, material implication, and material equivalence, respectively); modal operators: the necessity symbol ‘
’ (connectives of negation, disjunction, conjunction, material implication, and material equivalence, respectively); modal operators: the necessity symbol ‘ ’ and the possibility symbol ‘
’ and the possibility symbol ‘ ’; and the brackets. By Form we denote the set of all modal formulas.
’; and the brackets. By Form we denote the set of all modal formulas.
The set Form includes the set of all classical formulas. Let Taut be the set of all classical tautologies. Besides, for any φ, ψ, χ ∈Form, let χ[φ∕ψ] be any formula that results from χ by replacing one, none, or more than one occurrence of φ, in χ, by ψ.
As usually, modal logics are sets of formulas. By a modal logic we mean a set L of modal formulas satisfying following conditions:
-
Taut ⊆L,
-
L includes the following set of formulas
 (rep □ )
(rep □ ) -
L is closed under the following two rules: modus ponens for ‘
 ’:
’:  (mp )
(mp ) -
and uniform substitution
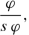 (sb )
(sb )where \( \mathop {s}\varphi \) is a result of the uniform substitution of formulas for propositional variables in φ.
If we skip the first condition we can say about modal logics in a broader sense or non-classical modal logics.
By the uniform substitution, every modal logic includes the set PL of modal formulas being substitution instances of elements of Taut.
By ( rep □ ), every modal logic has the following thesis:

In this paper the term ‘modal logic’ is always understood as a set of modal formulas. All members of a logic are called its theses.
2.2 Discussive Logic
Discussive formulas are again formed in the standard way using propositional variables, but this time from truth-value operators: ‘\( \mathop {\neg }\)’ and ‘ ’ (negation and disjunction); discussive connectives: ‘
’ (negation and disjunction); discussive connectives: ‘ ’, ‘
’, ‘ ’, ‘
’, ‘ ’ (conjunction, implication and equivalence); and the brackets. In the case of a discussive modal logic, we use also discussive modal operators
’ (conjunction, implication and equivalence); and the brackets. In the case of a discussive modal logic, we use also discussive modal operators  and
and  —‘discussive’, since these operators have also an explication in the model of discussion.
—‘discussive’, since these operators have also an explication in the model of discussion.
Let Ford (\(\mathrm {For}^{\mathrm {d}}_{\mathrm {m}}\)) be the set of all discussive formulas (respectively, discussive modal formulas) in this language.
2.2.1 Translation from Ford into Form
Let i0 be the translation from Ford into Form such that:
-
1.
i0(a) = a, for any propositional variable a,
-
2.
for any A, B ∈Ford:
-
\(\mathrm {i}_0( \mathop {\neg } A)=\ulcorner \mathop {\neg } \mathrm {i}_0(A)\urcorner \),
-
 ,
, -
 ,
, -
 ,
, -
 .
.
-
2.2.2 Historical Reminder
As it was mentioned, Jaśkowski used discussive operators to express some basic interactions that can hold between debaters. The first interaction has been expressed by Jaśkowski in the following way ‘if anyone states that p, then q’ (see [1, p. 67]). This phrase is treated as an intuitive understanding of Jaśkowski’s discussive implication. As one might see, we apply the custom to denote discussive implication by: ‘ ’. Taking into account the intuitive meaning of discussive implication, Jaśkowski proposes the formula
’. Taking into account the intuitive meaning of discussive implication, Jaśkowski proposes the formula

The technical reason for such interpretation of discussive implication is its ability to ensure the closure of the set of theses on modus ponens. In particular, Jaśkowski observes [2, p. 44], [1, p. 67]:
In every discussive system two theses, one of the form:
and the other of the form:
$$\displaystyle \begin{aligned} \mathfrak P\, , \end{aligned} $$entail the thesis
$$\displaystyle \begin{aligned} \mathfrak Q\, , \end{aligned} $$and that on the strength of the theorem
(M 2 1)
In[3]Footnote 1 a discussive conjunction (notation:  ) has been introduced:
) has been introduced:

It is usually understood as a summary made by a debater who expressed p. In the very same paper, discussive equivalence  is expressed by the formula:
is expressed by the formula:

2.3 The Discussive Logic D 2 as a Set of Discussive Formulas
Jaśkowski’s discussive logic D 2 can be treated either as a set of discussive formulas or as some consequence relation on the set of all discussive formulas. Nowadays, the discussive logic D 2 is usually understood in the first way and formulated with the help of the modal logic S5 as follows:

As one can see such a formulation corresponds to both levels of the modal interpretation recalled and sketched above. As one can also easily see, the set D
2 is closed under substitution. Besides, as it was planned by Jaśkowski, D
2 is closed on modus ponens for ‘ ’. It is achieved by the use of the formula (M21), which belongs to S5. Using this formula we see that for A, B ∈Ford, if A ∈D
2,
’. It is achieved by the use of the formula (M21), which belongs to S5. Using this formula we see that for A, B ∈Ford, if A ∈D
2,  , i.e.,
, i.e.,  , then
, then  , so B ∈D
2.
, so B ∈D
2.


the following formulas


belong to D 2.
As a standard counterexample, consider \(\ulcorner p\to (\neg p \to q)\urcorner \) that is not a thesis of D 2.
3 Discussive Modal Logic
3.1 Extension of Jaśkowski’s Translation
The first step while working on a modal extension of D 2 is to save modalities in the object language of discussive logic. So, we keep Jaśkowski’s intuitive model of discussion but add to the language modalities that are interpreted standardly. By considering this modal extension of D 2 ‘we allow’ participants of a discussion to explicitly use possibility and necessity operators. Such extension was investigated in [6].
While formulating a modal logic over D 2 we consider an extension i1 of the translation i0 onto the set of modal formulas by adding to the previously given conditions, two clauses:
-
 ,
, -
 .
.
The obtained logic is denoted as mD 2, where:

As an outcome, we can consider, for example, formulas of the form:



Using both translations we obtain:



We see that (∗), (K d) ∈mD 2 and (K1d)∉mD 2, while


and of course

To make a readable comparison of mD 2 with standard modal logics, we apply a function e from \(\mathrm {For}^{\mathrm {d}}_{\mathrm {m}}\) into Form which removes the subscript ‘d’.
Using the above mentioned examples and definitions we give the following resume of some basic facts on mD 2:
Fact 3.1 ([6])
-
1.
S5 and e[mD 2] cross each other.
-
2.
The set mD 2 is not closed under necessitation rule
 (3.1)
(3.1) -
3.
The set mD 2 is closed under modus ponens (mp) and is closed under uniform substitution (sb), hence mD 2 is a logic. In particular, it is a non-classical modal logic.
-
4.
-
(a)
\(\mathbf {CL}^{+} \varsubsetneq \mathrm {e}[\mathbf {m}\mathbf {D}_{ \mathbf {2}}]\)
-
(b)
\(\mathbf {CL} \nsubseteq \mathbf {m}\mathbf {D}_{ \mathbf {2}}\)
-
(c)
\(\mathbf {D}_{ \mathbf {2}}\varsubsetneq \mathbf {m}\mathbf {D}_{ \mathbf {2}}\) and mD 2 is a conservative extension of the logic D 2.
-
(a)
-
5.
The following formulas are theses of mD 2

-
6.
The following formulas are not theses of mD 2

-
7.
mD 2 (as D 2 ) is not closed on rules of contraposition
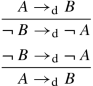
(in fact,
 , while
, while
 ).
).
-
8.
mD 2 (as D 2 ) is not extensional. Indeed

since

-
9.
For any \(A\in \mathrm {For}^{\mathrm {d}}_{\mathrm {m}}\) , such that i1(A) is a thesis of S5 , then A is a thesis of mD 2.
We can see that  and
and  are not dual on the basis of mD
2. Points 7 and 8, of the above fact 3.1, lead us to the following observations:
are not dual on the basis of mD
2. Points 7 and 8, of the above fact 3.1, lead us to the following observations:
Fact 3.2 ([6])
The set mD 2 is not closed under the congruence and extensionality rules:

As a result, mD 2 is also not closed on the monotonicity nor regularity rule:

3.2 Semantics for the Modal Discussive Logic
We focus here on semantical analysis, however, the logic under consideration can be also expressed purely syntactically—for axiomatisation of the logic mD 2, please see [6]. The given semantics is natural, it uses respective modal meanings of the considered connectives and when applied to the language without modalities can be used to determine of D 2.
A relational frame for a discussive modal logic (a frame) is a pair 〈W, R〉 consisting of a nonempty set W and a binary relation R on W. As usually, elements of sets W are called (accessible) worlds, while R is the accessibility relation.
A model for the logic mD 2 is a triple 〈W, R, V 〉, where 〈W, R〉 is a frame and the function \(V\colon \mathrm {For}^{\mathrm {d}}_{\mathrm {m}}\times W \longrightarrow \{0,1\}\) preserves classical truth conditions for negation and disjunction

standardly understood conditions for discussive connectives:

and usual conditions for modalities:

where \(R(w)= \{x\in W : w \mathop {\mbox{{$R$}}} x\}\). As usually, V is determined by its restriction to the set of all propositional variables. We say that the model 〈W, R, V 〉 is based on the frame 〈W, R〉.
Definition 3.3
A formula A is discussively true in a model M = 〈W, R, V 〉 iff for each w ∈ W, there is x ∈ R(w) such that V (A, x) = 1.
We say that a formula \(A\in \mathrm {For}^{\mathrm {d}}_{\mathrm {m}}\) is discussively valid in a frame iff A is discussively true in all models based on this frame.
Fact 3.4 ([6])
For any \(A\in \mathrm {For}^{\mathrm {d}}_{\mathrm {m}}\) and a model M:
A is discussively true in M iff
 is standardly true in M.
is standardly true in M.
We can vary the conditions that are imposed on the relation R.
Definition 3.5
Let F = 〈W, R〉. The frame F (or the accessibility relation R) is
-
(i)
trivial iff R = ∅,
-
(ii)
serial iff ∀x ∈ W∃y ∈ W xRy,
-
(iii)
reflexive iff ∀x ∈ W xRx,
-
(iv)
symmetric iff ∀x,y ∈ W(xRy ⇒ yRx),
-
(v)
transitive iff
 ,
, -
(vi)
Euclidean iff
 .
.
Fact 3.6
The set of all formulas from \(\mathrm {For}^{\mathrm {d}}_{\mathrm {m}}\) that are discussively valid in every frame is empty. In particular, the set of all formulas that discussively valid in a frame with a world w with no alternatives (that is in a frame which is not serial) is empty.
As an introductory step to the issue of the square of opposition for mD 2, we recall some facts concerning positive and negative examples of discussive validity for specific classes of frames, extending slightly results given in Fact 3.1. Below, we also refer to the issue of completeness for mD 2.
Fact 3.7 ([6])
-
1.
The formula

is discussively valid in every frame with a serial accessibility relation.
-
2.
It is not the case that

is discussively valid in every serial frame.
-
3.
The formulas

are discussively valid in every reflexive frame but also in those fulfilling the condition:
$$\displaystyle \begin{aligned} \forall_w\exists_{u}\Big(wRu\wedge \exists_{v}(u R v\wedge w R v)\Big).\end{aligned} $$While
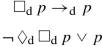
is valid in every serial and symmetric frame but also fulfilling the condition
$$\displaystyle \begin{aligned} \mathop{\forall}\limits_{z} \mathop{\exists}\limits_{u}(z R u \wedge \mathop{\forall}\limits_{x} (uRx\to \mathop{\exists}\limits_{w} (xRw \wedge z R w))). \end{aligned} $$ -
4.
For the formula

it is not the case that it is discussively valid in every symmetric frame or even frames that are both symmetric and serial.
We know that (see [6] and [5]):
Theorem 3.8 ([6])
-
1.
A formula belongs to mD 2 iff it is discussively valid in every reflexive and Euclidean frame.
-
2.
The logic mD 2 is determined by the class of reflexive and transitive frames.
-
3.
The logic mD 2 is determined by the class of serial and transitive frames.
-
4.
The logic mD 2 is determined by the class frames fulfilling
$$\displaystyle \begin{gathered} \forall_w\exists_{u}\Big( wRu\wedge \forall_{x}(uR x\rightarrow w R x)\Big)\\ \forall_w\exists_{u} \Big(wRu \wedge \forall_{x}\forall_{y} (u R x\wedge xRy\rightarrow w R y)\Big). \end{gathered} $$
4 Another Modal Extension of D 2
Fact 4.1 ([6])
The following two formulas belong to mD 2:

However, although these equivalences hold, it is still intriguing to consider calculuses with  and
and  , since D
2 and mD
2 are not closed under the rule of extensionality (see Fact 3.2).
, since D
2 and mD
2 are not closed under the rule of extensionality (see Fact 3.2).
So, the added modalities give a variant of the model of discussion in which a given participant expresses his own modal views. In what follows, we refer to the next extension of D 2, where we extend also the model of discussion.
4.1 Semantics for General/Public Discussive Modalities
We consider a model of discussion in which next to the discussive group, there is possibly a broader community of people whose statements will be used as an intuitive explication of new modalities  and
and  . In this way we obtain the set \(\mathrm {For}^{\mathrm {dg}}_{\mathrm {m}}\) being another extension of Ford but also of the set \(\mathrm {For}^{\mathrm {d}}_{\mathrm {m}}\). The semantics considered here is a natural extension of the previously given semantical conditions for discussive modalities: it uses respective modal meaning of the considered connectives with respect to another—not smaller then W in the sense of inclusion—domain W
g, and when applied to the language without modalities, i.e., when W
g is dropped, it comes down to the semantics that can be used for determination of D
2 or mD
2. Intuitively, the set W
g corresponds to the voices that express the external points of view that can be taken into account by members of the given discussive group.
. In this way we obtain the set \(\mathrm {For}^{\mathrm {dg}}_{\mathrm {m}}\) being another extension of Ford but also of the set \(\mathrm {For}^{\mathrm {d}}_{\mathrm {m}}\). The semantics considered here is a natural extension of the previously given semantical conditions for discussive modalities: it uses respective modal meaning of the considered connectives with respect to another—not smaller then W in the sense of inclusion—domain W
g, and when applied to the language without modalities, i.e., when W
g is dropped, it comes down to the semantics that can be used for determination of D
2 or mD
2. Intuitively, the set W
g corresponds to the voices that express the external points of view that can be taken into account by members of the given discussive group.
An relational frame for a discussive modal logic with public modalities is a quadruple 〈W, W g, W × W, W g × W g〉 consisting of a nonempty set W, and a set W g ⊇ W. Elements of the set W are still called (accessible) worlds, while elements of the set W g—general worlds.
A model for an extended discussive modal logic is any 5-tuple 〈W, W g, W × W, W g × W g, V 〉, where 〈W, W g, W × W, W g × W g〉 is a frame and \(V\colon \mathrm {For}^{\mathrm {dg}}_{\mathrm {m}}\times W_g \longrightarrow \{0,1\}\) is a function that preserves classical truth conditions (3.2) and (3.3) for negation and disjunction; discussive conditions for modalities adapted for the current context:

and the following conditions for new ‘general’/‘public’ modalities:

As usually, V is determined by its restriction to the set of all propositional variables. As we observed, we can consider discussive modalities expressed by discussive connectives:


We say that the model 〈W, W g, W × W, W g × W g, V 〉 is based on the frame 〈W, W g, W × W, W g × W g〉.
Since we consider full accessibility relations, in fact as frames we could treat just pairs 〈W, W g〉, while 〈W, W g, V 〉—as models, stipulating only that W ⊆ W g. We repeat the notation of validity for the introduced notions of model and frame referred to definitions given in this subsection:
Definition 4.2
A formula A is discussively true in a model M = 〈W, W g, W × W, W g × W g, V 〉 iff for each w ∈ W, there is x ∈ W such that V (A, x) = 1.
We say that a formula is discussively valid in a frame iff it is discussively true in all models based on this frame.
The set of all formulas discussively valid in the class of frames of the form 〈W, W g〉 is noted by m g D 2. We easily see:
Fact 4.3
D 2 ⊆m g D 2.Footnote 2
5 Square of Opposition
Now we consider theses of mD 2 that are connected to the square:Footnote 3
Fact 5.1
Suppose that \(A\in \mathrm {For}^{\mathrm {d}}_{\mathrm {m}}\), e(A) is a thesis of S5 and each atom a of A occurs in subformulas of the form  ,
,  ,
,  or
or  . Then A ∈mD
2.
. Then A ∈mD
2.
Below, a formula of the form \( \mathop {\neg } A\vee B\) is denoted as  .
.
Fact 5.2
The following formulas are theses of mD 2:

or using
 for the case of contraries, subalternation, and contradictories
for the case of contraries, subalternation, and contradictories

Moreover the respective connections also hold if the discussive connectives are used:

-
Taking into account the above theses and the fact that mD 2 as a logic is closed on substitution, we have the square for discussive modalities within mD 2, where respective connections can be understood both: classically and discussively.

One can observe that similar result holds for the logic m g D 2. Again e is the function that removes subscripts refereeing to discussive connectives but also indexes referring to the ‘global’ modalities:
Fact 5.3
Given \(A\in \mathrm {For}^{\mathrm {dg}}_{\mathrm {m}}\) formulated in the sublanguage solely with ∨, ¬,  ,
,  , and such that e(A) is a thesis of S5
, then A ∈m
g
D
2.
, and such that e(A) is a thesis of S5
, then A ∈m
g
D
2.
So, similarly as for mD 2, we have:Footnote 4
Fact 5.4
The following formulas are theses of m g D 2

or using
 for the case of contraries, subalternation, and contradictories
for the case of contraries, subalternation, and contradictories

Again, the respective connections also hold, if instead of ‘ ’, discussive implication is used. To see this, using the semantical characterisation of m
g
D
2, first we easily can observe that:
’, discussive implication is used. To see this, using the semantical characterisation of m
g
D
2, first we easily can observe that:
Fact 5.5
The following formulas are theses of m g D 2:

Hence, we have:
Lemma 5.6
The following formulas are theses of m g D 2:


Hence, we have the similar square for the pair of ‘public’ modalities in m g D 2.

Taking into account Fact 5.5 we obtain the extended square, where again, the respective relations can be expressed either in terms of classical implication, but—what is more interesting—also with the help of discussive implication.
We can connect both these squares by putting one onto another:

References
S. Jaśkowski, Rachunek zdań dla systemów dedukcyjnych sprzecznych. Studia Societatis Scientiarum Torunensis, Sect. A, I no. 5 (1948), 57–77. The first English version: Propositional calculus for contradictory deductive systems. Studia Logica 24 (1969), 143–157. https://doi.org/10.1007/BF02134311
S. Jaśkowski, A propositional calculus for inconsistent deductive systems. Logic and Logical Philosophy 7 (1999), 35–56; the second English version of [1]. https://doi.org/10.12775/LLP.1999.003
S. Jaśkowski, O koniunkcji dyskusyjnej w rachunku zdań dla systemów dedukcyjnych sprzecznych. Studia Societatis Scientiarum Torunensis, Sect. A, I no. 8 (1949), 171–172.
S. Jaśkowski, On the discussive conjunction in the propositional calculus for inconsistent deductive systems. Logic and Logical Philosophy 7 (1999), 57–59; the English version of [3]. https://doi.org/10.12775/LLP.1999.004
M. Nasieniewski, A comparison of two approaches to parainconsistency: Flemish and Polish. Logic and Logical Philosophy 9 (2001): 47–74. https://doi.org/10.12775/LLP.2001.004
K. Mruczek-Nasieniewska, M. Nasieniewski and A. Pietruszczak, A modal extension of Jaśkowski’s discussive logic D 2. Logic Journal of the IGPL 27 No. 4 (2019), 451–477. https://doi.org/10.1093/jigpal/jzz014
K. Mruczek-Nasieniewska, M. Nasieniewski and A. Pietruszczak, On a Modal Discussive Logic corresponding to the Extended Model of Discussion. In preparation.
Acknowledgements
The authors would like to thank the referee of this paper for his/her careful reading of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Mruczek-Nasieniewska, K., Nasieniewski, M. (2022). On Modal Opposition Within Some Modal Discussive Logics. In: Beziau, JY., Vandoulakis, I. (eds) The Exoteric Square of Opposition. Studies in Universal Logic. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-90823-2_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-90823-2_12
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-90822-5
Online ISBN: 978-3-030-90823-2
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





 ’:
’: 
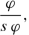
 ,
, ,
, ,
, .
.

 ,
, .
.


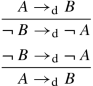
 , while
, while
 ).
).


 ,
, .
.