Abstract
We present a new public-key ABE for DFA based on the LWE assumption, achieving security against collusions of a-priori bounded size. Our scheme achieves ciphertext size \(\tilde{O}(\ell + B)\) for attributes of length \(\ell \) and collusion size B. Prior LWE-based schemes has either larger ciphertext size \(\tilde{O}(\ell \cdot B)\), or are limited to the secret-key setting. Along the way, we introduce a new technique for lattice trapdoor sampling, which we believe would be of independent interest. Finally, we present a simple candidate public-key ABE for DFA for the unbounded collusion setting.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Attribute-based encryption (ABE) [19, 24] is a generalization of public-key encryption to support fine-grained access control for encrypted data. Here, ciphertexts are associated with a description value x and keys with a policy M, and decryption is possible when \(M(x)=1\). One important class of policies we would like to support are those specified using deterministic finite automata (DFA). Such policies capture many real-world applications involving simple computation on data of unbounded size, such as network monitoring and logging, pattern matching in gene sequences, and processing tax returns. Since the seminal work of Waters [26] introducing ABE for DFA and providing the first instantiation from pairings, substantial progress has been made in the study of pairing-based ABE for DFA [2, 4, 7, 8, 13], culminating in adaptively secure public-key ABE for DFA against unbounded collusions based on the k-Lin assumption [14, 21].
In this work, we look at ABE for DFA based on the LWE assumption, which has seen fairly limited progress in spite of the exciting progress we have made in obtaining expressive ABE for circuits [9, 16]. Here, the state of the art is as follows:
-
a public-key scheme secure against collusions of a-prior bounded size (that is, the adversary gets to see a bounded number of secret keys), by combining the scheme of Agrawal and Singh [5] –henceforth AS17– for collusions of size one with generic amplification techniques for bounded collusions in [6, 15, 20];
-
a secret-key scheme for DFA (and NFA) secure against unbounded collusions [3].
Henceforth, we focus on the setting studied in AS17, namely public-key ABE for DFA secure against bounded collusions (indeed, most of the ABE literature consider the public-key setting). From a practical stand-point, the bounded collusion setting already captures a fairly realistic attack scenario. From a theoretical stand-point, it often already requires interesting and insightful techniques. In particular, the core technical novelty in the recent works on ABE for DFA from k-Lin [13, 14, 21] –both in the selective and the adaptive settings– lies in solving the problem in the one-collusion setting; amplification to unbounded collusions is achieved via the dual system encryption methodology [7, 25, 27], which unfortunately, we do not know how to instantiate from LWE.
1.1 Our Contributions
Our main result is a new public-key ABE for DFA based on the LWE assumption, in the bounded collusion setting:
-
Our scheme achieves ciphertext size \(\tilde{O}(\ell + B)\) for attributes of length \(\ell \) and collusion size B and only requires a \(\lambda ^{\omega (1)}\) modulus-to-noise ratio, whereas the AS17 scheme achieves ciphertext size \(\tilde{O}(\ell \cdot B)\) and requires a larger \(\lambda ^{\textsf {poly}(\log \lambda )}\) modulus-to-noise ratio; see Fig. 1 for a comparison.
-
As in AS17, our scheme achieves \( \textsf {sk}\)-selective security, where all the key queries are made before the adversary sees the public key or the ciphertext.
Our construction and its analysis are inspired by the pairing-based ABE for DFA in [13, 14, 26, 26], and is simpler than prior LWE-based schemes in [3, 5] in that we do not require an ABE for circuits [9, 16] as an intermediate building block. Our construction is very algebraic and entails the use of multiple LWE secrets in the ABE ciphertext, whereas the prior LWE-based schemes are more combinatorial. Along the way, we introduce a new technique for lattice trapdoor sampling, which we believe to be of independent interest. Finally, we present a simple candidate public-key ABE for DFA for the unbounded collusion setting (no such heuristic post-quantum candidate was known before, without assuming post-quantum iO).
Summary of LWE-based ABE schemes for DFA, secure against collusions of size B (cf. Sect. 2.1). In the table, Q is the number of states in the DFA M associated with \( \textsf {sk}\) and \(\ell \) is the length of x associated with \( \textsf {ct}\), and \(Q,\ell < \lambda ^{\omega (1)}\). Hardness refers to the modulus-to-noise ratio for the LWE assumption, for \(\lambda ^{\omega (1)}\)-security and \(\lambda ^{-\omega (1)}\) decryption error. We ignore factors polynomial in the security parameter \(\lambda \), \(|\Sigma |\), and \(\log \ell \).
ABE for DFA. Our ABE scheme follows the high-level structure of the pairing-based schemes in [13, 26]:
-
encryption of \(x \in \{0,1\}^\ell \) picks \(\ell +1\) fresh LWE secrets \(\mathbf {s}_0,\mathbf {s}_1,\ldots ,\mathbf {s}_\ell \) (row vectors);
-
a secret key for a DFA with Q states is associated with Q random row vectors \(\tilde{\mathbf {d}}_1,\ldots ,\tilde{\mathbf {d}}_Q\);
-
during decryption, we compute \(\mathbf {s}_i \tilde{\mathbf {d}}_{u_i}^{\!\scriptscriptstyle {\top }}\) (approximately), where \(u_i\) denotes the state reached upon the first i bits of x, for \(i=0,1,\ldots ,\ell \) (i.e., \(u_0\) is the DFA start state).
In a bit more detail,
-
the master public key specifies a pair of matrices \(\mathbf {A}_0,\mathbf {A}_1\) as well as \(\tilde{\mathbf {d}}^{\!\scriptscriptstyle {\top }}_{u_0}\);
-
the ciphertext contains \(\mathbf {s}_0 \tilde{\mathbf {d}}^{\!\scriptscriptstyle {\top }}_{u_0}\) and \(\mathbf {c}_i \approx (\mathbf {s}_{i-1} \Vert -\mathbf {s}_i) \mathbf {A}_{x_i}, i=1,\ldots ,\ell \);
-
the secret key contains \(\mathbf {k}^{\!\scriptscriptstyle {\top }}_{u,\sigma } \leftarrow \mathbf {A}_\sigma ^{-1}{\tilde{\mathbf {d}}^{\!\scriptscriptstyle {\top }}_u \atopwithdelims ()\tilde{\mathbf {d}}^{\!\scriptscriptstyle {\top }}_v}\) for all state transitions \((u,\sigma ) \in [Q] \times \{0,1\}\mapsto v \in [Q]\), where \(\mathbf {A}_\sigma ^{-1}(\cdot )\) denotes a Gaussian pre-image;
-
in order to compute \(\mathbf {s}_i\tilde{\mathbf {d}}_{u_i}^{\!\scriptscriptstyle {\top }}\), it suffices to compute the successive differences \(\mathbf {s}_{i-1} \tilde{\mathbf {d}}^{\!\scriptscriptstyle {\top }}_{u_{i-1}} - \mathbf {s}_i \tilde{\mathbf {d}}^{\!\scriptscriptstyle {\top }}_{u_i}\) as followsFootnote 1:
$$\mathbf {c}_i \cdot \mathbf {k}^{\!\scriptscriptstyle {\top }}_{u_i,x_i} \approx (\mathbf {s}_{i-1} \Vert -\mathbf {s}_i) \mathbf {A}_{x_i} \cdot \mathbf {A}_{x_i}^{-1}{\tilde{\mathbf {d}}^{\!\scriptscriptstyle {\top }}_{u_{i-1}} \atopwithdelims ()\tilde{\mathbf {d}}^{\!\scriptscriptstyle {\top }}_{u_i}} = \mathbf {s}_{i-1} \tilde{\mathbf {d}}^{\!\scriptscriptstyle {\top }}_{u_{i-1}} - \mathbf {s}_i \tilde{\mathbf {d}}^{\!\scriptscriptstyle {\top }}_{u_i}$$
In the proof of security, we will modify the ciphertext distribution in a way that traces the DFA computation path while keeping the secret key distribution unchanged. In contrast, prior ABE for DFA based on k-Lin modifies both the ciphertext and secret key distribution in the security proof (even for collusions of size one). Our proof strategy requires knowing the DFA while simulating the challenge ciphertext, and for that reason, we only achieve \( \textsf {sk}\)-selective security.
Lattice Trapdoor Sampling. We introduce a new lattice trapdoor notion and sampling technique for our proof of security. Given a wide LWE matrix \(\mathbf {A}\), the Micciancio-Peikert (MP) trapdoor [22] is a low-norm matrix \(\mathbf {T}\) such that \(\mathbf {A}\cdot \mathbf {T}= \mathbf {G}\), where \(\mathbf {G}\) is the gadget matrix. Such a matrix \(\mathbf {T}\) allows us to sample a random Gaussian preimage \(\mathbf {A}^{-1}(\mathbf {z})\) for all \(\mathbf {z}\), but it also breaks the LWE assumption with respect to \(\mathbf {A}\) (in fact, we can use \(\mathbf {T}\) to recover \(\mathbf {s}\) given \(\mathbf {s}\mathbf {A}+ \mathbf {e}\)).
In this work, we consider a “half trapdoor”, namely a low-norm matrix \(\mathbf {T}_{1/2}\) such that
That is, let \(\overline{\mathbf {A}},\underline{\mathbf {A}}\in \mathbb {Z}_q^{n \times m} \) denote the top and bottom halves of \(\mathbf {A}\). Then, \(\overline{\mathbf {A}}\cdot \mathbf {T}_{1/2}= \mathbf {0}\) and \(\underline{\mathbf {A}}\cdot \mathbf {T}_{1/2}= \mathbf {G}\), which means \(\mathbf {T}_{1/2}\) is a MP trapdoor for \(\underline{\mathbf {A}}\). We show that \(\mathbf {T}_{1/2}\) satisfies the following properties:
-
restricted trapdoor sampling: Given \(\mathbf {Z}\in \mathbb {Z}_q^{n \times Q},\mathbf {M}\in \{0,1\}^{Q \times Q}\), we can efficiently sample (using \(\mathbf {A},\mathbf {T}_{1/2}\)) a random Gaussian pre-image
$$\begin{aligned} \mathbf {A}^{-1}{\mathbf {D}\atopwithdelims ()\mathbf {D}\mathbf {M}+ \mathbf {Z}},\; \text{ for } \text{ random } \mathbf {D}\leftarrow \mathbb {Z}_q^{n \times Q} \end{aligned}$$(1)These Gaussian pre-images appear in the secret keys with \(\mathbf {D}= [\tilde{\mathbf {d}}_1^{\!\scriptscriptstyle {\top }}\mid \cdots \mid \tilde{\mathbf {d}}^{\!\scriptscriptstyle {\top }}_Q]\), \(\mathbf {M}\in \{0,1\}^{Q \times Q}\) being a DFA transition matrix, and \(\mathbf {Z}= \mathbf {0}\).
-
 : We also require computational hardness of the form \((\mathbf {A}, \mathbf {s}\overline{\mathbf {A}}+ \mathbf {e})\) is pseudorandom given \(\mathbf {T}_{1/2}\). However, such a statement is false since \((\mathbf {s}\overline{\mathbf {A}}+ \mathbf {e}) \cdot \mathbf {T}_{1/2}\approx \mathbf {0}\). Instead, we require that \((\mathbf {A}, \mathbf {s}\overline{\mathbf {A}}+ \mathbf {e})\) is pseudorandom even if the distinguisher gets adaptive queries to the restricted trapdoor sampling oracle in (1); we refer to this as \(\mathbf {T}_{1/2}\)-LWE.
: We also require computational hardness of the form \((\mathbf {A}, \mathbf {s}\overline{\mathbf {A}}+ \mathbf {e})\) is pseudorandom given \(\mathbf {T}_{1/2}\). However, such a statement is false since \((\mathbf {s}\overline{\mathbf {A}}+ \mathbf {e}) \cdot \mathbf {T}_{1/2}\approx \mathbf {0}\). Instead, we require that \((\mathbf {A}, \mathbf {s}\overline{\mathbf {A}}+ \mathbf {e})\) is pseudorandom even if the distinguisher gets adaptive queries to the restricted trapdoor sampling oracle in (1); we refer to this as \(\mathbf {T}_{1/2}\)-LWE.
As a sanity check for restricted trapdoor sampling, observe that it is easy to sample from each of \(\overline{\mathbf {A}}^{-1}(\mathbf {D})\) and \(\underline{\mathbf {A}}^{-1}(\mathbf {D}\mathbf {M}+\mathbf {Z})\), the latter since \(\mathbf {T}_{1/2}\) is a MP-trapdoor for \(\underline{\mathbf {A}}\). However, what we need is to sample from the “intersection” of these two distributions. With regards to \(\mathbf {T}_{1/2}\)-LWE, prior works [10, 18] showed that LWE implies \(\mathbf {T}_{1/2}\)-LWE for the special case where the oracle queries are restricted to \(\mathbf {M}= \mathbf {0}\); these in turn generalize a classic result in [12] showing pseudorandomness of \((\mathbf {A},\mathbf {s}\overline{\mathbf {A}}+ \mathbf {e})\) given \(\overline{\mathbf {A}}^{-1}(\mathbf {D})\) for random \(\mathbf {D}\).
1.2 Technical Overview I: \(\mathbf {T}_{1/2}\)
In the first part of the technical overview, we address the properties of \(\mathbf {T}_{1/2}\).
Restricted Trapdoor Sampling. We show how to sample from the distribution in (1) given \(\mathbf {T}_{1/2}\). Our sampler combines two ideas:
Step 1. First, we describe how to use \(\mathbf {T}_{1/2}\) to sample from a related distribution, namely:

where we replaced \(\mathbf {D}\mathbf {M}, \mathbf {M}\in \{0,1\}^{Q \times Q}\) with
 . We begin by writing (2) as
. We begin by writing (2) as

where the first \(\approx _s\) holds for all \(\mathbf {D}\), and the second \(\approx _s\) uses the fact that \(\mathbf {D}\) is random and a statistical lemma shown in [10, 18]. Next, observe that \((\underline{\mathbf {A}}- \mathbf {M}\overline{\mathbf {A}}) \cdot \mathbf {T}_{1/2}= \mathbf {G}\), which means we can use the MP trapdoor sampling algorithm [22] with \(\mathbf {T}_{1/2}\) as a trapdoor to sample from the distribution \((\underline{\mathbf {A}}- \mathbf {M}\overline{\mathbf {A}})^{-1}(\mathbf {Z})\).
Step 2. We rely on the vectorization operator \(\mathrm {vec}(\cdot )\) for matrices from linear algebra (see Sect. 2) to relate the distributions in (2) and (1). The vectorization of a matrix \(\mathbf {Z}\), denoted by \(\mathrm {vec}(\mathbf {Z})\), is the column vector obtained by stacking the columns of the matrix \(\mathbf {Z}\) on top off one another. Using a standard vectorization identity \(\mathrm {vec}(\mathbf {X}\mathbf {Y}\mathbf {Z}) = (\mathbf {Z}^{\!\scriptscriptstyle {\top }}\otimes \mathbf {X})\mathrm {vec}(\mathbf {Y})\), we have
This basically says that we can sample from the desired distribution in (1) by sampling from the distribution in (2) with \((\mathbf {M}^{\!\scriptscriptstyle {\top }}\otimes \mathbf {I}_n) \mathrm {vec}(\mathbf {D})\) in place of
 .
.
LWE Implies \(\mathbf {T}_{\mathbf {1/2}}\)-LWE. Next, we sketch a proof of the statement LWE implies \(\mathbf {T}_{1/2}\)-LWE, that is, \((\mathbf {A}, \mathbf {s}\overline{\mathbf {A}}+ \mathbf {e})\) is pseudorandom given the restricted trapdoor sampling oracle in (1). In the reduction, we sample \(\mathbf {A}\) as
where \(\mathbf {A}' \leftarrow \mathbb {Z}_q^{2n \times (m - n \log q)}, \mathbf {R}\leftarrow \{0,1\}^{(m-n \log q) \times n \log q}\).
-
Note that \(\mathbf {T}_{1/2}= {-\mathbf {R}\atopwithdelims ()\mathbf {I}}\) satisfies \(\mathbf {A}\cdot \mathbf {T}_{1/2}= {\mathbf {0} \atopwithdelims ()\mathbf {G}}\). This means that we can use \(\mathbf {R}\) to compute \(\mathbf {T}_{1/2}\) and to implement the restricted trapdoor sampling oracle in (1).
-
By LWE w.r.t. the public matrix \(\overline{\mathbf {A}}'\), we have
$$\mathbf {s}\overline{\mathbf {A}}+ \mathbf {e}\approx _s (\mathbf {s}\overline{\mathbf {A}}' + \mathbf {e}', (\mathbf {s}\overline{\mathbf {A}}' + \mathbf {e}') \mathbf {R}+ \mathbf {e}'') \approx _c (\mathbf {c}, \mathbf {c}\mathbf {R}+ \mathbf {e}''),\; \mathbf {c}\leftarrow \mathbb {Z}_q^{m - n \log q}$$This holds even if the distinguisher gets \(\mathbf {R}\), which we need to implement the oracle.
-
Now, observe that the oracle in (1) leaks no information about \(\mathbf {R}\) beyond \(\overline{\mathbf {A}}' \mathbf {R}\). By the left-over hash lemma, \(\mathbf {c}\mathbf {R}\) is statistically random given \(\mathbf {c},\overline{\mathbf {A}}',\overline{\mathbf {A}}'\mathbf {R}\). (A similar argument first appeared in [1].)
1.3 Technical Overview II: ABE for DFA
We proceed to provide a technical overview of our ABE for DFA. In this work, it is convenient to specify a DFA using vector-matrix notation. That is, a DFA \(M\) is a tuple \((\,Q,\Sigma ,\{\mathbf {M}_{\sigma }\}_{\sigma \in \Sigma },\mathbf {u}_0,\mathbf {f}\,)\) where \(\Sigma \) is the alphabet and
The DFA accepts an input \(x = (x_1,\ldots ,x_\ell ) \in \Sigma ^\ell \), denoted by \(M(x)=1\), if
ABE for B = 1. We begin with our ABE scheme for collusions of size one:
In the rest of this overview, we assume \(\Sigma = \{0,1\}\), and mostly ignore the error terms \(e_0,\mathbf {e}_i\) for notational simplicity. To see how decryption works, we first let
That is, \(\mathbf {u}_i^{\!\scriptscriptstyle {\top }}\) is the characteristic vector for the state reached upon reading \(x_1,\ldots ,x_i\). In addition, let \(\mathbf {d}_i^{\!\scriptscriptstyle {\top }}:= \mathbf {D}\cdot \mathbf {u}_i^{\!\scriptscriptstyle {\top }}\) denote the corresponding column in \(\mathbf {D}\) (denoted by \(\tilde{\mathbf {d}}^{\!\scriptscriptstyle {\top }}_{u_i}\) in Sect. 1.1). It is straight-forward (though a little tedious) to verify that
In particular, whenever \(M(x)=1\), we can recover \(\mu \) from \(\mathbf {c}_{\ell +2}\). Note that the noise growth in (5) grows with \(\ell \), and since we can only bound \(\ell \) by \(\lambda ^{\omega (1)}\), we require a \(\lambda ^{\omega (1)}\) modulus-to-noise ratio for decryption correctness. The security proof additionally uses noise smudging, which also requires a \(\lambda ^{\omega (1)}\) modulus-to-noise ratio.
Security. The main tool we have for the proof of security is \(\mathbf {T}_{1/2}\)-LWE, which we want to use to replace \(\mathbf {s}_{i-1} \overline{\mathbf {A}}_{x_i}\) in \(\mathbf {c}_i\) with random (while relying the oracle for restricted trapdoor sampling to simulate the corresponding secret keys). We cannot do so directly, since each \(\mathbf {s}_{i-1}\) also appears in \(\mathbf {c}_{i-1}\) (\(c_0\), in the case \(i=1\)). To resolve this issue, we start by using (5), which tells us that when \(M(x)=0\) as is the case for unauthorized keys in the proof of security, we have:
This allows us to write \(c_{0}\) as a function of \(\mathbf {c}_1,\ldots ,\mathbf {c}_\ell ,\mathbf {c}_{\ell +1}\) and \(\mathbf {K}_0,\mathbf {K}_1\) from \( \textsf {sk}_M\), thereby “eliminating” \(\mathbf {s}_0\) from \(c_0\). (Here, we use the fact that we are in the \( \textsf {sk}\)-selective setting.) At this point, we can replace \(\mathbf {s}_0 \overline{\mathbf {A}}_{x_1}\) in \(\mathbf {c}_1\) with random, and thus \(\mathbf {c}_1\) with random. This in “eliminates” \(\mathbf {s}_1\) from \(\mathbf {c}_1\), upon which we can replace \(\mathbf {s}_1 \overline{\mathbf {A}}_{x_2}\) in \(\mathbf {c}_2\) and thus \(\mathbf {c}_2\) with random. This continues until we have replaced \(\mathbf {c}_\ell \) with random. At this point, it suffices to argue that
hides \(\mu \), which can be handled using fairly standard techniques.
Handling B Collusions. Our basic scheme extends naturally to handle B collusions by sampling a fresh \(\mathbf {D}\) per secret key except one important caveat: the encryptor needs to know \(\mathbf {d}_0 = \mathbf {D}\cdot \mathbf {u}_0^{\!\scriptscriptstyle {\top }}\) in order to compute \(\mathbf {s}_0 \mathbf {d}_0\), and for the security proof, we need a fresh \(\mathbf {d}_0\) per secret key. To solve this problem, we modify the scheme as follows:
-
during set-up, we sample and publish \(\mathbf {d}_{0,j}, j \in [B]\) in \(\textsf {mpk}\);
-
the encryptor includes
 in \( \textsf {ct}\), which increases the ciphertext size by an additive factor of \(B \cdot \textsf {poly}(\lambda )\) (independent of \(\ell \));
in \( \textsf {ct}\), which increases the ciphertext size by an additive factor of \(B \cdot \textsf {poly}(\lambda )\) (independent of \(\ell \)); -
when issuing the j’th key, we sample a random \(\mathbf {D}\) such that \(\mathbf {D}\cdot \mathbf {u}_0^{\!\scriptscriptstyle {\top }}= \mathbf {d}_{0,j}\).
The security proof is similar to that for \(B=1\), except we start by using (5) to rewrite each \(\mathbf {c}_{0,j}\) in terms of \(\mathbf {c}_1,\ldots ,\mathbf {c}_{\ell +1}\).
Candidate ABE for DFA Against Unbounded Collusions. We start with our ABE for \(B=1\) in (4) and make the following modifications:
-
replace \(\mathbf {d}_0\) in \(\textsf {mpk}\) with a random matrix \(\mathbf {A}_{\text {st}}\);
-
replace \(\mathbf {s}_0\mathbf {d}_0^{\!\scriptscriptstyle {\top }}\) in \( \textsf {ct}\) with \(\mathbf {s}_0\mathbf {A}_{\text {st}}\);
-
add \(\mathbf {k}_{\text {st}} \leftarrow \mathbf {A}_{\text {st}}^{-1}(\mathbf {D}\mathbf {u}_0^{\!\scriptscriptstyle {\top }})\) to the secret key, where a fresh random \(\mathbf {D}\leftarrow \mathbb {Z}_q^{n \times Q}\) is chosen for each key.
Correctness follows as before, except we first compute \(\mathbf {s}_0 \mathbf {d}_0^{\!\scriptscriptstyle {\top }}\) using \(\mathbf {s}_0\mathbf {A}_{\text {st}} \cdot \mathbf {k}_{\text {st}}\). We believe that our candidate sheds new insights into both avenues and concrete difficulties for realizing a public-key ABE for DFA against unbounded collusions from LWE.
1.4 Prior Works
We provide a brief overview of prior LWE-based scheme, along with a folklore construction based on general circuits. We will refer to constructions secure against collusions of size 1 as a one-key scheme, and we use \(Q_{\max }\) to denote an upper bound on the number of DFA states.
A Folklore Construction via General Circuits. We can get bounded-collusion ABE for DFA by using bounded-collusion ciphertext-policy ABE for circuits; the latter can be constructed based on any semantically secure public-key encryption scheme –and thus LWE with \(\textsf {poly}(\lambda )\) hardness– via garbled circuits [15, 23]. Concretely, we encode the DFA M as a bit string of length \(O(Q \log Q)\) and the DFA input \(x \in \{0,1\}^\ell \) as a circuit of size \(O(\ell \cdot Q)\) that on input M, outputs M(x). The main draw-back is that the ciphertext size grows with \(Q_{\max }\), which we want to avoid.
The Agrawal-Singh AS17 Scheme. The AS17 scheme is a one-key \( \textsf {sk}\)-selective functional encryption (FE) scheme for DFA based on LWE. The construction uses the GKPVZ compact one-key FE \(\mathsf {cFE}\) for circuits, a symmetric-key encryption scheme \(\mathsf {SE}\), and a PRF \(\mathsf {PRF}\) (the AS17 scheme uses a pairwise-independent hashing instead of a PRF). We sketch a simplified variant of the AS17 scheme in the ABE setting:
-
Encryption of \(x \in \{0,1\}^\ell \) picks \(\ell \) PRF keys \(K_1,\ldots ,K_\ell \). During decryption, the decryptor computes \(\mathsf {PRF}(K_i,u_i)\) for \(i=1,\ldots ,\ell \), where \(u_i\) denotes the state reached upon the first i bits of x.
-
In order to go from \(\mathsf {PRF}(K_i,u_i)\) to \(\mathsf {PRF}(K_{i+1},u_{i+1})\), the decryptor would need to compute
$$\begin{aligned} \mathsf {SE}.\mathsf {Enc}_{\mathsf {PRF}(K_i,u_i)}(\mathsf {PRF}(K_{i+1},u_{i+1})) \end{aligned}$$To compute the quantity above, the decryptor first computes \(\mathsf {cFE}.\mathsf {Enc}(x_i,u_i,K_i,K_{i+1})\). The ABE secret key then contains \(\mathsf {cFE}\) secret keys that decrypts the \(\mathsf {cFE}\)-ciphertext to \(\mathsf {SE}.\mathsf {Enc}_{\mathsf {PRF}(K_i,u_i)}(\mathsf {PRF}(K_{i+1},u_{i+1}))\). This requires generating \(\mathsf {cFE}\) secret keys for circuits of depth \(O(\log Q)\), and hence a noise-to-modulus ratio \(\lambda ^{O(\log Q_{\max })} = \lambda ^{\textsf {poly}(\log \lambda )}\).Footnote 2
-
One question remains: how does the decryptor compute \(\mathsf {cFE}.\mathsf {Enc}(x_i,u_i,K_i,K_{i+1})\)? Note that the encryptor cannot compute this quantity because it does not know \(u_i\). The naive solution would be for the encryptor to publish in the ciphertext:
$$ \bigl \{\, \mathsf {SE}.\mathsf {Enc}_{\mathsf {PRF}(K_i,u)}(\mathsf {cFE}.\mathsf {Enc}(x_i,u,K_i,K_{i+1})) : u \in [Q_{\max }]\,\bigr \} $$However, this would mean that the final ABE ciphertext size grows with \(Q_{\max }\) instead of \(\log Q_{\max }\). Instead, AS17 shows how to compress the above quantity, using the fact that the \(\mathsf {cFE}\) ciphertext is “decomposable”.
An open problem is whether our techniques extend to functional encryption for DFA, as achieved in AS17.
The Agrawal-Maitra-Yamada AMY19 Scheme. The AMY19 scheme is a private-key ABE for NFA based on LWE; the scheme achieves \( \textsf {ct}, \textsf {sk}\)-selective security against unbounded ciphertext queries and against unbounded collusions. The AMY19 scheme uses two special ABE schemes:
-
(i)
a public-key ABE for the relation \(M(x) \wedge (|x| {\mathop {\le }\limits ^{?}} |M|)\);
-
(ii)
a secret-key ABE for the relation \(M(x) \wedge (|x| {\mathop {>}\limits ^{?}} |M|)\).
These two ABE schemes are constructed using the BGGHNSVV ABE for circuits [9] and using the fact that an NFA M for inputs of length \(\ell \) can be simulated using a circuit of size \(O(\ell \cdot |M|)\) and depth \(\textsf {poly}(\log \ell , \log |M|)\). The final ABE scheme for NFA contains BGGHNSVV ciphertexts into both the ciphertexts and the secret keys, and since the BGGHNSVV scheme is \( \textsf {sk}\)-selective, the AMY19 scheme is \( \textsf {ct}, \textsf {sk}\)-selective.
Prior k-Lin Based Schemes. As mentioned in the first step of our security proof, we essentially embed the DFA computation into the challenge ciphertext. In contrast, prior k-Lin based schemes embed the DFA computation into the secret key, which in turn requires using a computational assumption over the secret key space.
1.5 Discussion
ABE for DFA and More. In this work, we present new constructions and techniques for LWE-based ABE for DFA, achieving some improvements over prior works of AS17 and AMY19 along the way. Our techniques are largely complementary to those in AS17 and AMY19, and we believe there is much more to be gained by combining the techniques and insights from all three works. We conclude with two open problems:
-
Find an attack on our candidate ABE against unbounded collusions. Or, use the candidate as a starting point to design a simple secret-key ABE for DFA against unbounded collusions based on the LWE assumption, possibly by leveraging additional insights from AMY19.
-
It seems quite plausible that we can combine our techniques with ideas from [21] to obtain a simple one-collusion ABE for Turing machines M running in time T and space S, where \(| \textsf {ct}| = \textsf {poly}(\ell ) \cdot T \cdot S \cdot 2^S\) and \(| \textsf {sk}| = O(|M|)\). A more interesting problem is to design a simple and algebraic one-collusion ABE for Turing machines running in time T where \(| \textsf {ct}| = \textsf {poly}(\ell ,T)\) and \(| \textsf {sk}| = \textsf {poly}(|M| )\), as achieved in AS17.
LWE-based ABE with Multiple LWE Secrets. More broadly, we see this work as also taking a first step towards exploring the use of multiple LWE secrets in LWE-based ABE as well as bringing design ideas from more complex pairing-based schemes to the LWE setting. While the use of multiple LWE secrets is implicit also in AS17 and AMY19 (where the ciphertext contains multiple ciphertexts from some existing LWE-based scheme), our construction makes the connection more explicit.
2 Preliminaries
Notations. We use boldface lower case for row vectors (e.g. \(\mathbf {r}\)) and boldface upper case for matrices (e.g. \(\mathbf {R}\)). For integral vectors and matrices (i.e., those over \(\mathbb {Z}\)), we use the notation \(|\mathbf {r}|,|\mathbf {R}|\) to denote the maximum absolute value over all the entries. We use \(v \leftarrow \mathcal {D}\) to denote a random sample from a distribution \(\mathcal {D}\), as well as \(v \leftarrow S\) to denote a uniformly random sample from a set S. We use \(\approx _s\) and \(\approx _c\) as the abbreviation for statistically close and computationally indistinguishable.
Matrix Operations. The vectorization of a matrix \(\mathbf {Z}\), denoted by \(\mathrm {vec}(\mathbf {Z})\), is the column vector obtained by stacking the columns of the matrix \(\mathbf {Z}\) on top off one another. For instance, for the \(2\times 2\) matrix \(\mathbf {Z}= \begin{pmatrix} a &{} b \\ c &{} d \end{pmatrix}\), we have
We use \(\mathrm {vec}^{-1}(\cdot )\) to denote the inverse operator so that \(\mathrm {vec}^{-1}(\mathrm {vec}(\mathbf {Z}) = \mathbf {Z}\). For all matrices \(\mathbf {X},\mathbf {Y},\mathbf {Z}\) of the appropriate dimensions, we have \(\mathrm {vec}(\mathbf {X}\mathbf {Y}\mathbf {Z}) = (\mathbf {Z}^{\!\scriptscriptstyle {\top }}\otimes \mathbf {X})\mathrm {vec}(\mathbf {Y})\).
The tensor product (Kronecker product) for matrices \(\mathbf {A}= (a_{i,j}) \in \mathbb {Z}^{\ell \times m}\), \(\mathbf {B}\in \mathbb {Z}^{n\times p}\) is defined as
The mixed-product property for tensor product says that
DFA. We use \(M=(\,Q,\Sigma ,\{\mathbf {M}_{\sigma }\}_{\sigma \in \Sigma },\mathbf {u}_0,\mathbf {f}\,)\) to describe deterministic finite automata (DFA for short), where \(\mathbf {u}_0,\mathbf {f}\in \{0,1\}^Q, \mathbf {M}_\sigma \in \{0,1\}^{Q \times Q}\), and both \(\mathbf {u}_0\) and every column of \(\mathbf {M}_\sigma \) contains exactly one 1. For any \(x = (x_1,\ldots ,x_\ell ) \in \Sigma ^\ell \), we have:
2.1 Attribute-Based Encryption
Syntax. An attribute-based encryption (ABE) scheme for some class \(\mathcal {C}\) consists of four algorithms:
-
\(\mathsf {Setup}(1^\lambda ,\mathcal {C})\rightarrow (\textsf {mpk}, \textsf {msk})\). The setup algorithm gets as input the security parameter \(1^\lambda \) and class description \(\mathcal {C}\). It outputs the master public key \(\textsf {mpk}\) and the master secret key \( \textsf {msk}\).
-
\(\mathsf {Enc}(\textsf {mpk},x,\mu )\rightarrow \textsf {ct}_x\). The encryption algorithm gets as input \(\textsf {mpk}\), an input x and a message \(\mu \in \{0,1\}\). It outputs a ciphertext \( \textsf {ct}_{x}\). Note that x is public given \( \textsf {ct}_x\).
-
\(\mathsf {KeyGen}(\textsf {mpk}, \textsf {msk},M)\rightarrow \textsf {sk}_{M}\). The key generation algorithm gets as input \(\textsf {mpk}\), \( \textsf {msk}\) and \(M\in \mathcal {C}\). It outputs a secret key \( \textsf {sk}_{M}\). Note that \(M\) is public given \( \textsf {sk}_M\).
-
\(\mathsf {Dec}(\textsf {mpk}, \textsf {sk}_{M}, \textsf {ct}_x ) \rightarrow m\). The decryption algorithm gets as input \( \textsf {sk}_M\) and \( \textsf {ct}_x\) such that \(M(x)=1\) along with \(\textsf {mpk}\). It outputs a message \(\mu \).
Correctness. For all inputs x and \(M\) with \(M(x)=1\) and all \(\mu \in \{0,1\}\), we require
Security Definition. For a stateful adversary \(\mathcal {A}\), we define the advantage function
with the restriction that all queries \(M\) that \(\mathcal {A}\) sent to \(\mathsf {KeyGen}(\textsf {mpk}, \textsf {msk},\cdot )\) satisfy \(M(x^*) = 0\). An ABE scheme is \( \textsf {sk}\)-selectively secure if for all PPT adversaries \(\mathcal {A}\), the advantage \(\mathsf {Adv}^{\textsc {abe}}_{\mathcal {A}}(\lambda )\) is a negligible function in \(\lambda \). Note that \(\mathcal {A}\) only gets oracle access to \(\mathsf {KeyGen}\) at the beginning of the experiment before it sees \(\textsf {mpk}\). (The security experiment starts with \((\textsf {mpk}, \textsf {msk}) \leftarrow \mathsf {Setup}\) to generate the first two inputs to the \(\mathsf {KeyGen}\) oracle.)
Bounded-Collusion Setting. We say that an ABE scheme is B-bounded secure if \(\mathsf {Setup}\) gets an additional input \(1^B\), and the adversary is only allowed to make at most B queries to \(\mathsf {KeyGen}\). For simplicity, we focus on tag-based B-bounded security (sometimes referred to as stateful key generation in the literature) where:
-
\(\mathsf {KeyGen}\) takes an additional tag \(j \in [B]\) and correctness holds for all \(j \in [B]\);
-
In the security game, the queries made to \(\mathsf {KeyGen}\) must correspond to distinct tags.
It is easy to see that we can construct a tag-based B-bounded scheme from any 1-bounded scheme by running B independent copies of the 1-bounded scheme; this incurs a factor B blow-up in \(|\textsf {mpk}|,| \textsf {ct}|\) while \(| \textsf {sk}|\) remains the same. Furthermore, we can construct a B-bounded scheme from a tag-based O(B)-bounded scheme [6, 15, 20], with an additional \(O(\lambda ^2 (\log B)^2)\) multiplicative blow-up in \(|\textsf {mpk}|,| \textsf {ct}|\). We sketch a construction from [20] for removing tags with a bigger blow-up: take a tag-based \(O(B^2)\)-bounded scheme and generate secret keys for a random tag. Now, if the adversary gets at most B keys, then by a birthday bound, the advantage of the adversary is bounded by 1/4, and then we can apply hardness amplification to reduce the advantage to negligible.
2.2 Lattices Background
Learning with Errors. Given \(n,m,q,\chi \in \mathbb {N}\), the \(\mathsf {LWE}_{n,m,q,\chi }\) assumption states that
where
Trapdoor and Preimage Sampling. Given any \(\mathbf {z}\in \mathbb {Z}_q^n\), \(s>0\), we use \( \mathbf {A} ^{-1}(\mathbf {z},s)\) to denote the distribution of a vector \(\mathbf {y}\) sampled from \(\mathcal {D}_{\mathbb {Z}^m,s}\) conditioned on \( \mathbf {A} \mathbf {y}= \mathbf {z}\pmod q\). We sometimes suppress s when the context is clear.
There is a p.p.t. algorithm \(\mathsf {TrapGen}(1^n, 1^m, q)\) that, given the modulus \(q\ge 2\), dimensions n, m such that \(m \ge 2n\log q\), outputs \( \mathbf {A} \approx _s U(\mathbb {Z}^{n\times m}_q)\) with a trapdoor \(\tau \). Moreover, there is a p.p.t. algorithm that for \(s \ge 2\sqrt{n\log q}\), given \(( \mathbf {A} , \tau )\leftarrow \mathsf {TrapGen}(1^n, 1^m, q)\), \(\mathbf {z}\in \mathbb {Z}_q^n\), outputs a sample from \( \mathbf {A} ^{-1}(\mathbf {z}, s)\).
3 Trapdoor Sampling with \(\mathbf {T}_{1/2}\) and a Computational Lemma
We describe our new computational lemma, which we coin the “\(\mathbf {T}_{1/2}\)-LWE assumption” and which says that LWE holds in the presence of some oracle \(\mathcal {O}_\mathbf {A}(\cdot )\). Then, we show that the \(\mathbf {T}_{1/2}\)-LWE assumption follows from the LWE assumption.
3.1 LWE Implies \(\mathbf {T}_{1/2}\)-LWE
Theorem 1
(\(\mathbf {T}_{1/2}\)-LWE assumption). Fix parameters n, m, q. Under the \(\mathsf {LWE}_{n,m-n \log q,\chi }\) assumption, we have that
where
and where the distinguisher gets unbounded, adaptive queries to an oracle \(\mathcal {O}_\mathbf {A}(\cdot )\) that on input \(\mathbf {M}\in \mathbb {Z}_q^{Q \times Q}, \mathbf {Z}\in \mathbb {Z}_q^{n \times Q}\), outputs a sample from

where \(s^2 \ge O(m) + \omega (\log mQ + \log n)\).
Proof
We sample \(\mathbf {A}\) as
where \(\mathbf {A}' \leftarrow \mathbb {Z}_q^{2n \times (m - n \log q)}, \mathbf {R}\leftarrow \{0,\pm 1\}^{(m-n \log q) \times n \log q}\).Footnote 3 Setting \(\mathbf {T}_{1/2}:= {-\mathbf {R}\atopwithdelims ()\mathbf {I}}\), we have \(\mathbf {A}\cdot \mathbf {T}_{1/2}= {\mathbf {0} \atopwithdelims ()\mathbf {G}}\). We show in the next section that using \(\mathbf {A},\mathbf {T}_{1/2}\), we can efficiently simulate the oracle \(\mathcal {O}_\mathbf {A}\). We can then complete the current proof in two steps:
-
By the LWE assumption, we have:
$$\begin{aligned} (\mathbf {A}', \mathbf {s}\mathbf {A}' + \mathbf {e}') \approx _c (\mathbf {A}', \mathbf {c}') \end{aligned}$$where \(\mathbf {c}' \leftarrow \mathbb {Z}_q^{m - n \log q}, \mathbf {e}' \leftarrow \mathcal {D}_{\mathbb {Z}^{m-n \log q},\chi }\). This means that
$$\mathbf {s}\overline{\mathbf {A}}+ \mathbf {e}\approx _s (\mathbf {s}\overline{\mathbf {A}}' + \mathbf {e}' + \mathbf {e}''_0, (\mathbf {s}\overline{\mathbf {A}}' + \mathbf {e}') \mathbf {R}+ \mathbf {e}'') \approx _c (\mathbf {c}+ \mathbf {e}''_0, \mathbf {c}\mathbf {R}+ \mathbf {e}''),\; \mathbf {c}\leftarrow \mathbb {Z}_q^{m - n \log q}$$even given \(\mathbf {A},\mathbf {R}\), where the first \(\approx _s\) uses noise smudging. We can then use \(\mathbf {R}\) to simulate \(\mathcal {O}_\mathbf {A}(\cdot )\).
-
By left-over hash lemma, we can replace \(\mathbf {c}' \mathbf {R}\) with random, even given \((\mathbf {A}',\mathbf {c}',\mathbf {A}' \mathbf {R})\). Here, we crucially rely on the fact that the distribution \(\mathcal {O}_\mathbf {A}(\cdot )\) depends only on \(\mathbf {A}\) (and thus \(\mathbf {A}',\mathbf {A}' \mathbf {R}\)) and leaks no additional information about \(\mathbf {R}\).
3.2 Trapdoor Sampling with \(\mathbf {T}_{1/2}\)
Additional Notation. We adopt additional notation from [11]. We use \(\eta _\epsilon (\cdot )\) to denote the smoothing parameter of a lattice, and \(\Lambda ^\perp (\cdot )\) to denote the q-ary kernel lattice. We use  for probability distributions.
for probability distributions.
Lemma 1
([10, Lemma 4.1, 4.2]). Fix parameters \(\epsilon , s, n, m, q\) such that \(m > 18n \log q\). For all \(\mathbf {A}\in \mathbb {Z}_q^{2n \times m}\) satisfying \(\mathbf {A}\cdot \{0,1\}^m = \mathbb {Z}_q^{2n}\), and for all \(\mathbf {z}\in \mathbb {Z}_q^n\) and \(s > \eta _\epsilon (\Lambda ^\perp (\mathbf {A}))\), the distributions:

are \(2\epsilon \)-statistically close.
Note that the difference from the notation in [10] in that we switched the roles of \(\overline{\mathbf {A}},\underline{\mathbf {A}}\). Also, the condition in \(\mathbf {A}\) as stated in [10] is that \(\bigl \{\, \overline{\mathbf {A}}\cdot \mathbf {x}\mid \mathbf {x}\in \{0,1\}^m \cap \Lambda ^\perp (\underline{\mathbf {A}}) \,\bigr \} = \mathbb {Z}_q^n\), which is implied by \(\mathbf {A}\cdot \{0,1\}^m = \mathbb {Z}_q^{2n}\).
Theorem 2
Fix parameters \(n, q, m \ge O(n \log q)\). There is an efficient algorithm that on input \(\mathbf {A}\in \mathbb {Z}_q^{2n \times m}, \mathbf {T}_{1/2}\in \mathbb {Z}^{m \times n \log q}, \mathbf {M}\in \mathbb {Z}_q^{Q \times Q}, \mathbf {Z}\in \mathbb {Z}_q^{n \times Q},s \in \mathbb {N}\) such that \(\mathbf {A}\cdot \mathbf {T}_{1/2}= {\mathbf {0} \atopwithdelims ()\mathbf {G}}\), outputs a sample statistically close to the distribution

if the following conditions are satisfied:
As shown in [12], the conditions \(\mathbf {A}\cdot \{0,1\}^m = \mathbb {Z}_q^{2n}\) and \(\lambda _m(\Lambda ^\perp (\mathbf {A})) = O(1)\) are satisfied for all but a \(1-2q^{-2n}\) fraction of \(\mathbf {A}\).
Proof
We start by specifying the algorithm:
Algorithm. Output
where \((\mathbf {I}_Q \otimes \underline{\mathbf {A}}- \mathbf {M}^{\!\scriptscriptstyle {\top }}\otimes \overline{\mathbf {A}})^{-1}(\cdot )\) is computed using MP trapdoor sampling [22] with \(\mathbf {I}_Q \otimes \mathbf {T}_{1/2}\) as a trapdoor.
The analysis proceeds in three steps:
Step 1. We show that for all \(\mathbf {M},\mathbf {Z}\):

To show this, first observe that for all \(\mathbf {A},\mathbf {D},\mathbf {M},\mathbf {Z}\) and all \(\mathbf {K}\), we have:
where the second \(\Longleftrightarrow \) uses
This means that for all \(\mathbf {A},\mathbf {D},\mathbf {M},\mathbf {Z}\) and all s, the two distributions
are identically distributed.
Applying Lemma 1 to
we have

In Step 3, we check that \(\mathbf {A}'\) satisfies the conditions for Lemma 1.
Step 2. Observe that
which means that we can use \(\mathbf {I}_Q \otimes \mathbf {T}_{1/2}\) as a MP-trapdoor to sample from the distribution \((\mathbf {I}_Q \otimes \underline{\mathbf {A}}- \mathbf {M}^{\!\scriptscriptstyle {\top }}\otimes \overline{\mathbf {A}})^{-1}(\mathrm {vec}(\mathbf {Z}))\).
Step 3. To complete the analysis, we need to bound \(\eta _\epsilon (\mathbf {A}')\) and show that \(\mathbf {A}' \cdot \{0,1\}^{mQ} = \mathbb {Z}_q^{2nQ}\) (in order to invoke Lemma 1). Observe that
This means that \(\Lambda ^\perp (\mathbf {A}') = \Lambda ^\perp (\mathbf {I}_Q \otimes \mathbf {A})\), and that we can bound \(\eta _\epsilon (\Lambda ^\perp (\mathbf {I}_Q \otimes \mathbf {A}))\) using \(\lambda _m(\Lambda ^\perp (\mathbf {A})) = O(1)\). In addition, we have:
This completes the proof. \(\square \)
4 ABE for DFA Against Bounded Collusions
In this section, we present our ABE scheme for DFA against bounded collusions.
4.1 Our Scheme
-
\(\mathsf {Setup}(1^n,\Sigma ,1^B)\): Sample
$$(\mathbf {A}_\sigma ,\tau _{\sigma }) \leftarrow \mathsf {TrapGen}(1^{2n},1^m,q),\,\sigma \in \Sigma , \; (\mathbf {A}_{\text {end}},\tau _{\text {end}}) \leftarrow \mathsf {TrapGen}(1^n,1^m,q), \; \mathbf {d}_{0,j}, \mathbf {d}_{\text {end}} \leftarrow \mathbb {Z}_q^n,\,j \in [B]$$Output

-
\(\mathsf {Enc}(\textsf {mpk},(x_1,\ldots ,x_\ell ) \in \Sigma ^\ell , \mu \in \{0,1\})\). Sample
$$ \mathbf {s}_0,\mathbf {s}_1,\ldots ,\mathbf {s}_\ell \leftarrow \mathbb {Z}_q^n,\quad e_{0,j},e_{\ell +2} \leftarrow \mathcal {D}_{\mathbb {Z},\hat{\chi }},\,j \in [B], \quad \mathbf {e}_1,\ldots ,\mathbf {e}_\ell ,\mathbf {e}_{\ell +1} \leftarrow \mathcal {D}_{\mathbb {Z}^m,\chi } $$Output

-
\(\mathsf {KeyGen}( \textsf {msk},M_j,j)\): Parse \(M_j=(Q_j,\Sigma ,\left\{ \, \mathbf {M}_{\sigma ,j}\, \right\} _{\sigma \in \Sigma },\mathbf {u}_{0,j},\mathbf {f}_j)\). Sample
$$\mathbf {D}_j \leftarrow \mathbb {Z}_q^{n \times Q_j} \text{ s.t. } \mathbf {D}_j \cdot \mathbf {u}_{0,j}^{\!\scriptscriptstyle {\top }}= \mathbf {d}_{0,j}^{\!\scriptscriptstyle {\top }}, \quad \mathbf {K}_{\text {end},j} \leftarrow \mathbf {A}_{\text {end}}^{-1}(\mathbf {D}_j-\mathbf {d}^{\!\scriptscriptstyle {\top }}_{\text {end}} \otimes \mathbf {f}_j),\quad \mathbf {K}_{\sigma ,j} \leftarrow \mathbf {A}_{\sigma }^{-1}{\mathbf {D}_j \atopwithdelims ()\mathbf {D}_j \mathbf {M}_{\sigma ,j}},\,\sigma \in \Sigma $$using trapdoors \(\tau _{\text {end}},\left\{ \, \tau _\sigma \, \right\} _{\sigma \in \Sigma }\). Output
$$ \textsf {sk}_{M_j} := \bigl (\,\mathbf {K}_{\text {end},j},\; \left\{ \, \mathbf {K}_{\sigma ,j}\, \right\} _{\sigma \in \Sigma }\,\bigr )$$ -
\(\mathsf {Dec}( \textsf {sk}, \textsf {ct},j)\): For \(i=1,\ldots ,\ell \), compute \(\mathbf {u}_{i,j}^{\!\scriptscriptstyle {\top }}:= \mathbf {M}_{x_i,j} \cdots \mathbf {M}_{x_1,j}\mathbf {u}_{0,j}^{\!\scriptscriptstyle {\top }}\). Output
$$\begin{aligned} \mathsf {round}_{q/2}\bigl (\,c_{0,j} + \bigl (\sum _{i=1}^\ell \mathbf {c}_i \cdot \mathbf {K}_{x_i,j} \cdot {\mathbf {u}_{i-1,j}^{\!\scriptscriptstyle {\top }}}\bigr ) + \mathbf {c}_{\ell +1} \cdot \mathbf {K}_{\text {end},j} \cdot \mathbf {u}_{\ell ,j}^{\!\scriptscriptstyle {\top }}+ \mathbf {c}_{\ell +2}\,\bigr ) \end{aligned}$$where \(\mathsf {round}_{q/2}: \mathbb {Z}_q \rightarrow \{0,1\}\) denotes rounding to the nearest multiple of q/2.
Parameters. The Gaussians in \(\mathbf {A}_\sigma ^{-1}(\cdot ), \mathbf {A}_{\text {end}}^{-1}(\cdot )\) have parameters \(O(m + \log Q)\). The choice of \(n,m,q,\chi \) comes from the LWE assumption subject to
In particular, this means
where \(\tilde{O}(\cdot )\) hides \(\textsf {poly}(\log \lambda , \log \ell , \log \log Q)\) factors. To handle general a-prior unbounded \(\ell , Q\) as is necessarily the case in ABE for DFA, we just bound \(\ell ,Q\) by \(\lambda ^{\omega (1)}\).
Correctness. Fix \(x,j,M_j\) such that \(M_j(x) = 1\). Write \(\mathbf {d}_{i,j} := \mathbf {D}_j \cdot \mathbf {u}^{\!\scriptscriptstyle {\top }}_{i,j}\), for \(j=0,\ldots ,\ell \). First, we show that
This follows readily from
which in turns follows from
Next, since \(M_j(x) =1\), we have \(\mathbf {f}_j \mathbf {u}_{\ell ,j}^{\!\scriptscriptstyle {\top }}= 1\). It follows from (6) that
In particular, the error term is bounded by \(\hat{\chi }+(\ell +1) \dot{\chi }\).
4.2 \( \textsf {sk}\)-Selective Security
We assume that the adversary always makes exactly B key queries; this is WLOG, since we can always repeat some of the queries.
Game Sequence. The proof of security follows a sequence of games:
-
\(\mathsf {H}_0\): Real game where

-
\(\mathsf {H}'_0\): same as \(\mathsf {H}_0\), except we replace every \(c_{0,j}\) with
$$\begin{aligned} \Bigl (\sum _{i=1}^\ell \mathbf {c}_i \cdot \mathbf {K}_{x_i,j} \cdot {\mathbf {u}_{i-1,j}^{\!\scriptscriptstyle {\top }}}\Bigr ) + \mathbf {c}_{\ell +1} \cdot \mathbf {K}_{\text {end},j} \cdot \mathbf {u}_{\ell ,j}^{\!\scriptscriptstyle {\top }}+ e_{0,j} \end{aligned}$$(7)This game is well-defined because the adversary fixes all key queries \((M_j,j)\) before it chooses x in the \( \textsf {sk}\)-selective setting.
-
\(\mathsf {H}'_i, i=1,\ldots ,\ell \): same as \(\mathsf {H}'_0\), except we sample \(\mathbf {c}_1,\ldots ,\mathbf {c}_i \leftarrow \mathbb {Z}_q^m\). Note that this also changes the distribution of
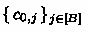 , since they depend on \(\mathbf {c}_1,\ldots ,\mathbf {c}_i\) as defined in (7).
, since they depend on \(\mathbf {c}_1,\ldots ,\mathbf {c}_i\) as defined in (7). -
\(\mathsf {H}_{\ell +1}\): same as \(\mathsf {H}_\ell \), except we replace \(c_{\ell +2}\) in \(\mathsf {H}_\ell \) with \(c'_{\ell +2} \leftarrow \mathbb {Z}_q\).
Lemma 2
\(\mathsf {H}_0 \approx _s \mathsf {H}'_0\).
Proof
It suffices to show that The only difference in the two games lies in the distribution of
 . Since \(M_j(x) = 0\), we have \(\mathbf {f}_j \mathbf {d}^{\!\scriptscriptstyle {\top }}_{\ell ,j} = 0\). It follows from (6) that
. Since \(M_j(x) = 0\), we have \(\mathbf {f}_j \mathbf {d}^{\!\scriptscriptstyle {\top }}_{\ell ,j} = 0\). It follows from (6) that
Combined with noise smudging using \(e_{0,j}\), namely
which in turn follows from \(\hat{\chi } \ge \chi \cdot (\ell +1)m \cdot \lambda ^{\omega (1)}\), we have

The lemma follows readily. \(\square \)
Lemma 3
For \(i=1,\ldots ,\ell \), \(\mathsf {H}'_{i-1} \approx _c \mathsf {H}'_i\).
Proof
Observe that the only difference between \(\mathsf {H}'_{i-1}\) and \(\mathsf {H}'_i\) lies in the distribution of \(\mathbf {c}_i\):
-
in \(\mathsf {H}'_{i-1}\), we have \(\mathbf {c}_i = \mathbf {s}_{i-1} \overline{\mathbf {A}}_{x_i} - \mathbf {s}_i \underline{\mathbf {A}}_{x_i} + \mathbf {e}_i\);
-
in \(\mathsf {H}'_i\), we have \(\mathbf {c}_i \leftarrow \mathbb {Z}_q^m\).
We show that \(\mathsf {H}'_{i-1} \approx _c \mathsf {H}'_i\) follows from the \(\mathbf {T}_{1/2}\)-LWE assumption.
As a simplifying assumption, we assume that the reduction knows \(x_i\) from the start. In the more general setting, the reduction simply guesses \(x_i\) at random at the beginning of the experiment, and aborts if the guess is wrong; this incurs a loss of \(|\Sigma |\) in the security reduction.
By the \(\mathbf {T}_{1/2}\)-LWE assumption applied to secret \(\mathbf {s}_{i-1}\) and public matrix \(\mathbf {A}_{x_i}\), we have:

given \(\mathbf {A}_{x_i}\) and oracle access to \(\mathcal {O}_{\mathbf {A}_{x_i}}(\cdot )\).
The reduction on input \(\mathbf {A}_{x_i}, \tilde{\mathbf {c}} \in \{\mathbf {s}_{i-1} \overline{\mathbf {A}}_{x_i},\mathbf {c}\},\mathbf {K}_{x_i,j}\) and oracle access to \(\mathcal {O}_{\mathbf {A}_{x_i}}(\cdot )\):
-
samples
$$ (\mathbf {A}_{\sigma },\tau _{\sigma }) \leftarrow \mathsf {TrapGen}(1^{2n},1^m,q), \sigma \ne x_i \quad (\mathbf {A}_{\text {end}},\tau _{\text {end}}) \leftarrow \mathsf {TrapGen}(1^n,1^m,q), \quad \mathbf {d}_{\text {end}} \leftarrow \mathbb {Z}_q^n$$ -
when \(\mathcal {A}\) makes a key query \((M_j,j)\) where \(M_j=(Q_j,\Sigma ,\left\{ \, \mathbf {M}_{\sigma ,j}\, \right\} _{\sigma \in \Sigma },\mathbf {u}_{0,j},\mathbf {f}_j)\):
-
queries \(\mathcal {O}_{\mathbf {A}_{x_i}}(\mathbf {M}_{x_i,j},\mathbf {0})\) to get \(\mathbf {K}_{x_i,j} \leftarrow \mathbf {A}_{x_i}^{-1}{\mathbf {D}_j \atopwithdelims ()\mathbf {D}_j \mathbf {M}_{x_i,j}}\);
-
computes \(\mathbf {D}_j = \overline{\mathbf {A}}_{x_i} \cdot \mathbf {K}_{x_i,j}\);
-
for all \(\sigma \ne x_i\), uses \(\tau _{\sigma }\) to compute \(\mathbf {K}_{\sigma ,j}\) as in \(\mathsf {KeyGen}\);
-
uses \(\tau _{\text {end}}\) to compute \(\mathbf {K}_{\text {end},j}\) as in \(\mathsf {KeyGen}\);
-
outputs \( \textsf {sk}_{M_j} := \bigl (\,\mathbf {K}_{\text {end},j},\; \left\{ \, \mathbf {K}_{\sigma ,j}\, \right\} _{\sigma \in \Sigma }\,\bigr )\)
-
-
computes
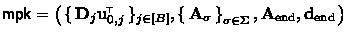
-
runs \(x=(x_1,\ldots ,x_\ell ),\mu _0,\mu _1 \leftarrow \mathcal {A}(\textsf {mpk})\)
-
picks \(\beta \leftarrow \{0,1\}\) and computes \( \textsf {ct}\) as follows:
-
samples random \(\mathbf {s}_0,\ldots ,\mathbf {s}_{\ell -1},\mathbf {s}_\ell \) except \(\mathbf {s}_{i-1}\);
-
computes \(\mathbf {c}_i := \tilde{\mathbf {c}}-\mathbf {s}_i\underline{\mathbf {A}}_{x_i}\);
-
computes the rest of \( \textsf {ct}\) as in \(\mathsf {H}'_{i-1}\);
-
-
outputs \(\mathcal {A}( \textsf {ct})\).
Now, observe that when
-
if \(\tilde{\mathbf {c}} = \mathbf {s}_{i-1}\overline{\mathbf {A}}_{x_i} + \mathbf {e}_i\), this matches \(\mathsf {H}'_{i-1}\).
-
if \(\tilde{\mathbf {c}} = \mathbf {c}\), this matches \(\mathsf {H}'_i\) since \(\mathbf {c}- \mathbf {s}_i\underline{\mathbf {A}}_{x_i}\) is uniformly random.
This completes the proof. \(\square \)
Lemma 4
(final transition). \(\mathsf {H}'_\ell \approx _c \mathsf {H}_{\ell +1}\).
Proof
By the LWE assumption, we have

The reduction on input \(\mathbf {A}_{\text {end}},\mathbf {d}_{\text {end}}, \mathbf {c}_{\ell +2},\tilde{c}\), where \(\tilde{c} \in \{\mathbf {s}_\ell \mathbf {d}^{\!\scriptscriptstyle {\top }}_{\text {end}}+e_{\ell +2}, c'_{\ell +2}\}\),
-
samples
$$\begin{aligned} (\mathbf {A}_{\sigma },\tau _{\sigma }) \leftarrow \mathsf {TrapGen}(1^{2n},1^m,q), \sigma \in \Sigma \end{aligned}$$ -
when \(\mathcal {A}\) makes a key query \((M_j,j)\) where \(M_j=(Q_j,\Sigma ,\left\{ \, \mathbf {M}_{\sigma ,j}\, \right\} _{\sigma \in \Sigma },\mathbf {u}_{0,j},\mathbf {f}_j)\):
-
samples \(\mathbf {K}_{\text {end},j} \leftarrow \mathcal {D}_{\mathbb {Z}^{m \times Q_j}}\)
-
programs \(\mathbf {D}_j = \mathbf {A}_{\text {end}} \mathbf {K}_{\text {end},j} + \mathbf {d}^{\!\scriptscriptstyle {\top }}_{\text {end}} \otimes \mathbf {f}_j\);
-
for all \(\sigma \in \Sigma \), computes \(\mathbf {K}_{\sigma ,j}\) using \(\tau _\sigma \) as in \(\mathsf {KeyGen}\);
-
outputs \( \textsf {sk}_{M_j} := \bigl (\,\mathbf {K}_{\text {end},j},\; \left\{ \, \mathbf {K}_{\sigma ,j}\, \right\} _{\sigma \in \Sigma }\,\bigr )\)
-
-
computes

-
runs \(x=(x_1,\ldots ,x_\ell ),\mu _0,\mu _1 \leftarrow \mathcal {A}(\textsf {mpk})\)
-
picks \(\beta \leftarrow \{0,1\}\) and computes \( \textsf {ct}\) as follows:
-
samples random \(\mathbf {c}_1,\ldots ,\mathbf {c}_{\ell }\);
-
for all \(j \in [B]\), compute \(c_{0,j}\) using (7) except replacing \(\mathbf {s}_\ell \mathbf {d}_{\ell ,j}^{\!\scriptscriptstyle {\top }}\) with
$$\begin{aligned} \mathbf {c}_{\ell +1} \cdot \mathbf {K}_{\text {end},j} \cdot \mathbf {u}^{\!\scriptscriptstyle {\top }}_{\ell ,j} \end{aligned}$$ -
outputs
 .
.
-
-
outputs \(\mathcal {A}( \textsf {ct})\).
Here, we use
This completes the proof. \(\square \)
5 Candidate ABE for DFA Against Unbounded Collusions
In this section, we describe a candidate ABE scheme for DFA against unbounded collusions:
-
\(\mathsf {Setup}(1^n,\Sigma )\): Sample
$$\begin{aligned}&(\mathbf {A}_\sigma ,\tau _{\sigma }) \leftarrow \mathsf {TrapGen}(1^{2n},1^m,q),\,\sigma \in \Sigma , \quad (\mathbf {A}_{\text {end}},\tau _{\text {end}}) \leftarrow \mathsf {TrapGen}(1^n,1^m,q), ,\\&(\mathbf {A}_{\text {st}},\tau _{\text {st}}) \leftarrow \mathsf {TrapGen}(1^n,1^m,q),\quad \mathbf {d}_{\text {end}} \leftarrow \mathbb {Z}_q^n, \end{aligned}$$Output
$$ \textsf {mpk}:= \bigl (\,\left\{ \, \mathbf {A}_\sigma \, \right\} _{\sigma \in \Sigma }, \mathbf {A}_{\text {end}}, \mathbf {A}_{\text {st}}, \mathbf {d}_{\text {end}}\,\bigr ), \quad \textsf {msk}:= \bigl (\,\left\{ \, \tau _{\sigma }\, \right\} _{\sigma \in \Sigma }, \tau _{\text {end}}\,\bigr )$$ -
\(\mathsf {Enc}(\textsf {mpk},(x_1,\ldots ,x_\ell ) \in \Sigma ^\ell , \mu \in \{0,1\})\). Sample
$$ \mathbf {s}_0,\mathbf {s}_1,\ldots ,\mathbf {s}_\ell \leftarrow \mathbb {Z}_q^n,\quad e_{\ell +2} \leftarrow \mathcal {D}_{\mathbb {Z},\hat{\chi }},\,j \in [B], \quad \mathbf {e}_0,\mathbf {e}_1,\ldots ,\mathbf {e}_\ell ,\mathbf {e}_{\ell +1} \leftarrow \mathcal {D}_{\mathbb {Z}^m,\chi } $$Output
$$ \textsf {ct}:= \bigl (\, \overbrace{\mathbf {s}_0 \mathbf {A}_{\text {st}} + \mathbf {e}_0}^{\mathbf {c}_0} ,\quad \{ \, \overbrace{(\mathbf {s}_{i-1} \overline{\mathbf {A}}_{x_i} - \mathbf {s}_i \underline{\mathbf {A}}_{x_i} + \mathbf {e}_i}^{\mathbf {c}_i}\, \}_{i \in [\ell ]},\quad \overbrace{\mathbf {s}_\ell \mathbf {A}_{\text {end}} + \mathbf {e}_{\ell +1}}^{\mathbf {c}_{\ell +1}},\quad \overbrace{\mathbf {s}_\ell \mathbf {d}^{\!\scriptscriptstyle {\top }}_{\text {end}} + e_{\ell +2} + \mu \cdot \lfloor \tfrac{q}{2} \rfloor }^{c_{\ell +2}} \,\bigr ) $$ -
\(\mathsf {KeyGen}( \textsf {msk},M)\): Parse \(M=(Q,\Sigma ,\left\{ \, \mathbf {M}_{\sigma }\, \right\} _{\sigma \in \Sigma },\mathbf {u}_{0},\mathbf {f})\). Sample
$$\mathbf {D}\leftarrow \mathbb {Z}_q^{n \times Q}, \quad \mathbf {k}^{\!\scriptscriptstyle {\top }}_{\text {st}} \leftarrow \mathbf {A}_{\text {st}}^{-1}(\mathbf {D}\cdot \mathbf {u}_{0}^{\!\scriptscriptstyle {\top }}),\quad \mathbf {K}_{\text {end}} \leftarrow \mathbf {A}_{\text {end}}^{-1}(\mathbf {D}-\mathbf {d}^{\!\scriptscriptstyle {\top }}_{\text {end}} \otimes \mathbf {f}),\quad \mathbf {K}_{\sigma } \leftarrow \mathbf {A}_{\sigma }^{-1}{\mathbf {D}\atopwithdelims ()\mathbf {D}\mathbf {M}_{\sigma }},\,\sigma \in \Sigma $$using trapdoors \(\tau _{\text {st}},\tau _{\text {end}},\left\{ \, \tau _\sigma \, \right\} _{\sigma \in \Sigma }\). Output
$$ \textsf {sk}_M := \bigl (\,\mathbf {k}_{\text {st}},\;\mathbf {K}_{\text {end}},\; \left\{ \, \mathbf {K}_{\sigma }\, \right\} _{\sigma \in \Sigma }\,\bigr )$$ -
\(\mathsf {Dec}( \textsf {sk}, \textsf {ct})\): For \(i=1,\ldots ,\ell \), compute \(\mathbf {u}_{i}^{\!\scriptscriptstyle {\top }}:= \mathbf {M}_{x_i} \cdots \mathbf {M}_{x_1}\mathbf {u}_{0}^{\!\scriptscriptstyle {\top }}\). Output
$$\begin{aligned} \mathsf {round}_{q/2}\bigl (\,\mathbf {c}_0 \mathbf {k}^{\!\scriptscriptstyle {\top }}_{\text {st}} + \sum _{i=1}^\ell \mathbf {c}_i \cdot \mathbf {K}_{x_i} \cdot {\mathbf {u}_{i-1}^{\!\scriptscriptstyle {\top }}} + \mathbf {c}_{\text {end}} \cdot \mathbf {K}_{\text {end}} \cdot \mathbf {u}_{\ell }^{\!\scriptscriptstyle {\top }}+ \mathbf {c}_{\ell +2}\,\bigr ) \end{aligned}$$where \(\mathsf {round}_{q/2}: \mathbb {Z}_q \rightarrow \{0,1\}\) denotes rounding to the nearest multiple of q/2.
Preliminary Cryptanalysis. We make two small observations:
-
Given unbounded keys, the adversary can recover a full short basis for the matrices
$$[\mathbf {A}_{\text {st}} \mid \overline{\mathbf {A}}_\sigma ], \forall \sigma $$This follows from the fact that for each key,
$$[\mathbf {A}_{\text {st}} \mid \overline{\mathbf {A}}_\sigma ] {\mathbf {k}_{\text {st}} \atopwithdelims ()-\mathbf {K}_\sigma \mathbf {u}^{\!\scriptscriptstyle {\top }}_0} = \mathbf {D}\cdot \mathbf {u}_0^{\!\scriptscriptstyle {\top }}- \mathbf {D}\cdot \mathbf {u}_0^{\!\scriptscriptstyle {\top }}= \mathbf {0}$$However, we do not know how to use such a collection of short basis to break security of the scheme.
-
Suppose we replace each \(\mathbf {k}^{\!\scriptscriptstyle {\top }}_{\text {st}}\) with \(\mathbf {c}_0 \mathbf {k}^{\!\scriptscriptstyle {\top }}_{\text {st}} + \mathbf {e}'_0\) for some fresh \(\mathbf {e}'_0\), then the scheme is indeed \( \textsf {sk}\)-selective secure, via essentially the same analysis as our bounded-collusion scheme. (Recall that the role of \(\mathbf {k}^{\!\scriptscriptstyle {\top }}_{\text {st}}\) for correctness is indeed only to compute \(\mathbf {c}_0 \mathbf {k}^{\!\scriptscriptstyle {\top }}_{\text {st}}\), so this change does not ruin functionality.) This means that any attack on our candidate scheme must crucially exploit access to \(\mathbf {k}^{\!\scriptscriptstyle {\top }}_{\text {st}}\) (beyond approximating \(\mathbf {c}_0 \mathbf {k}^{\!\scriptscriptstyle {\top }}_{\text {st}}\)), for instance, to recover a short basis as in the previous bullet.
Notes
- 1.
To facilitate comparison with Waters’ pairing-based scheme, we note that the terms corresponding to \(\mathbf {c}_i\) and \(\mathbf {k}_{u,\sigma }\) there-in are given by:
$$(g_1^{s_{i-1}}, g_1^{s_{i-1} z + s_i w_{x_i}}, g_1^{s_i}), \;\; (g_2^{-\tilde{d}_{u}+zr}, g_2^r, g_2^{-\tilde{d}_{v}+w_{\sigma }r})$$where \(g_1,g_2\) are the respective generators the group \(\mathbb {G}_1,\mathbb {G}_2\) in a bilinear group \(e : \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\). We can then compute a pairing-product over these terms to derive \(e(g_1,g_2)^{s_{i-1} \tilde{d}_{u_{i-1}} -s_{i} \tilde{d}_{u_{i}}}\).
- 2.
It seems plausible (with some considerable changes to the scheme and the proof) that we can replace \(\mathsf {cFE}\) for depth \(O(\log Q)\) circuits with an ABE for branching programs of size \(\textsf {poly}(Q)\). The latter can realized from LWE with a polynomial modulus-to-noise ratio [16, 17].
- 3.
Following [22, Section 5.2], we choose each entry of \(\mathbf {R}\) to be 0 with probability 1/2, and \(\pm 1\) each with probability 1/4. This yields \(|\mathbf {R}| = 1\) and \(s_1(\mathbf {R}) = O(\sqrt{m})\) w.h.p. Moreover, \((\mathbf {A},\mathbf {A}\mathbf {R}) \approx _s \text{ uniform }\).
References
Agrawal, S., Boneh, D., Boyen, X.: Efficient lattice (H)IBE in the standard model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 553–572. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_28
Agrawal, S., Chase, M.: Simplifying design and analysis of complex predicate encryption schemes. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 627–656. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_22
Agrawal, S., Maitra, M., Yamada, S.: Attribute based encryption (and more) for nondeterministic finite automata from LWE. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11693, pp. 765–797. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_26
Agrawal, S., Maitra, M., Yamada, S.: Attribute based encryption for deterministic finite automata from \(\sf DLIN\). In: Hofheinz, D., Rosen, A. (eds.) TCC 2019. LNCS, vol. 11892, pp. 91–117. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36033-7_4
Agrawal, S., Singh, I.P.: Reusable garbled deterministic finite automata from learning with errors. In: Chatzigiannakis, I., Indyk, P., Kuhn, F., Muscholl, A. (eds.) ICALP 2017, volume 80 of LIPIcs, pp. 36:1–36:13. Schloss Dagstuhl, July 2017
Ananth, P., Vaikuntanathan, V.: Optimal bounded-collusion secure functional encryption. In: Hofheinz, D., Rosen, A. (eds.) TCC 2019. LNCS, vol. 11891, pp. 174–198. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36030-6_8
Attrapadung, N.: Dual system encryption via doubly selective security: framework, fully secure functional encryption for regular languages, and more. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 557–577. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_31
Attrapadung, N.: Dual system encryption framework in prime-order groups via computational pair encodings. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 591–623. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_20
Boneh, D., et al.: Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 533–556. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_30
Chen, Y., Vaikuntanathan, V., Wee, H.: GGH15 beyond permutation branching programs: proofs, attacks, and candidates. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 577–607. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_20
Genise, N., Micciancio, D., Peikert, C., Walter, M.: Improved discrete Gaussian and subgaussian analysis for lattice cryptography. In: Kiayias, A., Kohlweiss, M., Wallden, P., Zikas, V. (eds.) PKC 2020. LNCS, vol. 12110, pp. 623–651. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45374-9_21
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: Ladner, R.E., Dwork, C. (eds.) 40th ACM STOC, pp. 197–206. ACM Press, May 2008
Gong, J., Waters, B., Wee, H.: ABE for DFA from k-Lin. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11693, pp. 732–764. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_25
Gong, J., Wee, H.: Adaptively secure ABE for DFA from k-Lin and more. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12107, pp. 278–308. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45727-3_10
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_11
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 545–554. ACM Press, June 2013
Gorbunov, S., Vinayagamurthy, D.: Riding on asymmetry: efficient ABE for branching programs. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 550–574. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_23
Goyal, R., Koppula, V., Waters, B.: Collusion resistant traitor tracing from learning with errors. In: Diakonikolas, I., Kempe, D., Henzinger, M. (eds.) 50th ACM STOC, pp. 660–670. ACM Press, June 2018
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: Juels, A., Wright, R.N., De Capitani di Vimercati, S. (eds.) ACM CCS 2006, pp. 89–98. ACM Press, October/November 2006. Available as Cryptology ePrint Archive Report 2006/309
Itkis, G., Shen, E., Varia, M., Wilson, D., Yerukhimovich, A.: Bounded-collusion attribute-based encryption from minimal assumptions. In: Fehr, S. (ed.) PKC 2017. LNCS, vol. 10175, pp. 67–87. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54388-7_3
Kowalczyk, L., Wee, H.: Compact adaptively secure ABE for NC\(^{1}\) from k-Lin. J. Cryptol. 33(3), 954–1002 (2019). https://doi.org/10.1007/s00145-019-09335-x
Micciancio, D., Peikert, C.: Trapdoors for lattices: simpler, tighter, faster, smaller. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 700–718. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_41
Sahai, A., Seyalioglu, H.: Worry-free encryption: functional encryption with public keys. In: Al-Shaer, E., Keromytis, A.D., Shmatikov, V. (eds.) ACM CCS 2010, pp. 463–472. ACM Press, October 2010
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_27
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_36
Waters, B.: Functional encryption for regular languages. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 218–235. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_14
Wee, H.: Dual system encryption via predicate encodings. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 616–637. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_26
Acknowledgments
I would like to thank Yilei Chen and Vinod Vaikuntanathan for illuminating discussions on lattice trapdoor sampling, as well as the reviewers for meticulous and constructive feedback.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 International Association for Cryptologic Research
About this paper
Cite this paper
Wee, H. (2021). ABE for DFA from LWE Against Bounded Collusions, Revisited. In: Nissim, K., Waters, B. (eds) Theory of Cryptography. TCC 2021. Lecture Notes in Computer Science(), vol 13043. Springer, Cham. https://doi.org/10.1007/978-3-030-90453-1_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-90453-1_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-90452-4
Online ISBN: 978-3-030-90453-1
eBook Packages: Computer ScienceComputer Science (R0)






 : We also require computational hardness of the form
: We also require computational hardness of the form  in
in 


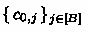 , since they depend on
, since they depend on 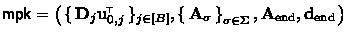

 .
.