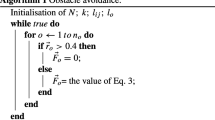Keywords

1 Introduction

Flocking of social animals is a commonly observed behaviour in many biological systems from tiny bacterial community to social animals such as fish school [9], sheep herds [14] and birds flocking [7]. Flocking, also known as collective motion, has been widely implemented in swarm robotic systems [16] such as exploration in precision agriculture [1] and unmanned aerial vehicles swarm coordination control [21].

The underlying mechanism of flocking behaviour steers a group of individuals to coherently move with an approximately identical speed and direction. Hence, the entire swarm moves together like a super-organism with astounding elegance and flexibility [19]. This large-scale swarm flocking presents the same universal property that, the emergent flocking behaviour only relies on the local interactions between robots without any need for global communication and any central control law. Researchers from physics to biology have proposed different collective motion models [2, 4, 8, 12, 20]. These models effectively reveal and describe the collective motion principles in large-scale swarm scenarios. One of the most important models is proposed by Vicsek et al. [20], which was followed by other study like [3]. It is a minimal agent-based model where individuals follow velocity alignment rule. This model establishes a fundamental and explicit interaction principle called the alignment rule. Despite many subsequent complex models were introduced to achieve self-organised flocking in a more precise and natural way [2, 3, 10], they can be considered as the variants of Vicsek model since they all strongly rely on the velocity-based alignment interaction to perform self-organised collective motion. However, this pioneering model still has limitations to fully depict self-organised flocking motion, especially for swarm robotic applications. Firstly, the velocity-based algorithm not only requires robots to obtain the orientation of neighbouring robots in short communication range, but it also needs their relative positions to determine the neighbouring topology. Hence, the robots must have a strong computational ability and a reliable inter-robot communication to address the issue, e.g. by using local communication methods [11]. Secondly, the swarm achieves collective motion in an infinite and ideal space without any physical boundary restriction, e.g. walls. Therefore, it is not practical for a real-world swarm robotic system where robots encounter obstacles and in a cluttered environment. In addition, velocity-based model assumes that each robot is set up with a fixed speed, and only orientation can be adjusted in each step. It significantly restricts the swarm in terms of flexibility and adaptability in case of the complex environments. Considering the limitations of the velocity alignment, another collective mechanism for flocking was proposed by Ferrante et al. [5, 6], which developed a novel position-based decentralised algorithm for achieving a collective motion. They abstracted self-propelled particle swarm in two-dimensional active solids, and introduced the Active Elastic Sheet (AES) model. The individual interaction is based on attractive-repulsive forces. Robot’s motion is driven by the combination of linear elastic forces from its fixed neighbouring topology. Therefore, the agent-based model only rely on the exchange information of relative position, rather than including the heading orientation of neighbouring robots, which significantly alleviates the requirement of hardware computation and perception. In addition, in [15, 22], both simulated and real robot experiments demonstrated the feasibility of AES model in the real swarm robot applications.

The AES model does not consider the limitations of the real-world environments since it is derived from the collective behaviour of the perfect active crystal. Inevitably, in a real-world scenario, there exists plenty of physical boundaries including obstacles and walls. Therefore, in this work, we developed a new flocking method based on the AES model, that facilitates application of the flocking in real-world scenarios with several obstacles– cluttered environments. In this work, we investigated different states of the swarm trajectory when an interaction between the swarm and obstacles happens in a cluttered environment. We modelled a repulsive force for collision avoidance and combined it with the AES model’s attraction-repulsion force. In addition, the impact of the proposed model in presence of obstacles with different collective forces was investigated.

2 Flocking Method

2.1 Active Elastic Sheet Model

The agent-based AES model [5] can produce the self-organised collective motion, even in the presence of noise. It can also start from swarm system with random initial orientation and position. Rather than orientation and alignment interaction, each pairwise of robots only exchange the position information, then generate the corresponding elastic force to affect the robot’s motion state. Its simplicity contributes to implementing self-organised flocking in swarm robotic applications. As introduced before, in a swarm system including N robots, individual’s motion dynamics is determined by the spring-like forces from its fixed neighbouring robot set. The attraction-repulsion forces affect both the linear and angular velocities of the robot during flocking. This continuous-time model can be illustrated mathematically as:

$$\begin{aligned} \dot{\; \overrightarrow{x}_i} = v_0 \hat{n}_i + \alpha [(\overrightarrow{F}_i + D_r \hat{\xi }_r) \cdot \hat{n}_i] \hat{n}_i , \end{aligned}$$
(1)
$$\begin{aligned} \dot{\theta _i} = \beta [(\overrightarrow{F}_i + D_r \hat{\xi }_r) \cdot \hat{n}_i^\perp ] + D_\theta \xi _\theta , \end{aligned}$$
(2)

where, \(\overrightarrow{x}_i\) and \(\theta _i\) are position and orientation of the ith robot. \(v_0\) is the self-propelled forward biasing speed that is imposed into all robots. \(\hat{n}_i\) and \(\hat{n}_i^\perp \) are two unit vectors pointing parallel and perpendicular to the heading direction of the ith robot, and two parameters \(\alpha \) and \(\beta \) are inverse translation and rotation damping coefficients, respectively. The motion essence of AES model is that the robot adjusts its linear and angular velocities based on the projection of forces in parallel to its heading and perpendicular to its heading.

This model also concentrates on the impact of noise from both measurement and actuation; \(D_r \hat{\xi }_r\) is the error from the measured forces and \(D_\theta \xi _\theta \) is the fluctuation of the individual motion. \(\hat{\xi }_r\) is a randomly generated unit vector for noise strength coefficient \(D_r\). Also, \(\hat{\xi }_r\) is a random variable with standard, zero-centred normal probability distribution for noise strength coefficient of \(D_\theta \). The total linear elastic force, \(\overrightarrow{F}_i\), is originated from those neighbouring robots interacting with the ith robot. It can be calculated as follow:

$$\begin{aligned} \overrightarrow{F}_i = \sum _{j\in S_i}\frac{-k}{l_{ij}}(|\overrightarrow{r}_{ij}| - l_{ij}) \frac{\overrightarrow{r}_{ij}}{|\overrightarrow{r}_{ij}|}, \end{aligned}$$
(3)
$$\begin{aligned} \overrightarrow{r}_{ij} = \overrightarrow{x}_j - \overrightarrow{x}_i , \end{aligned}$$
(4)

where, \(l_{ij}\) is the equilibrium distance where the force between ith and jth robot will become zero, and \(\frac{k}{l_{ij}}\) is the spring constant. Each neighbouring robot set \(S_i\) contains all robots that connect with the focal robot through the “virtual springs” at the beginning of each experiment. This connection would not be broken up regardless of the distance between this pair of the robots. Similar to spring, once the interaction network of neighbouring robots is defined, it will remain fixed throughout the experiment. In addition, according to Eq. (5), the inducing force would become large as the distance to equilibrium position increase. Overall, the total elastic force drives the robot to move toward the equilibrium position.

In order to implement our experiments, we followed experimental setup proposed in [15] and modified the original AES model with adding the goal direction, \(F_g\), which coordinates the swarm to achieve a collective motion with a specific direction. In addition, this modification can also lead to faster convergence of the collective motion. Hence, the goal direction is added to the swarm as a “virtual external force” described as:

$$\begin{aligned} \overrightarrow{F}_g = \omega _g \overrightarrow{\hat{v}_d}. \end{aligned}$$
(5)

The goal force is parallel to the desired velocity unit vector \(\overrightarrow{\hat{v}_d}\) and its magnitude is determined by the weighting coefficient \(\omega _g\). The modification steers the swarm system moving towards the region of obstacles by adjusting the desired velocity unit vector.

2.2 Extended AES Model

The robots’ interaction with obstacles based on the original AES model purely relies on attraction-repulsion force, which provides a natural benchmark to design obstacle interaction from the point of force. Indeed, the obstacle force can be treated as a repulsive force and its magnitude is also based on the distance between the robot and the obstacle. In contrast to elastic force in AES model, as the robot approaches to obstacle, its magnitude should become significantly large to avoid the collision. It should be close to the infinity when the distance is nearly zero. When a robot detects the existence of an obstacle, the repulsive obstacle force will appear will be imposed into the robot.

Obviously, the previous spring-like force cannot satisfy the requirement. There are some other virtual physical-based models with more complicated relation with distance and are utilised especially for robotic control. One of most widely used virtual physical-based models is the Lennard-Jones (LJ) potential model [17, 18], which was proposed to interpret motion of atoms or molecules in molecular dynamics. The obstacle force \(\overrightarrow{F}_{obs,i}\) that acts against the ith robot was designed based on the following equation:

$$\begin{aligned} \overrightarrow{F}_{obs,i} = \sum _{o\in O_i} \epsilon _{obs} [(\frac{\sigma _{obs}}{||\overrightarrow{r}_{io}||})^{2\alpha _{LJ}} - 2(\frac{\sigma _{obs}}{||\overrightarrow{r}_{io}||})^{\alpha _{LJ}}]\overrightarrow{r}_{io} \end{aligned}$$
(6)

There are some parameters that need to be explained and set for the experiments. Here, \(\overrightarrow{r_{io}}\) is the distance vector from an obstacle, o, to ith robot, and obstacle set \(O_i\) is the set of all obstacles within the detecting range of ith robot. \(\epsilon _{obs}\) corresponds to the depth of potential function and \(\alpha _{LJ}\) defines the rate of change of the potent versus distance by changing its power. The value of \(\alpha _{LJ}\) is set to 2, which contributes to improve the smoothness of collective behaviour. The final important parameter is \(\sigma _{obs}\), which is related to the equilibrium distance at which the Eq. (6) is equal to zero. According to Eq. (6), by setting the obstacle force to zero and solving it, the proper value for \(\sigma _{obs}\) parameter can be obtained in following relation:

$$\begin{aligned} \sigma _{obs} = \sqrt{2} d_{0,obs}, \end{aligned}$$
(7)

where \(d_{0,obs}\) represents the equilibrium distance where the obstacle force magnitude is equal to zero. Using the above equation, the \(\sigma _{obs}\) can be tuned automatically and its value can be determined as a function of equilibrium distance \(d_{0,obs}\). In order to maintain the repulsion force only, it is necessary to adjust the parameter \(\sigma _{obs}\) in a way that the obstacle exceeds the sensing range of robot before reaching the equilibrium point, i.e. \(d_{0,obs} > r_{sens}\), where \(r_{sens}\) is the sensing range of the robots. One suggestion is to define \(d_{0,obs}\) in a way that the obstacle force turns to zero at the verge of detection zone as follow:

$$\begin{aligned} \sigma _{obs} = \sqrt{2} d_{0,obs} = \sqrt{2} r_{sens}. \end{aligned}$$
(8)

In this case, when the robot perceive the obstacle, the repulsive obstacle force would appear and impose on the robot. In addition, as the robot approaches to an obstacle, the magnitude will increase significantly.

Designing all the forces affect the collective behaviour of robots, and consequently the whole swarm system. The motion dynamics of each robot would be redefine to consider the impact from external forces including goal force and obstacle force. The total force in Eq. (1) and Eq. (2) need be substituted by the total force which is simply modelled as the combination of collective force in Eq. (3), goal force in Eq. (5) and obstacle force in Eq. (6). The corresponding equation is illustrated below:

$$\begin{aligned} \overrightarrow{F}_{tot,i} = \overrightarrow{F}_{c,i} + \overrightarrow{F}_g + \overrightarrow{F}_{obs,i}, \end{aligned}$$
(9)

where, in the new definition, the total force \(\overrightarrow{F}_{tot,i}\) replaces the force in original AES motion dynamic, and the \(\overrightarrow{F}_i\) in Eq. (3) is viewed as the collective force \(\overrightarrow{F}_{c,i}\).

2.3 Metrics

The main aim of flocking behaviour is to achieve a common direction within the swarm members. In addition, the robots should move collectively, which can be characterised by an essential property, so called the coherency. The coherency depicts the likelihood of individual remaining in the swarm system. This principle feature can also serve as the performance index of flocking when swarm encounters obstacles in a cluttered environment. In order to evaluate the swarm coherency, a metric was introduced in this work. The metric is the average distance between the swarm individuals. It is also a common method to evaluate the coherency of swarm for collective motion [13]. The coherency is presented as:

$$\begin{aligned} d_s = \frac{2\sum _{i=1}^{N-1}\sum _{j=1}^{N}{||\overrightarrow{r}_{ij}||}}{N(N-1)}. \end{aligned}$$
(10)

This metric describes the mean value of each pair of robot’s distance. It should keep unchanged if the swarm maintains a stable motion without an abruption or squeeze deformation.

2.4 Experimental Setup

After defining the obstacle interaction and modifying the AES model, all the prerequisites are fully prepared to implement the simulated experiments. The aim of these experiments is to investigate the performance of self-organised flocking based on AES model in a cluttered environment. We designed three different environmental conditions to implement the experiments, including ideal environment without obstacle, single-obstacle environment and multi-obstacle environment. There are some basic parameters (listed in Table 1) that need to be determined. There are also some critical assumptions needed to be mentioned: i) the simulated experiments do not consider the impact of noise, ii) the network topology of robot swarm is determined prior to flocking and fixed. Each robot establishes a connection within its sensing range, and iii) the equilibrium distance \(l_{ij}\) in Eq. (3) is set to the initial distance between robots i and j.

Table 1. Setting values of related parameters in the experiments
Full size table

There are essential factors that will affect the flocking behaviour in the cluttered environment such as population size (N), equilibrium distance (\(l_{ij}\)) and the magnitude of collective force (k); however, we only considered \(l_{ij}\) and k in this work. In order to eliminate the accidental error in observation, repeatability principle need to be considered in these experiments. Therefore, each set of experiments was repeat 10 times.

Experiments without Obstacles: In this set of experiment, swarm moves in a given \(L\times {L}\) square arena with the physical boundaries. Their initial distance between two nearest neighbouring robots is set to equilibrium distance. The initial orientations and positions of the robots were selected randomly and uniformly distributed in the left-hand side of the arena. In this set of experiments, only goal force and collective force are imposed into the individual robots. The set goal force drags the swarm on the x-axis, and the collective force contributes to configure the swarm into a stable structure.

Experiments with a Single Obstacle: This set of experiments simulate a single obstacle environment, where the obstacle was located at a fixed point, where the swarm will encounter. In this experiment, the obstacle avoidance interaction was introduced into the collective motion. Similar with the first set of experiments, the related parameters still remain unchanged.

Experiments with Multiple Obstacles: This set experiments study the self-organised flocking in cluttered environment, with several obstacles which appear in front of robots which they are moving to right-hand side of the arena. There are three obstacles which form a triangle shape to block the motion of the flock. Except for this, other parameters are the same as the previous experiments. Compared with the single obstacle case, the obstacles’ force will provide a complex situation. Therefore, the robots will detect more than one obstacle force from different directions at the same time.

3 Results and Discussion

Figure 1 shows examples of the randomly selected flocking trajectories in three different scenarios with \(l_{ij} = 3.5\) m and \(N = 15\). In the diagrams, the small blue circles represent the robots in a swarm. The red arrows on each robot represent orientation of the robot. The large red circles indicate the obstacles which are nearly 4 times larger than the robots. Obviously, the swarm could achieve a collective motion in an ideal environment without obstacles as shown in Fig. 1(a). In addition, robotic swarm is also capable of avoiding the obstacles in all the scenarios, shown in the rest of Fig. 1. In Fig. 1(b) and (c), the parameter k associated with the collective force is set to 0.05. It can be viewed that the flock will be separated by the obstacle, and it is difficult to recover to the original structure. The swarm was divided into several small clusters by obstacle forces. Figure 1(d) and (e) present the flocking behaviour of the swarm with the same initial conditions (position and orientation). The only difference is to improve the magnitude of the collective force by setting it to \(k = 3\). In this case, The flocking performance in the ideal environment does not manifest any significant change. Hence, the swarm still can move collectively like a solid entity with a common direction. However, even if the robots in the swarm were segmented by the obstacles’ force, they were able to converge into a single cluster with a stable structure and maintain the self-organised flocking. In addition, this flocking behaviour possesses higher flexibility and robustness. It goes through the obstacles smoothly like a liquid flow in nature.

To analyse the behaviour of swarm in detail, we investigated the average distance of the swarm during flocking. Figure 1(a) shows that the form of the swarm do not change during the flocking in the environment without obstacle. Therefore, the results if the average distance for the first case is shown with dashed lines. Figure 2 illustrates the average distance of swarm for two different collective forces, \(k \in \{0.05 , 3\}\). Figure 2(a) depicts the results for \(l_{ij} = 3\) m from single-obstacle flocking motion. It takes approximately \(t=\)150 sec to encounter the obstacle and the average distance of swarm becomes bigger while they are crossing the region. This disturbance is recovered and reached the original stable state for large collective force. In contrast, in case of the small collective force, the average distance was increased after the swarm passed the obstacles. The main reason is that the swarm is divided into several clusters that were formed in different positions far from each other. Similarly, this result also appears in multi-obstacle cases shown in Fig. 2(b). In addition, the average distance was much larger than the single-obstacle cases. Figure 2(c) and (d) show the results for \(l_{ij}=3.5\) m. It illustrates that the equilibrium distance has minor impact on the flocking performance in cluttered environments.

Fig. 1.
figure 1

Flocking behaviour in three environmental cases with \(k=0.05\); (a) without an obstacle, (b) with a single obstacle, and (c) with multi-obstacle. (d) with \(k=3\) and a single obstacle, and (e) with \(k=3\) and multi-obstacle.

Full size image
Fig. 2.
figure 2

Average distance with two different collective forces (a) with \(l_{ij}=3\) in a single obstacle, (b) with \(l_{ij}=3\) in multi-obstacle, (c) with \(l_{ij}=3.5\) in a single obstacle, and (d) with \(l_{ij}=3.5\) in multi-obstacle. Line and dashed line indicate the median and shaded area represent the first and third quartiles.

Full size image

4 Conclusion

This work proposed a self-organised collective motion method based on the AES model. The main aim is to improve the AES collective motion behaviour to make it possible for use in a real-world application. This work designed an appropriate obstacle force and added it into the basic model. The simulation results illustrated the proposed method can achieve the self-organised flocking and obstacle avoidance in the complex environments. In addition, we investigated the flocking performance under the different parameters setting for collective force with a constant obstacle force. The results showed that the relationship between these two essential forces could have a significant impact on the flocking performance. The different equilibrium distances in the AES model were also investigated to illustrate the functionality of the proposed method. Further work will continue to investigate the obstacle interaction mechanisms in AES model using real-robot experiments.