Impact of Private Observation in the Bayesian Persuasion Game

Abstract

In the Bayesian persuasion setting, the sender aims at persuading the decision maker, so called the decoder, to choose a certain action among a set of possible actions. This paper considers two Bayesian persuasion games: one that involves the observation of a private signal by the decoder in addition to the signal transmitted by the encoder, and another version where no private signal is accessible by the decoder. Our goal is to examine the impact of this private signal on the encoder’s optimal utility. In order to do so, we investigate an example involving a binary state, a binary private signal and a binary receiver’s actions set. We identify the optimal splitting of the decoder’s beliefs satisfying the information constraint imposed by the restricted communication channel, and we compute the encoder’s optimal utility value, with and without private signal. Varying the parameters such as the prior belief, the precision of the private signal and the channel capacity, we aim at determining which of the two settings is more favorable to the encoder.

M. Le Treust—Gratefully acknowledges financial support from INS2I CNRS, DIM-RFSI, SRV ENSEA, UFR-ST UCP, The Paris Seine Initiative and IEA Cergy-Pontoise. This research has been conducted as part of the project Labex MME-DII (ANR11-LBX-0023-01).

1 Introduction

In [5], Kamenica-Gentzkow investigate a persuasion game in which the sender observes the realization of a state variable and commits to some signalling mechanism, then the receiver chooses the best-reply action corresponding to its posterior belief. Communication in persuasion games may be constrained by a limited channel’s capacity and messages distorted by some source of noise, as in [9]. Moreover, the receiver may privately observe a signal correlated to the state, as in the source coding problem of Slepian-Wolf and Wyner-Ziv, in [12] and [13]. In such settings, the persuasion problem is hard to solve even for simple models. Tools from information theory, involving entropy and mutual information, provided a solution for certain scenarios of repeated persuasion problems. The optimal solution to the noisy persuasion problem relies on a specific concavification involving an auxiliary utility function for the sender that accounts for the private observation of the receiver as in [8, 9] and [10].

Fig. 1.

Bayesian persuasion game with noisy channel $\mathcal {T}(y|x)$, with or without decoder’s side information Z. The utility functions of the encoder $\mathcal {E}$ and decoder $\mathcal {D}$ are denoted by $\phi _e(u,v)$ and $\phi _d(u,v)$.

1.1 State of the Art

Channel coding and communication problems originally introduced in [11] have been studied in several settings, particularly with the side information setting as in [1] where a hierarchical communication game is considered to treat information disclosure problems originated in economics and involving different objectives for the encoder and the decoder. In [2], Alonso-Cãmara provide necessary and sufficient conditions under which a sender benefits from persuading decoders with distinct prior beliefs. The computational aspects of the persuasion game are considered in [4], where the impact of the channel’s capacity on the optimal utility is investigated. Persuasion of a privately informed receiver was also investigated in [6], in which the optimal persuasion mechanisms are characterized. In [7], Laclau-Renou depicted the constraints imposed on the sender when multiple receivers have multiple beliefs.

1.2 Contributions

In this paper, we consider a persuasion game with binary source/state and binary decoder’s actions and we investigate the effect of the decoder’s side observation on the encoder’s optimal utility. We compute numerically the two values of the persuasion problems, with and without decoder’s side information, depending on two keys parameters, 1) the channel capacity and 2) the precision of the decoder’s side information. Depending on these two parameters, the decoder’s side information may increase or decrease the encoder’s utility.

The paper is organized as follows. The notations are defined in Sect. 2. In Sect. 3, we formulate the two concavification problems. In Sect. 4, we introduce the example of a binary source and state, and we formulate the optimal solutions for the case with no private observation in Sect. 4.1, and for the case where private observation is available at the decoder Sect. 4.2. In Sect. 5, we provide the results of our numerical simulations.

2 Notations

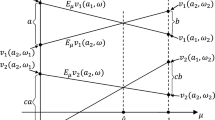
This paper considers a communication model that is illustrated in Fig. 1. Let $\mathcal {E}$ denote the encoder and $\mathcal {D}$ denote the decoder. Notations U, Z, X, Y,  and V denote the random variables of information source $u \in \mathcal {U}$, side information $z \in \mathcal {Z}$, channel inputs $x \in \mathcal {X}$, channel outputs $y \in \mathcal {Y}$, and decoder’s actions $v \in \mathcal {V}$ respectively. Calligraphic fonts $\mathcal {U},$ $\mathcal {Z},$ $\mathcal {X},$ $\mathcal {Y},$ and $\mathcal {V},$ denote the alphabets and lowercase letters u,  z,  x,  y,  and v denote the signal realizations. Notation $\mathcal {P}_U$ stands for the probability distribution of the state U of the game. The private observation Z of the receiver is correlated to U according to the conditional probability distribution $\mathcal {P}_{Z|U}$. We will denote the beliefs of the decoder by $p \in \varDelta (\mathcal {U})$ whereas p(u) belongs to [0, 1] for each $u \in \mathcal {U}$. The i.i.d. memoryless channel distribution will be denoted by $\mathcal {T}_{Y|X}.$ We denote by $\varDelta (\mathcal {X})$ the probability simplex, i.e. the set of probability distributions over $\mathcal {X}.$ We denote by $\mathcal {Q}_X$ the probability distribution over $\mathcal {X},$ i.e. the posterior beliefs of the decoder. The joint probability distribution $\mathcal {Q}_{XV} \in \varDelta (\mathcal {X} \times \mathcal {V})$ decomposes as follows, $\mathcal {Q}_{XV} =\mathcal {Q}_{X}\times \mathcal {Q}_{V|X}.$ The channel’s capacity will be denoted by C. Notations H(U),  H(U|Z) and I(X; Y) refer to Shannon’s entropy, conditional entropy and mutual information respectively [3, pp. 12], and are given below.

$$\begin{aligned} H(U)=&\sum _{u\in \mathcal {U}}p(u)\log _2 \frac{1}{p(u)}, \qquad H(U|Z)= \sum _{z\in \mathcal {Z}}\sum _{u\in \mathcal {U}}p(z,u)\log _2 \frac{1}{p(u)}, \end{aligned}$$

(1)

$$\begin{aligned} I(X;Y) =&\sum _{x\in \mathcal {X}}\sum _{y\in \mathcal {Y}}p(x,y)\log _2\frac{p(x,y)}{p(x)p(y). }, \qquad C = \underset{\mathcal {P}(x)}{\max }\; I(X;Y). \end{aligned}$$

(2)

3 Concavification Problems

Given a capacity value $C\ge 0$, we consider the two concavification problems below, stated in [10, Def. III.1] and [9, Def. 2.4].

$$\begin{aligned} \varGamma _0 =&\sup _{(\lambda _w,p_w)_{w\in \mathcal {W}}}\Bigg \{\sum _{w \in \mathcal {W}}\lambda _w\cdot \varPhi _e(p_w) \ s.t. \ \sum _{w \in \mathcal {W}}\lambda _w \cdot p_w =\mathcal {P}_U,\nonumber \\&\sum _w\lambda _w\cdot H(p_w) \ge H(U)-C,|\mathcal {W}|=\min (|\mathcal {U}|+1,|\mathcal {V}|)\Bigg \},\end{aligned}$$

(3)

$$\begin{aligned} \varGamma =&\sup _{(\lambda _w,p_w)_{w\in \mathcal {W}}}\Bigg \{\sum _{w \in \mathcal {W}}\lambda _w\cdot \varPsi _e(p_w) \ s.t. \ \sum _{w \in \mathcal {W}}\lambda _w \cdot p_w =\mathcal {P}_U,\nonumber \\&\sum _w\lambda _w\cdot h(p_w) \ge H(U|Z)-C,|\mathcal {W}|=\min (|\mathcal {U}|+1,|\mathcal {V}|^{|\mathcal {Z}|})\Bigg \}, \end{aligned}$$

(4)

where

$$\begin{aligned} \varPhi _e(p) =&\mathbb {E}_p\Big [\phi _e(U,v^{\star }(p))\Big ], \qquad H(p)= H(U), \end{aligned}$$

(5)

(6)

and

$$\begin{aligned} \forall z\in \mathcal {Z},\quad q_z\in \varDelta (\mathcal {U}),\quad q_z(u) =&\frac{p(u)\cdot \mathcal {P}(z|u)}{\sum _{u'}p(u')\cdot \mathcal {P}(z|u')},\qquad \forall u\in \mathcal {U},\end{aligned}$$

(7)

$$\begin{aligned} \varPsi _e(p) =&\sum _{u,z}p(u)\cdot \mathcal {P}(z|u)\cdot \varPhi _e \big (q_z \big ), \end{aligned}$$

(8)

$$\begin{aligned} h(p)=&\sum _{u,z}p(u)\cdot \mathcal {P}(z|u)\cdot \log _2\frac{\sum _{u'}p(u')\cdot \mathcal {P}(z|u')}{p(u)\cdot \mathcal {P}(z|u)}. \end{aligned}$$

(9)

The notation $v^{\star }(p) \in V$ stands for the decoder’s best reply action with respect to its posterior belief $p \in \varDelta (\mathcal {U})$. If several actions maximize the utility of the decoder, we assume that it chooses the one that minimizes the encoder’s utility. Thus, the encoder’s expected utility $\varPhi _e(p)$ is evaluated with respect to the decoder’s belief $p\in \varDelta (\mathcal {U})$. In the presence of side information $z \in Z$, the decoder’s belief is denoted by $q_z \in \varDelta (\mathcal {U})$. As a consequence, the encoder’s expected utility $\varPsi _e(p)$ is a convex combination between the utilities $\varPhi _e \big (q_z \big )$ evaluated at different possible beliefs $(q_z)_{z\in \mathcal {Z}}$. The supremum in (4) and (3) are taken over the set of splittings $(\lambda _w,p_w)_{w\in \mathcal {W}}$ of the prior probability distribution $\mathcal {P}_U \in \varDelta (\mathcal {U})$, that satisfy the cardinality bound, either $|\mathcal {W}|=\min (|\mathcal {U}|+1,|\mathcal {V}|)$ or $|\mathcal {W}|=\min (|\mathcal {U}|+1,|\mathcal {V}|^{|\mathcal {Z}|})$.

Formulas (3) and (4) are solutions to the persuasion game with noisy channel. The value $\varGamma$ corresponds to the persuasion problem in which the decoder has a private observation Z correlated with the state U according to the conditional probability distribution $P_{Z|U}$, whereas the value $\varGamma _0$ corresponds to the persuasion problem in which the decoder has no access to a side information, or equivalently, has a private observation Z that is independent from the state U. When removing the entropy-based constraints in $\varGamma _0$, the concavification problem boils down to the optimal solution provided by Kamenica-Gentzkow in [5].

4 Example with Binary Source and State

In this section, we will illustrate a particular scenario of a strategic communication involving binary source and state and decoder’s action. Let $\mathcal {U}=\{u_0,u_1\}$ the state space, $\mathcal {V}=\{v_0,v_1\}$ the action space, and $p_{0} = \mathrm {P}(U=u_1) \in [0,1]$ the decoder’s prior belief. We consider a binary symmetric noisy channel where $\mathcal {X}=\{x_0,x_1\}$ denotes the set of channel inputs, $\mathcal {Y}=\{y_0,y_1\}$ denotes the set of channel outputs. The channel’s capacity for noise level $\epsilon \in [0,\frac{1}{2}]$ is given by $C = 1-H_b(\epsilon )$ where $H_b(p)$ denotes the binary entropy. Utility functions of both encoder and decoder are given in Tables 1 and 2.

Table 1. Encoder’s utility

Table 2. Decoder’s utility

As shown in the decoder’s expected utility graph Fig. 2a, the red lines represent the decoder’s best reply action. Therefore, the action of the decoder will only change from $v_0$ to $v_1$ depending on the utility threshold $\gamma .$

In this example, we consider the prior $p_0=0.4$ and the utility threshold $\gamma =0.6$.

4.1 Persuasion Without Side Information (Equation for $\varGamma _0$)

The optimal number of posterior beliefs when no side information is available at the decoder is two [9, lemma 6.1]. These posterior beliefs of the decoder need to satisfy the splitting condition and information constraint

$$\begin{aligned}&\lambda q_1 + (1- \lambda ) q_2 = p_0 \Longleftrightarrow \lambda = \frac{p_0-q_2}{q_1-q_2} \Longleftrightarrow 1-\lambda = \frac{q_1-p_0}{q_1-q_2},\end{aligned}$$

(10)

$$\begin{aligned}&\lambda H_b(q_1) + (1- \lambda ) H_b(q_2) \ge H_b(p_0) - C. \end{aligned}$$

(11)

Assuming the information constraint is binding at the optimal, we get

$$\begin{aligned}&\lambda H_b(q_1) + (1- \lambda ) H_b(q_2) = H_b(p_0) - C \end{aligned}$$

(12)

$$\begin{aligned} \Longleftrightarrow&H_b(q_1) = \frac{p_0 H_b(q_2) -q_2 (H_b(p_0) - C)}{(p_0-q_2)} + q_1\frac{ (-H_b(q_2) + H_b(p_0) - C) }{(p_0-q_2)} \end{aligned}$$

(13)

The encoder’s expected utility function $\varPhi _e$ depicted in Fig. 2b is defined over [0, 1] by $\varPhi _e(q)=\mathbbm {1}_{q\in [\gamma ,1]}.$ For each $q_2\in [p_0,1]$, we denote by $q_1(q_2)$ the unique solution of (13) for a given pair $(p_0,C)$ . We assume that the decoder’s threshold $\gamma > p_0,$ hence at the optimum $q_2 = \gamma$, thus

$$\begin{aligned} \varGamma _0 =&\sup _{q_2\in [0,1]} \bigg (\lambda \varPhi _e(q_1(q_2)) + (1- \lambda ) \varPhi _e(q_2)\bigg ) = \frac{q_1(\gamma )-p_0}{q_1(\gamma )-\gamma }. \end{aligned}$$

(14)

Figure 2b shows an unrestricted communication without decoder’s side information. The green dotted line is the concavification of the encoder’s expected utility function represented in the red lines. The optimal utility value corresponds to the evaluation of this concavification at the prior belief $p_0$.

Fig. 2.

Encoder and Decoder’s Expected Utilities

4.2 Persuasion with Side Information (Equation for $\varGamma$)

When side information $\mathcal {Z}=\{z_0, z_1\}$ is observed by the decoder, then [9, Lemma 6.3] ensures that the optimal number of posterior beliefs is three. The posterior distributions $(q_1,q_2,q_3)$ from observing the message delivered by the encoder, must satisfy the information constraint given by

$$\begin{aligned} \lambda _1\cdot h(q_1) +\lambda _2\cdot h(q_2)+\lambda _3\cdot h(q_3) \ge H(U|Z) - \underset{\mathcal {P}(x)}{\max }I(X;Y) \end{aligned}$$

(15)

Thus $(\lambda _1,\lambda _2,\lambda _3)$ can be computed from the above information constraint, the splitting lemma $\lambda _1q_1 + \lambda _2q_2 + \lambda _3q_3 =p_0$ and the fact that $\lambda _1 + \lambda _2 + \lambda _3 =1.$ We assume that the information constraint is binding. From [10, Eq. (57)-(59)], we have

$$\begin{aligned} \lambda _1=&\frac{IC\cdot (q_2-q_3)+h(q_2)\cdot (q_3-p_0)+h(q_3)\cdot (p_0-q_2)}{h(q_1)\cdot (q_2-q_3)+h(q_2)\cdot (q_3-q_1)+h(q_3)\cdot (q_1-q_2)},\end{aligned}$$

(16)

$$\begin{aligned} \lambda _2=&\frac{IC\cdot (q_3-q_1)+h(q_3)\cdot (q_1-p_0)+h(q_1)\cdot (p_0-q_3)}{h(q_1)\cdot (q_2-q_3)+h(q_2)\cdot (q_3-q_1)+h(q_3)\cdot (q_1-q_2)},\end{aligned}$$

(17)

$$\begin{aligned} \lambda _3=&\frac{IC\cdot (q_1-q_2)+h(q_1)\cdot (q_2-p_0)+h(q_2)\cdot (p_0-q_1)}{h(q_1)\cdot (q_2-q_3)+h(q_2)\cdot (q_3-q_1)+h(q_3)\cdot (q_1-q_2)}. \end{aligned}$$

(18)

Given a interim belief parameter $q\in [0,1]$, the decoder’s side information might be $z_0$ or $z_1$, thus inducing the two following posterior beliefs

$$\begin{aligned} p_1(q)=&\frac{q.\delta }{(1-q).(1-\delta )+q.\delta },\qquad p_2(q)=\frac{q.(1-\delta )}{(1-q).\delta +q.(1-\delta )}. \end{aligned}$$

(19)

Fig. 3.

Splitting over 2 posteriors $(q_1=0;q_2=0.4468)$ with $C=0.25,\ p_0=0.4, \ \delta =0.35, \ \gamma =0.6.$

The decoder’s threshold $\gamma$ induces the two corresponding threshold $\nu _1$ and $\nu _2$ for the interim belief parameter $q\in [0,1]$

$$\begin{aligned} \nu _1=&\frac{\gamma .(1-\delta )}{\delta .(1-\gamma )+\gamma (1-\delta )},\qquad \nu _2=\frac{\gamma .\delta }{\gamma .\delta +(1-\delta ).(1-\gamma )}. \end{aligned}$$

(20)

Thus the encoder’s utility function $\varPsi _e(q)$ represented by the red lines in Fig. 3 and the conditional entropy h(q) reformulate as

$$\begin{aligned} \varPsi _e(q) =&0\cdot \mathbbm {1}_{\{q \in ]0,\nu _2]\}}+((1-q)\cdot \delta +q\cdot (1-\delta ))\cdot \mathbbm {1}_{\{q \in ]\nu _2,\nu _1]}+ 1\cdot \mathbbm {1}_{\{q \in ]\nu _1,1]\}}, \end{aligned}$$

(21)

$$\begin{aligned} h(q) =&((1-q)\cdot (1-\delta )+q\cdot \delta )\cdot H_b(p_1(q))+((1-q)\cdot \delta +q\cdot (1-\delta )) H_b(p_2(q). \end{aligned}$$

(22)

The encoder’s optimal utility value is given by

$$\begin{aligned} \varGamma =&\sup _{q_1\in [0,\nu _2],q_2\in [\nu _2,\nu _1],\atop q_3\in [\nu _1,1]} \bigg (\lambda _1\cdot \varPsi _e(q_1)+\lambda _2\cdot \varPsi _e(q_2)+ \lambda _3\cdot \varPsi _e(q_3) \bigg ) \end{aligned}$$

(23)

$$\begin{aligned} =&\sup _{q_1\in [0,\nu _2],q_2\in [\nu _2,\nu _1],\atop q_3\in [\nu _1,1]} \bigg (\frac{(h(p_0)-C)\big ((q_3-q_1 )\cdot \big (q_2\cdot (1-2\delta )+\delta \big )+(q_1-q_2)\big ) }{h(q_1)\cdot (q_2-q_3)+h(q_2)\cdot (q_3-q_1)+h(q_3)\cdot (q_1-q_2)} \nonumber \\ +&\frac{\big (h(q_3)\cdot (q_1-p_0) +h(q_1)\cdot (p_0-q_3)\big )\cdot \big (q_2\cdot (1-2\delta )+\delta \big )}{h(q_1)\cdot (q_2-q_3)+h(q_2)\cdot (q_3-q_1)+h(q_3)\cdot (q_1-q_2)} \nonumber \\&+ \frac{h(q_1)\cdot (q_2-p_0)+h(q_2)\cdot (p_0-q_1)}{h(q_1)\cdot (q_2-q_3)+h(q_2)\cdot (q_3-q_1)+h(q_3)\cdot (q_1-q_2)}\bigg ) \end{aligned}$$

(24)

Fig. 4.

Optimal Splittings over 3 posteriors $(q_1=0.012;q_2=0.4468;q_3=0.7358)$ with $C=0.25,\ p_0=0.4, \ \delta =0.35, \ \gamma =0.6.$

In some cases, the optimal splitting has only two posterior instead of three. Fig. 3 and Fig. 4 represent the optimal utility of the encoder depending on belief parameter q over a constrained communication channel with capacity $C=0.25$ and with decoder’s private observation $\delta =0.35$. Splitting over three posteriors instead of two, improves the encoder’s optimal payoff.

5 Numerical Simulations

In this section we investigate the impact of the private observation on the encoder’s optimal utility. Numerical simulations over (C, $\delta$) regions are performed for both concavification problems $\varGamma _0$ and $\varGamma$, revealing the encoder’s optimal payoff values with and without decoder’s private observation.

5.1 Encoder’s Optimal Payoff Values

The optimal splitting of the prior over 3 posterior beliefs results in the encoder’s optimal payoff values shown in Fig. 5 with respect to the $(C,\delta )$ regions.

Fig. 5.

Encoder’s optimal payoff evaluated with three posteriors w.r.t. $\delta$ and C for $p_0=0.4$ and $\gamma =0.6.$

As the channel’s capacity increases, the encoder’s utility is improved without decoder’s side information. This is due to the fact that more capacity allows the transmission of more information and hence information can be optimally disclosed. However; with low capacity, the decoder’s side observation can enhance the utility of the encoder until the encoder has no capacity at all, it becomes optimal to have private information up to some threshold $\delta ^{\star }$ evaluated in Proposition 1 below.

5.2 Impact of the Decoder’s Private Signal

Proposition 1

Let $C=0$.

• If $p_0 < \gamma$ and $\delta \in [0,\ \frac{p_0\cdot (\gamma -1)}{p_0\cdot (-1+2\gamma )-\gamma }]\ \cup \ [\frac{\gamma \cdot (1-p_0)}{p_0\cdot (1-2\gamma )+\gamma }, \ 1]$, then $\varGamma > \varGamma _0.$

• If $p_0 \ge \gamma$ then $\varGamma _0 \ge \varGamma .$

Fig. 6.

$(\delta ,C)$ regions for encoder’s optimal utility with (blue) and without (green) decoder’s private observation for $p_0=0.4$ and $\gamma =0.6.$ (Color figure online)

5.3 Impact of the Number of Posteriors

The encoder could potentially achieve a greater payoff by splitting the prior over three posterior beliefs instead of splitting over two posteriors only (Fig. 7).

Fig. 7.

Difference between optimal utility values obtained by splitting with three posteriors and two posteriors.