Keywords

1 Introduction

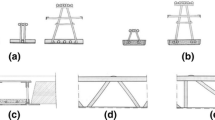
Steel-reinforced concrete structural constructions in the form of spatial truss elements with an upper reinforced concrete slab or beam are most used in the construction of bridge crossings and span structures of a coating of considerable length.

Examples of the use of steel-reinforced concrete composite truss structures in bridges are given by K. Flaga and K. Furtak in [1] and Jose J. Oliveira Pedro et al. in [2, 3]. A survey analysis of the evolution of the construction of composite truss bridges, which was carried out by a group of scientists led by L. Yongjian in [4, 5], showed the economic efficiency of their construction.

At the same time, despite the widespread use of composite truss bridges in construction practice, generalized norms and standards for their design are absent in most leading countries of the world, as noted by A. Sharma, P.K.Singh, K.K. Pathak in [6]. Therefore, today there is a need to develop and improve a practical methodology for calculating the bending strength of steel–concrete truss elements, which are structural components of composite bridges and spans of considerable lengths.

The goal of research is to develop the general procedure and analytical dependencies of the calculation of the flexural strength of steel-reinforced concrete (SRC) composite structural span elements (CSSE), depending on the stress–strain state of their design section at the breaking moment.

The scientific developments of the authors of the article are associated with their preliminary studies, which are set out in the works [7, 8, 9], and are also a further development of the research of leading scientists Piskunov V. [10, 11], Pavlikov A. & Kochkarev D. [12, 13, 19], Storozhenko L. [14, 15], Semko O. [16] with their co-authors.

2 Analytical Model of Calculation of the Flexural Strength of SRC CSSE

The analytical model for the calculation of the flexural strength of steel-reinforced concrete (SRC) composite structural span elements (CSSE) is the continuation of the authors’ scientific research results aimed to improve their calculation procedure. The main theoretical methodological prerequisites for the calculation of the SRC CSSE have been previously developed by the authors in the following academic papers [17, 18].

In order to work out the analytical model for the calculation of the flexural strength of steel-reinforced concrete (SRC) composite structural span elements (CSSE) we have defined the following prerequisites:

  • strain distribution in section at plastic (Composite-PSD) or elastic–plastic (Composite-SC) stages is carried out jointly by linear dependencies. The steel profile in the section of SRC truss elements has rigid vertical or inclined connections with the top concrete slab;

  • the criterion for the limit state at the breaking moment of the design section of the SRC CSSE is the extremum criterion for achieving deformations of the compressive zone of the concrete with the limit value \(\varepsilon_{cu}\), at which the flexural strength of \(M_{Rb}\) elements will be maximum:

    case a: \(M_{plRb} (\varepsilon_{cu} , \varepsilon_{a} > \varepsilon_{au} ) = max\)– is the plastic stage of destruction of SRC CSSE (Composite-PSD);

    case b: \(M_{Rb} (\varepsilon_{cu} , \varepsilon_{a} = \varepsilon_{au} ) = max\)– boundary stage of destruction of SRC CSSE – the border set between plastic stage (Composite-PSD) and elastic–plastic stage of destruction (Composite-SC);

    case c: \(M_{Rb} (\varepsilon_{cu} , \varepsilon_{a} < \varepsilon_{au} ) = max\)– elastic–plastic stage of destruction of SRC CSSE (Composite-SS);

    The extremum criterion for the destruction of \(M_{Rb} (\varepsilon_{cu} , \varepsilon_{a} = \varepsilon_{au} ) = max\) was formulated similarly to the criterion \(N(\varepsilon_{cu} , \varepsilon_{s} = \varepsilon_{su} ) = max\), which was recommended by Mitrofanov V.P. in article [20] in order to calculate optimal compression RC elements (Fig. 1).

  • the effort \(N_{c}\) in the compression area of the SRC CSSE’s cross-section is determined by mathematical relations, proposed by the scientists James K. Wight and James G. Macgregor and is now the basis for calculating the flexural strength of RC beams in Eurocode 2 [21] and SRC beams in Eurocode 4 [22];

  • the analysis of cross sections of SRC truss elements revealed that most part of cross-sections can be corrected to generalized characteristic design sections, which will be reduced to their vertical axis. The steel profile in the cross section of the SRC truss elements can be in the form of an I-beam (a), a rectangle (a square) (b) or a circular pipe (c). This steel profile can be arranged in conjunction or at some distance from the top concrete cap.

  • typological analysis of cross sections of SRC truss elements has showed that all their cross-sections for generalization of the calculation methodology for the flexural strength of SRC CSSE can be transformed to one deduced design section. The transformed design cross section of the SRC CSSE consists of a top concrete slab and an I- girder (steel profile) (Fig. 2);

    Fig. 1
    figure 1

    Typological series of characteristic design sections of SRC truss elements

    Full size image
    Fig. 2
    figure 2

    The overall transformed cross section of the SRC CSSE

    Full size image

  • as a result of the generalization, we have selected four isolated cases of strain–stress state of the design section of the SRC CSSE at determining the flexural strength (Fig. 3). Differentiation of cases of the SRC CSSE’s limit state depending on the position of the neutral axis in their section allows us to work out a stepwise algorithm of the analytical calculation model of their flexural strength and to obtain the basic calculated correspondences.

    Fig. 3
    figure 3

    Cases of the limit stress–strain state of the SRC CSSE’s design transformed cross section at determining their flexural strength

    Full size image

2.1 The algorithm for SRC CSSE’s Flexural Strength Calculation

The purpose of the mathematical method of design of the SRC CSSE’s flexural strength is to determine the limit value of the bending beam moment \(M_{Rb}\), which takes up its design section, and to compare it with the external moment M from the load action: \(M_{Rb} \ge M\) or \(M_{plRb} \ge M\).

The succession of determining the SRC CSSE’s flexural strength according to the proposed mathematical method of design (analytical method of calculation) is shown in the block diagram (Fig. 4).

Fig. 4
figure 4

The block diagram of the succession of determining the SRC CSSE’s flexural strength

Full size image

At the first stage of calculation the flexural strength of the SRC CSSE at present parameters, dimensions of the design section and strength of the composites (\(\varepsilon_{cu}\), \(\varepsilon_{au}\), \(E_{C}\), \(E_{a}\), \(f_{cd}\), \(f_{y}\). \(A_{C}\), \(A_{a}\) and \(h_{w}\) are calculated using Eqs. (1), (2) and (3)), we will find the following:

$$A_{C} = B_{f} \cdot T_{f}$$
(1)
$$A_{a} = 2 \cdot t_{f} \cdot b_{f} + h_{w} \cdot t_{w}$$
(2)
$$h_{w} = h_{a} - 2 \cdot t_{f}$$
(3)

  • the result of the product \(a_{a} \cdot \mu\) Eq. (4) and the value of internal forces \(N_{cf}\) Eq. (5) and \(N_{pl,a}\) Eq. (6):

    $$N_{cf} = 0,85 \cdot f_{cd} \cdot B_{f} \cdot T_{f}$$
    (4)
    $$N_{pl,a} = A_{a} \cdot f_{y}$$
    (5)
    $$a_{a} \cdot \mu = E_{a} \cdot A_{a} /\left( {E_{C} \cdot A_{C} } \right)$$
    (6)

  • let us check the constraint:

    $$a_{a} \cdot \mu \ge a_{a} \cdot \mu_{onm} ,$$

where \(a_{a} \cdot \mu_{onm}\) is the optimal value of the product, at which the maximum flexural strength will be equal to the mathematical relation: \(M_{Rb} (\varepsilon_{cu} , \varepsilon_{a} = \varepsilon_{au} ) = max\), when the deformations in the extreme fiber of the compressive zone of the concrete reach the value \(\varepsilon_{C} = \varepsilon_{cu}\), and in the steel segment they reach the value \(\varepsilon_{a} = \varepsilon_{au}\). The values of the product quantities \(a_{a} \cdot \mu_{onm}\) can be determined from the data in the tables given in the authors’ research works [7, 8], or using the mathematical relations given in Eqs. (7), (8), (9), (10) and (11):

$$a_{a} = E_{a} /E_{C}$$
(7)
$$\mu_{onm} = [2 \cdot \Delta_{Z} \cdot \Delta_{\varepsilon } \cdot (1 + \Delta_{h} ) - \Delta_{\varepsilon } - 1]/\{ a_{a} \cdot [2 \cdot \Delta_{Z} \cdot (1 + \Delta_{h} ) - \Delta_{h} \cdot (1 + \Delta_{\varepsilon } )]\}$$
(8)
$$\Delta_{Z} = Z_{a} /\left( {T_{f} + h_{a} /2} \right)$$
(9)
$$\Delta_{\varepsilon } = \varepsilon_{u} /\varepsilon_{au}$$
(10)
$$\Delta_{h} = h_{a} /T_{f}$$
(11)

At the second stage of calculation, we determine the possibility of the arrangement of the neutral horizontal axis of the section at the height (\(T_{f}\)) of the concrete slab on exposure to the external moment (\(M\)), under the following condition:

$$N_{cf } > N_{pl,a} .$$

If the condition \(N_{cf } > N_{pl,a}\), is satisfied, then the neutral horizontal axis of the element’s section falls within the limits of the height of the top concrete cap \(T_{f}\). Next, we determine the height of the compressive zone of the concrete (\(x_{C}\)) and the value of the bending beam moment (\(M_{Rd}\)) for the SRC CSSE’s design section in strain–stress state in cases 1a or 1b, c (Fig. 3) according to the mathematical relations, stated below in Table 1.

Table 1. Analytical dependences of the calculation of flexural strength \(M_{Rd}\) of the SRC CSSE depending on the case of strain–stress state of their design section
Full size table

At the third stage of calculation, under condition \(N_{cf } < N_{pl,a}\), we determine in the design section of the SRC CSSE the value \(Y_{B}\) (height) from the upper fiber under compression to the neutral axis and compare it with the condition:

$$Y_{B } \le h - h_{a} .$$

If the conditions \(N_{cf } < N_{pl,a}\), and are satisfied, then the neutral horizontal axis of the element’s section falls within the limits of the difference of the heights of. Next, we determine the height of the compressive zone of the concrete (\(Y_{B }\)) and the value of the bending beam moment (\(M_{Rd}\)) for the design section of the SRC CSSE in the strain–stress state in cases 2a or 2b,c (Fig. 3) according to the mathematical relations, stated above in Table 1.

At the fourth stage of calculation, when the value (height) \(Y_{B } \le h - h_{a}\), the value of the bending beam moment (\(M_{Rd}\)) for the design section of the SRC CSSE is determined in the strain–stress state in cases 3a or 3b,c (Fig. 4), 4a or 4b,c according to the mathematical relations, stated above in Table 1.

The value of flexural strength (\(M_{Rd}\)) of the design section of the SRC CSSE is compared with the value of the torque from external forces (\(M\)). The strength of the SRC CSSE section will be ensured with the requirement that:

$$M_{Rd} \ge M.$$

If the condition of the SRC CSSE’s flexural strength is not satisfied, then it is necessary to increase the size of their design section and to take the materials of their components with larger values of strength characteristics (shear properties), and then to do the calculation again.

2.2 Analytical Dependences of SRC CSSE’s Flexural Strength Depending on the Case of Strain–Stress State of the Design Section at the Breaking Moment

Analytical dependences of calculation flexural strength of steel-reinforced concrete (SRC) composite structural span elements (CSSE), depending on the case of strain–stress state of their design section at the breaking are shown in Table 1.

3 Comparisons between Experimental and Analytical Results of Bending Strength Calculation SRC CSSE

In order to compare the proposed analytical model of calculation of flexural strength of SRC CSSE, we have used the results of experimental studies of national and foreign scientists, such as: T. P. Kuch (specimens of beams B-1, B-2–1, B-2–2-1, B-2–3, B-3–1, B-3–2-1, B-3–3) [23]; F. S Shkoliar (specimens of beams B-1.1, B-1.2, B-2.1, B-2.2, B-3.1,) [24]; L. Luo (Lisheng Luo) (specimens of beams B-1… B-3) [25]; J. Bujnak (a specimen beam without marking) [26].

When comparing the results, we have determined arithmetic mean (\(\overline{X}\)), root-mean-square deviation (\(\sigma_{n - 1}\)) and coefficient of variation (\(\nu\)).

The comparisons of experimental results (\(M^{test}\)) and analytical findings of the calculation of flexural strength of SRC truss elements (\(M^{calc}\)) are given in Table 2.

Table 2 Comparison of experimental bending moments with theoretical meanings
Full size table

Comparison of experimental and theoretical strength values of 16 specimens of reinforced concrete truss beams, which components are bond, leads to the following statistical indicators:

  • for partial factors for concrete \(\gamma_{C} = 1,0\) and for material property, also accounting for model uncertainties and dimensional variations \(\gamma_{M} = 1,0\)- \(\overline{X} = 1,094;\;\sigma_{n - 1} = 0,006;\;\nu = 0,52\%\);

  • for partial factors for concrete \(\gamma_{C} > 1,0\) and for material property, also accounting for model uncertainties and dimensional variations \(\gamma_{M} > 1,0\)- \(\overline{X} = 1,261;\;\sigma_{n - 1} = 0,014;\;\nu = 1,13\%\).

4 Conclusions

The algorithms and analytical dependences of the method for calculating the flexural strength of steel-reinforced concrete (SRC) composite structural span elements (CSSE) are presented in the academic paper. Comparative analysis of the experimental findings with theoretical calculations of flexural strength of SRC CSSE has showed their adequate convergence, which allows to apply the proposed analytical dependencies in the design practice.

Further scientific research in this area will be aimed at improvement of the proposed method for calculating the SRC CSSE and its comparison with a wider range of experimental studies of the elements.

figure a