Abstract
Multi-signatures enable a group of signers to produce a joint signature on a joint message. Recently, Drijvers et al. (S&P’19) showed that all thus far proposed two-round multi-signature schemes in the pure DL setting (without pairings) are insecure under concurrent signing sessions. While Drijvers et al. proposed a secure two-round scheme, this efficiency in terms of rounds comes with the price of having signatures that are more than twice as large as Schnorr signatures, which are becoming popular in cryptographic systems due to their practicality (e.g., they will likely be adopted in Bitcoin). If one needs a multi-signature scheme that can be used as a drop-in replacement for Schnorr signatures, then one is forced to resort either to a three-round scheme or to sequential signing sessions, both of which are undesirable options in practice.
In this work, we propose \(\mathsf {MuSig2} \), a simple and highly practical two-round multi-signature scheme. This is the first scheme that simultaneously i) is secure under concurrent signing sessions, ii) supports key aggregation, iii) outputs ordinary Schnorr signatures, iv) needs only two communication rounds, and v) has similar signer complexity as ordinary Schnorr signatures. Furthermore, it is the first multi-signature scheme in the pure DL setting that supports preprocessing of all but one rounds, effectively enabling a non-interactive signing process without forgoing security under concurrent sessions. We prove the security of \(\mathsf {MuSig2} \) in the random oracle model, and the security of a more efficient variant in the combination of the random oracle and the algebraic group model. Both our proofs rely on a weaker variant of the OMDL assumption.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Multi-signature schemes [17] enable a group of signers (each possessing an own secret/public key pair) to run an interactive protocol to produce a single signature \(\sigma \) on a message m. A recent spark of interest in multi-signatures is motivated by the idea of using them as a drop-in replacement for ordinary (single-signer) signatures in applications such as cryptocurrencies that support signatures already. For example the Bitcoin community, awaiting the adoption of Schnorr signatures [32] as proposed in BIP 340 [38], is seeking for practical multi-signature schemes which are fully compatible with Schnorr signatures: multi-signatures produced by a group of signers should just be ordinary Schnorr signatures and should be verifiable like Schnorr signatures, i.e., they can be verified using the ordinary Schnorr verification algorithm given only a single aggregate public key that can be computed from the set of public keys of the signers and serves as a compact representation of it.
This provides a number of benefits that reach beyond simple compatibility with an upcoming system: Most importantly, multi-signatures enjoy the efficiency of Schnorr signatures, which are very compact and cheap to store on the blockchain. Moreover, if multi-signatures can be verified like ordinary Schnorr signatures, the additional complexity introduced by multi-signatures remains on the side of the signers and is not exposed to verifiers who need not be concerned with multi-signatures at all and can simply run Schnorr signature verification. Verifiers, who are just given the signature and the aggregate public key, in fact do not even learn whether the signature was created by a single signer or by a group of signers (or equivalently, whether the public key is an aggregation of multiple keys), which is advantageous for the privacy of users.
Multi-signatures Based on Schnorr Signatures. A number of modern and practical proposals [2, 4, 11, 20, 22, 28, 29, 36] for multi-signature schemes are based on Schnorr signatures. The Schnorr signature scheme [32] relies on a cyclic group  of prime order p, a generator g of
of prime order p, a generator g of  , and a hash function H. A secret/public key pair is a pair
, and a hash function H. A secret/public key pair is a pair  where \(X=g^x\). To sign a message m, the signer draws a random integer r in \(\mathbb {Z}_p\), computes a nonce \(R=g^r\), the challenge \(c=H(X,R,m)\), and \(s=r+cx\). The signature is the pair (R, s), and its validity can be checked by verifying whether \(g^s=RX^c\).
where \(X=g^x\). To sign a message m, the signer draws a random integer r in \(\mathbb {Z}_p\), computes a nonce \(R=g^r\), the challenge \(c=H(X,R,m)\), and \(s=r+cx\). The signature is the pair (R, s), and its validity can be checked by verifying whether \(g^s=RX^c\).
The naive way to design a multi-signature scheme fully compatible with Schnorr signatures would be as follows. Say a group of n signers want to sign a message m, and let \(L=\{X_1=g^{x_1},\ldots ,X_n=g^{x_n}\}\) be the multisetFootnote 1 of all their public keys. Each signer randomly generates and communicates to others a nonce \(R_i=g^{r_i}\); then, each of them computes \(R=\prod _{i=1}^n R_i\), \(c=H(\widetilde{X},R,m)\) where \(\widetilde{X}=\prod _{i=1}^n X_i\) is the product of individual public keys, and a partial signature \(s_i=r_i+cx_i\); partial signatures are then combined into a single signature (R, s) where \(s=\sum _{i=1}^n s_i \bmod p\). The validity of a signature (R, s) on message m for public keys \(\{X_1,\ldots ,X_n\}\) is equivalent to \(g^s=R\widetilde{X}^c\) where \(\widetilde{X}= \prod _{i=1}^n X_i\) and \(c=H(\widetilde{X},R,m)\). Note that this is exactly the verification equation for an ordinary key-prefixed Schnorr signature with respect to the aggregate public key \(\widetilde{X}\). However, as already pointed out many times [16, 19, 23, 24], this simplistic protocol is vulnerable to a rogue-key attack where a corrupted signer sets its public key to \(X_1= g^{x_1}(\prod _{i=2}^n X_i)^{-1}\), allowing him to produce signatures for public keys \(\{X_1,\ldots ,X_n\}\) by himself.
One way to generically prevent rogue-key attacks is to require that users prove possession of the secret key, e.g., by attaching a zero-knowledge proof of knowledge to their public keys [9, 31]. However, this makes key management cumbersome, complicates implementations, and is not compatible with existing and widely used key serialization formats.
The MuSig Scheme. A more direct defense against rogue-key attacks proposed by Bellare and Neven [4] is to work in the plain public-key model, where public keys can be aggregated without the need to check their validity. To date, the only multi-signature scheme provably secure in this model and fully compatible with Schnorr signatures is \(\mathsf {MuSig} \) (and the variant \(\mathsf {MuSig\text {-}DN}\) [28]) by Maxwell et al. [22], independently proven secure by Boneh, Drijvers, and Neven [9].
In order to overcome rogue-key attacks in the plain public-key model, \(\mathsf {MuSig} \) computes partial signatures \(s_i\) with respect to “signer-dependent” challenges \( c_i = \mathsf {H}_{\mathrm {agg}}(L,X_i)\cdot \mathsf {H}_{\mathrm {sig}}(\widetilde{X},R,m), \) where \(\widetilde{X}\) is the aggregate public key corresponding to the multiset of public keys \(L=\{X_1,\ldots ,X_n\}\). It is defined as \( \widetilde{X}= \prod _{i=1}^n X_i^{a_i} \) where \(a_i=\mathsf {H}_{\mathrm {agg}}(L,X_i)\) (note that the \(a_i\)’s only depend on the public keys of the signers). This way, the verification equation of a signature (R, s) on message m for public keys \(L=\{X_1,\ldots ,X_n\}\) becomes \( g^s=R\prod _{i=1}^n X_i^{a_ic} = R\widetilde{X}^c, \) where \(c=\mathsf {H}_{\mathrm {sig}}(\widetilde{X},R,m)\). This recovers the key aggregation property enjoyed by the naive scheme, albeit with respect to a more complex aggregate key \(\widetilde{X}=\prod _{i=1}^n X_i^{a_i}\).
In order to be able to simulate an honest signer in a run of the signing protocol via the standard way of programming the random oracle \(\mathsf {H}_{\mathrm {sig}}\), \(\mathsf {MuSig} \) has an initial commitment round (like the scheme by Bellare and Neven [4]) where each signer commits to its share \(R_i\) before receiving the shares of other signers.
As a result, the signing protocol of \(\mathsf {MuSig} \) requires three communication rounds, and only the initial commitment round can be preprocessed without knowing the message to be signed [26].
Two-Round Schemes. Following the scheme by Bellare and Neven [4], in which signing requires three rounds of interaction, multiple attempts to reduce this number to two rounds [2, 4, 22, 36] were foiled by Drijvers et al.. [11]. In their pivotal work, they show that all thus far proposed two-round schemes in the pure DL setting (without pairings) cannot be proven secure and are vulnerable to attacks with subexponential complexity when the adversary is allowed to engage in an arbitrary number of concurrent sessions (concurrent security), as required by the standard definition of unforgeability.
If one prefers a scheme in the pure DL setting with fewer communication rounds, only two options remain, and none of them is fully satisfactory. The first option is the \(\mathsf {mBCJ}\) scheme by Drijvers et al. [11], a repaired variant of the scheme by Bagherzandi, Cheon, and Jarecki [2]. While \(\mathsf {mBCJ}\) needs only two rounds, it does not output ordinary Schnorr signatures and is thus not suitable as a drop-in replacement for Schnorr signatures, e.g., in cryptocurrencies whose validation rules support Schnorr signatures (such as proposed for Bitcoin). The second option is \(\mathsf {MuSig\text {-}DN}\) (\(\mathsf {MuSig}\) with Deterministic Nonces) [28], which however relies on heavy zero-knowledge proofs to prove a deterministic derivation of the nonce to all cosigners. This increases the complexity of the implementation significantly and makes \(\mathsf {MuSig\text {-}DN}\), even though it needs only two rounds, in fact less efficient than three-round \(\mathsf {MuSig}\) in common settings. Moreover, in neither of these two-round schemes is it possible to reduce the rounds further by preprocessing the first round without knowledge of the message to be signed.
1.1 Our Contribution
We propose a novel and simple two-round variant of the \(\mathsf {MuSig} \) scheme that we call \(\mathsf {MuSig2} \). In particular, we remove the preliminary commitment phase, so that signers start right away by sending nonces. However, to obtain a scheme secure under concurrent sessions, each signer i sends a list of \(\nu \ge 2\) nonces \(R_{i,1},\ldots ,R_{i,\nu }\) (instead of a single nonce \(R_i\)), and effectively uses a linear combination \(\hat{R}_i=\prod _{j=1}^{\nu } R_{i,j}^{b^{j-1}}\) of these \(\nu \) nonces, where b is derived via a hash function.
\(\mathsf {MuSig2} \) is the first multi-signature scheme that simultaneously i) is secure under concurrent signing sessions, ii) supports key aggregation, iii) outputs ordinary Schnorr signatures, iv) needs only two communication rounds, and v) has similar signer complexity as ordinary Schnorr signatures. Furthermore, it is the first scheme in the pure DL setting that supports preprocessing of all but one rounds, effectively enabling non-interactive signing without forgoing security under concurrent sessions. \(\mathsf {MuSig\text {-}DN} \) [28], which relies on rather complex and expensive zero-knowledge proofs (proving time \(\approx 1\,\)s), only enjoys the first four properties and does not allow preprocessing of the first round without knowledge of the message.
In comparison to other multi-signature schemes based on Schnorr signatures, the price we pay for saving a round is a stronger cryptographic assumption: instead of the DL assumption, we rely on the algebraic one-more discrete logarithm (AOMDL) assumption, a weaker and falsifiable variant of the one-more discrete logarithm (OMDL) assumption [3, 5], which states that it is hard to find the discrete logarithm of \(q+1\) group elements by making at most q queries to an oracle solving the DL problem.
We give two independent security proofs which reduce the security of \(\mathsf {MuSig2} \) to the AOMDL assumption. Our first proof relies on the random oracle model (ROM), and applies to \(\mathsf {MuSig2} \) with \(\nu = 4\) nonces. Our second proof additionally assumes the algebraic group model (AGM) [12], and for this ROM+AGM proof, \(\nu =2\) nonces are sufficient.
Assuming a group element is as large as a collision-resistant hash of a group element, the overhead for every \(\mathsf {MuSig2} \) signer as compared to normal three-round \(\mathsf {MuSig} \) is broadcasting \(\nu -2\) group elements as well as \(\nu -1\) exponentiations plus one multi-exponentiation of size \(\nu -1\). As a result, for the optimal choice of \(\nu =2\), the computational overhead of a signing session of \(\mathsf {MuSig2} \) is just two exponentiations as compared to the state-of-the-art scheme \(\mathsf {MuSig} \). This makes \(\mathsf {MuSig2} \) highly practical.
A further optimized variant of \(\mathsf {MuSig2} \), which we call \(\mathsf {MuSig2^*} \) and discuss in the full version [27], reduces the size of the multi-exponentiation in the key aggregation algorithm from n to \(n-1\).
1.2 Concurrent Work
Concurrently to our work, two other works rely on a similar idea of using a linear combination of multiple nonces in order to remove a communication round while achieving security under concurrent sessions.
FROST. Komlo and Goldberg [18] use this idea for their \(\mathsf {FROST} \) scheme in the context of the more general setting of threshold signatures: in a “t-of-n” threshold signature scheme, any subset of size t of some set of n signers can create a signature. By setting \(t=n\) (as supported in \(\mathsf {FROST} \)), it is possible to obtain a multi-signature scheme as a special case. In comparison, the scope of our work is restricted to only “n-of-n” multi-signatures, which enables us to optimize for this case and achieve properties which, in the pure DL setting, are unique to multi-signatures, namely non-interactive key generation as well as non-interactive public key aggregation, two features not offered by \(\mathsf {FROST} \).
A major difference between our work and their work is the cryptographic model. The \(\mathsf {FROST} \) security proof relies on a non-standard heuristic which models the hash function (a public primitive) used for deriving the coefficients for the linear combination as a one-time VRF (a primitive with a secret key) in the security proof. This treatment requires an additional communication round in \(\mathsf {FROST} \) preprocessing stage and to disallow concurrent sessions in this stage, resulting in a modified scheme \(\mathsf {FROST\text {-}Interactive} \). As a consequence, the \(\mathsf {FROST\text {-}Interactive} \) scheme that is proven secure is in fact a three-round scheme and as such differs significantly from the two-round \(\mathsf {FROST} \) scheme that is recommended for deployment. Komlo and Goldberg [18] show that the security of \(\mathsf {FROST\text {-}Interactive} \) is implied by the DL assumption. In contrast, our \(\mathsf {MuSig2} \) proofs use the well-established ROM (or alternatively, AGM+ROM) to model the hash function as a random oracle and rely on a falsifiable and weaker variant of the OMDL assumption.
DWMS. Again concurrently, Alper and Burdges [1] use the idea of a linear combination of multiple nonces to obtain a two-round multi-signature scheme \(\mathsf {DWMS} \), which resembles \(\mathsf {MuSig2} \) closely but lacks several optimizations present in \(\mathsf {MuSig2} \). Concretely, \(\mathsf {DWMS} \) does not aggregate the first-round messages of all signers, an optimization which saves bandwidth and ensures that each signer needs to perform only a constant number of exponentiations. Moreover, \(\mathsf {DWMS} \) does not make use of the optimizations of setting the coefficient of one nonce to the constant 1, which saves one more exponentiation per signer when aggregating nonces, as well as setting the coefficient of one public key to the constant 1, which saves one exponentiation when aggregating keys (see the variant \(\mathsf {MuSig2^*} \) of our scheme in the full version [27]).
In terms of provable security, Alper and Burdges [1] provide a proof only in the combination of ROM+AGM, whereas we additionally provide a proof that does not rely on the AGM.
2 Technical Overview
2.1 The Challenge of Constructing Two-Round Schemes
Already an obsolete preliminary version [21] of the \(\mathsf {MuSig} \) paper [22] proposed a two-round variant of \(\mathsf {MuSig} \) in which the initial commitment round is omitted. We call this scheme \(\mathsf {InsecureMuSig} \) in the following. Maxwell et al. [21] claimed concurrent security under the OMDL assumption but their proof turned out be flawed: it fails to cover a subtle problem in the simulation of the signing oracle, which in fact had been described (and correctly sidestepped by restricting concurrency) already 15 years earlier in a work on two-party Schnorr signatures by Nicolosi et al. [29].
Drijvers et al. [11] rediscovered the flaw in the security proof of \(\mathsf {InsecureMuSig} \) and show that similar flaws appear also in the proofs of the other two-round DL-based multi-signature schemes by Bagherzandi et al. [2] and Ma et al. [20].Footnote 2 Moreover, they show through a meta-reduction that the concurrent security of these schemes cannot be reduced to the DL or OMDL problem using an algebraic black-box reduction (assuming the OMDL problem is hard).Footnote 3 In addition to the meta-reduction, Drijvers et al. [11] also gave a concrete attack of subexponential complexity based on Wagner’s algorithm [37] for solving the Generalized Birthday Problem [37], which has led to similar attacks on Schnorr blind signatures [33]. Their attack breaks \(\mathsf {InsecureMuSig} \) and the other aforementioned multi-signature schemes and inherently exploits the ability to run multiple sessions concurrently. Recently, Benhamouda et al. [7] gave a novel, simple, and very efficient attack of polynomial complexity, which confirms and extends these negative results.
A Concrete Attack. We outline the attack by Drijvers et al. [11] in order to provide an intuition for how we can overcome their negative results. The attack relies on Wagner’s algorithm for solving the Generalized Birthday Problem [37], which can be defined as follows for the purpose of this paper: Given a constant value \(t\in \mathbb {Z}_p\), an integer \(k_{\mathrm {max}}\), and access to random oracle H mapping onto \(\mathbb {Z}_p\), find a set \(\{q_1, \ldots , q_{k_{\mathrm {max}}}\}\) of \(k_{\mathrm {max}}\) queries such that \( \sum _{k=1}^{k_{\mathrm {max}}} H(q_{k}) = t. \) While for \(k_{\mathrm {max}}\le 2\), the complexity of this problem is the same as finding a preimage (\(k_{\mathrm {max}}=1\)) or a collision (\(k_{\mathrm {max}}=2\)) in the random oracle, the problem becomes, maybe surprisingly, easy for large \(k_{\mathrm {max}}\). In particular, Wagner [37] gives a subexponential algorithm assuming that \(k_{\mathrm {max}}\) is not bounded.
The attack proceeds as follows. The adversary opens \(k_{\mathrm {max}}\) concurrent signing sessions, in which it plays the role of the signer with public key \(X_2=g^{x_2}\), and receives \(k_{\mathrm {max}}\) nonces \(R_1^{(1)}, \ldots , R_1^{(k_{\mathrm {max}})}\) from the honest signer with public key \(X_1=g^{x_1}\). Let \( \widetilde{X}=X_1^{a_1} X_2^{a_2}\) be the corresponding aggregate public key. Given a forgery target message \(m^*\), the adversary computes \(R^* = \prod _{k=1}^{k_{\mathrm {max}}} R_1^{(k)}\) and uses Wagner’s algorithm to find nonces \(R_2^{(k)}\) to reply with such that
Having received \(R_2^{(k)}\), the honest signer will reply with partial signatures \(s_1^{(k)} = r_1^{(k)} + c^{(k)} \cdot a_1x_1\). Let \(r^* = \sum _{k=1}^{k_{\mathrm {max}}} r_1^{(k)} = \log _g(R^*)\). The adversary is able to obtain
where the last equality follows from Eq. (1). The adversary can further complete \(s_1^*\) to the full value
In other words, \((R^*, s^*)\) is a valid forgery on message \(m^*\) with signature hash \(c^*=\mathsf {H}_{\mathrm {sig}}(\widetilde{X}, R^*, m^*)\). In this example, the forgery is valid for the aggregate public key \(\widetilde{X}\), which is the result of aggregating public keys \(X_1\) and \(X_2\). It is however straightforward to adapt the attack to produce a forgery under a different aggregate public key as long as it is the result of aggregating the honest signer’s public key \(X_1\) with any multiset of adversarial public keys.
The complexity of this attack is dominated by the complexity of Wagner’s algorithm, which is \(O(k_{\mathrm {max}}\, 2^{\log _2(p)/(1+\lfloor (\log _2(k_{\mathrm {max}})\rfloor )})\). While this is super-polynomial, the attack is practical for common parameters and moderately large numbers \(k_{\mathrm {max}}\) of sessions. For example, for a group size of \(p \approx 2^{256}\) as common for elliptic curves, a value of \(k_{\mathrm {max}}=128\) brings the complexity of the attack down to approximately \(2^{39}\) operations, which is practical even on off-the-shelf hardware. If the attacker is able to open more sessions concurrently, the improved polynomial-time attack by Benhamouda et al. [7] assumes \(k_{\mathrm {max}}> \log _2 p\) sessions, but then has complexity \(O(k_{\mathrm {max}}\log _2 p)\) and a negligible running time in practice.
2.2 Our Solution
The attack by Drijvers et al. (and similarly the attack by Benhamouda et al.) relies on the ability to control the signature hash by controlling the aggregate nonce \(R_1^{(k)}R_2^{(k)}\) (on the LHS of Eq. (1)) in the first round of each of the concurrent signing sessions. Since all signers must know the aggregate nonce at the end of the first round, it seems hard to prevent the adversary from being able to control the aggregate nonce on the LHS without adding a preliminary commitment round. Our high-level idea to solve this problem and to foil the attacks is to accept that the adversary can control the LHS of the equation but prevent it from controlling the RHS instead.
The main novelty in our work is to let every signer i send a list of \(\nu \ge 2\) nonces \(R_{i,1},\ldots ,R_{i,\nu }\) and let it effectively use a random linear combination \(\hat{R}_i=\prod _{j=1}^{\nu }R_{i,j}^{b^{j-1}}\) of those nonces in lieu of the former single nonce \(R_i\). The scalar b is derived via a hash function \(\mathsf {H}_{\mathrm {non}}\) (modeled as a random oracle) applied the nonces of all signers, i.e., \(b = \mathsf {H}_{\mathrm {non}}(\widetilde{X}, (\prod _{i=1}^n R_{i,1},\ldots ,\prod _{i=1}^n R_{i,\nu }), m)\).
As a result, whenever the adversary tries different values for \(R_2\), the coefficient b changes, and so does the honest signer’s effective nonce \(\hat{R}_1 =\prod _{j=1}^{\nu }R_{1,j}^{b^{j-1}}\). This ensures that the sum of the honest signer’s effective nonces taken over all open sessions, i.e., value \(R^* = \prod _{k=1}^{k_{\mathrm {max}}} \hat{R}_1^{(k)}\) in the RHS of Eq. (1), is no longer a constant value. Without a constant RHS, the adversary lacks an essential prerequisite in the definition of the Generalized Birthday Problem and Wagner’s algorithm is not applicable.
With this idea in mind, it is tempting to fall back to only a single nonce (\(\nu = 1\)) but instead rely just on the coefficient b such that \(\hat{R}_1 = R_1^b\). However, then the adversary can effectively eliminate b by redefining \(R^* = \prod _{k=1}^{k_{\mathrm {max}}} R_1^{(k)}\) (which is independent of all \(b^{(k)}\)) and considering the equation
instead of Eq. (1) in order to perform the attack.
2.3 Proving Security
Before we describe how to prove \(\mathsf {MuSig2} \) secure, we first take a step back to \(\mathsf {InsecureMuSig} \) in order to understand the flaw in its purported security proof. Then, we explain how the usage of more than once nonce in \(\mathsf {MuSig2} \) enables us to fix that flaw.
The Difficulty of Simulating Signatures. Following the textbook security proof of Schnorr signatures, a natural but necessarily flawed approach to reduce the security of \(\mathsf {InsecureMuSig} \)Footnote 4 to the DL problem in the ROM will be to let the reduction announce the challenge group element \(X_1\) as the public key of the honest signer and fork the execution of the adversary in order to extract the discrete logarithm of \(X_1\) from the two forgeries output by the adversary in its two executions (using the Forking Lemma [4, 30]).
The insurmountable difficulty for the reduction in this approach is to simulate the honest signer in signing sessions without knowledge of the secret key of the honest signer. From the perspective of the reduction, simply omitting the preliminary commitment phase enables the adversary to know the combined nonce R before the reduction learns it, which prevents the reduction from simulating the signing oracle using the standard technique of programming the random oracle on the signature challenge \(\mathsf {H}_{\mathrm {sig}}(\widetilde{X}, R, m)\). In more details, observe that in \(\mathsf {InsecureMuSig} \), an adversary (controlling public key \(X_2\)) can impose the value of \(R=R_1R_2\) used in signing sessions since it can choose \(R_2\) after having received \(R_1\) from the honest signer (with public key \(X_1=g^{x_1}\)). This forbids the textbook way of simulating the honest signer in the ROM without knowing \(x_1\) by randomly drawing \(s_1\) and c, computing \(R_1=g^{s_1}(X_1)^{-a_1c}\), and programming \(\mathsf {H}_{\mathrm {sig}}(\widetilde{X},R,m) = c\), since the adversary might have made the random oracle query \(\mathsf {H}_{\mathrm {sig}}(\widetilde{X},R,m)\) before making the corresponding signing query.
The Flawed Security Proof of \(\mathsf {InsecureMuSig} \). The hope of Maxwell et al. [21] was to rely on the stronger OMDL assumption instead of the DL assumption in order to solve this problem without a commitment round. The DL oracle in the formulation of the OMDL problem enables the reduction to answer a signing query by obtaining the partial signature \(s_1\) of the honest signer via a DL oracle query for the discrete logarithm of \(R_1(X_1)^{a_1c}\). The reduction does not generate the nonce \(R_1\) of the honest signer randomly, but instead sets it to a DL challenge freshly drawn from the OMDL problem at the start of each signing session. As in the standard security proof of Schnorr signatures, the reduction forks the adversary and extracts the discrete logarithm \(x_1\) of the first DL challenge \(X_1\) from the forgeries that the adversary outputs in its different executions. This allows computing the discrete logarithm of each challenge \(R_1\) from \(s_1\) as \(r_1 = s_1 - a_1cx_1\).
With the adversary opening \(q_s\) signing sessions, if the reduction was not flawed, it would return the DL of \(q_s+1\) challenge elements (including the DL challenge \(X_1\) used as public key of the honest signer) using only \(q_s\) DL oracle calls, i.e., the reduction would solve the OMDL problem.
This simulation technique however fails in a subtle way when combined with the Forking Lemma, since the adversary might be forked in the middle of a signing session, when it has received \(R_1\) but has not returned \(R_2\) to the reduction yet. This can be seen as follows. Assume that the adversary sends a different value \(R_2\) and \(R_2'\) in the two executions after the fork, resulting in different signature hashes c and \(c'\) respectively. This implies that in order to correctly simulate the signing oracle in the forked execution, the reduction needs two queries to the DL oracle, both of which are related to the same single challenge \(R_1\). Since the answer of the first DL oracle query will already be enough to compute the discrete logarithm of \(R_1\) later on, the second query does not provide any additional useful information to the reduction (neither about the discrete logarithm of \(R_1\) nor about the discrete logarithm of another DL challenge) and is thus wasted. As a result, the reduction forgoes any hope to solve the OMDL problem when making the second query.Footnote 5
How Multiple Nonces in \(\mathsf {MuSig2} \) Help the Reduction. With \(\mathsf {MuSig2} \) however, the reduction can handle this situation. Now assume \(\nu =2\), i.e., the reduction will obtain two (instead of one) group elements \(R_{1,1}, R_{1,2}\) as DL challenges from the OMDL challenger during the first round of each signing session. This will allow the reduction to make two DL queries per signing session, and thus be able to simulate signatures even if the adversary forces different signature hashes \(c\ne c'\) in the two executions.
The natural question is how the reduction ensures that it is able to answer both DL challenges \(R_{1,1}, R_{1,2}\) for each signing session. \(\mathsf {MuSig2} \) solves this by having signers effectively use the linear combination \(\hat{R}_1 = R_{1,1} R_{1,2}^{b}\) as nonce where \(b = \mathsf {H}_{\mathrm {non}}(\widetilde{X}, (\prod _{i=1}^n R_{i,1},\prod _{i=1}^n R_{i,2}), m)\). As a result, the reduction is able to program the \(\mathsf {H}_{\mathrm {non}}\) and \(\mathsf {H}_{\mathrm {sig}}\) such that whenever the adversary gives a different response to a signing query in the second execution such that \(c\ne c'\), then also b and \(b'\) differ between the two executions. Consequently, the two DL queries made by the reduction will be answered with some \(s_1\) and \(s_1'\) that give rise to two linear independent equations \(s_1 = r_{1,1} + b r_{1,2} + a_1c x_1\) and \(s_1' = r_{1,1} + b'r_{1,2} + a_1c' x_1\). After the reduction has extracted \(x_1\) from the forgeries output by the adversary in the two executions, it can solve those equations for the unknowns \(r_{1,1}\) and \(r_{1,2}\), the discrete logarithms of the DL challenges \(R_{1,1}\) and \(R_{1,2}\).
Similarly, in the case that \(c=c'\), the reduction ensures that \(b=b'\) and therefore needs only one DL query to simulate the honest signer in both executions. Thus, it can use the free DL query to obtain a second linear independent equation.
Note that for this simulation technique, it is not important how the adversary controls the signature hashes c and \(c'\). So far we only considered the case that the adversary influences c and \(c'\) by choosing its nonces depending on the honest signer’s nonce. The reduction works equally for an adversary which controls the signature hash computed as \(\mathsf {H}_{\mathrm {sig}}(\widetilde{X}, R, m)\) not by influencing R but instead by being able to choose the message m or the set of signers L (and thus the aggregate public key \(\widetilde{X}\)) only in the second round of the signing protocol, i.e., after having seen the honest signer’s nonce. This explains why our scheme enables preprocessing and broadcasting the nonces (the first round) without having determined the message and the set of signers. This is in contrast to existing schemes, which are vulnerable to essentially the same attack as explained above if the adversary is given the ability to select the message or the set of signers after having seen the honest signer’s nonce [26].
So far we discussed only how the reduction is able to handle two different executions of the adversary (due to a single fork). However, since our reduction needs to fork the adversary twice to support key aggregation, it needs to handle four possible executions of the adversary. As a consequence, it will need four DL queries as well as \(\nu = 4\) nonces.
2.4 A More Efficient Solution in the Algebraic Group Model
In the algebraic group model (AGM) [12], the adversary is assumed to be algebraic, i.e., whenever it outputs a group element, it outputs a representation of this group element in the base formed by all group elements it has received so far. While the AGM is idealized, it is a strictly weaker model than the generic group model (GGM) [34], i.e., security proofs in the AGM carry over to the GGM but the AGM imposes fewer restrictions on the adversary. Security proofs in the AGM work via reductions to hard problems (similar to the standard model) because computational problems such as DL and OMDL are not information-theoretically hard in the AGM (as opposed to the GGM). In the AGM, Schnorr signatures (and related schemes such Schnorr blind signatures [10]) can be proven secure using a straight-line reduction without forking the execution of the adversary [13].
The main technical reason why our ROM proof works only for \(\mathsf {MuSig2} \) with as many as \(\nu = 4\) nonces is that our reduction needs to handle four executions of the adversary due to two applications of the Forking Lemma. Since this fundamental reason for requiring \(\nu = 4\) in the plain ROM simply disappears in the AGM, we are able to prove \(\mathsf {MuSig2} \) with \(\nu =2\) nonces secure in the combination ROM+AGM.
Due to space limitations, our results in the AGM+ROM can be found in the full version of the paper [27].
2.5 Algebraic OMDL: A Falsifiable Variant of OMDL
A cryptographic assumption is algorithmically falsifiable if it can be decided in p.p.t. whether a given algorithm breaks it.Footnote 6 While this is true for most standard assumptions such as the RSA assumption or the DL assumption, it is notably not true for the OMDL assumption, where the OMDL challenger needs to provide the adversary with a DL oracle that cannot be implemented in p.p.t. (unless the DL problem is easy, but then the OMDL assumption does not hold anyway).
While we believe that the OMDL has withstood the test of time, it is still desirable to avoid non-falsifiable assumptions whenever possible. We observe that the DL oracle can be in fact implemented in p.p.t. when the solving algorithm is required to be algebraic. In the context of OMDL, this translates to the requirement that whenever the adversary queries the discrete logarithm of a group element via the DL oracle, it outputs a representation of this group element in the basis formed by the generator and all DL challenges it has received thus far (which together constitute all group elements it has received thus far). As a result we obtain a falsifiable variant of the OMDL assumption that we call the algebraic OMDL (AOMDL) assumption. Since every algebraic algorithm is also a normal algorithm, the AOMDL assumption is immediately implied by the well-established OMDL assumption.
Since our reductions in both the ROM and in the AGM+ROM are algebraic in this sense, we can rely on the falsifiable AOMDL assumption. We would like to stress that being algebraic here refers to a property of the reduction, which acts as the algorithm solving (A)OMDL, and our reductions are algebraic independent of whether the unforgeability adversary, to which the reduction has access internally, is algebraic. As such, the use of the AOMDL assumption is independent and orthogonal of our use of the AGM as described in the previous subsection. In particular we can rely on the AOMDL assumption even in our ROM-only proof.
We believe that the AOMDL problem is helpful beyond the scope of this paper, as it turns out that essentially all security proofs in the literature use the OMDL problem in an algebraic and thus falsifiable fashion [e.g., 5, 6, 13, 29]. We do not claim that our observation about algebraic algorithms is a deep insight—in fact implementing the DL oracle is straight-forward given an algebraic solving algorithm—we simply believe it is useful for the evaluation of security results.
3 Preliminaries
The security parameter is denoted  . A group description is a triple
. A group description is a triple  where
where  is a cyclic group of order p and g is a generator of
is a cyclic group of order p and g is a generator of  . A (prime-order) group generation algorithm is an algorithm \(\mathsf {GrGen}\) which on input
. A (prime-order) group generation algorithm is an algorithm \(\mathsf {GrGen}\) which on input  returns a group description
returns a group description  where p is a \(\lambda \)-bit prime. The group
where p is a \(\lambda \)-bit prime. The group  is denoted multiplicatively, and we conflate group elements and their encoding when given as input to hash functions. Given an element
is denoted multiplicatively, and we conflate group elements and their encoding when given as input to hash functions. Given an element  , we let \(\log _g(X)\) denote the discrete logarithm of X in base g, i.e., the unique
, we let \(\log _g(X)\) denote the discrete logarithm of X in base g, i.e., the unique  such that \(X=g^x\).
such that \(X=g^x\).
Algebraic OMDL Problem. We introduce the algebraic OMDL (AOMDL) problem, which is at least as hard as the standard one-more discrete logarithm (OMDL) problem [3, 5].
Definition 1 (AOMDL Problem)
Let \(\mathsf {GrGen}\) be a group generation algorithm, and let game  be as defined in Fig. 1. The algebraic one-more discrete logarithm (AOMDL) problem is hard for \(\mathsf {GrGen}\) if for any p.p.t. algorithm
be as defined in Fig. 1. The algebraic one-more discrete logarithm (AOMDL) problem is hard for \(\mathsf {GrGen}\) if for any p.p.t. algorithm  ,
,

We highlight the changes from the standard OMDL problem to the AOMDL problem
 in Fig. 1. Since every algorithm solving AOMDL can be turned into an algorithm solving OMDL by dropping the representation from the \({ \textsc {DLog}}_g\) oracle queries, the AOMDL problem is hard for some \(\mathsf {GrGen}\) if the OMDL problem is hard for \(\mathsf {GrGen}\).
in Fig. 1. Since every algorithm solving AOMDL can be turned into an algorithm solving OMDL by dropping the representation from the \({ \textsc {DLog}}_g\) oracle queries, the AOMDL problem is hard for some \(\mathsf {GrGen}\) if the OMDL problem is hard for \(\mathsf {GrGen}\).
It is immediate that the entire  game runs in p.p.t. whenever
game runs in p.p.t. whenever  runs in p.p.t., i.e., the assumption that the AOMDL problem is hard is falsifiable as defined for instance by Gentry and Wichs [14].
runs in p.p.t., i.e., the assumption that the AOMDL problem is hard is falsifiable as defined for instance by Gentry and Wichs [14].
3.1 Syntax and Security Definition of Multi-signature Schemes
To keep the notation simple, we make a few simplifying assumptions. In particular, we restrict our syntax and security model to two-round signing algorithms, and in order to model that the first round can be preprocessed without having determined a message to be signed or the public keys of all signers, and without accessing the secret key, those inputs are given only to the second round of the signing algorithm.
Syntax. A two-round multi-signature scheme \(\Sigma \) with key aggregation consists of algorithms \((\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {KeyAgg}, (\mathsf {Sign},\mathsf {SignAgg},\mathsf {Sign}',\mathsf {SignAgg}',\mathsf {Sign}''), \mathsf {Ver})\) as follows. System-wide parameters \( par \) are generated by the setup algorithm \(\mathsf {Setup}\) taking as input the security parameter. For notational simplicity, we assume that \( par \) is given as implicit input to all other algorithms. The randomized key generation algorithm takes no input and returns a secret/public key pair  . The deterministic key aggregation algorithm \(\mathsf {KeyAgg}\) takes a multiset of public keys
. The deterministic key aggregation algorithm \(\mathsf {KeyAgg}\) takes a multiset of public keys  and returns an aggregate public key
and returns an aggregate public key  .
.
The interactive signature algorithm \((\mathsf {Sign},\mathsf {SignAgg},\mathsf {Sign}',\mathsf {SignAgg}',\mathsf {Sign}'')\) is run by each signer i and proceeds in a sequence of two communication rounds. \(\mathsf {Sign}\) does not take explicit inputs and returns a signer’s first-round output \( out _i\) and some first-round secret state \( state _i\). \(\mathsf {SignAgg}\) is a deterministic algorithm that aggregates the first-round outputs \(( out _1, \ldots , out _n)\) from all signers into a single first-round output \( out \) to be broadcast to all signers. Similarly, \(\mathsf {Sign}'\) takes the first-round secret state \( state _i\) of signer i, the aggregate first-round output \( out \), the secret key  of signer i, a message m to sign, public keys
of signer i, a message m to sign, public keys  of all cosigners, and returns this signer’s second-round output \( out '_i\) and some second-round secret state \( state '_i\), and \(\mathsf {SignAgg}'\) is a deterministic algorithm that aggregates the second-round outputs \(( out '_1,\ldots , out '_n)\) from all signers into a single second-round output \( out '\) to be broadcast to all signers. Finally, \(\mathsf {Sign}''\) takes the second-round secret state \( state '_i\) of signer i and the aggregate second-round output \( out '\) and outputs a signature \(\sigma \).
of all cosigners, and returns this signer’s second-round output \( out '_i\) and some second-round secret state \( state '_i\), and \(\mathsf {SignAgg}'\) is a deterministic algorithm that aggregates the second-round outputs \(( out '_1,\ldots , out '_n)\) from all signers into a single second-round output \( out '\) to be broadcast to all signers. Finally, \(\mathsf {Sign}''\) takes the second-round secret state \( state '_i\) of signer i and the aggregate second-round output \( out '\) and outputs a signature \(\sigma \).
The purpose of the aggregation algorithms \(\mathsf {SignAgg}\) and \(\mathsf {SignAgg}'\) is to enable savings in the broadcast communication in both signing rounds: An aggregator node [18, 35], which will be untrusted in our security model and can for instance be one of the signers, can collect the outputs of all signers in both rounds, aggregate the outputs using \(\mathsf {SignAgg}\) and \(\mathsf {SignAgg}'\), respectively, and broadcast only the aggregate output back to all signers. This optimization is entirely optional. If it is not desired, each signer can simply broadcast its outputs directly to all signers, which then all run \(\mathsf {SignAgg}\) and \(\mathsf {SignAgg}'\) by themselves.
The deterministic verification algorithm \(\mathsf {Ver}\) takes an aggregate public key  , a message m, and a signature \(\sigma \), and returns \(\mathtt {true}\) iff \(\sigma \) is valid for
, a message m, and a signature \(\sigma \), and returns \(\mathtt {true}\) iff \(\sigma \) is valid for  and m.
and m.
Security. Our security model is the same as in previous works on multi-signatures for multi-signatures with key aggregation [9, 11, 22] and requires that it is infeasible to forge multi-signatures involving at least one honest signer. As in previous work [4, 8, 23], we assume without loss of generality that there is a single honest public key (representing a honest signer) and that the adversary has corrupted all other public keys (representing possible cosigners), choosing corrupted public keys arbitrarily and potentially as a function of the honest signer’s public key.
The security game  is defined as follows. A key pair \((\) is generated for the honest signer and the adversary
is defined as follows. A key pair \((\) is generated for the honest signer and the adversary  is given
is given  . The adversary can engage in any number of (concurrent) signing sessions with the honest signer. Formally,
. The adversary can engage in any number of (concurrent) signing sessions with the honest signer. Formally,  has access to oracles \({ \textsc {Sign}}\), \({ \textsc {Sign}}'\), and \({ \textsc {Sign}}''\) implementing the three steps \(\mathsf {Sign}\), \(\mathsf {Sign}'\), and \(\mathsf {Sign}''\) of the signing algorithm with the honest signer’s secret key. This in particular means that the adversary can pass the same L, containing
has access to oracles \({ \textsc {Sign}}\), \({ \textsc {Sign}}'\), and \({ \textsc {Sign}}''\) implementing the three steps \(\mathsf {Sign}\), \(\mathsf {Sign}'\), and \(\mathsf {Sign}''\) of the signing algorithm with the honest signer’s secret key. This in particular means that the adversary can pass the same L, containing  multiple times, and the same m to multiple \({ \textsc {Sign}}'\) calls, effectively obtaining a signing session in which the honest signer participates multiple times.
multiple times, and the same m to multiple \({ \textsc {Sign}}'\) calls, effectively obtaining a signing session in which the honest signer participates multiple times.
Note that oracles \({ \textsc {Sign}}'\) and \({ \textsc {Sign}}''\) expect as input aggregate values \( out \) and \( out '\), purported to be the aggregation of all signers’ outputs from the respective previous round. This leaves the task performed by the algorithms \(\mathsf {SignAgg}\) and \(\mathsf {SignAgg}'\) to the adversary and models that the aggregator node (if present) is untrusted. We omit explicit oracles for \(\mathsf {SignAgg}\) and \(\mathsf {SignAgg}'\). This is without loss of generality because these algorithms do not take secret inputs and can be run by the adversary locally.
Eventually, the adversary returns a multiset  of public keys, a message m, and a signature \(\sigma \). The game returns \(\mathtt {true}\) (representing a win of
of public keys, a message m, and a signature \(\sigma \). The game returns \(\mathtt {true}\) (representing a win of  ) if
) if  , the forgery is valid, i.e., \(\mathsf {Ver}(\mathsf {KeyAgg}(L),m,\sigma )=\mathtt {true}\), and the adversary never made a \({ \textsc {Sign}}'\) query for multiset L and message m.
, the forgery is valid, i.e., \(\mathsf {Ver}(\mathsf {KeyAgg}(L),m,\sigma )=\mathtt {true}\), and the adversary never made a \({ \textsc {Sign}}'\) query for multiset L and message m.
Definition 2 (EUF-CMA)
Given a multi-signature scheme with key aggregation \(\Sigma =(\mathsf {Setup},\mathsf {KeyGen},\mathsf {KeyAgg},(\mathsf {Sign},\mathsf {SignAgg},\mathsf {Sign}',\mathsf {SignAgg}',\mathsf {Sign}''),\mathsf {Ver})\), let game  be as defined above. Then \(\Sigma \) is existentially unforgeable under chosen-message attacks (EUF-CMA) if for any p.p.t. adversary
be as defined above. Then \(\Sigma \) is existentially unforgeable under chosen-message attacks (EUF-CMA) if for any p.p.t. adversary  ,
,

Our security model is based on the model by Bellare and Neven [4] which was proposed in the context of multi-signatures without key aggregation. Even though this security model has been used previously for multi-signatures with key aggregation [9, 11, 22], one may wonder if it is at all suitable in this context. We argue in the full version [27] that it is indeed suitable.
4 The Multi-signature Scheme \(\mathsf {MuSig2} \)
Our new multi-signature scheme \(\mathsf {MuSig2} \) is parameterized by a group generation algorithm \(\mathsf {GrGen}\) and by an integer \(\nu \), which specifies the number of nonces sent by each signer. The scheme is defined in Fig. 2. Note that verification is exactly the same as for ordinary key-prefixed Schnorr signatures with respect to the aggregate public key \(\widetilde{X}\).
The multi-signature scheme \(\mathsf {MuSig2} [\mathsf {GrGen},\nu ]\). Public parameters \( par \) returned by \(\mathsf {Setup}\) are implicitly given as input to all other algorithms. We use a helper algorithm \(\mathsf {MuSigCoef}\) as a wrapper for \(\mathsf {H}_{\mathrm {agg}}\) to make the description of the scheme more modular, which will help us describe a variant \(\mathsf {MuSig2^*} \) of the scheme with optimized key aggregation (see the full version [27]).
Implementers should be aware that derandomizing techniques often applied to the signing algorithm of single-signer signatures are in general not secure in the case of multi-signatures, and that care has to be taken when implementing the stateful signing algorithm of \(\mathsf {MuSig2} \). We discuss these issues as well as further practical considerations and optimizations in the full version [27].
5 Security of \(\mathsf {MuSig2} \) in the ROM
In this section, we establish the security of \(\mathsf {MuSig2} \) with \(\nu =4\) nonces in the random oracle model.
Theorem 1
Let \(\mathsf {GrGen}\) be a group generation algorithm for which the AOMDL problem is hard. Then the multi-signature scheme \(\mathsf {MuSig2} [\mathsf {GrGen},\nu =4]\) is EUF-CMA in the random oracle model for \(\mathsf {H}_{\mathrm {agg}}\), \(\mathsf {H}_{\mathrm {non}}\), \(\mathsf {H}_{\mathrm {sig}}:\{0,1\}^*\rightarrow \mathbb {Z}_p\).
Precisely, for any adversary  against \(\mathsf {MuSig2} [\mathsf {GrGen},\nu =4]\) running in time at most t, making at most \(q_s\) \({ \textsc {Sign}}\) queries and at most \(q_h\) queries to each random oracle, and such that the size of L in any signing session and in the forgery is at most N, there exists an algorithm
against \(\mathsf {MuSig2} [\mathsf {GrGen},\nu =4]\) running in time at most t, making at most \(q_s\) \({ \textsc {Sign}}\) queries and at most \(q_h\) queries to each random oracle, and such that the size of L in any signing session and in the forgery is at most N, there exists an algorithm  taking as input group parameters
taking as input group parameters  , running in time at most
, running in time at most
where \(q=2q_h+q_s+1\) and \(t_\mathrm{exp}\) is the time of an exponentiation in  , making at most \(4 q_s\) \({ \textsc {DLog}}_g\) queries, and solving the AOMDL problem with an advantage
, making at most \(4 q_s\) \({ \textsc {DLog}}_g\) queries, and solving the AOMDL problem with an advantage

Before proving the theorem, we start with an informal explanation of the key techniques used in the proof. Let us recall the security game defined in Sect. 3.1, adapting the notation to our setting. Group parameters  and a key pair \((x^*,X^*)\) for the honest signer are generated. The target public key \(X^*\) is given as input to the adversary
and a key pair \((x^*,X^*)\) for the honest signer are generated. The target public key \(X^*\) is given as input to the adversary  . Then, the adversary can engage in protocol executions with the honest signer by providing a message m to sign and a multiset L of public keys involved in the signing process where \(X^*\) occurs at least once, and simulating all signers except one instance of \(X^*\).
. Then, the adversary can engage in protocol executions with the honest signer by providing a message m to sign and a multiset L of public keys involved in the signing process where \(X^*\) occurs at least once, and simulating all signers except one instance of \(X^*\).
The Double-Forking Technique. This technique is already used by Maxwell et al. in the security proof for \(\mathsf {MuSig} \) [22]. We are repeating the idea below with slightly modified notation.
The first difficulty is to extract the discrete logarithm \(x^*\) of the challenge public key \(X^*\). The standard technique for this would be to “fork” two executions of the adversary in order to obtain two valid forgeries (R, s) and \((R',s')\) for the same multiset of public keys \(L=\{X_1,\ldots ,X_n\}\) with \(X^*\in L\) and the same message m such that \(R=R'\), \(\mathsf {H}_{\mathrm {sig}}(\widetilde{X},R,m)\) was programmed in both executions to some common value \(h_{\mathrm {sig}}\), \(\mathsf {H}_{\mathrm {agg}}(L,X_i)\) was programmed in both executions to the same value \(a_i\) for each i such that \(X_i\ne X^*\), and \(\mathsf {H}_{\mathrm {agg}}(L,X^*)\) was programmed to two distinct values \(h_{\mathrm {agg}}\) and \(h_{\mathrm {agg}}'\) in the two executions, implying that
where \(n^*\) is the number of times \(X^*\) appears in L. This would allow to compute the discrete logarithm of \(X^*\) by dividing the two equations above.
However, simply forking the executions with respect to the answer to the query \(\mathsf {H}_{\mathrm {agg}}(L,X^*)\) does not work: indeed, at this moment, the relevant query \(\mathsf {H}_{\mathrm {sig}}(\widetilde{X},R,m)\) might not have been made yet by the adversary,Footnote 7 and there is no guarantee that the adversary will ever make this same query again in the second execution, let alone return a forgery corresponding to the same \(\mathsf {H}_{\mathrm {sig}}\) query. In order to remedy this situation, we fork the execution of the adversary twice: once on the answer to the query \(\mathsf {H}_{\mathrm {sig}}(\widetilde{X},R,m)\), which allows us to retrieve the discrete logarithm of the aggregate public key \(\widetilde{X}\) with respect to which the adversary returns a forgery, and on the answer to \(\mathsf {H}_{\mathrm {agg}}(L,X^*)\), which allows us to retrieve the discrete logarithm of \(X^*\).
As in Bellare and Neven [4], our technical tool to handle forking of the adversary is a “generalized Forking Lemma” which extends Pointcheval and Stern’s Forking Lemma [30] and which does not mention signatures nor adversaries and only deals with the outputs of an algorithm  run twice on related inputs.
run twice on related inputs.
However, the generalized Forking Lemma of Bellare and Neven [4] is not general enough for our setting, and we rely on the following variant.
Lemma 1
Fix integers q and m. Let  be a randomized algorithm which takes as input a main input \( inp \) generated by some probabilistic algorithm \(\mathsf {InpGen}()\), elements \(h_1,\ldots ,h_q\) from some sampleable set H, elements \(v_1,\ldots ,v_m\) from some sampleable set V, and random coins from some sampleable set R, and returns either a distinguished failure symbol \(\bot \), or a tuple \((i,j, out )\), where \(i\in \{1,\ldots ,q\}\), \(j\in \{0,\ldots ,m\}\), and \( out \) is some side output. The accepting probability of
be a randomized algorithm which takes as input a main input \( inp \) generated by some probabilistic algorithm \(\mathsf {InpGen}()\), elements \(h_1,\ldots ,h_q\) from some sampleable set H, elements \(v_1,\ldots ,v_m\) from some sampleable set V, and random coins from some sampleable set R, and returns either a distinguished failure symbol \(\bot \), or a tuple \((i,j, out )\), where \(i\in \{1,\ldots ,q\}\), \(j\in \{0,\ldots ,m\}\), and \( out \) is some side output. The accepting probability of  , denoted
, denoted  , is defined as the probability, over \( inp \leftarrow \mathsf {InpGen}()\),
, is defined as the probability, over \( inp \leftarrow \mathsf {InpGen}()\),  ,
,  , and the random coins of
, and the random coins of  , that
, that  returns a non-\(\bot \) output. Consider algorithm
returns a non-\(\bot \) output. Consider algorithm  , taking as input \( inp \) and \(v_1,v'_1,\ldots ,v_m,v'_m\in V\), described in Fig. 3. Let \( frk \) be the probability (over \( inp \leftarrow \mathsf {InpGen}()\),
, taking as input \( inp \) and \(v_1,v'_1,\ldots ,v_m,v'_m\in V\), described in Fig. 3. Let \( frk \) be the probability (over \( inp \leftarrow \mathsf {InpGen}()\),  , and the random coins of
, and the random coins of  ) that
) that  returns a non-\(\bot \) output. Then
returns a non-\(\bot \) output. Then

Since the proof of the lemma is very similar to the one of [4, Lemma 1], it is deferred to the full version [27].
Simulating the Honest Signer. For now, consider the scheme with \(\nu = 1\). (We will illustrate the problem of this choice further down in this section.) The adversary has access to an interactive signing oracle, which enables it to open sessions with the honest signer. The signing oracle consists of three sub-oracles \({ \textsc {Sign}}\), \({ \textsc {Sign}}'\), and \({ \textsc {Sign}}''\) but note that we can without loss of generality ignore \({ \textsc {Sign}}''\), which computes the final signature \(s=\sum _{i=1}^n s_i \bmod p\), because it does not depend on secret state and thus the adversary can simply simulate it locally.
The reduction’s strategy for simulating the signing oracle is to use the DL oracle available in the formulation of the AOMDL problem as follows. Whenever the adversary starts the k-th signing session by querying \({ \textsc {Sign}}\), the reduction uses a fresh DL challenge \(R_{1,1}\) from the AOMDL challenge oracle and returns it as its nonce to the adversary. At any later time the adversary queries \({ \textsc {Sign}}'\) with session counter k, a nonce R (purported to be obtained as \(R = \prod _{i=1}^n R_{i,1}\)), a message m to sign, and \(n - 1\) public keys \(X_2, \ldots , X_n\). The reduction then sets \(L=\{X_1=X^*,X_2,\ldots ,X_n\}\), computes \(\widetilde{X}\) and \(c = \mathsf {H}_{\mathrm {sig}}(\widetilde{X},R,m)\), and uses the DL oracle in the formulation of the AOMDL problem to compute \(s_1\) as
where the required algebraic representation of \(R_{1,1}(X^*)^{ca_1}\) is omitted in this informal description and can be computed naturally by the reduction. The reduction then returns \(s_1\) to the adversary. Since a fresh DL challenge is used as \(R_{1,1}\) in each signing query, the reduction will be able to compute its discrete logarithm \(r_{1,1}\) once \(x^*\) has been retrieved via \( r_{1,1} = c a_1 x^* - s_1. \)
Leveraging Two or More Nonces. The main obstacle in the proof and the novelty in this work is to handle adversaries whose behavior follows this pattern: The adversary initiates a signing session by querying the oracle \({ \textsc {Sign}}\) to obtain \(R_{1,1}\), then makes a query \(\mathsf {H}_{\mathrm {sig}}(\widetilde{X},R,m)\), for which it will output a forgery later, and only then continues the signing session with a query to \({ \textsc {Sign}}'\) with arguments \(m, R, (X_2, \ldots , X_n)\). Our goal is to fork the execution of the adversary at the \(\mathsf {H}_{\mathrm {sig}}\) query. But then, the adversary may make \({ \textsc {Sign}}'\) queries with different arguments \(m, R, (X_2, \ldots , X_{n})\), and \(m', R', (X_2', \ldots , X'_{n'})\) in the two executions. In that case, this results in different signature hashes \(c\ne c'\) and requires the reduction simulating the honest signer to make two DL oracle queries in order to answer the \({ \textsc {Sign}}'\) query. Consequently, the reduction will lose the AOMDL game because it had only requested the single AOMDL challenge \(R_{1,1}\).
This is exactly where \(\nu \ge 2\) nonces will come to the rescue. Now assume \(\nu =2\), i.e., the reduction will obtain two (instead of one) group elements \(R_{1,1}, R_{1,2}\) as challenges from the AOMDL challenger. This will allow the reduction to make two DL queries. In order to answer \({ \textsc {Sign}}'\), the reduction follows the \(\mathsf {MuSig2} \) scheme by computing \(\widetilde{X}\) from the public keys, and b by hashing \(\widetilde{X}\), m and all R values of the signing session with \(\mathsf {H}_{\mathrm {non}}\). The reduction then aggregates the nonces of the honest signer into its effective nonce \(\hat{R}_1 = R_{1,1} R_{1,2}^b\), queries the signature hash c and replies to the adversary with \(s_1 = { \textsc {DLog}}_g(\hat{R}_1(X^*)^{a_1c},\ldots )\).
Now since the reduction has obtained two AOMDL challenges, it can make a second \({ \textsc {DLog}}_g\) query to compute \(s_1'={ \textsc {DLog}}_g(\hat{R}'_1(X^*)^{a_1'c'},\ldots )\) and answer the \({ \textsc {Sign}}'\) query in the second execution. Moreover, to ensure that the AOMDL challenge responses \(r_{1,1}\) and \(r_{1,2}\) can be computed after extracting \(x^*\), the reduction programs \(\mathsf {H}_{\mathrm {non}}\) to give different responses in each execution after a fork. Let us assume for now that the signing session was started with a \({ \textsc {Sign}}\) query after the \(\mathsf {H}_{\mathrm {agg}}\) fork. We can distinguish the following two cases depending on when \(\mathsf {H}_{\mathrm {non}}\) is queried with the inputs corresponding to the signing session:
-
\(\mathsf {H}_{\mathrm {non}}\) is queried after the \(\mathsf {H}_{\mathrm {sig}}\) fork. Regardless of what values the adversary sends in \({ \textsc {Sign}}'\), hashing with \(\mathsf {H}_{\mathrm {non}}\) ensures that with overwhelming probability the second execution will use a value \(b'\) that is different from b in the first execution. In order to answer the \({ \textsc {Sign}}'\) queries, the reduction uses \({ \textsc {DLog}}_g\) to compute \(s_1\) and \(s_1'\) resulting in a system of linear equations
$$\begin{aligned} r_{1,1} + b r_{1,2}&= s_1 - a_1cx^* \bmod p \\ r_{1,1} + b' r_{1,2}&= s_1' - a_1'c'x^* \bmod p \end{aligned}$$with unknowns \(r_{1,1}\) and \(r_{1,2}\). As the system is linearly independent (as \(b \ne b'\)) the reduction can solve it and forward the solutions to the AOMDL challenger.
-
\(\mathsf {H}_{\mathrm {non}}\) is queried before the \(\mathsf {H}_{\mathrm {sig}}\) fork. This implies that b in the first execution is equal to \(b'\) in the second execution and requires the reduction to ensure that \(a_1'\) and \(c'\) are identical in both executions. Then the input to the \({ \textsc {DLog}}_g\) query is also identical and the reduction can simply cache and reuse the result of the \({ \textsc {DLog}}_g\) query from the first execution to save the \({ \textsc {DLog}}_g\) query in the second execution. (Without this caching, the reduction would waste a second \({ \textsc {DLog}}_g\) query to compute \(s_1'=s_1\), which it knows already, and then would not have a second, linearly independent equation that allows solving for \(r_{1,1}\) and \(r_{1,2}\).) The value \(a_1\) is equal to \(a_1'\) because the inputs of \(\mathsf {H}_{\mathrm {non}}\) contain \(\widetilde{X}\) which implies that the corresponding \(\mathsf {H}_{\mathrm {agg}}\) happened before \(\mathsf {H}_{\mathrm {non}}\) and therefore before the fork. Similarly, \(\mathsf {H}_{\mathrm {sig}}\) requires the aggregate nonce R of the signing session and therefore \(\mathsf {H}_{\mathrm {non}}\) must be queried before the corresponding \(\mathsf {H}_{\mathrm {sig}}\). In order to argue that \(c = c'\), observe that from the inputs (and output) of a \(\mathsf {H}_{\mathrm {non}}\) query it is possible to compute the inputs of the \(\mathsf {H}_{\mathrm {sig}}\) query. Therefore, the reduction can make such an internal \(\mathsf {H}_{\mathrm {sig}}\) query for every \(\mathsf {H}_{\mathrm {non}}\) query it receives. This \(\mathsf {H}_{\mathrm {sig}}\) query is before the fork point implying \(c = c'\) as desired. (The reduction does not need to handle the case that this \(\mathsf {H}_{\mathrm {sig}}\) query is the fork point, because then the values L and m of forgery were queried in a signing session and thus the forgery is invalid.) Now the reduction has a \({ \textsc {DLog}}_g\) query left to compute the discrete logarithm of \(R_{1,1}\), which enables to compute the discrete logarithm of \(R_{1,2}\) after \(x^*\) has been extracted.
More generally, if the signing session can be started before the \(\mathsf {H}_{\mathrm {agg}}\) fork, the reduction may have to provide different signatures in all four executions. To answer the signature queries nonetheless, the reduction requires four DL queries and therefore requires \(\mathsf {MuSig2} \) with \(\nu = 4\) nonces. Similar to the above, whenever \(\mathsf {H}_{\mathrm {non}}\) is queried after the \(\mathsf {H}_{\mathrm {sig}}\) fork, the reduction ends up with up to four equations, which are constructed to be linearly independent with high probability. Whenever \(\mathsf {H}_{\mathrm {non}}\) is queried before the \(\mathsf {H}_{\mathrm {sig}}\) fork, the \({ \textsc {DLog}}_g\) queries in the corresponding executions will be identical and the result can be cached and reused. The \({ \textsc {DLog}}_g\) queries saved due to caching can then be used to complete the linear system to \(\nu =4\) linearly independent equations, and the reduction can solve for the unknowns \(r_{1,1}, \ldots , r_{1,4}\).
5.1 Security Proof
Proof Overview. We first construct a “wrapping” algorithm  which essentially runs the adversary
which essentially runs the adversary  and returns a forgery together with some information about the adversary execution, unless some bad events happen. Algorithm
and returns a forgery together with some information about the adversary execution, unless some bad events happen. Algorithm  simulates the random oracles \(\mathsf {H}_{\mathrm {agg}}\), \(\mathsf {H}_{\mathrm {non}}\), and \(\mathsf {H}_{\mathrm {sig}}\) uniformly at random and the signing oracle by obtaining \(\nu \) DL challenges from the AOMDL challenge oracle for each \({ \textsc {Sign}}\) query and by making a single query to the DL oracle for each \({ \textsc {Sign}}'\) query. Then, we use
simulates the random oracles \(\mathsf {H}_{\mathrm {agg}}\), \(\mathsf {H}_{\mathrm {non}}\), and \(\mathsf {H}_{\mathrm {sig}}\) uniformly at random and the signing oracle by obtaining \(\nu \) DL challenges from the AOMDL challenge oracle for each \({ \textsc {Sign}}\) query and by making a single query to the DL oracle for each \({ \textsc {Sign}}'\) query. Then, we use  to construct an algorithm
to construct an algorithm  which runs the forking algorithm
which runs the forking algorithm  as defined in Sect. 3 (where the fork is w.r.t. the answer to the \(\mathsf {H}_{\mathrm {sig}}\) query related to the forgery), allowing it to return a multiset of public keys L together with the discrete logarithm of the corresponding aggregate public key. Finally, we use
as defined in Sect. 3 (where the fork is w.r.t. the answer to the \(\mathsf {H}_{\mathrm {sig}}\) query related to the forgery), allowing it to return a multiset of public keys L together with the discrete logarithm of the corresponding aggregate public key. Finally, we use  to construct an algorithm
to construct an algorithm  computing the DL of the public key of the honest signer by running
computing the DL of the public key of the honest signer by running  (where the fork is now w.r.t. the answer to the \(\mathsf {H}_{\mathrm {agg}}\) query related to the forgery). Throughout the proof, the reader might find helpful to refer to Fig. 4 which illustrates the inner working of
(where the fork is now w.r.t. the answer to the \(\mathsf {H}_{\mathrm {agg}}\) query related to the forgery). Throughout the proof, the reader might find helpful to refer to Fig. 4 which illustrates the inner working of  .
.
Due to  and
and  carefully relaying DL challenges, it is ensured that the \(\nu \ge 4\) DL challenges that
carefully relaying DL challenges, it is ensured that the \(\nu \ge 4\) DL challenges that  obtains in each \({ \textsc {Sign}}\) query are identical across all executions of
obtains in each \({ \textsc {Sign}}\) query are identical across all executions of  . Since
. Since  (via
(via  and
and  ) obtains \(1+\nu q_s\) DL challenges (one for the public key of the honest signer and \(\nu \) for each of the \(q_s\) signing sessions) and solves all of these challenges using at most \(\nu q_s\) queries to the DL oracle (one for each of the \(q_s\) signing session in at most \(4\le \nu \) executions due to double-forking), algorithm
) obtains \(1+\nu q_s\) DL challenges (one for the public key of the honest signer and \(\nu \) for each of the \(q_s\) signing sessions) and solves all of these challenges using at most \(\nu q_s\) queries to the DL oracle (one for each of the \(q_s\) signing session in at most \(4\le \nu \) executions due to double-forking), algorithm  solves the AOMDL problem.
solves the AOMDL problem.
A possible execution of algorithm  . Each path from left to right represents an execution of the adversary
. Each path from left to right represents an execution of the adversary  . Each vertex symbolizes a call to random oracles \(\mathsf {H}_{\mathrm {agg}}\) and \(\mathsf {H}_{\mathrm {sig}}\), and the edge originating from this vertex symbolizes the response used for the query. Leaves symbolize the forgery returned by the adversary.
. Each vertex symbolizes a call to random oracles \(\mathsf {H}_{\mathrm {agg}}\) and \(\mathsf {H}_{\mathrm {sig}}\), and the edge originating from this vertex symbolizes the response used for the query. Leaves symbolize the forgery returned by the adversary.
Normalizing Assumptions and Conventions. Let a \((t,q_s,q_h,N)\)-adversary be an adversary running in time at most t, making at most \(q_s\) \({ \textsc {Sign}}\) queries, at most \(q_h\) queries to each random oracle, and such that |L| in any signing session and in the forgery is at most N.
In all the following, we assume that the adversary only makes “well-formed” random oracles queries, meaning that \(X^* \in L\) and \(X\in L\) for any query \(\mathsf {H}_{\mathrm {agg}}(L,X)\). This is without loss of generality, since “ill-formed” queries are irrelevant and could simply be answered uniformly at random in the simulation.
We further assume without loss of generality that the adversary makes exactly \(q_h\) queries to each random oracle and exactly \(q_s\) queries to the \({ \textsc {Sign}}\) oracle, and that the adversary closes every signing session, i.e., for every \({ \textsc {Sign}}\) query it will also make a corresponding \({ \textsc {Sign}}'\) query at some point. This is without loss of generality because remaining queries can be emulated after the adversary has terminated (in the case of \({ \textsc {Sign}}'\) queries using a set of public keys and a message m which are different from the adversary’s forgery to make sure not to invalidate a valid forgery).
We ignore the \({ \textsc {Sign}}''\) oracle in the simulation. This is without loss of generality because it does not depend on secret state and thus the adversary can simply simulate it locally.
Lemma 2
Given some integer \(\nu \), let  be a \((t,q_s,q_h,N)\)-adversary in the random oracle model against the multi-signature scheme \(\mathsf {MuSig2} [\mathsf {GrGen},\nu ]\), and let \(q=2q_h+q_s+1\). Then there exists an algorithm
be a \((t,q_s,q_h,N)\)-adversary in the random oracle model against the multi-signature scheme \(\mathsf {MuSig2} [\mathsf {GrGen},\nu ]\), and let \(q=2q_h+q_s+1\). Then there exists an algorithm  that takes as input group parameters
that takes as input group parameters  , uniformly random group elements
, uniformly random group elements  , and uniformly random scalars \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\), \(h_{\mathrm {non},1},\ldots ,h_{\mathrm {non},q}\), \(h_{\mathrm {sig},1},\ldots ,h_{\mathrm {sig},q} \in \mathbb {Z}_p\), makes at most \(q_s\) queries to a discrete logarithm oracle \({ \textsc {DLog}}_g\), and with accepting probability (as defined in Lemma 1)
, and uniformly random scalars \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\), \(h_{\mathrm {non},1},\ldots ,h_{\mathrm {non},q}\), \(h_{\mathrm {sig},1},\ldots ,h_{\mathrm {sig},q} \in \mathbb {Z}_p\), makes at most \(q_s\) queries to a discrete logarithm oracle \({ \textsc {DLog}}_g\), and with accepting probability (as defined in Lemma 1)

outputs a tuple \((i_{\mathrm {agg}},j_{\mathrm {agg}},i_{\mathrm {sig}},j_{\mathrm {sig}},L,R,s,\vec {a})\) where \(i_{\mathrm {agg}},i_{\mathrm {sig}}\in \{1,\ldots ,q\}\), \(j_{\mathrm {agg}},j_{\mathrm {sig}}\in \{0,\ldots ,q\}\), \(L=\{X_1,\ldots ,X_n\}\) is a multiset of public keys such that \(X^*\in L\), \(\vec {a}=(a_1,\ldots ,a_n) \in \mathbb {Z}_p^n\) is a tuple of scalars such that \(a_i=h_{\mathrm {agg},i_{\mathrm {agg}}}\) for any i such that \(X_i=X^*\), and
Proof
We construct algorithm  as follows. It initializes three empty sets \(T_{\mathrm {agg}}\), \(T_{\mathrm {non}}\) and \(T_{\mathrm {sig}}\) for storing key-value pairs (k, v), which we write in assignment form “
as follows. It initializes three empty sets \(T_{\mathrm {agg}}\), \(T_{\mathrm {non}}\) and \(T_{\mathrm {sig}}\) for storing key-value pairs (k, v), which we write in assignment form “ ” for a set T. The sets represent tables for storing programmed values for respectively \(\mathsf {H}_{\mathrm {agg}}\), \(\mathsf {H}_{\mathrm {non}}\) and \(\mathsf {H}_{\mathrm {sig}}\). It also initializes four counters \( ctrh _{\mathrm {agg}}\), \( ctrh _{\mathrm {non}}\), \( ctrh _{\mathrm {sig}}\), and \( ctrs \) (initially zero), an empty set \(S\) for keeping track of open signing sessions, an empty set Q for keeping track of completed signing sessions, an empty set K for keeping track of aggregate keys resulting from queries to \(\mathsf {H}_{\mathrm {agg}}\), and two flags \(\mathsf {BadOrder}\) and \(\mathsf {KeyColl}\) (initially \(\mathtt {false}\)) that will help keep track of bad events. Then, it picks random coins \(\rho _A\), runs the adversary
” for a set T. The sets represent tables for storing programmed values for respectively \(\mathsf {H}_{\mathrm {agg}}\), \(\mathsf {H}_{\mathrm {non}}\) and \(\mathsf {H}_{\mathrm {sig}}\). It also initializes four counters \( ctrh _{\mathrm {agg}}\), \( ctrh _{\mathrm {non}}\), \( ctrh _{\mathrm {sig}}\), and \( ctrs \) (initially zero), an empty set \(S\) for keeping track of open signing sessions, an empty set Q for keeping track of completed signing sessions, an empty set K for keeping track of aggregate keys resulting from queries to \(\mathsf {H}_{\mathrm {agg}}\), and two flags \(\mathsf {BadOrder}\) and \(\mathsf {KeyColl}\) (initially \(\mathtt {false}\)) that will help keep track of bad events. Then, it picks random coins \(\rho _A\), runs the adversary  on
on  and public key \(X^*\) as input and answers its queries as follows.
and public key \(X^*\) as input and answers its queries as follows.
-
Hash query \(\mathsf {H}_{\mathrm {agg}}(L,X)\): (Recall that by assumption, \(X^*\in L\) and \(X\in L\).) If \(T_{\mathrm {agg}}(L,X)\) is undefined, then
 increments \( ctrh _{\mathrm {agg}}\), randomly assigns
increments \( ctrh _{\mathrm {agg}}\), randomly assigns  for all \(X'\in L\setminus \{X^*\}\), and assigns
for all \(X'\in L\setminus \{X^*\}\), and assigns  . Then,
. Then,  computes the aggregate key corresponding to L, namely
computes the aggregate key corresponding to L, namely  where
where  and
and  . If \(\widetilde{X}\) is equal to the first argument of some defined entry in \(T_{\mathrm {sig}}\) (i.e., there exists R and m such that \(T_{\mathrm {sig}}(\widetilde{X},R,m) \ne \bot \)), then
. If \(\widetilde{X}\) is equal to the first argument of some defined entry in \(T_{\mathrm {sig}}\) (i.e., there exists R and m such that \(T_{\mathrm {sig}}(\widetilde{X},R,m) \ne \bot \)), then  sets
sets  . If \(\widetilde{X}\in K\), then
. If \(\widetilde{X}\in K\), then  sets
sets  , otherwise it sets
, otherwise it sets  . Finally, it returns \(T_{\mathrm {agg}}(L,X)\).
. Finally, it returns \(T_{\mathrm {agg}}(L,X)\). -
Hash query \(\mathsf {H}_{\mathrm {non}}(\widetilde{X}, (R_1,\ldots ,R_\nu ), m)\): If \(T_{\mathrm {non}}(\widetilde{X}, (R_1,\ldots ,R_\nu ), m)\) is undefined, then
 increments \( ctrh _{\mathrm {non}}\) and assigns
increments \( ctrh _{\mathrm {non}}\) and assigns  . Then
. Then  sets
sets  and computes
and computes  . If \(T_{\mathrm {sig}}(\widetilde{X},R,m)\) is undefined, then
. If \(T_{\mathrm {sig}}(\widetilde{X},R,m)\) is undefined, then  makes an internal query to \(\mathsf {H}_{\mathrm {sig}}(\widetilde{X},R,m)\). Finally, it returns b.
makes an internal query to \(\mathsf {H}_{\mathrm {sig}}(\widetilde{X},R,m)\). Finally, it returns b. -
Hash query \(\mathsf {H}_{\mathrm {sig}}(\widetilde{X},R,m)\): If \(T_{\mathrm {sig}}(\widetilde{X},R,m)\) is undefined, then
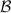 increments \( ctrh _{\mathrm {sig}}\) and assigns
increments \( ctrh _{\mathrm {sig}}\) and assigns  . Then, it returns \(T_{\mathrm {sig}}(\widetilde{X},R,m)\).
. Then, it returns \(T_{\mathrm {sig}}(\widetilde{X},R,m)\). -
Signing query \({ \textsc {Sign}}()\):
 increments \( ctrs \), adds \( ctrs \) to \(S\), lets
increments \( ctrs \), adds \( ctrs \) to \(S\), lets  and sends
and sends  to the adversary.
to the adversary. -
Signing query
 : If \(k \notin S\) then the signing query is answered with \(\bot \). Otherwise,
: If \(k \notin S\) then the signing query is answered with \(\bot \). Otherwise,  removes k from \(S\). Let
removes k from \(S\). Let  and
and  . Let
. Let  for each \(i\in \{2,\ldots ,n\}\) and let
for each \(i\in \{2,\ldots ,n\}\) and let  . If \(T_{\mathrm {agg}}(L,X^*)\) is undefined,
. If \(T_{\mathrm {agg}}(L,X^*)\) is undefined,  makes an internal query to \(\mathsf {H}_{\mathrm {agg}}(L,X^*)\) which ensures that \(T_{\mathrm {agg}}(L,X_i)\) is defined for each \(i\in \{1,\ldots ,n\}\). It sets
makes an internal query to \(\mathsf {H}_{\mathrm {agg}}(L,X^*)\) which ensures that \(T_{\mathrm {agg}}(L,X_i)\) is defined for each \(i\in \{1,\ldots ,n\}\). It sets  , computes
, computes  , and sets
, and sets  . Then
. Then  sets
sets  . If \(T_{\mathrm {non}}(\widetilde{X}, (R_1,\ldots ,R_\nu ), m)\) is undefined, then
. If \(T_{\mathrm {non}}(\widetilde{X}, (R_1,\ldots ,R_\nu ), m)\) is undefined, then  makes an internal query to \(\mathsf {H}_{\mathrm {non}}(\widetilde{X}, (R_1,\ldots ,R_\nu ), m)\). It sets
makes an internal query to \(\mathsf {H}_{\mathrm {non}}(\widetilde{X}, (R_1,\ldots ,R_\nu ), m)\). It sets  , aggregates the nonces as
, aggregates the nonces as 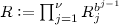 ,Footnote 8 and sets
,Footnote 8 and sets  , where \(T_{\mathrm {sig}}(\widetilde{X},R,m)\) is defined due to the internal \(\mathsf {H}_{\mathrm {sig}}\) query when handling the internal \(\mathsf {H}_{\mathrm {non}}\) query. Then,
, where \(T_{\mathrm {sig}}(\widetilde{X},R,m)\) is defined due to the internal \(\mathsf {H}_{\mathrm {sig}}\) query when handling the internal \(\mathsf {H}_{\mathrm {non}}\) query. Then,  computes the honest signer’s effective nonce
computes the honest signer’s effective nonce  . It sets
. It sets and
and 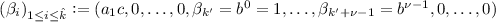 for
for  , and obtains
, and obtains  by querying the DL oracle. Finally,
by querying the DL oracle. Finally,  returns \(s_1\).
returns \(s_1\).
If  returns \(\bot \) or if \(\mathsf {BadOrder}= \mathtt {true}\) or \(\mathsf {KeyColl}= \mathtt {true}\) at the end of the game, then
returns \(\bot \) or if \(\mathsf {BadOrder}= \mathtt {true}\) or \(\mathsf {KeyColl}= \mathtt {true}\) at the end of the game, then  outputs \(\bot \). Otherwise, let (L, m, (R, s)) denote the output of the adversary, where (R, s) is a purported forgery for a public key multiset L such that \(X^*\in L\) and a message m. Then,
outputs \(\bot \). Otherwise, let (L, m, (R, s)) denote the output of the adversary, where (R, s) is a purported forgery for a public key multiset L such that \(X^*\in L\) and a message m. Then,  parses L as \(\{X_1=X^*,\ldots ,X_n\}\) and checks the validity of the forgery as follows. If \(T_{\mathrm {agg}}(L,X^*)\) is undefined, it makes an internal query to \(\mathsf {H}_{\mathrm {agg}}(L,X^*)\) which ensures that \(T_{\mathrm {agg}}(L,X_i)\) is defined for each \(i\in \{1,\ldots ,n\}\), sets
parses L as \(\{X_1=X^*,\ldots ,X_n\}\) and checks the validity of the forgery as follows. If \(T_{\mathrm {agg}}(L,X^*)\) is undefined, it makes an internal query to \(\mathsf {H}_{\mathrm {agg}}(L,X^*)\) which ensures that \(T_{\mathrm {agg}}(L,X_i)\) is defined for each \(i\in \{1,\ldots ,n\}\), sets  , and computes
, and computes  . If \(T_{\mathrm {sig}}(\widetilde{X},R,m)\) is undefined, it makes an internal query to \(\mathsf {H}_{\mathrm {sig}}(\widetilde{X},R,m)\) and lets
. If \(T_{\mathrm {sig}}(\widetilde{X},R,m)\) is undefined, it makes an internal query to \(\mathsf {H}_{\mathrm {sig}}(\widetilde{X},R,m)\) and lets  . If \(g^s\ne R\widetilde{X}^c\), i.e., the forgery is not a valid signature, or if \((L, m)\in Q\), i.e., the forgery is invalid because the adversary made a \({ \textsc {Sign}}'\) query for L and m,
. If \(g^s\ne R\widetilde{X}^c\), i.e., the forgery is not a valid signature, or if \((L, m)\in Q\), i.e., the forgery is invalid because the adversary made a \({ \textsc {Sign}}'\) query for L and m,  outputs \(\bot \). Otherwise, it takes the following additional steps. Let
outputs \(\bot \). Otherwise, it takes the following additional steps. Let
-
\(i_{\mathrm {agg}}\) be the index such that \(T_{\mathrm {agg}}(L,X^*)=h_{\mathrm {agg},i_{\mathrm {agg}}}\),
-
\(j_{\mathrm {agg}}\) be the value of \( ctrh _{\mathrm {non}}\) at the moment \(T_{\mathrm {agg}}(L, X^*)\) is assigned,
-
\(i_{\mathrm {sig}}\) be the index such that \(T_{\mathrm {sig}}(\widetilde{X},R,m)=h_{\mathrm {sig},i_{\mathrm {sig}}}\),
-
\(j_{\mathrm {sig}}\) be the value of \( ctrh _{\mathrm {non}}\) at the moment \(T_{\mathrm {sig}}(\widetilde{X},R,m)\) is assigned.
Then  returns \((i_{\mathrm {agg}},j_{\mathrm {agg}},i_{\mathrm {sig}},j_{\mathrm {sig}},L,R,s,\vec {a})\), where \(\vec {a}=(a_1,\ldots ,a_n)\). By construction, \(a_i=h_{\mathrm {agg},i_{\mathrm {agg}}}\) for each i such that \(X_i=X^*\), and the validity of the forgery implies Equation (2).
returns \((i_{\mathrm {agg}},j_{\mathrm {agg}},i_{\mathrm {sig}},j_{\mathrm {sig}},L,R,s,\vec {a})\), where \(\vec {a}=(a_1,\ldots ,a_n)\). By construction, \(a_i=h_{\mathrm {agg},i_{\mathrm {agg}}}\) for each i such that \(X_i=X^*\), and the validity of the forgery implies Equation (2).
\(\mathsf {H}_{\mathrm {agg}}\) is called at most \(q_h\) times by the adversary, at most once per \({ \textsc {Sign}}'\) query, and at most once when verifying the forgery, hence at most \(q_h+q_s+1\) times in total. Similarly, \(\mathsf {H}_{\mathrm {non}}\) is called at most \(q_h\) times by the adversary and at most once per \({ \textsc {Sign}}'\) query, hence at most \(q_h+q_s\) times in total. Finally, \(\mathsf {H}_{\mathrm {sig}}\) is called at most \(q_h\) times by the adversary, at most once per \(\mathsf {H}_{\mathrm {non}}\) query, and at most once when verifying the forgery, hence at most \(2q_h+q_s+1\) times in total. Hence, each random oracle is called at most \(q=2q_h+q_s+1\) times in total.
We now lower bound the accepting probability of  . Since \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\), \(h_{\mathrm {non},1},\ldots ,h_{\mathrm {non},q}\) and \(h_{\mathrm {sig},1},\ldots ,h_{\mathrm {sig},q}\) are uniformly random,
. Since \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\), \(h_{\mathrm {non},1},\ldots ,h_{\mathrm {non},q}\) and \(h_{\mathrm {sig},1},\ldots ,h_{\mathrm {sig},q}\) are uniformly random,  perfectly simulates the security experiment to the adversary. Moreover, when the adversary eventually returns a forgery,
perfectly simulates the security experiment to the adversary. Moreover, when the adversary eventually returns a forgery,  returns a non-\(\bot \) output unless \(\mathsf {BadOrder}\) or \(\mathsf {KeyColl}\) is set to \(\mathtt {true}\). Hence, by the union bound,
returns a non-\(\bot \) output unless \(\mathsf {BadOrder}\) or \(\mathsf {KeyColl}\) is set to \(\mathtt {true}\). Hence, by the union bound,

It remains to upper bound \(\Pr \left[ \mathsf {BadOrder} \right] \) and \(\Pr \left[ \mathsf {KeyColl} \right] \). Note that for any query \(\mathsf {H}_{\mathrm {agg}}(L',X')\), either \(T_{\mathrm {agg}}(L',X')\) is already defined, in which case \(\mathsf {H}_{\mathrm {agg}}\) returns immediately and neither \(\mathsf {BadOrder}\) nor \(\mathsf {KeyColl}\) can be set to \(\mathtt {true}\), or \(T_{\mathrm {agg}}(L',X')\) is undefined, in which case \(T_{\mathrm {agg}}(L',X'')\) is undefined for every \(X'' \in L'\) since all these table values are set at the same time when the first query \(\mathsf {H}_{\mathrm {agg}}(L',*)\) happens. In the latter case, the corresponding aggregate key is
where \(n^*\ge 1 \) is the number of times \(X^*\) appears in \(L'\) and \(h_{\mathrm {agg},i}\) (where i is the value of \( ctrh _{\mathrm {agg}}\) when \(T_{\mathrm {agg}}(L',X^*)\) is set) is uniformly random in \(\mathbb {Z}_p\) and independent of Z which accounts for public keys different from \(X^*\) in \(L'\). Hence, \(\widetilde{X}'\) is uniformly random in  of size
of size  . Since there are always at most q defined entries in \(T_{\mathrm {sig}}\) and at most q queries to \(\mathsf {H}_{\mathrm {agg}}\), \(\mathsf {BadOrder}\) is set to \(\mathtt {true}\) with probability at most
. Since there are always at most q defined entries in \(T_{\mathrm {sig}}\) and at most q queries to \(\mathsf {H}_{\mathrm {agg}}\), \(\mathsf {BadOrder}\) is set to \(\mathtt {true}\) with probability at most  . Similarly, the size of K is always at most q (since at most one element is added per \(\mathsf {H}_{\mathrm {agg}}\) query), hence \(\mathsf {KeyColl}\) is set to \(\mathtt {true}\) with probability at most
. Similarly, the size of K is always at most q (since at most one element is added per \(\mathsf {H}_{\mathrm {agg}}\) query), hence \(\mathsf {KeyColl}\) is set to \(\mathtt {true}\) with probability at most  . Combining all of the above, we obtain
. Combining all of the above, we obtain

\(\square \)
Using  , we now construct an algorithm
, we now construct an algorithm  which returns a multiset of public keys L together with the discrete logarithm of the corresponding aggregate key.
which returns a multiset of public keys L together with the discrete logarithm of the corresponding aggregate key.
Lemma 3
Given some integer \(\nu \), let  be a \((t,q_s,q_h,N)\)-adversary in the random oracle model against the multi-signature scheme \(\mathsf {MuSig2} [\mathsf {GrGen},\nu ]\) and let \(q=2q_h+q_s+1\). Then there exists an algorithm
be a \((t,q_s,q_h,N)\)-adversary in the random oracle model against the multi-signature scheme \(\mathsf {MuSig2} [\mathsf {GrGen},\nu ]\) and let \(q=2q_h+q_s+1\). Then there exists an algorithm  that takes as input group parameters
that takes as input group parameters  , uniformly random group elements
, uniformly random group elements  , and uniformly random scalars \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\), \(h_{\mathrm {non},1},h_{\mathrm {non},1}',\ldots ,h_{\mathrm {non},q},h_{\mathrm {non},q}'\in \mathbb {Z}_p\), makes at most \(2q_s\) queries to a discrete logarithm oracle \({ \textsc {DLog}}_g\), and with accepting probability (as defined in Lemma 1)
, and uniformly random scalars \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\), \(h_{\mathrm {non},1},h_{\mathrm {non},1}',\ldots ,h_{\mathrm {non},q},h_{\mathrm {non},q}'\in \mathbb {Z}_p\), makes at most \(2q_s\) queries to a discrete logarithm oracle \({ \textsc {DLog}}_g\), and with accepting probability (as defined in Lemma 1)

outputs a tuple \((i_{\mathrm {agg}},j_{\mathrm {agg}},L,\vec {a},\tilde{x})\) where \(i_{\mathrm {agg}}\in \{1,\ldots ,q\}\), \(j_{\mathrm {agg}}\in \{0,\ldots ,q\}\), \(L=\{X_1,\ldots ,X_n\}\) is a multiset of public keys such that \(X^*\in L\), \(\vec {a}=(a_1,\ldots ,a_n)\in \mathbb {Z}_p^n\) is a tuple of scalars such that \(a_i=h_{\mathrm {agg},i_{\mathrm {agg}}}\) for any i such that \(X_i=X^*\), and \(\tilde{x}\) is the discrete logarithm of \(\widetilde{X}=\prod _{i=1}^n X_i ^{a_i}\) in base g.
Proof
Algorithm  runs
runs  with
with  as defined in Lemma 2 and takes additional steps as described below. The mapping with notation of our Forking Lemma (Lemma 1) is as follows:
as defined in Lemma 2 and takes additional steps as described below. The mapping with notation of our Forking Lemma (Lemma 1) is as follows:
-
 , \(X^*\), \(U_1,\ldots ,U_{\nu q_s}\), and \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\) play the role of \( inp \),
, \(X^*\), \(U_1,\ldots ,U_{\nu q_s}\), and \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\) play the role of \( inp \), -
\(h_{\mathrm {non},1},h_{\mathrm {non},1}',\ldots ,h_{\mathrm {non},q},h_{\mathrm {non},q}'\) play the role of \(v_1,v'_1,\ldots ,v_m,v'_m\),
-
\(h_{\mathrm {sig},1},\ldots ,h_{\mathrm {sig},q}\) play the role of \(h_1,\ldots ,h_q\),
-
\((i_{\mathrm {sig}},j_{\mathrm {sig}})\) play the role of (i, j),
-
\((i_{\mathrm {agg}},j_{\mathrm {agg}},L,R,s,\vec {a})\) play the role of \( out \).
In more details,  picks random coins \(\rho _B\) and uniformly random scalars \(h_{\mathrm {sig},1},\ldots ,h_{\mathrm {sig},q} \in \mathbb {Z}_p\), and runs algorithm
picks random coins \(\rho _B\) and uniformly random scalars \(h_{\mathrm {sig},1},\ldots ,h_{\mathrm {sig},q} \in \mathbb {Z}_p\), and runs algorithm  on coins \(\rho _B\), group description
on coins \(\rho _B\), group description  , group elements
, group elements  , and scalars \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\), \(h_{\mathrm {non},1},\ldots , h_{\mathrm {non},q}\), \(h_{\mathrm {sig},1},\ldots ,h_{\mathrm {sig},q} \in \mathbb {Z}_p\). Recall that scalars \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\) and \(h_{\mathrm {non},1},h_{\mathrm {non},1}',\ldots ,,h_{\mathrm {non},q},h_{\mathrm {non},q}'\) are part of the input of
, and scalars \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\), \(h_{\mathrm {non},1},\ldots , h_{\mathrm {non},q}\), \(h_{\mathrm {sig},1},\ldots ,h_{\mathrm {sig},q} \in \mathbb {Z}_p\). Recall that scalars \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\) and \(h_{\mathrm {non},1},h_{\mathrm {non},1}',\ldots ,,h_{\mathrm {non},q},h_{\mathrm {non},q}'\) are part of the input of  and the former will be the same in both runs of
and the former will be the same in both runs of  . All \({ \textsc {DLog}}_g\) oracle queries made by
. All \({ \textsc {DLog}}_g\) oracle queries made by  are relayed by
are relayed by  to its own \({ \textsc {DLog}}_g\) oracle. If
to its own \({ \textsc {DLog}}_g\) oracle. If  returns \(\bot \),
returns \(\bot \),  returns \(\bot \) as well. Otherwise, if
returns \(\bot \) as well. Otherwise, if  returns a tuple \((i_{\mathrm {agg}},j_{\mathrm {agg}},i_{\mathrm {sig}},j_{\mathrm {sig}},L,R,s,\vec {a})\), where \(L=\{X_1,\ldots ,X_n\}\) and \(\vec {a}=(a_1,\ldots ,a_n)\),
returns a tuple \((i_{\mathrm {agg}},j_{\mathrm {agg}},i_{\mathrm {sig}},j_{\mathrm {sig}},L,R,s,\vec {a})\), where \(L=\{X_1,\ldots ,X_n\}\) and \(\vec {a}=(a_1,\ldots ,a_n)\),  picks uniformly random scalars \(h_{\mathrm {sig},i_{\mathrm {sig}}}',\ldots ,h_{\mathrm {sig},q}' \in \mathbb {Z}_p\) and runs
picks uniformly random scalars \(h_{\mathrm {sig},i_{\mathrm {sig}}}',\ldots ,h_{\mathrm {sig},q}' \in \mathbb {Z}_p\) and runs  again with the same random coins \(\rho _B\) on input
again with the same random coins \(\rho _B\) on input

Again, all \({ \textsc {DLog}}_g\) oracle queries made by  are relayed by
are relayed by  to its own \({ \textsc {DLog}}_g\) oracle. If
to its own \({ \textsc {DLog}}_g\) oracle. If  returns \(\bot \) in this second run,
returns \(\bot \) in this second run,  returns \(\bot \) as well. If
returns \(\bot \) as well. If  returns a second tuple \((i_{\mathrm {agg}}',j_{\mathrm {agg}}',i_{\mathrm {sig}}',j_{\mathrm {sig}}',L',R',s',\vec {a}')\), where \(L'=\{X'_1,\ldots ,X'_{n'}\}\) and \(\vec {a}'=(a'_1,\ldots ,a'_{n'})\),
returns a second tuple \((i_{\mathrm {agg}}',j_{\mathrm {agg}}',i_{\mathrm {sig}}',j_{\mathrm {sig}}',L',R',s',\vec {a}')\), where \(L'=\{X'_1,\ldots ,X'_{n'}\}\) and \(\vec {a}'=(a'_1,\ldots ,a'_{n'})\),  proceeds as follows. Let \(\widetilde{X}=\prod _{i=1}^nX_i^{a_i}\) and \(\widetilde{X}'=\prod _{i=1}^{n'}(X'_i)^{a'_i}\) denote the aggregate public keys from the two forgeries. If \(i_{\mathrm {sig}}\ne i_{\mathrm {sig}}'\), or \(i_{\mathrm {sig}}=i_{\mathrm {sig}}'\) and \(h_{\mathrm {sig},i_{\mathrm {sig}}}=h_{\mathrm {sig},i_{\mathrm {sig}}}'\), then
proceeds as follows. Let \(\widetilde{X}=\prod _{i=1}^nX_i^{a_i}\) and \(\widetilde{X}'=\prod _{i=1}^{n'}(X'_i)^{a'_i}\) denote the aggregate public keys from the two forgeries. If \(i_{\mathrm {sig}}\ne i_{\mathrm {sig}}'\), or \(i_{\mathrm {sig}}=i_{\mathrm {sig}}'\) and \(h_{\mathrm {sig},i_{\mathrm {sig}}}=h_{\mathrm {sig},i_{\mathrm {sig}}}'\), then  returns \(\bot \). Otherwise, if \(i_{\mathrm {sig}}=i_{\mathrm {sig}}'\) and \(h_{\mathrm {sig},i_{\mathrm {sig}}}\ne h_{\mathrm {sig},i_{\mathrm {sig}}}'\), we will prove shortly that
returns \(\bot \). Otherwise, if \(i_{\mathrm {sig}}=i_{\mathrm {sig}}'\) and \(h_{\mathrm {sig},i_{\mathrm {sig}}}\ne h_{\mathrm {sig},i_{\mathrm {sig}}}'\), we will prove shortly that
which implies in particular that \(\widetilde{X}=\widetilde{X}'\). By Lemma 2, the two outputs returned by  are such that
are such that
which allows  to compute the discrete logarithm of \(\widetilde{X}\) as
to compute the discrete logarithm of \(\widetilde{X}\) as

Then  returns \((i_{\mathrm {agg}},j_{\mathrm {agg}},L,\vec {a},\tilde{x})\).
returns \((i_{\mathrm {agg}},j_{\mathrm {agg}},L,\vec {a},\tilde{x})\).
 returns a non-\(\bot \) output if
returns a non-\(\bot \) output if  does, so that by Lemmas 1 and 2, and letting
does, so that by Lemmas 1 and 2, and letting  ,
,  ’s accepting probability satisfies
’s accepting probability satisfies

It remains to prove the equalities of Eq. (3). In  ’s first execution, \(h_{\mathrm {sig},i_{\mathrm {sig}}}\) is assigned to \(T_{\mathrm {sig}}(\widetilde{X},R,m)\), while is
’s first execution, \(h_{\mathrm {sig},i_{\mathrm {sig}}}\) is assigned to \(T_{\mathrm {sig}}(\widetilde{X},R,m)\), while is  ’s second execution, \(h_{\mathrm {sig},i_{\mathrm {sig}}}'\) is assigned to \(T_{\mathrm {sig}}(\widetilde{X}',R',m')\). Note that these two assignments can happen either because of a direct query to \(\mathsf {H}_{\mathrm {sig}}\) by the adversary, during a query to \(\mathsf {H}_{\mathrm {non}}\), during a \({ \textsc {Sign}}'\) query, or during the final verification of the validity of the forgery. Up to these two assignments, the two executions are identical since
’s second execution, \(h_{\mathrm {sig},i_{\mathrm {sig}}}'\) is assigned to \(T_{\mathrm {sig}}(\widetilde{X}',R',m')\). Note that these two assignments can happen either because of a direct query to \(\mathsf {H}_{\mathrm {sig}}\) by the adversary, during a query to \(\mathsf {H}_{\mathrm {non}}\), during a \({ \textsc {Sign}}'\) query, or during the final verification of the validity of the forgery. Up to these two assignments, the two executions are identical since  runs
runs  on the same random coins and input, uses the same values \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\) for \(T_{\mathrm {agg}}(\cdot ,X^*)\) assignments, the same values \(h_{\mathrm {sig},1},\ldots ,h_{\mathrm {sig},i_{\mathrm {sig}}-1}\) for \(T_{\mathrm {sig}}\) assignments, and the same values \(h_{\mathrm {non},1},\ldots ,h_{\mathrm {non},j_{\mathrm {sig}}}\) for \(T_{\mathrm {non}}\) assignments, \(T_{\mathrm {agg}}(\cdot ,X\ne X^*)\) assignments, and DL oracle outputs \(s_1\) in \({ \textsc {Sign}}'\) queries. Since both executions are identical up to the two assignments
on the same random coins and input, uses the same values \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\) for \(T_{\mathrm {agg}}(\cdot ,X^*)\) assignments, the same values \(h_{\mathrm {sig},1},\ldots ,h_{\mathrm {sig},i_{\mathrm {sig}}-1}\) for \(T_{\mathrm {sig}}\) assignments, and the same values \(h_{\mathrm {non},1},\ldots ,h_{\mathrm {non},j_{\mathrm {sig}}}\) for \(T_{\mathrm {non}}\) assignments, \(T_{\mathrm {agg}}(\cdot ,X\ne X^*)\) assignments, and DL oracle outputs \(s_1\) in \({ \textsc {Sign}}'\) queries. Since both executions are identical up to the two assignments  and
and  , the arguments of the two assignments must be the same, which in particular implies that \(R=R'\) and \(\widetilde{X}=\widetilde{X}'\). Assume that \(L\ne L'\). Then, since \(\widetilde{X}=\widetilde{X}'\), this would mean that \(\mathsf {KeyColl}\) is set to \(\mathtt {true}\) in both executions, a contradiction since
, the arguments of the two assignments must be the same, which in particular implies that \(R=R'\) and \(\widetilde{X}=\widetilde{X}'\). Assume that \(L\ne L'\). Then, since \(\widetilde{X}=\widetilde{X}'\), this would mean that \(\mathsf {KeyColl}\) is set to \(\mathtt {true}\) in both executions, a contradiction since  returns a non-\(\bot \) output in both executions. Hence, \(L=L'\). Since in both executions of
returns a non-\(\bot \) output in both executions. Hence, \(L=L'\). Since in both executions of  , \(\mathsf {BadOrder}\) is not set to \(\mathtt {true}\), assignments
, \(\mathsf {BadOrder}\) is not set to \(\mathtt {true}\), assignments  and
and  necessarily happened before the fork. This implies that \(i_{\mathrm {agg}}=i_{\mathrm {agg}}'\), \(j_{\mathrm {agg}}=j_{\mathrm {agg}}'\), and \(\vec {a}=\vec {a}'\). \(\square \)
necessarily happened before the fork. This implies that \(i_{\mathrm {agg}}=i_{\mathrm {agg}}'\), \(j_{\mathrm {agg}}=j_{\mathrm {agg}}'\), and \(\vec {a}=\vec {a}'\). \(\square \)
We are now ready to prove Theorem 1 by constructing from  an algorithm
an algorithm  solving the AOMDL problem.
solving the AOMDL problem.
Proof of Theorem 1. Fix some integer \(\nu \ge 4\).Footnote 9 Algorithm  runs
runs  with
with  as defined in Lemma 3 and takes additional steps as described below. The mapping with the notation in our Forking Lemma (Lemma 1) is as follows:
as defined in Lemma 3 and takes additional steps as described below. The mapping with the notation in our Forking Lemma (Lemma 1) is as follows:
-
 , \(X^*\), \(U_1,\ldots ,U_{\nu q_s}\) play the role of \( inp \),
, \(X^*\), \(U_1,\ldots ,U_{\nu q_s}\) play the role of \( inp \), -
\((h_{\mathrm {non},1},h_{\mathrm {non},1}')\), \((h_{\mathrm {non},1}'',h_{\mathrm {non},1}''')\), ..., \((h_{\mathrm {non},q},h_{\mathrm {non},q}')\), \((h_{\mathrm {non},q}'',h_{\mathrm {non},q}''')\) play the role of \(v_1\), \(v'_1\), ..., \(v_m\), \(v'_m\),
-
\(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\) play the role of \(h_1,\ldots ,h_q\),
-
\((i_{\mathrm {agg}},j_{\mathrm {agg}})\) play the role of (i, j),
-
\((L,\vec {a},\tilde{x})\) play the role of \( out \).
In more details, algorithm  makes \(\nu q_s +1\) queries to its challenge oracle \(X^*,U_1,\ldots ,U_{\nu q_s} \leftarrow { \textsc {Ch}}()\), picks random coins \(\rho _C\) and scalars \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\), \(h_{\mathrm {non},1},h_{\mathrm {non},1}',\ldots , h_{\mathrm {non},q},h_{\mathrm {non},q}'\in \mathbb {Z}_p\), and runs
makes \(\nu q_s +1\) queries to its challenge oracle \(X^*,U_1,\ldots ,U_{\nu q_s} \leftarrow { \textsc {Ch}}()\), picks random coins \(\rho _C\) and scalars \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\), \(h_{\mathrm {non},1},h_{\mathrm {non},1}',\ldots , h_{\mathrm {non},q},h_{\mathrm {non},q}'\in \mathbb {Z}_p\), and runs  on coins \(\rho _C\), group description
on coins \(\rho _C\), group description  , group elements \(X^*,U_1,\ldots ,U_{\nu q_s}\in \mathbb {Z}_p\), and scalars \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\), \(h_{\mathrm {non},1},h_{\mathrm {non},1}',\ldots , h_{\mathrm {non},q},h_{\mathrm {non},q}'\in \mathbb {Z}_p\). It relays all \({ \textsc {DLog}}_g\) oracle queries made by
, group elements \(X^*,U_1,\ldots ,U_{\nu q_s}\in \mathbb {Z}_p\), and scalars \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},q}\), \(h_{\mathrm {non},1},h_{\mathrm {non},1}',\ldots , h_{\mathrm {non},q},h_{\mathrm {non},q}'\in \mathbb {Z}_p\). It relays all \({ \textsc {DLog}}_g\) oracle queries made by  to its own \({ \textsc {DLog}}_g\) oracle, caching pairs of group elements and responses to avoid making multiple queries for the same group element. If
to its own \({ \textsc {DLog}}_g\) oracle, caching pairs of group elements and responses to avoid making multiple queries for the same group element. If  returns \(\bot \),
returns \(\bot \),  returns \(\bot \) as well. Otherwise, if
returns \(\bot \) as well. Otherwise, if  returns a tuple \((i_{\mathrm {agg}},j_{\mathrm {agg}},L,\vec {a},\tilde{x})\),
returns a tuple \((i_{\mathrm {agg}},j_{\mathrm {agg}},L,\vec {a},\tilde{x})\),  picks uniformly random scalars \(h_{\mathrm {agg},i_{\mathrm {agg}}}',\ldots ,h_{\mathrm {agg},q}'\in \mathbb {Z}_p\) and \(h_{\mathrm {non},j_{\mathrm {agg}}+1}'',h_{\mathrm {non},j_{\mathrm {agg}}+1}''',\ldots ,h_{\mathrm {non},q}'',h_{\mathrm {non},q}'''\in \mathbb {Z}_p\), and runs
picks uniformly random scalars \(h_{\mathrm {agg},i_{\mathrm {agg}}}',\ldots ,h_{\mathrm {agg},q}'\in \mathbb {Z}_p\) and \(h_{\mathrm {non},j_{\mathrm {agg}}+1}'',h_{\mathrm {non},j_{\mathrm {agg}}+1}''',\ldots ,h_{\mathrm {non},q}'',h_{\mathrm {non},q}'''\in \mathbb {Z}_p\), and runs  again with the same random coins \(\rho _C\) on input \(X^* ,U_1,\ldots ,U_{\nu q_s}\),
again with the same random coins \(\rho _C\) on input \(X^* ,U_1,\ldots ,U_{\nu q_s}\),
It relays all \({ \textsc {DLog}}_g\) oracle queries made by  to its own \({ \textsc {DLog}}_g\) oracle after looking them up in its cache to avoid making duplicate queries. If
to its own \({ \textsc {DLog}}_g\) oracle after looking them up in its cache to avoid making duplicate queries. If  returns \(\bot \) in this second run,
returns \(\bot \) in this second run,  returns \(\bot \) as well. If
returns \(\bot \) as well. If  returns a second tuple \((i_{\mathrm {agg}}',j_{\mathrm {agg}}',L',\vec {a}',\tilde{x}')\),
returns a second tuple \((i_{\mathrm {agg}}',j_{\mathrm {agg}}',L',\vec {a}',\tilde{x}')\),  proceeds as follows. Let \(L=\{X_1,\ldots ,X_n\}\), \(\vec {a}=(a_1,\ldots ,a_n)\), \(L'=\{X'_1,\ldots ,X'_{n'}\}\), and \(\vec {a}'=(a'_1,\ldots ,a'_n)\). Let \(n^*\) be the number of times \(X^*\) appears in L. If \(i_{\mathrm {agg}}\ne i_{\mathrm {agg}}'\), or \(i_{\mathrm {agg}}=i_{\mathrm {agg}}'\) and \(h_{\mathrm {agg},i_{\mathrm {agg}}}=h_{\mathrm {agg},i_{\mathrm {agg}}}'\),
proceeds as follows. Let \(L=\{X_1,\ldots ,X_n\}\), \(\vec {a}=(a_1,\ldots ,a_n)\), \(L'=\{X'_1,\ldots ,X'_{n'}\}\), and \(\vec {a}'=(a'_1,\ldots ,a'_n)\). Let \(n^*\) be the number of times \(X^*\) appears in L. If \(i_{\mathrm {agg}}\ne i_{\mathrm {agg}}'\), or \(i_{\mathrm {agg}}=i_{\mathrm {agg}}'\) and \(h_{\mathrm {agg},i_{\mathrm {agg}}}=h_{\mathrm {agg},i_{\mathrm {agg}}}'\),  returns \(\bot \). Otherwise, if \(i_{\mathrm {agg}}=i_{\mathrm {agg}}'\) and \(h_{\mathrm {agg},i_{\mathrm {agg}}}\ne h_{\mathrm {agg},i_{\mathrm {agg}}}'\), then we will show below that
returns \(\bot \). Otherwise, if \(i_{\mathrm {agg}}=i_{\mathrm {agg}}'\) and \(h_{\mathrm {agg},i_{\mathrm {agg}}}\ne h_{\mathrm {agg},i_{\mathrm {agg}}}'\), then we will show below that

By Lemma 3, we have that
Thus,  can compute the discrete logarithm of \(X^*\) as
can compute the discrete logarithm of \(X^*\) as

We will now prove the equalities in Eq. (4). In the two executions of  run within the first execution of
run within the first execution of  , \(h_{\mathrm {agg},i_{\mathrm {agg}}}\) is assigned to \(T_{\mathrm {agg}}(L,X^*)\), while in the two executions of
, \(h_{\mathrm {agg},i_{\mathrm {agg}}}\) is assigned to \(T_{\mathrm {agg}}(L,X^*)\), while in the two executions of  run within the second execution of
run within the second execution of  , \(h_{\mathrm {agg},i_{\mathrm {agg}}}'\) is assigned to \(T_{\mathrm {agg}}(L',X^*)\). Note that these two assignments can happen either because of a direct query \(\mathsf {H}_{\mathrm {agg}}(L,X)\) made by the adversary for some key \(X\in L\) (not necessarily \(X^*\)), during a signing query, or during the final verification of the validity of the forgery. Up to these two assignments, the four executions of
, \(h_{\mathrm {agg},i_{\mathrm {agg}}}'\) is assigned to \(T_{\mathrm {agg}}(L',X^*)\). Note that these two assignments can happen either because of a direct query \(\mathsf {H}_{\mathrm {agg}}(L,X)\) made by the adversary for some key \(X\in L\) (not necessarily \(X^*\)), during a signing query, or during the final verification of the validity of the forgery. Up to these two assignments, the four executions of  are identical since
are identical since  runs
runs  on the same random coins and the same input, uses the same values \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},i_{\mathrm {agg}}-1}\) for \(T_{\mathrm {agg}}(\cdot ,X^*)\) assignments, the same values \(h_{\mathrm {sig},1},\ldots ,h_{\mathrm {sig},q}\) for \(T_{\mathrm {sig}}\) assignments, the same values \(h_{\mathrm {non},1},\ldots ,h_{\mathrm {non},j_{\mathrm {agg}}}\) for \(T_{\mathrm {non}}\) assignments, \(T_{\mathrm {agg}}(\cdot ,X\ne X^*)\) assignments, and the DL oracle outputs \(s_1\) in \({ \textsc {Sign}}'\) queries (note that this relies on the fact that in the four executions of
on the same random coins and the same input, uses the same values \(h_{\mathrm {agg},1},\ldots ,h_{\mathrm {agg},i_{\mathrm {agg}}-1}\) for \(T_{\mathrm {agg}}(\cdot ,X^*)\) assignments, the same values \(h_{\mathrm {sig},1},\ldots ,h_{\mathrm {sig},q}\) for \(T_{\mathrm {sig}}\) assignments, the same values \(h_{\mathrm {non},1},\ldots ,h_{\mathrm {non},j_{\mathrm {agg}}}\) for \(T_{\mathrm {non}}\) assignments, \(T_{\mathrm {agg}}(\cdot ,X\ne X^*)\) assignments, and the DL oracle outputs \(s_1\) in \({ \textsc {Sign}}'\) queries (note that this relies on the fact that in the four executions of  , \(\mathsf {BadOrder}\) is not set to \(\mathtt {true}\)). Since the four executions of
, \(\mathsf {BadOrder}\) is not set to \(\mathtt {true}\)). Since the four executions of  are identical up to the assignments
are identical up to the assignments  and
and  , the arguments of these two assignments must be the same, which implies that \(L=L'\). Besides, all values \(T_{\mathrm {agg}}(L,X)\) for \(X\in L\setminus \{X^*\}\) are chosen uniformly at random by
, the arguments of these two assignments must be the same, which implies that \(L=L'\). Besides, all values \(T_{\mathrm {agg}}(L,X)\) for \(X\in L\setminus \{X^*\}\) are chosen uniformly at random by  using the same coins in the four executions, which implies that \(a_i=a'_i\) for each i such that \(X_i\ne X^*\). This shows the equalities in Eq. (4).
using the same coins in the four executions, which implies that \(a_i=a'_i\) for each i such that \(X_i\ne X^*\). This shows the equalities in Eq. (4).
Recall that  internally ran four executions of
internally ran four executions of  (throughout forking in
(throughout forking in  and in
and in  ). Consider a \({ \textsc {Sign}}\) query handled by
). Consider a \({ \textsc {Sign}}\) query handled by  , and let i be the index such that the group elements \(U_i, \ldots , U_{i+\nu -1}\) queried by
, and let i be the index such that the group elements \(U_i, \ldots , U_{i+\nu -1}\) queried by  to \({ \textsc {Ch}}\) were assigned to \(R_{1,1}, \ldots R_{1,\nu }\) by
to \({ \textsc {Ch}}\) were assigned to \(R_{1,1}, \ldots R_{1,\nu }\) by  when handling this query. In the corresponding \({ \textsc {Sign}}'\) query, algorithm
when handling this query. In the corresponding \({ \textsc {Sign}}'\) query, algorithm  has computed \(a_1\), b and c and has queried the DL oracle with
has computed \(a_1\), b and c and has queried the DL oracle with

(and the appropriate algebraic representation, which we do not repeat here). Note that all four executions of  have been passed the same group elements \(U_i, \ldots , U_{i+\nu -1}\) as input to be used in \({ \textsc {Sign}}\) queries. However, when handling the corresponding \({ \textsc {Sign}}'\) queries,
have been passed the same group elements \(U_i, \ldots , U_{i+\nu -1}\) as input to be used in \({ \textsc {Sign}}\) queries. However, when handling the corresponding \({ \textsc {Sign}}'\) queries,  may have made different queries to the DL oracle in the four executions.Footnote 10
may have made different queries to the DL oracle in the four executions.Footnote 10
Algorithm  initializes a flag \(\mathsf {LinDep}\) representing a bad event and attempts to deduce the discrete logarithm of all challenges which were used in each \({ \textsc {Sign}}\) query in all four executions of
initializes a flag \(\mathsf {LinDep}\) representing a bad event and attempts to deduce the discrete logarithm of all challenges which were used in each \({ \textsc {Sign}}\) query in all four executions of  as follows.
as follows.
For each \({ \textsc {Sign}}'(k,\ldots )\) query with session index \(k\), algorithm  proceeds to build a system of \(\nu \) linear equations with unknowns \(r_1, \ldots , r_\nu \), the discrete logarithms of \(R_{1,1},\dots ,R_{1,\nu }\). Let \(P_k\) be the partition of the four executions of
proceeds to build a system of \(\nu \) linear equations with unknowns \(r_1, \ldots , r_\nu \), the discrete logarithms of \(R_{1,1},\dots ,R_{1,\nu }\). Let \(P_k\) be the partition of the four executions of  such that two executions are in the same component if they were identical up to assignment of the \(T_{\mathrm {non}}\) entry accessed by the \({ \textsc {Sign}}'(k,\ldots )\) query handler when defining
such that two executions are in the same component if they were identical up to assignment of the \(T_{\mathrm {non}}\) entry accessed by the \({ \textsc {Sign}}'(k,\ldots )\) query handler when defining  .Footnote 11 Consider the variables \(b, a_1, c, s_1\) in the \({ \textsc {Sign}}'(k, \ldots )\) query handler within all executions within some component \(\ell \in P_k\). We will show below that all executions in component \(\ell \in P_k\) assign identical values
.Footnote 11 Consider the variables \(b, a_1, c, s_1\) in the \({ \textsc {Sign}}'(k, \ldots )\) query handler within all executions within some component \(\ell \in P_k\). We will show below that all executions in component \(\ell \in P_k\) assign identical values  to these variables. As a consequence, all executions in component \(\ell \) pass identical group elements as inputs to their DL oracles in the \({ \textsc {Sign}}'(k,\ldots )\) query handler (see Eq. (5)). Thus, due to the caching of DL oracle replies in
to these variables. As a consequence, all executions in component \(\ell \) pass identical group elements as inputs to their DL oracles in the \({ \textsc {Sign}}'(k,\ldots )\) query handler (see Eq. (5)). Thus, due to the caching of DL oracle replies in  , algorithm
, algorithm  has used only \(|P_k|\) DL queries to its own DL oracle to answer the DL oracle queries originating by all four executions of
has used only \(|P_k|\) DL queries to its own DL oracle to answer the DL oracle queries originating by all four executions of  . Then
. Then  has a system of \(|P_k|\,\le 4 \le \nu \) linear equations
has a system of \(|P_k|\,\le 4 \le \nu \) linear equations

with unknowns \(r_1, \ldots , r_\nu \). If the values \({b^{(\ell )}}\) for \(\ell \in \{1, \ldots , |P_k|\}\) are not pairwise distinct, then  sets
sets  and returns \(\bot \).
and returns \(\bot \).
Otherwise,  completes the linear system with \(\nu - |P_k|\) remaining DL queries as follows. For each \(\ell \in \{|P_k| + 1, \ldots , \nu \}\), it picks a value \(b^{(\ell )}\) from \(\mathbb {Z}_p\) such that \(b^{(\ell )}\ne b^{(\ell ')}\) for all \(\ell '<\ell \) and obtains the additional equations
completes the linear system with \(\nu - |P_k|\) remaining DL queries as follows. For each \(\ell \in \{|P_k| + 1, \ldots , \nu \}\), it picks a value \(b^{(\ell )}\) from \(\mathbb {Z}_p\) such that \(b^{(\ell )}\ne b^{(\ell ')}\) for all \(\ell '<\ell \) and obtains the additional equations
\(\ell \in \{|P| + 1, \ldots , \nu \}\), computing the algebraic representations of the queried group elements appropriately as  and
and  .
.
The coefficient matrix
of the complete linear system (Eqs. (6) and (7)) is a square Vandermonde matrix with pairwise distinct \(b^{(\ell )}\) values, and thus has full rank \(\nu \). At this stage,  has a system of \(\nu \) linear independent equations with \(\nu \) unknowns. Because the system is consistent by construction, it has a unique solution \(r_1, \ldots , r_\nu \), which is computed and output by
has a system of \(\nu \) linear independent equations with \(\nu \) unknowns. Because the system is consistent by construction, it has a unique solution \(r_1, \ldots , r_\nu \), which is computed and output by  .
.
It remains to show that if for some given \({ \textsc {Sign}}'(k, \ldots )\) query, two executions of  are in the same component of \(P_k\), then
are in the same component of \(P_k\), then
where here and in the following, non-primed and primed terms are the values used in the \({ \textsc {Sign}}'\) query in the respective execution. By definition, the executions were identical up to the assignments of \(T_{\mathrm {non}}(\widetilde{X},(R_1,\dots ,R_{\nu }),m)\) and \(T_{\mathrm {non}}(\widetilde{X}',(R_1',\dots ,R_{\nu }'),m')\), which implies that \(\widetilde{X}=\widetilde{X}'\), \((R_1,\dots ,R_{\nu }) = (R_1',\dots ,R_{\nu }')\), \(m=m'\), and \(T_{\mathrm {non}}(\widetilde{X},(R_1,\dots ,R_{\nu }),m)=T_{\mathrm {non}}(\widetilde{X}',(R_1',\dots ,R_{\nu }'),m')\). The equality \(b=b'\) follows immediately.
To prove \(c=c'\), note that previous equalities imply that \(\prod _{j=1}^\nu R_j^{b^{j-1}} = \prod _{j=1}^\nu (R_j')^{(b')^{j-1}}\), i.e. \(R=R'\). Hence, c and \(c'\) were defined using the same table entry \(T_{\mathrm {sig}}(\widetilde{X},R,m)\) in both executions. If entry \(T_{\mathrm {sig}}(\widetilde{X}, R, m)\) had already been set when \(T_{\mathrm {non}}(\widetilde{X}, (R_1, \ldots , R_\nu ), m)\) was set, then \(c=c'\) due to the executions being identical. Otherwise, if the value \(T_{\mathrm {sig}}(\widetilde{X}, R, m)\) had not already been set when \(T_{\mathrm {non}}(\widetilde{X}, (R_1, \ldots , R_\nu ), m)\) was set, then the internal \(\mathsf {H}_{\mathrm {sig}}\) query in the \(\mathsf {H}_{\mathrm {non}}\) query handler set \(T_{\mathrm {sig}}(\widetilde{X}, R, m)\) exactly when the query \(\mathsf {H}_{\mathrm {non}}(\widetilde{X}, (R_1, \ldots , R_\nu ), m)\) was handled. Since  did not receive a forgery which is invalid due to the values m and L from the forgery having been queried in a \({ \textsc {Sign}}'\) query, the internal \(\mathsf {H}_{\mathrm {sig}}\) query was not the \(\mathsf {H}_{\mathrm {sig}}\) fork point. Therefore, both executions are still identical when \(T_{\mathrm {sig}}(\widetilde{X},R,m)\) is set, which implies that \(c=c'\).
did not receive a forgery which is invalid due to the values m and L from the forgery having been queried in a \({ \textsc {Sign}}'\) query, the internal \(\mathsf {H}_{\mathrm {sig}}\) query was not the \(\mathsf {H}_{\mathrm {sig}}\) fork point. Therefore, both executions are still identical when \(T_{\mathrm {sig}}(\widetilde{X},R,m)\) is set, which implies that \(c=c'\).
To prove \(a_1=a_1'\) we first note that in the first execution, \(\mathsf {H}_{\mathrm {agg}}(L,X^*)\) was set before \(T_{\mathrm {sig}}(\widetilde{X},R,m)\) (as otherwise  would have set
would have set  ), hence before \(T_{\mathrm {non}}(\widetilde{X}, (R_1, \ldots , R_\nu ), m)\) since as proved above \(T_{\mathrm {sig}}(\widetilde{X},R,m)\) was set before or at the same time as \(T_{\mathrm {non}}(\widetilde{X}, (R_1, \ldots , R_\nu ), m)\). Similarly, in the second execution, \(\mathsf {H}_{\mathrm {agg}}(L',X^*)\) was set before \(T_{\mathrm {non}}(\widetilde{X}, (R_1, \ldots , R_\nu ), m)\). Because both executions are identical up to the assignment of \(T_{\mathrm {non}}(\widetilde{X}, (R_1, \ldots , R_\nu ), m)\), \(\mathsf {H}_{\mathrm {agg}}(L,X^*)\) and \(\mathsf {H}_{\mathrm {agg}}(L',X^*)\) were set in both executions. Assume that \(L \ne L'\). Then \(\mathsf {KeyAgg}(L) = \widetilde{X}= \widetilde{X}' =\mathsf {KeyAgg}(L')\), a contradiction since
), hence before \(T_{\mathrm {non}}(\widetilde{X}, (R_1, \ldots , R_\nu ), m)\) since as proved above \(T_{\mathrm {sig}}(\widetilde{X},R,m)\) was set before or at the same time as \(T_{\mathrm {non}}(\widetilde{X}, (R_1, \ldots , R_\nu ), m)\). Similarly, in the second execution, \(\mathsf {H}_{\mathrm {agg}}(L',X^*)\) was set before \(T_{\mathrm {non}}(\widetilde{X}, (R_1, \ldots , R_\nu ), m)\). Because both executions are identical up to the assignment of \(T_{\mathrm {non}}(\widetilde{X}, (R_1, \ldots , R_\nu ), m)\), \(\mathsf {H}_{\mathrm {agg}}(L,X^*)\) and \(\mathsf {H}_{\mathrm {agg}}(L',X^*)\) were set in both executions. Assume that \(L \ne L'\). Then \(\mathsf {KeyAgg}(L) = \widetilde{X}= \widetilde{X}' =\mathsf {KeyAgg}(L')\), a contradiction since  has not set
has not set  in either of the executions. This implies that \(a_1\) and \(a_1'\) were defined using the same table entry \(\mathsf {H}_{\mathrm {agg}}(L,X^*)\) which was set when executions were identical, hence \(a_1=a_1'\).
in either of the executions. This implies that \(a_1\) and \(a_1'\) were defined using the same table entry \(\mathsf {H}_{\mathrm {agg}}(L,X^*)\) which was set when executions were identical, hence \(a_1=a_1'\).
The equality \(s_1=s_1'\) follows from Eq. (5) together with \(b=b'\), \(a_1=a_1'\), and \(c=c'\). This shows the equalities in Eq. (8).
Altogether,  makes |P| DL queries initiated by
makes |P| DL queries initiated by  (as in Eq. (6)) and \(\nu -|P|\) additional DL queries (as in Eq. (7)) per initiated signing session. Thus, the total number of DL queries is exactly \(\nu q_s\).
(as in Eq. (6)) and \(\nu -|P|\) additional DL queries (as in Eq. (7)) per initiated signing session. Thus, the total number of DL queries is exactly \(\nu q_s\).
Neglecting the time needed to compute discrete logarithms and solve linear equation systems, the running time \(t'\) of  is twice the running time of
is twice the running time of  , which itself is twice the running time of
, which itself is twice the running time of  . The running time of
. The running time of  is the running time t of
is the running time t of  plus the time needed to maintain tables \(T_{\mathrm {agg}}\), \(T_{\mathrm {non}}\), and \(T_{\mathrm {sig}}\) (we assume each assignment takes unit time) and answer signing and hash queries. The sizes of \(T_{\mathrm {agg}}\), \(T_{\mathrm {non}}\), and \(T_{\mathrm {sig}}\) are at most qN, q, and q respectively. Answering signing queries is dominated by the time needed to compute the aggregate key as well as the honest signer’s effective nonce, which is at most \(Nt_\mathrm{exp}\) and \((\nu -1) t_\mathrm{exp}\) respectively. Answering hash queries is dominated by the time to compute the aggregate nonce which is at most \((\nu -1) t_\mathrm{exp}\). Therefore, \(t'=4(t+q(N+2\nu -2))t_\mathrm{exp}+O(qN)\).
plus the time needed to maintain tables \(T_{\mathrm {agg}}\), \(T_{\mathrm {non}}\), and \(T_{\mathrm {sig}}\) (we assume each assignment takes unit time) and answer signing and hash queries. The sizes of \(T_{\mathrm {agg}}\), \(T_{\mathrm {non}}\), and \(T_{\mathrm {sig}}\) are at most qN, q, and q respectively. Answering signing queries is dominated by the time needed to compute the aggregate key as well as the honest signer’s effective nonce, which is at most \(Nt_\mathrm{exp}\) and \((\nu -1) t_\mathrm{exp}\) respectively. Answering hash queries is dominated by the time to compute the aggregate nonce which is at most \((\nu -1) t_\mathrm{exp}\). Therefore, \(t'=4(t+q(N+2\nu -2))t_\mathrm{exp}+O(qN)\).
Clearly,  is successful if
is successful if  returns a non-\(\bot \) answer and \(\mathsf {LinDep}\) is not set to \(\mathtt {true}\). \(\mathsf {LinDep}\) is set to \(\mathtt {true}\) if, in the linear system corresponding to some \({ \textsc {Sign}}(k,\dots )\) query, there are two identical values \(b^{(\ell )} = b^{(\ell ')}\) in two different execution components \(\ell , \ell ' \le |P_k|\). By construction, \(b^{(\ell )}\) and \(b^{(\ell ')}\) were assigned to two of the scalars \( h_{\mathrm {non},1}, h_{\mathrm {non},1}', h_{\mathrm {non},1}'', h_{\mathrm {non},1}''', \ldots , h_{\mathrm {non},q}, h_{\mathrm {non},q}', h_{\mathrm {non},q}'', h_{\mathrm {non},q}'''. \) Since these 4q scalars are drawn from \(\mathbb {Z}_p\) with
returns a non-\(\bot \) answer and \(\mathsf {LinDep}\) is not set to \(\mathtt {true}\). \(\mathsf {LinDep}\) is set to \(\mathtt {true}\) if, in the linear system corresponding to some \({ \textsc {Sign}}(k,\dots )\) query, there are two identical values \(b^{(\ell )} = b^{(\ell ')}\) in two different execution components \(\ell , \ell ' \le |P_k|\). By construction, \(b^{(\ell )}\) and \(b^{(\ell ')}\) were assigned to two of the scalars \( h_{\mathrm {non},1}, h_{\mathrm {non},1}', h_{\mathrm {non},1}'', h_{\mathrm {non},1}''', \ldots , h_{\mathrm {non},q}, h_{\mathrm {non},q}', h_{\mathrm {non},q}'', h_{\mathrm {non},q}'''. \) Since these 4q scalars are drawn from \(\mathbb {Z}_p\) with  , we have
, we have  Let
Let  . By Lemmas 1 and 3, the success probability of
. By Lemmas 1 and 3, the success probability of  is at least
is at least

Altogether, the advantage of  is at least
is at least

\(\square \)
Notes
- 1.
Since we do not impose any constraint on the key setup, the adversary can choose corrupted public keys arbitrarily and duplicate public keys can appear in L.
- 2.
- 3.
We refer the interested reader to the full version [27] for a high-level explanation of why the meta-reduction cannot be adapted to work with our scheme.
- 4.
Observe that \(\mathsf {InsecureMuSig} \) is identical to an imaginary \(\mathsf {MuSig2} \) with a just a single nonce, i.e., \(\nu = 1\).
- 5.
- 6.
- 7.
In fact, it is easy to see that the adversary can only guess the value of the aggregate public key \(\widetilde{X}\) corresponding to L at random before making the relevant queries \(\mathsf {H}_{\mathrm {agg}}(L,X_i)\) for \(X_i\in L\), so that the query \(\mathsf {H}_{\mathrm {sig}}(\widetilde{X},R,m)\) can only come after the relevant queries \(\mathsf {H}_{\mathrm {agg}}(L,X_i)\) except with negligible probability.
- 8.
This computation can be saved by caching the result when handling the internal \(\mathsf {H}_{\mathrm {non}}\) query.
- 9.
Theorem 1 states the security of \(\mathsf {MuSig2} \) only for \(\nu =4\), because there is no reason to use more than four nonces in practice. The proof works for any \(\nu \ge 4\).
- 10.
For example, the adversary may have replied with different L, m or R values in different executions, or algorithm
 may have received different “\(h_{\mathrm {non}}\)” values.
may have received different “\(h_{\mathrm {non}}\)” values. - 11.
For example, all four executions (as visualized in Fig. 4) are in the same component if the corresponding \(T_{\mathrm {non}}\) value was set before the \(\mathsf {H}_{\mathrm {agg}}\) fork point, and two executions in the same branch of the \(\mathsf {H}_{\mathrm {agg}}\) fork are in the same component if the \(T_{\mathrm {non}}\) value was set before the \(\mathsf {H}_{\mathrm {sig}}\) fork point.
References
Alper, H.K., Burdges, J.: Two-round trip schnorr multi-signatures via delinearized witnesses. In: CRYPTO 2021, 2021. https://eprint.iacr.org/2020/1245
Bagherzandi, A., Cheon, J.H., Jarecki, S.: Multisignatures secure under the discrete logarithm assumption and a generalized forking lemma. In: Ning, P., Syverson, P.F., Jha, S. (eds.) ACM CCS 2008, pp. 449–458. ACM Press, October 2008. https://doi.org/10.1145/1455770.1455827
Bellare, M., Namprempre, C., Pointcheval, D., Semanko, M.: The one-more-RSA-inversion problems and the security of Chaum’s blind signature scheme. J. Cryptol. 16(3), 185–215 (2003). https://doi.org/10.1007/s00145-002-0120-1
Bellare, M., Neven, G.: Multi-signatures in the plain public-key model and a general forking lemma. In: Juels, A., Wright, R.N., De Capitani di Vimercati, S. (eds.) ACM CCS 2006, pp. 390–399. ACM Press, October/November 2006. https://doi.org/10.1145/1180405.1180453
Bellare, M., Palacio, A.: GQ and schnorr identification schemes: proofs of security against impersonation under active and concurrent attacks. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 162–177. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_11
Bellare, M., Shoup, S.: Two-tier signatures, strongly unforgeable signatures, and Fiat-Shamir without Random Oracles. In: Okamoto, T., Wang, X. (eds.) PKC 2007. LNCS, vol. 4450, pp. 201–216. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-71677-8_14
Benhamouda, F., Lepoint, T., Loss, J., Orrù, M., Raykova, M.: On the (in)security of ROS. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021. LNCS, vol. 12696, pp. 33–53. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77870-5_2
Boldyreva, A.: Threshold signatures, multisignatures and blind signatures based on the gap-Diffie-Hellman-group signature scheme. In: Desmedt, Y.G. (ed.) PKC 2003. LNCS, vol. 2567, pp. 31–46. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36288-6_3
Boneh, D., Drijvers, M., Neven, G.: Compact multi-signatures for smaller blockchains. In: Peyrin, T., Galbraith, S. (eds.) ASIACRYPT 2018. LNCS, vol. 11273, pp. 435–464. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03329-3_15
Chaum, D., Pedersen, T.P.: Wallet databases with observers. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 89–105. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-48071-4_7
Drijvers, M., et al.: On the security of two-round multi-signatures. In: 2019 IEEE Symposium on Security and Privacy, pp. 1084–1101. IEEE Computer Society Press, May 2019. https://doi.org/10.1109/SP.2019.00050
Fuchsbauer, G., Kiltz, E., Loss, J.: The algebraic group model and its applications. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 33–62. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_2
Fuchsbauer, G., Plouviez, A., Seurin, Y.: Blind schnorr signatures and signed ElGamal encryption in the algebraic group model. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12106, pp. 63–95. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45724-2_3
Gentry, C., Wichs, D.: Separating succinct non-interactive arguments from all falsifiable assumptions. In: Fortnow, L., Vadhan, S.P. (eds.) 43rd ACM STOC, pp. 99–108. ACM Press, June 2011. https://doi.org/10.1145/1993636.1993651
Goldwasser, S., Kalai, Y.T.: Cryptographic assumptions: A position paper. Cryptology ePrint Archive, Report 2015/907 (2015). https://eprint.iacr.org/2015/907
Horster, P., Michels, M., Petersen, H.: Meta-multisignature schemes based on the discrete logarithm problem. In: IFIP/Sec ’95, IFIP Advances in Information and Communication Technology, pp. 128–142. Springer (1995)
Itakura, K., Nakamura, K.: A public-key cryptosystem suitable for digital multisignatures. NEC Res. Dev. 71, 1–8 (1983)
Komlo, C., Goldberg, I.: FROST: flexible round-optimized schnorr threshold signatures. In: SAC 2020, 2020. To be published. https://eprint.iacr.org/2020/852
Langford, S.K.: Weaknesses in some threshold cryptosystems. In: Koblitz, N. (ed.) CRYPTO 1996. LNCS, vol. 1109, pp. 74–82. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68697-5_6
Ma, C., Weng, J., Li, Y., Deng, R.H.: Efficient discrete logarithm based multi-signature scheme in the plain public key model. Des. Codes Cryptogr. 54(2), 121–133 (2010). https://doi.org/10.1007/s10623-009-9313-z
Maxwell, G., Poelstra, A., Seurin, Y., Wuille, P.: Simple Schnorr multi-signatures with applications to Bitcoin. IACR Cryptology ePrint Archive, 2018/068, Version 20180118:124757, 2018. Preliminary obsolete version of [22]. https://eprint.iacr.org/2018/068/20180118:124757
Maxwell, G., Poelstra, A., Seurin, Y., Wuille, P.: Simple Schnorr multi-signatures with applications to Bitcoin. Des. Codes Cryptogr. 87(9), 2139–2164 (2019). https://eprint.iacr.org/2018/068.pdf
Micali, S., Ohta, K., Reyzin, L.: Accountable-subgroup multisignatures: extended abstract. In: Reiter, M.K., Samarati, P., (eds.) ACM CCS 2001, pp. 245–254. ACM Press, November 2001. https://doi.org/10.1145/501983.502017
Michels, M., Horster, P.: On the risk of disruption in several multiparty signature schemes. In: Kim, K., Matsumoto, T. (eds.) ASIACRYPT 1996. LNCS, vol. 1163, pp. 334–345. Springer, Heidelberg (1996). https://doi.org/10.1007/BFb0034859
Naor, M.: On cryptographic assumptions and challenges. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 96–109. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_6
Nick, J.: Insecure shortcuts in MuSig (2019). https://medium.com/blockstream/insecure-shortcuts-in-musig-2ad0d38a97da
Nick, J., Ruffing, T., Seurin, Y.: MuSig2: simple two-round schnorr multi-signatures. Cryptology ePrint Archive, Report 2020/1261 (2020). https://eprint.iacr.org/2020/1261
Nick, J., Ruffing, T., Seurin, Y., Wuille, P.: MuSig-DN: schnorr multi-signatures with verifiably deterministic nonces. In: Ligatti, J., Ou, X., Katz, J., Vigna, G., (eds.) ACM CCS 20, pp. 1717–1731. ACM Press, November 2020. https://doi.org/10.1145/3372297.3417236
Nicolosi, A., Krohn, M.N., Dodis, Y., Mazières, D.: Proactive two-party signatures for user authentication. In: NDSS 2003. The Internet Society, February 2003. https://www.ndss-symposium.org/ndss2003/proactive-two-party-signatures-user-authentication/
Pointcheval, D., Stern, J.: Security arguments for digital signatures and blind signatures. J. Cryptol. 13(3), 361–396 (2000). https://doi.org/10.1007/s001450010003
Ristenpart, T., Yilek, S.: The power of proofs-of-possession: securing multiparty signatures against rogue-key attacks. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 228–245. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-72540-4_13
Schnorr, C.-P.: Efficient signature generation by smart cards. J. Cryptol. 4(3), 161–174 (1991). https://doi.org/10.1007/BF00196725
Schnorr, C.P.: Security of blind discrete log signatures against interactive attacks. In: Qing, S., Okamoto, T., Zhou, J. (eds.) ICICS 2001. LNCS, vol. 2229, pp. 1–12. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45600-7_1
Shoup, V.: Lower bounds for discrete logarithms and related problems. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 256–266. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-69053-0_18
Stinson, D.R., Strobl, R.: Provably secure distributed schnorr signatures and a (t, n) threshold scheme for implicit certificates. In: Varadharajan, V., Mu, Y. (eds.) ACISP 2001. LNCS, vol. 2119, pp. 417–434. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-47719-5_33
Syta, E., et al.: Keeping authorities “honest or bust” with decentralized witness cosigning. In: 2016 IEEE Symposium on Security and Privacy, pages 526–545. IEEE Computer Society Press, May 2016. https://doi.org/10.1109/SP.2016.38
Wagner, D.: A generalized birthday problem. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 288–304. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_19
Wuille, P., Nick, J., Ruffing, T.: Schnorr signatures for secp256k1. Bitcoin Improvement Proposal 340 (2020). https://github.com/bitcoin/bips/blob/master/bip-0340.mediawiki
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 International Association for Cryptologic Research
About this paper
Cite this paper
Nick, J., Ruffing, T., Seurin, Y. (2021). MuSig2: Simple Two-Round Schnorr Multi-signatures. In: Malkin, T., Peikert, C. (eds) Advances in Cryptology – CRYPTO 2021. CRYPTO 2021. Lecture Notes in Computer Science(), vol 12825. Springer, Cham. https://doi.org/10.1007/978-3-030-84242-0_8
Download citation
DOI: https://doi.org/10.1007/978-3-030-84242-0_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-84241-3
Online ISBN: 978-3-030-84242-0
eBook Packages: Computer ScienceComputer Science (R0)






 OMDL problem. The changes from the OMDL problem to the
OMDL problem. The changes from the OMDL problem to the
 OMDL problem are
OMDL problem are
 .
.

 built from
built from  .
.
 increments
increments  for all
for all  . Then,
. Then,  computes the aggregate key corresponding to L, namely
computes the aggregate key corresponding to L, namely  where
where  and
and  . If
. If  sets
sets  . If
. If  sets
sets  , otherwise it sets
, otherwise it sets  . Finally, it returns
. Finally, it returns  increments
increments  . Then
. Then  sets
sets  and computes
and computes  . If
. If  makes an internal query to
makes an internal query to  increments
increments  . Then, it returns
. Then, it returns  increments
increments  and sends
and sends  to the adversary.
to the adversary. : If
: If  removes k from
removes k from  and
and  . Let
. Let  for each
for each  . If
. If  makes an internal query to
makes an internal query to  , computes
, computes  , and sets
, and sets  . Then
. Then  sets
sets  . If
. If  makes an internal query to
makes an internal query to  , aggregates the nonces as
, aggregates the nonces as 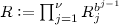 ,
, , where
, where  computes the honest signer’s effective nonce
computes the honest signer’s effective nonce  . It sets
. It sets and
and 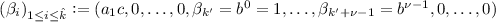 for
for  , and obtains
, and obtains  by querying the DL oracle. Finally,
by querying the DL oracle. Finally,  returns
returns 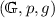 ,
,  ,
,  may have received different “
may have received different “