Inertial Morphing as a Novel Concept in Attitude Control and Design of Variable Agility Acrobatic Autonomous Spacecraft

Abstract

This book chapter presents a systematic overview of the novel concept of “inertial morphing (IM)”, first introduced by the authors in 2017 and further expanded in their following publications. It involves deliberate changes of the inertial properties of the system for control of the attitude of the spacecraft.

The “inertial morphing” control concept is essentially based on the realisation that the spinning spacecraft can be seen and utilised as gyroscope itself, instead of utilisation of complex, heavy and energy-consuming gyroscopic devices on-board. Utilisation of the concept, therefore, enables reduction of the weight and dimensions of the conventional systems.

It has been discovered and demonstrated via versatile numerical simulations that IM can be used to enable spacecraft with wide range of attitude control capabilities (e.g. 90° and 180° inversions, de-tumbling and controlled agility acrobatic manoeuvrings). Moreover, it has been also discovered that control of very complex manoeuvres can be achieved with a few only controlled inertial morphing actions (two and three morphings correspondingly for 180° and 90° inversions).

The general control methods presented in this chapter are based on the geometric interpretation of the arbitrary 3D rotational motion of the spacecraft, using angular momentum sphere and kinetic energy ellipsoid in the non-dimensional coordinates. The key control strategies involve combination of installing the angular momentum vector into transition polhodes and installing into transition separatrices.

Reduction in weight and dimensions, simplicity of the implementation of the inertial morphing and simplicity of the attitude control, requiring two or three discrete control actions, make this technology attractive for a variety of applications, especially involving autonomous spacecraft.

One of the remarkable features of the IM control is the ability to access a range of solutions between agile (fast) and prolonged (slow) types and select the most appropriate speed of the undertaking attitude manoeuvre. This added variable agility may be useful, for example, to perform for autonomous spacecraft surveillance, landing or manoeuvring. In particular, the IM may foster effective protection of the spacecraft from hostile environments (asteroids, radiation, etc.), as the spacecraft would be able to quickly expose the most protective surfaces to the sources of danger, hence prolonging survivability of the system. In the other cases of capturing the tumbling spacecraft, the prolonged mode can be selected, allowing more time for the capture and handling.

For the practical implementation of the IM concept, this book chapter also presents a range of conceptual mechanical designs. As Euler’s equation for the rotational motion of the rigid bodies paved the way for the development of the theory of gyroscopes and design of various gyroscopic systems, the paradigm of “inertial morphing” may prompt development of new generation of the acrobatic spacecraft with significantly reduced weight and dimensions, reduced cost and enhanced operational capabilities. It may be also possible to design new classes of gyroscopes, possessing an added-on sense of time, which is in contrast to the classical gyroscopes that only possess a sense of orientation.

With a wide spectrum of the presented examples, related to the application of a novel design concept of “inertial morphing”, it is believed that presented concept, modelling and simulation of the spinning systems and attitude control method of the spinning systems will be useful not only for the specialists but for a very wide audience, including engineers, scientists, students and enthusiasts of science and space technology.

1 Introduction

There are almost 4900 satellites orbiting the Earth [1], and this number will be non-linearly increasing with time. Continuous control of the attitude is a vital function for spacecraft vehicles. Indeed, communication and observation satellites require directional pointing of their antennae and equipment, for using a single thruster for breaking (used initially for boost) may require 180° attitude reorientation of the spacecraft body (“inversion”) to apply thruster force against the motion of the spacecraft, etc. Therefore, attitude dynamics, guidance, navigation and control are the modern research disciplines, requiring new and the most innovative solutions for making new challenging space missions possible and stimulating attention of space engineering community.

Continuous development of new technologies (including miniaturisation of electronic hardware, introduction of new materials) allows significant reduction of the mass of satellites [2]. However, this reduction is in conflict with heavy mass and complexity of the modern attitude control systems, employing gyroscopes. An attractive alternative of controlling spacecraft without employment of the traditional gyroscopic devices has been proposed by the authors. It involves deliberate changes of the inertial properties of the system, called “inertial morphings (IM)”, used for control of the attitude of the spacecraft. “Inertial morphing” control concept is essentially based on realisation that the spinning spacecraft can be seen and utilised as gyroscope itself, instead of utilisation of complex, heavy and energy-consuming gyroscopic devices on-board. It has been recently discovered and demonstrated via versatile numerical simulations that IM can be used to enable spacecraft with wide range of attitude control capabilities (e.g. 90° and 180° inversions, de-tumbling and controlled agility acrobatic manoeuvrings). Moreover, it has been also discovered that control of very complex manoeuvres can be achieved with a few only control inertial morphing actions (two and three morphings correspondingly for 180° and 90° inversions). This book chapter aims to present a systematic overview of the concept of the “inertial morphing”, firstly introduced by the authors in 2017 [3] and further expanded in [4,5,6,7,8,9,10].

The novel concept of IM enables design and construction of the inertially morphed spacecraft, possessing acrobatic capabilities, and may allow design of new class of gyroscopic systems with a “sense” of time.

2 Historical Background

2.1 Discovery of the “Garriott’s-Dzhanibekov’s Effect” in Space

Development of the “inertial morphing” concept was prompted by the flipping motion of the rigid bodies, observed and demonstrated in space.

During his fifth space flight, on June 25, 1985, Vladimir Aleksandrovich Dzhanibekov discovered a spectacular phenomenon: a spinning wing nut in stable flight suddenly, without apparent reasons, changed its orientation by 180° and continued its flight backwards, simultaneously changing its direction of rotation to the opposite. The pattern of the observed as unprovoked 3D flipping motion of the rigid body, which is initially provided with only a one-axis spin, repeated itself in a periodic sequence. This phenomenon was initially widely referred to as Dzhanibekov’s effect [11–12]. Vladimir Dzhanibekov himself explained his discovery in various lectures, TV programs and interviews (see Fig. 5.1a).

Fig. 5.1

(a) Vladimir A. Dzhanibekov, interview at the “Secret Signs” TV program, explaining flipping of the wing nut, observed in 1985 [11–12]; (b) Owen K. Garriott, demonstration on-board of “Skylab 3” of the flipping instrument, spun about its intermediate axis, observed in 1973 [13]

Performing detailed literature search, we were able to find even earlier demonstrations in space of the flipping motion of the spinning rigid body, dated by 1973. Indeed, interestingly, an experiment with box-shaped space instrument by famous US scientist-astronaut Owen Kay Garriott on-board Skylab 3 in 1973, 12 years before Dzhanibekov’s experiments, demonstrated the flipping motion of the rigid body [13], initiated on purpose by providing it manually with initial energetic spin about the intermediate axis. This immediately resulted in the periodic flipping motion of the instrument in weightless environment (see Fig. 5.1b). This earlier reference suggests that the use of the “Garriott’s-Dzhanibekov’s effect” in the future would be more precise name to the observed flipping phenomenon. In both cases, spin to the rigid body was applied in zero gravity by providing a torque impulse about the intermediate axis of inertia of the body, which instantly results in the peculiar rotational motion of the boxed object about this axis with clearly observed periodic flipping about this axis.

Similar experiments have subsequently been run on the International Space Station (ISS), including 30th, 34th and 38th NASA missions. One of the well-known spectacular demonstration involved unscrewed from the base T-handle [14]. These experiments in space clearly demonstrated that a spinning object always rotates in the same direction relative to the observation camera (fixed to the inertial coordinates frame): that means that in the reference frame of the rotating handle, the direction of rotation flips changes each time its orientation flips.

Garriott’s-Dzhanibekov’s effect has prompted development of theories suggesting that the Earth, similar to the wing nut, performs periodic flips estimated to be at the order of 12,000 years. Evidence in support of this theory includes changes in the Earth’s magnetic field [15]. These theories are still debated in the scientific programs [16].

Surprisingly, the Garriott’s-Dzhanibekov effect or the “tennis racket theorem” as it is sometimes referred to [17] can be explained by Euler’s equations, published in their canonical form in 1758 [18]. During the mid-nineteenth century, Louis Poinsot, a French geometer, developed a geometric interpretation of the physics of rotating bodies that provided a much-welcomed visual counterpart to Euler’s algebraic equations [19]. Interestingly, Euler’s equations paved the theoretical ground to many scientific manifestations, including Coriolis forces, predicted by Euler but interpreted to the world many years later by French scientist Gaspard-Gustave de Coriolis in 1835. So, heritage by Euler often required time for his ideas to be adopted by scientists. In case of the Euler’s equations, it took more than 250 years for scientists to relate the beautiful phenomenon of the flipping motion to these equations. The phenomenon had been conceptually predicted in 1971 by Beachley [20]; however, his work was unnoticed for a very long time and has been left unnoticed, and an in-depth explanation of the phenomenon has only been very recently presented in journal publication [21]. During the last 5 years, interest in the phenomenon has been exponentially increasing. One of the recent interesting references on the topic is authored by Cleve Moler, the founder of Mathworks Company (developing world-famous MATLAB and SIMULINK computer simulation environments), who has been also fascinated with this phenomenon and has a dedicated publication [22].

Derek A. Muller, an Australian-born Canadian science communicator, filmmaker, television personality and inventor, founder of the popular “Veritasium” channel on YouTube, on September 20, 2019, presented a special program [16] dedicated to “Dzhanibekov effect” or “tennis racket theorem”, which during the 6 following months attracted almost 7.5 million views, showing an unprecedented interest not only from the scientists and engineers but from the broad community in the discussed topic and its applications.

2.2 Demonstrations of the “Garriott’s-Dzhanibekov’s Effect” on-Board of the ISS

Due to its simplicity and spectacular nature, the Garriott’s-Dzhanibekov’s effect has become one of the most popular educational and scientific experiments on-board of the International Space Station. It has been reproduced with various rigid-body objects and even liquids. Various videos on these experiments, available in the media and on YouTube, are excellent educational resources.

An amazing visual demonstration in space of the “Garriott’s-Dzhanibekov’s effect” or “tennis racket theorem” was performed in 2008 by Richard Allen Garriott de Cayeux [23], a pioneer in commercial space travel and a son of the US scientist-astronaut Owen Kay Garriott. Using nothing more complex than a deck of cards, Richard Allen Garriott demonstrated both stable rotation and tumbling rotation and explained why you can easily spin a rectangular box around two axes but it quickly wobbles out of control if you try to spin it along its intermediate axis (see Fig. 5.2a).

Fig. 5.2

Demonstrations of the “Garriott’s-Dzhanibekov’s effect” on-board of the ISS: (a) Richard Garriott; (b) Dan Burbank and Anton Shkaplerov, 30th expedition to ISS, 2011; (c) Kevin Ford (NASA), 34th expedition to ISS, 2013’ (d) Koichi Wakata (JAXA), 38th expedition, 2014; (e–f) “Dancing T-handle” on board of the ISS

Influence of the shape of the rigid bodies, thus mass distribution in various rigid bodies, including cylinders, cubes and right rectangular prisms, was demonstrated on-board of the ISS by Dan Burbank and Anton Shkaplerov (see Fig. 5.2b), members of the 30th expedition [24].

American astronaut Kevin Ford (NASA) (34th expedition) [25] (see Fig. 5.2c) and Japanese astronaut Koichi Wakata (JAXA) (38th expedition) [26] (see Fig. 5.2d) experimented on-board of the ISS with nothing more complex that pliers. They used this adjustable geometry tool as an object, capable of intriguing spinning, flipping and tumbling in zero gravity.

One of the most fascinating movies is a continuous short-period flipping of the T-handle on-board of the ISS, fairly called as “dancing T-handle” [14] (see Fig. 5.2e–f). This is a wonderful demonstration of the “Garriott’s-Dzhanibekov’s effect”, which very convincingly illustrates instability of rotation of the rigid body with distinct principal moments of inertia, if the main spin is provided about its principal axis, associated with intermediate moment of inertia.

All these and other demonstrations can be explained with famous Euler’s equation.

2.3 Leonard Euler and His Famous Equations for the Rigid-Body Dynamics

Leonhard Euler (April 15, 1707–Sept. 18, 1783) was a famous Swiss physicist and mathematician (the most eminent of the eighteenth century and one of the greatest in history), who made key contributions to various fields of mathematics and mechanics, leaving long-lasting heritage of more than 500 books and papers (His portrait is presented in Fig. 5.3a.). It has been computed that his publications during his working life averaged about 800 pages a year.

Fig. 5.3

Leonard Euler and his equations for the rigid-body dynamics: (a) Leonard Euler’s portrait from the University of Tartu collection [29]; (b) the title of the historic Leonard Euler’s work [18], dated 1758; (c) Euler’s equations as they appeared in the original L. Euler’s work [30]

His “Euler’s identity” is considered an example of mathematical beauty:

$$ {e}^{i\pi}+1=0 $$

(5.1)

called “the most remarkable formula in mathematics” by Richard P. Feynman [27], for its single uses of the notions of addition, multiplication, exponentiation and equality and the single uses of the important constants 0, 1, e, i and π.

In 1988, readers of the Mathematical Intelligencer voted it “The Most Beautiful Mathematical Formula Ever”. In total, Euler was responsible for three of the top 5 formulae in that poll [28].

His interests are amazingly versatile. Even when dealing with music, Euler’s approach is mainly mathematical. His writings on music are not particularly numerous (a few 100 pages, in his total production of about 30,000 pages), but they reflect an early preoccupation and one that did not leave him throughout his life.

Among numerous Euler’s works, he developed rigid-body dynamics; very influential publication has a very special place in history. It presented Euler’s equations for the dynamics of a rigid body, widely used in modern engineering and science.

Being always fascinated with Euler’s scientific work and heritage, the authors were delighted to find in the Euler’s archive his original work. It is with greatest pleasure and a profound sense of tribute to Great Euler that we are reproducing in Fig. 5.3a Euler’s portrait from the University of Tartu collection [29] and in Fig. 5.3b the title of the Euler’s publication, available from the Euler’s archive, and in Fig. 5.3c we show the famous Euler’s equations, exactly as they appeared in Euler’s original work [30].

In modern language, the Euler’s equations in Fig. 5.3c can be written as follows:

$$ \left\{\begin{array}{c}\sum {N}_x={I}_{xx}\;{\dot{\omega}}_x+\left({I}_{zz}-{I}_{yy}\right)\;{\omega}_y{\omega}_z\ \\ {}\sum {N}_y={I}_{yy}\;{\dot{\omega}}_y+\left({I}_{xx}-{I}_{zz}\right)\;{\omega}_z{\omega}_x\\ {}\sum {N}_z={I}_{zz}\;{\dot{\omega}}_z+\left({I}_{yy}-{I}_{xx}\right)\;{\omega}_x{\omega}_y\end{array}\right. $$

(5.2)

where x, y, z are the principal axes of inertia fixed to the body; the components of angular velocity in this system are ω = (ω _x, ω _y, ω _z); the torque is N = (N _x, N _y, N _z); and the diagonal elements of the inertia tensor are I _xx, I _yy and I _zz.

Equations (5.2) are known as “Euler’s equations” for a rigid body. They are referred to as equations in principal inertia axes, with the angular velocity components in terms of the angles α, β, γ, which are the angles subtended by the rotation axes with the principal ones fixed in the body. It could be said that these are the Euler angles, although actually they are usually defined by applying the rotation operator to the axes fixed on the body, so that each angle is related to the angular velocities of rotation known as precession, nutation and spin.

3 Numerical Modelling and Simulation of the “Garriott’s-Dzhanibekov’s Effect”

3.1 Equations of Motion

Euler’s Eq. (5.2), in the general case, can be applied for moments summed about any point P, where P is a point on the rigid body that is attached to a fixed pivot in the inertial reference system. However, in this case the inertia properties should be calculated relative to the point P.

In this work, we will apply the Euler’s equations for moments summed about the centre of mass G of the rigid body, free from any external torques (N _x = N _y = N _z = 0), and in the further notations, we will imply that I _xx, I _yy and I _zz are principal moments of inertia of the body with respect to the G (which, for brevity, are often denoted as I _x, I _y and I _z):

$$ \left\{\begin{array}{c}{I}_{xx}\;{\dot{\omega}}_x-\left({I}_{yy}-{I}_{zz}\right)\;{\omega}_y\;{\omega}_z=0\\ {}{I}_{yy}\;{\dot{\omega}}_y-\left({I}_{zz}-{I}_{xx}\right)\;{\omega}_z\;{\omega}_x=0\\ {}{I}_{zz}\;{\dot{\omega}}_z-\left({I}_{xx}-{I}_{yy}\right)\;{\omega}_x{\omega}_y=0\end{array}\right. $$

(5.3)

The matrix form of the above is:

$$ \left[\begin{array}{ccc}{I}_{xx}& 0& 0\\ {}0& {I}_{yy}& 0\\ {}0& 0& {I}_{zz}\end{array}\right]\left\{\begin{array}{c}{\dot{\omega}}_x\\ {}{\dot{\omega}}_y\\ {}{\dot{\omega}}_z\end{array}\right\}=\left\{\begin{array}{c}\left({I}_{yy}-{I}_{zz}\right)\;{\omega}_y\;{\omega}_z\\ {}\left({I}_{zz}-{I}_{xx}\right)\;{\omega}_z\;{\omega}_x\\ {}\left({I}_{xx}-{I}_{yy}\right)\;{\omega}_x\;{\omega}_y\end{array}\right\} $$

(5.4)

In order to be able to describe instantaneous orientation of a rigid body with respect to a fixed coordinate system, we will use the angles ψ, θ and ϕ, the 3-1-3 Euler angles [31]:

$$ \left\{\begin{array}{c}{\omega}_x\kern0.5em =\dot{\psi}\;\sin \theta\;\sin \phi +\dot{\theta}\;\cos \phi \\ {}{\omega}_y\kern0.5em =\dot{\psi}\;\sin \theta\;\cos \phi -\dot{\theta}\;\sin \phi \\ {}{\omega}_z\kern0.5em =\kern0.5em \dot{\psi}\;\cos \theta +\dot{\phi}\kern4.5em \end{array}\right. $$

(5.5)

which can also be written in the matrix form:

$$ \left[\begin{array}{ccc}\sin \theta\;\sin \phi & \kern1em \cos \phi & 0\\ {}\sin \theta\;\cos \phi & -\sin \phi & 0\\ {}\cos \theta & 0& 1\end{array}\right]\left\{\begin{array}{c}\dot{\psi}\\ {}\dot{\theta}\\ {}\dot{\phi}\end{array}\right\}=\left\{\begin{array}{c}{\omega}_x\\ {}{\omega}_y\\ {}{\omega}_z\end{array}\right\} $$

(5.6)

For solving the rigid-body dynamics problems, using numerical methods, we combine matrix Eqs. (5.4) and (5.6) into a single equation:

$$ \left[\begin{array}{cccccc}{I}_{xx}& 0& 0& 0& 0& 0\\ {}0& {I}_{yy}& 0& 0& 0& 0\\ {}0& 0& {I}_{zz}& 0& 0& 0\\ {}0& 0& 0& \sin \theta\;\sin \phi & \cos \phi & 0\\ {}0& 0& 0& \sin \theta\;\cos \phi & -\sin \phi & 0\\ {}0& 0& 0& \cos \theta & 0& 1\end{array}\right]\left\{\begin{array}{c}{\dot{\omega}}_x\\ {}{\dot{\omega}}_y\\ {}{\dot{\omega}}_z\\ {}\dot{\psi}\\ {}\dot{\theta}\\ {}\dot{\phi}\end{array}\right\}=\left\{\begin{array}{c}\left({I}_{yy}-{I}_{zz}\right)\;{\omega}_y{\omega}_z\\ {}\left({I}_{zz}-{I}_{xx}\right)\;{\omega}_z{\omega}_x\\ {}\left({I}_{xx}-{I}_{yy}\right)\;{\omega}_x{\omega}_y\\ {}{\omega}_x\\ {}{\omega}_y\\ {}{\omega}_z\end{array}\right\} $$

(5.7)

This matrix equation can be solved directly, or task for more robust solution can be reformulated in terms of quaternions.

3.2 Programming Considerations

Ordinary differential equations can be efficiently solved using Runge-Kutta methods.

MATLAB^® has a set of specialised procedures, including ode45, ode23, ode113, ode15s, ode23s, ode23t, ode23tb, ode15i, to deal with various tasks, for example, described by the ordinary differential equation in the classical form:

$$ \left\{\overset{.}{\mathbf{x}}\right\}=\left\{f\left(t,\mathbf{x}\right)\right\} $$

(5.8)

There is also a very useful option enabling solution of the problems, involving the so-called “mass” matrix M:

$$ \left[M\left(t,\mathbf{x}\right)\right]\left\{\overset{.}{\mathbf{x}}\right\}=\left\{f\left(t,\mathbf{x}\right)\right\} $$

(5.9)

This option, accessible via the odeset, in some cases can improve efficiency and can also handle cases when the mass matrix is singular (non-invertible). As it can be seen, our matrix Eq. (5.7) corresponds to the format given with Eq. (5.9); therefore, we use MATLAB^® ode procedure in conjunction with the “mass matrix” option to simulate dynamic behaviour of the simulated spacecraft models.

3.3 Non-dimensional Formulation of the Equations

For the main derivations in this chapter, it will be typically assumed that the system has three distinct principal moments of inertia, which are arranged in the following order: I _xx < I _yy < I _zz. For more generic formulations, two non-dimensional parameters, η and ξ, both restricted in their values within the range between 0 and 1 can be introduced:

$$ \eta =\frac{I_{xx}}{I_{zz}};\kern2em \xi =\frac{I_{yy}-{I}_{xx}}{I_{zz}-{I}_{xx}};\kern2em \left(0<\eta <1;\kern1em 0<\xi <1\right) $$

(5.10)

Parameter ξ in this case would have a similar meaning of the non-dimensional coordinate “counterpart” from the finite element method, defining the current position within the finite element. In the context of this study, ξ is specifying the non-dimensional relative position coordinate of the intermediate value of the moment of inertia between the minimum value of the moment of inertia I _xx and the maximum value of the moment of inertia I _zz (see Fig. 5.4). In other words, it can be said that ξ is the non-dimensional parameter in the Hermite functions, enabling calculation of I _yy using I _xx and I _zz, using the following relationship:

$$ {I}_{yy}={I}_{xx}\left(1-\xi \right)+{I}_{zz}\;\xi $$

(5.11)

Fig. 5.4

Introduction of the non-dimensional parameters, describing relative values of the principal moments of inertia of the system

The zero value of ξ would now correspond to I _xx, and unit value of ξ would correspond to I _zz and any intermediate value of ξ, expressed via 0 < ξ < 1, would correspond to I _yy. With these notations, we can also derive several relationships, enabling useful conversions in the future:

$$ {I}_{yy}={I}_{xx}\left(1-\xi +\frac{1}{\eta}\right);\kern3em {I}_{zz}=\frac{I_{xx}}{\eta }. $$

(5.12)

As illustration, we take I _xx = 2; I _yy = 3; I _zz = 4 [all in kg × m²] and can see from Eqs. (5.10, 5.11 and 5.12) that these system’s parameters would correspond to ξ = 0.5 and η = 0.5.

Furthermore, in many cases, additional advantages could be gained if the Euler equations can be also rewritten in the non-dimensional quantities [32]:

$$ {\displaystyle \begin{array}{l}\frac{d}{d\overline{t}}{\overline{H}}_{xx}+\left(1-\frac{I_{yy}}{I_{zz}}\right){\overline{H}}_{yy}{\overline{H}}_{zz}=0,\\[10pt] {}\frac{d}{d\overline{t}}{\overline{H}}_{yy}+\left(\frac{I_{yy}}{I_{zz}}-\frac{I_{yy}}{I_{xx}}\right){\overline{H}}_{zz}{\overline{H}}_{xx}=0,\\[10pt] {}\frac{d}{d\overline{t}}{\overline{H}}_{zz}+\left(\frac{I_{yy}}{I_{xx}}-1\right){\overline{H}}_{xx}{\overline{H}}_{yy}=0,\end{array}} $$

(5.13)

where non-dimensional time is calculated as:

$$ \overline{t}=\left(\sqrt{2{K}_0/{I}_{yy}}\right)\;t $$

(5.14)

where K ₀ is the elliptic integral of the first kind.

3.4 Numerical Simulation of the “Garriott’s-Dzhanibekov’s Effect”: Illustration Case

We reproduce simulation results from [3] for the case study, in which the following parameters were employed: I _xx = 0.3, I _yy = 0.35, I _zz = 0.4 (all in kg × m²), corresponding to ξ = 0.5 and η = 0.75, with the initial conditions ω _x0 = 0.1, ω _y0 = 15, ω _z0 = 0.1 (all in rad/s). The main results are shown in Fig. 5.5 for completeness of the presentation.

Fig. 5.5

Time histories of the key for the Garriott’s-Dzhanibekov’s effect flipping motion: (a) moments of inertia, angular velocity components and non-dimensional angular momentum components; (b) Euler angles

Figure 5.5a shows that in this illustration case, the initial dominant angular velocity about the system’s y-body axis is subject to the periodical change of its initial value to the opposite in sign value, symbolising the flipping motion with 180° change in the orientation of the rigid body. From the simulation results, it can be seen that the period of the flips is equal to T = 12.3 s.

Figure 5.5a confirms that during the “flipping” motion, the angular momentum in the system is conserved.

At last, Fig. 5.5b shows that while ψ is monotonically increasing, the ϕ pattern is quite different: there are evident “plateau” segments corresponding to small changes in ϕ around 0°, 180°, 360°, etc. However, the most important observation in the context of this work is the presence of the multiple zero crossings for various components of the angular velocity, in particular, for ω _x, ω _y and ω _z in the presented test case.

4 Calculation of the Period of the Flipping Motion

We assume that I _yy is intermediate value of the principal moment of inertia. Then the period of the observed unstable motion can be estimated, using Eq. (37.12) in page 154 from the L.D. Landau’s reference [33]:

$$ \mathrm{If}\;{H}^2>2{K}_0\;{I}_{yy}, $$

(5.15)

then

$$ T=4K\sqrt{\frac{I_{xx}{I}_{yy}{I}_{zz}}{\left({I}_{zz}-{I}_{yy}\right)\left({H}^2-2{K}_0{I}_{xx}\right)}} $$

(5.16)

$$ \mathrm{If}\;{H}^2<2{K}_0\;{I}_{yy}, $$

(5.17)

then

$$ T=4K\sqrt{\frac{I_{xx}{I}_{yy}{I}_{zz}}{\left({I}_{xx}-{I}_{yy}\right)\left({H}^2-2{K}_0{I}_{zz}\right)}}, $$

(5.18)

where K is complete elliptic integral of the first kind:

$$ K=\underset{0}{\overset{1}{\int }}\frac{ds}{\sqrt{\left(1-{s}^2\right)\left(1-{k}^2{s}^2\right)}}=\underset{0}{\overset{\pi /2}{\int }}\frac{du}{\sqrt{1-{k}^2\;{\sin}^2u}} $$

(5.19)

As an illustrative example, let us assume the following parameters of the system: I _xx = 3, I _zz = 3.5 (all in kg × m²), corresponding to η = 0.8571 with the initial conditions ω _x0 = 0.1, ω _y0 = 15, ω _z0 = 0.1 (all in rad/s). For this case we will use Eqs. (5.15, 5.16, 5.17, 5.18 and 5.19) and will illustrate the influence of the intermediate moment of inertia I _yy of the system on the period T of the unstable flipping motion. Resulting plot is presented in Fig. 5.6.

Fig. 5.6

Period T of the unstable flipping motion (“Garriott’s-Dzhanibekov’s effect” case) as a function of intermediate moment of inertia I _yy (for the following example: I _xx = 3; I _zz = 3.5 [kg × m²] ; ω _x,i = 0.1, ω _y,i = 15, ω _z,i = 0.1 [rad/s])

The shape of the plot in Fig. 5.6 is clearly asymmetrical, but enabling variation of the period T within the wide range. Most significantly, Fig. 5.6 shows that the period T of flipping motion is bounded with particular minimum value, and there are two values of I _yy, providing with local minima values of the flipping periods T within the range of I _yy between the minimum value of the moment of inertia I _xx and maximum value of the moment of inertia I _zz.

Setting I _xx to a fixed value, and running variation for I _zz and I _yy, we can also calculate more generic plot, showing influence of these two other principal moments of inertia on the period of the unstable motion. The resultant plot is shown in Fig. 5.7, giving higher resolution for smaller values of T by changing the T-axis limits. This is a very interesting plot, which shows more generic nature of the asymmetry, observed in Fig. 5.6. The plot has also very recognisable “ridge” over the combination of moments of inertia I _yy and I _zz which results in very high periods.

Fig. 5.7

Period T of the unstable flipping motion (“Garriott’s-Dzhanibekov’s effect” case) of the rigid body, as a function of its moments of inertia I _yy and I _zz

As a second illustrative example, let us assume the following parameters of the system, in which I _xx = 3, I _zz = 3.5 (all in kg×m²), corresponding to η = 0.8571, with the initial conditions ω _x0 = 0.1, ω _y0 = 15, ω _z0 = 0.1 (all in rad/s). For this case we will use Eqs. (5.15, 5.16, 5.17, 5.18 and 5.19) and will illustrate the influence of the intermediate moment of inertia I _yy of the system on the period of the unstable flipping motion. The resulting plot, presented in Fig. 5.7, is clearly being asymmetrical and could be easily regarded by many as counter-intuitive, as there may be a wrongly perceived assumption of the “symmetrical” influence of I _yy on period T.

This plot prompts that variation in the intermediate value of the moment of inertia between I _xx and I _zz (i.e. changing the ξ value) can allow changes of the period T of the flipping motion within wide range. However, there is a minimum value of the period, which could not be reduced further. For the example shown, the lower threshold of the period is slightly higher than 22.2 s. Also, there is a specific value of the I _yy which leads to the infinitely large value of the T. For the example shown, this corresponding value of I _yy is approximately 3.27 kg × m².

Allowing variation of the I _yy and I _zz values (i.e. ξ and η non-dimensional parameters), we can also calculate more generic plot, showing influence of these principal moments of inertia on the period T of the unstable motion. The resultant plot is shown in Fig. 5.7. This is an interesting plot, which shows more generic nature of the asymmetry, observed in Fig. 5.6. However, most significant observation in Fig. 5.7 is that for each of the I _zz values, there is a value of I _yy which leads to the infinitely large period of the flipping motion. We named this area as “high periods ridge”.

The plot in Fig. 5.7 is similar in shape to the plot in Fig. 5.6a, and it similarly prompts that when I _yy is approaching any of the other moments of inertia, I _xx or I _zz, then the period of the flipping is asymptotically approaching infinite values.

Similarly to the examples above, in the second illustrative example, we initially assume initial conditions ω _x0 = 0.01, ω _y0 = 1.5, ω _z0 = 0.01 (all in rad/s) for the system with I _xx = 2, I _zz = 4 (all in kg × m²), which corresponds to η = 0.5 (see Eq. 5.10) and plot the flipping period as a function of the intermediate moment of inertia I _yy, varying its value in-between the minimum value of the moment of inertia I _xx and maximum value of the moment of inertia I _zz. The resultant plot is shown in Fig. 5.8a with continuous red line. It allows determination of the flipping period. This value is equal to 47.16 s. Let us now, in addition to the above, consider a similar “variable I _yy” experiment, changing only the maximum moment of inertia value from I _zz = 4 to I _zz = 5, which would correspond to η = 0.4. The resultant plot for the period is shown with dotted blue line in Fig. 5.8a. Comparison of the two curves allows to suggest another avenue for manipulation with the period of the flipping motion by changing the ratio between I _xx and I _zz, i.e. η value. Figure 5.8b also shows a ridge with high values of the flipping periods. It can be observed that for the higher values of I _zz, this ridge has more offset towards I _zz, than towards I _xx.

Fig. 5.8

Period of the unstable flipping motion (“Garriott’s-Dzhanibekov’s effect” case) of the rigid body, as a function of its moments of inertia I _yy and I _zz for two variation experiments: (a) variation of I _yy only in two cases I _xx = 2; I _zz = 4; and I _xx = 2; I _zz = 5 [kg × m²] ; ω _x,i = 0.01, ω _y,i = 1.5, ω _z,i = 0.01 [rad/s]; (b) variation of both, I _yy and I _zz in the case I _xx = 2 [kg × m²] ; ω _x,i = 0.01, ω _y,i = 1.5, ω _z,i = 0.01 [rad/s]

4.1 Influence of the Value of the Angular Velocity ω_y of the Predominant Spin on the Period T of the Flipping Motion

In this subsection, we consider systems with non-zero initial angular momentum H ₀. In case of the system with predominant spin about its intermediate axis, the major contributors to H ₀ are the ω _y and I _yy.

Using Eqs. (5.15, 5.16, 5.17, 5.18 and 5.19), we can represent T as a 3D surface plot, explaining influence on the T(ω _y, I _yy) function of its two argument. The resultant plot is shown in Fig. 5.9. It clearly reveals the tendency of the periods to become very large, when I _yy is approaching to I _xx or I _zz. However, the plot also reveals the ridge of high value of periods, being asymmetrically in-between I _xx and I _zz. As surface gradient is very high in vicinity of the ridge, it should be avoided for practical implementations, because in this area T would be very sensitive to small changes in I _yy, which would make control of the system period impractical.

Fig. 5.9

Variation of the period T(ω _y, I _yy) of the flipping motion with the changes in the predominant spinning angular velocity ω _y and value of the intermediate moment of inertia I _yy for the system with I _xx = 3, I _zz = 3.5 kg × m² (i.e. η = 0.8571)

As an example, in Fig. 5.9 we also intersect the T surface with two illustrative level values of the period: T = 30s and T = 50s. The intersection lines show that for the desired value of the flipping period T, there are multiple matching combinations of ω _y and I _yy; however, if the goal of the selection is to minimise the spin rate, then, there may be two local minimum specific values of I _yy. Two contour lines for T = 30s and T = 50s are shown separately in Fig. 5.10. It shows, that, if, for example, the aim of the design process is to keep ω _y low, for the T = 50, there are two solutions for I _yy, approximately equal to I _yy = 3.335 and I _yy = 3.18.

Fig. 5.10

Two labelled contour lines for the ω _y (T, I _yy) surface in Fig. 5.9, corresponding to the values of the flipping periods equal to T = 30 s and T = 50 s

4.2 Influence of the Value of the Period T of the Flipping Motion on the Angular Velocity ωy of the Predominant Spin

Results in Fig. 5.9 are presented for the ω _y = ω _y (T, I _yy), being a function of two arguments, T and I _yy. This function is shown in Fig. 5.11 as a 3D surface plot. For the illustration purposes, we assume interest in two special values of angular velocity of the predominant rotation: ω _y = 6 and ω _y = 12 rad/s. The intersection lines of these level panes and the ω _y surface, together with other contour curves, are given in Fig. 5.12.

Fig. 5.11

Variation of the period ω _y (T, I _yy) of the flipping motion with the changes in the predominant spinning angular velocity T and value of the intermediate moment of inertia I _yy for the system with I _xx = 3, I _zz = 3.5 kg × m² (i.e. η = 0.8571)

Fig. 5.12

Contour lines for the T(ω _y, I _yy) surface in Fig. 5.11 with in-between bands individually coloured. Red band corresponds to the ω _y = 4–6 (rad/s) spin rate range, yellow band to the ω _y = 6–8 range, green band to the ω _y = 8–10, cyan band to the ω _y = 10–12, blue band to the ω _y = 12–14 range and purple band to the ω _y = 14–16 range

5 Geometric Interpretation of the 3D Rotational Dynamics of Rigid Objects

5.1 General Comments

In this section, we will present geometric interpretation of the 3D rotational dynamics of the rigid body, employing angular momentum spheres, kinetic energy ellipsoids and hodographs – lines produced by the tip of the vector of the non-dimensional angular momentum, changing with time. The current angular momentum is then represented by the vector from the origin to a point on the hodograph.

5.2 Angular Momentum Sphere

Let us consider arbitrary free motion of the rigid body. In the context of the rigid-body dynamics, the angular momentum vector is defined as the product of matrix of the moments of inertia and the angular velocity vector. In the following presentation, for the modelling purposes, we will use the Cartesian coordinate system with its origin at the centre of the mass of the system and its axes x, y and z being the principal axes of inertia of the modelled rigid body. With these, the angular momentum vector can be represented with its components H _x, H _y and H _z:

$$ {\overrightarrow{\mathbf{H}}}_G={H}_x{\overrightarrow{\mathbf{e}}}_x+{H}_y{\overrightarrow{\mathbf{e}}}_y+{H}_z{\overrightarrow{\mathbf{e}}}_z $$

(5.20)

where ${\overrightarrow{\mathbf{e}}}_x$, ${\overrightarrow{\mathbf{e}}}_y$ and ${\overrightarrow{\mathbf{e}}}_z$ are unit vectors along x, y and z orthogonal directions.

For exploring 3D rotational dynamics, including “Garriott’s-Dzhanibekov’s effect”, we will utilise the fundamental law of conservation of angular momentum, implying that the angular momentum can be exchanged between objects in a closed system, but total angular momentum before and after an exchange remains constant (is conserved). Therefore, at any moment of the simulation, the length of the angular momentum vector must remain constant. We can express the squared length of the vector ${\overrightarrow{\mathbf{H}}}_G$ and equate it to the initial value, which would be known at the beginning of the simulation:

$$ {\left[{H}_x(t)\right]}^2+{\left[{H}_y(t)\right]}^2+{\left[{H}_z(t)\right]}^2={\left|{\overrightarrow{\mathbf{H}}}_G(0)\right|}^2 $$

(5.21)

This can be rewritten as follows:

$$ {\left[\frac{H_x(t)}{H(0)}\right]}^2+{\left[\frac{H_y(t)}{H(0)}\right]}^2+{\left[\frac{H_z(t)}{H(0)}\right]}^2=1 $$

(5.22)

Now, let us rewrite previous equation in terms of the non-dimensional quantities, ${\overline{H}}_x$, ${\overline{H}}_y$and ${\overline{H}}_z$

$$ {\left[{\overline{H}}_x(t)\right]}^2+{\left[{\overline{H}}_y(t)\right]}^2+{\left[{\overline{H}}_z(t)\right]}^2=1 $$

(5.23)

where

$$ {\displaystyle \begin{array}{l}{\overline{H}}_x(t)=\frac{H_x(t)}{H_0}=\frac{I_{xx}{\omega}_x}{\sqrt{{\left({I}_{xx}{\omega}_x\right)}^2+{\left({I}_{yy}{\omega}_y\right)}^2+{\left({I}_{zz}{\omega}_z\right)}^2}}\\[11pt] {}{\overline{H}}_y(t)=\frac{H_y(t)}{H_0}=\frac{I_{yy} \omega_y}{\sqrt{{\left({I}_{xx}{\omega}_x\right)}^2+{\left({I}_{yy}{\omega}_y\right)}^2+{\left({I}_{zz}{\omega}_z\right)}^2}}\\[11pt] {}{\overline{H}}_z(t)=\frac{H_z(t)}{H_0}=\frac{I_{zz} \omega_z}{\sqrt{{\left({I}_{xx}{\omega}_x\right)}^2+{\left({I}_{yy}{\omega}_y\right)}^2+{\left({I}_{zz}{\omega}_z\right)}^2}}\end{array}} $$

(5.24)

Equation (5.23) represents a unit sphere, called angular momentum sphere (AMS).

The graphical interpretation of Eq. (5.23) is a sphere with unit radius in the non-dimensionalised angular momentum coordinates and is shown in Fig. 5.13a. Amazingly, it would correspond to all rigid bodies and all possible torque-free motions of the rigid bodies.

Fig. 5.13

Angular momentum sphere (AMS): (a) 3D view of the unit AMS in the non-dimensionalised angular momentum coordinates; (b) + H _x view with visible “parking” points #2, #3, #4, #5 and #6 shown; (b) −H _x view with visible “parking” points #1, #3, #4, #5 and #6 shown

5.3 Utilisation Angular Momentum Sphere and Its Feasible Godographs for the Non-dimensional Angular Momentum Vector as Strategic Basis for the Methods of Attitude Control of the Rotating Systems

In case of a typical Garriott’s-Dzhanibekov’s effect “flipping” motion, spinning of the system could be seen as a periodic travel of the hodograph (line, drawn by the tip of the non-dimensional angular momentum vector $\overline{\mathbf{H}}$ on the unit AMS) along the closed path on the AMS. The angular momentum godograph is also called polhode and will be discussed in the next section. The motion of the hodograph in the vicinity of the pole (potential “parking” point) is rather slow, and the switch between two points of the intersection of the AMS with the y-axis – negative y point [0, −1, 0] and positive y point [0, 1, 0] – is occurring rather rapidly.

For the demo case, these points are numbered as #3 and #4 in Fig. 5.13b and c. For the selected y rotation example, the simple inversion method [5, 6] can be used, and the spacecraft could be stabilised around these two opposite points, which we will call “potential parking” points or just “parking” points. However, there are two more pairs of the “parking” points on the axes x and z. All six “parking” points are shown in Fig. 5.13b and c.

We have a special interest in the poles, as we see them as parking points to be utilised when the arbitrary 3D motion is to be stabilised and reduced to the regular spin about the body axes. Often, transformation of motion would involve a transfer of the tip of the non-dimensional angular momentum vector from one parking point to another. This could only be achieved if there is a feasible godograph for the vector $\overline{\mathbf{H}}$. And, as it will be seen in the next section, there are only special types of trajectories, separatrices, which are crossing the poles, and these trajectories are for the special type of the rotational motion of the rigid body – “Garriott’s-Dzhanibekov’s effect” flipping motion. Therefore, we place special emphasis on the establishment of the connection between the two transfer points for the vector $\overline{\mathbf{H}}$, which can be constructed from segments of polhodes and/or separatrices.

In this work, we are proposing to use IM for controlled transfer of the system into unstable “flipping” motion and use transition from one parking point to another parking point for switching trajectory of the hodograph of the vector ${\overrightarrow{\mathbf{H}}}_G(t)$ to other parking points, i.e. not necessarily being opposite to the established flipping.

If this is achieved, the spacecraft could be stabilised around desired/targeted parking point, as per the morphing procedure in [3, 4]. Stabilisation of the angular momentum vector in any of the six parking points would mean that the system would perform most predominant rotation, associated with only one of the selected body axis, x, y or z, passing through the targeted parking point and almost no rotation about two other orthogonal body axes. This is the reason for aiming to get to any of these points and then to stop flipping motion, as per [3,4,5,6,7,8,9,10].

5.4 Polhodes on the Angular Momentum Sphere

Let us solve Euler’s equations in the matrix form (5.7) and calculate time responses of the same rigid body due to different initial conditions. As contrast illustrations, we consider three cases A, B and C with the following initial conditions, applied to the rigid body with I _xx = 2, I _xx = 3, I _xx = 4 (all in kg × m²):

• Case-A: ω _x0 = 0.01, ω _y0 = 1.5, ω _z0 = 0.01 (all in rad/s)

• Case-B: ω _x0 = 0.4, ω _y0 = 1, ω _z0 = 0.8 (all in rad/s)

• Case-C: ω _x0 = 1.3, ω _y0 = 0.6, ω _z0 = 0.3 (all in rad/s)

Time histories for the angular velocity components for these three cases are presented in Fig. 5.14.

Fig. 5.14

Time histories for angular velocity components ω _x, ω _y, ω _z for three contrast cases of initial conditions: (A) ω _x,i = 0.01, ω _y,i = 1.5, ω _z,i = 0.01; (B) ω _x,i = 0.4, ω _y,i = 1, ω _z,i = 0.8; (C) ω _x,i = 1.3, ω _y,i = 0.6, ω _z,i = 0.3 (here and further all angular velocities are given in rad/s)

From a distinct response in Fig. 5.14a, we can conclude that the case-A response corresponds to a classical “Garriott’s-Dzhanibekov’s effect” flipping motion, whereas two other responses correspond to tumbling motion.

Angular momentum sphere can be used in the cases A, B and C not only to mark their respective initial conditions but also to show the corresponding resultant motion as lines on the AMS, called polhodes. Polhodes are trajectories of the tips of the non-dimensional angular momentum vectors, ${\overline{\mathbf{H}}}_A$, ${\overline{\mathbf{H}}}_B$ and ${\overline{\mathbf{H}}}_C$ (these three polhodes are marked with the red colour in Fig. 5.15), where we also show for comprehensive visualisation three quiver plots for the ${\overline{\mathbf{H}}}_A$, ${\overline{\mathbf{H}}}_B$ and ${\overline{\mathbf{H}}}_C$ vectors, superimposed over the AMS and polhodes.

Fig. 5.15

Polhodes: (a) for cases A, B and C in Fig. 5.14; (b) examples of broad coverage of initial conditions and associated responses

We should emphasise that for plotting polhodes on the AMS we are using non-dimensional angular momentum coordinates ${\overline{H}}_x,\kern0.5em {\overline{H}}_y,\kern0.5em {\overline{H}}_z$, defined as per Eq. (5.24).

5.5 Kinetic Energy Ellipsoid

Let us express the kinetic energy of the rotating body in terms of the angular momentum components:

$$ \frac{1}{2}{I}_{xx}{\omega}_x^2+\frac{1}{2}{I}_{yy}{\omega}_y^2+\frac{1}{2}{I}_{zz}{\omega}_z^2={\left[\frac{H_x(t)}{\sqrt{2{I}_{xx}}}\right]}^2+{\left[\frac{H_y(t)}{\sqrt{2{I}_{yy}}}\right]}^2+{\left[\frac{H_z(t)}{\sqrt{2{I}_{zz}}}\right]}^2=K(t) $$

(5.25)

The classical demonstrations of the “Garriott’s-Dzhanibekov’s effect” are typically considered rigid bodies with fixed values of the inertial properties.

However, in our study, it is essential to consider more general case, allowing for the moments of inertia to change with time. The imperative importance of this feature will be explained later.

$$ {\left[\frac{H_x(t)}{\sqrt{2{I}_{xx}(t)}}\right]}^2+{\left[\frac{H_y(t)}{\sqrt{2{I}_{yy}(t)}}\right]}^2+{\left[\frac{H_z(t)}{\sqrt{2{I}_{zz}(t)}}\right]}^2=K(t) $$

(5.26)

We, then, divide both sides of this equation by constant H ²(0) and rearrange result in terms of non-dimensional quantities ${\overline{H}}_x$, ${\overline{H}}_y$ and ${\overline{H}}_z$:

$$ {\left[\frac{H_x(t)}{H(0)}\frac{1}{\sqrt{2{I}_{xx}(t)}}\right]}^2+{\left[\frac{H_y(t)}{H(0)}\frac{1}{\sqrt{2{I}_{yy}(t)}}\right]}^2+{\left[\frac{H_z(t)}{H(0)}\frac{1}{\sqrt{2{I}_{zz}(t)}}\right]}^2=\frac{K(t)}{{\left[H(0)\right]}^2}\vspace*{-10pt} $$

(5.27)

$$ {\left[\frac{{\overline{H}}_x}{\sqrt{2{I}_{xx}(t)}}\right]}^2+{\left[\frac{{\overline{H}}_y}{\sqrt{2{I}_{yy}(t)}}\right]}^2+{\left[\frac{{\overline{H}}_z}{\sqrt{2{I}_{zz}(t)}}\right]}^2=\frac{K(t)}{{\left[H(0)\right]}^2} $$

(5.28)

Equation (5.26), finally, can be written in its useful final form as follows:

$$ {\left[\frac{{\overline{H}}_x(t)}{\frac{\sqrt{2K(t){I}_{xx}(t)}}{H(0)}}\right]}^2+{\left[\frac{{\overline{H}}_y(t)}{\frac{\sqrt{2K(t){I}_{yy}(t)}}{H(0)}}\right]}^2+{\left[\frac{{\overline{H}}_z(t)}{\frac{\sqrt{2K(t){I}_{zz}(t)}}{H(0)}}\right]}^2=1 $$

(5.29)

or

$$ {\left[\frac{{\overline{H}}_x(t)}{a_x(t)}\right]}^2+{\left[\frac{{\overline{H}}_y(t)}{a_y(t)}\right]}^2+{\left[\frac{{\overline{H}}_z(t)}{a_z(t)}\right]}^2=1 $$

(5.30)

Equation (5.30) corresponds to the ellipsoid in the ${\overline{H}}_x$, ${\overline{H}}_y$ and ${\overline{H}}_z$ axis, with the following values of the semi-major axes:

$$ {\displaystyle \begin{array}{l}{a}_x(t)=\frac{\sqrt{2\;K(t)\;{I}_{xx}(t)}}{H(0)}\\[12pt] {}{a}_y(t)=\frac{\sqrt{2\;K(t)\;{I}_{yy}(t)}}{H(0)}\\[12pt] {}{a}_z(t)=\frac{\sqrt{2\;K(t)\;{I}_{zz}(t)}}{H(0)}\end{array}} $$

(5.31)

5.6 Polhodes on the Kinetic Energy Ellipsoids

Kinetic energy ellipsoids (KEEs) can be used in the study cases A, B and C not only to mark their respective initial conditions but also to show the corresponding resultant motion as lines on the KEEs, called polhodes. Polhodes are trajectories of the tips of the non-dimensional angular momentum vectors, ${\overline{\mathbf{H}}}_A$, ${\overline{\mathbf{H}}}_B$ and ${\overline{\mathbf{H}}}_C$ (these three polhodes are marked with the blue colour in Fig. 5.16b, e, h), where we also show for comprehensive visualisation three quiver plots for the ${\overline{\mathbf{H}}}_A$, ${\overline{\mathbf{H}}}_B$ and ${\overline{\mathbf{H}}}_C$ vectors, superimposed over the KEEs and polhodes.

Fig. 5.16

(a), (d), (g) Angular momentum unit spheres (left column); (b), (e), (h) kinetic energy ellipsoids (middle column) for cases A, B, C; (c), (f), (i) superimposed AMSs and KEEs

We should emphasise that for plotting polhodes on the KEEs we are using non-dimensional angular momentum coordinates ${\overline{H}}_x,\kern0.5em {\overline{H}}_y,\kern0.5em {\overline{H}}_z$, defined as per Eq. (5.24).

Therefore, in Fig. 5.16, in addition to the angular momentum spheres with specific polhodes for the cases A, B and C (Fig. 5.16, left column), we also plotted corresponding kinetic energy ellipsoids (Fig. 5.16, middle column). Then, combining the surfaces in these two columns, we can see that specific polhodes are, in fact, lines of intersection between the corresponding AMSs and KEEs (Fig. 5.16 right column).

5.7 Polhodes for Systems with Equal Moments of Inertia

Let us consider a special case, when two out of three moments of inertia have the same values. For illustration, we simulate the case with I _xx = I _zz = 5, I _yy = 3 (all in kg × m²) and ω _x,i = 0.2; ω _y,i = 1; ω _z,i = 0.6 (all in rad/s). A snapshot from the 3D animation is shown in Fig. 5.17a, time histories of the main spacecraft dynamics parameters are shown in Fig. 5.17b and the co-centred KEE and AMS surfaces are shown in Fig. 5.17c. Figure 5.17a shows that the y-body axis is circling, indicating that the motion of the spacecraft is “coning”. This is confirmed with the godograph of the y-body axis, drawing in 3D a yellow circle, while other body axes, x and z, are drawing more complex curves (see Fig. 5.17a).

Fig. 5.17

3D rotational motion of the spacecraft with two equal moments of inertia: (a) 3D view; (b) time histories of the moment of inertia, angular velocity and non-dimensional angular momentum components; (3) collocated AMS and KEE

Figure 5.17c shows that KEE is bulging above the AMS in the xz plane and AMS is intersecting with KEE along the circle, and during the animation process, the tip of the non-dimensional vector $\overline{\mathbf{H}}$ is sliding along this intersection line, called polhode. Velocities of the tip of the vector $\overline{\mathbf{H}}$ are shown with black arrows in Fig. 5.17c. Because vector $\overline{\mathbf{H}}$ has a unit length, it is fully embraced by the AMS and KEE. In order to visualise its current orientation in the body axes, its magnified version with increased length and added small black sphere at the end is shown in Fig. 5.17c. Simulation results show that the values of the semi-major axes of the KEE are equal to a _x = a _z = 1.1471 and a _y = 0.8885.

For another interesting special case, when all moments of inertia are given with the same number, for example, with I _xx = I _yy = I _zz = 5 (all in kg × m²) and ω _x,i = 0.2; ω _y,i = 1; ω _z,i = 0.6 (all in rad/s), similar results are presented in Fig. 5.18. In this case, both surfaces, AMS and KEE, are given by unit spheres, displayed in Fig. 5.18a on the simulation control panel on the right side with mosaic surface. It is interesting to observe that all body axes, x, y and z, are drawing perfect circles with their tips, as shown in Fig. 5.18a. In this case, components of the angular velocities are not changing their values with time (see Fig. 5.18b), and the angular momentum vector is not changing its orientation in the body axes (see Fig. 5.18).

Fig. 5.18

3D rotational motion of the spacecraft with two equal moments of inertia: (a) 3D view; (b) time histories of the moment of inertia, angular velocity and non-dimensional angular momentum components; (3) collocated AMS and KEE

6 Geometric Interpretation of the “Garriott’s-Dzhanibekov’s Effect”, Using Angular Momentum Sphere and Kinetic Energy Ellipsoid

6.1 Collocated Angular Momentum Sphere and Kinetic Energy Ellipsoid for the Garriott’s-Dzhanibekov’s Flipping Motion Example

Figure 5.19 shows collocated $\overline{H}$ sphere (shown in light blue colour) and K ellipsoid (shown in red colour) for the case, considered in Sect. 5.3.4 : I _xx = 0.3; I _yy = 0.35; I _zz = 0.4 (all in kg × m²); ω _x,i = 0.1, ω _y,i = 15, ω_z0 = 0.1 (all in rad/s). It is clearly seen from Fig. 5.19a that the value of the z semi-major axis of the K ellipsoid is larger than 1, and therefore, around the “north” and “south” poles, it is extending (extruding/bulging/swelling) outside the $\overline{H}$ unit sphere. The values of the semi-major axes of the KEE can be calculated, using Eq. (5.28), giving the following values: a _x = 0.9258; a _y = 1; a _z = 1.0690. As solution points of the attitude dynamics problem are simultaneously restricted by $\overline{H}$ sphere and K ellipsoid, they must belong to the intersection of $\overline{H}$ and K surfaces.

Fig. 5.19

Angular momentum sphere and Kinetic energy ellipsoid for the flipping object (typical “Garriott’s-Dzhanibekov’s effect” case): (a) 3D view of collocated $\overline{H}$ sphere and K ellipsoid; (b) 2D “minus” ${\overline{H}}_y$ view with $\overline{H}$ hodograph marked; (c) enlarged $\overline{H}$ hodograph with the selected discrete time points shown; (d) “flipping” fast phase and “sleeping” slow phases

In order to indicate the direction of motion of the $\overline{H}$ hodograph, in Fig. 5.19c we mark some of the discrete instants for the tip of the $\overline{H}$ vector with their corresponding times. In addition, we are adding the quiver arrow plot, indicating the speed of vector $\overline{H}$ along of the hodograph. Figure 5.19c shows that close to the point, where y-axis intersects with $\overline{H}$ sphere, the density of the points is getting larger, and the length of the quiver arrows is smaller. It indicates that the $\overline{H}$ vector is slowing down, when it is getting more aligned with y-axis, which is an intermediate axis for the system.

The 3D marked plots in Fig. 5.19 conform with the pattern of motion, observed in “Garriott’s-Dzhanibekov’s effect” experiments, where there is local (in time) stabilisation of the system, where its main rotation is getting closer to the y-axis, and then, the flip is happening rather rapidly (see Fig. 5.19b, c and d).

6.2 Conceptual Spacecraft Model, Based on the Flipping Motion

The periodic flipping motion of the system about its intermediate axis prompts design of the spacecraft utilising this peculiar motion. Indeed, if the spacecraft is provided with rotation about its intermediate axis, it would start flipping and would start exposing its instruments to different directions, without any additional involvement of attitude control devices and systems. If, in one particular case, the spacecraft has a camera, scanning instrument or antenna, externally attached to the spacecraft, it could be directed to various directions on its own, due to the flipping motion of the body of the spacecraft. What makes this concept attractive is the following:

• Simplicity of the design and robustness of the flipping motion, which may allow use of the concept for far space autonomous missions, where no real-time interference by the mission specialist would be possible

• Ability to control the period of the flipping motion by proper selection of the principal moments of inertia of the system, which may allow selection of the most efficient agility of the spacecraft

In the presentation of the concept of the flipping spacecraft, we need to make two important comments:

• (a) The main disadvantage of the “continuously flipping” spacecraft concept in its basic configuration is its inability to switch flips ON only when they are needed: indeed, it would be impractical for the system to perform flips all the time, including launching and deployment stages. Therefore, it would be imperative to learn on how to switch ON and OFF the flipping motions. The method of initiation of the flipping motion on the spacecraft in stable spin and transferring flips into the stable spin has been discovered in [3] and will be presented in the following section.

• (b) Observing the flipping motion of the T-handle [14] or other rigid bodies in the flipping motion demonstrations [23,24,25,26], one may get the impression that the instrument, attached to any side of the flipping body, would scan the spacecraft surrounding, pointing in all possible directions. However, our study [8] showed that this impression about full scanning coverage of the instruments on the flipping spacecraft is wrong, and it also showed that attachment of the instrument to different sides of the flipping spacecraft may result in restricted hemispheres for the intended coverage. This aspect is analysed in the next subsection.

6.3 Investigating Orientation of the Sides of the Spacecraft Exposed to the Specific Directions

As spacecraft may have directional sensing equipment, attached to the sides, let us explore possible exposure of this equipment to the specified directions of interest. For this purpose, let us introduce a semi-transparent green coloured spherical dome, embracing the rotating spacecraft (which, in turn, has its rotating body axes system xyz with unit orts e ₁, e ₂ and e ₃). We collocate the centre of the dome (point O) with the centre of the mass of the rotating body. However, most significant, we fix the dome in the global coordinates XYZ, so it is not rotating with the body and its body axes xyz. Then we consecutively plot lines of intersection of the rotating orts e ₁, e ₂ and e ₃ with the dome. It must be emphasised that the spheres in Fig. 5.20 are not the bodies of the spacecraft (which may have any arbitrary shape), but the embracing imagined domes.

Fig. 5.20

Lines of intersection of the rotating orts e ₁, e ₂ and e ₃ with the spherical dome (green), fixed in the global axes system XYZ: “ball of wool” lines. (a) e ₁ diagrams (t = 0, 12 and 120 s), (b) e ₂ diagrams (t = 0, 12 and 120 s), (c) e ₃ diagrams (t = 0, 12 and 120 s) and (d) e ₁, e ₂ and e ₃ diagrams, presented together (t = 0, 12 and 120 s)

For the illustration purposes, let us simulate the motion of the spacecraft with the following parameters: I _xx = 2, I _yy = 4, I _zz = 3 (all in kg × m²). Let us for t = 0 align xyz body axes with XYZ global inertial axes as follows: x is aligned with X, y is aligned with Z and z is aligned with −Y. If the spacecraft is installed in orbit with initially provided angular velocity ω _x,i = 0.01, ω _y,i = 0.01, ω _z,i = 1 (all in rad/s), the spacecraft starts “flipping” along axis z, being an intermediate axis of inertia (as I _xx < I _zz < I _yy).

During this flipping process, we trace all intersections of the orts e ₁, e ₂ and e ₃ with the dome and present them as continuous lines with different colours. Results are shown in Fig. 5.20. It should be noted that for each of the computer screen snapshots in this figure, the individual viewpoint was selected for better observation of the simulation results. Selection of the viewpoints could be clearly understood using the vector of the angular momentum H as a reference, as it is pointing in the same direction in the global coordinates XYZ for all presented snapshots.

Last images for the e ₂ in Fig. 5.20b are remarkably interesting and illustrate our new finding! They show that y-body rotating axis, associated in this example with the maximum moment of inertia, is “drawing” e ₂ intersection lines on the dome only on one hemisphere, bulging towards the angular momentum vector H (we call it H ₊ hemisphere), and is never pointing towards the other hemisphere of the dome (shown as H ₋ hemisphere in Fig. 5.21). This is valid for the direction of y with positive component of the angular velocity along this direction (ω _y,i > 0). We have run many other various simulations, confirming that it is a general pattern, so the side, perpendicular to the axis with maximum moment of inertia and associated with positive angular velocity component, is never turned away from the vector H direction.

Fig. 5.21

(a) H ₊ and H ₋ hemispheres of the “dome” (I _xx = 2, I _yy = 4, I _zz = 3, all in kg × m² ; ω _x = 0.01, ω _y = 0.01, ω _z = 1, all in rad/s); (b) H ₊ and H ₋ hemispheres of the “dome” shown on the flipping acrobatic spacecraft (on the left) concurrently with the AMS/KEE simulation Virtual Reality control panel (on the right)

In Fig. 5.20, initially, vector H is almost aligned with z body axis (which is, in turn, is initially positioned along the –Y global axis); this is because initial values of ω _x,i and ω _z,i (and ultimately H _x,i and H _z,i) are small compared with ω _y,i (and ultimately H _y,i). Therefore, the 2D plane surface, subdividing H ₊ and H ₋, is almost parallel to the XZ plane. Discovery of the H ₊ and H ₋ planes is also illustrated on the model of the spacecraft (see Fig. 5.21b), flipping about x body axis and “drawing” godograph on the surrounding dome with its “y” body axis. Figure 5.21b also shows on the right the simulation Virtual Reality control panel, displaying AMS and KEE of the system with enlarged non-dimensional angular momentum vector, sliding along the separatrix.

H ₊ and H ₋ are also shown in Fig. 5.22, where we consider additional contrast case with the following parameters: I _xx = 2, I _yy = 4, I _zz = 3 (all in kg × m²) and initial angular velocities ω _x,i = 0.5, ω _y,i = 0.5, ω _z,i = 1 (all in rad/s), which has much more significant initial values of ω _x,i and ω _y,i, than in the previous example, hence has large components of H _x,i and H _z,i, as compared with H _y,i. It results in the subdivision of the dome into two parts (H ₊ and H ₋) by the inclined 2D plane, shown in white in Fig. 5.22a. Results of the intersection lines of the e ₂ ort with the dome are shown in Fig. 5.22a. They somehow resemble “ball of wool” (see Fig. 5.22b), especially with the knitting needles resembling the H and e ₂ vectors. However, the simulated resulting “ball of wool” lines are “sitting” on one hemisphere only! This hemisphere is on the side of the plane, perpendicular to H vector (and we will call it H ₊ hemisphere). The other side of the hemisphere (H ₋) does not have any threads of the “ball of wool”.

Fig. 5.22

“Ball of wool” lines: (a) simulation results for the case I _xx = 2, I _yy = 4, I _zz = 3 (all in kg × m²) and initial angular velocities ω _x,i = 0.5, ω _y,i = 0.5, ω _z,i = 1 (all in rad/s); (b) original “balls of wool”, which prompted the used analogy and terminology

This discovered new result can be used in the design of various spacecraft missions. For example, in case of the communication mission, if the spacecraft is installed in orbit with predominant rotation about an intermediate axis of inertia and is carrying an antenna, it should be ensured that the initial direction of the angular momentum vector H is consistent with the “source”, sensed by antenna, i.e. with H ₊ hemisphere facing the “source”; otherwise, spacecraft communication would be blanked for all instants of the mission. So, it matters which side of the spacecraft, perpendicular to the axis with maximum moment of inertia, is selected: one side would be good for utilising antenna, and the other side would be inoperable/terminal. The exposure “efficiency” of the equipment on the selected sides was explored in reference [34].

On the same token, in some other cases, when, for example, the spacecraft is subject to directional adhere conditions (heat, radiation, flying debris), it may be advisable to “reinforce” the spacecraft, facing the intended H ₋ hemisphere, install the spacecraft in orbit with the direction of the initial angular momentum pointing outwards the “danger” and place all sensitive equipment on the side, perpendicular to the axis with maximum moment of inertia and with positive component of the angular velocity along this direction (i.e. “plus” e ₂ in the two previously considered illustration cases).

As a summary from this subsection, we present in Fig. 5.23 godographs of all body axes orts e ₁, e ₂ and e ₃, for the base case study in Subsect. 5.3.4 (I _xx = 0.3, I _yy = 0.35, I _zz = 0.4 (all in kg × m²), corresponding to ξ = 0.5 and η = 0.75, with the initial conditions ω _x0 = 0.1, ω_y0 = 15, ω _z0 = 0.1 (all in rad/s)).

Fig. 5.23

“Ball of wool” lines for body axes orts e ₁, e ₂ and e ₃ in base study case in Subsect. 5.3.4: (a) red ort e ₁ along axis with minimum moment of inertia; (b) yellow ort e ₂ along intermediate axis; (c) green ort e ₃ along axis with maximum moment of inertia

It shows that if the system performs classical “Garriott’s-Dzhanibekov’s” flipping motion, the godograph of the port with maximum moment of inertia is drawing on the half of the dome, surrounding a flipping object, therefore on this object, where will be a side, which will be only exposed to one half of the semi-space, pointed by the angular momentum vector H, and will never be exposed to the second semi-space.

7 Proposing New Spacecraft Designs/Missions, Utilising Garriott’s-Dzhanibekov’s Effect and Inertial Morphing

7.1 Proposing Method of “Switching ON/OFF” Garriott’s-Dzhanibekov’s Spacecraft Flipping Motion by Controlled Inertial Morphing

Flipping motion of the rigid body, during which the direction of the angular velocity of the main rotation, let’s say, ω _y, is intermittently changing to opposite, is called “Garriott’s-Dzhanibekov’s effect”. It is a consequence of the moment of inertia, associated with the main rotation, being between two other values of the moments of inertia, I _xx and I _zz, in other words, having an intermediate value among principal moments of inertia.

What if there is a need to stop or suspend for some time the unstable “flipping” motion of the object?

For this purpose, Beachley [20] proposed four types of mass translations. However, this proposition was rather conceptual, as it did not involve equations of motion of the spacecraft with variable inertial properties, did not explain the change in moments of inertia and did not investigate the inversion timing.

In [3], and then in [4,5,6,7,8,9,10], we have addressed all these issues in a systematic manner and for the purpose of control of the spacecraft attitude, proposed general method of inertial morphing of the spacecraft, mathematically linking these modifications to the changes in moments of inertia and simulating transitional spacecraft response, using rigorous equations of motion [3]. In particular, we showed that for stabilisation of the spacecraft, there exist two morphing strategies, and after implementation of which, the intermediate moment of inertia becomes the smallest or largest among all principal moments of inertia.

In the illustration case, where we selected “y” axis to be the axis of the main rotation, the condition for the unstable “Garriott’s-Dzhanibekov’s effect”-type motion can be written as:

$$ {I}_{xx}\kern1em <\kern1em {I}_{yy}\kern1em <\kern1em {I}_{zz} $$

(5.32)

However, if via special design of the spacecraft, enabling the change of its principal moments of inertia (via mechanical or other means), the targeted value of I _yy is in controllable way forcefully “moved” outside the embrace of I _xx and I _zz, then the condition of instability Eq. (5.32) would no longer be satisfied and the unstable motion would be “switched OFF”!

Conceptually, this proposition can be illustrated with the diagram in Fig. 5.24, which presents two sets of solutions. The first conceptual solution set involves reduction of initial value of I _yy (which we denote as I _yy,i) to its new (or final) value I _yy,f, being smaller than I _xx value. And the second solution involves increase of the initial value of I _yy (which we denote as I _yy,i) to its new value I _yy,f, being larger than I _zz.

Fig. 5.24

Possible conceptual solutions for stabilizing an unstable spacecraft with its main rotation about the y-axis

For the numerical verification of the concept, let us assume the following demonstration values: I _xx = 0.3, I _yy = 0.35 and I _zz = 0.4 (all in kg × m²), which are conforming with the general condition in Eq. (5.32) of the flipping unstable motion, which would result if the main rotation about y-axis is initiated. And in this case, in order to test the concept of “switching OFF” the flipping motion, we will change I _yy,i = 0.35 to its new value of I _yy,f = 0.2 (solution-1) or I _yy,f = 0.5 (solution-2).

However, in order to proceed with the numerical simulations, we need to expand Euler Eq. (5.3), allowing variations in the moments of inertia of the rigid body.

7.2 Extending Euler’s Equations for Rigid-Body Rotations, Allowing Variation of Moments of Inertia

In order to simulate the cases of the morphing spacecraft with variable moments of inertia, we need to extend classic Euler’s Eq. (5.3). We note that the sum of the moments about the centre of mass of a rigid body due to external forces and couples equals to the rate of change of the angular momentum about the centre of mass [35]:

$$ \sum \overrightarrow{\mathbf{N}}={\left.\frac{d\overrightarrow{\mathbf{H}}}{dt}\right|}_{Inertial}={\left.\frac{d\overrightarrow{\mathbf{H}}}{dt}\right|}_{Body}+\overrightarrow{\boldsymbol{\upomega}}\times \overrightarrow{\mathbf{H}} $$

(5.33)

Also, the components of the angular momentum vector, $\overrightarrow{\mathbf{H}}$, with respect to the body-axis frame can be expressed by the product between the principal moment of inertia matrix I _G and the components of the angular velocity vectors as follows:

$$ \overrightarrow{\mathbf{H}}(t)=\left[\begin{array}{ccc}{I}_{xx}& 0& 0\\ {}0& {I}_{yy}& 0\\ {}0& 0& {I}_{zz}\end{array}\right]\left\{\begin{array}{l}{\omega}_x\\ {}{\omega}_y\\ {}{\omega}_z\end{array}\right\} $$

(5.34)

Therefore, extended Euler’s equations can now be written as:

$$ \left[\begin{array}{ccc}{\dot{I}}_{xx}& 0& 0\\ {}0& {\dot{I}}_{yy}& 0\\ {}0& 0& {\dot{I}}_{zz}\end{array}\right]\left\{\begin{array}{l}{\omega}_x\\ {}{\omega}_y\\ {}{\omega}_z\end{array}\right\}+\left[\begin{array}{ccc}{I}_{xx}& 0& 0\\ {}0& {I}_{yy}& 0\\ {}0& 0& {I}_{zz}\end{array}\right]\left\{\begin{array}{l}{\dot{\omega}}_x\\ {}{\dot{\omega}}_y\\ {}{\dot{\omega}}_z\end{array}\right\}\\{}+\left[\begin{array}{ccc}0& -{\omega}_z& -{\omega}_y\\ {}-{\omega}_z& 0& -{\omega}_x\\ {}-{\omega}_y& -{\omega}_x& 0\end{array}\right]\left[\begin{array}{ccc}{I}_{xx}& 0& 0\\ {}0& {I}_{yy}& 0\\ {}0& 0& {I}_{zz}\end{array}\right]\left\{\begin{array}{l}{\omega}_x\\ {}{\omega}_y\\ {}{\omega}_z\end{array}\right\}=\left\{\begin{array}{l}0\\ {}0\\ {}0\end{array}\right\} $$

(5.35)

For solving the morphing rigid-body dynamics problems, using numerical methods, we combine matrix Eqs. (5.35) and (5.6) into a single equation:

$$ \left[\begin{array}{cccccc}{I}_{xx}& 0& 0& 0& 0& 0\\ {}0& {I}_{yy}& 0& 0& 0& 0\\ {}0& 0& {I}_{zz}& 0& 0& 0\\ {}0& 0& 0& \sin \theta\;\sin \phi & \kern1.5em \cos \phi & 0\\ {}0& 0& 0& \sin \theta\;\cos \phi & -\sin \phi & 0\\ {}0& 0& 0& \cos \theta & 0& 1\end{array}\right]\left\{\begin{array}{c}{\dot{\omega}}_x\\ {}{\dot{\omega}}_y\\ {}{\dot{\omega}}_z\\ {}\dot{\psi}\\ {}\dot{\theta}\\ {}\dot{\phi}\end{array}\right\}=\left\{\begin{array}{c}\left({I}_{yy}-{I}_{zz}\right)\;{\omega}_y{\omega}_z-{\dot{I}}_{xx}\;{\omega}_x\\ {}\left({I}_{zz}-{I}_{xx}\right)\;{\omega}_z{\omega}_x-{\dot{I}}_{yy}\;{\omega}_y\\ {}\left({I}_{xx}-{I}_{yy}\right)\;{\omega}_x{\omega}_y-{\dot{I}}_{zz}\;{\omega}_z\\ {}{\omega}_x\\ {}{\omega}_y\\ {}{\omega}_z\end{array}\right\} $$

(5.36)

Equation (5.33) is the main equation, used in this work and solved using MATLAB^® ode MATLAB Runge-Kutta solver, with “mass matrix” option, as per Eq. (5.9). This equation is applicable to the systems which moments of inertia are changing with time.

7.3 Six-Mass Conceptual Model of the Spacecraft with Inertial Morphing Capabilities

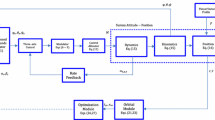
To demonstrate the feasibility of the controllable behaviour of the spacecraft, let us consider a simple conceptual model of the morphing spacecraft, constructed as an axisymmetric set of three orthogonal dumbbells, each of which has negligible mass of the rod, connecting two equal concentrated masses at its ends. Let us also assume, for conceptual simplicity, that three dumbbells are connected at the middle points of their rods, and the corresponding masses m _x, m _y and m _z are located at the distances r _x, r _y and r _z from the axes of rotation x, y and z, as shown in Fig.5.25. In the illustrated conceptual design, morphing of the spacecraft is achieved via independent synchronized control of the position coordinates r _x = r _x(t), r _y = r _y(t) and r _z = r _z(t) of the masses m _x, m _y and m _z.

Fig. 5.25

Six-mass conceptual model of the morphing spacecraft

The principal moments of inertia of the system can be calculated as follows:

$$ {\displaystyle \begin{array}{l}{I}_{xx}=2{m}_y{r}_y^2+2{m}_z{r}_z^2\\ {}{I}_{yy}=2{m}_z{r}_z^2+2{m}_x{r}_x^2\\ {}{I}_{zz}=2{m}_x{r}_x^2+2{m}_y{r}_y^2\end{array}} $$

(5.37)

Then by adding all equations in (5.34), and taking only a half of the left and right hand sides, we can get:

$$ \frac{1}{2}\left({I}_{xx}+{I}_{yy}+{I}_{zz}\right)=2\left({m}_x{r}_x^2+{m}_y{r}_y^2+{m}_z{r}_z^2\right) $$

(5.38)

Then, subtracting from Eq. (5.35) consecutively each of Eq. (5.34), we can obtain:

$$ {\displaystyle \begin{array}{l}{r}_x(t)=\sqrt{\frac{I_{yy}(t)\kern1em +\kern1em {I}_{zz}(t)\kern1em -\kern1em {I}_{xx}(t)}{4\;{m}_x}}\\[10pt] {}{r}_y(t)=\sqrt{\frac{I_{zz}(t)\kern1em +\kern1em {I}_{xx}(t)\kern1em -\kern1em {I}_{yy}(t)}{4\;{m}_y}}\\[10pt] {}{r}_z(t)=\sqrt{\frac{I_{xx}(t)\kern1em +\kern1em {I}_{yy}(t)\kern1em -\kern1em {I}_{zz}(t)}{4\;{m}_z}}\end{array}} $$

(5.39)

Equations (5.39) are very important equations, as they mathematically represent a basis for the concept of “inertial morphing”, as formulated for the six-mass model of the morphed spacecraft. They show that at any instant of time t, the exact set of positions for the masses m _x, m _y and m _z in the model can be uniquely determined, based on the values of the required moments of inertia of the system for this instant of time. Equations (5.39) assume that masses m _x, m _y and m _z have constant values, but they are not imposing these as constraints. In fact, it may be possible in some IM designs to employ masses, which would have variable values, and in these cases, notations m _x, m _y and m _z in Eq. (5.39) should be replaced with m _x(t), m _y(t) and m _z(t). There rather exquisite designs may involve, for example, solidification, evaporation or ablation of the mass materials.

7.4 Conceptual Example of the Morphed Spacecraft, Self-Transferring from Unstable Flipping Motion to Stable No-Flips Spin

Let us assume, as an example, that the system’s parameters are given with the following numbers: m _x = m _y = m _z = 1 kg, I _xx = 0.3 kg × m², I _yy = 0.35 0.3 kg × m², I _zz = 0.40 kg × m², the same as in Sect. 5.3.4 example. Then, for the case of the tumbling spacecraft considered in Sect. 5.3.4, we can find the initial radial positions of the spacecraft masses, using Eq. (5.39):

$$ {r}_{x0}=0.2500\ \mathrm{m};\kern2em {r}_{y0}=0.2958\ \mathrm{m};\kern2em {r}_{z0}=0.3354\ \mathrm{m}. $$

(5.40)

These values for the unit masses would ensure that the inertial properties of the spacecraft are I _xx = 0.3 kg × m², I _yy = 0.35 kg × m², I _zz = 0.4 kg × m² (this can be proven via Eqs. 5.34). Note that in our example here I _yy has an intermediate value among all principal moments of inertia: I _{xx <} I _{yy <} I _zz; therefore, if the spacecraft is provided with the initial angular velocity ω _x0 = ω _z0 = 0.1 rad/s and ω _y0 = 15 rad/s, with the prevailing rotation about y-body axis, then the spacecraft rotation about this axis would be unstable and the classical “Garriott’s-Dzhanibekov’s effect” periodic flipping would be observed.

It will be shown in Sect. 9.1 that, if during the “flipping” motion, at the instant, when the angular velocities ω _x0 and ω _z0 are close to zeros, the moment of inertia I _yy,i = 0.35 kg × m² is rapidly changed to its new value, less than I _xx, for example, I _yy,f = 0.2 kg × m², then the nature of the followed motion of the system would change from unstable “flipping” to stable. This would happen, because with the deliberate assignment of the described new values of the moments of inertia, predominant rotation of the system would not be longer along the intermediate axis but would be instantly changed in favour of the rotation about the same body axis but now having its new status of the axis with minimum moment of inertia, and the resulting rotation would become stable, without flips. We call it “switching OFF” the flipping motion manoeuvre. Note: this would require a single instant inertial morphing.

The new values of the position radii, corresponding to this particular solution (being one out many solutions in the “solution-1” set), can be calculated using Eq. (5.39) and are shown in the graphical form in Fig. 5.26a and in the table form in Fig. 5.26b:

Fig. 5.26

Solution-1 for the conceptual six-mass design of the morphing spacecraft, self-transferring from unstable “Garriott’s-Dzhanibekov’s effect”-type flipping motion to stable spinning no-flips motion (and vice versa): (a) graphical representation, where white spheres correspond to unstable flipping about y – axis of predominant initial rotation and black spheres to stable no-flips spin; (b) table representation with radii for all masses specified for initial and final stages of the inertial morphing

$$ {r}_{xf}=0.1581\ \mathrm{m}; \ \ \ \ {r}_{yf}=0.3536\ \mathrm{m}; \ \ \ \ {r}_{zf}=0.2739\ \mathrm{m}. $$

(5.41)

The spacecraft masses at these final radius positions are shown in Fig. 5.26a with dark colour.

The flipping motion can be also stopped, using a solution from the “solution-2” set. One of the examples is shown in conceptual Fig. 5.24. For the purpose of the illustration of the concept, let us consider rapid increase of the I _yy from its initial value of I _yy,i = 0.35 kg × m² to its new (final) value of I _yy,f, being larger than I _zz, for example, I _yy,f = 0.5 kg × m². The new values of the position radii, corresponding to the “solution-2” in Fig. 5.27b, can be calculated using Eqs. (5.39):

Fig. 5.27

Solution-2 for the conceptual six-mass design of the morphing spacecraft, self-transferring from unstable “Garriott’s-Dzhanibekov’s effect”-type flipping motion to stable spinning no-flips motion (and vice versa): (a) graphical representation, where white spheres correspond to unstable flipping about y – axis of predominant initial rotation and black spheres to stable no-flips spin; (b) table representation with radii for all masses specified for initial and final stages of the inertial morphing

$$ {r}_{xf}=0.3162\;\mathrm{m}; \ \ \ \ {r}_{yf}=0.2236\;\mathrm{m}; \ \ \ \ {r}_{zf}=0.3873\;\mathrm{m}. $$

(5.42)

The spacecraft masses at these radius positions are shown in Fig. 5.27b with dark colour.

The morphing of the spacecraft from the initially unstable configuration [as per Eq. (5.40)], associated with the “flipping” motion, to its final stable configuration [as per Eqs. (5.41) or (5.42) and solution-1 or 2 in Fig. 5.24] is shown in Figs. 5.26a and 5.27a, where masses for the initial unstable (flips) configuration are shown in white, whereas the masses for the final (no-flips) stable configuration are shown in black colour.

Summary for both particular solutions is presented in Figs. 5.26b and 5.27b. It would be important to note that, in the presented cases, it was not obligatory during the morphing of the system and its transition from the “initial” to “final” states to keep both values of I _xx and I _zz unchanged. However, it was done for purpose to emphasize the role of the I _yy in the process of stabilisation of the system.

7.5 Geometric Interpretation of the Cases, Where “Garriott’s-Dzhanibekov’s Effect” Is Controlled

7.5.1 Stopping Flipping Motion, Using One Inertial Morphing: Solution-1

At last, in this section, we consider the case of “switching OFF” the flipping motion and fully stabilising the system.

As proposed and illustrated in [3] on the six-mass dumbbell model, full stabilisation of the spinning rigid body (e.g., spacecraft or rocket) can be achieved with a controllable change of all moments of inertia. However, in order to emphasise the importance of the I _yy in stabilisation of the system, I _xx and I _zz were not involved. Application of the applied changes in I _yy (shown in Fig. 5.28a) ensures that the periodic change in ω _y is stopped, as illustrated with Fig. 5.28b.

Fig. 5.28

Stopping the flipping motion (solution-1): (a) explanation of the inertial morphing applied; (b) time history of the resulting angular velocity components ω _x, ω _y, ω _z; (c) radii of the KEE; (d) geometric interpretation, showing the AMS and KEE before and after application of the inertial morphing

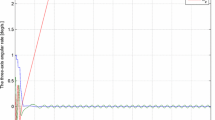
Figure 5.29a shows that while the angular momentum is conserved in the system, the kinetic energy may be a subject to variations. In the presented example, increase in the dominant angular velocity component ω _y triggers significant increase in the kinetic energy by 74%, as demonstrated in Fig. 5.29b.

Fig. 5.29

Time histories of the key characteristics of the inertially morphed system: (a) non-dimensional angular momentum $\overline{H}$, (b) kinetic energy E

Figure 5.28d of the associated controlled action shows that the kinetic energy ellipsoid has dramatically swollen and is now fully embracing and hiding (inside of the KEE) the angular momentum sphere, which is in great contrast with solution-2, to be illustrated in Fig. 5.30. Nevertheless, both surfaces are touching each other at two points: pole S and another pole on the opposite side of the y-axis.

Fig. 5.30

Stopping the flipping motion (solution-2): (a) explanation of the inertial morphing applied; (b) time history of the resulting angular velocity components ω _x, ω _y, ω _z; (c) radii of the KEE; (d) geometric interpretation, showing the AMS and KEE before and after application of the inertial morphing

Conclusion from this subsection is as follows: stabilisation of the flipping motion (i.e. switching OFF the “Garriott’s-Dzhanibekov’s effect”) manipulating with I _yy only may be achieved using two avenues – making I _yy the smallest moment of inertia or making it largest moment of inertia [3]. The first avenue has been illustrated in Figs. 5.28 and 5.29 .

7.5.2 Stopping Flipping Motion, Using One Inertial Morphing: Solution-2

One of the two types of solutions is presented in Fig. 5.30 .

Solution-2 has been achieved at the “expense” of the kinetic energy E, which has reduced its initial value after the morphing by 30% (see Fig. 5.31a). The geometric interpretation of this controlled action in Fig. 5.30 shows that the kinetic energy ellipsoid has dramatically shrunk and is now fully embraced by the angular momentum sphere, which is in great contrast with solution-1, illustrated in Fig. 5.28 . In solution-2, the final KEE is not seen, as is entirely residing inside the shrunk AMS. Nevertheless, both surfaces AMS and KEE are touching each other at just two points: pole S and the pole on the opposite side along the y-axis.

Fig. 5.31

Time histories of the key characteristics of the inertially morphed system: (a) kinetic energy E; (b) non-dimensional angular momentum $\overline{H}$

8 Attitude Dynamics of Spacecraft with Inertial Morphing

8.1 Study Case-2: “Switching OFF” Flipping Motion of the Spacecraft After One Flip (Solution-1)

Figure 5.32 shows that at the instant t = 6.77 s, the angular velocity ω _y has its highest value and ω _x changes its value from negative to positive. It is believed that this instant, corresponding to the most prominent rotation about the y-body axis, would be the best time to apply morphing to the spacecraft. In our demo case, the moment of inertia I _yy is changed from 0.35 to 0.2, as per Fig. 5.32a within relatively short period of time of 0.2 s. Results of the simulation are given with Fig. 5.32b and c. Figure 5.32b shows that the simulated morphing led to the step-type increase of the angular velocity ω _y of the body and did not initiate significant oscillations in ω _x and ω _z. In contrast to Case-1, where ω and H plots had similar shapes, in Case-2 these plots are different.

Fig. 5.32

Time histories for Case-2 (switching OFF the flipping motion of the system) of the key parameters: (a) controlled moment of inertia I _yy; (b) angular velocity components; (c) angular momentum components; (d) Euler angles

Figure 5.32b shows that morphing did not change the angular momentum H _y and after the morphing was completed, the value of H _y stayed almost unchanged, evidencing that attempt to stop the “flipping” motion was successful. At last, note that as the stabilised value of |ϕ| = 180°, the stabilised spacecraft is flying backwards, with its initial heading attitude changed by 180°!

8.2 Study Case-3: “Switching OFF” Flipping Motion of the Spacecraft After One Flip (Solution-2)

It is interesting to observe that stabilisation of the system, illustrated with Fig. 5.33, has been achieved with a controllable change of the moment of inertia I _yy (associated with the main rotation of the spacecraft), which initially had its value of I _yy,i = 0.35, being an intermediate value, surrounded by the smallest I _xx = 0.2 and largest I _zz = 0.4 moments of inertia:

$$ {I}_{xx}<{I}_{yy,i}<{I}_{zz}\vspace*{-13pt} $$

(5.43)

Fig. 5.33

Time histories for Case-3 (switching OFF the flipping motion of the system) of the key parameters: (a) controlled moment of inertia I _yy, (b) angular velocity components, (c) angular momentum components and (d) Euler angles

While keeping values of I _xx and I _zz unchanged, the value of I _yy in the presented experiment was changed from I _{yy, i} = 0.35 to the final value of I _yy,f = 0.5, as per Fig. 5.33a, after which it became the largest principal moment of inertia:

$$ {I}_{xx}<{I}_{zz}<{I}_{yy,f} $$

(5.44)

Figure 5.33 shows that one of the consequences of the increase of I _yy was a reduction from 15 to 10.5 rad/s of the associated angular velocity ω _y of the spacecraft. This simulation result is in perfect agreement with the conservation of the angular momentum of the system, suggesting that ω _y must be reduced by the ratio of 15*(I _yy,i/ I _yy,f) = 15*(0.35/0.5) = 10.5 rad/s.

In contrast to Case-1, where ω and H plots had similar shapes, in the Case-3 these plots are different.

Figure 5.33b shows that morphing did not change the angular momentum H _y and after the morphing was completed, the value of H _y stayed almost unchanged, evidencing that the stopping “flipping” motion has been successful.

8.3 Study Case-4: “Switching OFF” Flipping Motion of the Spacecraft After Two Flips (Solution-1)

We now demonstrate switching OFF the “flipping” motion of the morphing spacecraft after it performs two flips. The time history of morphing is similar to the one presented in Fig. 5.33, but morphing is starting at t = 13.54 s. Results of this Case-4 are presented in Fig. 5.34. Observed reduction of the angular velocity ω _y is the same, as for the Case-2; however, in Case-2 after the motion is stabilised, the spacecraft continues its flight backwards, whereas in the current case, the stabilised attitude of the spacecraft is the same as at the initial time.

Fig. 5.34

Time histories for Case-4 (switching OFF the flipping motion of the system) of the key parameters: (a) controlled moment of inertia I _yy, (b) angular velocity components, (c) angular momentum components and (d) Euler angles

8.4 Study Case-5: “Switching ON” Spacecraft Flipping Motion

In a similar way as stabilisation, described in Cases 2–4, was achieved, we can initiate the “flipping” motion of the spacecraft. For this, the axis of the major rotation of the system (let’s say, y) initially should coincide with the axis of minimal or maximal moments of inertia, i.e. one of the conditions should be satisfied: I _yy < min(I _xx, I _zz) or I _yy > max(I _xx, I _zz).

In this case, initiated rotation would be stable, without “flipping”. To activate the “flipping” motion, morphing of the system should be performed, which should result in I _yy becoming an intermediate value between I _xx and I _zz. In the study Case-5, as illustration, we use the following values: ω _x = 0.1, ω _y = 26.25, ω _z = 0.1 (all – in rad/s), I _xx = 0.3, I _yy,i = 0.2, I _yy,f = 0.35, I _zz = 0.4 (all – in kg*m²). The time history of applied morphing is presented in Fig. 5.35a, and the results of the simulation are shown in Fig. 5.35b and c.

Fig. 5.35

Time histories for Case-5 (switching ON the flipping motion of the system) of the key parameters: (a) controlled moment of inertia I _yy, (b) angular velocity components, (c) angular momentum components and (d) Euler angles

8.5 Study Case-6: “Switching ON” Spacecraft Flipping Motion with Following One Flip and “Switching OFF”

Case-6 represents further development of the Case-5 by switching OFF the “flipping” motion at t = 9.89 s, instant of the maximal value of ω _y. The time history of applied morphing is presented in Fig. 5.36a, and the results of the simulation are shown in Fig. 5.36b and c.

Fig. 5.36

Time histories for Case-6 (switching ON the flipping motion of the system with following one flip and switching OFF) of the key parameters: (a) controlled moment of inertia I _yy, (b) angular velocity components, (c) angular momentum components and (d) Euler angles

8.6 Study Case-7: Control of the Frequency of the Flipping Motion via “Inertial Morphing”

Case-7 demonstrates the ability of the proposed “inertia morphing” for control of the frequency of the “flipping” motion. In this demo, inertia properties of the “flipping” system are as follows:

• I _xx,i = 0.3, I _yy,i = 0.395, I _zz,i = 0.4 were changed after three 180° flips to

• I _xx,f = 0.3, I _yy,f = 0.35, I _zz,f = 0.3 = 0.4 (all in kg × m²), as per Fig. 5.37a.

Fig. 5.37

Time histories for Case-7 (control of the frequency) of the key parameters: (a) controlled moment of inertia I _yy, (b) angular velocity components, (c) angular momentum components and (d) Euler angles

However, the intermediate value of the moment of inertia I _yy was still kept within the values of I _xx and I _zz: I _xx < I _yy < I _zz. It is really interesting to observe that it was possible to achieve substantial change of the frequency of the flipping motion. Calculations of the flipping motion periods before and after “morphing” can be calculated, using Eqs. (5.15, 5.16, 5.17, 5.18 and 5.19): T _i = 21.5 s and T _f = 10.8 s (twice reduction!). This is in perfect correspondence with the results of the simulations, partially shown in Fig. 5.37.

9 Inertial Morphing and the Law of Conservation of Angular Momentum

The law of conservation of angular momentum is one of the fundamental laws in physics, mechanics and quantum mechanics, stating that the total angular momentum of a closed system remains constant. There are numerous fascinating qualitative demonstrations of this law, for example, involving Hoberman sphere [36], a plastic sphere frame that can be contracted by pulling on a string. Pulling on the string while the sphere is rotating causes the sphere’s moment of inertia to decrease and its angular speed to increase, demonstrating conservation of angular momentum.

Figure skaters in a spin (Fig. 5.38a) use conservation of angular momentum: changing their moments of inertia enables them to vary their rate of spin. For the same total angular momentum, they will spin faster by bringing their arms in (lower moment of inertia) and slower by extending their arms (higher moment of inertia). Reduction of the moment of inertia can be achieved by drawing skater’s arms and legs. Increase of the moment of inertia can be achieved by moving the skater’s arms outwards.

Fig. 5.38

A figure skater, employing manipulations with the moments of inertia of the human body to control the spin rate: (a) fast spin and (b) fastest spin by O. Oliver of 342 RMP or 5.7 Hz (19 January 2015, Guinness Book of World Records)

For example, let us assume the initial spin rate of the skater to be equal to 30 rad/s and ability to increase its angular momentum by a factor of 3. Then, using the law of conservation of energy, and ignoring energy losses due to the ice friction and air drag, etc. during the spin, we can estimate a new spin rate of the skater being equal to 10 rad/s.

Figure 5.38b shows Olivia Oliver, who achieved the fastest recorded spin on ice skates of 342 RPM (this record was achieved in Warsaw, Poland, on 19 January 2015 and is in the Guinness Book of World Records [37]). This spin speed corresponds to 5.7 Hz or the angular velocity of 35.81 rad/s.

All numerical demonstrations in Figs. 5.29a, 5.32b, 5.33b, 5.34b, 5.35b, 5.36b and 5.37b, involving inertial morphing, showed that the angular momentum was conserved: $\mid \overline{\mathbf{H}}\mid$, the absolute value of the magnitude of the non-dimensional vector of the angular momentum $\overline{\mathbf{H}}$, plotted with grey dashed line, remained its constant value.

Analysis of the numerically simulated changes in the angular velocity of the presented rotating systems was in full agreement with the law of conservation of angular momentum. In particular example, Study Case-3, applying inertial morphing, which resulted in increase of the angular momentum I _yy from 0.35 to 0.5 kg × m², has led to the reduction of the angular velocity from 15 to 10.5 rad/s. These changes allow us to express this observation as follows: I _yy,i ω _y,i = I _yy,f ω _y,f.

Figure 5.33 shows that one of the consequences of the increase of I _yy was a reduction from 15 to 10.5 rad/s of the associated angular velocity ω _y of the spacecraft. This simulation result is in perfect agreement with the conservation of the angular momentum of the system, suggesting that ω _y must be reduced by the ratio of 15*(I _yy,i/ I _yy,f) = 15*(0.35/0.5) = 10.5 rad/s.

On the surface, there is apparent similarity between the skaters and proposed inertially morphed spacecraft, manipulating with the inertial properties.

However, there is a significant difference: skater is “operating” within the stable modes of motion [38], whereas a morphed spacecraft is actually extracting most advantages from its inertial manipulations in its ability to manipulate with the attitude, as it is able to access unstable motions!

In this respect, we would like to suggest the following analogy, which could be easier understood by a wide audience. Let us consider nothing more complex than heating of water. When this is occurring for the water temperature, being within the range 0–100 °C, let us say 80 °C, then the heating energy, passed on to the water, leads to the quantitative change in the water’s temperature. However, if the energy is passed on the system, after we reached 100 °C, then we can observe conversion of the water from the liquid state to the gaseous state! This is a change in quality of the substance. In a similar way, considering an experiment with water to be cooled, where water has initial temperature, let us say 10 °C, we can see conversion of the matter from liquid to the solid state after we reached 0 °C. This would be also a case with a change in quality of the substance.

Similar to the heating/cooling of the water within the range 0–100 °C, manipulation with the moments of inertia, during which their order, let us say, I _xx,i < I _yy,i < I _zz,i is not changing with I _xx,f < I _yy,f < I _zz,f, rotational characteristics of the system (like angular velocity components) are changing only in a sense of their quantities, but without the change in the “quality” of the rotational motion. However, similar to the water being evaporated or frozen, with the change of the order of the moments of inertia (due to the applied IM), let us say, from I _xx,i < I _yy,i < I _zz,i to I _yy,f < I _xx,f < I _zz,f, (or I _yy,f < I _zz,f < I _xx,f or I _xx,f < I _zz,f < I _yy,f or I _zz,f < I _xx,f < I _yy,f), then, in addition to the quantitative changes in the rotational parameters of the system, we would be also expecting a qualitative change in the motion.

Therefore, it is proposed to distinguish between the inertial morphings, which do not employ non-stable modes of motion and is called the cold inertial morphings from the inertial morphings, which employ non-stable modes of motion and are called the “hot IM”. With these definitions, the most useful of the IM for spacecraft, allowing acrobatic capabilities, are “hot inertial morphings”.

10 Inertial Morphing in Novel Designs of Acrobatic Spacecraft for 180 Degrees Inversions: Method of “Installing into Separatrix” with Pole-Separatrix-Pole Transfer

10.1 Applications of Acrobatic Missions

It is believed that new results of this research may have multiple applications. We would like to propose and list a few of them, which may be useful in planning new space missions:

• 1. Assistance in establishing formation flight:

Eject one spacecraft in the forward direction, and then, after one flip, eject another spacecraft in the opposite direction, so that the formation flying is achieved in orbit around the Earth or other planet or celestial body (comet, asteroid).

• 2. Thruster direction control:

To boost (accelerate) or decelerate spacecraft velocity by only one thruster. Of course, deep space mission vehicles change its attitude to boost (escape from the Earth) and to decelerate its velocity when it enters to an orbit around another planet.

Usually other small thrusters (or reaction wheels) are used to change attitude of vehicles. In addition to this, our new proposed method could be also used for changing the attitude of the spacecraft and its following stabilisation in the fixed body frame.

• 3. Frequency of “flipping” motion control:

Inertial morphing can be used to control within wide range the frequency of the “flips” for the “Garriott’s-Dzhanibekov’s effect” mode. However, we showed that there is a minimum (i.e. low bounding limit) for the period of these oscillations.

10.2 Illustrated Description of Application of IM for Thruster Direction Control

Figure 5.39 is dedicated to one (out of many) possible application of the IM. It illustrates inversion of the spacecraft, using two morphing procedures: the first is to activate unstable flipping motion and second is to stop flipping motion. This enables for a single thruster to be used for acceleration of the spacecraft (boosting stage, Fig. 5.39a) and also for its deceleration (braking stage, Fig. 5.39f).

Fig. 5.39

Examples of application of inertial morphing for inversion of spacecraft [9]: (a–f) 180° inversion, allowing to use the same thruster for the boost and braking stages

10.3 Fast 180 Degrees Inversion of the Spacecraft

To demonstrate the feasibility of the proposed application, let us consider six-mass model of the spacecraft with corresponding numerical parameters m _x = 4 kg, m _y = 5 kg; m _z = 1 kg. The key requirement to this design would be the ability of the system to reposition six paired masses (e.g. via linear actuators), in accordance to the control considerations. Let us assume that the mission profile would enable instalment of the spacecraft with initial predominant spin about y-axis (with angular velocity ω _y,i = 8.57 and other components of ω being small: ω _x,i = ω _z,i = 0.01, all in rad/s). If the masses are initially positioned at their locations, shown in Fig. 5.40 with white spheres, with position radii equal to r _x,i = 548, r _y,i = 510, and r _z,i = 447 mm correspondingly, then the inertial properties of the spacecraft would be I _xx,i = 3; I _yy,i = 2.8; I _zz,i = 5 (all in kg × m²). With these selected parameters, the y spin of the system would be stable, as axis of rotation coincides with the minimal inertia axis.

Fig. 5.40

Positions of the masses during spacecraft inversions via inertial morphing for acrobatic manoeuvre in Fig. 5.39(a)–(e): 180 degrees inversion, illustrated for six-mass spacecraft conceptual model [9]

Let assume that at the instant t = 10 s we wish to initiate flipping motion of the system. This can be achieved by applying inertial “Morphing-1”, during which moment of inertia I _yy should become an intermediate axis. Aiming for the new moments of inertia to be I _xx,1 = 3; I _yy,1 = 3.4; I _zz,1 = 5 (kg × m²), we calculate new radii for the masses, using the following relationships, as per Eq. (5.39):

$$ {\displaystyle \begin{array}{l}{r}_{x1}=\frac{1}{2}\sqrt{\left(\kern0.5em {I}_{yy,1}\kern1em +\kern1em {I}_{zz,1}\kern1em -\kern1em {I}_{xx,1}\right)/{m}_x}\\[12pt] {}{r}_{y1}=\frac{1}{2}\sqrt{\left(\kern0.5em {I}_{zz,1}\kern1em +\kern1em {I}_{xx,1}\kern1em -\kern1em {I}_{yy,1}\right)/{m}_y}\\[12pt] {}{r}_{z1}=\frac{1}{2}\sqrt{\left(\kern0.5em {I}_{xx,1}\kern1em +\kern1em {I}_{yy,1}\kern1em -\kern1em {I}_{zz,1}\right)/{m}_y}\end{array}} $$

(5.45)

Resultant values of the new position radii, ensuring transition of the system from stable regular spin to the flipping unstable motion, are as follows: r _x1 = 581, r _y1 = 480 and r _z1 = 592 mm. Therefore, to trigger the spinning motion, it is just necessary to move paired masses from initial positions (shown in Fig. 5.40 with white spheres) to their new positions, shown with black spheres. For better perception of the 3D design, an imagined semi-transparent xz plane is added to the figure.

For the system, initially satisfying I _yy,i < I _xx,i < I _zz,i condition, rapid assignment at t = 10 s of the new moments of inertia, satisfying now I _xx,1 < I _yy,1 < I _zz,1 condition, transfers regular y spin motion into unstable spin. Its period can be calculated using Eqs. (5.15, 5.16, 5.17, 5.18 and 5.19) for the corresponding regular spin conditions at t = 10 s:

• I _xx,1 = 3, I _yy,1 = 4.8, I _zz,1 = 5, ω _x1 = −0.2917, ω _y1 = 5.0284, ω _z1 = −0.6714.

Calculations give us T = 17.784 s; therefore, the time to 180° flip would be T/2 = 8.8920 s. At this very moment, rapid “Morphing-2” should be applied to stop flipping phase and stabilise the system. For this morphing, in accordance with [3], any set of new moments of inertia can be selected, strictly satisfying any of the two conditions: I _yy,2 < I _xx,2 < I _zz,2 (“solution I _yy min” strategy) or I _xx,2 < I _zz,2 < I _yy,2 (“solution I _yy max” strategy). In one case scenario, return to the initial moments of inertia can be implemented. However, as an additional example, we illustrate implementation of the I _xx = 3, I _yy = 5.2, I _zz = 5 (“solution-1” strategy) scenario. To achieve these new inertia characteristics, as per Eq. (5.39), spacecraft control masses should be rapidly moved to their final positions: r _x2 = 671, r _y2 = 374 and r _z2 = 894 mm.

The described morphings (achieved via controlled changes in r _x(t), r _y(t) and r _z(t)), time histories for the resulting moments of inertia, angular velocity and angular momentum components are presented in Fig. 5.41. Interestingly, that rapid changes in ω _y and I _yy do not lead to similar changes in ${\overline{H}}_y$. Also, as evidenced by Fig. 5.41c, the total angular momentum $|\overline{\mathbf{H}}|$ is conserved during the flipping acrobatics (Figs. 5.42 and 5.43).

Fig. 5.41

Variation of the system’s parameters during fast 180 degrees inversion: (a) principal moments of inertia and their derivatives, (b) angular velocity and non-dimensional angular momentum components and (c) Euler angles

Fig. 5.42

Radii of the KEE and kinetic energy E of the system during 180 degrees inversion

Fig. 5.43

Collocated AMS and KEE for different stages of the 180° inversion: (a) t = 0.6 s, (b) t = 2.1 s, (c) t = 9.9 s, (d) t = 10s, (e) t = 13.1 s, (f) t = 14.2 s, (g) t = 14.7 s, (h) t = 16.4 s and (i) t = 19–28 s

10.4 Slow 180 Degrees Inversion of the Spacecraft (Figs. 5.44, 5.45 and 5.46)

The same principle can be used for complete reconfiguration (“repackaging”) of the articulated compound spacecraft, consisting, for example, of three segments A ₁-B ₁, B ₂-C ₂ and C ₃-D ₃. If all of these segments are un-docked, they can independently perform the same flipping manoeuver, as described above, and then (after stabilisation) docked to a new configuration: B ₁-A ₁, C ₂-B ₂ and D ₃-C ₃. Note that the reconfiguration can be applied to the selected segments only and to the spacecraft with any number of segments. For example, if only central segment B ₂-C ₂ is inverted, the new configuration would be A ₁-B ₁, C ₂-B ₂ and C ₃-D ₃.

Fig. 5.44

Variation of the system’s parameters during slow 180 degrees inversion: (a) principal moments of inertia and their derivatives, (b) angular velocity and non-dimensional angular momentum components and (c) Euler angles

Fig. 5.45

Variation of the system’s parameters during slow 180 degrees inversion: (a) values of the semi-major axes and (b) AMS and KEE for the initial instant (on the left) and after completion of the I (on the right)

Fig. 5.46

180 degrees inversion of the spacecraft, using IM: flipping acrobatic spacecraft “draws” on the dome with y intermediate body axis (on the left) concurrently with the AMS/KEE simulation Virtual Reality control panel (on the right): (a) spacecraft initially is in stable spin; (b–d) transition stage, when spacecraft flips after unstable mode is activated with first IM; and (e) spacecraft is in stable spin, stabilised with the second IM

11 Inertial Morphing in Novel Designs of Acrobatic Spacecraft for De-tumbling: Method of “Installing into Separatrix” with Polhode-Separatrix-Pole or Polhode-Polhode-Separatrix-Pole Transfer

11.1 Application of Inertial Morphing to the Tumbling Spacecraft Model: Observations

In the classical “Garriott’s-Dzhanibekov’s effect” cases, the rigid body is “given” and its inertial properties are assumed fixed. Moreover, typically, it is assumed that the rigid body/system is provided with most prominent rotation about the y-axis, with two other rotations being very small.

Let us explore more general case where we will also allow other rotations to be more significant. Assume, for example, the following parameters of the system: I _xx = 0.3, I _yy = 0.395, I _zz = 0.4 (all in kg × m²), with the initial conditions ω _x,i = 3, ω _y,i = 15, ω _z,i = 0.1 (all in rad/s). System can be simulated, using Eq. (5.7). The time history of the angular velocity components is given with Fig. 5.47 . Firstly it shows that the initially small x-rotation is quickly evolving and becoming comparable with initially dominant y-rotation. Also, it shows that the pattern of motion is different from the observations in the Garriott’s–Dzhanibekov’s effect cases: the angular velocity curves are free from distinct sharp gradients, which prompts that there are no intermitted fast and slow phases.

Fig. 5.47

Time histories of the parameters of the study case system with I _xx = 0.3, I _yy = 0.395, I _zz = 0.4 (all in kg × m²), with the initial conditions ω _x0 = 3, ω _y0 = 15, ω _z0 = 0.1 (all in rad/s): (a) angular velocities and (b) Euler angles

Quick analysis of the Euler angles in Fig. 5.47 suggests that the motion of the body can be characterised as tumbling, due to active involvement of several rotations.

The $\overline{H}$ sphere and K ellipsoid can be also constructed for the case. They are shown in Fig. 5.48, which shows two lines of intersection between $\overline{H}$ sphere and K ellipsoid, with only one being the solution hodograph. Figure 5.48 also confirms previous observation: the density of the step points on the hodograph is rather uniform, and the arrows of the quiver plot have almost the same length.

Fig. 5.48

Angular momentum sphere (AMS) and kinetic energy ellipsoid (KEE) for the system with compound rotations

In the following series of experiments, we will be using extended Euler’s equations, taking into account variations in the system’s moment of inertia.

In the next several experiments, we will be starting simulation of the system with these parameters, I _xx = 0.3, I _yy = 0.395, I _zz = 0.4 (all in kg × m²), with the initial conditions ω _x,i = 3, ω _y,i = 15, ω _z,i = 0.1 (all in rad/s), and then will initiate morphing of the system at different times in the experiments.

Firstly, let us apply morphing, as per Fig. 5.49 .

Fig. 5.49

Time history of the controlled manipulation with the moment of inertia I _yy

Reduction of the y moment of inertia leads to the slight increase in its y angular velocity, as evidenced by Fig. 5.50a with time histories of angular velocity components.

Fig. 5.50

Simulated results for the inertial morphing in Fig. 5.49 applied at t = 3.32 s: (a) time histories of the angular velocity components; (b) AMSs (blue) and KEEs (red) shown before (on the left) and after (on the right) inertial morphing was initiated at t = 3.32 s; (b) continuous hodograph of the non-dimensional angular momentum vector

In fact, as the angular momentum is conserved, the ω _y is expected to increase to 15*(0.395/0.350) = 16.9 rad/s. However, this leases to the change in the kinetic energy of the system: change from 45.79 to 51.32 [kg × m²/s²]. As a result of this, the semi-major axes of the energy ellipsoid should be re-calculated, using Eq. (5.12), giving us the following numbers:

• Initial semi-major axis of the KEE: 0.8746, 1.0036, 1.0099

• Final semi-major axis of the KEE: 0.9271, 1.0014, 1.0706.

These numbers suggest that the kinetic energy ellipsoid is now bulging more in the areas of its poles. In view of changed K shape, we now need to show two sets of collocated $\overline{H}$ sphere and K ellipsoid, corresponding to the stages before and after morphing (applied at 3.32 s), as shown in Fig. 5.50 .

Note that the angular velocity vector is now escaping from its initial hodograph, leaving it at the point S (corresponding to 3.32 s) and continuing its motion along another trajectory on another $\overline{H}$ sphere from point S.

It is interesting to realise that the hodograph trajectory is very sensitive to the instant of initiation of morphing. To illustrate this, we perform two more experiments, this time, applying morphing at 4 s. Geometric interpretation of this case, presented in Fig. 5.51, shows that the after-morphing hodograph is now circling around the z-axis, which is in contrast to Fig. 5.50, showing coning/circling about x-axis. Figure 5.51 is also suggesting that the period of the circling has been reduced after the morphing.

Fig. 5.51

Simulated results for the inertial morphing in Fig. 5.49 applied at t = 4 s: (a) time histories of the angular velocity components; (b) AMSs (blue) and KEEs (red) shown before (on the left) and after (on the right) inertial morphing was initiated at t = 4 s; (c) continuous hodograph of the non-dimensional angular momentum vector for the case of inertial morphing, initiated at t = 4 s

Two more cases are presented for completeness. They are illustrated with Figs. 5.52 and 5.53. They look similar in terms of the rotational motion; however, their hodographs are at the different poles of the $\overline{H}$ sphere, on the “North” and on the “South” poles.

Fig. 5.52

Simulated results for the inertial morphing in Fig. 5.49 applied at t = 5 s: (a) time histories of the angular velocity components; (b) AMSs (blue) and KEEs (red) shown before (on the left) and after (on the right) inertial morphing was initiated at t = 5 s; (c) continuous hodograph of the non-dimensional angular momentum vector for the case of inertial morphing, initiated at t = 5 s

Fig. 5.53

Simulated results for the inertial morphing in Fig. 5.49 applied at t = 8 s: (a) time histories of the angular velocity components; (b) AMSs (blue) and KEEs (red) shown before (on the left) and after (on the right) inertial morphing was initiated at t = 8 s; (c) continuous hodograph of the non-dimensional angular momentum vector

These simple experiments with the application of the same inertial morphing are showing importance of the instant, when this IM is applied, and also they show variety of results to be achieved. In particular, it was possible from common initial polhode to transfer to new polhodes around various body axes. Essentially, in all of these experiments, we were able to transfer from one polhode to another. In the next section, a rigorous method of selection of the new polhode and timing for the IM will be presented and illustrated with particular examples.

11.2 Formulation of the Conceptual Solution for De-tumbling of the Spacecraft, Using “Installing into Polhode” via “Polhode-to-Polhode” Transfer

Figure 5.54 shows a conceptual of the “installing into polhode” method with “polhode-to-polhode transfer, with the conjugate transition point shown as white dot. It is important that this can be seen as transition between polhodes, associated with different poles, being z and y poles in this example. As a particular case, the second polhode can be selected to be a separatrix. And this case is presented in the next section.

Fig. 5.54

Conceptual demonstration of the “installing into polhode” method with “polhode-to-polhode transfer, with the conjugate transition point shown as white dot

11.3 Detailed Example on “Installing into Polhode” via “Polhode-to-Polhode” Transfer (Fig. 5.55)

Fig. 5.55

Non-dimensional angular momentum spheres with polhodes and separatrices and truncated specific hodographs for (a) Phase-1 (before inertial morphing) conditions – I _xx = 2, I _yy = 3, I _zz = 4, ω _x,i = 0.4, ω _y,i = 1, ω _z,i = 0.8; specific hodograph shown with blue line – and (b) Phase-2 (after inertial morphing) conditions: I _xx = 3.5, I _yy = 3, I _zz = 4, ${\omega}_{x,t_Q}=0.7133,{\omega}_{y,t_Q}=-0.7318,{\omega}_{z,t_Q}=0.9016,{t}_Q=21.5\;s$; hodograph shown with red line

Figure 5.56(a) shows non-dimensional angular momentum sphere with two separatrices and sets of representative polhodes for the wide range initial conditions. It also shows, as a blue bold line, a specific polhode (or hodograph of the $\overline{\mathbf{H}}$ vector) for the Phase-1 conditions: I _xx = 2, I _yy = 3, I _zz = 4, ω _x,i = 0.4, ω _y,i = 1, ω _z,i = 0.8.

Fig. 5.56

Illustration of the transition between Phase-1 and Phase-2 of the inertial morphing of the system: (a) side 3D view; (b) z-axis 2D view

If the spacecraft possesses inertial morphing capabilities, then the “switch” to any new inertial properties can be simulated and illustrated graphically. Let us assume, for illustration purposes, that the new principal moments of inertia are I _xx = 3.5, I _yy = 3, I _zz = 4. Then, for the Phase-2, its own non-dimensional angular momentum sphere with two separatrices and sets of representative polhodes (for the wide range initial conditions) can be also produced (see Fig. 5.56b). Morphing can be applied at any stage during the execution of Phase-1. For certainty, let us also assume that the morphing is rapidly applied at t = 21.5 s instant. Then, the new corresponding angular velocities of the spacecraft could be calculated, using Eqs. (5.36).

11.4 Control Method of Installing into Separatrix Using Inertial Morphing: Geometric Interpretation

Using torque-free case Euler’s Eq. (5.3) and employing numerical simulator of the rotational motion of the morphing spacecraft [3], let us produce various sets of the feasible polhodes. Figure 5.57 presents three contrast cases, where I _xx < I _yy < I _zz and intermediate value of I _yy is (a) close to I _xx, (b) almost equally distant from I _xx and I _zz and (c) I _yy close to I _zz. These three cases are characterised with the following non-dimensional ratios between the principal moments of inertia I _xx: I _yy: I _zz: (a) 1:1.02:1.26; (b) 1:1.144:1.26; (c) 1:1.22:1.26.

Fig. 5.57

Feasible polhodes for three contrast cases, characterised with the same minimum and maximum values of principal moments of inertia but different intermediate values (hence, ratios I _xx: I _yy: I _zz): (a) I _xx = 2.5; I _yy = 2.55; I _zz = 3.15, (b) I _xx = 2.5; I _yy = 2.86; I _zx = 3.15, (c) I _xx = 2.5; I _yy = 3.05; I _zz = 3.15 (all in kg × m²); (d) x-view of Case (c); (e) minus y-view of Case (c); (f) z-view of Case (c)

It is quite clear that polhodes can be grouped, based on their “association” with the y (also coinciding with ${\overline{H}}_x$) and z (also coinciding with ${\overline{H}}_z$) axes, both being stable axes of rotation. Figure 5.57 distinguishes with bold black lines transition polhodes (called separatrices) between two areas of stable periodic rotations about the x and z axes. Note that separatrices pass through the y (coinciding with ${\overline{H}}_y$) – axis of intermediate inertia.

The separatrices, shown in Fig. 5.57, are critical for the explanation of the “Garriott’s-Dzhanibekov’s effect” and “tennis racket theorem” [3], during which the object being spun about their intermediate axis y is performing periodic flips, seen as the periodic change of its attitude in the global coordinate system by 180°. As it can be observed from the Fig. 5.57, during the Garriott’s-Dzhanibekov’s effect classical demonstration, for example, using T-handle [14], the system is usually provided with predominant rotation about its axis, coinciding with the intermediate moment of inertia axis. Using the geometric interpretation, it can be said that at the initial instant, the system is “inserted” in one of the saddle points on the y-axis (i.e. point #3 or #4 in Fig. 5.13 notations), where separatrices intersect.

Therefore, any small applied disturbance leads to the trigger of the unstable motion along one of the polhodes, standing very close to one of the separatrices, shown in bold black in Fig. 5.57.

For completeness, we should compare the shapes of the polhodes, as seen from various points of view. For this purpose, we take the AMS with plotted polhodes for the case shown in Fig. 5.5c (I _x: I _y: I _z = 2.5: 3.05: 3.15). Then we show in Fig. 5.57 (d)–(f) three orthogonal projections of the AMS for case (c).

Polhode projections on the $\left({\overline{H}}_y,{\overline{H}}_z\right)$ plane (shown in Fig. 5.57d) are represented by ellipses. In the illustrated case, these ellipses have small eccentricity and resemble circles. However, strictly speaking, they are ellipses.

Polhode projections on the $\left({\overline{H}}_x,{\overline{H}}_z\right)$ plane (shown in Fig. 5.57e) are represented by hyperbolas. However, projections of the separatrices are given by straight lines, and we will prove this shortly. These projections of the separatrices along the intermediate axis view are the key for the proposed method.

Polhode projections on the $\left({\overline{H}}_x,{\overline{H}}_y\right)$ plane (shown in Fig. 5.57f) are represented by ellipses. For the particular set of selected principal moments of inertia in the demo case, these ellipses have high eccentricity.

Comparison of the polhodes in Fig. 5.57a, b, c, viewed from the intermediate axis direction y shows that the tilt of the separatrices varies within substantial range and is a function of the relative location of the intermediate moment of inertia I _yy between the minimum value of the principal moments of inertia (I _xx) and the maximum value of the principal moments of inertia (I _zz). Next, we establish analytical relations for these parameters.

In this current study we consider various cases of the inertial morphing, during which each of the initially assigned body axes, x, y and z could become an intermediate axis. However, for derivation of some useful analytical relationships, let us assume first that:

$$ {I}_{xx}<{I}_{yy}<{I}_{zz} $$

(5.46)

This assumption would also mean that:

$$ {a}_x<{a}_y<{a}_z $$

(5.47)

If, in view of these assumptions, we divide Eq. (5.23) by ${a}_y^2$ and subtract resultant equation from Eq. (5.30), we can eliminate ${\overline{H}}_y$, which leads us to a very important relationship, describing slopes of the projections of the separatrices on the $\left({\overline{H}}_x,\kern0.5em {\overline{H}}_z\right)$ plane, being normal to the intermediate axis:

$$ \frac{{\overline{H}}_x}{{\overline{H}}_z}=\sqrt{\frac{a_x^2\left({a}_z^2-{a}_y^2\right)}{a_z^2\left({a}_y^2-{a}_x^2\right)}}=\sqrt{\frac{1-{a}_{yz}^2}{a_{yx}^2-1}};\kern2em \left(\mathrm{only}\ \mathrm{valid}\ \mathrm{if}\kern0.5em {I}_{xx}<{I}_{yy}<{I}_{zz}\right) $$

(5.48)

where a _yz = a _y/a _z and a _yx = a _y/a _x.

From Eq. (5.31) we can conclude that:

$$ \frac{I_{xx}}{a_x^2}=\frac{I_{yy}}{a_y^2}=\frac{I_{zz}}{a_z^2}= const $$

(5.49)

In view of this, we can present Eq.(5.48) in an alternative format:

$$ \frac{{\overline{H}}_x}{{\overline{H}}_z}=\sqrt{\frac{I_x\left({I}_z-{I}_y\right)}{I_z\left({I}_y-{I}_x\right)}} $$

(5.50)

Let us call the α-angle from the vertical direction ${\overline{H}}_z$ to the plane of separatrix a tilt angle. Then:

$$ \alpha =\arctan \left(\frac{{\overline{H}}_x}{{\overline{H}}_z}\right);\kern2em \left(\mathrm{only}\ \mathrm{valid}\ \mathrm{if}\kern0.5em {I}_{xx}<{I}_{yy}<{I}_{zz}\right) $$

(5.51)

As an example, we produce a particular plot of the values of the α-angle during variation of I _yy between given values of I _xx = 2.4 and I _zz = 3.15 to be used in the upcoming simulation cases (Fig. 5.58).

Fig. 5.58

Variation of the α-angle for separatrix (measured from vertical) due to the variation in I _yy, based on Eqs. 5.50 and 5.51

However, in this work we are dedicated to the non-dimensional construction of the analytical tools. With this in mind, let us represent results in Eqs. (5.44 and 5.45) in non-dimensional format. For this purpose, let us employ a non-dimensional variable ξ introduced with Eq. (5.10), enabling to express the value of the intermediate moment of inertia via Eq. (5.11), reproduced below:

$$ {I}_{yy}={I}_{xx}\left(1-\xi \right)+{I}_{zz}\xi $$

(5.52)

Zero value of ξ would now correspond to I _xx and unit value of ξ would correspond to I _zz and any intermediate value of I _yy could be expressed via 0 < ξ < 1.

With these notations, Eqs. (5.44 and 5.45) can be now expressed as a function ofξ:

$$ \alpha =\arctan \left(\sqrt{\left(\frac{I_{xx}}{I_{zz}}\right)\left(\frac{1}{\xi }-1\right)}\right);\kern1em \left(\mathrm{only}\ \mathrm{valid}\ \mathrm{if}\kern0.5em {I}_{xx}<{I}_{yy}<{I}_{zz}\ \mathrm{and}\ 0<\xi <1\right) $$

(5.53)

Equation (5.47) can be plotted as a 3D surface, corresponding to the α, being a function of two non-dimensional variables: (1) variable ξ, describing relative “location” of I _yy between I _xx and I _zz, and (2) ratio (η = I _xx/I _zz), which is subject to the inequalities 0 < I _xx/I _zz < 1. This 3D surface plot is shown in Fig. 5.59, together with superimposed plot from Fig. 5.58 and also level lines, corresponding to the angles α = [10°, 20°, 30°, 40°, 50°, 60°, 70°, 80°], i.e. with equal 10° increments.

Fig. 5.59

Variation of the α-angle for separatrix (measured from vertical) due to the variations in ξ and ratio (I _xx/I _zz)

As mentioned before, this study is not restricted to the cases, stipulated by Eq. (5.40), as in our work intermediate axes may vary during the simulated scenarios. In the cases of the change of the intermediate axes, for example, when intermediate axes change from y to x, (i.e. when after morphing is applied, the new moments of inertia would satisfy I _yy < I _xx < I _zz), Eqs. (5.44 and 5.45) must be rewritten as follows:

$$ \frac{{\overline{H}}_y}{{\overline{H}}_z}=\sqrt{\frac{a_y^2\left({a}_z^2-{a}_x^2\right)}{a_z^2\left({a}_x^2-{a}_y^2\right)}}=\sqrt{\frac{1-{a}_{xz}^2}{a_{xy}^2-1}};\kern2em \left(\mathrm{only}\ \mathrm{valid}\ \mathrm{if}\kern0.5em {I}_{yy}<{I}_{xx}<{I}_{zz}\right) $$

(5.54)

$$ \alpha =\arctan \left(\frac{{\overline{H}}_y}{{\overline{H}}_z}\right);\kern3em \left(\mathrm{only}\ \mathrm{valid}\ \mathrm{if}\kern0.5em {I}_{yy}<{I}_{xx}<{I}_{zz}\right) $$

(5.55)

Similarly, when intermediate axes change from y to z (i.e. when after morphing is applied, the new moments of inertia satisfy I _xx < I _zz < I _yy), Eqs. (5.50 and 5.51) must be rewritten as follows:

$$ \frac{{\overline{H}}_x}{{\overline{H}}_y}=\sqrt{\frac{a_x^2\left({a}_y^2-{a}_z^2\right)}{a_y^2\left({a}_z^2-{a}_x^2\right)}}=\sqrt{\frac{1-{a}_{zy}^2}{a_{zx}^2-1}};\kern2em \left(\mathrm{only}\ \mathrm{valid}\ \mathrm{if}\kern0.5em {I}_{xx}<{I}_{zz}<{I}_{yy}\right) $$

(5.56)

$$ \alpha =\arctan \left(\frac{{\overline{H}}_x}{{\overline{H}}_y}\right);\kern2em \left(\mathrm{only}\ \mathrm{valid}\ \mathrm{if}\kern0.5em {I}_{xx}<{I}_{zz}<{I}_{yy}\right) $$

(5.57)

As this has been mentioned before, if the spinning system is initially provided with a predominant spin about the intermediate axis of inertia, the flipping motion could be initiated. Essentially, this is a very special case of the motion, initiated with particular initial conditions. Geometrically, this would mean that the tip of the angular momentum vector of the system is initially “inserted” in one of the saddle points, where separatrices are intersecting. This means that the vector of initial angular momentum ${\overrightarrow{\mathbf{H}}}_G(0)$ is initially aligned with y-axis! And, as the angular momentum is conserved, the total vector of the angular momentum keeps its initial orientation in the global XYZ coordinate system all the time, allowing AMS to rotate about centre of the mass G in the body-axis system with y-axis periodically coming to the initial alignment with vector ${\overrightarrow{\mathbf{H}}}_G(t)$. With this, from Fig. 5.57, it is quite obvious that with this particular initial condition, the system has to follow one of the polhodes, located very close to the separatrix.

11.5 Control Method of Installing into Separatrix, Using Inertial Morphing: Selection of the IM Parameters and IM Activation Time

Let us consider a task of stabilisation of a spacecraft, which is initially in tumbling motion. Geometric interpretation of the inversion of the spinning body about its intermediate axis also offers an effective solution for this task.

Apart from traditional use of the flipping motion for spacecraft inversion, we are suggesting its another application: it can be used as a “vehicle”, pulling the angular momentum vector away from the tumbling polhode and “driving” it along the separatrix to the saddle point, which, after stabilisation at this point, can be called a “parking” point. However, the whole manoeuvre would require application of the inertial morphing a few (two or more) times!

First morphing would be required to transfer the system from its initial polhode into separatrix, corresponding to the supplementary case of unstable flipping motion. This is needed to force the $\overline{H}$ vector to get to the saddle point, where two of its components ${\overline{H}}_x$ and ${\overline{H}}_z$ are close to zero. Second morphing would be very similar to the one described in the previous section and would be required for stopping the flipping motion of the system.

During flipping process, the system’s angular velocity vector “spends” considerable time in the vicinity of the saddle points, where only one component of the angular momentum $\left({\overline{H}}_y\right)$ has the most prevailing value, with two other components $\left({\overline{H}}_x\ \mathrm{and}\ {\overline{H}}_z\right)$ having very small values. After leaving the saddle points, the angular momentum vector performs rapid transit to the opposite saddle point, using adjacent separatrix. During transition stage, all magnitudes of the angular velocity vector have comparable absolute values.

However, in the general case, when initial conditions are not selected in rather unique way, the system performs compound rotation, involving all, x, y and z rotations. One of the particular illustration cases [I _xx = 2.5, I _yy = 2.4, I _zz = 3.15 (all in kg × m²), with the initial conditions ω _x,i = −4.93, ω _y,i = 2.73, ω _z,i = 5.75 (all in rad/s)] is presented in Fig. 5.60, where polhode is shown as red line.

Fig. 5.60

Particular study case: I _xx = 2.4, I _yy = 2.5, I _zz = 3.15 (all in kg × m² ), ω _x0 = −4.93, ω _y0 = 2.73, ω _z0 = 5.75 (all in rad/s): (a) polhode (shown with red line), (b) separatrices (shown with black thick lines)

For the initiated motion shown, it may be desirable to stabilise spacecraft, reducing compound rotations (with all, ω _x, ω _y, ω _z) involved to a rotation with only y rotation.

This would mean that we need to reduce (shrink) current trajectory, given by the red polhode in Fig. 5.60 to a point, marked as #3. However, this point is only accessible from the polhode, close to the separatrix. Current separatrices, shown in Fig. 5.60b with bold black lines, are not accessible, as the current polhode does not intersect any of the separatrices.

Solving Euler’s Eqs.(5.3) for the particular case data, we can determine the maximum projected angle for the point on the polhode, denoted as α ₁ in Fig. 5.61. Its value is equal to |α ₁| = 36.1^°.

Fig. 5.61

Calculation of the important angles for the illustration study case [I _xx = 2.4, I _yy = 2.5, I _zz = 3.15, ω _x,i = −4.93, ω _y,i = 2.73, ω _z,i = 5.75]: (a) α ₁, minimum incline angle for the polhode; (b) α ₂, incline angle for the separatrix plane

Using Eqs. (5.60 and 5.61), we can calculate the incline angle of the separatrix, shown in Fig. 5.61 (being a semi-transparent y projection of the AMS in Fig. 5.60b) as α ₂. Its value is equal to |α ₂| = 65.8^°.

This prompts a solution to the task: in order for the current hodograph of the angular momentum vector trajectory (along polhode) to be switched to the saddle point, or “parking” point (shown as point #3 in Fig. 5.13), we need to aim to get to the separatrix, applying morphing to the system. In other words, we will aim to “insert” hodograph of the system into the separatrix. In order to achieve this objective, parameters of the morphing should be carefully selected to ensure that the associated incline angle |α _new|for the new inertial properties is increased and is exactly equal to |α ₁| = 36.1^°.

If we keep the values of I _xx and I _zz unchanged and if we keep the value of I _yy between I _xx and I _zz, then we can get from Eqs. (5.50 and 5.51) solution I _yy = 2.84 for this study case. Graphical solution of the task is illustrated in Fig. 5.62.

Fig. 5.62

Determination of the new morphing value of the principle intermediate moment of inertia I _yy for stabilising spin around the y-axis

Moreover, success of implementation of this solution (enabling to get to the hodograph of $\overline{H}$ vector to the parking point #3) is a subject to the right moment of activation of this morphing. In our case, we select the instant, when the angular momentum vector is in the $\left({\overline{H}}_x,{\overline{H}}_z\right)$ plane.

This concludes stage-1 (out of two) for the whole manoeuvre. When hodograph is on the orbit, which is close to the separatrix, “flipping” motion is activated. If we wish to stop flipping, another morphing is needed to convert unstable motion into stable. This can be done via application of the morphing, assigning I _yy a new value, which would be the smallest or largest value out of all moments of inertia. Therefore, there could be two classes of solutions to stabilisation of the second stage.

For demonstration purpose, we select solution-2 [5], assigning I _yy a value of 3.5, which would make I _zz a new intermediate value.

Similar to the stage-1 morphing-1, time of activation of the morphing-2 is also very important. We apply morphing at the instant, when hodograph reaches the desired one (out of two) parking point on the axis y.

11.6 Example of the “Flipping”-Assisted Stabilisation (De-tumbling) of the Tumbling Spacecraft, Using Inertial Morphing

We demonstrate in detail stabilisation of the tumbling spacecraft, using the proposed method. The key to understanding this method is with the graphical interpretation of the attitude dynamics.

Let us assume that the spacecraft with given initial values of the moments of inertia (I _xx = 2.5, I _yy = 2.4, I _zz = 3.15) is originally in arbitrary free rotation, involving all three angular velocities, as shown in Fig. 5.63a.

Fig. 5.63

Illustration of the spacecraft tumbling motion: (a) time history of ω _x, ω _y, ω _{z –} components of its angular velocity vector $\protect\overrightarrow{\boldsymbol{\upomega}}$; (b) graphical interpretation of the motion, using KEE and AMS

This motion can be visualised, using intersecting kinetic energy ellipsoid and angular momentum sphere, as shown in Fig. 5.63b. The genuine length $\overline{H}$ vector cannot be used for visualisation as its length is equal to 1, and it would not be seen at any instant, as it would be completely hidden by the embracing angular momentum sphere with unit radius. Therefore, for visualisation of the instantaneous orientation of $\overline{H}$ in Fig. 5.63b, we use a black line with a dot at its end and extruding beyond the surface of the sphere. The godograph of the $\overline{H}$ vector is shown with a black line on the surface of the angular momentum sphere, coming strictly along the intersection between the AMS and KEE.

Let us set a task to control rotations of the system, via the changes of the values of its principal moments of inertia.

In each case of using flipping mode for escaping from the closed smooth polhode, we need to apply change to moments of inertia, which could be calculated based on the parameters of the targeted separatrix, using Eqs. (5.50), (5.51) or (5.53).

An example of complete set of morphings, stabilising the system about the y-axis, being initially in the tumbling state as per Fig. 5.64, is presented in Figs. 5.65, 5.66, 5.67 and 5.68. Figure 5.65 explains the sequence and nature of inertial changes. Figure 5.66 gives consecutive snapshots from the simulation process, illustrating changes of the kinetic energy ellipsoid and polhodes – resultant feasible trajectories for the angular momentum vector. Figure 5.68 shows time histories for the angular momentum components and also values of the kinetic energy semi-major axes.

Fig. 5.64

Sets of feasible polhodes for the system with I _xx = 2.5, I _yy = 2.4, I _zz = 3.15

Fig. 5.65

Two-stage stabilisation (de-tumbling) of the tumbling spacecraft via morphing: time history of the I _xx, I _yy, I _zz

Fig. 5.66

Critical instances of spacecraft stabilisation: (a) start of the simulation; (b) initially, hodograph is “circling” around z-axis; (c) stage-1 ends, and transition to “flipping” is initiated, t = 9.792 s; (d) approach to the saddle point-1, t = 12 s; (e) near the saddle point-1 (possible “parking” or stabilisation point), t = 15 s; (f) passing saddle point-1, t = 19 s; (g) approach to the saddle point-2, t = 22 s; (h) stage-2 ends and third stage starts at t = 26 s, parking at the stable “saddle point-2 attractor” is activated and de-tumbling (stabilisation) is completed

Figure 5.65 explains the sequence and nature of the inertial changes, deliberately applied to the system. Figure 5.66 gives consecutive snapshots from the simulation process, illustrating changes of the kinetic energy ellipsoid and polhodes – resultant feasible trajectories for the angular momentum vector.

It is interesting to observe that at the initial stage of the motion of the system, its e ₂ body axis ort is “drawing” a pretty spread trajectory on the “dome” (Fig. 5.67a). However, after stabilisation is completed, this trajectory is essentially reduced to the point (Fig. 5.67b). Also, at the last stage of the simulation, trajectories for e ₁ and e ₃ are very close to the equatorial plane, which confirms that the stabilised motion is close to the rotation of the body along the direction of the angular momentum vector. The feature of the example is the final direction of the y-body axis system, selected for stabilisation in this example, which is opposite to the direction of H . If the goal of stabilisation was to have them both aligned, then third stage should be activated at instant close to 15 s, as evidenced by Fig. 5.68 .

Fig. 5.67

“Balls of wool” for (a) the first stage of spacecraft motion with tumbling/coning (t = 0 s); (b) last stage of stabilisation of the spacecraft (t = 0.6842 s) with e ₁, e ₂ and e ₃ intersection lines with the “dome”

Fig. 5.68

Time history of (a) H _total, H _x, H _y, H _z; (b) a _x, a _y and a _z during two-stage stabilisation (de-tumbling) of the tumbling spacecraft via inertial morphing

11.7 Reversing Vector of Angular Momentum on the Separatrix, Installing Its Godograph into the Same Separatrix

For any system with I _min, I _int and I _max, regardless of the values of the initial velocities ω _x , ω _y and ω _z , there is a set of two polhodes, which plane has an angle α _prime with the ${\overline{H}}_{\mathrm{max}}$ axis. For example, in case of I _xx < I _yy < I _zz, the α-angle can be calculated using Eq. (5.51) or Eq. (5.53). This can be illustrated with the pair of collocated surfaces, AMS and KEE, and for the particular illustration case, I _xx < I _yy < I _zz these two surfaces, which we will call prime surfaces, are shown in Fig. 5.69c. However, there is another pair of two surfaces, AMS and KEE, which we will call dual surfaces, with I _zz < I _yy < I _xx, which have the same intermediate axis and the same separatrix.

Fig. 5.69

Prime combinations of KEE and AMS for “Garriott’s-Dzhanibekov’s effect” flipping motion and their dual counterpart combinations: (a)–(b) for x being an intermediate axis; (c)–(d) for y being an intermediate axis; (e)–(f) for z being an intermediate axis

The “prime” and “dual” surfaces are shown in Fig. 5.69 in each row for the x, y and z flipping motions.

For the dual surfaces in the illustration example, the angle α _dual should be measured from the separatrix plane to the axis with maximum moment of inertia, and it is a complimentary angle to α _prime:

$$ {\alpha}_{\mathrm{dual}}={90}^{{}^{\circ}}-{\alpha}_{\mathrm{prime}}\kern1em \Rightarrow \kern1em \tan \left({\alpha}_{\mathrm{dual}}\right)={\tan}^{-1}\left({\alpha}_{\mathrm{prime}}\right) $$

(5.58)

The dual surfaces for Fig. 5.69c case are shown in Fig. 5.69d, located in the same row. New morphed moments of inertia for the dual case can be calculated as follows: we can first set any new values for the minimum and maximum values of the moments of inertia in a dual: I _{zz, dual} < I _{xx, dual}. And, then, the intermediate value can be calculated, using adjusted Eq. (5.53), solved for the value of the intermediate moment of inertia and for the current example, and can be written in the explicit form:

$$ {I}_{yy}=\frac{\left[{\left({\tan}^{-1}{\alpha}_{\mathrm{prime}}\right)}^2+1\right]{I}_{zz}}{{\left({\tan}^{=1}{\alpha}_{\mathrm{prime}}\right)}^2+\left(\frac{I_{zz}}{I_{xx}}\right)}=\frac{\left[{\left({\tan}^{-1}{\alpha}_{\mathrm{prime}}\right)}^2+1\right]}{{\left({\tan}^{-1}{\alpha}_{\mathrm{prime}}\right)}^2+\eta }{I}_{\mathrm{min}},\mathrm{where}\;\eta =\frac{I_{\mathrm{min}}}{I_{\mathrm{max}}}=\frac{I_{zz}}{I_{xx}} $$

(5.59)

As a particular numerical simulation example, let us consider the case of the system with initial I _xx,i = 0.3, I _yy,i = 0.35, I _zz,i = 0.4 (all in kg × m²), and ω _x,i = 0.1, ω _y,i = 15, ω _z,i = 0.1 (all in rad/s). With these conditions, the system starts classical “Garriott’s-Dzhanibekov’s” flips, during which the godograph of the non-dimensional angular momentum vector is sliding along the line, being close to the separatrix. Angle of the plane of the separatrix with the “z” axis can be determined, using Eqs. (5.50 and 5.51):

$$ \alpha =\mathrm{atan}\;\left(\mathrm{sqrt}\left(0.3\ast \left(0.4-0.35\right)/\left(0.4\ast \left(0.35-0.3\right)\right)\right)\right)\ast 180/ \pi={40.8934}^{{}^{\circ}} $$

This angle is related to the KEE, bulging over the AMS along the “z” axis. However, the same separatrix would characterise the “dual” KEE, which is bulging over the AMS along the “x” body axis, corresponding to:

$$ {I}_{xx,f}=0.4\;\mathrm{and}\;{I}_{zz,f}=0.3\left(\mathrm{all}\;\mathrm{in}\;\mathrm{kg}\times {\mathrm{m}}^2\right)\ \mathrm{and}\;{\alpha}_{\mathrm{dual}}={90}^{{}^{\circ}}-{40.8934}^{{}^{\circ}}={49.1066}^{{}^{\circ}} $$

(5.60)

Equation (5.50) can now be solved for I _yy,f or Eq. (5.59) can be used to obtain I _yy,f = 0.336.

If during the flipping motion at any stage, let say at t = 9.5 s if the values of I _xx,i = 0.3, I _yy,i = 0.35, I _zz,i = 0.4, are morphed to the new values I _xx,f = 0.4, I _yy,f = 0.336 and I _zz,f = 0.3, then the angular momentum vector, instead of continuation of its motion along the separatrix, would start moving along the same separatrix, but in the opposite direction, i.e. “backwards” along the previous path of the tip of the vector $\overline{\mathbf{H}}$, as shown in Fig. 5.70!

Fig. 5.70

Sliding of the tip of the non-dimensional angular momentum vector along the same separatrix for two different combinations of the moments of inertia: (a)–(g) direct sliding along “prime” separatrix, (h)–(i) reverse sliding along coincident “dual” separatrix

Results of the animation of the direct and reverse sliding of the godograph of the angular momentum along the same separatrix are shown in Fig. 5.70. On the snapshots, the floating view angle was used, enabling always to the extended in length vector $\overline{\mathbf{H}}$.

In addition to this case, when reversing was activated at the point, being in-between two poles, we also present results for the case, when revering was activated after the non-dimensional angular momentum vector performed full cycle along two semi-separatrices. Results of this simulation case are shown in Fig. 5.71. Figure 5.71b shows slight increase in ω _y immediately after the application of the IM at t = 13 s. This is because of the required switch for the I _yy value from 0.35 to 0.366, ensuring transition from the “prime” to the “dual” KEE, shown in Fig. 5.72. It is interesting to observe the change of the direction of the motion of the godograph on the “prime” from counterclockwise to opposite after the switch to the “dual” KEE. These directions are shown in Fig. 5.72 with red arrows. Also, the KEEs are shown as semi-transparent surfaces, enabling to see through and recognise the segments of the AMSs, covered by the KEEs.

Fig. 5.71

Simulation results for the “Garriott’s-Dzhanibekov’s effect” flipping motion with godograph sliding along “prime” and “dual” AMSs and KEEs: (a) principal moments of inertial and their rates; (b) components of the angular velocity non-dimensional angular momentum; (c) radii of the KEE

Fig. 5.72

(a) CCW is the direction of the godograph on “prime” AMS and KEE; (b) CW is the reversed direction of the godograph on “prime” AMS and KEE

11.8 Summary of the Method of Installing of the Godograph of the Non-dimensional Vector of Angular Momentum of Tumbling Spacecraft into Conjugate Separatrix

In view of the importance of this method, we are presenting its brief summary. The tumbling spacecraft with assumed I _xx < I _yy < I _zz can be represented with the polhode (shown in Fig. 5.73 with red line). For the given I _xx , I _yy and I _zz the current separatrix has a dihedral angle with z body axis. As one of the simplest manoeuvres, leaving y-axis to be an intermediate axis after the applied morphing, it is proposed to use point #1 or #2 for installing godograph of the non-dimensional angular momentum into a new separatrix, touching polhode at points #1 and #2, being intersection points between the xz plane and polhode. (Another similar simple manoeuver can involve points #3 and #4 but would require to change intermediate axis from y to x.)

Fig. 5.73

System current separatrices shown together with the current polhode and points, enabling installing into separatrices for possible switch to the new separatrices, changing motion from tumbling to flipping type

For the given I _xx and I _zz, we can select I _yy, ensuring that the separatrix for the new set of moments of inertia is passing through points #1 and #2. For this selection, we determine α -angle of inclination of the separatrix plane with respect to the z-axis [3]:

$$ {\displaystyle \begin{array}{l}\kern2em \alpha =\arctan \left(\sqrt{\dfrac{I_x\left({I}_y-{I}_z\right)}{I_z\left({I}_x-{I}_y\right)}}\right)=\arctan \left(\sqrt{\eta \left(\dfrac{1}{\xi }-1\right)}\right)\\ {}\left(\mathrm{only}\ \mathrm{applicable}\ \mathrm{for}\ \mathrm{the}\ {I}_{xx}<{I}_{yy}<{I}_{zz}\ \mathrm{notations}\ \mathrm{and}\ 0<\eta <1\ \mathrm{and}\ 0<\xi <1\right)\end{array}} $$

(5.61)

Changes in the α-angle due to the variation in both, η and ξ, are shown in Fig. 5.74. Note that for convenience, values of α-angles are presented in degrees.

Fig. 5.74

Changes in the α-angle due to the variation in both η and ξ: (a) 3D surface plot for α(η, ξ) function with colorbar added; (b) 2D projection of the α(η, ξ) surface with its contour lines: η = 0 : 0.1 : 1; α = 0 : 10 : 90

The method, described in [3], was based on the calculation of the value of the intermediate moment of inertia I _yy for the specified α-angle and known values of I _xx = 2.4 and I _zz = 3.15. For this formulation, Eq. (5.61) can be rewritten as follows:

$$ \xi ={\left\{1+\left[{\left(\tan \alpha \right)}^2/\eta \right]\right\}}^{-1} $$

(5.62)

In the particular case considered in reference [4], for I _xx = 2.4 and I _zz = 3.15, the corresponding value of η is equal to η = 0.7619; furthermore, Eq. (5.62) gives ξ = 0.5907, which (as per Eq. (5.52)) corresponds to I _xx = 2.8430.

The generic graphical method, corresponding to this procedure, is illustrated in Fig. 5.75, where α-angle (shown in degrees) is plotted as a function of ξ for various values of η = [.1, .2, .3, .4, .5, .6, .7, .8, .9, 1].

Fig. 5.75

Changes in the α-angle due to the variation in ξ for selected values of η = [1:10]/10

Alternatively, if the minimum and maximum values of the moments of inertia are fixed and the α-angle is established, then the intermediate value of the moment of inertia can be calculated, using Eq. (5.50), solved for I _yy:

$$ {I}_{\mathrm{int}}=\frac{\left[{\left(\tan \alpha \right)}^2+1\right]{I}_{\mathrm{min}}}{{\left(\tan \alpha \right)}^2+\left(\frac{I_{\mathrm{min}}}{I_{\mathrm{max}}}\right)}=\frac{\left[{\left(\tan \alpha \right)}^2+1\right]}{{\left(\tan \alpha \right)}^2+\eta }{I}_{\mathrm{min}},\mathrm{where}\;\eta =\frac{I_{\mathrm{min}}}{I_{\mathrm{max}}} $$

(5.63)

12 Inertial Morphing in Novel Designs of Acrobatic Spacecraft for 90 Degrees Inversions: Method of “Installing into Separatrix” with Separatrix-to-Separatrix Transfer

Figure 5.76 is dedicated to another possible application of inertial morphing. It illustrates 90° change of the spacecraft spin axis, using three morphing procedures: the first is to activate unstable flipping motion; second is to switch to x separatrix; and the third is to stop tumbling motion with transfer of spacecraft spin from y to a new nominated body axis, being x in this illustration example.

Fig. 5.76

Example of application of inertial morphing for inversion of spacecraft [9]: (a–e) 90° inversion, allowing change of spacecraft rotation from longitudinal to lateral

System’s initial conditions are as follows: ω _x,i = 0.01, ω _y,i = 8.57, ω _z,i = 0.01 (all in rad/s), I _xx = 3, I _yy = 2.8, I _zz = 5 (all in kg × m²). It should be noted that in Fig. 5.76 initial and final spin axes are presented in body-axis system. And in the global axis system, due to the law of conservation of angular momentum, both initial and final spin orientations are aligned with the same direction of the non-dimensional angular momentum vector $\overline{\mathbf{H}}$.

Spacecraft morphing parameters, corresponding to Fig. 5.76, are shown in Table 5.1 and are also illustrated in Fig. 5.77.

Table 5.1 Spacecraft morphed parameters in the example with 90° inversion

Fig. 5.77

Positions of the masses during spacecraft 90° inversion via inertial morphing for acrobatic manoeuvre in Fig. 5.76 (a)–(e) [9]: illustrated for six-mass spacecraft model

Initially the system is in stable spin (shown as IM0 in table). IM1 was designed to insert the system into y separatrix, similar to shown in Fig. 5.69c. This initiates a y flip, during which IM2 is applied, forcing the system to transfer to x separatrix. So, this acrobatics involves two “installing into separatrices” actions. Important control consideration is as follows: IM2 is applied at the instant when in body axes vector $\overline{\mathbf{H}}$ (to be displayed in body axes, as in Fig. 5.69c) passes intersection of x and y separatrices. IM3 is designed to stop x flips in the way shown in Fig. 5.78a. Figure 5.78b shows components of the angular velocity of the spacecraft. It is remarkable that, initially, the system had y predominant angular velocity component ω _y,i, with two other components being close to zero ω _x,i = ω _z,i ≈ 0. After three morphings, the system has only one predominant component of the angular velocity, ω _x,i, with the values of two other components being close to zero: ω _y,i ≈ 0, ω _z,i ≈ 0. At last, Fig. 5.78c shows changes of the radii of the KEE, reflecting the applied changes to the values of the moments of inertia during controlled morphings.

Fig. 5.78

Time histories of the parameters of the system: (a) moments of inertia and their time rates, (b) components of the angular velocity and non-dimensional angular momentum and (c) radii of the KEE

13 Demo of Combined Multiphase Inertial Morphing: Consecutive “Parade” of All Three Orthogonal Inversions, Associated with x, y and z Body Axes

In order to demonstrate capability of the proposed method, in Fig. 5.79 we present results for a single simulation case, during which the spinning body is reconfigured four times. The carefully selected scenario for the applied inertial morphing (changes in the system, leading to the change of the values of the principal moments of inertia) enables to achieve the following:

• (1) Established flipping motion along the y-axis (with possibility for y inversion), distinguished with a white background in Fig. 5.79

• (2) Established flipping motion along the z-axis (with possibility for z inversion), distinguished with green background in Fig. 5.79

• (3) Established flipping motion along the x-axis (with possibility for x inversion) distinguished with pink background in Fig. 5.79

Fig. 5.79

Time history of the (a) I _xx, I _yy, I _zz; (b) ω _x, ω _y, ω _z; (c) H _total, H _x, H _y, H _z; (d) a _x, a _y and a _z during four-stage “all-axes inversion parade”

So, it has been demonstrated that the predominant spin can be consecutively passed on to any of the body axis with multiple possibilities for inversion at any stage of the stabilised motion and then stabilisation of the desirable orientation. In other words, if the object had a cube shape, based on this example, it was possible to perform transition of the spinning motion of the cube, allowing exposure of each of its six faces to the direction of the initial predominant spin. We call this compound demo case “all-axes inversion parade”.

In Fig. 5.79 areas with yellow and light blue backgrounds are the transition phases. It can be seen that the angular momentum is conserved. The total simulation time for this case was 240 s, and the instants, when inertial morphings were initiated, were 16.5555 s, 30.8525 s, 111.0420 s and 157.9995 s.

Some of the most critical stages of the “parade” scenario are also illustrated in Fig. 5.80 .

Fig. 5.80

Critical instances of spacecraft “parade” of all three orthogonal inversions: (a) y inversion stage (established “flipping”), (b) tumble (orbiting x-axis), (c) x inversion stage (established “flipping”), (d) tumble (orbiting y-axis) and (e) x inversion stage (established “flipping”) (f) at “parking” point: stabilisation opportunity

It can be observed that the period of inversion stages differs significantly. Periods for the “flipping” stages can be calculated analytically [8], using elliptic integrals. They are becoming very large, especially when the values of two moments of inertia come close.

14 Enhancement of the Reorientation and Change of the Spin Axis Using Moment Wheel

For completeness of this chapter, we need to mention another powerful aspect of further enhancement of the spinning spacecraft attitude control capabilities: adding one or a set of moment reaction wheels, which are often used on various space systems [39].

Differential equations of motion of the spacecraft, equipped with wheels, could be presented as follows:

$$ \left[\begin{array}{cccccc}{I}_{xx}& 0& 0& 0& 0& 0\\ {}0& {I}_{yy}& 0& 0& 0& 0\\ {}0& 0& {I}_{zz}& 0& 0& 0\\ {}0& 0& 0& \sin \theta \sin \phi & \cos \phi & 0\\ {}0& 0& 0& \sin \theta \cos \phi & -\sin \phi & 0\\ {}0& 0& 0& \cos \theta & 0& 1\end{array}\right]\left\{\begin{array}{c}{\dot{\omega}}_x\\ {}{\dot{\omega}}_y\\ {}{\dot{\omega}}_z\\ {}\dot{\psi}\\ {}\dot{\theta}\\ {}\dot{\phi}\end{array}\right\}=\left\{\begin{array}{c}\left({I}_{yy}-{I}_{zz}\right){\omega}_y{\omega}_z-{\dot{I}}_{xx}{\omega}_x\\ {}\left({I}_{zz}-{I}_{xx}\right){\omega}_z{\omega}_x-{\dot{I}}_{yy}{\omega}_y\\ {}\left({I}_{xx}-{I}_{yy}\right){\omega}_x{\omega}_y-{\dot{I}}_{zz}{\omega}_z\\ {}{\omega}_x\\ {}{\omega}_y\\ {}{\omega}_z\end{array}\right\}\\-\left\{\begin{array}{c}{n}_{\omega_1}+{\omega}_2{l}_3-{\omega}_3{l}_2\\ {}{n}_{\omega_2}+{\omega}_3{l}_1-{\omega}_1{l}_3\\ {}{n}_{\omega_3}+{\omega}_1{l}_2-{\omega}_2{l}_1\\ {}0\\ {}0\\ {}0\end{array}\right\} $$

(5.64)

Even simple preliminary cases, involving one wheel and not sophisticated wheel’s controls (with one of them presented in Fig. 5.81), enabled us to find significant influence of this enhancement on performance of the system. In particular, it was possible to significantly influence the period of inversion, make inversions asymmetrical, etc. Authors intend to explore these capabilities in more detail in the future works.

Fig. 5.81

Shift of stabilisation point, achieved with compounding use of the inertial morphing and reaction wheel

The proposed multistage transfer method can be called a method of “installing into the separatrices”. It enables conversion of the predominant rotation about any body axis into rotation about any other body axis.

With the capability of this axis-to-axis transfer, spacecraft essentially could perform three types of inversions, associated with any of three body axes.

In order to demonstrate capabilities of the method, “all-axes inversion parade” was presented, during which the spinning system was transitioned through three consecutive stages with inversion, associated with each of the body axes, x, y and z. This is in contrast with the classical Garriott’s-Dzhanibekov’s effect demonstration, where only one axis inversion was possible.

This method enables to get precision control of the spacecraft multi-axis inversion without using conventional gyroscopes.

The method is based on the geometric interpretation of the spinning systems. It employs angular momentum sphere and kinetic energy ellipsoid, polhodes and separatrices and their evolution due to the variation of the inertia properties of the system, called inertial morphing. In this chapter, we formalised non-dimensional constructions.

15 Animations in Virtual Reality

Computer capabilities of the spinning rigid-body simulator, intended to deal with systems, enabling “inertial morphing”, were enhanced with programming of the Virtual Reality block. It enables animated visualisation of the attitude dynamics of the spinning spacecraft.

It allows the operator/designer to observe results of the control actions on the spacecraft, initiating (on the operator’s request), for example, transfers of the spacecraft from stable spin to unstable, flipping, mode and vice versa. Virtual Reality not only provides the operator with instant impression on the quality of the executed manoeuvre but also enables observation of the progression of the manoeuvre from various coordinate systems (inertial and body axes).

An example of the simulation of the scenario is shown in Fig. 5.82. During this simulation, the stable spacecraft is transferred into the unstable mode, performs one flip (i.e. changes its axial attitude by 180°) to direct its antenna and then is stabilised by the operator, with flipping completely stopped. Various controls and diagnostics on the progression of the scenario are displayed on the screen, including notification on the current control status, for example, “Garriott’s-Dzhanibekov’s effect” is “OFF” or “ON”.

Fig. 5.82

Computer screen snapshot, presenting one of the instants in the animated scenario, involving control of the “Garriott’s-Dzhanibekov’s effect”

16 Examples of the Conceptual Designs of the Inertially Morphed Systems

16.1 Example-1 Design, Involving “Six-Masses” Repositioned Along Body Axes

Figure 5.83 shows a simple “six-mass” model of the rotating system, where masses in pairs can be independently repositioned along their respective axes. This reposition is done symmetrically in each pair and can be performed with independent actuators.

Fig. 5.83

Illustration of the “six-mass” model, with masses symmetrically repositioned in pairs via their translation along the x, y and z axes

Variation of the principal moments of the inertia of the system I _xx, I _yy and I _zz with controlled parameters r _x, r _y and r _z can be described with the following analytical relationships:

$$ {\displaystyle \begin{array}{l}{I}_{xx}=2\times \left[{m}_y{r_y}^2+{m}_z{r_z}^2\right]\\ {}{I}_{yy}=2\times \left[{m}_z{r_z}^2+{m}_x{r_x}^2\right]\\ {}{I}_{zz}=2\times \left[{m}_x{r_x}^2+{m}_y{r_y}^2\right]\end{array}} $$

(5.65)

These can be illustrated graphically as 3D surfaces. To be specific, three surfaces, corresponding to I _xx, I _yy and I _zz, are plotted in Fig. 5.84a for the example, given by the following parameters: m _1x = m _2x = m _1y = m _2y = 0.5 kg, m _1z = m _2z = 0.3 kg – and the radii for the masses m _1z and m _2z are equal to r _z = 0.3 m.

Fig. 5.84

Illustration of the “six-mass” model, with masses symmetrically repositioned in pairs along the x, y and z axes

Figure 5.84 shows that in the illustration example, there could be found numerous combinations of r _x and r _y for which the green surface, corresponding to I _yy, could take lowest, intermediate and highest positions. With this, if the system is provided with y initial predominant rotation, even for the fixed r _z, proper selection of varied r _x and r _y could switch the rotation about the y axis between the stable spin and unstable flipping motion. For example, if the system starts with r _x = 0.3 m, r _y = 0.1 m, r _z = 0.3 m, ω _x = 6 rad/s, ω _y = 0.01 rad/s, ω _z = 0.01 rad/s, we should expect this spin to be stable, because for the given parameters, I _yy would be the maximum moment of inertia (see point A in Fig. 5.84). If using translational actuators for the masses m _x and m _y can change position of these masses to the new values, let us say r _x = 0.1 m, r _y = 0.15 m, and no change to r _z = 0.3 m, then for the new radii of the masses, I _yy would become an intermediate moment of inertia (shown as point B in Fig. 5.84), and the unstable flipping motion would be triggered. If afterwards, at the time of passing the pole by the system’s angular momentum vector, another morphing is applied (setting r _y = 0.27 m), and with no changes applied to (leaving them at r _x = 0.15 m and r _y = 0.3 m), then the moment of inertia I _yy (shown as point C in Fig. 5.84) would become the minimal moment of inertia, and the flipping motion of the system would be transferred to the stable spin.

Figure 5.85 complements design process and shows periods of the flipping motions of the “six-mass” design for various combinations of r _x and r _z. This function is shown as a 3D surface for the fixed value of the distance r _y = 0.12 m. It confirms that proper selection of r _x, r _y and r _z would not only allow desired manipulations with the principle moments of inertia of the system but would also enable selection of the desired period of the flipping motion. This may be important for the cases, where agile or prolonged manoeuvre would be required.

Fig. 5.85

Period of the flipping motion T = T(r _x, r _z) as a function of the x and z positions of the m _x and m _z masses in the six-mass model for fixed r _y = 0.12 m

16.2 Example-2 Design: “Scissors” Model for Inertial Morphing

Figure 5.86 shows an example of using the “XZ scissors” mechanism for performing changes to the inertial properties of the system. It enables that the system remains dynamically balanced about any of the body axes. Figure 5.86 presents configuration of the same system, but with different angles β between the m _x-m _x links and the “x” axis (being kept by the mechanism the same as the angle between the m _z-m _z links and the x axis), which can be controlled with a single actuator, which will be called β-actuator (not shown in the Fig. 5.86). It is assumed in the presented example, the synchronously symmetric positions r _y of the y masses.

Fig. 5.86

Illustration of the “XZ scissors” mechanism, employed to perform controlled inertial morphing of the system: (a)–(h) correspond to the following angles between the m _x-m _x link and the x axis (also synchronised with the angle between the m _z-m _z link and the x axis): β = 10°, 20°, 30°, 40°, 50°, 60°, 70°, 80°

Variation of the principal moments of the inertia of the system I _xx, I _yy and I _zz with both controlled parameters, β and r _y, can be described with the following analytical relationships:

$$ {\displaystyle \begin{array}{l}{I}_{xx}=2\times \left[{m}_x{\left({r}_x\sin \beta \right)}^2+{m}_z{\left({r}_z\sin \beta \right)}^2+{m}_y{r}_y^2\right]\\[12pt] {}{I}_{yy}=2\times \left({m}_x{r}_x^2+{m}_z{r}_z^2\right)\\[12pt] {}{I}_{zz}=2\times \left[{m}_x{\left({r}_x\cos \beta \right)}^2+{m}_z{\left({r}_z\cos \beta \right)}^2+{m}_y{r}_y^2\right]\end{array}} $$

(5.66)

These can be illustrated graphically as 3D surfaces. To be specific, three surfaces, corresponding to I _xx, I _yy and I _zz, are plotted in Fig. 5.87(a) for the example, given by the following parameters: m _1x = m _2x = m _1z = m _2z = 0.3 kg, m _1y = m _2y = 0.5 kg – and the length L of all radii for the masses m _1x, m _2x, m _1y, m _2y, m _1z and m _2z is equal to r _x = r _y = r _z = L = 0.25 m.

Fig. 5.87

Principal moments of inertia of the system in Fig. 5.86 as functions of β and r _y variables, which can be controlled individually by two actuators: (a) 3D representation and (b) 2D representation

Figure 5.87b shows the same plot, but with different axes limits and as the top view. It is interesting to observe that if the design with r _y = 0.25 m β = 45° is initially provided with the predominant rotation about the y axis, the system would remain in the stable spin, and as for the specified parameters, I _yy would be the maximum moment of inertia, being larger than any other moments of inertia, I _xx and I _zz (I _xx < I _yy and I _zz < I _yy). However, should the angle θ be increased well above 49° or reduced well below 41° (with the r _y kept unchanged at r _y = 0.25 m), then the I _yy would become an intermediate moment of inertia, and the flipping motion would be triggered with the first, β-actuator. Similarly, the I _yy would become an intermediate moment of inertia if the angle β is kept unchanged at β = 45° but the r _y value is increased well above r _y = 0.1935 m, using the second, β-actuator. Therefore, in the illustration example, transition from stable spin to unstable flipping motion can be independently triggered by any of the two system’s actuators or by combined action of two actuators.

Figure 5.88 complements design process and shows periods of the flipping motions of the “scissors” design for various combinations of r _y and β. This function is shown as a 3D surface for the fixed value of the distance to the masses in the xz plane.

Fig. 5.88

Period of the flipping motion T = T(r _y, β) as a function of the r _y and β parameters in the “scissors” model: (a) T = T(r _y, β) presented as 3D surface, (b) T = T(r _y, β) presented as 2D plot

16.3 Example-3 Design: Rhombus Model for Inertial Morphing

Figure 5.89 shows an example of using the “XZ rhombus” mechanism for performing changes in the inertial properties of the system. It enables that the system remains dynamically balanced about any of the body axes. Figure 5.89 presents configuration of the same system, but with different angles β between the m _x-m _z links and the x axis, which can be controlled with a single actuator, which will be called β-actuator (not shown in Fig. 5.89). It is assumed in the presented example, the synchronously symmetric positions r _y of the y masses can be varied separately, with another r _y -actuator (also not shown in Fig. 5.89).

Fig. 5.89

Illustration of the “XZ rhombus” mechanism, employed to perform controlled inertial morphing of the system: (a)–(h) correspond to the following angles between the m _x-m _z links and the “x” axis: β = 10°, 20°, 30°, 40°, 50°, 60°, 70°, 80°

Variation of the principal moments of the inertia of the system I _xx, I _yy and I _zz with both controlled parameters, β and r _y, can be described with the following analytical relationships:

$$ {\displaystyle \begin{array}{l}{I}_{xx}=2\times \left[{m}_y{r}_y^2+{m}_z{\left(L\sin \beta \right)}^2\right]\\[12pt] {}{I}_{yy}=2\times \left[{m}_x{\left(L\cos \beta \right)}^2+{m}_z{\left(L\sin \beta \right)}^2\right]\\[12pt] {}{I}_{zz}=2\times \left[{m}_y{r}_y^2+{m}_x{\left(L\cos \beta \right)}^2\right]\end{array}} $$

(5.67)

These can be illustrated graphically as 3D surfaces. To be specific, three surfaces, corresponding to I _xx, I _yy and I _zz, are plotted in Fig. 5.90a for the example, given by the following parameters – m _1x = m _2x = m _1y = m _2y = m _1z = m _2z = 0.3 kg – and the length L of the m _x-m _z links is equal to 0.25 m.

Fig. 5.90

Principal moments of inertia of the system in Fig. 5.89 as functions of β and r _y variables, which can be controlled individually by two actuators: (a) 3D representation and (b) 2D representation

Figure 5.90b shows the same plot, but with different axes limits and as the top view. It is interesting to observe that if the design with r _y = 0.15 m, β = 45° is initially provided with the predominant rotation about the y axis, the system would remain in the stable spin, and as for the specified parameters, I _yy would be the maximum moment of inertia, being larger than any other moments of inertia, I _xx and I _zz (I _xx < I _yy and I _zz < I _yy). However, should the angle β be increased well above 53° or reduced well below 37° (with the r _y kept unchanged at r _y = 0.15 m), then the I _yy would become an intermediate moment of inertia, and the flipping motion would be triggered with the first, β-actuator. Similarly, the I _yy would become an intermediate moment of inertia if the angle β is kept unchanged at β = 45°, but the r _y value is increased well above r _y = 0.1767 m, using the second, β-actuator. Therefore, in the illustration example, transition from stable spin to unstable flipping motion can be independently triggered by any of the two system’s actuators or by combined action of two actuators.

16.4 Example-4 Design: Two Cylinders System

Figure 5.91 shows an example of using the two cylinders mechanism for performing changes in the inertial properties of the system. In this conceptual design, two cylinders of length L are synchronously translated in opposite directions to keep symmetry. Initial position of the cylinders is shown with green colour, and an example of the intermediate position with outwards translations is shown with yellow colour. Direction of morphing translations for cylinders is shown with equal size thick black arrows. It enables that the system remains dynamically balanced about any of the body axes. Figure 5.91 presents configuration of the same system, but with different positions of the cylindrical masses along y axis, which can be controlled with a single actuator, which will be called r _y-actuator (not shown in the figure), ensuring the synchronously symmetric repositioning r _y of the y masses.

Fig. 5.91

Illustration of the two cylinders conceptual mechanism, employed to perform controlled inertial morphing of the system: (a) cylinders are moved outwards; (b) cylinders are moved inwards

Variation of the principal moments of the inertia of the system I _xx, I _yy and I _zz with one controlled parameter, r _y, can be described with the following analytical relationships:

$$ {\displaystyle \begin{array}{l}{I}_{xx}=2\times \left(\dfrac{M\;{L}^2}{12}+M\;{r_y}^2\right)={I}_{yy}+{I}_{zz}\\[12pt] {}{I}_{yy}=2\times \left(M\;{r_y}^2\right)\\[12pt] {}{I}_{zz}=2\times \left(\dfrac{M\;{L}^2}{12}\right)\end{array}} $$

(5.68)

These can be illustrated graphically as 3D surfaces. To be specific, three surfaces, corresponding to I _xx, I _yy and I _zz, are plotted in Fig. 5.92 for the example, given by the following parameters: mass of each cylinders M = 0.9 kg – the length L is varied within 0.1–0.3 m range; and the position of the cylinder parameter is varied within 0.1–0.3 m range.

Fig. 5.92

Principal moments of inertia in the “two cylinders” model, as functions of the length of the cylinder L and its distance from the y-axis r _y

Figure 5.92 shows that the limited options exist for transition to flipping motion, if the initial predominant stable spin of the system is arranged about y or z axes. The feasible combination of L and r _y parameters corresponds to the areas, where I _yy and I _zz surfaces are changing their bottom-to-top order in the Fig. 5.92.

However, as it can be seen from Eq. (5.62) and from Fig. 5.92, surface I _xx is always staying above any of the I _yy or I _zz surfaces. Therefore, if there is a goal to use the mechanism for transition from stable rotation to unstable flipping motion, this mechanism would be inefficient for this intended change, if predominant rotation of the system is selected about x axis.

As Fig. 5.92 shows, at least for large values of a _y (0.1–0.3 m), change of the distances for these cylinders from the axis of rotation is not an effective mean for changing the “status” of the axis of rotation. With this model, the intermediate axis will stay intermediate axis, regardless of the controlled distance. [The green surface is always staying between the red and yellow surfaces.]

16.5 Suggestions on Some Practical Implementation of the Inertial Morphing

This section does not aim to present comprehensive collection of the implementation of the methods to control the principal moments of inertia of the spacecraft, which we called “inertial morphing”. Nevertheless, for completeness, we wish to present just a few of the methods/concepts, being considered as promising for realization in real spacecraft systems. In these examples, for simplicity of the illustrations, the conceptual model of the spacecraft (Fig. 5.25) will be used. As equations for the moments of inertia are functions of the distances r and masses m, conceptually, there could be two main approaches to the implementation of the inertial morphing: (a) based on variation of r - positions of the masses and (b) based on variation of masses. These approaches are briefly explained below.

• (a) The first approach to implementation of the inertial morphing is based on the controlled reposition of the spacecraft masses, using actuators. Let us consider the following case: m _x = m _y = m _z = 1 kg; these masses are initially located at their radii: r _x = 0.8 m; r _y = 1 m; r _z = 1.2 m. Let us assume that the system is equipped with linear actuator (motor and appropriate mechanical system), capable of translational repositioning of the masses m _z via changing the length of r _z from 1.2 to 0.6 m within 1 s. The morphing process is shown in Fig. 5.93a, where initial positions of the masses are shown with white spheres and the final positions with black spheres and where direction of the translations for two m _z masses is shown with two red arrows. Also, for better perception of the 3D design, a semi-transparent yz plane is added to the Fig. 5.93a.

Fig. 5.93

Particular example of inertial morphing via translational reposition of the z dumbbell masses m _z while keeping positions of the x and y masses unchanged (m _x = m _y = m _z = 1 kg): (a)3D view of the spacecraft model, (b) time history of the position of the masses and (c) time history of the resulting principal moments of inertia I _xx, I _yy and I _zz

In this example, the positions of the masses on the x and y axes remain unchanged; only r _z is subject to variation (as per Fig. 5.93b). Equation (5.65) permits the calculation of the associated resulting time history of the principal moments of inertia of the system. Figure 5.93c shows that while I _zz keeps its value unchanged, during morphing, the I _xx value is changing from 4.88 to 2.72 [kg × m²] and the I _yy is changing from 4.16 to 2.0 [kg × m²]. However, most significant in the context of this work is an observation that, in this example, the role of the intermediate moment of inertia (which initially “belongs” to I _yy) is “passed” from I _yy to I _zz (at t = 0.33 s) and then is further “passed” to I _xx (at t = 0.67 s). Consequently, using only one variable r _z in the morphing process, it was possible to arrange for each of the spacecraft axes x, y and z at different stages, to become the intermediate axis of rotation.

The method, presented above, can be extended to the actuation of all masses, including m _x and m _y. With this general arrangement, the morphing would permit continuous control of the position of all masses, hence enabling assignment of any arbitrary values to the principal moments of inertia of the system, as per requirements of the morphing scenarios. Of course, these assignments should be compatible with the mechanical/electrical/thermal constrains of the particular designs/implementations of the morphing systems.

A variation of the same method may involve application of the special actuators to reposition large segments of the spacecraft. This idea is illustrated with the controlled change of the angular positions θ _i of the solar panels to manipulate the inertial properties of the spacecraft (see Fig. 5.94).

Fig. 5.94

Spacecraft, deploying solar arrays [40]

We envisage that similar implementations of the illustrated principle can be achieved in some other ways. For example, deployment of the masses, to the new destination (in any, inwards, outwards or inclined directions), can be ensured via unconstraining the pre-compressed springs, as per Fig. 5.95. This, however, would permit only a single discrete actuation. Nevertheless, it can be a good choice for the small autonomous system, where the control actions should be minimized and simplified.

Fig. 5.95

Particular example of inertial morphing via translational reposition of the “z” dumbbell masses m _z (shown with black colour) via release of the pre-constrained compressed springs (shown with red colour): (a) initial configuration and (b) masses deployed inwards

Alternatively, for continuous actuation, instead of using solid masses, heavy liquids and/or liquid metals [41] can be used, which could be controlled via manipulation with valves and employment of the passive inertial forces and/or controlled magnetic field forces to move these liquid media.

• (b) The second approach to implementation of the inertial morphing is based on the controlled change of the spacecraft masses and may involve, for example, mass ejection, ablation, evaporation or solidification of the components of the structure, etc.

Geometric reconfigurations of the spacecraft systems (e.g. during deployment of the inflatable components or solar panels and reorientation of the antennae) are a widely used concept and proved to be successful for many space systems (e.g. Spartan-207, Hughes/Boeing HS-376, SMART-1 and RAE-B satellites, space probes Rosetta and Down, etc.). However, these are provided to ensure the functionality of the spacecraft, without any relevance to the attitude dynamics objectives [42]. In contrast, concept of spacecraft reconfiguration, explicitly aiming to assist in attitude manoeuvering [3,4,5,6,7,8,9,10], is a very new concept. Indeed, idea of the reconfigurable spacecraft systems, transformable spacecraft, which consist of multiple modules connected with each other by hinges or universal joints, proposed by JAXA [43, 44], is only 3 years old, and further development of the concept is underway [45].

It is believed that this chapter will further contribute to much wider application of the spacecraft reconfigurations with the primary goal to enhance the attitude dynamics capabilities of spacecraft.

17 Conclusions

This book chapter presented development of a series of conceptual controlled scenarios, useful for real life of small spacecraft missions. It explored the possible applications of the “inertial morphing” concept, together with the method of “installing into polhodes and separatrices” for the possible applications in efficient spacecraft missions, involving small, low-weight and low-cost autonomous spacecraft with acrobatic capabilities.

We are hopeful that the proposed efficient (few actions) control methods, using inertial morphing, will pave the way for the design of real autonomous spacecraft without using conventional gyroscopic devices or enhance the traditional gyroscopic systems, adding to their operational capabilities and agility or saving energy.

The “inertial morphing” offers a general control platform for spacecraft attitude dynamics manipulations. However, in view of the immediate readiness for the practical application due to simplicity, the 180° and 90° inversions and de-tumbling of the spacecraft should be specially mentioned.

It is believed that the remarkable simplicity of the “OFF” “one control action” method of stopping flipping motion of the systems, rotating about its intermediate axis (“Garriott’s-Dzhanibekov’s effect”), and the “ON” “one control action” activation of the flipping motion of the systems, being initially set into the regular stable spin about axes with maximum or minimum principal moments of inertia, can be very attractive for the autonomous microsatellites and deep space exploration apparatus. Combination of these results in the “two control actions” method for the 180° inversion of the spinning spacecraft, with additional ability to scale the final rotational speed. This enables to use single thruster for boost and braking. This may be also useful for protection of the most fragile on-board equipment by exposing mostly protected surface towards the environmental hazards (asteroids, radiation, etc.), hence contributing to the prolonged survivability of the spacecraft and adding to the probability of success of the missions with high environmental risks.

Similarly, combination of the “OFF” and “ON” single control actions with the proposed method of “Installing (or, using other word, Inserting) into Separatrix” leads to the “three control actions” method of 90° inversion of the spacecraft.

The third, very important application of the inertial morphing is in combination of the “Installing (or Inserting) into Polhode” or “Installing into Separatrix” (“single control action” each), and “OFF” method allows de-tumbling of the spacecraft from arbitrary spatial tumbling to the regular spin about any of the body axes, selected by the space mission operator. If future spacecraft are designed with the inertial morphing capabilities, de-tumbling manoeuvre, using only “two” or “three control actions”, can be useful for facilitating the capture of the spacecraft for servicing or removal of the spacecraft after its service lifespan. This feature can also be useful for changing axis of rotation to more stable option for the long station keeping.

In summary, the list of the discovered and proposed novel capabilities, offered in spacecraft design by inertial morphing, includes but is not limited to the following:

• 1. Ability to switch on and off the “Garriott-Dzhanibekov effect”, using meticulous inertial morphings

• 2. Peculiar exposure of the sides of the flipping object to the global axis directions, illustrated with the “ball of wool” method

• 3. Ability to control flipping periods within the wide range and discovery of the 3D ridge of the parameters with high periods and two valleys with minimum periods, using the proposed “instalment into separatrices” method and “pole-to-pole” transfers

• 4. Ability to perform 180° inversions with two discrete control actions and ability to perform 90° inversions with three discrete control actions

• 5. Ability to effectively manipulate with arbitrarily rotational motions of the tumbling systems, using the proposed method of “polhode-to-polhode transfer”

• 6. Ability to de-tumble spacecraft using combination of “polhode-to-polhode-to-separatrix transfer” or “polhode-to-separatrix” and “instalment into separatrix”

• 7. Ability to reverse the direction of the slide of the tip of the non-dimensional angular momentum vector, employing “prime” and “dual” separatrices

• 8. Ability to perform conjugated “parade” of all body axes inversions

• 9. Ability to enhancement of attitude control of the spacecraft with traditional reaction wheels via added inertial morphing

The novelty of the presented materials, based on [3,4,5,6,7,8,9], includes the following:

• Utilisation of deliberately applied changed to the inertial properties of the system for its attitude control and enhancement of the spinning spacecraft attitude dynamics capabilities using inertial morphing

• Generalised geometric interpretation of arbitrary attitude motions of the morphed systems, using non-dimensional angular momentum coordinates, angular momentum sphere and kinetic energy ellipsoid

• Determination of the required IM changes and their phasing

• Development of the methods and mechanisms for inertial morphing

• Development of a general method of de-tumbling of the spacecraft and transition of the rotational motion to the rotation about any nominated body axis

• Reduction of continuous control actions to a limited number of discrete control actions (e.g. two only inertial morphings for 180° inversion and three only morphings for 90° inversion)

• Discovery of the limited exposures of tumbling and flipping bodies to specific orientation

• Establishment of the ranges of the flipping periods

• Suggestion of new spacecraft designs, enabling agile space acrobatic or prolonged attitude capabilities

• Suggestion of new space applications

• Proposition of applications of inertial morphing for the possible future space missions

• Demonstration of the proposed concepts and methods, using versatile advanced non-linear numerical simulations and virtual reality

As Euler’s equations paved the way for the development of the theory of gyroscopes and design of various gyroscopic systems, the paradigm of “inertial morphing” may prompt development of new generation of the acrobatic spacecraft with significantly reduced weight and dimensions, reduced cost and enhanced operational capabilities. It may be also possible to design new classes of gyroscopes, possessing an added-on sense of time, which is in contrast to the classical gyroscopes that only possess a sense of orientation.

With a wide spectrum of the presented examples, related to the application of a novel design concept of “inertial morphing”, it is believed that presented concept, modelling and simulation of the spinning systems and attitude control method of the spinning systems will be useful not only for the specialists but for a very wide audience, including engineers, scientists, students and enthusiasts of science and space technology.

Appendixes

1.1 Nomenclature

ψ, θ, ϕ	Euler angles
ω x, ω y, ω z	Components of the angular velocity
ω x,i, ω y,i, ω z,i	Initial components of the angular velocity
a x, a y, a z	Values of the semi-major axes of the ellipsoid of the kinetic energy
α	Angle between the plane of the separatrix and axis with maximum moment of inertia
β	Masses position angle in the “scissors” and “rhombus” mechanisms
G	Centre of the mass of the spacecraft
$\overrightarrow{\mathbf{H}}(t)$	Angular momentum vector
$H=\mid \overrightarrow{\mathbf{H}}\mid$	Value of the system’s angular moment
${\overline{H}}_x,{\overline{H}}_y,{\overline{H}}_z$	Non-dimensionalised components of the angular momentum vector
I xx, I yy, I zz	Principal moments of inertia
k	Parameter in complete elliptic integral k
K(k)	Complete elliptic integral of the first kind
K 0	Kinetic energy of the system
l	Angular momentum vector of wheels, expressed in the body-fixed reference frame
m x, m y, m z	Dumbbell masses in six-mass spacecraft model
${n}_{\omega_i}$	Control torque applied to the i-th wheel
M	Mass matrix
N x, N y, N z	Torque components
P	Pivot point
P, Q, R	Torque components in original Euler’s work
r x, r y, r z	Axial positions of the spacecraft masses in the “six-mass” model
t	Time
T	Period of the flipping motion
x, y, z	Principal body axes of the rigid body
x	Vector of system’s states

1.2 Acronyms/Abbreviations

ISS	International Space Station
AMS	Angular momentum sphere
KEE	Kinetic energy ellipsoid
IM	Inertial morphing