Low Power Current-Mode Relaxation Oscillators for Temperature and Supply Voltage Monitoring

Abstract

This chapter presents a family of current-mode relaxation oscillators that can be designed either as a compensated digital clock source, or as an oscillator-based sensor whose frequency reports the temperature or supply voltage. One compensated timer implementation in 0.18 $\upmu$m CMOS achieves a figure of merit of 120 pW/kHz, making it one of the most efficient relaxation oscillators reported to date. The oscillator design is then extended to produce a $V_{DD}$-controlled oscillator and a temperature-controlled oscillator. Finally, we introduce a low-power hybrid oscillator sensor, which encodes measurements of both the supply voltage and temperature into the durations of its two alternating digital clock phases. The underlying dual-phase current-mode relaxation oscillator and the resulting sensor circuits are easy to implement, are area- and energy-efficient, and offer straightforward power and speed tradeoffs for a wide range of applications.

1 Introduction

Timers, temperature sensors, and supply voltage monitors are fundamental components of nearly all microelectronic systems. At the low-power end of the spectrum, small embedded sensors are constrained by battery capacity or unpredictable environments, and they must make the most of limited sources of energy [1, 2]. At the high-performance end, servers rely on temperature and voltage monitors to maximize performance and power efficiency, while balancing computational loads, scaling voltage and frequency, and avoiding overheating.

Some of the constraints in microelectronic devices are fundamentally thermal limits. Implantable medical devices, despite their comparatively low power, are often constrained to only a few degrees of heating to avoid damaging the surrounding biological tissue [3]. In higher power CPUs and GPUs, power dissipation is non-uniformly distributed, and localized hot spots can deviate significantly in temperature compared to other areas of the chip, exposing some areas of the device to potential hardware failure and reduced lifespan.

Other limitations come down to timing. Low-power devices often spend much of their time in idle modes to conserve energy, and as a result a large fraction of their total energy consumption may come from circuits like wake-up timers. There are important tradeoffs between precision, power, and area in low-power oscillators. Meeting timing specification is also clearly a main design constraint in high-performance systems, where logic timing is a function of local variations in process, supply voltage, and temperature, and there is always a tension between power efficiency and operating margin. Minimizing the area and energy associated with monitor circuits is key to supporting sensing at high spatial resolution with minimal cost and interference [4, 5].

The architect and designer Frank Lloyd Wright once said, “Simplicity and repose are the qualities that measure the true value of any work of art.” A similar philosophy can apply to power optimization in microelectronic circuits. Simpler circuits often use fewer transistors, reducing power. Keeping circuits in repose by minimizing their activity also improves efficiency. Although there are numerous potential strategies for performance improvements, if the aim is for straightforward design and reliability, beauty can often be found in small, simple, and low-power circuit solutions.

This chapter begins with a description of a low-power current-mode relaxation oscillator [6]. The oscillator is initially introduced with the goal of constant frequency across temperature and supply voltage. Then, we illustrate how the oscillator can be modified to use a reference voltage intentionally sensitive to either temperature or supply voltage [7]. Three sensor designs are proposed: one dedicated temperature sensor, one dedicated supply voltage sensor, and a hybrid sensor that senses both temperature and supply voltage in two alternating phases of one oscillator.

The circuits proposed here have the benefit of extremely low design complexity. There are only four key parameters (W and L of a key transistor, $I_{ref}$, and C) in the sensor design, which can be easily scaled to achieve speed and power trade-offs for different applications, while maintaining state-of-the-art performance. With a temperature sensor core area of 0.003 mm$^2$ and a supply voltage sensor core area of 0.005 mm$^2$, the two dedicated sensors have conversion energies of 0.28 and 0.35 nJ/conv respectively, each achieving the lowest conversion energy in its class.

Section 2 introduces the ultra-low-power and compact relaxation oscillator topology [6], and in Sect. 3 we extend the structure to design standard cells for temperature and supply-voltage monitoring. Section 4 describes two schemes for converting the analog oscillator period and duty cycle information to a digital readout. We then discuss suitable reference current generation for the oscillator, and Sect. 5 introduces a modified bandgap current reference. Section 6 highlights key design considerations, and analyzes the anticipated performance limitations. Specifically, we analyze transistor switching delays and sources of nonlinearity, which are key to building more accurate sensor designs based on relaxation oscillators. Section 7 presents experimental results from three sensor designs implemented in a standard 0.18 $\upmu$m CMOS process, and Sect. 8 concludes the chapter.

2 Dual-Phase Current-Mode Relaxation Oscillator

2.1 Operation Description

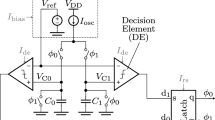
Figure 1 shows a dual-phase current-mode relaxation oscillator described in [6]. In this circuit, M2–M4 are matched transistors. Two identical capacitors C1 and C2 are alternately charged by $I_{ref}$ and reset to ground as dictated by the complementary output clocks Q and $\overline{Q}$, which are generated by a set-reset (SR) latch.

Fig. 1.

A dual-phase current-mode relaxation oscillator [6].

As illustrated by the timing diagram in Fig. 1, when $Q=1$ and $\overline{Q}=0$, $V_{C2}$ and node S at the drain of M4 are reset to ground. The voltage on C1 is charged up with a slope of $(I_{ref}/C1)$. Meanwhile, biased with $I_{ref}$, M3 compares $V_{C1}$ with the reference voltage $(V_{ref}=I_{ref}\cdot R_{ref})$ and provides an amplified difference to the R node. Once the voltage on the R node reaches the latch’s threshold voltage, the SR latch changes its state to $Q=0$ and $\overline{Q}=1$. In this state, there is no current flowing through M3 and C1, and $I_{ref}$ biases M4 while charging C2. The oscillation period can be expressed as:

$$\begin{aligned} T&= 2\left( \frac{V_{ref}}{I_{ref}/C}+t_{sw}+\tau _{SR} \right) \nonumber \\&= 2\left( \tau _{RC}+t_{sw}+\tau _{SR}\right) , \end{aligned}$$

(1)

where $C1=C2=C$, $\tau _{RC}=R_{ref}C$. $\tau _{SR}$ stands for the digital delay of SR latch. In low-power applications, current starving can be employed to reduce the dynamic power consumption of the SR latch.

Power and Design Notes: Since the same devices and current are reused for both the comparator bias and capacitor charging, source-coupled comparators such as this one can be highly power and area efficient [8]. To adjust the power, area, and accuracy for different applications and/or clock speeds, one can simply modify $I_{ref}$, C, and the dimensions of M2-M4.

Oscillator Period Components: The first component $\tau _{RC}$ and the third component $\tau _{SR}$ are straightforward to interpret: $\tau _{RC}$ is the time required for C1 or C2 to reach $V_{ref}$ from ground, and $\tau _{SR}$ is the digital delay of the SR latch after node S or R reaches the switching/triggering point of the SR latch.

The second component $t_{sw}$ is relatively more complicated. In general, when the current charges the capacitor to $V_{ref}$, the voltage on node S or R is not high enough to switch the SR latch. Therefore $t_{sw}$ is the delay between the capacitor voltage reaching $V_{ref}$ and node S/R reaching the switching point of the SR latch. $t_{sw}$ is affected by the finite comparator transistor gain and the parasitic capacitance at node S or R, so we call $t_{sw}$ the comparator delay. Due to the second component $t_{sw}$ and the third component $\tau _{SR}$, the final voltage on the capacitor ends up being higher than the reference voltage $V_{ref}$.

In Sect. 6, the oscillation period is analyzed using the current-split model. The idea is that a portion of $I_{ref}$ is used to charge up the capacitor C while the rest is charging up the parasitic capacitance on node S or R, until node S or R switches the SR latch. For more technique details for more accurate oscillator design, we refer the reader to Sect. 6.

2.2 Oscillator Variations and Extensions

In Fig. 1, the resistor $R_{ref}$ creates a reference voltage that is approximately constant. For other applications, it is possible to replace this fixed reference voltage with a voltage corresponding to a measurement quantity of interest, creating a voltage-controlled oscillator.

However, one obstacle to the extension of this structure is the finite input impedance at the node $V_{ref}$, looking into the source of M2. Supposing that there is a voltage sampled at a capacitor, we would like to generate a voltage-controlled frequency by connecting this sampling capacitor to the source node of M2. But this voltage will be quickly corrupted by the bias current flowing into M2 due to the resistive path at its source node. Instead, we want a constant voltage at the source node of M2, regardless of the loading effect.

Fig. 2.

Proposed voltage-controlled oscillator. $V_{IN}$ is buffered and replicated in place of $V_{ref}$, producing an oscillation period proportional to $V_{IN}$.

Figure 2 addresses this limitation by adding a high-impedance unity-gain buffer which replicates $V_{IN}$ at $V_{ref}$, in an arrangement which also reuses M2’s bias current. It can be viewed as an amplifier whose inputs are at the gates of M5-M6, and whose output is the drain node of M6. This amplifier is connected as a voltage follower, so that its output is regulated to be approximately equal to $V_{IN}$, assuming a reasonable loop gain. The open-loop gain $A_0$ of the amplifier made by M5-M6, M1-M2 and M7-M8 is:

$$\begin{aligned} A_{0} = g_{m5/6} [ r_{ds6}~||~( 1/g_{m2}+r_{ds8})], \end{aligned}$$

(2)

where $g_{m2}$ and $g_{m5/6}$ are the transconductances of M2 and M5/M6, and $r_{ds6}$ and $r_{ds8}$ are the drain-to-source resistances of M6 and M8, respectively. The static current consumption of the voltage sensor in Fig. 2 is 3 $\times \,I_{ref}$. Thanks to the current reuse, the current addition is only one $I_{ref}$ compared with the current-mode relaxation oscillator shown in Fig. 1.

The period of this voltage-controlled oscillator can be expressed as:

$$\begin{aligned} \tau _{V_{IN}} = 2 \left( \frac{V_{IN}}{I_{ref}/C} + t_{sw} + \tau _{SR} \right) \end{aligned}$$

(3)

If $t_{sw}$ and $\tau _{SR}$ are small, the period in (3) becomes linearly proportional to the in voltage, providing a time-encoded measurement of $V_{IN}$.

Now that $V_{IN}$ is buffered, we can connect it to an arbitary sampled voltage, either from a resistive voltage divider or a sampling capacitor. Section 3 details three possible extentions realizing temperature and/or supply voltage sensing.

3 Temperature and Supply Voltage Sensing

3.1 Supply Voltage Sensing

As shown Fig. 3, a natural step towards a supply-voltage-controlled oscillator would be to create $V_{IN}$ by a simple voltage division from $V_{DD}$, employing the configuration described in Fig. 2. The period of the supply-voltage-controlled oscillator is:

Fig. 3.

Proposed voltage sensor.

$$\begin{aligned} \tau _{V_{IN}} = 2 \left( \frac{2/5V_{DD}}{I_{ref}/C} + t_{sw} + \tau _{SR} \right) \end{aligned}$$

(4)

The first term in (4) dominates the oscillation period because the comparator delay $t_{sw}$ and the digital delay $\tau _{SR}$ are much faster than charging C to 2*$V_{DD}/5$. The period in (4) becomes linearly proportional to the supply voltage, providing a time-encoded measurement of $V_{DD}$.

Design Notes and Example: To trade off between power, area, and accuracy, the circuit designer can tune the three key parameters in this supply voltage sensor, $I_{ref}$, C, and the dimensions of M1-M4, to meet different specifications. Taking a $\upmu$W supply-voltage sensor operating around 10 MHz for example, $I_{ref}$ is 2.1 $\upmu$A and C is 50 fF. Transistors M2-M4 have W/L = 3 $\upmu$m/1 $\upmu$m, operating in the subthreshold region for high $g_m/I_D$ (transconductance efficiency). For the other design parameters, M5-M6 have W/L = 5 $\upmu$m/1 $\upmu$m, and operate in subthreshold, while M7-M8 have W/L = 2 $\upmu$m/4 $\upmu$m and operate in strong inversion.

3.2 Temperature Sensing

Biased with a constant current $I_{ref}$, a forward-biased diode has a voltage $V_{diode}$ with a complementary to absolute temperature (CTAT) coefficient, due to the exponential temperature dependence of its reverse saturation current $I_s$:

Fig. 4.

Proposed temperature sensor. By replacing $V_{ref}$ with $V_{diode}$, a temperature-dependent oscillation is obtained.

$$\begin{aligned} V_{diode}(T) = \frac{kT}{q} \ln \left( \frac{I_{ref}}{I_s(T)} \right) , \end{aligned}$$

(5)

where T is the absolute temperature, k is Boltzmann’s constant, and $V_{diode}$ is on the order of several hundred millivolts.

Considering the fact that both the diode and M2 can be biased by the same reference current, a low-power temperature sensor can be readily implemented by replacing $R_{ref}$ with a forward-biased diode from Fig. 1, as redrawn in Fig. 4. Now the period of this relaxation oscillator becomes:

$$\begin{aligned} \tau _{temp} = 2 \left( \frac{V_{diode}}{I_{ref}/C} + t_{sw} + \tau _{SR} \right) \end{aligned}$$

(6)

Since the first term in (6) dominates the oscillation period, the oscillation period will reflect the diode’s sensitivity to temperature. Excluding bias generation, the static current consumption of this temperature sensor is $2I_{ref}$.

Design Example: To implement a $\upmu$W temperature sensor operating at a speed around 10 MHz, $I_{ref}$, C, and the M2-M4 dimensions can be assigned the same values as those in the supply-voltage sensor design.

3.3 Hybrid Oscillator Sensing both Temperature and Supply Voltage

For ultra-low power applications like radio-frequency identification (RFID) tags which need both temperature and supply voltage monitoring, we can save power by combining the two sensors into one.

Fig. 5.

Proposed structure for a hybrid oscillator which senses both supply voltage and temperature (a) conceptual and its timing diagram, (b) transistor-level schematic.

Figure 5(a) presents a conceptual diagram, containing two halves: the left half has an input of $1/4V_{DD}$ generated from a voltage divider, and the input to the right half comes from the complementary-to-absolute-temperature (CTAT) voltage of a forward-biased diode. As a result, the digital output Q will be modulated by both the temperature and the supply voltage. The detailed transistor-level schematic is drawn in Fig. 5(b). Four identical PMOS transistors in series from $V_{DD}$ to ground form a supply voltage divider. To minimize power, a small W/L ratio is chosen for these four devices, which ensures that the current of the voltage divider is much less than $I_{ref}$; additionally, the high impedance combined with the gate capacitance of M5 helps to filter out high-frequency supply noise. Compared with two separate temperature and $V_{DD}$ sensors, this hybrid oscillator saves half of the dynamic power and reduces static current consumption by $I_{ref}$.

The logic “high” and “low” durations of the digital output Q are linearly proportional to $V_{DD}$ and temperature, respectively. If $t_{sw}$ and $\tau _{SR}$ are negligible, then

$$\begin{aligned} \tau _{high} \approx \frac{1/4~V_{DD}}{I_{ref}/C} \end{aligned}$$

(7)

$$\begin{aligned} \tau _{low} \approx \frac{V_{diode}}{I_{ref}/C} \end{aligned}$$

(8)

Design Notes: Some very careful readers may ask: why is the gate voltage of M5 $1/4V_{DD}$ in Fig. 5 but $2/5V_{DD}$ in Fig. 3? In order to make the unity-gain operational amplifier work, the gate voltage of M5 has to provide a gate-to-source voltage drop for M5, plus enough headroom for the $2I_{ref}$ current source beneath M5, which operates in the saturation region. We apply the circuit described in Fig. 5 to the ultra-low power domain. With $I_{ref}$ on the nA level, the gate-to-source voltage of M5 is lower than with a $\upmu$A level bias current, so the required M5 gate voltage is lower.

As a parameter example for a nanowatt hybrid sensor operating at several tens of kHz and nanowatts, $I_{ref}$ is set to be 6 nA and C to be 50 fF. Transistors M2-M4 have a dimension of W/L = 1 $\upmu$m/3 $\upmu$m.

4 Readout Circuit

When integrating the sensors in a System-on-Chip (SoC), a readout circuit is required to digitize the analog time information using a reference clock. There are two approaches to the frequency-to-digital conversion, depending on the relative reference clock speed.

With a reference clock faster than the sensor clock, the first approach is to count the fast reference clock cycles during N slow sensor cycles (N = 256). As depicted in Fig. 6, after N slow sensor cycles, the time-to-digital converter sends a DONE signal to latch the reference clock counting for DATA readout. Meanwhile, it clears the reference clock counter for the next round of conversion. This approach has a quick conversion time at the expense of high dynamic power due to the fast reference clock.

Fig. 6.

Frequency-to-digital conversion scheme used to digitize the sensor outputs, when the reference clock is much faster than the sensor clock.

The second approach is to count the sensor cycles during a fixed number (N) of reference clock cycles, when the reference clock is slower than the sensor clock. To implement this method, we can just swap the connections of the reference and sensor clock in Fig. 6. This approach is generally applied to ultra low power systems, where the reference clock is typically slow to reduce the power budget.

One similarity shared by the two approaches is that between the sensor clock and reference clock, a faster clock is counted during a fixed number (N) of the slower clock cycles. For the dedicated supply voltage and temperature sensors in Fig. 3 and Fig. 4, we can use either fast or slow reference clocks, depending on the data-conversion speed requirement.

Fig. 7.

Modification of the frequency-to-digital conversion scheme to digitize the hybrid sensor output.

For the hybrid sensor in Fig. 5, we have to measure the logic high and logic low duration separately with a fast reference clock, in order to obtain the temperature or supply voltage information, respectively. Figure 7 illustrates measurement of the sensor clock’s logic phase. An AND gate enables the fast reference clock counting only during sensor logic high. Similarly, to measure the logic low duration, we can replace the AND gate with an OR gate.

5 Reference Current Generation

In Fig. 1, 2, 3, 4 and 5, does $I_{ref}$ have to be a bandgap reference current insensitive to supply voltage and temperature (PVT)? Let us only consider the dominant term in each oscillation period, with the assumption that the comparator delay $t_{sw}$ and the SR latch delay $\tau _{SR}$ are much smaller.

For a Resistor-Capacitor (RC) relaxation oscillator, its linear component is:

$$\begin{aligned} T_{relx\_osc,linear} = 2 \times \frac{V_{ref}}{I_{ref}/C} = 2 \times \frac{I_{ref} \cdot R}{I_{ref}/C} = 2 \times RC \end{aligned}$$

(9)

We can see that the reference current $I_{ref}$ is cancelled out, leaving only RC. In other words, $I_{ref}$ does not have to be a PVT insensitive current to keep the linear dominant period components constant. In fact, a proportional-to-absolute-temperature (PTAT) current can bias the RC relaxation oscillator, while keeping a constant oscillation frequency over temperature and supply voltage, as in [6].

When it comes to the supply voltage and temperature sensor, Eq. (7) and (8) tell us that a constant reference current $I_{ref}$ is required in order to make the period component linear with $V_{DD}$ or $V_{diode}$.

Fig. 8.

A compact and easy-to-design bandgap current reference modified from [9] with removal of the operational amplifier. Copies of the reference current are created with mirrors from MP2.

Figure 8 depicts a compact and easy-to-design bandgap current reference circuit. This circuit is modified from [9] with removal of the operational amplifier. It places a resistor $\text {R}_1$ in parallel with the diodes in order to reduce the minimum supply voltage compared to a classical bandgap configuration. The identical NMOS pair MN1-MN2 will regulate their source voltages to be equal. By selecting a proper ratio of $R_1$ to $R_2$ and a diode area ratio of N, one can generate a temperature-independent current $I_{BGR}$,

$$\begin{aligned} I_{BGR} = \frac{V_d}{R_1} + \frac{\Delta {V_d}}{R_2} = \frac{1}{R_1} \left( V_d + \frac{R_1}{R_2} \frac{kT}{q} \ln N \right) , \end{aligned}$$

(10)

where $V_d$ is the voltage across the P+/N-well junction diodes, and $\Delta V_d$ is the difference between the two diodes’ forward voltages, which appears across $\text {R}_2$. $V_d$ has a CTAT coefficient, while the second term is PTAT. Similar to other bandgap circuits, the basic principle is to compensate a CTAT coefficient with a weighted PTAT coefficient, by choosing the correct value of $(R_1/R_2\times \ln N)$ in (10).

It is worth noting that the resistor temperature coefficient can affect the temperature variation of $I_{BGR}$. This could be addressed by implementing $\text {R}_1$ and $\text {R}_2$ with two series resistors having opposite temperature coefficients.

6 Design Considerations

The dominant linear component in the oscillation period represents the ideal oscillation behavior. To design an accurate sensor, we have to suppress the nonlinear components in the oscillation period as much as possible. This section takes a detailed look at these nonidealities, using the current-split model. The expressions and delay model in this section apply to both constant frequency oscillators and extended voltage or voltage sensors.

6.1 Delay Model of the Amplifying Transistor

As illustrated in Fig. 9, $I_{ref}$ splits into two branches. One branch $I_{chrg}$ flows into M3 to charge up the capacitor C while the remainder charges the parasitic capacitance at the drain node of M3. The voltage change at the drain node of M3, $\Delta (V_{d,M3})$, can be written in terms of its charging current ($I_{ref}-I_{chrg}$) and the internal parasitic capacitance $C_{int}$:

Fig. 9.

Current splitting when both the drain and source of M3 are ramping up.

$$\begin{aligned} \Delta (V_{d,M3}) = \frac{I_{ref}-I_{chrg}}{C_{int}}~\Delta t \end{aligned}$$

(11)

If M3 has a gain of $A_{M3}$, the voltage change at the drain node of M3, $\Delta (V_{d,M3})$, also equals the ramping rate on C amplified with $A_{M3}$,

$$\begin{aligned} \Delta (V_{d,M3}) = A_{M3} \times \frac{I_{chrg}}{C}~\Delta t, \end{aligned}$$

(12)

we can use (11) and (12) to solve for $I_{chrg}$:

$$\begin{aligned} I_{chrg} = \frac{I_{ref}}{1+A_{M3}C_{int}/C} \end{aligned}$$

(13)

Equation (13) tells us that the gain of M3 affects the current splitting. When M3 works in the linear region, $A_{M3,lin}$ is small, and the denominator is approximately 1. Thus almost all the $I_{ref}$ flows into M3 to charge up C ($I_{ref} \approx I_{chrg}$). As M3 enters the saturation region, or $A_{M3,sat}$ is large, $A_{M3,sat}C_{int}$ becomes comparable to C, and a fraction of $I_{ref}$ begins to charge up $C_{int}$. At this phase, we could also say that $C_{int}$ requires more current than C, since M3 is amplifying the changes in $V_C$. From the small-signal perspective, dV/dt at the output of M3 could approach $(A_{M3,sat} \times I_{ref}/C)$ only if M3 had infinite bandwidth (no $C_{int}$, and thus no current splitting). But in practice, $C_{int}$ limits the bandwidth.

Fig. 10.

The delay model and illustrated transition of the source-coupled amplifier transistors (M3 and M4).

As shown in Fig. 10, the source voltage of M3 ramps up from zero until its drain voltage reaches $V_{SW}$, the switching threshold of the SR latch. We divide the total period into two phases $\tau _1$ and $\tau _2$ based on the operation of M3 (linear and saturation). We use the capacitor ramping voltage $V_C$ and M3 drain voltage $V_{d,M3}$, to calculate $\tau _1$ and $\tau _2$ respectively, as illustrated by the two yellow segments in Fig. 10. We use $V_{d,M3}$ rather than $V_C$ to derive $\tau _2$, because it is simpler to obtain the initial and final voltages of $V_{d,M3}$ during $\tau _2$.

During $\tau _1$, M3 is in the linear region, with its drain-to-source voltage below $V_{dsat}$. Here M3 operates as a resistor, and initially the drain of M3 ($V_{d,M3}$) directly follows the capacitor voltage $V_C$. The gain $A_{M3,linear}$ is small, and the voltage is charging at a rate of $I_{ref}/C$ based on (13).

This first phase ends when the drain-to-source voltage of M3 equals $V_{dsat}$, which corresponds to a capacitor voltage $V_{C,sat}$. The duration of the first phase $\tau _1$ can be derived as:

$$\begin{aligned} \tau _{1} = \frac{V_{C,sat}}{I_{ref}/C} \end{aligned}$$

(14)

In order to derive $\tau _1$, we need to find $V_{C,sat}$, the capacitor voltage at which M3 enters saturation.

At the end of $\tau _1$, M2 and M3 form a differential amplifier, whose input voltage is the difference between the two source voltages and whose output is the difference between the two drain voltages. Their source and drain node voltages at the end of $\tau _1$ are described in Table 1.

Table 1. Node voltages at the end of $\tau _1$.

Given that the gain of M3 is $A_{M3,sat}$, $V_{C,sat}$ can be obtained from:

$$\begin{aligned} A_{M3,sat}(V_{IN} - V_{C,sat}) = V_{IN}+V_{gs,M2}-V_{C,sat}-V_{dsat}, \end{aligned}$$

(15)

where $(V_{IN}-V_{C,sat})$ on the left is the source voltage difference between M2 and M3, and the expression on the right is the drain voltage difference of M2 and M3, the amplifier’s output. We can use Eq. (15) to solve for $V_{C,sat}$, and from there solve for $\tau _1$ using Eq. (14).

During $\tau _2$, M3 operates in the saturation region, amplifying the voltage difference between the two source voltages $V_{IN}$ and $V_{C}$, and current splitting occurs. The drain voltage of M3, $V_{d,M3}$, is $(V_{dsat}+V_{C,sat})$ at the start of $\tau _2$ and slews to $V_{SW}$, at a rate of $(A_{M3,sat}I_{chrg}/C)$, to trigger the SR latch, as illustrated by the second yellow segment line in Fig. 10. From (13), the total time of the second phase $\tau _2$ is:

$$\begin{aligned} \tau _{2}&= \frac{V_{SW}-(V_{dsat}+V_{C,sat})}{A_{M3,sat}I_{chrg}/C} \nonumber \\&= \frac{V_{SW}-(V_{dsat}+V_{C,sat})}{A_{M3,sat}I_{ref}/(C+A_{M3,sat}C_{int})} \end{aligned}$$

(16)

Substituting the expression of $V_{C,sat}$ obtained from (15) into $\tau _1$ and $\tau _2$ in (14) and (16), we can reach to the overall oscillation half-period:

$$\begin{aligned}&\tau _1 + \tau _2 = \frac{V_{IN}}{I_{ref}/C} + \frac{V_{SW}-V_{dsat}-V_{IN}}{I_{ref}/C_{int}} \nonumber \\&+ \frac{V_{SW}-V_{gs,M2}-V_{IN}}{A_{M3,sat}I_{ref}/C} + \frac{V_{gs,M2}-V_{dsat}}{(A_{M3,sat}-1)I_{ref}/C_{int}} \end{aligned}$$

(17)

The last term in (17) is negligible, because its ratio to the first term is on the order of $(\frac{1}{A_{M3,sat}}\cdot \frac{C_{int}}{C})$ assuming $V_{IN}$ and $(V_{gs,M2}-V_{dsat})$ have the same order of magnitude. In a sensor design example at the 0.18 $\upmu$m CMOS process node, $A_{M3,sat}$ is about 100, C is 50 fF and $C_{int}$ is <5 fF. Thus, the last term contributes less than 0.1% to the overall conversion time. Similarly, the contributions of the second and third terms can be justified numerically by substituting $A_{M3,sat}$ and $C_{int}$ into their ratios to the first term. Moreover, the contribution of the second term can be further reduced by decreasing $|V_{SW}-V_{dsat}-V_{IN}|$. We can achieve this reduction by adjusting the transistor dimensions of NOR gates in the SR latch ($V_{SW}$ adjustment).

6.2 Curvature Error/Nonlinearity

In (17), the first term describes the ideal behavior, in which the oscillation period $\tau _1 + \tau _2$ is linear with $V_{IN}$, and $V_{IN}$ can represent a resistor voltage, temperature or supply voltage. The second and third terms highlight important sources of nonlinearity.

In this subsection, we can begin to understand the nonlinearity of the oscillation period by building an expression for errors in (17) in terms of several partial derivatives, and then considering the magnitude and temperature dependence of each term, assuming that $V_{IN}$ is ideal:

$$\begin{aligned} \Delta (\tau _1 + \tau _2) ~&\approx ~ \frac{-V_{IN}}{I_{ref}^2/C} \cdot \Delta I_{ref} \nonumber \\&+ \frac{1}{I_{ref}/C_{int}} \cdot \Delta (V_{SW}-V_{dsat}-V_{IN}) \nonumber \\&+ \frac{1}{I_{ref}/C} \cdot \Delta \left[ \frac{V_{SW}-V_{gs,M2}-V_{IN}}{A_{M3,sat}} \right] \end{aligned}$$

(18)

The first term in this expansion approximates the sensitivity to errors in $I_{ref}$. When analyzing the other terms in (18), $I_{ref}$ is assumed constant.

Fig. 11.

Simulated switching threshold of the SR latch versus temperature.

Since $C_{int}$ has minimal temperature and voltage dependences [8], the second error term will vary primarily with the switching threshold $V_{SW}$. For the SR latch design, we suggest adding current sources ($mI_{ref}$) on top of the PMOS devices in series with $V_{DD}$ to limit the peak dynamic current, which is also called current starvation. Using this technique will make $V_{SW}$ more robust to the supply voltage variation. Assuming subthreshold operation near the switching threshold, $V_{SW}$ can thus be formulated as:

$$\begin{aligned} V_{SW} = \eta V_T \ln {\left( \frac{mI_{ref}}{V_T^2 \upmu C_{ox} (W/L)_{n,SR}} \right) }+V_{TH,n} \end{aligned}$$

(19)

This expression predicts that $V_{SW}$ will be complementary to absolute temperature, as plotted in Fig. 11. Assuming M2 and M3 are also subthreshold, $V_{gs,M2}$ follows (19) and the gain of M3 is:

$$\begin{aligned} A_{M3,sat} = g_{m3}r_{ds,m3}=\frac{V_A}{\eta V_T}, \end{aligned}$$

(20)

where $V_A$ is the early voltage (which has minimal temperature dependence), $\eta$ is the subthreshold slope factor, and $V_T = kT/q$ is the thermal voltage.

Substituting (19) and (20) into (18), one can observe that the second term scales linearly with temperature. The third term introduces second-order temperature curvature error.

Based on this analysis, we can recognize the importance of minimizing $C_{int}$ to reduce the second term in (18), and maximizing $A_{M3,sat}$ to reduce the third term. Therefore, in our designs, we increased the lengths of the amplifying transistors, and minimized the sizes of the transistors in the SR latch. The importance of minimizing $C_{int}$ indicates that the proposed circuit can continue to benefit from CMOS technology scaling.

7 Measured Performance

Sensing circuits based on relaxation oscillators can be applied across a wide range of applications, from low-power sensor nodes to high-performance thermal monitors on multicore processors.

This section gives three oscillator-based sensor examples: one nW hybrid oscillator (Fig. 5), one $\upmu$W $V_{DD}$ sensor (Fig. 3), and one $\upmu$W temperature sensor (Fig. 4), in a standard $0.18\upmu$m CMOS process. A micrograph of the fabricated chip is shown in Fig. 12. One bandgap reference circuit based on Fig. 8 is also included. The bandgap draws 2.0 $\upmu$A and occupies 0.0156 mm$^2$, including several current mirrors to distribute $I_{ref}$ to multiple sensors.

As depicted in Fig. 6 and Fig. 7, the experimental sensor readout is performed using a time-to-digital converter (TDC) implemented on an FPGA module (Opal Kelly XEM6310). The TDC counts reference clock cycles during N sensor cycles (N = 256 in the $\upmu$W sensors and N = 10 in the nW hybrid sensor), which is the equivalent conversion time.

Fig. 12.

Die photo of the proposed temperature and voltage sensors, fabricated in 0.18 $\upmu$m CMOS.

7.1 State of the Art

Before we introduce the current-mode relaxation oscillator-based supply voltage and temperature sensors, let us first briefly review the state-of-the-art in each category.

There are several options for producing digital outputs that represent the supply voltage. One of the simplest arrangements is a voltage-controlled oscillator, which is often used for supply monitoring [10, 11]. Digital critical path monitors (CPMs) [12, 13] have very low latency and can be used to respond to power supply transients, but they are less precise for continuous monitoring, and CPMs are often combined with other complementary sensors.

Fig. 13.

CMOS smart temperature sensors [14] are compared by plotting (a) energy per conversion versus temperature resolution, and (b) an energy-resolution figure-of-merit (FoM, with unit of nJ$\cdot$K$^2$) versus normalized circuit area.

Temperature sensors use a wider variety of approaches. Resistive [15,16,17] and thermal-diffusivity [18] temperature sensors are able to achieve high resolution (often <0.1 ℃), but demand sophisticated frequency-locked loops or $\Sigma \Delta$-ADCs to digitize the temperature-dependent information. Their area, power consumption, and design complexity increase accordingly. Oscillator-based temperature sensors, which employ frequency [4, 19,20,21] or duty cycle modulation [22], are appealing for thermal monitoring as they are straightforward to implement.

Low-latency temperature measurements are important to track thermal transients, which can swing 10–20 ℃ within 2–3 ms in smartphone SoCs [23]. Ultimately, a monitor circuit must be evaluated by a combination of factors [14] including its area, power, resolution, conversion time, and accuracy. Some of these metrics are quantified for a survey of temperature sensors in Fig. 13.

7.2 Hybrid nW Temperature/$V_{DD}$ Sensor

The hybrid nW oscillator has an active area of 46 $\upmu$m $\times$ 68 $\upmu$m in a standard $0.18~\upmu$m CMOS process. At room temperature, with a supply voltage of 1.3 V, the circuit oscillates at 35.7 kHz while consuming 40 nA. The duration of the temperature phase ($\tau _{low}$) is 16.0 $\upmu$s, and the $V_{DD}$ sensing phase ($\tau _{high}$) is 12.0 $\upmu$s.

The time-to-digital converter (TDC) described in Fig. 7 is also simulated in 0.18 $\upmu$m CMOS. Its simulated power is 1.2 $\upmu$W for the temperature phase data readout, and is 0.9 $\upmu$W for the $V_{DD}$ phase data readout, under a 0.8 V digital supply. Its estimated area is 3000 $\upmu$m$^2$, using low-power D-flip-flops based on [24]. In more advanced process nodes, the TDC power and area would decrease further.

Fig. 14.

Measurements of the temperature-sensitive phase of five hybrid sensor samples, showing (a) pulse width versus temperature, (b) nonlinearity error after 2-point trimming, and (c) supply sensitivity.

Figure 14(a) shows a temperature sweep of the hybrid sensor measured across five chips when $V_{DD}$ is 1.3 V. The duration of the temperature phase is linear with temperature, while the $V_{DD}$ phase has minimal temperature dependence. The peak-to-peak temperature nonlinearity error is +0.68/−0.51℃ after two-point linear calibration, as plotted in Fig. 14(b). In Fig. 14(c), measured on five chips, the mean voltage sensitivity of the temperature phase is 2.03 ℃/V without calibration when $V_{DD}$ varies from 1.2 V to 1.8 V. Based on the time-to-digital converter described in Fig. 7, each reading was conducted by counting a 100 MHz reference clock only during the temperature sensitive phase for 10 sensor cycles, yielding a conversion time of 280 $\upmu$s. The corresponding root-mean-squared (RMS) temperature resolution is 0.17 ℃.

Fig. 15.

Measurements of the $V_{DD}$-sensitive phase of five hybrid sensor samples, showing (a) pulse width versus $V_{DD}$, (b) nonlinearity error after 2-point trimming, and (c) temperature sensitivity.

Figure 15(a) shows a supply voltage sweep for the hybrid sensor from 1.2 V to 1.8 V at room temperature. The duration of the $V_{DD}$ phase has a peak-to-peak nonlinearity error of +9.73/–13.98 mV after two-point calibration. In Fig. 15(c), from −15 ℃ to 100 ℃, the duration of the $V_{DD}$ phase shows an average temperature dependence of 0.54 mV/℃ without any calibration. The RMS $V_{DD}$ resolution is 1.8 mV via 100 consecutive $V_{DD}$ readings at 1.3 V $V_{DD}$. Each reading was conducted by counting a 100 MHz reference clock only during the $V_{DD}$ sensitive phase for 10 sensor cycles, corresponding to a conversion time of 280 $\upmu$s.

7.3 Dedicated $\upmu$W Temperature Sensor

The $\upmu$W temperature sensor has an active area of 60 $\upmu$m $\times$ 55 $\upmu$m. It consumes 6.57 $\upmu$A and operates at 12.0 MHz with $V_{DD}$ = 1.3 V at room temperature. Figure 16(a) shows a temperature sweep of the temperature sensor measured across 15 sample test chips when $V_{DD}$ is 1.3 V, in which the periods are linear with temperature. The peak-to-peak temperature nonlinearity error is +0.85/–0.94℃ after two-point linear calibration, as plotted in the upper panel of Fig. 16(b). In the lower panel of Fig. 16(b), measured on 15 samples, the mean voltage sensitivity is 2.28 ℃/V after the removal of the systematic non-linearity when $V_{DD}$ varies from 1.2 V to 1.8 V. The RMS temperature resolution is 210 mK via 1000 consecutive temperature readings at room temperature. Each reading was conducted by counting a 100 MHz reference clock for 256 sensor cycles as shown in Fig. 6, yielding a conversion time of 21.4 $\upmu$s. The simulated power of the time-to-digital converter described by Fig. 6 is 2.1 $\upmu$W in 0.18 $\upmu$m CMOS.

Fig. 16.

Measurements of the $\upmu$W temperature sensor, illustrating (a) oscillation period versus temperature, (b) temperature nonlinearity error after two-point calibration with 15 samples, (c) oscillation period versus $V_{DD}$, and (d) supply sensitivity without calibration (upper) and supply sensitivity after curvature correction (lower).

7.4 Dedicated $\upmu$W $V_{DD}$ Sensor

The $V_{DD}$ sensor core occupies an area of 60 $\upmu$m $\times$ 86 $\upmu$m. Its current consumption is 8.34 $\upmu$A, measured with $V_{DD}$ = 1.3 V at room temperature. Figure 17(a) shows a supply voltage sweep for the $V_{DD}$ sensor from 1.2 V to 1.8 V at room temperature. As shown in the lower panel of Fig. 17(b), the period has a peak-to-peak nonlinearity error of +28.7/−30.0 mV after two-point calibration. Based on 1000 consecutive $V_{DD}$ readings at 1.3 V $V_{DD}$, with a conversion time of 256 sensor cycles (22.4 $\upmu$s), the corresponding RMS $V_{DD}$ resolution is 0.94 mV.

Fig. 17.

Measurements of the $\upmu$W $V_{DD}$ sensor, showing (a) oscillation period versus $V_{DD}$, (b) $V_{DD}$ nonlinearity error, (c) oscillation period versus temperature, (d) temperature sensitivity before (upper) and after curvature correction (lower).

7.5 Performance Summary

Table 2 summarizes the nW and $\upmu$W temperature sensor performance, and Table 3 summarizes the performance of the two $V_{DD}$ sensors. When we evaluate the energy per conversion, the power consumption of the bandgap reference and the time-to-digital converter are also taken into account. In particular, the time-to-digital converter consumes more power than the nW sensor itself, due to the fast reference clock.

Table 2. Temperature sensor specifications

Table 3. Supply voltage sensor specifications

8 Conclusion

Before we conclude, perhaps we can take a broader perspective, and ask what the current-mode relaxation oscillator and the bandgap circuit structure have in common, which enables their power efficiency. One feature they share is that they save power by obviating the operational amplifiers used in the conventional oscillator and bandgap. In most operational amplifiers, signal amplification is obtained by sharing a common source node and comparing the differential gate voltages between two transistors. In the oscillator and proposed bandgap, the amplifying transistors share a common gate voltage but compare their source nodes, allowing current reuse in the capacitor charging or bias branches. Recognizing that voltage amplification is not constrained to gate comparison is essential to understanding the performance of the designs in this chapter.