Keywords

1 Introduction

When they perform mathematical modeling of magnetic fields for applied magnetostrictive level gauges (AMRLG), there is the problem of solving the systems of finite-difference equations with a large number of unknowns. This problem was formulated and solved in the works of many authors, for example in [1, 2]. The determination of the sought magnetic potentials was carried out using numerical methods that require significant computational resources and time when they simulate an AMRLG with a complex geometry of the acoustic path for bypass systems.

However, the practice of solving the systems of equations, similar in structure to the finite-difference equations obtained for the AMRLG magnetic field, makes it possible to develop some ways to reduce the calculation time while maintaining and sometimes increasing the result accuracy [2]. In particular, a modification of the Richardson method with the calculation of the optimal set of parameters by the rotation method gives a good gain in time and accuracy. Let’s consider this technique in more detail.

As is known, the system of Maxwell’s equations, describing, in particular, the distribution of AMRLG magnetic fields, can be approximated by a system of finite-difference equations of the form [3] via one method or another:

$$Au = b$$
(1)

where \(A = \left\| {a_{{i,j}} } \right\|\)—the matrix of the system coefficients, u—the column of unknowns (potentials), \(b\)—the column of the right parts.

Moreover, it is known about the matrix A that it is sparse and ill-conditioned, and the system of equations has a large number of unknowns, commensurate with the number of grid nodes [4].

It is known from various sources [3–6] that to solve the systems of difference equations of the form (1) in the computational domain with complex geometry, it is most expedient to use the Richardson method, the alternating triangular method, and various iterative methods of the variational type. Moreover, all of them, except for the first one, require a preliminary calculation of many parameters, while allowing solve the problem in the areas with a pronounced inhomogeneity of the media.

Within the framework of the problem being solved, the computational domain of the AMRLG type for bypass systems does not have significant heterogeneity, therefore, in this case, the use of the Richardson method will be effective. The main difficulty of this method use is the partial problem of finding the eigenvalues \(\lambda _{{\max }}\) and \(\lambda _{{\min }}\) of the array \(A\). At that, when they solve the problem on a computer, it seems most expedient to use the rotation method to find the indicated eigenvalues [4].

2 Materials and Methods

The approach to an iterative Richardson scheme development is to study the behavior of the error \(\delta = f\left( n \right)\). Such an analysis makes it possible to choose a parameter \(\tau\), considering the nature of the error \(\delta ^{n}\) change during the transition from the nth to (n + 1)th iteration, and

$$\delta ^{n} = u^{n} - u^{T}$$
(2)

where \(u^{T}\)—the array of exact potential values.

Indeed, boundary conditions are specified at the computational domain boundaries, and their error is equal to zero. Therefore, inside the region, the function \(\delta ^{n}\) can be expanded in a Fourier series, which will have the following form:

$$\delta _{{i,j}}^{n} = \mathop \sum \limits_{{k,m}} C_{{km}} \sin \frac{{k\pi }}{N}i \cdot \sin \frac{{m\pi }}{M}j$$
(3)

where the expansion coefficients \(C_{{km}}\) depend on the parameter \(\tau\) the iteration number n [4]. The smaller the value of the coefficient \(C_{{km}}\), the less influence the k, m harmonic makes on the total error \(\delta ^{n}\).

Therefore, the choice of the optimal value \(\tau _{o}\) should be carried out from the criterion of error harmonics best suppression in the middle part of the spectrum. We also take into account that the harmonic composition of the error \(\delta ^{n}\) can be changed from one iteration to another, and a new value \(\tau _{o}^{n}\) should be chosen at each step for the maximum efficiency of the method [4].

The main advantage of the Richardson method is in the use of a set of optimal values \(\tau _{o}^{n}\). The slow convergence of other methods (simple iteration, Seidel, upper relaxation method) is explained by the fact that the low and high frequency harmonics of the error \(\delta ^{n}\) are suppressed at the same rate and the overall convergence of the method is determined only by the extreme boundaries of the error spectrum. The introduction of a set of optimal values \(\tau _{o}^{n}\) ensures successive suppression of all error harmonics and its uniform rapid decrease during a small number of iterations.

Let’s consider the ways to obtain a set of optimal values \(\tau _{o}^{n}\).

For this, assuming that \(\tau ^{n}\) depends on the iteration number, we put down the Richardson iteration scheme in the following form [4]:

$$u^{{n + 1}} = \left( {1 - \tau ^{n} A + b} \right)u^{n}$$
(4)

Due to the fact that a relation similar to (4) will be fulfilled for an array of exact potentials \(u^{T}\) and taking into account (2), it is possible to write the following for the error \(\delta ^{n}\):

$$\delta ^{{n + 1}} = \left( {1 - \tau ^{n} A + b} \right)\delta ^{n}$$
(5)

Then, after denoting the initial error (for n = 0) via \(\delta ^{0}\), we get an expression for the error after \(n_{1}\) of iterations:

$$\delta ^{{n_{1} }} = \delta ^{0} \mathop \prod \limits_{{n = 0}}^{{n_{1} }} \left( {1 - \tau ^{n} A + b} \right)$$
(6)

Using (6), it can be shown that for the best suppression of the error with \(n_{1}\) of iterations, the parameters \(\tau ^{n}\) should be selected based on the condition [4]:

$$\left\| {\mathop \prod \limits_{{n = 0}}^{{n_{1} }} \left( {1 - \tau ^{n} A + b} \right)} \right\| = \min$$
(7)

In practice, the search for a set of parameters \(\tau ^{n}\), minimizing the norm (7) is usually replaced by the search of \(\tau ^{n} \in \left[ {\lambda _{{\max }}^{{ - 1_{{\min }}^{{ - 1}} }} } \right]\), at which the Chebyshev polynomials of the first kind of the degree \(~n_{1}\) take the values closest to zero. Then, as is known [4]:

$$\tau ^{n} = 2\left( {\lambda \cos \frac{{\left( {2n - 1} \right)\pi }}{{2n_{1} }}\min \max ^{{ - 1}} _{1} \min _{{\max }} } \right)$$
(8)

3 Results

Calculated in accordance with (8), the first elements of the sequence \(\tau ^{n}\) have the order \(1/\lambda _{{\max }}\), and therefore, the error harmonics corresponding to the right side of the spectrum are most actively suppressed during the first iterations. The components of the left side of the spectrum are suppressed slowly with these iterations. However, they are actively suppressed by the higher order sequence elements \(\tau ^{n}\), with the order \(1/\lambda _{{\min }}\), i.e., at \(\tau ^{n} \to \tau ^{{n_{1} }}\). Thus, there is a significant uniform decrease of the error \(\delta ^{n}\) during \(n_{1}\) of iterations [2].

When they solve practical problems on a computer by the Richardson method, they are usually set with a relatively small number \(n_{1} \sim 10 \ldots 50\), the parameters \(\tau ^{{n_{1} }}\) are calculated using the formula (7), and a series of \(n_{1}\) iterations (4) with the same parameters \(\tau ^{{n_{1} }}\) until the accuracy criterion is met.

Richardson’s method is characterized by a high convergence rate. It is known that when they use an optimal set of parameters \(\tau _{o}^{n}\) the number of iterations \(n\) on a mesh with \(N \times M\) of nodes depends on the specified accuracy as follows [4]:

$$n = 0.32NM\ln \frac{2}{\varepsilon }$$
(9)

Since the main difficulty during the implementation of this method is finding the eigenvalues \(\lambda _{{\max }}\) and \(\lambda _{{\min }}\) of the array \(A\), we will further consider some approximate methods for their calculation, suitable for the arrays with the marked properties.

Currently, a large number of methods are known solving such problems. These are the methods of direct expansion, iteration, rotation, etc. [1, 4,7,8]. All these methods are classified into partial (allowing find only some, often arbitrary, eigenvalues of a matrix) and complete one (finding all eigenvalues). Since in the context of this problem it is necessary to find only the minimum and maximum eigenvalues, the use of partial methods is ineffective, due to the arbitrariness of the obtained eigenvalues. Therefore, we will search for all eigenvalues by the full method, and then select the maximum and minimum from them.

The most effective complete method used for large symmetric matrices is the rotation method [2]. The essence of this method is as follows.

The method is based on the transformation of the original symmetric matrix A similarity using the orthogonal matrix H. An orthogonal matrix is taken as a matrix H for the rotation method, such that \(HH^{T} = H^{T} H = E\), where E is the single matrix.

Because of the orthogonality property of the similarity transformation, the original matrix A and the matrix \(A^{{\left( i \right)}}\), obtained after the transformation retain their trace and eigenvalues \(\lambda _{i}\), i.e. the following equality holds:

$${\text{tr}}A = \mathop \sum \limits_{i} a_{{ii}} = A\mathop \sum \limits_{i} \lambda _{i} = {\text{tr}}A^{{\left( i \right)}}$$
(10)

The rotation method idea is in repeated application of a similarity transformation to the original matrix:

$$A^{{\left( {k + 1} \right)}} = \left( {H^{{\left( k \right)}} } \right)^{{ - 1}} \cdot A^{{\left( k \right)}} \cdot H^{{\left( k \right)}} = \left( {H^{{\left( k \right)}} } \right)^{T} \cdot A^{{\left( k \right)}} \cdot H^{{\left( k \right)}} ,\quad k = 0,1,2, \ldots$$
(11)

The formula (11) defines an iterative process, during which an orthogonal matrix \(H^{{\left( k \right)}}\) is determined at the kth iteration, for an arbitrarily chosen off-diagonal element \(a_{{ij}}^{{\left( k \right)}}\), \(i \ne j\), that transforms this element and the element \(a_{{ji}}^{{\left( k \right)}}\) into \(a_{{ij}}^{{\left( {k + 1} \right)}} = a_{{ji}}^{{\left( {k + 1} \right)}} \approx 0\). In this case, at each iteration, the off-diagonal element \(a_{{ij}}^{{\left( k \right)}}\) is selected among the maximum ones. At that, the matrix \(H^{{\left( k \right)}}\) is called the Jacobi rotation matrix. It depends on the rotation angle \(\phi ^{{\left( k \right)}}\), determined from the following expression:

$$tg2\phi ^{{\left( k \right)}} = \frac{{2a_{{ij}}^{{\left( k \right)}} }}{{a_{{ii}}^{{\left( k \right)}} - a_{{jj}}^{{\left( k \right)}} }}$$
(12)

At that \(\left| {2\phi ^{{\left( k \right)}} < \frac{\pi }{2}} \right|,\,i < j\), and it has the following form [3]:

$$H^{{(k)}} = \left( {\begin{array}{*{20}c} 1 & \ldots & 0 & 0 & 0 & \ldots & 0 & 0 & 0 & \ldots & 0 \\ \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & \ldots & 1 & 0 & 0 & \ldots & 0 & 0 & 0 & \ldots & 0 \\ 0 & \ldots & 0 & {\cos \phi ^{{(k)}} } & 0 & \ldots & 0 & { - \sin \phi ^{{(k)}} } & 0 & \ldots & 0 \\ 0 & \ldots & 0 & 0 & 1 & \ldots & 0 & 0 & 0 & \ldots & 0 \\ \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & \ldots & 0 & 0 & 0 & \ldots & 1 & 0 & 0 & \ldots & 0 \\ 0 & \ldots & 0 & {\sin \phi ^{{(k)}} } & 0 & \ldots & 0 & {\cos \phi ^{{(k)}} } & 0 & \ldots & 0 \\ 0 & \ldots & 0 & 0 & 0 & \ldots & 0 & 0 & 1 & \ldots & 0 \\ \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & \ldots & 0 & 0 & 0 & \ldots & 0 & 0 & 0 & \ldots & 1 \\ \end{array} } \right)$$
(13)

In the course of the iterative process (10) at \(k \to \infty\) the moduli of all off-diagonal elements \(a_{{ij}}^{{\left( k \right)}}\), \(i \ne j\) tend to zero, and the matrix itself \(A^{{\left( k \right)}} \to {\text{diag}}\left( {\lambda _{1} ,\lambda _{2} , \ldots \lambda _{n} } \right)\). The criterion for achieving the required accuracy of the rotation method is [4]:

$$\mathop {\max }\limits_{{i \ne j}} \left| {a_{{ij}}^{{\left( k \right)}} } \right| < \varepsilon$$
(14)

4 Discussion

The implementation of the rotation algorithm for finding the eigenvalues of the system ratio matrix made it possible to evaluate the efficiency of the Richardson method with an optimal set of parameters \(\tau _{o}^{n}\), calculated by the formula (8). The experimental dependences of the number of iterations \(n\) on a given accuracy \(\varepsilon\), obtained at various sets of parameters \(\tau ^{n}\), are shown on Fig. 1.

Fig. 1
figure 1

Influence of a set of parameters \(\tau ^{n}\) on the number of iterations n according to the Richardson method

Full size image

As you can see, the number of iterations n with a set of parameters \(\tau _{o}^{n}\), calculated by the formula (8) using the rotation method (line 2) differs slightly from the ideal theoretical one (line 3) determined by the expression (9). With a random selection of a set of parameters \(\tau ^{n}\) (line 1), the number of iterations increases by 2–3 times.

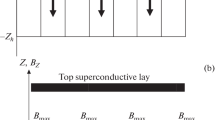
Figure 2 shows the results of the magnetic field calculations of AMRLG, when YUNDK24B alloy is selected as a permanent magnet [9].

Fig. 2
figure 2

The picture of the magnetic field strength of the applied AMRLG

Full size image

Figure 3 shows the results of the magnetic field modeling of AMRLG using ELCUT system, when YUNDK24B alloy is selected as a permanent magnet [10,11,13].

Fig. 3
figure 3

The picture of the magnetic field strength of the applied AMRLG in ELCUT

Full size image

So, the results of calculating the magnetic field of AMRLG by the proposed method and using the known modeling system turned out to be similar.

5 Conclusion

Thus, the use of the developed methodology to calculate AMRLG magnetic fields for bypass systems reduces the number of iterations and the solution time, proving its effectiveness.