Abstract
In the multiparty equality problem, each of the n nodes starts with a k-bit input. If there is a mismatch between the inputs, then at least one node must be able to detect it. The cost of a multiparty equality protocol is the total number of bits sent in the protocol. We consider the problem of minimizing this communication cost under the local broadcast model for the case where the underlying communication graph is undirected. In the local broadcast model of communication, a message sent by a node is received identically by all of its neighbors. This is in contrast to the classical point-to-point communication model, where a message sent by a node to one of its neighbors is received only by its intended recipient.
Under point-to-point communication, there exists a simple protocol which is competitive within a factor 2 of the lower bound [1]. In this protocol, a rooted spanning tree is fixed and each node sends its entire input to its parent in the tree. On receiving a value from its child, a node compares it against its own input to check if the two values match. Ignoring lower order additive terms, a more complicated protocol comes within a factor \({4/3}\) of the lower bound and is tight for certain classes of graphs [1]. Tight results, ignoring lower order terms, are also known for complete graphs [2, 9].
We study the multiparty equality problem under the local broadcast model. Recently, our work has shown that the connectivity requirements for Byzantine consensus are lower in the local broadcast model as compared to the classical model [7, 8]. In this work,
-
1.
we identify a lower bound for the multiparty equality problem in this model.
-
2.
we first identify simple protocols, wherein nodes are restricted to either transmit their entire input or not transmit anything at all, and find that these can cost \(\varOmega (\log n)\) times the lower bound using existing example for the set cover problem [12].
-
3.
we then design a protocol to solve the problem within a constant factor of the lower bound.
This research is supported in part by the National Science Foundation awards 1409416 and 1733872, and Toyota InfoTechnology Center. Any opinions, findings, and conclusions or recommendations expressed here are those of the authors and do not necessarily reflect the views of the funding agencies or the U.S. government.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
In this paper, we study the multiparty equality problem, wherein n nodes are connected via an arbitrary undirected graph \(G = (V, E)\). Each node \(u \in V\) starts with a k-bit input x(u). If \(x(u) \ne x(v)\) for two distinct nodes \(u, v \in V\), then at least one node in the graph must be able to detect the mismatch. The cost of a multiparty equality protocol is the total number of bits sent in the protocol. We want to minimize this communication cost.
This problem has been studied under the point-to-point communication model by Alon et al. [1] and Liang and Vaidya [9]. Under the point-to-point communication model, all links are private so that when a node transmits a message to a neighbor in the network, the other neighbors do not receive the message. Here, we consider the local broadcast communication model where a message sent by a node is received identically by all of its neighbors in the communication network. This communication model is inspired by wireless networks where a message sent by a wireless device is received by all devices in its immediate vicinity. Recently, it has been shown that the connectivity requirements for the Byzantine consensus problem are lower in the local broadcast model as compared to the point-to-point model [7, 8].
To see the difference between the two communication models, consider the scenario where a node u intends to communicate its entire k-bit input with all of its neighbors. In the point-to-point communication model, node u will have to transmit its entire input on each of the incident edges separately. In contrast, in the local broadcast model, node u will have to transmit its input only once and all of its neighbors will receive the input identically.
When a node u transmits \(\ell \) bits, under point-to-point channels, exactly \(\ell \) bits are received by the recipient node. However, under local broadcast, each neighbor of u receives \(\ell \) bits. So while the total number of bits transmitted in a protocol under the point-to-point model is exactly the same as the total number of bits received, this is not the case under the local broadcast model. The optimal protocols can be different depending on whether they minimize the number of bits transmitted or the number of bits received. We discuss these two different cost functions in Sect. 3. In this paper, we focus on the transmission cost.
We study static protocols [1, 9], where the transmitting nodes (as well as the number of bits transmitted by the nodes) for each round of the protocol are pre-determined and independent of the inputs. We make the following contributions.
-
1.
We give a lower bound on the transmission cost of multiparty equality under the local broadcast model.
-
2.
We first introduce simple protocols, where each node can either transmit its entire input or not transmit at all. When a node receives a value from its neighbor, it compares it against its own input to check if the two values match. Under local broadcast, such simple protocols are related to special dominating sets. With point-to-point channels, the simple protocols consist of fixing a rooted spanning tree, with each node transmitting its input value to its parent. In the classical setting, these are competitive within a factor 2 of the corresponding lower bound [1]. Unfortunately, under the local broadcast model, we find that the simple protocols can be a factor \(\varOmega ( \log n )\) worse than the identified lower bound.
-
3.
We show that there exist static protocols that solve the multiparty equality problem within a constant factor of the lower bound. These are linear protocols in the sense that the value transmitted by any node is a linear function (over a finite field) of its input. This is in contrast with the point-to-point model where linear protocols do not perform any better than the simple protocols [1].
The best known protocol for arbitrary graphs under point-to-point communication is by Alon et al. [1]. It is a non-linear protocol that achieves a competitive factor of \({4/3}\) against the lower bound, ignoring lower order additive terms. For certain classes of graphs, it is in fact optimal. Tight results, ignoring lower order terms, are also known for complete graphs [2, 9] using non-linear protocols. Our results show that while there is no separation between linear and simple protocols in the point-to-point model, there is a clear separation between them in the local broadcast model.
The rest of the paper is organized as follows. We introduce the notation in Sect. 2. In Sect. 3, we formalize the problem and discuss the cost measure under the local broadcast model. A lower bound is given in Sect. 4. We present and analyze simple protocols in Sect. 5. In Sect. 6, we design a protocol that is competitive within factor 4 of the lower bound. Finally, we conclude in Sect. 7 and identify some open problems.
2 Notation
We consider an undirected communication graph \(G = (V, E)\) of size  , which is fixed in advance. Throughout, we assume that the communication graph is connected, since the problem is not solvable in disconnected graphs. Each node u has a k-bit binary input x(u).
, which is fixed in advance. Throughout, we assume that the communication graph is connected, since the problem is not solvable in disconnected graphs. Each node u has a k-bit binary input x(u).
Two nodes u and v are neighbors if \(uv \in E\) is an edge in G. The neighborhood of a node u is the set of neighbors of u. It is denoted

The number of neighbors of u is the degree of node u, denoted by

We use \(N^+(u)\) to denote the set containing neighbors of u and u itself,

Above, “\(+\)” denotes the union of a set with a singleton. We extend the definition of neighborhood to sets so that the neighborhood of a set S is the set of nodes not in S that have a neighbor in S,

For a set of nodes \(S \subset V\),
-
\(\overline{S}\) is the set \(V - S\).
-
a cut is a partition \((S, \overline{S})\) of V.
-
the set of edges that cross a cut \((S, \overline{S})\) is denoted by

-
the boundary \(B (S, \overline{S})\) of a cut \((S, \overline{S})\) is the set of nodes that have a neighbor on the other side of the cut, i.e.,

-
edges within the set S are denoted by

A subgraph of G is a graph whose node set and edge set are subsets of V and E respectively.
-
For a subset of nodes \(U \subset V\), G[U] is a subgraph of G node-induced by U, with node set U and edge set E[U].
-
With a slight abuse of terminology, for a subset of edges \(F \subset E\), G[F] is a subgraph of G edge-induced by F, where all the endpoints of edges in F form the node set and F is the edge set. More specifically, the node set of G[F] is given by
 .
.
3 Problem Statement and Cost Function
In the Multiparty Equality Problem, each node u starts with a k-bit binary input x(u) and must output a single bit 0 or 1, meeting the following criteria. If all nodes have the same input, then all nodes must output 0. However, if there is a mismatch \(x(u) \ne x(v)\), for any two distinct nodes u, v, then at least one node in the graph must output 1Footnote 1.
Communication between nodes is via local broadcast. A message sent by a node u is received identically and reliably by each neighbor of u. Moreover, each neighbor can correctly identify u to be the transmitter of the message.
As in [1] and [9], we consider only the static protocols where the transmitters at each time step are pre-determined by the protocol and are independent of the inputs. We consider protocols where the total number of bits \(c(u)\) transmitted by a node u is independent of the inputs. Note that under the local broadcast model, when a node u transmits \(c(u)\) bits, a total of \(d(u) c(u)\) bits are received by all the neighbors of u combined.
In the point-to-point model, a message transmitted by a node u is received by exactly one neighbor of u. So the total number of bits transmitted in a protocol is exactly the same as the total number of bits received. In contrast, in the local broadcast model, the number of bits transmitted is smaller than the number of bits received by factor equal to the degree of the transmitting node. Correspondingly, there are the following two cost functions. The transmission cost of a protocol is the total number of bits transmitted by all the nodes in the graph,
The reception cost of a protocol is the total number of bits received by all the nodes in the graph,
In this paper, we consider the transmission cost of protocols.
4 Lower Bound
The two party equality problem was introduced by Yao [13], who showed that both parties combined must transmit at least k bits to solve the problem. Note that, for two parties, the point-to-point model and the local broadcast model are equivalent. This argument can be extended for \(n \ge 3\) parties by considering two-way partitions of the node set [1, 3]. Let \((S, \overline{S})\) be an arbitrary cut of V. Consider the set of executions where all nodes in S always have the same input and all nodes in \(\overline{S}\) always have the same input. Then this is equivalent to the two party equality problem. Thus, by the two party lower bound, there must be at least k bits shared across the cut.
Consider any multiparty equality protocol under the local broadcast model. Let c(u) be the number of bits transmitted by a node u in the protocol. Then for any cut \((S, \overline{S})\), we have that there must be at least k bits transmitted across the cut. Under the local broadcast model, when a node transmits a message, it is sent identically on all its incident edges. Therefore, the total number of bits transmitted by the nodes at the boundary of the cut \((S, \overline{S})\) must be at least k, i.e.,
Using \(y(u) := {c(u)/k}\) to normalize the transmission by each node, we get the following linear program.

We use \(\mathcal {P}\) to denote the above linear program given by Eqs. 1–3. The cost of \(\mathcal {P}\) is the value of its optimal solution.
Theorem 1
The cost of any static protocol that solves the multiparty equality problem under the local broadcast model is at least the cost of \(\mathcal {P}\).
The proof is an extension of the arguments for two parties. For any cut \((S, \overline{S})\), one can contract all nodes in S into one node and all nodes in \(\overline{S}\) into another to get a two party problem.
Proof
Suppose, for the sake of contradiction, that a static protocol solves the multiparty equality problem but has a cost less than the optimal solution to \(\mathcal {P}\). Then, there exists a cut \((S, \overline{S})\) such that \(\sum _{u \in B (S, \overline{S})} c(u) < k\) for this protocol. By the pigeon hole principle, there exist two inputs \(\alpha \) and \(\beta \) such that the nodes in \(B (S, \overline{S})\) all transmit the same messages in the following three cases:
-
1.
every node in the graph has input \(\alpha \).
-
2.
every node in the graph has input \(\beta \).
-
3.
all nodes in S have input \(\alpha \) and all nodes in \(\overline{S}\) have input \(\beta \).
Since all nodes in S (resp. \(\overline{S}\)) output 0 in case 1 (resp. case 2), therefore, all nodes output 0 in case 3, a contradiction.
5 Simple Protocols
In this section, we consider simple protocols where some subset of nodes is chosen to transmit their entire input. On receiving transmission from any of its neighbors, a node u compares the received value against its own input. If the values match for all the received messages, then u outputs 0. Otherwise, u outputs 1.
Definition 1
A protocol is simple if every node either transmits its entire input, or does not transmit at all.
This set of protocols is related to what is called the weakly connected dominating set of a graph. Consider a subset \(S \subset V\) of nodes. Let  be the set of edges that are incident on at least one node in S. Let
be the set of edges that are incident on at least one node in S. Let  be the subgraph of G edge-induced by F. Then S is a weakly connected dominating set of G if H is a connected spanning subgraph of G.
be the subgraph of G edge-induced by F. Then S is a weakly connected dominating set of G if H is a connected spanning subgraph of G.
Proposition 1
A simple protocol solves the multiparty equality problem if and only if the set \(S \subset V\) of nodes chosen to transmit their entire input is a weakly connected dominating set of G.
Proof
We consider the two directions separately:
-
\(\Rightarrow \) Consider a simple protocol that solves the multiparty equality problem by choosing a set \(S \subset V\) of nodes to transmit their entire input. We show that S is a weakly connected dominating set of G. Let
 .
.-
1.
H is a spanning subgraph of G: Suppose for the sake of contradiction that there is a node \(u \not \in H\). Then u neither sends nor receives any transmissions. Then no node in the graph G can distinguish between the case where all nodes in G have the same input and the case where u has a different input than the rest of the graph. This is a contradiction to the initial assumption that the protocol solves the multiparty equality problem.
-
2.
H is a connected graph: Suppose for the sake of contradiction that H is not a connected graph so that there are at least two connected components A and B of H. Note that no messages are transmitted between A and B. Then no node in G can distinguish between the case where all nodes in G have the same input and the case where nodes in A have a different input than nodes in B. This is a contradiction to the initial assumption that the protocol solves the multiparty equality problem.
-
1.
-
\(\Leftarrow \) Suppose that \(S \subset V\) is a weakly connected dominating set of G. As before, let
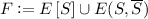 and
and  . Consider the corresponding simple protocol where nodes in S transmit their entire input, while all nodes compare the received values against their own input. Clearly no mismatch is detected when all nodes in G have the same input, and so all nodes output 0. So consider the case where two nodes u, v have mismatching inputs \(x(u) \ne x(v)\). Since H is a connected spanning subgraph of G, so there exists at least one uv-path P in H. Furthermore, because \(x(u) \ne x(v)\) so there exist two adjacent nodes w, z in P such that \(x(w) \ne x(z)\). By construction of H, either \(w \in S\) or \(z \in S\) (or both). WLOG assume that \(w \in S\) and it transmits its entire input in the protocol. Then z will receive a value different than its input and will output 1.
. Consider the corresponding simple protocol where nodes in S transmit their entire input, while all nodes compare the received values against their own input. Clearly no mismatch is detected when all nodes in G have the same input, and so all nodes output 0. So consider the case where two nodes u, v have mismatching inputs \(x(u) \ne x(v)\). Since H is a connected spanning subgraph of G, so there exists at least one uv-path P in H. Furthermore, because \(x(u) \ne x(v)\) so there exist two adjacent nodes w, z in P such that \(x(w) \ne x(z)\). By construction of H, either \(w \in S\) or \(z \in S\) (or both). WLOG assume that \(w \in S\) and it transmits its entire input in the protocol. Then z will receive a value different than its input and will output 1.
Note that the total cost of transmission is  where
where  is the size of the weakly connected dominating set. The minimum weakly connected dominating set problem has been studied in the literature [4,5,6, 11] and is known to be NP-complete.
is the size of the weakly connected dominating set. The minimum weakly connected dominating set problem has been studied in the literature [4,5,6, 11] and is known to be NP-complete.
As mentioned in Sect. 1, simple protocols in the point-to-point model are supported on a rooted spanning tree of G. These are within a factor 2 of the optimal and one can not do any better with linear protocols [1]. Even on complete graphs, non-linear protocols are needed to achieve the optimal cost [2, 9]. Under local broadcast, it is easy to see that simple protocols are optimal for complete graphs (one node transmits its entire input). Unfortunately, the simple protocols suffer a gap of \(\varOmega (\log n)\) against the lower bound on arbitrary graphs.
Proposition 2
There exist a family of graphs such that the cost of \(\mathcal {P}\) is O(k) while any dominating set has size \(\varOmega (k \cdot \log n)\).
Proof (Proof Sketch)
The family of graphs is based on Example 13.4 in [12] for establishing a lower bound on the integrality gap of a linear programming relaxation of the set cover problem. Using a common approximation preserving reduction from the set cover to the dominating set problem, one can get a graph G with the following properties. G has two parts A and B, both of size \({n/2}\). A is a complete graph and B is an independent set. Each node in A (resp. B) has exactly \({(n+2)/4}\) neighbors in B (resp. A). Furthermore, any dominating set has size at least \(\log _2({(n+2)/2})\).
We now give a solution y to \(\mathcal {P}\). Pick an arbitrary node \(s \in A\). Assign \(y(s) := 1\). For each node \(u \in A - s\), assign

For each node \(u \in B\), assign \(y(u) := 0\). To see that y is indeed a solution to \(\mathcal {P}\), consider an arbitrary cut \((S, \overline{S})\). WLOG assume that \(s \in S\). By construction of G (recall that A is a complete graph), if \(A - S\) is non-empty, then \(s \in B (S, \overline{S})\) and we have that
as required. So assume that \(S \supseteq A\). Consider any node \(t \in \overline{S} \subseteq B\). We have that

The first inequality follows from the fact that all of t’s neighbors are in \(A \subseteq S\), and so  . The second inequality follows from \(y(u) \ge {4/(n+2)}\) for each
. The second inequality follows from \(y(u) \ge {4/(n+2)}\) for each  , since
, since  . Finally, the equality follows from the fact that t has exactly \({(n+2)/4}\) neighbors by construction.
. Finally, the equality follows from the fact that t has exactly \({(n+2)/4}\) neighbors by construction.
Recall that, by construction, any dominating set has size at least \(\log _2({(n+2)/2})\). This is a lower bound for any weakly connected dominating set as well. Therefore, any simple protocol has cost at least \(k \cdot \log _2({(n+2)/2})\). On the other hand, the solution y to \(\mathcal {P}\) given above has value

Therefore, the cost of \(\mathcal {P}\) is at most 3k.
6 Upper Bound
In this section, we constructively establish an upper bound on the multiparty equality problem, as stated in the following theorem.
Theorem 2
For sufficiently large k, there exists a protocol that solves the multiparty equality problem with a cost of at most 4 times the cost of \(\mathcal {P}\).
We design a protocol that solves the multiparty equality problem under the local broadcast model. We start with an optimal solution y of the linear program \(\mathcal {P}\) in Sect. 4. Note that y is an optimal solution to \(\mathcal {P}\) for all values of \(k>0\). Since the linear program has integer entries, y(u) is rational for each node u. Let q be an even integer such that \(q \cdot y(u)\) is an integer for all u. Define two integers m and \(\ell \) as follows.
For simplicity, we assume k is an integral multiple of both q and \(\ell \). To design our protocol, we will use an \((m,\ell )\)-Reed-Solomon code [10] over Galois field \(GF(2^{{k/\ell }})\). Note that a code-word in this code consists of m symbols, with each symbol size being \({k/\ell }\) bits. Such a Reed-Solomon code exists so long as \(2^{{k/\ell }}> m\). To satisfy this property, we assume that k is sufficiently large. In a Reed-Solomon (RS) code, k input bits are represented using \(\ell \) symbols from \(GF(2^{{k/\ell }})\), each symbol representing \(k/\ell \) bits of the input. These \(\ell \) symbols are then encoded into m symbols to obtain the corresponding code-word. Given any \(\ell \) out of the m symbols of a code-word, the corresponding k-bit input can be correctly determined. We view the encoding of each of the m symbols as a function  , since we will be applying the encodings to different inputs. Of the m total symbols in the code-word, each node u is assigned \(q {\cdot } y(u)\) of them in the protocol. We describe how the nodes use these symbols later.
, since we will be applying the encodings to different inputs. Of the m total symbols in the code-word, each node u is assigned \(q {\cdot } y(u)\) of them in the protocol. We describe how the nodes use these symbols later.
In the protocol, nodes are either red or blue. We describe how they are colored later. A red node broadcasts its entire input to its neighbors and always outputs 0. A blue node u computes its \(q {\cdot } y(u)\) code symbols on its input x(u) and broadcasts them to its neighbors. A blue node u performs checks (as discussed below) on all transmissions received from its neighbors. If all checks pass, then it outputs 0. Otherwise, it outputs 1. On receiving a transmission from a red neighbor r, u checks if the received value x(r) is the same as x(u). On receiving a transmission from a blue neighbor b, u computes the corresponding \(q \cdot y(b)\) code symbols on its own input x(u) and checks if they match with the received code symbols from b.
We now describe how to color the nodes for the protocol. We color the nodes in rounds. Initially, all nodes are colored white. In each round, at least one white node gets colored either red or blue. At the end, all nodes will be colored either red or blue. Let \(W_i\), \(B_i\), and \(R_i\) denote the set of white, blue, and red nodes at the end of round i, with \(W_0 = V\) and \(B_0 = R_0 = \emptyset \). In each round, we maintain that
-
1.
the red and blue subgraph \(G[R_i \cup B_i]\) is connected, and
-
2.
no white node is a neighbor of a red node.
In round 1, we select an arbitrary node and color it red. All its neighbors are colored blue. In round i, we select an arbitrary white neighbor  of a blue node. Note that until all nodes are colored red or blue, such a white node always exists. There are two cases to consider.
of a blue node. Note that until all nodes are colored red or blue, such a white node always exists. There are two cases to consider.
-
1.
If
$$\begin{aligned} \sum _{v \in N^+(u) \cap W_{i-1}} y(v) \ge \frac{1}{2}, \end{aligned}$$then we color u red and its white neighbors blue:

-
2.
Otherwise we have that

The first equality follows from the fact that 1) u itself is white, and 2) each neighbor of u is either white or blue, so that \(N^+(u)\) can be partitioned into \(N^+(u) \cap W_{i-1}\) and
 . The inequality follows because
. The inequality follows because 
In this case, we color u blue:
$$\begin{aligned} R_{i}&:= R_{i-1}, \\ B_{i}&:= B_{i-1} + u, \\ W_{i}&:= W_{i-1} - u. \end{aligned}$$
Note that while the design of the protocol relies on knowing the solution to \(\mathcal {P}\), the protocol itself is distributed where each red or blue node can run its part locally. In the following lemma, we use the coloring rounds \(i \ge 1\) to inductively prove the correctness of the protocol.
Lemma 1
For each \(i \ge 1\), the protocol solves the multiparty equality problem in the subgraph \(G[R_{i} \cup B_{i}]\).
Proof
We proceed inductively. For the base case, \(i = 1\). We have that \(R_{1} = r\) and  . If there is no mismatch between inputs, then clearly all nodes output 0. If there is a mismatch, then it must necessarily be between r and a blue node
. If there is no mismatch between inputs, then clearly all nodes output 0. If there is a mismatch, then it must necessarily be between r and a blue node  . Since node r broadcasts its entire input, so node b is able to check that \(x(r) \ne x(b)\) and so outputs 1, as required.
. Since node r broadcasts its entire input, so node b is able to check that \(x(r) \ne x(b)\) and so outputs 1, as required.
For the inductive step, assume that the protocol solves the multiparty equality problem in the subgraph \(G[R_{i-1} \cup B_{i-1}]\). We show that it also solves the problem in the subgraph \(G[R_{i} \cup B_{i}]\). If there is a mismatch between inputs of two nodes in \(R_{i-1} \cup B_{i-1}\), then we are done by induction. So assume that all nodes in \(R_{i-1} \cup B_{i-1}\) have the same input. Let  be the white node selected in round i. There are two corresponding cases to consider.
be the white node selected in round i. There are two corresponding cases to consider.
-
1.
u got colored red in round i. Let
 be a neighbor of u which was blue at the end of round \(i-1\). Recall that all nodes in \(R_{i-1} \cup B_{i-1}\) have identical input. If \(x(u) \ne x(b)\), then b will output 1, as required. So suppose \(x(u) = x(b)\). Therefore all nodes in \(R_{i} \cup B_{i-1}\) have identical input. Consider an arbitrary node \(b' \in B_{i} - B_{i-1}\) which got colored blue in round i. By construction,
be a neighbor of u which was blue at the end of round \(i-1\). Recall that all nodes in \(R_{i-1} \cup B_{i-1}\) have identical input. If \(x(u) \ne x(b)\), then b will output 1, as required. So suppose \(x(u) = x(b)\). Therefore all nodes in \(R_{i} \cup B_{i-1}\) have identical input. Consider an arbitrary node \(b' \in B_{i} - B_{i-1}\) which got colored blue in round i. By construction,  . So \(b'\) receives the entire input of u. If \(x(b') \ne x(u)\), then \(b'\) will output 1. If \(x(b') = x(u)\), then \(b'\) will output 0, as required.
. So \(b'\) receives the entire input of u. If \(x(b') \ne x(u)\), then \(b'\) will output 1. If \(x(b') = x(u)\), then \(b'\) will output 0, as required. -
2.
u got colored blue in round i. Recall that u is the only node that got colored either red or blue in round i, i.e.,
 . Also, we have that
. Also, we have that 
So u must have received a total of at least
 code symbols from nodes in \(B_{i-1}\). u re-computes these code symbols on its own input x(u) and checks against the received values. Since all nodes in \(B_{i-1}\) have the same input, by the property of RS codes, u outputs 0 if and only if x(u) is the same as the inputs of nodes in \(B_{i-1}\).
code symbols from nodes in \(B_{i-1}\). u re-computes these code symbols on its own input x(u) and checks against the received values. Since all nodes in \(B_{i-1}\) have the same input, by the property of RS codes, u outputs 0 if and only if x(u) is the same as the inputs of nodes in \(B_{i-1}\).
Therefore the protocol solves the multiparty equality problem in the subgraph \(G[R_{i} \cup B_{i}]\), as required.
The following lemma bounds the transmission cost of the protocol.
Lemma 2
The cost of transmission of the protocol is at most \(4k \cdot \sum _{u \in V} y(u)\).
Proof
The total number of bits transmitted by the red nodes is k times the number of red nodes, say t. Let \(i_1< i_2< \dots < i_t\) be the rounds where nodes \(r_1, r_2, \dots , r_t\) got colored red. We have that

For the first inequality, recall that  for all
for all  since \(r_j\) got colored red in round \(i_j\). For the last inequality, note that \(N^+(r_j) \cap W_{i_j-1}\) and \(N^+(r_{j'}) \cap W_{i_{j'}-1}\) are disjoint for any distinct
since \(r_j\) got colored red in round \(i_j\). For the last inequality, note that \(N^+(r_j) \cap W_{i_j-1}\) and \(N^+(r_{j'}) \cap W_{i_{j'}-1}\) are disjoint for any distinct  . To see this, assume \(j < j'\) so that \(N^+(r_j) \cap W_{i_{j'}-1}\) is empty because \(r_j\) got colored red and its neighborhood blue in round \(i_j\). Thus, the total number of bits transmitted by red nodes is upper bounded by \(2k \cdot \sum _{u \in V} y(u)\).
. To see this, assume \(j < j'\) so that \(N^+(r_j) \cap W_{i_{j'}-1}\) is empty because \(r_j\) got colored red and its neighborhood blue in round \(i_j\). Thus, the total number of bits transmitted by red nodes is upper bounded by \(2k \cdot \sum _{u \in V} y(u)\).
For the blue nodes, recall that each blue node u transmits \(q \cdot y(u)\) code symbols, each of which consists of \({k/\ell }\) bits. So, the total number of bits transmitted by the blue nodes is at most

where the first equality follows from \(\ell = {q/2}\).
It follows that the total number of bits transmitted by both the red and the blue nodes in the protocol is at most \(4k \cdot \sum _{u \in V} y(u)\).
Proof
(Proof of Theorem 2). A protocol that solves the multiparty equality problem is given in this section. The proof of correctness follows from Lemma 1 while the transmission cost is bounded in Lemma 2.
7 Conclusion and Open Problems
In this paper we have studied the multiparty equality problem under the local broadcast model on arbitrary graphs. We established a lower bound to the transmission cost using two-way partitions of nodes. We identified simple protocols and observed that they can cost \(\varOmega (\log n)\) times the lower bound in certain graphs. This is in contrast to the point-to-point model where simple protocols are within a factor 2 of the lower bound [1]. We also presented linear protocols, based on Reed-Solomon codes, that cost at most 4 times the lower bound.
We finish the paper with some open problems:
-
1.
Can the lower bound be improved? Note that the lower bound for the point-to-point communication model [1] is also based on two-way partitions of nodes. If a better lower bound exists for the local broadcast model, can the same technique be used to improve the lower bound for the point-to-point model, or vice versa?
-
2.
Can we improve on the given upper bound?
-
3.
In this work, we considered the transmission costs of the protocols (Sect. 3). What do the protocols look like if they minimize reception cost instead? Let \(\text {cost}_{P}(G)\) be the cost of an optimal protocol under point-to-point communication on a graph G. Let \(\text {cost}_{T}(G)\) and \(\text {cost}_{R}(G)\) be the transmission and reception costs of corresponding optimal protocols under local broadcast on a graph G. Then we have the following relationship between the three quantities.
$$\begin{aligned} \text {cost}_{T}(G) \le \text {cost}_{P}(G) \le \text {cost}_{R}(G). \end{aligned}$$The first inequality follows from the fact that any protocol \(P_p\) designed for the point-to-point model can be converted into a protocol \(P_b\) for the local broadcast model by having each node broadcast all the messages it transmits in P, without paying any additional transmission cost. The second inequality follows from the fact that any protocol \(P_b\) designed for the local broadcast model can be converted into a protocol \(P_p\) for the point-to-point model by having each node transmit all of its messages in \(P_b\) to all of its neighbors via point-to-point transmissions in \(P_p\), without paying any additional reception cost.
-
4.
A more generalized problem is where each node is assigned a weight. This weight is the per bit cost paid for communication by the node. This model generalizes both the transmission and reception cost variants.
-
5.
In this work, we have considered static protocols (see Sect. 3) where the transmitters at each time step and the number of bits transmitted by each node are both independent of the input. Do “dynamic” protocols perform any better under local broadcast?
Notes
- 1.
Note that the node detecting a mismatch between inputs can propagate this to the rest of the graph with an overhead that is independent of k, but not of n.
References
Alon, N., Efremenko, K., Sudakov, B.: Testing equality in communication graphs. IEEE Trans. Inf. Theory 63(11), 7569–7574 (2017)
Alon, N., Moitra, A., Sudakov, B.: Nearly complete graphs decomposable into large induced matchings and their applications. In: Proceedings of the Forty-Fourth Annual ACM Symposium on Theory of Computing, STOC 2012, pp. 1079–1090. Association for Computing Machinery, New York (2012). https://doi.org/10.1145/2213977.2214074
Chattopadhyay, A., Rudra, A.: The range of topological effects on communication. In: Halldórsson, M.M., Iwama, K., Kobayashi, N., Speckmann, B. (eds.) ICALP 2015. LNCS, vol. 9135, pp. 540–551. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47666-6_43
Chen, Y.P., Liestman, A.L.: Approximating minimum size weakly-connected dominating sets for clustering mobile ad hoc networks. In: Proceedings of the 3rd ACM International Symposium on Mobile Ad Hoc Networking & Computing, MobiHoc 2002, pp. 165–172. Association for Computing Machinery, New York (2002). https://doi.org/10.1145/513800.513821
Dubhashi, D., Mei, A., Panconesi, A., Radhakrishnan, J., Srinivasan, A.: Fast distributed algorithms for (weakly) connected dominating sets and linear-size skeletons. J. Comput. Syst. Sci. 71(4), 467–479 (2005). https://doi.org/10.1016/j.jcss.2005.04.002. http://www.sciencedirect.com/science/article/pii/S002200000500053X
Dunbar, J.E., Grossman, J.W., Hattingh, J.H., Hedetniemi, S.T., McRae, A.A.: On weakly connected domination in graphs. Discrete Math. 167–168, 261–269 (1997). Selected Papers 15th British Combinatorial Conference. https://doi.org/10.1016/S0012-365X(96)00233-6. http://www.sciencedirect.com/science/article/pii/S0012365X96002336
Khan, M.S., Naqvi, S.S., Vaidya, N.H.: Exact Byzantine consensus on undirected graphs under local broadcast model. In: Proceedings of the 2019 ACM Symposium on Principles of Distributed Computing, PODC 2019, pp. 327–336. Association for Computing Machinery, New York (2019). https://doi.org/10.1145/3293611.3331619
Khan, M.S., Tseng, L., Vaidya, N.H.: Exact Byzantine consensus on arbitrary directed graphs under local broadcast model. In: 23rd International Conference on Principles of Distributed Systems (OPODIS 2019). Leibniz International Proceedings in Informatics (LIPIcs), vol. 153, pp. 30:1–30:16. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, Dagstuhl, Germany (2020). https://doi.org/10.4230/LIPIcs.OPODIS.2019.30. https://drops.dagstuhl.de/opus/volltexte/2020/11816
Liang, G., Vaidya, N.: Multiparty equality function computation in networks with point-to-point links. In: Kosowski, A., Yamashita, M. (eds.) SIROCCO 2011. LNCS, vol. 6796, pp. 258–269. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22212-2_23
Reed, I.S., Solomon, G.: Polynomial codes over certain finite fields. J. Soc. Ind. Appl. Math. 8(2), 300–304 (1960)
Swaminathan, V.: Weakly connected domination in graphs. Electron. Notes Discrete Math. 33, 67–73 (2009). International Conference on Graph Theory and Its Applications. https://doi.org/10.1016/j.endm.2009.03.010. http://www.sciencedirect.com/science/article/pii/S1571065309000298
Vazirani, V.V.: Approximation Algorithms. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-662-04565-7
Yao, A.C.C.: Some complexity questions related to distributive computing (preliminary report). In: Proceedings of the Eleventh Annual ACM Symposium on Theory of Computing, STOC 1979, pp. 209–213. Association for Computing Machinery, New York (1979). https://doi.org/10.1145/800135.804414
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Khan, M.S., Vaidya, N.H. (2021). Testing Equality Under the Local Broadcast Model. In: Jurdziński, T., Schmid, S. (eds) Structural Information and Communication Complexity. SIROCCO 2021. Lecture Notes in Computer Science(), vol 12810. Springer, Cham. https://doi.org/10.1007/978-3-030-79527-6_15
Download citation
DOI: https://doi.org/10.1007/978-3-030-79527-6_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-79526-9
Online ISBN: 978-3-030-79527-6
eBook Packages: Computer ScienceComputer Science (R0)








 .
. .
.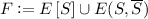 and
and  . Consider the corresponding simple protocol where nodes in S transmit their entire input, while all nodes compare the received values against their own input. Clearly no mismatch is detected when all nodes in G have the same input, and so all nodes output 0. So consider the case where two nodes u, v have mismatching inputs
. Consider the corresponding simple protocol where nodes in S transmit their entire input, while all nodes compare the received values against their own input. Clearly no mismatch is detected when all nodes in G have the same input, and so all nodes output 0. So consider the case where two nodes u, v have mismatching inputs 

 . The inequality follows because
. The inequality follows because 
 be a neighbor of u which was blue at the end of round
be a neighbor of u which was blue at the end of round  . So
. So  . Also, we have that
. Also, we have that 
 code symbols from nodes in
code symbols from nodes in