22.1 Introduction

The terminology vehicle-bridge interaction (VBI) came out in the 1990s when people were trying to figure out the dynamic responses of bridges and high-speed trains [12, 16]. The interaction between the bridge and vehicle occurs naturally as the moving vehicle excites the vibration to the bridge, and the bridge turns back the vibration to the vehicle at the same time. Such an interaction loop makes the VBI system possible for practical applications, including health monitoring of structures, damage detection of bridges, design of bridges and mobile sensors, etc. Nowadays, VBI has become one prosperous research direction in the world. For readers interested in a detailed review of VBI topics, recent publications are referred to the state-of-the-art review [14] and the book [15], Vehicle Scanning Method, by Yang and his co-workers.

In a VBI system, it is known that the key components are the bridge and vehicle although there are factors affecting the interaction between the bridge and vehicle [3, 8, 9, 11]. In the literature [7, 10, 13], the vehicle is mostly treated as a moving load. Particularly, a single-degree-of-freedom (SDOF) sprung mass is adopted due to its simplicity. Nevertheless, by carefully examining the SDOF vehicle model, there is room for improvement of the vehicle model in order to effectively obtain bridge frequencies. For instance, a two-mass vehicle model was proposed to consider both sprung mass and unsprung mass [6]. As the test vehicle is assumed to be in contact with the road via its wheels, the dynamic responses of both vehicle and bridge can be better reflected when the unsprung mass is included. Nevertheless, the assumption of direct contact of the wheel at a particular point in the presence of road surface roughness is still not realistic since the wheels are of finite size in general. Therefore, a massless disk model was proposed by including the influence of wheel size [4]. In this work, a comparison of the disk model and the SDOF vehicle model was made. It was shown that the moving paths obtained by these two models are different under road surface roughness, and the moving path of the disk model is the envelope of that of the point model. In view of the aforementioned models, the present work further proposes a wheel size embedded two-mass vehicle model. By combining the wheel size and unsprung mass, a wider application is easily seen in the future. The interested readers are referred to the authors’ recent publication [5] for complete description of the VBI model.

The structure of this work is arranged in the following: the VBI formulation for the proposed vehicle model is briefly introduced in Sect. 22.2. In Sect. 22.3, the proposed vehicle model is first verified by comparing it with an analytical solution. Then, a numerical investigation is given. Section 22.4 concludes this work.

22.2 VBI Formulation

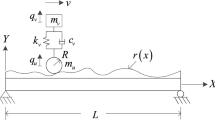
The schematic diagram of the proposed VBI system, wheel size embedded two-mass vehicle model, is depicted in Fig. 22.1. The symbols are introduced as follows: \(m_v\) is the sprung mass representing the vehicle body; \(m_u\) is the unsprung mass representing the axle mass; R is the wheel radius; the two masses are connected by a spring of stiffness \(k_v\) and a dashpot of damping coefficient \(c_v\). For the VBI system in consideration, the vehicle is assumed to move with a constant velocity v on the road with surface roughness denoted by r(x). A simply supported beam of length L is adopted for the bridge.

The corresponding equations of motion for the vehicle and beam element are given as follows:

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{m_v}}&{}0\\ 0&{}{{m_u}} \end{array}} \right] \left\{ {\begin{array}{*{20}{c}} {{{\ddot{q}}_v}}\\ {{{\ddot{q}}_u}} \end{array}} \right\} + \left[ {\begin{array}{*{20}{c}} {{c_v}}&{}{ - {c_v}}\\ { - {c_v}}&{}{{c_v}} \end{array}} \right] \left\{ {\begin{array}{*{20}{c}} {{{\dot{q}}_v}}\\ {{{\dot{q}}_u}} \end{array}} \right\} + \left[ {\begin{array}{*{20}{c}} {{k_v}}&{}{ - {k_v}}\\ { - {k_v}}&{}{{k_v}} \end{array}} \right] \left\{ {\begin{array}{*{20}{c}} {{q_v}}\\ {{q_u}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} 0\\ {{m_v}{{\ddot{q}}_v} + {m_u}{{\ddot{q}}_u}} \end{array}} \right\} \end{aligned}$$
(22.1)
$$\begin{aligned} \left[ {{m_b}} \right] \left\{ {{{\ddot{q}}_b}} \right\} + \left[ {{c_b}} \right] \left\{ {{{\dot{q}}_b}} \right\} + \left[ {{k_b}} \right] \left\{ {{q_b}} \right\} = - {f_c}\left\{ {N\left( {{{\bar{x}}_c}} \right) } \right\} - {M_c}\left\{ {N'\left( {{{\bar{x}}_c}} \right) } \right\} \end{aligned}$$
(22.2)
Fig. 22.1
figure 1

Schematic diagram of the VBI system

Full size image

In Eq. (22.1), \(q_v\) and \(q_u\) represent the displacements of the vehicle body and unsprung mass, respectively; g is the gravitational constant. In Eq. (22.2), \([m_b]\), \([c_b]\), and \([k_b]\) are the mass, damping, and stiffness matrices of the beam element, with \(\{q_b\}\) the corresponding displacement vector. \(\{N\}\) and \(\{N'\}\) denote the vector composed of the cubic Hermitian interpolation functions and the first-order derivative of the vector. \(\bar{x}_c\) is the location of contact point. The expressions for \(f_c\) and \(M_c\) are

$$\begin{aligned} f_c = (m_v + m_u) g + m_v \ddot{q}_v + m_u \ddot{q}_u \end{aligned}$$
(22.3)

and

$$\begin{aligned} M_c = f_c \, \Delta x \end{aligned}$$
(22.4)

The following displacement relation is adopted:

$$\begin{aligned} {q_u} = {\left\{ {N\left( {{{\bar{x}}_c}} \right) } \right\} ^\mathrm{{T}}}\left\{ {{q_b}} \right\} + \bar{r}\left( {{x_c}} \right) \end{aligned}$$
(22.5)

where \(\bar{r}(x_c)\) represents the lift of the entire wheel, and \(x_c\) represents the location of wheel center.

Substituting Eqs. (22.3)–(22.5) into Eqs. (22.1) and (22.2) leads to the following matrix form of the equations of VBI system:

$$\begin{aligned} \mathbf{{M}}\left\{ \begin{array}{l} {{\ddot{q}}_v}\\ \left\{ {{{\ddot{q}}_b}} \right\} \end{array} \right\} + \mathbf{{C}}\left\{ \begin{array}{l} {{\dot{q}}_v}\\ \left\{ {{{\dot{q}}_b}} \right\} \end{array} \right\} + \mathbf{{K}}\left\{ \begin{array}{l} {q_v}\\ \left\{ {{q_b}} \right\} \end{array} \right\} = \mathbf{{F}} \end{aligned}$$
(22.6)

To reach the above equation, the detailed derivation is given in the authors’ recent publication [5]. In Eq. (22.6), the boldface denotes the matrix form, and the corresponding components in the matrices are given as follows:

$$\begin{aligned} \mathbf{{M}}&= \left[ {\begin{array}{*{20}{c}} {{m_v}}&{}\mathbf{{0}}\\ \mathbf{{M}}_{vu}&{}\mathbf{{M}}_{uu} \end{array}} \right] , \nonumber \\&\mathbf{{M}}_{vu} = {{m_v}\left( {\left\{ {N\left( {{{\bar{x}}_c}} \right) } \right\} + \left\{ {N'\left( {{{\bar{x}}_c}} \right) } \right\} \Delta x} \right) } , \nonumber \\&\mathbf{{M}}_{uu} = {\left[ {{m_b}} \right] + \left\{ {N\left( {{{\bar{x}}_c}} \right) } \right\} {{\left\{ {N\left( {{{\bar{x}}_c}} \right) } \right\} }^\mathrm{{T}}}{m_u} + \left\{ {N'\left( {{{\bar{x}}_c}} \right) } \right\} {{\left\{ {N\left( {{{\bar{x}}_c}} \right) } \right\} }^\mathrm{{T}}}{m_u}\Delta x}\end{aligned}$$
(22.7)
$$\begin{aligned} \mathbf{{C}}&= \left[ {\begin{array}{*{20}{c}} {{c_v}}&{}{ - {c_v}{{\left\{ {N\left( {{{\bar{x}}_c}} \right) } \right\} }^\mathrm{{T}}}}\\ \mathbf{{0}}&{}{\left[ {{c_b}} \right] + 2v{m_u}\left( {\left\{ {N\left( {{{\bar{x}}_c}} \right) } \right\} {{\left\{ {N'\left( {{{\bar{x}}_c}} \right) } \right\} }^\mathrm{{T}}} + \left\{ {N'\left( {{{\bar{x}}_c}} \right) } \right\} {{\left\{ {N'\left( {{{\bar{x}}_c}} \right) } \right\} }^\mathrm{{T}}}\Delta x} \right) } \end{array}} \right] \end{aligned}$$
(22.8)
$$\begin{aligned} \mathbf{{K}}&= \left[ {\begin{array}{*{20}{c}} {{k_v}}&{}{ - {c_v}v{{\left\{ {N'\left( {{{\bar{x}}_c}} \right) } \right\} }^\mathrm{{T}}} - {k_v}{{\left\{ {N\left( {{{\bar{x}}_c}} \right) } \right\} }^\mathrm{{T}}}}\\ \mathbf{{0}}&{}{\left[ {{k_b}} \right] + {v^2}{m_u}\left( {\left\{ {N\left( {{{\bar{x}}_c}} \right) } \right\} {{\left\{ {N''\left( {{{\bar{x}}_c}} \right) } \right\} }^\mathrm{{T}}} + \left\{ {N'\left( {{{\bar{x}}_c}} \right) } \right\} {{\left\{ {N''\left( {{{\bar{x}}_c}} \right) } \right\} }^\mathrm{{T}}}\Delta x} \right) } \end{array}} \right] \end{aligned}$$
(22.9)
$$\begin{aligned} \mathbf{{F}}&= \left\{ {\begin{array}{*{20}{c}} {{f_v}}\\ {\left\{ {{f_b}} \right\} } \end{array}} \right\} \nonumber \\ \mathrm{{ }}&= \left\{ {\begin{array}{*{20}{c}} {{c_v}v\bar{r}'\left( {{x_c}} \right) + {k_v}\bar{r}\left( {{x_c}} \right) }\\ { - \left[ {\left( {{m_v} + {m_u}} \right) g\mathrm{{ + }}{m_u}{v^2}\bar{r}''\left( {{x_c}} \right) } \right] \left( {\left\{ {N\left( {{{\bar{x}}_c}} \right) } \right\} \mathrm{{ + }}\left\{ {N'\left( {{{\bar{x}}_c}} \right) } \right\} \Delta x} \right) } \end{array}} \right\} \end{aligned}$$
(22.10)

In Eqs. (22.7)–(22.10), the parameters including \(\bar{x}_c\), \(x_c\), and \(\bar{r}(x_c)\) are unknowns to be determined numerically. Therefore, the procedure for finding these parameters is crucial in this work. Due to limited space, it is referred to the work given in [5].

22.3 Numerical Results

22.3.1 Verification

The following parameters and material properties are adopted for verifying the proposed vehicle model [5]. For the bridge, \(\bar{m} = 1000~\text {kg/m}\), \(L = 30~\text {m}\), \(E = 27.5~\text {GPa}\), and \(I = 0.175~\text {m}^4\); for the vehicle, \(m_v = 1500~\text {kg}\), \(m_u = 150~\text {kg}\), \(k_v = 170~\text {kN/m}\), \(R = 0.3~\text {m}\), and \(v = 5~\text {m/s}\). In the finite element simulation, 40 beam elements are adopted. The dynamic equations are solved by using a time interval \(\Delta t = 0.001~\text {s}\). The damping effect is ignored for both bridge and vehicle.

As depicted in Figs. 22.2 and 22.3, the dynamic responses including deflection and acceleration of both bridge and vehicle obtained by the present vehicle model agree well with the analytical solutions derived by Biggs [2].

Fig. 22.2
figure 2

Dynamic responses of the bridge: a deflection; b acceleration

Full size image
Fig. 22.3
figure 3

Dynamic responses of the vehicle: a deflection; b acceleration

Full size image

22.3.2 Identification of Bridge Frequencies

In this study, the same information about bridge and vehicle given in Sect. 22.3.1 is adopted again while the damping ratio 0.2 is considered in the test vehicle. In addition, a high level of road irregularity is adopted. The numerical generation of road irregularity is referred to ISO 8608 [1]. Figure 22.4 shows the moving path of the wheel together with the road irregularity. Obviously, the moving path of the wheel encloses the periphery of the profile of road irregularity, which indicates the effect of wheel size.

Fig. 22.4
figure 4

Moving path of the wheel corresponding to road irregularity

Full size image

Next, the ability of the proposed vehicle model to identify bridge frequencies is investigated. As shown in Fig. 22.5a, the overview of vehicle’s spectrum is presented. By zooming in this figure, as shown in Fig. 22.5b, the marked high peaks in the spectrum are corresponding to bridge frequencies. In particular, it is observed that the first four bridge frequencies can be identified clearly even under a high level of road irregularity. By examining the maximal relative error of the identified bridge frequencies, it is found that the proposed vehicle model can extract at least the first five bridge frequencies with maximal relative error less than \(5\%\).

Fig. 22.5
figure 5

Vehicle’s spectra: a overview of the spectrum; b enlargement of the spectrum

Full size image

22.4 Conclusion

In this work, an advanced vehicle model is proposed for the identification of bridge frequencies. Aiming at effectively and efficiently scanning bridge frequencies, the wheel size is embedded in the two-mass vehicle model. From numerical investigation, it is easily seen that the major contribution of this work is the ability to scan high bridge frequencies even under a high level of road irregularity. In particular, no additional technique such as empirical mode decomposition (EMD) is involved to process the vehicle’s spectra, thereby making the proposed VBI model practical. Through the spectral analysis of dynamic responses recorded by the vehicle, both the vehicle and bridge frequencies can be identified directly. The efficacy of the proposed VBI model is therefore demonstrated.