Optimal Control for a Space Rendezvous

Abstract

We consider the transfer of a chaser vehicle to a space station using impulsive control with minimal fuel consumption. It is assumed that the space station moves on a circular Keplerian orbit in a rotational symmetric gravitational field and that the chaser vehicle has already reached the station’s orbital plane. The vehicle is steered by impulsive burns of the rockets. The problem is solved numerically using Pontryagin’s maximum principle for impulsive controls by a multiple shooting method and a continuation procedure to study the variation of the optimal control strategy for varying time constraints. The problem is studied using a local linearized system and the fully nonlinear system using local Cartesian and polar coordinates.

21.1 Introduction

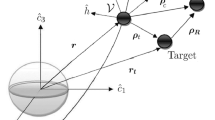
We investigate the energy-optimal impulsive control of a chaser vehicle (C) to a space station (S), which moves on a circular Keplerian orbit (Fig. 21.1). The chaser is steered by impulsive burns of its rockets. Finding the control strategy, which uses the least amount of propellant, is one of the most important tasks in manoeuvre planning.

Fig. 21.1

A chaser vehicle (C) should be transferred to the vicinity of the space station by impulsive thrusts

The transfer problem between different Keplerian orbits has already been solved by Hohmann [1]. He suggested applying two thrusts in a tangential direction, which yields the optimal solution, as long as the orbits are not too far apart.

In this article we investigate the control problem using Pontryagin’s Maximum principle, which is discussed in depth in [2]. In this reference also the problem with impulsive control thrusts is considered and the proof relies on a previous article by Blaquiere [3].

While most applications of Optimal Control Theory assume quadratic control costs, we are interested in the more relevant $L_1$-norm of the cost, the actually burned fuel. This choice leads to a complication, because from the Maximum Principle we cannot directly derive the optimal control depending on the state and costate variables, as is the case for quadratic control costs.

A further topic in this article is the comparison between different sets of coordinate systems: While localized coordinates around the space station lead to the frequently used linear Clohessy-Wiltshire equations, we are also interested in the results for the full nonlinear equations using either a local co-rotating Cartesian frame or localized polar coordinates. While the Cartesian coordinates reflect the view from the space station, the polar coordinates better reflect the orbital dynamics of the system. The computed results demonstrate that one has to be careful in stating the initial conditions, otherwise one obtains significant differences in the solutions. Although the considered distances are very small compared to the orbital radius, the small differences in the different coordinate descriptions cause quite large effects in the optimal solution.

The article is organized as follows: First, we introduce the used coordinate systems and the equations of motion for the chaser vehicle in these coordinates. Then we derive the difference equations for the considered impulsive control and state the necessary optimality conditions following from Pontryagin’s Maximum Principle for systems with impulsive controls, as given in [2]. Finally, we apply the method to the chasing problem in the different coordinate systems.

21.2 Equations of Motion

During free flight, the chaser vehicle’s motion is governed by the equations of a body in the earth’s gravitational field. In planar Cartesian coordinates, the equations of motion read

Fig. 21.2

Local Cartesian (X, Y) and polar coordinate ($X_P, Y_P$) systems

$$\begin{aligned} \ddot{\boldsymbol{x}} = -\frac{k \boldsymbol{x}}{|\boldsymbol{x}|^3}, \end{aligned}$$

(21.1)

with $k=G m_E$, where G is the gravitational constant and $m_E$ is the mass of the earth. The space station rotates on a circular part of radius $r_S$ with angular velocity $\omega$, where $k = r_S^3 \omega ^2$.

$$\begin{aligned} \boldsymbol{x}_S = \mathbf {B}(t) \begin{pmatrix} r_S \\ 0 \end{pmatrix}, \quad \text {where } \mathbf {B}(t) = \begin{pmatrix} \cos \omega t &{} -\sin \omega t\\ \sin \omega t &{} \cos \omega t \end{pmatrix}. \end{aligned}$$

(21.2)

Introducing a relative rotating reference frame (see Fig.  21.2), in which the space station S rests at the origin,

$$\begin{aligned} \boldsymbol{x} =\boldsymbol{x}_S + \mathbf {B}(t) \boldsymbol{X} \end{aligned}$$

(21.3)

and rescaling the time by $\tau = \omega t$, we obtain the near-field dynamics

$$\begin{aligned} \ddot{X}&= 2 \dot{Y} + r_S+X - \frac{r_S^3(r_S+X)}{\left( (r_S+X)^2 + Y^2\right) ^{3/2}}, \end{aligned}$$

(21.4a)

$$\begin{aligned} \ddot{Y}&= -2 \dot{X} + Y - \frac{r_S^3 Y}{\left( (r_S+X)^2 + Y^2\right) ^{3/2}}, \end{aligned}$$

(21.4b)

where the dots now denote derivatives with respect to orbital time $\tau$. For $|\boldsymbol{X}| \ll r_S$, Eq. (21.4) can be approximated by the linear system, well known as Clohessy-Wiltshire equations [4],

$$\begin{aligned} \ddot{X}&= 2 \dot{Y} + 3 X, \end{aligned}$$

(21.5a)

$$\begin{aligned} \ddot{Y}&= -2 \dot{X}. \end{aligned}$$

(21.5b)

A second possible choice of coordinates are polar coordinates: $\boldsymbol{x} = r (\cos \varphi , \sin \varphi )^T$. In these coordinates, the equations of motion are given by

$$\begin{aligned} \ddot{r} - r \dot{\varphi }^2&= -\frac{k}{r^2}, \end{aligned}$$

(21.6a)

$$\begin{aligned} \frac{d}{dt} r^2 \dot{\varphi } = r^2 \ddot{\varphi } + 2 r \dot{r} \dot{\varphi }&= 0. \end{aligned}$$

(21.6b)

Now we again introduce local variables $X_P=r-r_S$ and $Y_P = r_S (\varphi -\omega t)$ (see Fig. 21.2), which agree with the Cartesian coordinates at first order. The positions in the polar and Cartesian coordinate systems are related by

$$\begin{aligned} X&= (r_S + X_P) \cos (Y_P/r_S) - r_S, \end{aligned}$$

(21.7a)

$$\begin{aligned} Y&= (r_S + X_P) \sin (Y_P/r_S). \end{aligned}$$

(21.7b)

We obtain the rescaled equations

$$\begin{aligned} \ddot{X}_P - (r_S+X_P) \left( 1 + \frac{\dot{Y}_P}{r_S}\right) ^2&= - \frac{r_S^3}{(r_S+X_P)^2}, \end{aligned}$$

(21.8a)

$$\begin{aligned} 2 \dot{X}_P \left( 1+\frac{\dot{Y}_P}{r_S}\right) + (r_S + X_P) \frac{\ddot{Y}_P}{r_S}&= 0. \end{aligned}$$

(21.8b)

As expected, at leading order we again obtain the linear system (21.5).

21.2.1 Impulsive Control Actions

In order to steer the chaser to its target position, a series of impulsive controls is applied by firing the engine for infinitely short intervals. We assume, that the direction and magnitude of these impulses can be chosen arbitrarily. During firing, the position of the vehicle remains unaltered, but the velocity changes instantaneously. If the scaled impulsive control at time $\tau _i$ is denoted by $\boldsymbol{v}_i$, the change in the velocities is given by

$$\begin{aligned} \Delta \dot{X}(\tau _i)&= \dot{X}(\tau _i^+) - \dot{X}(\tau _i^-) = v_{i,1}, \end{aligned}$$

(21.9a)

$$\begin{aligned} \Delta \dot{Y}(\tau _i)&= \dot{Y}(\tau _i^+) - \dot{Y}(\tau _i^-) = v_{i,2}, \end{aligned}$$

(21.9b)

where $\dot{X}(\tau _i^+)$ and $\dot{X}(\tau _i^-)$ denote the values of $\dot{X}$ immediately before and after the impulsive control action, respectively.

In polar coordinates, the impulse control leads to

$$\begin{aligned} \Delta \dot{r}(\tau _i)&= v_{i,r},&\text {with } v_{i,r}&= v_{i,1} \cos \varphi + v_{i,2} \sin \varphi , \end{aligned}$$

(21.10a)

$$\begin{aligned} \Delta (r^2 \dot{\varphi })(\tau _i)&= r v_{i,\varphi },&v_{i, \varphi }&= -v_{i,1}\sin \varphi + v_{i,2} \cos \varphi , . \end{aligned}$$

(21.10b)

Since r is unaffected by the impulse, (21.10b) becomes

$$\begin{aligned} \Delta \dot{\varphi } (\tau _i) = v_{i,\varphi }/r. \end{aligned}$$

(21.10c)

In local variables, (21.10) becomes

$$\begin{aligned} \Delta \dot{X}_P(\tau _i)&= v_{i,r}, \end{aligned}$$

(21.11a)

$$\begin{aligned} \Delta \dot{Y}_P(\tau _i)&= r_S v_{i,\varphi }/(r_S+X_P). \end{aligned}$$

(21.11b)

In these coordinates, the jump in $\dot{Y}_P$ also depends on the state variable $X_P$; since $|X_P| \ll r_S$, this dependency vanishes in the linearized equations, but has to be taken into consideration in the treatment of the nonlinear system. We further note that $|(v_{i,r}, v_{i,\varphi })|=|(v_{i,1}, v_{i,2})|$ holds.

21.2.2 Optimal Control Problem

In space missions, the propellant consumption is one of the most important topics, therefore we search for a control strategy, which steers the chaser vehicle to its target position and uses the least amount of fuel. Under some circumstances, it might be necessary to reach the target in a shorter time at the cost of higher energy expenditure. In this case, we prescribe the time interval for the manoeuvre, otherwise the final time is left to be determined by optimizing fuel consumption alone.

We search for an optimal sequence of impulsive controls, which minimizes the cost

$$\begin{aligned} C = \sum _{i=1}^k |\boldsymbol{v}_i|, \end{aligned}$$

(21.12)

where the number k of impulses, the time instances $\tau _i$, the impulse vectors $\boldsymbol{v}_i$, and possibly the time interval T have to be chosen optimally.

Let us stress here that we search the minimum propellant usage in the $L_1$-norm, which corresponds to the real costs. Quadratic cost functions are usually easier to handle, but do not properly describe the minimal cost.

The necessary conditions for optimal control problems with impulsive controls were already stated in [2, 3] and apply to the general optimal control problem with continuous controls $u_i(t)$, impulsive controls $\boldsymbol{v}_i$, utility functions $F(\boldsymbol{q}(t), \boldsymbol{u}(t), t)$, and $G(\boldsymbol{q}(\tau _i^-), \boldsymbol{v}_i, \tau _i)$ for the continuous and discrete controls, respectively, and a terminal value $S(\boldsymbol{q}(T^+))$:

$$\begin{aligned} \max _{\boldsymbol{u}, k, \tau _i, \boldsymbol{v}_i} \{J&= \int _0^T F(\boldsymbol{q}(t), \boldsymbol{u}(t), t) dt + \sum _{i=1}^k G(\boldsymbol{q}(\tau _i^-), \boldsymbol{v}_i, \tau _i) + S(\boldsymbol{q}(T^+))\}, \end{aligned}$$

(21.13)

such that

$$\begin{aligned} \dot{\boldsymbol{q}}(t)&= \boldsymbol{f}(\boldsymbol{q}(t), \boldsymbol{u}(t), t), \quad \boldsymbol{q}(0^-)=\boldsymbol{q}_0, \end{aligned}$$

(21.14)

$$\begin{aligned} \boldsymbol{q}(\tau _i^+) - \boldsymbol{q}(\tau _i^-)&= \boldsymbol{g}(\boldsymbol{q}(\tau _i^-), \boldsymbol{v}_i, \tau _i). \end{aligned}$$

(21.15)

Similarly to the Maximum Principle by Pontryagin, one defines two Hamilton functions, one for the continuous part, and one for the discontinuities

$$\begin{aligned} H(\boldsymbol{q}, \boldsymbol{p}, \boldsymbol{u}, t)&= F(\boldsymbol{q}(t),\boldsymbol{u}(t), t) + \boldsymbol{p}^T \boldsymbol{f}(\boldsymbol{q}(t), \boldsymbol{u}(t), t), \end{aligned}$$

(21.16)

$$\begin{aligned} \mathcal {H}(\boldsymbol{q}, \boldsymbol{p}, \boldsymbol{v}, t)&= G(\boldsymbol{q}(t),\boldsymbol{v}, t) + \boldsymbol{p}^T \boldsymbol{g}(\boldsymbol{q}(t), \boldsymbol{v}, t). \end{aligned}$$

(21.17)

As usual, the (piecewise) optimal continuous control $\boldsymbol{u}^\star$ is obtained from the Maximum Principle for the Hamiltonian H, and the differential equations for the costate variables are also determined by H. The optimal impulse controls $\boldsymbol{v}_i^\star$ are given by maximizing $\mathcal {H}$:

$$\begin{aligned} \boldsymbol{u}^\star&= \arg \max _{\boldsymbol{u}} H(\boldsymbol{q}^{\star }(t), \boldsymbol{p}(t), \boldsymbol{u}, t), \end{aligned}$$

(21.18)

$$\begin{aligned} \dot{\boldsymbol{p}}&= -\partial H(\boldsymbol{q}^{\star }(t), \boldsymbol{p}(t), \boldsymbol{u}^{\star }, t)/\partial \boldsymbol{q}, \end{aligned}$$

(21.19)

$$\begin{aligned} \boldsymbol{v}_i^\star&= \arg \max _{\boldsymbol{v}_i} \mathcal {H}(\boldsymbol{q}^\star (\tau _i^{*-}), \boldsymbol{p}(\tau _i^{*+}), \boldsymbol{v}_i, \tau _i^\star ), \end{aligned}$$

(21.20)

$$\begin{aligned} \boldsymbol{p}(\tau _i^{*+})-\boldsymbol{p}(\tau _i^{*-})&= -\partial \mathcal {H}(\boldsymbol{q}^\star (\tau _i^{*-}), \boldsymbol{p}(\tau _i^{*+}), \boldsymbol{v}_i^\star , \tau _i^\star )/\partial \boldsymbol{q}, \end{aligned}$$

(21.21)

$$\begin{aligned} H(\boldsymbol{q}^\star (\tau _i^{*+}), \boldsymbol{p}(\tau _i^{*+}),&\, \boldsymbol{u}^\star (\tau _i^{*+}), \tau _i^\star ) - H(\boldsymbol{q}^\star (\tau _i^{*-}), \boldsymbol{p}(\tau _i^{*-}), \boldsymbol{u}^\star (\tau _i^{*-}), \tau _i^\star ) \nonumber \\ \begin{Bmatrix} > \\ = \\ < \end{Bmatrix}&\frac{\partial \mathcal {H}(\boldsymbol{q}^\star (\tau _i^{*-}), \boldsymbol{p}(\tau _i^{*+}), \boldsymbol{v}_i^\star , \tau _i^\star )}{\partial \tau } \quad \text {for } \tau _i^\star {\left\{ \begin{array}{ll} = 0 \\ \in (0, T), \\ = T.\end{array}\right. } \end{aligned}$$

(21.22)

Here starred quantities denote optimal values for the controls, states, and firing times.

From (21.21), it follows that the adjoint variables become discontinuous, if the jump conditions depend on the state variables, which is the case in our system for the polar coordinates.

Finally, we see from (21.22), which ensures the optimality of the impulse instances $\tau _i$, that the Hamiltonian H is continuous at interior impulse times $\tau _i$, if $\mathcal {H}$ doesn’t depend on $\tau$ explicitly.

Since our model is autonomous, the optimal final time $T^\star$ is obtained by the boundary condition

$$\begin{aligned} H(\boldsymbol{q}^\star (T^\star ), \boldsymbol{p}^\star (T^\star ), \boldsymbol{u}^\star ) = 0. \end{aligned}$$

(21.23)

No continuous controls $u_i$ are present and the considered cost depends on the impulsive controls $\boldsymbol{v}_i$, therefore the utility function F doesn’t show up in the Hamiltonian, and the Maximum condition (21.18) doesn’t apply.

21.3 Optimal Control Problem for the Linearized System

Since during the considered phase of the chasing manoeuvre the chaser is already quite close to the space station, the approximation (21.5) together with the jump conditions (21.9) provides a good approximation for the dynamics. Rewriting (21.5) as a first- order system, one obtains the Hamiltonian H and the adjoint differential equations

$$\begin{aligned} \dot{q}_1&= q_2, \end{aligned}$$

(21.24a)

$$\begin{aligned} \dot{q}_2&= -q_1 + 2 q_4, \end{aligned}$$

(21.24b)

$$\begin{aligned} \dot{q}_3&= -2 q_1 + q_4, \end{aligned}$$

(21.24c)

$$\begin{aligned} \dot{q}_4&= 0, \end{aligned}$$

(21.24d)

$$\begin{aligned} H(\boldsymbol{q}, \boldsymbol{p})&= p_1 q_2 + p_2 (-q_1 + 2q_4) + p_3 (-2q_1 + q_4), \end{aligned}$$

(21.24e)

$$\begin{aligned} \dot{p}_1&= p_2 + 2 p_3, \end{aligned}$$

(21.24f)

$$\begin{aligned} \dot{p}_2&= -p_1, \end{aligned}$$

(21.24g)

$$\begin{aligned} \dot{p}_3&= 0, \end{aligned}$$

(21.24h)

$$\begin{aligned} \dot{p}_4&= -2 p_2 - p_3, \end{aligned}$$

(21.24i)

where the state variables $q_i$ are given by $q_1 = X$, $q_2 = \dot{X}$, $q_3 = Y$, and $q_4 = \dot{Y} + 2 X$. The choice of these variables is motivated by the rotational symmetry of the system, by which the angular momentum $d=r^2 \dot{\varphi }$ is a first integral. In the linearized system, the variable $q_4=\dot{Y} + 2X$ is constant, as can be seen from (21.5b).

In these state variables, the jump conditions (21.9) read

$$\begin{aligned} \boldsymbol{q}(\tau _i^+) - \boldsymbol{q}(\tau _i^-) = \boldsymbol{g}(\boldsymbol{q}(\tau _i^-), \boldsymbol{v}_i) = (0, v_{i,1}, 0, v_{i, 2})^{\text {T}}. \end{aligned}$$

(21.25)

With $G=-C$ the Hamiltonian for the impulsive controls is therefore given by

$$\begin{aligned} \mathcal {H}(\boldsymbol{q}(\tau _i), \boldsymbol{p}(\tau _i), \boldsymbol{v}_i, \tau _i) = -\sqrt{v_{i,1}^2+v_{i,2}^2} + p_2 v_{i,1} + p_4 v_{i,2} . \end{aligned}$$

(21.26)

Now we find from (21.20)

$$\begin{aligned} \frac{v_{i,1}}{\sqrt{v_{i,1}^2 + v_{i,2}^2}} = p_2, \quad \frac{v_{i,2}}{\sqrt{v_{i,1}^2 + v_{i,2}^2}} = p_4, \end{aligned}$$

(21.27)

from which it follows that

$$\begin{aligned} \boldsymbol{v}_i \parallel (p_2, p_4) \quad \text {and } \sqrt{p_2^2 + p_4^2} = 1. \end{aligned}$$

(21.28)

So we know only the direction of the impulsive controls; their magnitude has to be obtained by solving the boundary value problem. We also know that at the instances $\tau _i$, the adjoint variables must satisfy $|(p_2, p_4)|=1$.

Since $\mathcal {H}$ doesn’t depend on the state variables $q_i$ and on $\tau _i$, the costate variables $\boldsymbol{p}$ are continuous at $\tau _i$ by (21.21), and also the Hamilton function H is continuous by (21.22). By (21.25), the continuity condition for H becomes

$$\begin{aligned} \Delta H = p_1 v_{i,1} + (2 p_2+p_3) v_{i,2} = 0, \end{aligned}$$

(21.29)

which is equivalent to the condition $d (p_2^2+p_4^2)/d\tau =0$ by (21.28).

The boundary conditions state that the chaser should be steered from a starting position to a target point at the station’s orbit:

$$\begin{aligned} q_1(0)&= X_0,&q_1(T)&= 0, \end{aligned}$$

(21.30a)

$$\begin{aligned} q_2(0)&= \dot{X}_0,&q_2(T)&= 0, \end{aligned}$$

(21.30b)

$$\begin{aligned} q_3(0)&= Y_0,&q_3(T)&= 0, \end{aligned}$$

(21.30c)

$$\begin{aligned} q_4(0)&= \dot{Y}_0 + 2 X_0,&q_4(T)&= 0. \end{aligned}$$

(21.30d)

Since the final position is an equilibrium, the Hamiltonian $H(\boldsymbol{q}(T), \boldsymbol{p}(T))$ vanishes for all choices of T. Therefore, the condition (21.23) for the optimal planning period T has to be stated immediately before the last impulse.

We note that since $q_4$ can only reach its final value by impulses in the horizontal direction, the difference $|q_4(T)-q_4(0)|$ provides a lower bound for fuel consumption. The Hohmann transfer [1] with two horizontal burns provides an energy-optimal solution.

The boundary value problem (BVP) (21.24) and (21.30) is solved numerically by the Multiple Shooting Method Boundsco [5], which is especially designed for Optimal control problems with discontinuous state variables.

The following results are calculated for the initial conditions:

$$\begin{aligned} X(0)&= -5 \,\text {km},&\dot{X}(0)&= 0, \end{aligned}$$

(21.31a)

$$\begin{aligned} Y(0)&= -50 \,\text {km},&\dot{Y}(0)&= 50 \,\text {km}/\text {rev} \overset{\wedge }{\approx }9\,\text {m/s}, . \end{aligned}$$

(21.31b)

and orbit radius $r_S=6778\,\text {km}$.

In the first step, a Hohmann transfer for the energy-optimal trajectory with two horizontal burns is calculated. The first impulse occurs when the chaser reaches the proper elliptical orbit, the second one occurs when it reaches its target position at $t=T\approx 1.492T_0$.

Starting with this solution, a continuation method [6] is employed to decrease the time interval from the value needed for an energetically optimal manoeuvre. By monitoring the switching function $S(\tau )=\sqrt{p_2^2 + p_4^2}$ (see Fig. 21.3), we observe that close to $T=1.465\,T_0$, where $T_0=2\pi /\omega$ denotes the revolution period, it crosses the line $S=1$ at $t \approx 0.2 T$, where a new firing event should occur. The trajectories for $T=1.492\,T_0$, and $T=1.465\,T_0$ are displayed in Fig. 21.4. Although the thrusts have different directions, the trajectories are almost the same.

Fig. 21.3

Variation of the switching function $S=\sqrt{p_2^2+p_4^2}$ for different time intervals

Fig. 21.4

Trajectories and directions of impulsive thrusts for different planning intervals

Fig. 21.5

Impulse times for the linear system (21.5) and for the system written in local polar coordinates (21.8). The firing instances $\tau _i$ are sorted chronologically

Fig. 21.6

Impulse times for the nonlinear system (21.4) in local Cartesian coordinates

Reducing T further, the new firing time decreases down to $t=0$, as can be seen in Fig. 21.5. The firing time $\tau _2$ also decreases and vanishes at $T \approx 0.65\,T_0$: The impulse magnitude $|\boldsymbol{v}_2|$ shrinks to zero and the switching function $S(\tau )$ separates from the line $S=1$. For shorter time horizons, only firings at the start and at the end of the manoeuvre are executed.

The cost C depending on the permitted manoeuvre duration T is displayed in Fig. 21.7; for quick transfers the fuel consumption increases strongly. The labels in Fig. 21.7 denote the firing instances: “S” at the start, “I” in the interior, and “E” at the end of the transfer.

21.4 Optimal Control Problem for the Nonlinear System

For validation of the linear approximation (21.5) also, the optimal control for the nonlinear systems (21.4) and (21.8) was computed.

21.4.1 Optimal Control Problem for the Local Cartesian Frame

Using the local Cartesian system (21.4), the equations of motion become nonlinear, but the cost function C and the equations for the impulsive control (21.9) remain the same as in the linear system (21.5). Since the jumps in (21.9) do not depend on the state variables and time $\tau$, the costate variables $p_i$ and the Hamiltonian remain continuous at the firing instances $\tau _i$.

As initial values, we choose the same ones as in the linear system and obtain the results shown in Fig. 21.8, which differ significantly from the results obtained with the linear system (21.5) and for the polar coordinates (21.8). Also the sequence of impulse instances $\tau _i$ differs between these calculations, as can be seen from Figs. 21.5 and 21.6. The optimal time $T^\star$ for the least propellant consuming solution increases from approximately 1.5 revolutions to 1.85 revolutions.

Fig. 21.7

Dependence of fuel cost on the permitted manoeuvre duration T for systems (21.5) and (21.8)

Fig. 21.8

Dependence of fuel cost on the permitted transfer duration T for systems (21.4)

21.4.2 Optimal Control Problem for the Polar Coordinate Frame

When using the local polar coordinate system (21.8), the jump conditions (21.11) lead to the maximum condition

$$\begin{aligned} \boldsymbol{v}_i^\star = \arg \max _{\boldsymbol{v}_i}\left( -\sqrt{v_{i,r}^2 + v_{i, \varphi }^2} + p_2 v_{i,r} + p_4 \frac{r_S v_{i,\varphi }}{r_S + X_P}\right) , \end{aligned}$$

(21.32)

giving

$$\begin{aligned} \frac{v_{i,r}}{\sqrt{v_{i,r}^2 + v_{i, \varphi }^2}} = p_2, \quad \frac{v_{i,\varphi }}{\sqrt{v_{i,r}^2 + v_{i, \varphi }^2}} = \frac{r_S p_4}{r_S + X_P}. \end{aligned}$$

The switching function $S(\tau )$ which governs the impulse time instances becomes

$$\begin{aligned} S = \sqrt{p_2^2 + \frac{r_S^2 p_4^2}{(r_S+X_P)^2}}. \end{aligned}$$

Since (21.11) is time-independent, due to (21.22) the Hamiltonian H is continuous at the firing times. The occurrence of the state variable $q_1=X_P$ in the jump condition (21.11) leads to the jump

$$\begin{aligned} p_1(\tau _i^{*+}) - p_1(\tau _i^{*-}) = \left. \frac{r_S p_4}{(r_S+X_P)^2}\right| _{\tau =\tau _i^\star } \end{aligned}$$

(21.33)

in the costate variable $p_1$, according to (21.21).

As initial values, we choose

$$\begin{aligned} X_P(0)&= -5 \,\text {km},&\dot{X}_P(0)&=0, \end{aligned}$$

(21.34a)

$$\begin{aligned} Y_P(0)&= -50 \,\text {km},&\dot{Y}_P(0)&=50\,\text {km}/\text {rev} \end{aligned}$$

(21.34b)

and obtain the results shown in Figs. 21.5 and 21.7, which agree very well with the results for the linear system.

Fig. 21.9

Comparison of the energy-optimal trajectories for the different choices of coordinate systems. The arrows indicate the direction and magnitude of the impulsive controls

Now it remains to explain the significant difference between the results for the two nonlinear variants: One might think that the difference between the initial positions is negligible, since $50\,\text {km}$ is much smaller than the earth circumference. Indeed the positions given by $(X,Y)=(-5\,\text {km}, -50\,\text {km})$ and $(X_P,Y_P)=(-5\,\text {km}, -50\,\text {km})$ differ only by approximately $200\,\text {m}$. In Fig. 21.9, the energy-optimal trajectories for the different initial conditions are displayed. The initial values for solution A are again given by (21.31), and those for solution B in (21.34), corresponding to

$$\begin{aligned} X(0)&\approx -5.184\,\text {km},&\dot{X}(0)&\approx 0.369\,\text {km}/\text {rev}, \\ Y(0)&\approx -49.962\,\text {km},&\dot{Y}(0)&\approx 49.962 \,\text {km}/\text {rev}. \end{aligned}$$

Using the same initial conditions in both systems gives of course the same solutions.

Fig. 21.10

Dependence of the required time T for the energy-optimal solution on the initial height $X_P(0)$

Fig. 21.11

Different trajectories starting at the initial height $X_P(0)=-4.6\,\text {km}$

In order to study the dependence of the required time T of the energy-optimal solution on the initial height, a continuation with varying values of $X_P(0)$ was carried out, with the remaining initial conditions kept fixed. The obtained curve is displayed in Fig. 21.10: It shows an increase of $T/T_0$ from 1.488 to 1.936, when $X_P(0)$ varies from $-5\,\text {km}$ to $-4.8\,\text {km}$. Close to $X_P(0)=-4.55\,\text {km}$, a series of turning points can be seen along the curve, leading to a series of different energy-optimal solutions for the same initial conditions. In Fig. 21.11, three different trajectories are displayed starting at the same initial position $X_P(0)=-4.6\,\text {km}$, corresponding to the points in Fig. 21.10. After reaching the final orbit height, the system performs an increasing number of oscillations, until it ends up in its target position.

21.5 Conclusions

The energy-optimal chasing strategy for a space rendezvous using the $L_1$-norm for the fuel consumption has been investigated for different sets of coordinate systems. Using a homotopy strategy to reduce the time duration of the manoeuvre shows a quite complicated variation of the applied impulsive control. In the considered range of initial conditions, the control strategy and the optimal path depend sensitively on the initial height X(0). When comparing the results calculated in different coordinate systems, the seemingly small differences must therefore not be neglected. The linear system governing the near-field dynamics, which approximates the equations in the polar and the Cartesian frame, agrees better with the nonlinear system in polar coordinates.