Breaking the Circuit Size Barrier for Secure Computation Under Quasi-Polynomial LPN

Abstract

In this work we introduce a new (circuit-dependent) homomorphic secret sharing (HSS) scheme for all $\log /\log \log$-local circuits, with communication proportional only to the width of the circuit, and polynomial computation, assuming the super-polynomial hardness of learning parity with noise ($\mathsf {LPN}$). At the heart of our new construction is a pseudorandom correlation generator (PCG), which allows two partie to locally stretch, from short seeds, pseudorandom instances of an arbitrary $\log /\log \log$-local additive correlation.

Our main application, and the main motivation behind this work, is a generic two-party secure computation protocol for every layered (boolean or arithmetic) circuit of size s with total communication $O(s/\log \log s)$ and polynomial computation, assuming the super-polynomial hardness of the standard learning parity with noise assumption (a circuit is layered if its nodes can be partitioned in layers, such that any wire connects adjacent layers). This expands the set of assumptions under which the ‘circuit size barrier’ can be broken, for a large class of circuits. The strength of the underlying assumption is tied to the sublinearity factor: we achieve communication O(s/k(s)) under the $s^{2^{k(s)}}$-hardness of LPN, for any $k(s) \le \log \log s / 4$.

Previously, the set of assumptions known to imply a PCG for correlations of degree $\omega (1)$ or generic secure computation protocols with sublinear communication was restricted to LWE, DDH, and a circularly secure variant of DCR.

1 Introduction

In this work, we present a novel (circuit dependent) homomorphic secret sharing (HSS) scheme for any $(\log /\log \log )$-local circuit which is secure under the super-polynomial hardness of the learning parity with noise ($\mathsf {LPN}$) assumption. The main application, and motivation for this work, is a new protocol for securely computing layered arithmetic and boolean circuits with communication sublinear in the circuit size, under the quasi-polynomial hardness of $\mathsf {LPN}$.

Homomorphic Secret Sharing (HSS). An HSS is a compact secret sharing scheme equipped with homomorphism: the parties can locally convert compact (additive) shares of an input into (additive) shares of some function of it, without interaction. Compactness here means that the input shares should be much smaller than, and ideally independent of, the size of the evaluated circuit. More precisely, HSS for a circuit class allows the parties to homomorphically convert their shares for any circuit in the class. This powerful primitive has been instantiated for all circuits under LWE [BKS19], or for $\mathsf {NC} ^1$ under DDH [BGI16a], or a circularly secure variant of DCR [FGJS17], and for the class of constant degree polynomials from LPN [BCG+19b].

The Circuit Size Barrier in Secure Computation. Secure computation allows mutually distrustful parties to securely compute a public function of their joint private inputs, concealing all information beyond the output. Since its introduction in the seminal works of Yao [Yao86], and Goldreich, Micali, and Wigderson [GMW87b, GMW87a], secure computation has received a constant attention. For a long time, however, all standard approaches to secure computation have been stuck at an intriguing circuit-size barrier, in that they require an amount of communication (at least) proportional to the size of the circuit being computed. In contrast, insecure computation only requires exchanging the inputs, which might be considerably smaller than the entire circuit. Getting beyond this limitation has been a major challenge in secure computation. Early positive results required exponential computation [BFKR91, NN01], or were limited to very simple functions such as point functions [CGKS95, KO97, CG97] or constant-depth circuits [BI05].

The situation changed with the breakthrough result of Gentry [Gen09] on fully-homomorphic encryption (FHE), which led to optimal communication protocols in the computational setting [DFH12, AJL+12]. On the downside, the set of assumptions under which we know how to build FHE is very narrow; it is restricted to lattice-based assumptions such as LWE, and in particular does not include any of the traditional assumptions which were used in the 20th century. More recently, the elegant work of [BGI16a] showed for the first time that secure computation with sublinear communication could be based on assumptions not known to imply FHE, by building a two-party secure computation protocol under the DDH assumption, with communication $O(s/\log s)$ for layered circuits of size s.¹ [FGJS17] later followed this blueprint and switched out the DDH assumption for the circular security of the Pallier encryption scheme. It remains open whether secure computation with sublinear communication can be based on any other traditional and well-studied assumption, such as code-based assumptions.

1.1 Our Contribution

We show that circuit-dependent homomorphic secret sharing, i.e. HSS where the share generation requires knowing in advance the circuit to be evaluated homomorphically, for the class of log-local circuits exists, conditioned on (the quasi-polynomial hardness of) a well-studied 20th century assumption: the learning parity with noise (LPN) assumption [BFKL94]. Informally, the LPN assumption captures the hardness of solving an overdetermined system of linear equations over $\mathbb {F}_2$, when a small subset of the equations is perturbed with a random noise. The LPN assumption has a long history in computational learning theory, where it emerged. Furthermore, our results only require a flavour of LPN where the adversary is given a very limited number of samples (typically, O(n) equations in n indeterminates). In this regime, LPN is equivalent to the hardness of decoding random linear codes over $\mathbb {F}_2$, which is the well-known syndrome decoding problem in the coding theory community, where it has been studied since the 60’s [Pra62].

Details on the Underlying Assumption. In a bit more detail, given a security parameter $\lambda$, the (T, n, N, r)-LPN assumption with dimension $n = n(\lambda )$, number of samples $N = N(\lambda )$ and noise rate $r = r(\lambda )$ states that for every adversary $\mathsf {Adv}$ running in time at most $T = T(\lambda )$,

$$\begin{aligned} \Pr \left[ A {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {F}_2^{N\times n}, \vec e {\mathop {\leftarrow }\limits ^{{}_\$}}\mathsf {Ber} _r^N, \vec s {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {F}_2^n\;:\; \mathsf {Adv}(A, A\cdot \vec s + \vec e) = \vec s\right] = \mathrm {negl}(\lambda ), \end{aligned}$$

where $\mathsf {Ber} _r$ denotes the Bernouilli distribution which outputs 1 with probability r, and $\mathrm {negl}$ denote some negligible function. When T can be any polynomial (resp. any super-polynomial function, some super-polynomial function), we say that we assume the polynomial (resp. quasi-polynomial, super-polynomial) hardness of LPN. For arithmetic circuits, we need to assume LPN over large fields, or equivalently syndrome decoding for random linear codes over large fields; this is also a well-founded and well-studied assumption, used in several previous works, e.g. [BCGI18, BCG+19b].

HSS for Any Loglog-Depth Circuit. We introduce a new circuit-dependent HSS scheme for the class of all $\log \log$-depth circuits. More precisely,

Main Theorem 1

(HSS for any loglog-Depth Circuit, Informal). Let C be a size-s, n-input, m-output, $(\epsilon \cdot \log \log )$-depth arithmetic circuit over $\mathbb {F}$ (for some $\epsilon <1/4$). If the $\mathbb {F}\hbox {-}\mathsf {LPN}$ assumption with super-polynomial dimension $\ell$, $O(\ell )$ samples, and inverse super-polynomial rate holds, then there exists a secure HSS scheme for the class $\{C\}$ with share size $n+O(m\cdot s\cdot \log s/ c^{\log ^{1-\epsilon }s-\log ^{1-2\epsilon }s})$ (for some constant c) and computational complexity $O(m\cdot \mathsf {poly} (s)\cdot (\log |\mathbb {F}|)^2)$.

Restricting the circuit class to depth-k size-s circuits where $k(s)\le \log \log s /4$ leads to quantitative improvements in the size of the shares, the computational complexity of expanding shares, and the strength of the LPN assumption.

Application to Sublinear Computation. Our HSS scheme has (non black-box) implications for sublinear computation. As in [BGI16a], our results holds for all layered (boolean or arithmetic) circuits, in the two-party setting.

Main Theorem 2

(Sublinear Computation of Layered Circuits, Informal). For any layered arithmetic circuit C of polynomial size $s = s(\lambda )$ with n inputs and m outputs, for any function $k(s) \le \log \log s - \log \log \log s + O(1)$, there exists a two party protocol for securely computing C in the honest-but-curious model, with total communication $[2(n + m + s/k)]\cdot \log |\mathbb {F}| +o(s/k)$ and computation bounded by $s^3\cdot \mathsf {polylog} s \cdot (\log |\mathbb {F}|)^2$ under a set of $\mathsf {LPN}$ assumptions, the exact nature of which depends on the sublinearity factor k.

In particular, setting $k \leftarrow O(\log \log s)$ leads to a protocol with total communication $O(n+m+s/\log \log s)$, secure under the super-polynomial hardness of:

• $\mathbb {F}\hbox {-}\mathsf {LPN}$ with super-polynomial dimension $\ell$, $O(\ell )$ samples, and inverse super-polynomial rate,

• $\mathbb {F}_2\hbox {-}\mathsf {LPN}$ with super-polynomial dimension $\ell '$, $O(\ell ')$ samples, and inverse polynomial rate $1/s^{O(1)}$ (which is implied by the above if $\mathbb {F}=\mathbb {F}_2$).

Furthermore (but with a slighly different choice of parameters than the one described above), as k is reduced to an arbitrarily small $k = \omega (1)$, we need only assume the quasi-polynomial hardness of:

• $\mathbb {F}\hbox {-}\mathsf {LPN}$ with quasi-polynomial dimension $\ell$, $O(\ell )$ samples, and inverse quasi-polynomial rate,

• $\mathbb {F}_2\hbox {-}\mathsf {LPN}$ with quasi-polynomial dimension $\ell '$, $O(\ell ')$ samples, and inverse polynomial rate $1/s^{O(1)}$ (which is implied by the above if $\mathbb {F}=\mathbb {F}_2$).

and the computation is reduced to $O(s^{1+o(1)}\cdot (\log |\mathbb {F}|)^2)$.

Remark 1

While we require security against super-polynomial-time adversaries, this remains a relatively weak flavour of LPN where the dimension is very high, i.e. super-polynomial as well (and the adversary is allowed to run in time $O(\ell ^2)$ where $\ell$ is the dimension), and the number of samples which the adversary gets is very limited, $O(\ell )$. On the other hand, we require a very small noise rate $\lambda /N$. For example, instantiating the above with $k = (\log \log s) /5$, we obtain a secure computation protocol with total communication $O(\ell + m + s/\log \log s)$ (sublinear in s) and polynomial computation, assuming that LPN is hard against adversaries running in super-polynomial time $\lambda ^{O(\log \lambda )}$, with dimension $\ell = \lambda ^{O(\log \lambda )}$, $N = 2\ell$ samples, and noise rate $\lambda /N$. More generally, for any super-constant function $\omega (1)$, there is a two-party protocol with communication $O(n+m+s/\log \omega (1))$ assuming the $\lambda ^{\omega (1)}$-hardness of LPN (i.e., the quasi-polynomial hardness of LPN).

We note that, in this regime of parameters, the best known attacks are the information set decoding attack [Pra62] and its variants (which only shave constant in the exponents, hence have the same asymptotic complexity), which require time $2^{O(\lambda )}$.² Therefore, assuming hardness against $\lambda ^{O(\log \lambda )}$-time adversaries is a very plausible assumption.

Remark 2

(On the Generality of Layered Circuits). Our construction is restricted to the class of (boolean or arithmetic) layered circuits. This restriction stems from the blockwise structure of the construction, and was also present in the previous works of [BGI16a] and [Cou19]. As noted in [Cou19], layered circuits are a relatively large and general class of circuits, which furthermore capture many “real-world” circuits such as FFT-like circuits (used in signal processing, integer multiplication, or permutation networks [Wak68]), Symmetric crypto primitives (e.g. AES and algorithms that proceed in sequences of low-complexity rounds are naturally “layered by blocks”), or dynamic-programming algorithm (e.g. the Smith-Waterman distance, or the Levenshtein distance and its variants).

Generalisation to the Malicious Setting. Our result can directly be generalised to the malicious setting using a generic GMW-style compiler [GMW87a], which is communication preserving when instantiated with succinct zero-knowledge arguments [NN01]. Such arguments exist under collision-resistant hash functions; hence, Theorem 2 extends to the malicious setting as well, at the cost of further assuming collision-resistant hash functions (which is a mild assumption). We note that CRHFs have recently been built from (sub-exponentially strong) flavours of LPN [AHI+17, YZW+19, BLVW19].

1.2 Our Techniques

Our starting point is the construction of pseudorandom generator (PCG) from the work of [BCG+19b], under the LPN assumption. At a high level, a PCG allows to distributively generate long pseudorandom instances of a correlation. More precisely, a PCG for a correlation $\mathsf {corr}$ (seen as a distribution over pairs of elements) is a pair $(\mathsf{Gen}, \mathsf {Expand})$ where $\mathsf{Gen} (1^\lambda )$ generates a pair of seeds $(\mathsf{k}_0,\mathsf{k}_1)$ and $\mathsf {Expand} (b, \mathsf{k}_b)$ output a string $R_b$. A PCG must satisfy two properties: (correctness) $(R_0,R_1)$ is indistinguishable from a random sample from $\mathsf {corr}$, and (security) for $b\in \{0,1\}$, the string $R_b$ is indistinguishable, even given $\mathsf{k}_{1-b}$, from a string $R'_b$ sampled randomly conditioned on satisfying the correlation with $R_{1-b}$.

The technical contribution at the heart of this paper is to show that, under a certain LPN assumption, there exists a 2-party PCG for the following correlation, which we call substrings tensor powers ($\mathsf {stp}$) correlation. It is (publicly) parametrised by

• a string length n;

• subsets $S_1,\dots ,S_{\mathsf {n}_{\mathsf {s}}}\in \left( {\begin{array}{c}[n]\\ \le K\end{array}}\right)$ of at most $K=\log n / \log \log n$ many coordinates each;

• a tensor power parameter $\mathsf {tpp}$ (which can be super-constant, as high as K);

and generates additive shares of all the tensor powers of the prescribed substrings of a random string, i.e.

$$({\vec r}, ({(1_\mathbb {F}\;||\;{\vec r}[S_i])}^{\otimes \mathsf {tpp}})_{1\le i \le \mathsf {n}_{\mathsf {s}}}),\text { where } \vec r\in \mathbb {F}^n\text { is (pseudo)random}.$$

In the above, $\vec a^{\otimes b}$ denotes a vector $\vec a$ tensored with itself b rimes. In order to build shares of $(\vec r, \vec r^{\otimes 2})$ for some (pseudo)random $\vec r\in \mathbb {F}^n$ (the bilinear correlation), the PCG of [BCG+19b] uses a multi-point function secret sharing scheme (MPFSS) (defined in Sect. 3.1) to give the parties small seeds which can be expanded locally to shares of $(\vec e, \vec e^{\otimes 2})$ for some random sparse vector $\vec e\in \mathbb {F}^n$. Thence, if H is some suitable public matrix the parties can get shares of , which is pseudorandom under LPN, and of $\vec r^{\otimes 2}=H^{\otimes 2}\cdot \vec e^{\otimes 2}$ by locally multiplying their shares of $\vec e$ and $\vec e^{\otimes 2}$ by H and $H^{\otimes 2}$ respectively. The main issue in using this approach directly is that performing the expanding $\vec r ^{\otimes \mathsf {tpp}} = H[S_i]^{\otimes \mathsf {tpp}}\cdot \vec e^{\otimes \mathsf {tpp}}$ (where $H[S_i]$–abusively–denotes the submatrix of H with only the rows indexed by elements of $S_i$) would require super-polynomial computation, as $H[S_i]$ has n columns.

The core idea of our work is to develop a very careful modified strategy. Instead of letting each $\vec r$ be a (pseudo)random mask, we construct $\vec r$ as a sum of $n\cdot \log n$ vectors $\vec r_{j}$, each associated with a public subset of at most K coordinates: these K coordinates are random, but all others are zero. The crucial property achieved by this construction is the following: with high probability, the sum of these sparse vectors will be pseudorandom, but every size-K substring of $\vec r$ (and in particular $S_1,\dots ,S_{\mathsf {n}_{\mathsf {s}}}$) will be expressible as a sum of ‘not too many’ of the $\vec r_{j}$. This allows the expanding to be done by raising to the tensor power $\mathsf {tpp}$ a matrix whose dimensions are both $K^{O(1)}$, and not n as before. Thus computation remains polynomial.

If we were to stop here, the size of the seeds would grow linearly with $\mathsf {n}_{\mathsf {s}}$, the number of subsets; this would violate the compactness requirement. Instead, we show that we can batch the subsets into $\mathsf {n}_{\mathsf {s}}/\beta$ groups of at most $\beta$ subsets each, for some parameter $\beta$ to be refined, to reduce the share size and recover compactness, without harming computational efficiency. Indeed, so long as $\beta$ is not too large, the substring of $\vec r$ associated with the union of any $\beta$ size-K subsets of coordinates will still be expressible as a sum of ‘not too many’ of the $\vec r_{j}$. Our computations reveal a sweet spot for the choice of $\beta$, for which the PCG seeds are compact and yet the complexity of expanding them remains polynomial.

1.3 Related Work

Pseudorandom correlation generators were first studied (under the name of cryptocapsules) in [BCG+17]. Constructions of PCGs for various correlations, under variants of the LPN assumptions, and applications of PCGs to low-communication secure computation, have been described in [BCGI18, BCG+19b, BCG+19a, SGRR19, BCG+20b, BCG+20a].

Early works on sublinear-communication secure computation either incurred some exponential cost, or were restricted to very limited types of computations. The first protocols to break the circuit size barriers was shown in [BFKR91] (which gave a protocol with optimal communication, albeit with exponential computation and only for a number of parties linear in the input size). The work of [NN01] gave a sublinear protocol, but with exponential complexity. The work of [BI05] gives a low-communication protocol for constant-depth circuit, for a number of parties polylogarithmic in the circuit size, and the works of [CGKS95, KO97, CG97] gave sublinear protocols for the special case of point functions. The result of Gentry [Gen09] led to the first optimal communication protocols in the computational setting [DFH12, AJL+12] under LWE-style assumptions, for all circuits and without incurring any exponential cost. The work of [IKM+13] gave an optimal communication protocol in the correlated randomness model, albeit using an exponential amount of correlated randomness. More recently, [Cou19] constructed an unconditionally secure $\mathsf {MPC}$ protocol with sublinear communication for layered circuits, in the two-party setting, with a polynomial amount of correlated randomness. Finally, progress in breaking the circuit-size barrier for layered circuits in the computational setting is closely tied to the advances in HSS for super-constant depth circuits [BGI16a, FGJS17].

2 Technical Overview

Notations. We say that a function $\mathrm {negl}:\mathbb {N}\rightarrow \mathbb {R}^+$ is negligible if it vanishes faster than every inverse polynomial. For two families of distributions $X = \{X_\lambda \}$ and $Y = \{Y_\lambda \}$ indexed by a security parameter $\lambda \in \mathbb {N}$, we write $X {\mathop {\approx }\limits ^\mathrm{c}}Y$ if X and Y are computationally indistinguishable (i.e. any family of circuits of size $\mathsf {poly} (\lambda )$ has a negligible distinguishing advantage), $X {\mathop {\approx }\limits ^\mathrm{s}}Y$ if they are statistically indistinguishable (i.e. the above holds for arbitrary, unbounded, distinguishers), and $X \equiv Y$ if the two families are identically distributed.

We usually denote matrices with capital letters (A, B, C) and vectors with bold lowercase ($\vec {x},\vec {y}$). By default, vectors are assumed to be column vectors. If $\vec x$ and $\vec y$ are two (column) vectors, we use $\vec x || \vec y$ to denote the (column) vector obtained by their concatenation. We write $\vec x \otimes \vec y$ to denote the tensor product between $\vec x$ and $\vec y$, i.e., the vector of length $n_xn_y$ with coordinates $x_iy_j$ (where $n_x$ is the length of $\vec x$ and $n_y$ is the length of $\vec y$). We write $\vec x^{\otimes 2}$ for $\vec x \otimes \vec x$, and more generally, $\vec x^{\otimes n}$ for the n-th tensor power of $\vec x$, $\vec x \otimes \vec x \otimes \cdots \otimes \vec x$. Given a vector $\vec {x}$ of length $|\vec {x}| = n$, the notation $\mathsf {HW}\left( x\right)$ denotes the Hamming weight $\vec {x}$, i.e., the number of its nonzero entries. Let k be an integer. We let $\{0,1\} ^k$ denote the set of bitstrings of length k. For two strings (x, y) in $\{0,1\} ^k$, we denote by $x\oplus y$ their bitwise xor.

Circuits. An arithmetic circuit C with n inputs and m outputs over a field $\mathbb {F}$ is a directed acyclic graph with two types of nodes: the input nodes are labelled according to variables $\{x_1, \cdots , x_n\}$; the (computation) gates are labelled according to a base B of arithmetic functions. In this work, we will focus on arithmetic circuits with indegree two, over the standard basis $\{+, \times \}$. C contains m gates with no children, which are called output gates. If there is a path between two nodes $(v,v')$, we say that v is an ancestor of $v'$. In this work, we will consider a special type of arithmetic circuits, called layered arithmetic circuits ($\mathsf {LBC}$). An $\mathsf {LBC}$ is a arithmetic circuit C whose nodes can be partitioned into $D = \mathsf {depth} (C)$ layers $(L_1, \cdots , L_{d})$, such that any edge (u, v) of C satisfies $u \in L_i$ and $v\in L_{i+1}$ for some $i\le d-1$. Note that the width of a layered arithmetic circuit is also the maximal number of non-output gates contained in any single layer. Evaluating a circuit C on input $\vec x \in \mathbb {F}^n$ is done by assigning the coordinates of $\vec x$ to the variables $\{x_1, \cdots , x_n\}$, and then associating to each gate g of C (seen as an arithmetic function) the value obtained by evaluating g on the values associated to its parent nodes. The output of C on input $\vec x$, denoted $C(\vec x)$, is the vector of values associated to the output gates.

2.1 PCG and HSS

Much like a PCG for the bilinear correlation yields an HSS for degree-two circuits [BCG+19b], given a PCG for the $\mathsf {stp}$ correlation with $\mathsf {tpp} =K$, it is almost immediate to build an HSS scheme for any singleton class comprised of a log/loglog-local circuit C (which is the case in particular if its depth is at most $\log \log -\log \log \log$, since the gates have in-degree at most 2). Since the circuit to be homomorphically evaluated on the input shares is known, the Share procedure can depend on it (which is not usually the case for HSS). Let $S_1,\dots ,S_m$ be the subsets of inputs on which each output depends, and let K denote the locality of C; we build a (circuit dependent) HSS scheme as follows:

• $\mathsf{HSS}.\mathsf{Share} (\vec x)$: Generates compact PCG key $(k_0,k_1)$ which expand to shares of $({\vec r}, ({(1_\mathbb {F}\;||\;{\vec r}[S_i])}^{\otimes \mathsf {tpp}})_{1\le i \le m})$, set $\vec x'\leftarrow \vec x\oplus \vec r$, and give to each party $P_\sigma$ a share $s_\sigma =(k_\sigma ,\vec x')$.

• $\mathsf{HSS}.\mathsf {Eval} (\sigma ,s_\sigma )$: Expand $s_\sigma$ and, for each $i=1\dots m$, extract a share of $(1_\mathbb {F}\;||\;{\vec r}[S_i])^{\otimes \mathsf {tpp}}$. Use it to generate shares of the coefficients of the “degree-K polynomial” on $|S_i|\le K$ variables $P_i$ satisfying $P_i(X)=C(X-\vec r[S_i])$. Output the inner product of the vector of coefficient shares with the vector $(1_\mathbb {F}\;||\;\vec x')^{\otimes K}$. (This linear product is a share of $P_i(\vec x')$.)

Correctness and security follow from inspection, along the same lines as [BCG+19b]. Usually, $\mathsf{HSS}.\mathsf{Share}$ is given only a circuit class as auxiliary input, not a specific circuit, and the parties should be able to homomorphically evaluate any circuit in the class. In our case however the HSS is circuit-dependent, because the subsets $S_1,\dots ,S_m$ are intrinsically tied to the evaluated circuit. An alternative formulation is that our HSS scheme supports singleton circuit classes (or, more generally, local circuits with the same pattern of subsets).

2.2 Generating Correlated Randomness from a PCG

From now on, we set the number of parties to $N = 2$. The work of [BCG+19b, Section 6] provides a pseudorandom correlation generator under the LPN assumption, generates correlated (pseudo) random strings for the low-degree polynomial correlation, i.e. shares of $(\vec r,\vec {r}^{\otimes 2},\dots ,\vec {r}^{\otimes d})$ for some constant d, where $\vec r$ is a (pseudo)random vector. With the construction from the previous paragraph, this yields an HSS for constant-depth circuits. Our goal is to design a PCG which would lead to an HSS for super-constant depth circuits. More specifically, and keeping our end application in mind, we would like for our PCG to have short enough seeds to lead to a compact HSS scheme (i.e., shares of an input x should be at most O(x)). This is fundamental when using the scheme to generate correlated randomness in the protocol of [Cou19], which achieves sublinear communication in the correlated randomness model, and which is the starting point of our application to sublinear secure computation.

Our approach is therefore to directly plug in the construction of [BCG+19b] and see where it fails. Two issues emerge: the computation is super-polynomial, and the communication not sublinear. Below, we outline each of these issues, and explain how we overcome them.

First Issue: Too Many Polynomials. The first problem which appears when plugging the PCG of [BCG+19b] in the protocol of [Cou19] is that the latter requires distributing many shares of multivariate polynomials $\hat{Q}$ – more precisely, s/k such polynomials (one for each coordinate of each first layer of a bloc). While the PCG of [BCG+19b] allows to compress pseudorandom pairs $(\vec r, Q(\vec X-\vec r))$ into short seeds, these seeds will still be of length at least $\omega (\log \lambda )$, where $\lambda$ is the security parameter, for the PCG to have any hope of being secure. That means that even if we could manage to securely distribute all these seeds with optimal communication protocols, the overall communication would still be at the very least $\omega ((s\log \lambda )/\log \log s)$, which cannot be sublinear since $\log \log s = o(\log \lambda )$ (as s is polynomial in $\lambda$).

We solve this first issue as follows: we fix a parameter $\beta$, and partition each $\vec y_i$ into $w/\beta$ subvectors, each containing $\beta$ consecutive coordinates of $\vec y_i$. Then, the core observation is that a simple variant of the PCG of [BCG+19b] allows in fact to generate shares of $(\vec r, \vec r^{\otimes 2}, \cdots , \vec r^{\otimes 2^k})$ for some pseudorandom r, where $\vec r^{\otimes j}$ denotes the tensor product of $\vec r$ with itself j times (which we call from now on the j-th tensor power of $\vec r$): this correlation is enough to generate shares of all degree-$2^k$ polynomial in $\vec r$ rather than a single one. We will build upon this observation to show how to generate a batch of $\beta$ shares of multivariate polynomials from a single tensor-power correlation, thus reducing the number of PCG seeds required in the protocol by a factor of $\beta$, at the tolerable cost of slightly increasing the size of each seed.

Solution: Batching $\beta$ Multivariate Polynomials. Consider the first length-$\beta$ subvector of $\vec y_{i+1}$, which we denote $\vec v$. Observe that the entire subvector $\vec v$ can depend on at most $\beta \cdot 2^k$ coordinates of $\vec y_i$, since each coordinate of $\vec v$ depends on at most $2^k$ coordinates of $\vec y_i$. Therefore, we can now see the computation of $\vec v$ from $\vec y_i$ as evaluating $\beta$ multivariate polynomials $(Q_1 \cdots , Q_\beta )$, where all multivariate polynomials take as input the same size-$(\beta 2^k)$ subset of coordinates of $\vec y_i$. To securely compute shares of $\vec v$ from shares of $\vec y_i$, the parties can use the following type of correlated randomness: they will have shares of $(\vec r, \vec r^{\otimes 2}, \cdots \vec r^{\otimes 2^k})$, where $\vec r$ is a random mask of length $\beta \cdot 2^k$. Consider the following polynomials:

$$\begin{aligned} (\hat{Q}_1(\vec X), \cdots , \hat{Q}_\beta (\vec X)) {\mathop {=}\limits ^{{}_{\mathsf {def}}}}(Q_1(\vec X - \vec r), \cdots , Q_\beta (\vec X - \vec r)). \end{aligned}$$

Each coefficient of each $\hat{Q}$ can be computed as a degree-$2^k$ multivariate poynomial in the coordinates of $\vec r$ – or, equivalently, as a linear combination of the coordinates of $(\vec r, \vec r^{\otimes 2}, \cdots \vec r^{\otimes 2^k})$. Hence, given additive shares of $(\vec r, \vec r^{\otimes 2}, \cdots \vec r^{\otimes 2^k})$, the parties can locally compute additive shares of the coefficients of all the polynomials $(\hat{Q}_1, \cdots \hat{Q}_\beta )$. Using the PCG of [BCG+19b], the seeds for generating pseudorandom correlations of the form $(\vec r, \vec r^{\otimes 2}, \cdots \vec r^{\otimes 2^k})$ have length:

$$\begin{aligned} O\left( \lambda ^{2^k}\cdot \log \left( \left( \beta \cdot 2^k\right) ^{2^k}\right) \right) , \end{aligned}$$

where $\lambda$ is some security parameter related to the hardness of the underlying LPN assumption. Or more simply, using the fact the computational cost of generating the correlations contains the term $\left( \beta \cdot 2^k\right) ^{2^k}$ which must remain polynomial in s. Therefore, the total number of bits which the parties have to distribute (for all $(d/k)\cdot (w/\beta ) = s/(\beta k)$ such seeds) is $O(({s}/{k})\cdot (\lambda ^{2^k} \cdot \log s)/\beta )$.

Choosing the Parameter $\beta$. Suppose for simplicity that we already have at hand an MPC protocol allowing to securely distribute such seeds between the parties, with linear overhead over the total length of the seeds generated. This means that generating the full material will require a total communication of $c \cdot s\cdot \lambda ^{2^k} \cdot \log s/(\beta k)$. By setting $\beta$ to be larger than $c \cdot \lambda ^{2^k} \cdot \log s$, the total communication will be upper bounded by $O(s/k) = O({s}/\log \log s)$ when setting $k \leftarrow O(\log \log s)$, which is the highest our techniques will allow it to be pushed. The most important remaining question is whether we can execute this process in polynomial time given such a large $\beta$. Put more simply, the core issue is that the computational complexity of expanding short seeds to shares of $(\vec r, \vec r^{\otimes 2}, \cdots \vec r^{\otimes 2^k})$ with the PCG of [BCG+19b] contains a term of the form $(\beta \cdot 2^k)^{2^k}$. To make the computation polynomial, we must therefore ensure that $\beta$ is at most $s^{O(2^{-k})}$, which is subpolynomial. Fortunately, this can be done by setting the security parameter $\lambda$ of the underlying PCG to be $s^{O(2^{-2k})}$. For instance, for any constant $\epsilon \in ]0,1[$, we can set $\lambda \leftarrow 2^{\log ^\epsilon s}$, $k\leftarrow \log \log s/c_{\epsilon }$, and $\beta \leftarrow s^{O(2^{-k})}$ for some explicit constant $c_\epsilon >2$, at the cost of now having to assume the quasi-polynomial security of the LPN assumption.

Second Issue: Too Much Communication. In the previous paragraphs, we focused on generating the appropriate correlated random coins using sublinear total communication. But doing so, we glossed over the fact that in the full protocol, the parties must also broadcast (shares of) values of the form $\vec y + \vec r$, where $\vec y$ contains values of some layer, and $\vec r$ is some mask. Recall that with the method which we just outlined, the parties must generate such a length-$(\beta 2^k)$ mask $\vec r$ for the k-ancestors of each length-$\beta$ subvector of each last layer of a block. Since there are d/k blocks, whose first layers contain $w/\beta$ subvector each, and since each $\vec y + \vec r$ is of length $\beta \cdot 2^k$, this requires to communicate a total of $(d/k)\cdot (w/\beta )\cdot \beta 2^k = s\cdot 2^k/k$ values – and this cannot possibly be sublinear in s. In fact, this issue already appears in [Cou19], where it was solved as follows: rather than picking an independent mask for each vector of ancestors of a node on a layer (or, in our case, of a length-$\beta$ block of nodes), pick a single $\vec r_i$ to mask a full layer $\vec y_i$, and define the mask for the subset $S_{i,j}$ of ancestors of a target value $y_{i+1,j}$ to be $\vec r_i[S_{i,j}]$. This implies that the parties must mow broadcast a single masked vector $\vec y_i+\vec r_i$ for each first layer of a block, reducing the overall communication back to O(s/k). The correlated randomness which the parties must securely distribute now consists of tensor powers of many subsets of the coordinates of each mask.

Using the PCG of [BCG+19b] for ‘Subvectors Tensor Powers Correlations’. However, attemping to construct a PCG for generating this kind of correlated randomness from the PCG of [BCG+19b] blows up the computation to the point that it can no longer be polynomial. To explain this issue, we briefly recall the high level construction of the PCG of [BCG+19b]. To share a pseudorandom vector $(\vec r, \cdots , \vec r^{\otimes 2^k})$ where $\vec r$ is of length w, the PCG will first generate a very sparse vector $\vec r'$, with some number t of nonzero coordinates. Then, each $(\vec {r'})^{\otimes n}$ for some $n\le 2^k$ is itself a $t^n$-sparse vector, of length $w^n$. Using multi-point function secret sharing (MPFSS, a primitive which was developed in a recent line of work [GI14, BGI15, BGI16b, BCGI18] and can be built from one way functions), one can compress shares of $(\vec {r'})^{\otimes n}$ to length-$t^n\cdot \log w$ seeds. Then, the final pseudorandom correlation is obtained by letting the parties locally compress $\vec r'$ by multiplying it with a large public matrix H, giving a vector $\vec r = H \cdot \vec r'$. Similarly, $\vec r^{\otimes n}$ can be reconstructed by computing $H^{\otimes n}\cdot (\vec {r'})^{\otimes n} = (H\cdot \vec r')^{\otimes n} = \vec r^{\otimes n}$, using the multilinearity of tensor powers. The security relies on the fact that if H is a large compressing public random matrix, then its product with a random sparse noise vector $\vec r'$ is indistinguishable from random, under the dual LPN assumption (which is equivalent to the standard LPN assumption). Concretely, one can think of $\vec r'$ as being of length 2w, and of H as being a matrix from $\mathbb {F}^{w\times 2w}$ which compresses $\vec r'$ to a pseudorandom length-w vector.

Now, the issue with this construction is that even if we need only tensor powers of small subvectors (of length $\beta \cdot 2^k$ in our construction) of the vector $\vec r$, the computation for expanding the seed to these pseudorandom tensor powers will grow super-polynomially with the length of entire vector w. Indeed, consider generating the $2^k$-th tensor power of a subvector $\vec r[S]$ of $\vec r$, for some size-$\beta \cdot 2^k$ subset S of [w]. Then with the PCG of [BCG+19b], this requires computing $\left( H[S]\right) ^{\otimes 2^k}\cdot (\vec r'[S])^{\otimes 2^k}$, where the share of $(\vec r'[S])^{\otimes 2^k}$ are obtained from a short seed using MPFSS, and $H[S] \in \mathbb {F}^{|S|\times 2w}$ is the submatrix of H whose columns are indexed by S. The core issue becomes now visible: even though H[S] has only |S| rows, it still has 2w columns, and computing $H[S]^{\otimes 2^k}$ requires roughly $(|S|\cdot w)^{2^k}$ arithmetic operation. But since we want ultimately to have k be some increasing function of s, the above will contain a term of the form $w^{2^k}=w^{\omega (1)}$, where w (the circuit width) can be polynomial in the circuit size s, leading to an overall computational complexity of $s^{\omega (1)}$, which is super-polynomial.

Solution: Covering the Private Values with the Sum of Separable Masks. Our solution to circumvent the above problem is to generate $\vec r$ as the sum of a certain number m of shorter masks $\vec r^1,\vec r^2,\dots$ which each only cover $\theta$ values (note that they may – and will – overlap). This way the $2^k$-th tensor power of a subvector $\vec v$ can be obtained from appropriate linear combinations of coordinates of the $2^k$-th tensor power of the concatenation of only the $\vec r^j$ which overlap with $\vec v$. The amount of computation grows super-polynomially in the length of this concatenated vector only (instead of w as before).

More formally, we have a list of $w/\beta$ target subsets $S_1,\dots ,S_{w/\beta }$ (each one corresponding to the $2^k\beta$ ancestors of a batch of $\beta$ outputs) for which we want to compute the $2^k$-th tensor power of $\vec r[S_i]$, for some random $\vec r\in \mathbb {F}^w$. We want to find M size-K sets $\alpha _1,\alpha _2,\dots ,\alpha _M\in \left( {\begin{array}{c}[w]\\ K\end{array}}\right)$ such that each $S_i$ intersects with a small number B of $\alpha _j$s, while $\cup _{i=1}^M\alpha _i=[w]$. We associate each $\alpha _j$ with a vector $\vec r^j\in \mathbb {F}^K$: together they define a sparse subvector of $\mathbb {F}^w$. If we let $\vec r$ be the sum of these sparse vectors, it is clear that for any $i\in [w/\beta ]$, each element of $(1_\mathbb {F}\ ||\ \vec r[S_i])^{\otimes 2^k}$ can be obtained by a linear combination of the elements of the $2^k$-th tensor power of the vector of size $(1+BK)$ obtained by concatenating $(1_\mathbb {F})$ and the $\vec r^j$s such that $\alpha _j\cap S_i\ne \emptyset$. The amount of computation required is then of the order $(BK)^{2^k}$.

The problem of deterministically finding such subsets $\alpha _1,\dots ,\alpha _M$ – which we call a B-Good Cover of $(S_i)_{i\in [w/\beta ]}$ – turns out to be difficult in the general case. Fortunately, there is a straightforward probabilistic solution: choosing them independently and at random works with high probability. More specifically, taking $M\leftarrow O(w\cdot \ln w)$ i.i.d. uniformly random submasks covering $K\leftarrow \beta 2^k$ values each means that the $\beta 2^k$ ancestral inputs of any batch of $\beta$ outputs will be covered by only a total of roughly $B=\log w$ submasks (the proof of this relies on standard concentration bounds). This effectively lifts the cost of the computation from being super-polynomial in w to being only super-polynomial in $\beta 2^{k}\log w$, which remains polynomial overall when setting $\beta$ and k to be appropriately small.

2.3 Application to Sublinear Secure Computation

The work of [Cou19] gives a generic secure protocol with sublinear communication for layered circuits. It works in the corruptible correlated randomness model: before the protocol, a trusted dealer lets the adversary choose the strings that the corrupted parties will get, samples the correlated random coins of the remaining parties afterwards, and distributes them to the parties. As shown in [BCG+19b], generating this corruptible randomness using a PCG leads to a secure protocol in the standard model. In a bit more detail, the parties use a generic secure protocol to generate the short seeds $(\mathsf{k}_0,\mathsf{k}_1)$ then expand them locally; it might have a high overhead, but it will not be a bottleneck since the seeds are very small. We show that our new PCG can be used for just this purpose.

The general idea is to split a layered circuit of size s into carefully chosen blocks, each containing $O(\log \log s)$ consecutive layers. The precise block decomposition is detailed in [Cou19]. Using our PCG cast as an HSS scheme for $O(\log \log s)$-depth circuits (with the duality described in Sect. 2.1) allows the parties to evaluate the circuit in a block-by-clock fashion: for each block the parties start with additive shares of

• the inputs of the circuit;

• the values of the first layer of the block;

and, using HSS, compute additive shares of

• the outputs of the circuit which are in the block;

• the values of the last layer, which are also the values of the first layer of the next block.

Let us note that since the circuit and its blocks are publicly known to both parties, so the fact our HSS scheme is circuit-dependent is not an issue here. This block-by-block approach allows the parties to ‘skip’ a fraction $O(\log \log (s))$ of the gates when computing the circuit, by communicating at each block rather than at each gate. Unfortunately, combining all these blocks together involves pesky technicalities which prohibit a very modular approach and require us to consider the protocol in its entirety. Indeed, the inputs can appear arbitrarily many times–up to O(s) even–across many blocks, so the randomness used to mask them has to be reused, and we cannot deal with each block using an independent instance of HSS. However, dealing with this problem does not require any additional insight, only more cumbersome notations.

In the above outline, we assumed that we had access to a sufficiently low-communication MPC protocol to distribute the generation of the seeds to our new PCG. To obtain our claimed result, it remains to show that this building block can be instantiated under the quasi-polynomial hardness of LPN. In fact, this MPC protocol needs not have linear communication in the seed size; it turns out that by tuning the parameters appropriately, any fixed polynomial in the seed size suffices to guarantee the existence of a “soft spot” for the parameters of our PCG such that we simultaneously get sublinear total communication $O(s/{\log \log s})$ and polynomial computation. Distributing the generation procedure of our PCG essentially boils down to generating (many) seeds for a multi-point function secret sharing scheme, which itself boils down mainly to securely generating seeds for a standard length-doubling pseudorandom generator (PRG), and securely executing about $\log (\mathsf {domsize})$ expansions of these short seeds, where $\mathsf {domsize}$ denotes the domain size of the MPFSS. Using a standard LPN-based PRG and GMW-style secure computation, instantiated with an LPN-based oblivious transfer protocol, suffices to securely generate the MPFSS seeds we need.

3 Preliminaries

3.1 Function Secret Sharing

Informally, an FSS scheme for a class of functions $\mathcal {C}$ is a pair of algorithms $\mathsf{FSS} = (\mathsf{FSS}.\mathsf{Gen},\mathsf{FSS}.\mathsf {Eval})$ such that:

• $\mathsf{FSS}.\mathsf{Gen}$ given a function $f\in \mathcal {C}$ outputs a pair of keys $(K_0,K_1)$;

• $\mathsf{FSS}.\mathsf {Eval}$, given $K_b$ and input x, outputs $y_b$ such that $y_0$ and $y_1$ form additive shares of f(x).

The security requirement is that each key $K_b$ computationally hide f, except for revealing the input and output domains of f. For the formal definition of FSS, we refer the reader to the full version of this paper. Our application of FSS requires applying the evaluation algorithm on all inputs. Following [BGI16b, BCGI18, BCG+19b, BCG+19a], given an FSS scheme $(\mathsf{FSS}.\mathsf{Gen},\mathsf{FSS}.\mathsf {Eval})$, we denote by $\mathsf{FSS}.\mathsf {FullEval}$ an algorithm which, on input a bit b, and an evaluation key $K_b$ (which defines the input domain I), outputs a list of |I| elements of $\mathbb {G}$ corresponding to the evaluation of $\mathsf{FSS}.\mathsf {Eval} (b,K_b,\cdot )$ on every input $x\in I$ (in some predetermined order). Below, we recall some results from [BGI16b] on FSS schemes for useful classes of functions.

Distributed Point Functions. A distributed point function (DPF) [GI14] is an FSS scheme for the class of point functions $f_{\alpha ,\beta }:\{0,1\} ^\ell \rightarrow \mathbb {G}$ which satisfies $f_{\alpha ,\beta }(\alpha ) = \beta$, and $f_{\alpha ,\beta }(x)=0$ for any $x\ne \alpha$. A sequence of works [GI14, BGI15, BGI16b] has led to highly efficient constructions of DPF schemes from any pseudorandom generator (PRG).

Theorem 3

(PRG-based DPF [BGI16b]). Given a PRG $G:\{0,1\} ^\lambda \rightarrow \{0,1\} ^{2\lambda +2}$, there exists a DPF for point functions $f_{\alpha ,\beta }:\{0,1\} ^\ell \rightarrow \mathbb {G}$ with key size $\ell \cdot (\lambda +2) + \lambda + \lceil \log _2|\mathbb {G}|\rceil$ bits. For $m=\lceil \frac{\log |\mathbb {G}|}{\lambda +2} \rceil$, the key generation algorithm $\mathsf{Gen}$ invokes G at most $2(\ell +m)$ times, the evaluation algorithm $\mathsf {Eval}$ invokes G at most $\ell +m$ times, and the full evaluation algorithm $\mathsf {FullEval}$ invokes G at most $2^\ell (1+m)$ times.

FSS for Multi-Point Functions. Similarly to [BCGI18, BCG+19b, BCG+19a], we use FSS for multi-point functions. A k-point function evaluates to 0 everywhere, except on k specified points. When specifying multi-point functions we often view the domain of the function as [n] for $n=2^\ell$ instead of $\{0,1\}^\ell$.

Definition 4

(Multi-Point Function [BCGI18]). An (n, t)-multi-point function over an abelian group $(\mathbb {G},+)$ is a function $f_{S,\vec {y}}:[n]\rightarrow \mathbb {G}$, where $S = (s_1, \cdots , s_t )$ is an ordered subset of [n] of size t and $\vec {y} = (y_1, \cdots , y_t)\in \mathbb {G}^t$, defined by $f_{S,\vec {y}}(s_i) = y_i$ for any $i\in [t]$, and $f_{S,y}(x) = 0$ for any $x\in [n]\setminus S$.

We assume that the description of S includes the input domain [n] so that $f_{S,\vec {y}}$ is fully specified. A Multi-Point Function Secret Sharing (MPFSS) is an FSS scheme for the class of multi-point functions, where a point function $f_{S,\vec {y}}$ is represented in a natural way. We assume that an MPFSS scheme leaks not only the input and output domains but also the number of points t that the multi-point function specifies. An MPFSS can be easily obtained by adding t instances of a DPF.

3.2 Learning Parity with Noise

Our constructions rely on the Learning Parity with Noise assumption [BFKL93] (LPN) over a field $\mathbb {F}$ (the most standard variant of LPN typically assumes $\mathbb {F}= \mathbb {F}_2$, but other fields can be considered). Unlike the LWE assumption, in LPN over $\mathbb {F}$ the noise is assumed to have a small Hamming weight. Concretely, the noise is a random field element in a small fraction of the coordinates and 0 elsewhere. Given a field $\mathbb {F}$, $\mathsf {Ber} _r(\mathbb {F})$ denote the distribution which outputs a uniformly random element of $\mathbb {F}\setminus \{0\}$ with probability r, and 0 with probability $1-r$.

Definition 5

(LPN). For dimension $k=k(\lambda )$, number of samples (or block length) $q=q(\lambda )$, noise rate $r = r(\lambda )$, and field $\mathbb {F}= \mathbb {F}(\lambda )$, the $\mathbb {F}\hbox {-}\mathsf {LPN} (k,q,r)$ assumption states that

$$\begin{aligned}&\{(A, \vec {b}) \;|\; A{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {F}^{q\times k}, \vec {e}{\mathop {\leftarrow }\limits ^{{}_\$}}\mathsf {Ber} _r(\mathbb {F})^q, \vec {s}{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {F}^k, \vec {b}\leftarrow A\cdot \vec s + \vec {e} \} \\ {\mathop {\approx }\limits ^\mathrm{c}}&\{(A, \vec {b}) \;|\; A{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {F}^{q\times k}, \vec {b}{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {F}^q\} \end{aligned}$$

Here and in the following, all parameters are functions of the security parameter $\lambda$ and computational indistinguishability is defined with respect to $\lambda$. Note that the search LPN problem, of finding the vector can be reduced to the decisional LPN assumption [BFKL93, AIK09]. In this paper, our protocols will mostly rely on a variant of LPN, called exact LPN ($\mathsf {xLPN}$) [JKPT12]. In this variant, the noise vector $\vec e$ is not sampled from $\mathsf {Ber} _r(\mathbb {F})^q$, but it is sampled uniformly from the set $\mathsf {HW} _{rq}(\mathbb {F}^q)$ of length-q vectors over $\mathbb {F}$ with exactly rq nonzero coordinates (in contrast, a sample from $\mathsf {Ber} _r(\mathbb {F})^q$ has an expected number $r\cdot q$ of nonzero coordinates). While standard LPN is usually preferred since the Bernouilli distribution is convenient to analyze, $\mathsf {xLPN}$ is often preferred in concrete implementations, since it offers a potentially higher level of security for similar parameters (by avoiding weak instances with a low amount of noise). Furthermore, as outlined in [JKPT12], $\mathsf {xLPN}$ and LPN are equivalent: $\mathsf {xLPN}$ reduces to its search version using the sample-preserving reduction of [AIK07], and search-$\mathsf {xLPN}$ is easily seen to be polynomially equivalent to search-LPN.

Dual LPN. In our protocols, it will also prove convenient to work with the (equivalent) alternative dual formulation of LPN.

Definition 6

(Dual LPN). For dimension $k=k(\lambda )$, number of samples (or block length) $q=q(\lambda )$, noise rate $r = r(\lambda )$, and field $\mathbb {F}= \mathbb {F}(\lambda )$, the dual-$\mathbb {F}\hbox {-}\mathsf {LPN} (k,q,r)$ assumption states that

$$\begin{aligned}&\{(H, \vec {b}) \;|\; H{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {F}^{q-k\times q}, \vec {e}{\mathop {\leftarrow }\limits ^{{}_\$}}\mathsf {Ber} _r(\mathbb {F})^q, \vec {b}\leftarrow H\cdot \vec {e} \} \\ {\mathop {\approx }\limits ^\mathrm{c}}&\{(H, \vec {b}) \;|\; H{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {F}^{q-k\times q}, \vec {b}{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {F}^q\} \end{aligned}$$

Solving the dual LPN assumption is easily seen to be at least as hard as solving LPN: given a sample $(A,\vec b)$, define $H\in \mathbb {F}^{q-k\times q}$ to be the parity-check matrix of A (hence $H\cdot A = 0$), and feed $(H, H\cdot \vec b)$ to the dual LPN solver. Note that the parity check matrix of a random matrix is distributed as a random matrix. Furthermore, when $\vec b = A\cdot \vec s + \vec e$, we have $H\cdot \vec b = H\cdot (A\cdot \vec s + \vec e) = H\cdot \vec e$. For discussions regarding existing attacks on LPN and their efficiency, we refer the reader to [BCGI18, BCG+19b].

3.3 Pseudorandom Correlation Generators

Pseudorandom correlation generators (PCG) have been introduced in [BCG+19b]. Informally, a pseudorandom correlation generator allows to generate pairs of short keys (or seeds) $(\mathsf{k}_0,\mathsf{k}_1)$ such that each key $\mathsf{k}_\sigma$ can be expanded to a long string $R_\sigma = \mathsf {Expand} (\sigma ,\mathsf{k}_\sigma )$, with the following guarantees: given the key $\mathsf{k}_{1-\sigma }$, the string $R_\sigma$ is indistinguishable from a random string sampled conditioned on satisfying the target correlation with the string $R_{1-\sigma } = \mathsf {Expand} (1-\sigma ,\mathsf{k}_{1-\sigma })$. The formal definition of PCGs is given in the full version of this paper

4 Secure Computation from Super-Constant-Degree Low-Locality Polynomial Correlated Randomness

4.1 Block Decomposition of Layered Circuits

Given an arithmetic circuit C and an input vector $\vec x$, we call value of the gate g on input $\vec x$ the value carried by the output wire of a given gate g of C during the evaluation of $C(\vec x)$. The following decomposition of layered circuits is implicit in [Cou19]; for completeness, we give the proof in the full version.

Lemma 7

(Block-Decomposition of Layered Circuits). Let C be a layered arithmetic circuit over a field $\mathbb {F}$ with n inputs and m outputs, of size s and depth $d = d(n)$. For any integer k, denoting $t=t(k) = \lceil d/k\rceil$, there exists $2t+1$ integers $(s_0 = 0, s_1, \cdots , s_{t-1},s_t = 0)$, $(m_0, \cdots , m_{t-1})$, and functions $(f_0, \cdots , f_{t - 1})$ with $f_i: \mathbb {F}^n \times \mathbb {F}^{s_i} \rightarrow \mathbb {F}^{s_{i+1}} \times \mathbb {F}^{m_i}$, such that:

• The algorithm A given below satisfies, for any input vector $\vec x \in \mathbb {F}^n$, $A(\vec x) = C(\vec x)$ (that is, A computes C);

  

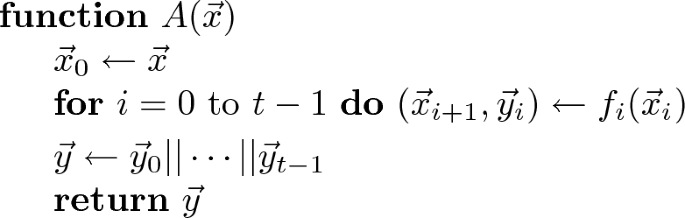
• For any $i \in [\![0, t-1]\!]$, $j \le s_{i+1} + m_i$, the j-th output³ of $f_i: \mathbb {F}^n\times \mathbb {F}^{s_i} \mapsto \mathbb {F}^{s_{i+1}}\times \mathbb {F}^{m_i}$ can be computed by a multivariate polynomial $P_{i,j}$ over $\mathbb {F}^{2^k}$ of degree $\deg P_{i,j} \le 2^{k}$;

• $\sum _{i=0}^{t-1} s_i \le s/k$ and $\sum _{i=0}^{t-1} m_i = m$.

4.2 Securely Computing C in the Correlated Randomness Model

We represent in Fig. 1 the ideal functionality for securely evaluating the layered arithmetic circuit C.

Fig. 1.

Ideal functionality $\mathcal {F} _C$ for securely evaluating an arithmetic circuit C among N parties.

We represent on Fig. 2 an ideal functionality for distributing (function-dependent) correlated randomness between the parties.

Theorem 8

Let $k\le \log \log s-\log \log \log s$. There exists a protocol $\varPi _C$ which (perfectly) securely implements the N-party functionality $\mathcal {F} _C$ in the $\mathcal {F} _\mathsf {corr}$-hybrid model, against a static, passive, non-aborting adversary corrupting at most $N-1$ out of N parties, with communication complexity upper bounded by $O(N\cdot (n +\frac{s}{k} + m)\cdot \log |\mathbb {F}|)$ and polynomial computation.

Fig. 2.

Ideal corruptible functionality $\mathcal {F} _\mathsf {corr}$ to deal out correlated randomness to the parties.

The protocol follows closely the construction of [Cou19], with some tedious technical adaptations which are necessary to rely on the specific type of correlated randomness which we will manage to securely generate with low communication overhead. The protocol and its security analysis are given in the full version.

5 Generating Correlated Randomness from LPN

In this section, we construct a protocol $\varPi _\mathsf {corr}$, which implements the ideal functionality $\mathcal {F} _\mathsf {corr}$ with small communication, under the quasi-polynomial LPN assumption. A very natural approach to realise a functionality that distributes correlated random coins using a small amount of communication is to rely on pseudorandom correlation generators, a primitive recently defined an constructed (for various types of correlations, and under a variety of assumptions) in [BCG+19b]. At a high level, [BCG+19b] suggests to distribute correlated randomness with the following approach:

• Use a generic secure computation protocol $\varPi _\mathsf{Gen}$ to distributively execute the $\mathsf{PCG}.\mathsf{Gen}$ functionality of the pseudorandom correlation generator. Note that $\mathsf{PCG}.\mathsf{Gen}$ outputs short seeds, much smaller than the correlated pseudo-random strings which can be stretched from these seeds. Therefore, $\varPi _\mathsf{Gen}$ can potentially have a relatively high communication overhead in its inputs and outputs, while maintaining the overall communication overhead of $\varPi _\mathsf {corr}$ small.

• Expand the distributively generated seeds locally using the $\mathsf {Expand}$ algorithm of the PCG. Each such string is guaranteed, by the security of the PCG, to be indistinguishable (from the viewpoint of the other parties) from a uniformly random string sampled conditioned on satisfying the target correlation with the expanded strings held by the other parties.

While this approach does not necessarily leads to a secure implementation of an ideal functionality generating correlated random coins, it was shown in [BCG+19b] (Theorem 19 in [BCG+19b]) that it provides a provably secure implementation for all corruptible ideal functionalities for distributing correlated random coins. Note that this property is satisfied by our functionality $\mathcal {F} _\mathsf {corr}$. Our protocol $\varPi _\mathsf {corr}$ will follow this approach. We start by constructing a pseudorandom correlation generator for the type of correlated randomness produced by $\mathcal {F} _\mathsf {corr}$, building upon an LPN-based construction of [BCG+19b].

5.1 Substrings Tensor Powers Correlations ($\mathsf {stp}$)

We now describe our construction of a PCG for generating the type of correlated randomness produced by $\mathcal {F} _\mathsf {corr}$. As all constructions of [BCG+19b], our construction will be restricted to the two-party setting; hence, we focus on $N=2$ parties from now on. Abstracting out the unnecessary details, the functionality $\mathcal {F} _\mathsf {corr}$ does the following. It is parametrised with a vector length w, subsets $(S_i)_{1\le i \le \mathsf {n}_{\mathsf {s}}}\in \left( {\begin{array}{c}[w]\\ \le K\end{array}}\right) ^{\mathsf {n}_{\mathsf {s}}}$, a tensor power parameter $\mathsf {tpp}$, and generates shares of:

$$({\vec r}, ({(1_\mathbb {F}\;||\;{\vec r}[S_i])}^{\otimes \mathsf {tpp}})_{1\le i \le \mathsf {n}_{\mathsf {s}}}),\text { where } \vec r\in \mathbb {F}^w\text { is random}.$$

We call $\mathcal {C}$ the correlation generator associated with $\mathcal {F} _\mathsf {corr}$, i.e. the PPT algorithm that, on input the security parameter in unary $1^\lambda$, samples correlated random string as above (where the parameters $(\mathsf {n}_{\mathsf {s}},K,\mathsf {tpp})$ are functions of $\lambda$). It is straightforward to see that $\mathcal {C}$ is a reverse-samplable correlation generator , since it is an additive correlation: given any fixed share $\mathsf{share} _0$, a matching share can be reverse-sampled by sampling $\vec r$ and setting $\mathsf{share} _1 \leftarrow ({\vec r}, ({(1_\mathbb {F}\;||\;{\vec r}[S_i])}^{\otimes \mathsf {tpp}})_{1\le i \le \mathsf {n}_{\mathsf {s}}}) - \mathsf{share} _0$. We call this type of correlated randomness a subsets tensor powers ($\mathsf {stp}$). Below, we describe a pseudorandom correlation generator for such correlations.

5.2 Good Cover

Before we proceed with the description of a PCG to generate such correlations, we need to introduce a concept, that of a good cover. The notations in this subsection are completely self-contained, and may conflict with the parameters defined for the main protocol. In the course of our construction we will want to solve the following problem: given a vector $\vec v$ of size n, a family $(S_i)_{i\in [t]}\in \mathcal {P}([n])^t$ of t (short) subsets of coordinates of $\vec v$, and a (small) bound $B>0$, the problem is to find a family $(\vec v_j)_{j\in [M]}$ of some number m of size-K subvectors of $\vec v$ such that:

• 1. The subvectors collectively cover $\vec v$;

• 2. For each $i\in [t]$, there are at most B subvectors in $(\vec v_j)_{j\in [M]}$ whose coordinates intersect $S_i$.

We call such a family a B-Good Cover of $(\vec v, (S_i)_{i\in [t]})$. First of all we note that the values of the vectors and subvectors do not matter, so we will conflate them with sets and subsets (of coordinates) for simplicity, which leads to a more natural formulation.

Definition 9

(Good Cover – Set Formulation). Let $n,B,K,t,q,M\in \mathbb {N}$ and $(S_i)_{i\in [t]}\in \left( {\begin{array}{c}[n]\\ \le q\end{array}}\right) ^t$ a family of t subsets of [n] of size at most q each. A family $A=(\vec \alpha ^j)_{j\in [M]}\in {[n]\atopwithdelims ()K}^M$ is a B-Good Cover of $(S_i)_{i\in [t]}$ if:

• 1. A covers [n]: $\bigcup _{j=1}^M \vec \alpha ^j= [n]$

• 2. Each $S_i$ intersects at most B elements of A: $\forall i\in [t], |\{j\in [M]:\vec \alpha ^j\cap S_i\ne \emptyset \}|\le B.$

We abusively conflate the two views, where a good cover is just a family of subsets $A\in \left( {\begin{array}{c}[n]\\ K\end{array}}\right) ^M$ and where the good cover is a family of sparse vectors—given by a set of coordinates and a short vector of values—$A\in (\left( {\begin{array}{c}[n]\\ K\end{array}}\right) \times \mathbb {F}^K)^M$.

Lemma 10

(Random Covers are Good Covers.). Let $n,\kappa ,\kappa '\in \mathbb {N}\smallsetminus \{0,1\}$, and $(S_i)_{i\in [t]}\in \left( {\begin{array}{c}[n]\\ \le q\end{array}}\right) ^t$ a family of t subsets of [n] of size at most q each. Let $A=(\vec \alpha ^j)_{j\in [M]}\in {[n]\atopwithdelims ()K}^M$ be a sequence of M i.i.d. uniform random size-K subsets of [n], with $M=\kappa \cdot n\ln n/K$. Let $B\leftarrow \kappa '\kappa \cdot q\cdot \ln n$.

It holds that $A=(\vec \alpha ^j)_{j\in [M]}$ is a B-Good Cover of $(S_i)_{i\in [t]}$ with probability at least:

$$1-\frac{1}{n^{\kappa -1}}-\frac{t}{n^{(\kappa '-2)\kappa \cdot q/2}}.$$

The proof is given in the full version.

5.3 PCG for Subsets Tensor Powers ($\mathsf {PCG}_{\mathsf {stp}}$)

We now proceed with the description of a pseudorandom correlation generator for subsets tensor powers.

PCG for Low-Degree Polynomials from [BCG+19b]. We start by recalling a natural variant of pseudorandom correlation generator of [BCG+19b, Section 6], which generates shares of $\vec r^{\otimes \mathsf {tpp}}$, for a parameter $\mathsf {tpp}$ and a pseudorandom $\vec r$. It relies on the $\mathsf {xLPN}$ assumption with dimension n, number of samples $n' > n$, and a number $\lambda$ of noisy coordinates. In our instantiation, we will typically consider $n' = O(n)$, e.g. $n' = 12n$; this corresponds to a particularly conservative variant of LPN with a very limited number of samples, and is equivalent to the hardness of decoding a random constant-rate linear code (which is known as the syndrome decoding problem). As discussed in Sect. 3, all known attacks on the syndrome decoding problem for constant-rate codes have complexity $2^{O(\lambda )}$. The PCG of [BCG+19b] is parametrised by integers $1^\lambda , n, n', \lambda , \mathsf {tpp} \in \mathbb {N}$ (where $n' > n$), a field $\mathbb {F}$, and a random parity-check matrix $H_{n',n} {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {F}^{(n'-n)\times n'}$ (Fig. 3).

Fig. 3.

PCG for low-degree polynomials from [BCG+19b].

Correctness follows from the fact that $\vec v_0 + \vec v_1 = \vec e^{\otimes \mathsf {tpp}}$ by the correctness of $\mathsf{MPFSS}$, and $H_{n',n}^{\otimes \mathsf {tpp}}\cdot \vec e^{\otimes \mathsf {tpp}} = (H_{n',n} \cdot \vec e)^{\otimes \mathsf {tpp}}$ by multilinearity of the tensor product. Hence, denoting $\vec r = H_{n',n}\cdot \vec e$, it holds that $\vec r_0 + \vec r_1 = \vec r^{\otimes \mathsf {tpp}}$. For security, we must show that the following distributions are indistinguishable for any $\sigma = 0, 1$:

$$\begin{aligned}&\{(\mathsf{k}_\sigma , \vec r_{1-\sigma })\;:\; (\mathsf{k}_0,\mathsf{k}_1) {\mathop {\leftarrow }\limits ^{{}_\$}}\mathsf{Gen} (1^\lambda ), \vec r_{1-\sigma } \leftarrow \mathsf {Expand} (1-\sigma ,\mathsf{k}_{1-\sigma })\}\\ {\mathop {\approx }\limits ^\mathrm{c}}&\{(\mathsf{k}_\sigma , \vec r_{1-\sigma })\;:\; (\mathsf{k}_0,\mathsf{k}_1) {\mathop {\leftarrow }\limits ^{{}_\$}}\mathsf{Gen} (1^\lambda ), \vec r_{\sigma } \leftarrow \mathsf {Expand} (\sigma ,\mathsf{k}_{\sigma }), \vec r{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {F}^n,\\&{ \vec r_{1-\sigma } \leftarrow \vec r^{\otimes \mathsf {tpp}} - \vec r_\sigma \}} \end{aligned}$$

Proof

We sketch the analysis for the sake of completeness; the full proof is given in [BCG+19b]. Security is shown with the following sequence of hybrids: first generate $(\mathsf{k}_\sigma , \vec r_{1-\sigma })$ as in the first distribution above. Then, generate $(\mathsf{k}_\sigma , \vec r_{1-\sigma })$ as before, and generate an alternative key $\mathsf{k}'_\sigma$ solely from the parameters $(1^\lambda ,\mathbb {F},n,n',t,\mathsf {tpp})$, using the simulator of the MPFSS. Output $(\mathsf{k}'_\sigma , \vec r_{1-\sigma })$; under the security of the MPFSS, this distribution is indistinguishable from the previous one. Note that $\mathsf{k}'_\sigma$ does not depend anymore on the noise vector $\vec e$. In the next hybrid, generate $\vec r {\mathop {\leftarrow }\limits ^{{}_\$}}H_{n',n}\cdot \vec e$ and set $\vec r_{1-\sigma } \leftarrow \vec r^{\otimes \mathsf {tpp}} -\mathsf {Expand} (\sigma ,\mathsf{k}_{\sigma })$; this game is perfectly indistinguishable from the previous one. Finally, replace $\vec r {\mathop {\leftarrow }\limits ^{{}_\$}}H_{n',n}\cdot \vec e$ by $\vec r {\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {F}^n$; under the LPN assumption, this last game (which correspond exactly to the second distribution) is computationally indistinguishable from the previous one, and security follows.    $\square$

Our New PCG. We now describe a variant of the above PCG, tailored to computing the tensor powers of many short subsets. The PCG is parametrised by $(S_i)_{i\in [K]}\in \left( {\begin{array}{c}[w]\\ \le K\end{array}}\right) ^{\mathsf {n}_{\mathsf {s}}}$, $\mathsf {n}_{\mathsf {s}}$ subsets of at most K indices taken from [w]. We assume for simplicity, but morally without loss of generality⁴, that $\bigcup _{i=1}^{\mathsf {n}_{\mathsf {s}}}S_i=[w]$. Our goal is for the parties to obtain shares of some pseudorandom vector $\vec r\in \mathbb {F}^w$ as well as shares of $(1\ ||\ \vec r[S_i])^{\otimes \mathsf {tpp}}\in \mathbb {F}^{w\cdot \mathsf {tpp}}$ for each $i\in [\mathsf {n}_{\mathsf {s}} ]$.

We start by generating a B-good cover (for some integer B) of the $(S_i)_i$ of the form $(\alpha _j,\vec r_j)_{j\in [m]}\in (\left( {\begin{array}{c}[w]\\ \theta \end{array}}\right) \times \mathbb {F}^\theta )^m$ where each $\vec r_j$ is pseudorandom. We generate each of the m pseudorandom masks $\vec r_j$ using a different instance of $\mathsf {xLPN}$, i.e. $\vec r_j\leftarrow H_j\cdot \vec e_j$, where $\vec e_j\in \mathbb {F}^{\theta '}$ is $\lambda$-sparse and $H_j{\mathop {\leftarrow }\limits ^{{}_\$}}\mathbb {F}^{\theta \times \theta '}$ for some $\theta '=O(\theta )$. For each $S_i$, we denote the set of the indices of the masks which ‘intersect’ with $S_i$. Note that $\forall i\in [\mathsf {n}_{\mathsf {s}} ],|I_i|\le B$ by definition of a B-good cover. We can now proceed with our main goal: generating shares of a subsets tensor powers correlation.

We define , where $f_{\alpha _j,\vec r_j}\in \mathbb {F}^w$ is the sparse vector defined by $(f_{\alpha _j,\vec r_j})_{|\alpha _j}=\vec r_j$ (and which is equal to $0_\mathbb {F}$ on $[w]\smallsetminus \alpha _j$). Since $\bigcup _{i=1}^{\mathsf {n}_{\mathsf {s}}}S_i=[w]$ and each of the $\vec r_j$ is pseudorandom, $\vec r$ is also pseudorandom.

Note that for any given $i\in [\mathsf {n}_{\mathsf {s}} ]$, $(1_\mathbb {F}\ ||\ \vec r[S_i])$ is a subvector of the vector $\tilde{\vec r}_i$ obtained by multiplying the block-diagonal matrix $H'_i=\textsf {Diag}((1_\mathbb {F}),H_{j_1},\dots ,H_{j_{|I_i|}})$ with the vector $\vec e'_i=(1_\mathbb {F}|| e_{j_1} || \cdots || e_{j_{|I_i|}})$. Therefore for any tensor power $\mathsf {tpp}$ (i.e. the degree of the polynomial correlation), $\tilde{\vec r}_i^{\otimes \mathsf {tpp}}=(H'_i \cdot \vec e'_i)^{\otimes \mathsf {tpp}} = (H'_i)^{\otimes \mathsf {tpp}} \cdot (\vec e'_i)^{\otimes \mathsf {tpp}}$. If the parties use an MPFSS scheme to generate small seeds which expand to $(\vec e'_i)^{\otimes \mathsf {tpp}}$, they can then locally obtain shares of $\tilde{\vec r}_i^{\otimes \mathsf {tpp}}$ (since $(H'_i)^{\otimes \mathsf {tpp}}$ is public), and therefore of $(1_\mathbb {F}\ ||\ \vec r[S_i])^{\otimes \mathsf {tpp}}$. From all these shares of all the $(1_\mathbb {F}\ ||\ \vec r[S_i])^{\otimes \mathsf {tpp}}, i\in [\mathsf {n}_{\mathsf {s}} ]$ the parties can locally extract shares of all the $\vec r[S_i]$ and thence shares of $\vec r$ (since $\bigcup _{i=1}^{\mathsf {n}_{\mathsf {s}}}S_i=[w]$). The protocol is given in Fig. 4.

Fig. 4.

Pseudorandom correlation generator $\mathsf {PCG}_{\mathsf {stp}}$ for generating pseudorandom instances of the subsets tensor powers correlation over a field $\mathbb {F}$.

Theorem 11

Let $w>0$, and $(S_i)_{i\in [\mathsf {n}_{\mathsf {s}} ]}$ a list of $\mathsf {n}_{\mathsf {s}}$ subsets of [w]. Let $B,\theta '$ such that there exists a B-good cover of $(S_i)_{i\in [\mathsf {n}_{\mathsf {s}} ]}$ comprised of size-$\theta '$ vectors, and let $\theta < \theta '$. Assume that the $\mathbb {F}\hbox {-}\mathsf {xLPN} (\theta ,\theta ',\lambda )$ assumption holds, and that $\mathsf{MPFSS}$ is a secure multi-point function secret-sharing scheme for the family of $(1+\mu \cdot \lambda )^\mathsf {tpp}$-point functions from $[(1+\mu \cdot \theta ')^\mathsf {tpp} ]$ to $\mathbb {F}$ for all $\mu \in [{B}]$. Then $\mathsf {PCG}_{\mathsf {stp}}$ is a secure pseudorandom correlation generator, which generates pseudorandom shares of a subsets tensor powers correlation $(\vec r, ({(1_\mathbb {F}\;||\;\vec r[S_i])}^{\otimes \mathsf {tpp}})_{1\le i\le \mathsf {n}_{\mathsf {s}}})$ where $\vec r\in \mathbb {F}^w$.

• Communication: If the $\mathsf{MPFSS}$ seeds have size $O[\lambda \cdot (1+B\lambda )^\mathsf {tpp} \cdot \log ((1+B\theta ')^\mathsf {tpp})]$ and $\mathsf{MPFSS}.\mathsf {FullEval}$ can be computed with $O((1+B\lambda )^\mathsf {tpp} \cdot (1+B\theta ')^\mathsf {tpp} \cdot \frac{\log |\mathbb {F}|}{\lambda })$ invocations of a pseudorandom generator $\mathsf{PRG}:\{0,1\} ^{\lambda }\mapsto \{0,1\} ^{2\lambda +2}$, then $\mathsf {PCG}_{\mathsf {stp}}.\mathsf{Gen}$ outputs seeds of size:

  $$\begin{aligned} |\mathsf{k}_\sigma | = O\left( \mathsf {n}_{\mathsf {s}} \cdot \lambda \cdot \left( 1+B\lambda \right) ^\mathsf {tpp} \cdot \log \left( (1+B\theta ')^\mathsf {tpp} \right) \right) . \end{aligned}$$

• Computation: The computational complexity of $\mathsf {PCG}_{\mathsf {stp}}.\mathsf {Expand}$ is predominantly that of $O(\mathsf {n}_{\mathsf {s}} \cdot (1+B\lambda )^\mathsf {tpp} \cdot (1+B\theta ')\cdot \frac{\log |\mathbb {F}|}{\lambda })$ invocations of a PRG, plus $\mathsf {n}_{\mathsf {s}}$ matrix-vector products with a matrix of dimensions $(1+B\theta )^\mathsf {tpp} \times (1+B\theta ')^\mathsf {tpp}$ which requires at most $O(\mathsf {n}_{\mathsf {s}} \cdot (B\theta )^\mathsf {tpp} \cdot (B\theta ')^\mathsf {tpp})\subseteq O(\mathsf {n}_{\mathsf {s}} \cdot (B\theta ')^{2\cdot \mathsf {tpp}})$ arithmetic operations over $\mathbb {F}$.

The proof of the above theorem is omitted in this version of the paper.

5.4 Instantiating the MPFSS

Theorem 11 assumes the existence of an MPFSS scheme $\mathsf{MPFSS}$ for the family of all $(1+\mu \cdot \lambda )^\mathsf {tpp}$-point functions from $[(1+\mu \cdot \theta ')^\mathsf {tpp} ]$ to $\mathbb {F}$ for some $\mu \in [B]$ (or, equivalently, an MPFSS for each $\mu$ which can then all be combined into one scheme), with the following efficiency guarantees: $\mathsf{MPFSS}.\mathsf{Gen} (1^\lambda )$ outputs seeds of size $O((1+B\lambda )^\mathsf {tpp} \cdot \lambda \cdot \log ((1+B\theta ')^\mathsf {tpp}))$, and $\mathsf{MPFSS}.\mathsf {FullEval}$ can be computed with $O((1+B\lambda )^\mathsf {tpp} \cdot (1+B\theta ')^\mathsf {tpp} \cdot \frac{\log |\mathbb {F}|}{\lambda })$ invocations of a pseudorandom generator $\mathsf{PRG}:\{0,1\} ^{\lambda }\mapsto \{0,1\} ^{2\lambda +2}$. The works of [BGI16b, BCGI18] provides exactly such a construction, which makes a black box use of any pseudorandom generator $\mathsf{PRG}:\{0,1\} ^{\lambda }\mapsto \{0,1\} ^{2\lambda +2}$. We instantiate the PRG using the LPN-based construction of [BKW03], which we recall in the full version of the paper.

5.5 Securely Distributing $\mathsf{MPFSS}.\mathsf{Gen}$ an $\varPi _\mathsf {stp}$

The seeds of the MPFSS scheme of [BCGI18] can be securely generated by using parallel instances of a generic secure computation protocols to securely evaluate the above PRG. Using GMW to instantiate the generic protocol, we have:

Corollary 12

There exists a semi-honest secure two-party protocol $\varPi _\mathsf{MPFSS}$ which distributes the seeds of a multi-point function secret-sharing scheme $\mathsf{MPFSS}$ for the family of $t'$-point functions from $[(1+B\theta ')^\mathsf {tpp} ]$ to $\mathbb {F}$, using $O(t'\cdot \nu \cdot \lambda ^2)$ calls to an ideal oblivious transfer functionality, where $\nu =\log ((1+B\theta ')^\mathsf {tpp})$ and $t' = (1+B\lambda ')^\mathsf {tpp}$, with an additional communication of $O(t'\cdot \nu \cdot \lambda ^2)$ bits, and total computation polynomial in $t'\cdot \nu \cdot \lambda$.

We prove the above corollary by exhibiting $\varPi _\mathsf{MPFSS}$ in the full version. As a direct corollary of Corollary 12, since the seeds of $\mathsf {PCG}_{\mathsf {stp}}$ contain exactly $\mathsf {n}_{\mathsf {s}}$ independent MPFSS seeds, we have:

Corollary 13

There exists a semi-honest secure two-party protocol $\varPi _\mathsf {stp}$ which distributes the seeds of the pseudorandom correlation generator $\mathsf {PCG}_{\mathsf {stp}}$ represented on Fig. 4, using $O(\mathsf {n}_{\mathsf {s}} \cdot t'\cdot \nu \cdot \lambda ^2)$ calls to an ideal oblivious transfer functionality, where $\nu =\log ((B\theta '+1)^\mathsf {tpp})$ and $t' = (1+B\lambda )^\mathsf {tpp}$, with an additional communication of $O(\mathsf {n}_{\mathsf {s}} \cdot t'\cdot \nu \cdot \lambda ^2)$ bits, and total computation $O(\mathsf {n}_{\mathsf {s}} \cdot \mathsf {poly} (t'\cdot \nu \cdot \lambda ))$.

Instantiating the oblivious transfer. To execute the GMW protocol, we need an oblivious transfer. Under the $\mathbb {F}_2\hbox {-}\mathsf {LPN} (\lambda , O(\lambda ), 1/\lambda ^\delta )$ assumption ($\delta$ is any small constant), there exists oblivious transfers (with simulation security) with $\mathsf {poly} (\lambda )$ communication and computation; see for example [DGH+20].

Constructing $\varPi _\mathsf {corr}$. The work of [BCG+19b] shows that any corruptible functionality distributing the output of a correlation generator $\mathcal {C}$ can be secure instantiated using any semi-honest secure two-party protocol $\varPi$ for distributing the $\mathsf{Gen}$ procedure of a PCG for $\mathcal {C}$, with the same communication as $\varPi$, and with computational complexity dominated by the computational complexity of $\varPi$ plus the computational complexity for computing the $\mathsf{PCG}.\mathsf {Expand}$ procedure. Therefore, using their result together with our protocol $\varPi _{\mathsf {stp}}$ for generating the seeds of a PCG for subsets tensor powers correlation allows to securely instantiate $\mathcal {F} _\mathsf {corr}$ (with $N=2$).

Recall that the computation of $\mathsf {PCG}_{\mathsf {stp}}.\mathsf {Expand}$ is dominated by $O(\mathsf {n}_{\mathsf {s}} \cdot (1+B\lambda )^\mathsf {tpp} \cdot (1+B\theta ')^\mathsf {tpp} \cdot \frac{\log |\mathbb {F}|}{\lambda })$ invocations of a PRG – which requires at most $O(\lambda ^2\cdot \mathsf {n}_{\mathsf {s}} \cdot (1+B\lambda )^\mathsf {tpp} \cdot (1+B\theta ')^\mathsf {tpp} \cdot \frac{\log |\mathbb {F}|}{\lambda })$ operations over $\mathbb {F}_2$ using the simple LPN-based PRG from [BKW03] –, plus an additional $O(\mathsf {n}_{\mathsf {s}} \cdot (1+B\theta )^\mathsf {tpp} \cdot (1+B\theta ')^\mathsf {tpp})$ arithmetic operations over $\mathbb {F}$. Since each operation over $\mathbb {F}$ can be computed with $O(\log |\mathbb {F}|)^2)$ boolean operations, combining the two, we get computation $O(\lambda \cdot \mathsf {n}_{\mathsf {s}} \cdot (1+B\theta )^\mathsf {tpp} \cdot (1+B\theta ')^\mathsf {tpp} \cdot (\log |\mathbb {F}|)^2)$.

All that remains is for the parties to generate the necessary material for $\mathsf {PCG}_{\mathsf {stp}}$: m random $\mathbb {F}^{\theta \times \theta '}$ matrices and m size-$\theta '$ subsets of [w]. At its core, this is just a matter for the parties to generate and hold the same $m\cdot (\theta \cdot \theta '\cdot \log |\mathbb {F}|+\log \left( {\begin{array}{c}w\\ \theta '\end{array}}\right) )$ (pseudo)-random bits. This can be achieved by having one party sample a seed of size $\lambda$, send it to the other, and both parties can expand it locally by calling the length-doubling PRG from [BKW03] (and used above) $m\cdot \theta '\cdot (\theta \cdot \log |\mathbb {F}|+\log w)/\lambda$ times (in a GGM tree-like approach). This requires $\lambda$ bits of communication and $O(m\cdot \theta '\cdot (\theta \cdot \log |\mathbb {F}|+\log w)\cdot \lambda )$ bits of local computation. This is summarised in an intermediate theorem, omitted from this version. Wrapping up, using $\varPi _\mathsf {stp}$ with an appropriate good cover suffices to construct a protocol $\varPi _\mathsf {corr}$ for securely implementing the functionality $\mathcal {F} _\mathsf {corr}$. The detailed choice of parameters is deferred to the full version. Below, we describe a specific choice of parameters for the full construction which suffices to arrive at the claimed result.

6 Choice of Parameters

In this section, we tune the parameters of our protocol. We want to ensure the scheme is correct with all but negligible probability, that it is secure, that the communication is sublinear, and that the computation is polynomial. We make two sets of choices for the parameters: the first optimising for communication, and the other for computation (and incidentally for the strength of the security assumption). The full discussion is deferred to the full version.

Combining Theorem 8–which provides a secure protocol in the $\mathcal {F} _\mathsf {corr}$-hybrid model–and the instantiation of the $\mathcal {F} _\mathsf {corr}$ as provided in the full version, with an appropriate choice of parameters, also made explicit in the full version, we get our main theorem, Main Theorem 1 below.

Main Theorem 1

(Sublinear Computation of Layered Circuits – Optimised for Communication). Assuming the super-polynomial security of

• $\mathbb {F}\hbox {-}\mathsf {LPN}$ with super-polynomial dimension $\ell$, $O(\ell )$ samples, and inverse super-polynomial rate,

• $\mathbb {F}_2\hbox {-}\mathsf {LPN}$ with super-polynomial dimension $\ell '=s^{O((1))}$, $O(\ell ')$ samples, and inverse polynomial rate (which is implied by the above if $\mathbb {F}=\mathbb {F}_2$),

there exists a probabilistic semi-honest two-party protocol which securely evaluates any layered arithmetic circuit over $\mathbb {F}$ with success probability $1-\mathrm {negl}(s)$ and which uses $O\left( \left[ n+s/\log \log s+m\right] \cdot \log |\mathbb {F}|\right)$ bits of communication and $s^3\cdot \mathsf {polylog} {s}\cdot (\log |\mathbb {F}|)^2$ bits of computation (where s, n, and m are respectively the number of gates, inputs, and outputs of the circuit).

Instantiating the protocol with an alternative choice of parameters, also detailed in the full version, instead yields the following.

Main Theorem 2

(Sublinear Computation of Layered Circuits – Optimised for Computation). Assuming the quasi-polynomial security of

• $\mathbb {F}\hbox {-}\mathsf {LPN}$ with quasi-polynomial dimension $\ell$, $O(\ell )$ samples, and inverse quasi-polynomial rate,

• $\mathbb {F}_2\hbox {-}\mathsf {LPN}$ with quasi-polynomial dimension $\ell '$, $O(\ell ')$ samples, and inverse polynomial rate (which is implied by the above if $\mathbb {F}=\mathbb {F}_2$),

there exists a probabilistic semi-honest two-party protocol which securely evaluates any layered arithmetic circuit over $\mathbb {F}$ with success probability $1-\mathrm {negl}(s)$ and which uses $O\left( \left[ n+o(s)+m\right] \cdot \log |\mathbb {F}|\right)$ bits of communication and $s^{1+o(1)}\cdot (\log |\mathbb {F}|)^2$ bits of computation (where s, n, and m are respectively the number of gates, inputs, and outputs of the circuit).