Keywords

1 Introduction

A footbridge may be flexible and is potentially prone to vibrate due to human excitation. The dynamic forces caused by pedestrians might not cause ultimate-limit-state issues, but the serviceability limit state may be of concern.

A well-known and critical scenario was that occurring on the Millennium Bridge in London [1]. Here, both vertical and horizontal motion caused by pedestrians showed to be a problem. The problematic conditions often relate to coincidence between bridge natural frequencies and frequencies of human in motion. In this case excessive structural vibrations may occur and if not properly designed, the bridge may be unfit for its intended use.

In this paper focus is on the vertical action of pedestrians. The action has for decades been modelled as a deterministic load [2,3,4]. More recently, in for instance [5,6,7,8], the stochastic nature of the action has been considered and modelled.

Hence, this paper will adapt the stochastic line of thinking, hereby modelling central walking parameters as random variables. Doing so recognises that parameters such as pedestrian step frequency, step length and dynamic load factors are in fact stochastic properties by nature.

A comprehensive line-up of the probabilistic scenario is introduced in [9]. The present paper takes off-set in the general approach, but also considers, adapts and evaluates simplifications along the way.

For all investigations off-set is taken in artificial footbridges. They will be assumed pin-supported, and focus will be on the vertical bridge response at midspan in the form of accelerations. As a result of the fact that the loading is stochastic, the response will be stochastic too, and the output of calculations will be the acceleration quantiles. These are derived combining Newmark time integration with Monte Carlo simulations.

The paper aims at exploring how sensitive the stochastic nature of footbridge vibration is to decisions related to defining dynamic load factors and how sensitive it is in regard to assumptions made for the stochastic nature of step frequencies of the pedestrians.

Section 2 describes basic model assumptions.

Section 3 describes the different study angles of the paper, and Sect. 4 summarises conclusions.

2 Modelling of Walking Loads

The walking load models considered in this paper rely on a modal load assumption in which the modal load Q(t) acting on the footbridge and generated by the pedestrian is derived using Eq. (1).

$$ Q(t)=\Phi (t)F(t) $$
(1)

F(t) represents the vertical force imparted at the position of the pedestrian while crossing the bridge, and Ф(t) is the mode shape function. Only the first bending mode is considered to dominate the response, and hence this will be taken as a half-sine sinusoidal. It will depend on the pacing speed v of the pedestrian, and in consequence hereof on the step frequency f s and step length l s of the pedestrian as a result of the relationship shown in Eq. (2).

$$ v={f}_{\mathrm{s}}{l}_{\mathrm{s}} $$
(2)

The mode shape function is calculated using Eq. (3).

$$ \Phi (t)=\sin \left(\pi vt/L\right) $$
(3)

This load model, F(t), is the model introduced in [9]. The mathematical expression for F(t) is seen in Eqs. (4–6):

$$ F(t)=\sum_{i=1}^5{F}_i(t)+\sum_{i=1}^5{F}_i^S(t) $$
(4)
$$ {F}_i(t)={W\alpha}_i\sum_{{\overline{f}}_j=i-0.25}^{i+0.25}{\overline{\alpha}}_i\left({\overline{f}}_j\right)\cos \left(2\pi {\overline{f}}_j{f}_{\mathrm{s}}t+\theta \left({\overline{f}}_j\right)\right) $$
(5)
$$ {F}_i^S(t)={W\alpha}_i^S\sum_{{\overline{f}}_j^S=i-0.75}^{i-0.25}{\overline{\alpha}}_i^S\left({\overline{f}}_j^S\right)\cos \left(2\pi {\overline{f}}_j^S{f}_{\mathrm{s}}t+\theta \left({\overline{f}}_j^S\right)\right) $$
(6)

Reference is made to [9], for a detailed description.

Here it suffices to mention that W represents the static weight of the pedestrian. Furthermore, that f s represents the step frequency.

The model consists of main load harmonics (Eq. 5) and subharmonics (Eq. 6). The latter due to the fact that “the fundamental period of the force time history is equal to the time required to make two successive steps, rather than one” [9].

A governing parameter for the loading is the dynamic load factors, α i, (i = 1, 2, …, 5).

For the main harmonic, α 1 (the first load harmonic), the following mean value, μ, and a standard variation, σ, is assumed.

$$ \mu =-0.2649{f}_{\mathrm{S}}^3+1.3206{f}_{\mathrm{S}}^2-1.7597{f}_{\mathrm{S}}+0.7613;\kern0.75em \sigma =0.16\mu $$
(7)

As would appear, the dynamic load factor is modelled as a random variable, and the distribution is assumed Gaussian.

Table 1 defines the assumptions made for the dynamic load factors, for α i(i = 2, 3, 4, 5), and the corresponding mean values (μ) and standard deviations (σ).

Table 1 Mean values and standard deviations
Full size table

The subharmonic load factors \( {\alpha}_i^S \) are derived from the main harmonic load factor, α 1, in the way described in [9].

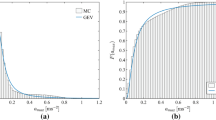
Having set up the load, Newmark time-integration allows for computing bridge response and Monte Carlo simulations for establishing a statistical basic for the response. From this, acceleration quantiles can be derived, such as the acceleration quantile a 95, which will be the parameter in focus in this paper for describing the acceleration level of the considered footbridges.

For each bridge 100.000 simulations were conducted.

3 Studies of This Paper

3.1 Impact of Decisions Related to Modelling the Load Amplification Factor

The purpose of this study is to explore how different decisions related to modelling the dynamic load factor influence estimates of the stochastic bridge response in the form of the acceleration quantile a 95.

A simplified load model is assumed, namely one that only considers the first harmonic, α 1. Leakage of energy around this load harmonic is also disregarded.

The following assumptions were made as regards the walking parameters, see Table 2.

Table 2 Mean values and standard deviations
Full size table

Hence, it is assumed that step length and step frequency are random variables, and Gaussian distributions are assumed to apply.

By this approach, the load amplification factor (Eq. 7) would vary depending on the outcome of f s in simulations from one pedestrian crossing to the next.

An alternative assumption for the calculations could be to assume that the load amplification factor assumes a constant value, namely the value that can be calculated by assuming the mean value of the step frequency f s for the calculations of the dynamic load factor (in Eq. 7).

This was done for the SDOF footbridges listed in Table 3.

Table 3 Modal properties of bridges and bridge lengths (L)
Full size table

The combination of values of f 1, m 1, and L is believed to be fairly realistic for SDOF pin-supported footbridges, as m 1 and L drop with increase in f 1.

In terms of the deviations between outcomes of calculations of a 95, obtained by the two approaches, Table 4 shows the results. The difference between results is normalised to the result obtained assuming that the dynamic load factor would vary from one bridge crossing to the next.

Table 4 Deviations in terms of estimates of a 95
Full size table

The results signify that it may not be totally off to employ a simplified approach for computations, when it comes to settling on the dynamic load factor. Even though the simplified approach somewhat violates the stochastic nature of the problem, fairly reasonable results are obtained.

It is underlined that the investigations presented here do not reflect the uncertainty of the stochastic nature of the dynamic load factor. For such information see for instance [8].

3.2 Impact of Decisions Related to Modelling the Step Frequency

To this end of investigation different sets of assumptions related to modelling the stochastic nature of step frequency are considered.

The step frequency will be modelled as a random variable, but assumptions related to mean value and standard deviation need to be made.

For the investigations of this paper, the assumptions listed in Table 5 are considered.

Table 5 Mean values and standard deviations
Full size table

The models represent different proposals that can be found in literature [8].

Here, they are considered as input data for computing a 95 for different footbridges.

For the study, the bridges tabulated in Table 6 are considered.

Table 6 Modal properties of bridges and bridge lengths (L)
Full size table

The dynamic characteristics for the bridges do not exactly correspond to those in the previous study, but this is not of primary importance.

In terms of bridge response, and focusing on the response characteristic a 95, Table 7 summarises the results computed for footbridge A, B, and C. Values of a 95 are provided for the three different step frequency models.

Table 7 Acceleration quantile a 95
Full size table

For bridge A there is a maximum difference of (0.3093–0.1750=) 0.1343 m/s2 between results obtained for the three stochastic models for step frequency. If this value is normalised by the minimum number 0.1750 m/s2, one obtains a 77% difference in results for bridge A.

Doing the same calculations for bridge B and C results in 24% and 83% differences, respectively.

Hence, the choice of step frequency model assumed for computing a 95 has a relative high impact on the result.

4 Conclusion and Discussion

In the paper the influence of decisions as regards settling on a framework for pedestrian load models for evaluating footbridge response at the design stage was examined. Focus was on estimation of the footbridge acceleration response occurring at midspan of footbridges. The acceleration quantile a 95 (the acceleration level exceeded in 5% of the pedestrian crossings) was chosen for investigation.

For the investigations, different artificial SDOF and pin-supported bridges were considered so as to widen the perspective of conclusions.

One issue addressed was on ways for choosing the dynamic load amplification factor for a computational prediction of footbridge response. Another issue was on choosing parameters of a stochastic model for the step frequency of pedestrians for entering into the calculations.

Both choices might potentially affect the outcome of the predicted stochastic nature of bridge response and hence serviceability-limit-state evaluations for footbridges.

As for the dynamic load factor, different methods for extracting the main governing load amplification factor were examined. It turned out that a simplified technique not fully in accordance with the stochastic nature of the pedestrian traffic provided fairly reasonable results (errors in predictions of a 95 of maximum 20% for the investigated bridges).

Whereas the investigations in terms of the dynamic load factor focused on a technique for simpler processing of data, the investigations in terms of choosing parameters for a stochastic model for step frequency directly relate to actual uncertainties.

Solutions to this challenge are not provided here but it is interesting to notice that the calculations of this paper suggest up to 83% deviations in estimates of a 95 depending on which bridge is considered and which input parameters are chosen for modelling the stochastic nature of step frequencies.