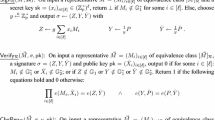Keywords

1 Introduction

Digital identity management systems become an increasingly important corner stone of digital workflows. Self-sovereign identity (SSI) systems such as SovrinFootnote 1 are of central interest as underlined by a recent push in the European Union for a cross-border SSI system.Footnote 2 But all these systems face a similar issue, namely that of efficient revocation. Regardless of whether they are built from signatures, group signatures or anonymous credentials, such systems have to consider mechanisms to revoke a user’s identity information. Especially for identity management systems with a focus on privacy, revocation may threaten those privacy guarantees. As such various forms of privacy-preserving revocations have emerged in the literature including approaches based on various forms of deny- or allowlists including [3, 13, 31] among many others.

One promising approach regarding efficiency is based on denylists (or allowlists) via cryptographic accumulators which were introduced by Benaloh and de Mare [11]. They allow one to accumulate a finite set \(\mathcal {X}\) into a succinct value called the accumulator. For every element in this set, one can efficiently compute a witness certifying its membership, and additionally, some accumulators also support efficient non-memberships witnesses. However, it should be computationally infeasible to find a membership witness for non-accumulated values and a non-membership witness for accumulated values, respectively. Accumulators facilitate privacy-preserving revocation mechanisms, which is especially relevant for privacy-friendly authentication mechanisms like group signatures and credentials. For a denylist approach, the issuing authority accumulates all revoked users and users prove in zero-knowledge that they know a non-membership witness for their credential. Alternatively, for a allowlist approach, the issuing authority accumulates all users and users then prove in zero-knowledge that they know a membership witness. As both approaches may involve large lists, efficient accumulator updates as well as efficient proofs are important for building an overall efficient system. For example, in Sovrin [37] and Hyperledger IndyFootnote 3 such an accumulator-based approach with allowlists following the ideas of [31] is used. Their credentials contain a unique revocation ID attribute, \(i_R\), which are accumulated. Each user obtains a membership witness proving that their \(i_R\) is contained in the accumulator. Once a credential is revoked, the corresponding \(i_R\) gets removed from the accumulator and all users have to update their proofs accordingly. The revoked user is no longer able to prove knowledge of a verifying witness and thus verification fails.

Accumulators are an important primitive and building block in many cryptographic protocols. In particular, Merkle trees [44] have seen many applications in both the cryptographic literature but also in practice. For example, they have been used to implement Certificate Transparency (CT) [38] where all issued certificates are publicly logged, i.e., accumulated. Accumulators also find application in credentials [13], ring, and group signatures [26, 39], anonymous cash [45], among many others. When looking at accumulators deployed in practice, many systems rely on Merkle trees. Most prominently we can observe this fact in CT. Even though new certificates are continuously added to the log, the system is designed around a Merkle tree that gets recomputed all the time instead of updating a dynamic public-key accumulator. The reason is two-fold: first, for dynamic accumulators to be efficiently computable, knowledge of the secret trapdoor used to generate the public parameters is required. Without this information, witness generation and accumulator updates are simply too slow for large sets (cf. [35]). Secondly, in this setting it is of paramount importance that the log servers do not have access to the secret trapdoor. Otherwise malicious servers would be able to present membership witnesses for every certificate even if it was not included in the log.

The latter issue can also be observed in other applications of public-key accumulators. The approaches due to Garman et al. [31] and the one used in Sovrin rely on the Strong-RSA and q-SDH accumulators, respectively. Both these accumulators have trapdoors: in the first case the factorization of the RSA modulus and in the second case a secret exponent. Therefore, the security of the system requires those trapdoors to stay secret. Hence, these protocols require to put significant trust in the parties generating the public parameters. If they would act maliciously and not delete the secret trapdoors, they would be able to break all these protocols in one way or another. To circumvent this problem, Sander [47] proposed a variant of an RSA-based accumulator from RSA moduli with unknown factorization. Alternatively, secure multi-party computation (MPC) protocols enable us to compute the public parameters and thereby replace the trusted third party. As long as a large enough subset of parties is honest, the secret trapdoor is not available to anyone. Over the years, efficient solutions for distributed parameter generation have emerged, e.g., for distributed RSA key generation [16, 17, 29], or distributed ECDSA key generation [41].

Based on the recent progress in efficient MPC protocols, we ask the following question: what if the parties kept their shares of the secret trapdoor? Are the algorithms of the public-key accumulators exploiting knowledge of the secret trapdoor faster if performed within an (maliciously-secure) MPC protocol than their variants relying only on the public parameters?

1.1 Our Techniques

We give a short overview of how our construction works which allows us to positively answer this question for accumulators in the discrete logarithm setting. Let us consider the accumulator based on the \(q\)-SDH assumption which is based on the fact that given powers \(g^{s^i} \in \mathbb {G} \) for all i up to q where \(s \in \mathbb {Z} _p\) is unknown, it is possible to evaluate polynomials \(f \in \mathbb {Z} _p[X]\) up to degree q at s in the exponent, i.e., \(g^{f(s)}\). This is done by taking the coefficients of the polynomial, i.e., \(f = \sum _{i=0}^q a_i X^i\), and computing \(g^{f(s)}\) as \( \prod _{i=0}^q (g^{s^i})^{a_i} \text {.} \) The accumulator is built by defining a polynomial with the elements as roots and evaluating this polynomial at \(s\) in the exponent. A witness is simply the corresponding factor canceled out, i.e., \(g^{f(s)(s-x)^{-1}}\). Verification of the witness is performed by checking whether the corresponding factor and the witness match \(g^{f(s)}\) using a pairing equation.

If \(s\) is known, all computations are more efficient: \(f(s)\) can be directly evaluated in \(\mathbb {Z} _p\) and the generation of the accumulator only requires one exponentiation in \(\mathbb {G} \). The same is true for the computation of the witness. For the latter, the asymptotic runtime is thereby reduced from \(\mathcal {O}(|\mathcal {X}|)\) to \(\mathcal {O}(1)\). This improvement comes at a cost: if \(s\) is known, witnesses for non-members can be produced.

On the other hand, if multiple parties first produce \(s\) in an additively secret-shared fashion, these parties can cooperate in a secret-sharing based MPC protocol. Thereby, all the computations can still benefit from the knowledge of \(s\). Indeed, the parties would compute their share of \(g^{f(s)}\) and \(g^{f(s)(s-x)^{-1}}\) respectively and thanks to the partial knowledge of \(s\) could still perform all operations – except the final exponentiation – in \(\mathbb {Z} _p\). Furthermore, all involved computations are generic enough to be instantiated with MPC protocols with different trust assumptions. These include the dishonest majority protocol SPDZ [21, 24] and honest majority threshold protocols based on Shamir secret sharing [48].

1.2 Our Contribution

Starting from the very recent treatment of accumulators in the UC model [15] by Baldimtsi et al. [4], we introduce the notion of (threshold) secret-shared accumulators. As the name suggests, it covers accumulators where the trapdoor is available in a (potentially full) threshold secret-shared fashion with multiple parties running the parameter generation as well as the algorithms that profit from the availability of the trapdoor. Since the MPC literature discusses security in the UC model, we also chose to do so for our accumulators.

Based on recent improvements on distributed key generation of discrete logarithms, we provide dynamic public-key accumulators without trusted setup. During the parameter generation, the involved parties keep their shares of the secret trapdoor. Consequently, we present MPC protocols secure in the semi-honest and the malicious security model, respectively, implementing the algorithms for accumulator generation, witness generation, and accumulator updates exploiting the shares of the secret trapdoor. Specifically, we give such protocols for q-SDH accumulators [25, 46], which can be build from dishonest-majority full-threshold protocols (e.g., SPDZ [21, 24]) and from honest-majority threshold MPC protocols (e.g., Shamir secret sharing [48]). In particular, our protocol enables updates to the accumulator independent of the size of the accumulated set. For increased efficiency, we consider this accumulator in bilinear groups of Type-3. Due to their structure, the construction nicely generalizes to any number of parties.

We provide a proof-of-concept implementation of our protocols in two MPC frameworks, MP-SPDZ [36] and FRESCO.Footnote 4 We evaluate the efficiency of our protocols and compare them to the performance of an implementation, having no access to the secret trapdoors as usual for the public-key accumulators. We evaluate our protocol in the LAN and WAN setting in the semi-honest and malicious security model for various choices of parties and accumulator sizes. For the latter, we choose sizes up to \(2^{14}\). Specifically, for the \(q\)-SDH accumulator, we observe the expected \(\mathcal {O}(1)\) runtimes for witness creation and accumulator updates, which cannot be achieved without access to the trapdoor. Notably, for the tested numbers of up to 5 parties, the MPC-enabled accumulator creation algorithms are faster for \(2^{10}\) elements in the LAN setting than its non-MPC counterpart (without access to the secret trapdoor). For \(2^{14}\) elements the algorithms are also faster in the WAN setting.

Finally, we discuss how our proposed MPC-based accumulators might impact revocation in distributed credential systems such as Sovrin [37]. In this scenario, the trust in the nodes run by the Sovrin foundation members can further be reduced. In addition, this approach generalizes to any accumulator-based revocation scheme and can be combined with threshold key management systems. We also discuss applications to CT and its privacy-preserving extension [35].

1.3 Related Work

When cryptographic protocols are deployed that require the setup of public parameters by a trusted third party, issues similar to those mentioned for public-key accumulators may arise. As discussed before, especially cryptocurrencies had to come up with ways to circumvent this problem for accumulators but also the common reference string (CRS) of zero-knowledge SNARKs [14]. Here, trust in the CRS is of paramount importance on the verifier side to prevent malicious provers from cheating. But also provers need to trust the CRS as otherwise zero-knowledge might not hold. We note that there are alternative approaches, namely subversion-resilient zk-SNARKS [9] to reduce the trust required in the CRS generator. Groth et al. [33] recently introduced the notion of an updatable CRS where first generic compilers [1] are available to lift any zk-SNARK to an updatable simulation sound extractable zk-SNARK. There the CRS can be updated and if the initial generation or one of the updates was done honestly, neither soundness nor zero-knowledge can be subverted. In the random oracle model (ROM), those considerations become less of a concern and the trust put into the CRS can be minimized, e.g., as done in the construction of STARKs [10].

Approaches that try to fix the issue directly in the formalization of accumulators and corresponding constructions have also been studied. For example, Lipmaa [42] proposed a modified model tailored to the hidden order group setting. In this model, the parameter setup is split into two algorithms, \(\mathsf {Setup}\) and \(\mathsf {Gen}\) where the adversary can control the trapdoors output by \(\mathsf {Setup}\), but can neither influence nor access the randomness used by \(\mathsf {Gen}\). However, constructions in this model so far have been provided using assumptions based on modules over Euclidean rings, and are not applicable to the efficient standard constructions we are interested in. More recently, Boneh et al. [12] revisited the RSA accumulator without trapdoor which allows the accumulator to be instantiated from unknown order groups without trusted setup such as class groups of quadratic imaginary orders [34] and hyperelliptic curves of genus 2 or 3 [27].

The area of secure multiparty computation has seen a lot of interest both in improving the MPC protocols itself to a wide range of practical applications. In particular, SPDZ [21, 24] has seen a lot of interest, improvements and extensions. This interest also led to multiple MPC frameworks, e.g., MP-SPDZ [36], FRESCO and SCALE-MAMBA,Footnote 5 enabling easy prototyping for researchers as well as developers. For practical applications of MPC, one can observe first MPC-based systems turned into products such as Unbound’s virtual hardware security model (HSM).Footnote 6 For such a virtual HSM, one essentially wants to provide distributed key generation [29] together with threshold signatures [22] allowing to replace a physical HSM. Similar techniques are also interesting for securing wallets for the use in cryptocurrencies, where especially protocols for ECDSA [32, 41] are of importance to secure the secret key material. Similarly, such protocols are also of interest for securing the secret key material of internet infrastructure such as DNSSEC [20]. Additionally, addressing privacy concerns in machine learning algorithms has become increasingly popular recently, with MPC protocols being one of the building blocks to achieve private classification and private model training as in [50] for example. Recent works [49] also started to generalize the algorithms that are used as parts of those protocols allowing group operations on elliptic curve groups with secret exponents or secret group elements.

2 Preliminaries

In this section, we introduce cryptographic primitives we use as building blocks. For notation and assumptions, we refer to the full version.

2.1 UC Security and ABB

In this paper, we mainly work in the UC model first introduced by Canetti [15]. The success of the UC model stems from its universal composition theorem, which, informally speaking, states that it is safe to use a secure protocol as a sub-protocol in a more complex one. This strong statement enables one to analyze and proof the security of involved protocols in a modular way, allowing us to build upon work that was already proven to be secure in the UC model.

The importance of the UC model for secure multiparty computation stems from the arithmetic black box (ABB) [23]. The ABB models a secure general-purpose computer in the UC model. It allows performing arithmetic operations on private inputs provided by the parties. The result of these operations is then revealed to all parties. Working with the ABB provides us with a tool of abstracting arithmetic operations, including addition and multiplication in fields.

2.2 SPDZ, Shamir, and Derived Protocols

Our protocols build upon SPDZ [21, 24] and Shamir secret sharing [48], concrete implementations of the abstract ABB. SPDZ itself is based on an additive secret-sharing over a finite field \(\mathbb {F} _{p}\) with information-theoretic MACs making the protocol statistically UC secure against an active adversary corrupting all but one player. On the other hand, Shamir secret sharing is a threshold sharing scheme where \(k\le n\) out of n parties are enough to evaluate the protocol correctly. Therefore, it is naturally robust against parties dropping out during the computation; however, it assumes an honest-majority amongst all parties for security. Shamir secret sharing can be made maliciously UC secure in the honest-majority setting using techniques from [18] or [40].

We will denote the ideal functionality of the online protocol of SPDZ and Shamir secret sharing by \(\mathcal {F}_{\text {Abb}}\). For an easy use of these protocols later in our accumulators, we give a high-level description of the functionality together with an intuitive notation. We assume that the computations are performed by n (or k) parties and we denote by \(\langle s\rangle \in \mathbb {F} _p\) a secret-shared value between the parties in a finite field with p elements, where p is prime. The ideal functionality \(\mathcal {F}_{\text {Abb}}\) provides us with the following basis operations: Addition \(\langle a+b\rangle \leftarrow \langle a\rangle +\langle b\rangle \) (can be computed locally), multiplication \(\langle ab\rangle \leftarrow \langle a\rangle \cdot \langle b\rangle \) (interactive 1-round protocol), sampling , and opening a share \(\langle a\rangle \). For convenience, we assume that we have also access to the inverse function \(\langle a^{-1}\rangle \). Computation of the inverse can be efficiently implemented using a standard form of masking as first done in [5]. Given an opening of \(\langle z\rangle = \langle r\cdot a\rangle \), the inverse of \(\langle a\rangle \) is then equal to \(z^{-1}\langle r\rangle \). However, there is a small failure probability if either a or r is zero. In our case, the field size is large enough that the probability of a random element being zero is negligible.

There is one additional sub-protocol which we will often need. Recent work [49] introduced protocols – in particular based on SPDZ – for group operations of elliptic curve groups supporting secret exponents and secret group elements. For this work, we only need the protocol for exponentiation of a public point with a secret exponent. Let \(\mathbb {G} \) be a cyclic group of prime order \(p\) and \(g\in \mathbb {G} \). Further, let \(\langle a\rangle \in \mathbb {F} _p\) be a secret-shared exponent.

  • \(\mathsf {Exp}_\mathbb {G} (\langle a\rangle ,g):\) The parties locally compute \(\langle g^a\rangle \leftarrow g^{\langle a\rangle }\).

Since the security proof of this sub-protocol in [49] does not use any exclusive property of an elliptic curve group, it applies to any cyclic group of prime order.

All protocols discussed so far are secure in the UC model, making them safe to use in our accumulators as sub-protocols. Therefore, we will refer to their ideal functionality as \(\mathcal {F}_{\text {ABB+}}\). As a result, our protocols become secure in the UC model as long as we do not reveal any intermediate values.

2.3 Accumulators

We rely on the formalization of accumulators by Derler et al. [25]. We recall definitions of static and dynamic accumulators in the full version.

figure a

2.4 Pairing-Based Accumulator

We recall the q-SDH-based accumulator from [25], which is based on the accumulator by Nguyen [46]. The idea here is to encode the accumulated elements in a polynomial. This polynomial is then evaluated for a fixed element and the result is randomized to obtain the accumulator. A witness consists of the evaluation of the same polynomial with the term corresponding to the respective element cancelled out. For verification, a pairing evaluation is used to check whether the polynomial encoded in the witness is a factor of the one encoded in the accumulator. As it is typically more efficient to work with bilinear groups of Type-3 [30], we state the accumulator as depicted in Scheme 1 in this setting. Correctness is clear, except for the \(\mathsf {WitUpdate}\) subroutine: To update witness \(\mathsf {wit}_{x_i}\) of the element \(x_i\) after the element x was added to the accumulator \(\varLambda _{\mathcal {X}}\) to create the new accumulator \(\varLambda _{\mathcal {X}'} = \varLambda _{\mathcal {X}}^{(x + s)}\), one computes:

$$\begin{aligned} \varLambda _\mathcal {X}\cdot \mathsf {wit}_{x_i}^{(x-x_i)}&= \varLambda _\mathcal {X}^{(x_i+s)\cdot (x_i + s)^{-1}}\cdot \varLambda _\mathcal {X}^{(x-x_i)\cdot (x_i + s)^{-1}} \\&= \varLambda _\mathcal {X}^{(x+s)\cdot (x_i + s)^{-1}} = \varLambda _\mathcal {X'}^{(x_i + s)^{-1}} \end{aligned}$$

which results in the desired updated witness. Similar, if the element x gets removed instead, one computes the following to get the desired witness:

$$\begin{aligned} (\varLambda _{\mathcal {X}'}^{-1}\cdot \mathsf {wit}_{x_i})^{(x-x_i)^{-1}}&= \varLambda _{\mathcal {X}'}^{-(x_i+s)\cdot (x_i+s)^{-1}\cdot (x-x_i)^{-1}} \cdot \varLambda _{\mathcal {X}'}^{(x+s)\cdot (x_i+s)^{-1}\cdot (x-x_i)^{-1}} \\&= \varLambda _{\mathcal {X}'}^{(x_i + s)^{-1}\cdot (x-x_i)^{-1}\cdot (x-x_i + s -s)} = \varLambda _\mathcal {X'}^{(x_i + s)^{-1}} \end{aligned}$$

The proof of collision freeness follows from the q-SDH assumption. For completeness, we still restate the theorem from [25] adopted to the Type-3 setting. For the proof, we refer to the full version.

Theorem 1

If the q-SDH assumption holds, then Scheme 1 is collision-free.

Remark 1

Note that for support of arbitrary accumulation domains, the accumulator requires a suitable hash function mapping to \(\mathbb {Z} _p^*\). For the MPC-based accumulators that we will define later, it is clear that the hash function can be evaluated in public. For simplicity, we omit the hash function in our discussion.

2.5 UC Secure Accumulators

Only recently, Baldimtsi et al. [4] formalized the security of accumulators in the UC framework. Interestingly, they showed, that any correct and collision-free standard accumulator is automatically UC secure. We, however, want to note, that their definitions of accumulators are slightly different then the framework by Derler et al. (which we are using). Hence, we adapt the ideal functionality \(\mathcal {F}_{\text {Acc}}\) from [4] to match our setting: First our ideal functionality \(\mathcal {F}_{\text {Acc}}\) consists of two more sub-functionalities. This is due to a separation of the algorithms responsible for the evaluation, addition, and deletion. Secondly, our \(\mathcal {F}_{\text {Acc}}\) is simplified to our purpose, whereas \(\mathcal {F}_{\text {Acc}}\) from Baldimtsi et al. is in their words “an entire menu of functionalities covering all different types of accumulators”. Thirdly, we added identity checks to sub-functionalities (where necessary) to be consistent with the given definitions of accumulators.

The resulting ideal functionality can be found in the full version. Note that the ideal functionality has up to three parties. First, the party which holds the set \(\mathcal {X}\) is the accumulator manager \(\mathcal {AM}\), responsible for the algorithms \(\mathsf {Gen},\mathsf {Eval},\mathsf {WitCreate},\mathsf {Add}\) and \(\mathsf {Delete}\). The second party \(\mathcal {H}\) owns a witness and is interested in keeping it updated and for this reason, performs the algorithm \(\mathsf {WitUpdate}\). The last party \(\mathcal {V}\) can be seen as an external party. \(\mathcal {V}\) is only able to use \(\mathsf {Verify}\) to check the membership of an element in the accumulated set.

In the following theorem we adapt the proof from [4] to our setting:

Theorem 2

If \(\varPi _{Acc}=(\mathsf {Gen},\mathsf {Eval},\mathsf {WitCreate},\mathsf {Verify},\mathsf {Add},\mathsf {Delete},\mathsf {WitUpdate})\) is a correct and collision-free dynamic accumulator with deterministic \(\mathsf {Verify}\), then \(\varPi _{Acc}\) UC emulates \(\mathcal {F}_{\text {Acc}}\).

For the proof we refer to the full version. As a direct consequence of Theorems 1 and 2, the accumulator from Scheme 1 is also secure in the UC model of [4] since it is correct and collision-free:

Corollary 1

Scheme 1 emulates \(\mathcal {F}_{\text {Acc}}\) in the UC model.

3 Multi-Party Public-Key Accumulators

With the building blocks in place, we are now able to go into the details of our construction. We first present the formal notion of (threshold) secret-shared accumulators, their ideal functionality, and then present our constructions.

For the syntax of the MPC-based accumulator, which we dub (threshold) secret-shared accumulator, we use the bracket notation \(\langle s\rangle \) from Sect. 2.2 to denote a secret shared value. If we want to explicitly highlight the different shares, we write \(\langle s\rangle =(s_1,\dots ,s_n)\), where the share \(s_i\) belongs to a party \(P_i\). We base the definition on the framework of Derler et al. [25], where our algorithms behave in the same way, but instead of taking an optional secret trapdoor, the algorithms are given shares of the secret as input. Consequently, \(\mathsf {Gen}\) outputs shares of the secret trapdoor instead of the secret key. The static version of the accumulator is defined as follows:

Definition 1

(Static (Threshold) Secret-Shared Accumulator). Let us assume that we have a (threshold) secret sharing-scheme. A static (threshold) secret-shared accumulator for \(n\in \mathbb {N} \) parties \(P_1,\dots ,P_n\) is a tuple of PPT algorithms \((\mathsf {Gen}, \mathsf {Eval}, \mathsf {WitCreate}, \mathsf {Verify})\) which are defined as follows:

  • \(\mathsf {Gen}(1^\kappa , q):\) This algorithm takes a security parameter \(\kappa \) and a parameter q. If \(q \ne \infty \), then q is an upper bound on the number of elements to be accumulated. It returns a key pair \((\mathsf {sk}_{\varLambda }^i,\mathsf {pk}_{\varLambda })\) to each party \(P_i\) such that \(\mathsf {sk}_{\varLambda }=\mathsf {Open}(\mathsf {sk}_{\varLambda }^1,\dots ,\mathsf {sk}_{\varLambda }^n)\), denoted by \(\langle \mathsf {sk}_{\varLambda }\rangle \). We assume that the accumulator public key \(\mathsf {pk}_\varLambda \) implicitly defines the accumulation domain \(\mathsf {D}_\varLambda \).

  • \(\mathsf {Eval}((\langle \mathsf {sk}_{\varLambda }\rangle , \mathsf {pk}_{\varLambda }), \mathcal {X}):\) This algorithm takes a secret-shared private key \(\langle \mathsf {sk}_{\varLambda }\rangle \) a public key \(\mathsf {pk}_{\varLambda }\) and a set \(\mathcal {X}\) to be accumulated and returns an accumulator \(\varLambda _{\mathcal {X}}\) together with some auxiliary information \(\mathsf aux\) to every party \(P_i\).

  • \(\mathsf {WitCreate}((\langle \mathsf {sk}_{\varLambda }\rangle , \mathsf {pk}_{\varLambda }), \varLambda _{\mathcal {X}}, \mathsf {aux}, x):\) This algorithm takes a secret-shared private key \(\langle \mathsf {sk}_{\varLambda }\rangle \) a public key \(\mathsf {pk}_{\varLambda }\), an accumulator \(\varLambda _{\mathcal {X}}\), auxiliary information \(\mathsf aux\) and a value x. It returns \(\bot \), if \(x\notin \mathcal {X}\), and a witness \(\mathsf {wit}_{x}\) for x otherwise to every party \(P_i\).

  • \(\mathsf {Verify}(\mathsf {pk}_\varLambda , \varLambda _{\mathcal {X}}, \mathsf {wit}_{x}, x):\) This algorithm takes a public key \(\mathsf {pk}_{\varLambda }\), an accumulator \(\varLambda _{\mathcal {X}}\), a witness \(\mathsf {wit}_{x}\) and a value x. It returns \(1\) if \(\mathsf {wit}_{x}\) is a witness for \(x\in \mathcal {X}\) and \(0\) otherwise.

In analogy to the non-interactive case, dynamic accumulators provide additional algorithms to add elements to the accumulator and remove elements from it, respectively, and update already existing witnesses accordingly.

Definition 2

(Dynamic (Threshold) Secret-Shared Accumulator). A dynamic (threshold) secret-shared accumulator is a static (threshold) secret-shared accumulator with an additional tuple of PPT algorithms \((\mathsf {Add}, \mathsf {Delete},\mathsf {WitUpdate})\) which are defined as follows:

  • \(\mathsf {Add}((\langle \mathsf {sk}_{\varLambda }\rangle , \mathsf {pk}_{\varLambda }), \varLambda _{\mathcal {X}}, \mathsf {aux}, x):\) This algorithm takes a secret-shared private key \(\langle \mathsf {sk}_{\varLambda }\rangle \) a public key \(\mathsf {pk}_{\varLambda }\), an accumulator \(\varLambda _{\mathcal {X}}\), auxiliary information \(\mathsf {aux}\), as well as an element x to be added. If \(x \in \mathcal {X}\), it returns \(\bot \) to every party \(P_i\). Otherwise, it returns the updated accumulator \(\varLambda _{\mathcal {X}'}\) with \(\mathcal {X}' \leftarrow \mathcal {X}\cup \{ x \}\) and updated auxiliary information \(\mathsf {aux}'\) to every party \(P_i\).

  • \(\mathsf {Delete}((\langle \mathsf {sk}_{\varLambda }\rangle , \mathsf {pk}_{\varLambda }), \varLambda _{\mathcal {X}}, \mathsf {aux}, x):\) This algorithm takes a secret-shared private key \(\langle \mathsf {sk}_{\varLambda }\rangle \) a public key \(\mathsf {pk}_{\varLambda }\), an accumulator \(\varLambda _{\mathcal {X}}\), auxiliary information \(\mathsf {aux}\), as well as an element x to be added. If \(x \not \in \mathcal {X}\), it returns \(\bot \) to every party \(P_i\). Otherwise, it returns the updated accumulator \(\varLambda _{\mathcal {X}'}\) with \(\mathcal {X}' \leftarrow \mathcal {X}\setminus \{ x \}\) and updated auxiliary information \(\mathsf {aux}'\) to every party \(P_i\).

  • \(\mathsf {WitUpdate}((\langle \mathsf {sk}_{\varLambda }\rangle , \mathsf {pk}_{\varLambda }), \mathsf {wit}_{x_i}, \mathsf {aux}, x):\) This algorithm takes a secret-shared private key \(\langle \mathsf {sk}_{\varLambda }\rangle \) a public key \(\mathsf {pk}_{\varLambda }\), a witness \(\mathsf {wit}_{x_i}\) to be updated, auxiliary information \(\mathsf aux\) and an element x which was added to/deleted from the accumulator, where \(\mathsf {aux}\) indicates addition or deletion. It returns an updated witness \(\mathsf {wit}'_{x_i}\) on success and \(\bot \) otherwise to every party \(P_i\).

Correctness and collision-freeness naturally translate from the non-interactive accumulators to the (threshold) secret-shared ones.

For our case, the ideal functionality for (threshold) secret-shared accumulators, dubbed \(\mathcal {F}_{\text {MPC-Acc}}\) is more interesting. \(\mathcal {F}_{\text {MPC-Acc}}\) is very similar to \(\mathcal {F}_{\text {Acc}}\) and can be found in the full version. The only difference in describing the ideal functionality for accumulators in the MPC setting arises from the fact that we now have not only one accumulator manager but n, denoted by \(\mathcal {AM}_1,\dots ,\mathcal {AM}_n\). More concretely, whenever a sub-functionality of \(\mathcal {F}_{\text {MPC-Acc}}\) – that makes use of the secret key – gets a request from a manager identity \(\mathcal {AM}_i\), it now also gets a participation message from the other managers identities \(A_j\) for \(j\ne i\). Furthermore, the accumulator managers take the role of the witness holder. The party \(\mathcal {V}\), however, stays unchanged.

3.1 Dynamic (Threshold) Secret-Shared Accumulator from the \(q\)-SDH Assumption

For the generation of public parameters \(\mathsf {Gen}\), we can rely on already established methods to produce ECDSA key pairs and exponentiations with secret exponents, respectively. These methods can directly be applied to the accumulators. Taking the \(q\)-SDH accumulator as an example, the first step is to sample the secret scalar \(s \in \mathbb {Z} _p\). Intuitively, each party samples its own share \(s_i\) and the secret trapdoor \(s\) would then be \(s = \mathsf {Open}(s_1, \dots , s_n)\). The next step, the calculation of the basis elements \(g^{s^j}\) for \(j=1, \ldots , q\), is optional, but can be performed to provide public parameters, that are useful even to parties without knowledge of \(s\). All of these elements can be computed using \(\mathsf {Exp}_\mathbb {G} \) and the secret-shared \(s\), respectively its powers. For the accumulator evaluation, \(\mathsf {Eval}\), the parties first sample their shares of \(r\). Then, they jointly compute shares of \(r \cdot f(s)\) using their shares of \(r\) and \(s\). The so-obtained exponent and \(\mathsf {Exp}_\mathbb {G} \) produce the final result.

For witness creation, \(\mathsf {WitCreate}\), it gets more interesting. Of course, one could simply run \(\mathsf {Eval}\) again with one element removed from the set. In this case, we can do better, though. The difference between the accumulator and a witness is that in the latter, one factor of the polynomial is canceled. Since \(s\) is available, it is thus possible to cancel this factor without recomputing the polynomial from the start. Indeed, to compute the witness for an element \(x\), we can compute \((s + x)^{-1}\) and then apply that inverse using \(\mathsf {Exp}_\mathbb {G} \) to the accumulator to get the witness. Note though, that before the parties perform this step, they need to check if \(x\) is actually contained in \(\mathcal {X}\). Otherwise, they would produce a membership witness for a non-member. In that case, the verification would check whether \(f(s) (s+x)^{-1}(s+x)\) matches \(f(s)\), which of course also holds even if \(s+x\) is not a factor of \(f(s)\). In contrast, when performing \(\mathsf {Eval}\) with only the publicly available information, this issue does not occur since there the witness will not verify. \(\mathsf {Add}\) and \(\mathsf {Delete}\) can be implemented in a similar manner. When adding an element to the accumulator, the polynomial is extended by one factor. Removal of an element requires that one factor is canceled. Both operations can be performed by first computing the factor using the shares of \(s\) and then running \(\mathsf {Exp}_\mathbb {G} \).

Now, we present the MPC version of the \(q\)-SDH accumulator in Scheme 2 following the intuition outlined above. Note, that the algorithm for \(\mathsf {WitUpdate}\) is unlikely to be faster than its non-MPC version from Scheme 1. Indeed, the non-MPC version requires only exponentiations in \(\mathbb {G} _1\) and a multiplication without the knowledge of the secret trapdoor. We provide the version using the trapdoor for completeness but will use the non-MPC version of the algorithm in practical implementations. Note further that we let \(\mathsf {Gen}\) choose the bilinear group \(\mathsf {BG}\), but this group can already be fixed a priori.

figure b

Theorem 3

Scheme 2 UC emulates \(\mathcal {F}_{\text {Acc-MPC}}\) in the \(\mathcal {F}_{\text {ABB+}}\)-hybrid model.

Proof

At this point, we make use of the UC model. Informally speaking, accumulators are UC secure, and SPDZ, Shamir secret sharing, and the derived operations UC emulate \(\mathcal {F}_{\text {ABB+}}\). Therefore, according to the universal composition theorem, the use of these MPC protocols in the accumulator Scheme 2 can be done without losing UC security. For a better understanding, we begin by showing the desired accumulator properties for Scheme 2.

The proof of the correctness follows directly from the correctness proof from Scheme 1 for the case where the secret key is known. Collision-freeness is also derived from the non-interactive q-SDH accumulator. (It is true that now each party has a share of the trapdoor, but without the other shares no party can create a valid witness.) Since \(\mathsf {Verify}\) is obviously deterministic, Scheme 2 fulfills all necessary assumption of Theorem 2. After applying Theorem 2, we get a simulator \(\mathcal {S}_{Acc}\) interacting with the ideal functionality \(\mathcal {F}_{\text {Acc}}\). Since we now also have to simulate the non-interactive sub-protocols, we have to extend \(\mathcal {S}_{Acc}\). We construct \(\mathcal {S}_{\text {Acc-MPC}}\) by building upon \(\mathcal {S}_{\text {Acc}}\) and in addition internally simulate \(\mathcal {F}_{\text {ABB+}}\). As described in Sect. 2.2, the MPC protocols used in the above algorithms are all secure in the UC model. Since we do not open any secret-shared values besides uniformly random elements and the output or values that can be immediately derived from the output, the algorithms are secure due to the universal composition theorem.    \(\square \)

Remark 2

In \(\mathsf {Gen}\) of Scheme 2 we explicitly do not compute \(h_i \leftarrow g_1^{s^i}\). Hence, using \(\mathsf {Eval}\) without access to s is not possible. But the public key is significantly smaller and so is the runtime of the \(\mathsf {Gen}\) algorithm. If, however, these values are needed to support a non-secret-shared \(\mathsf {Eval}\), one can modify \(\mathsf {Gen}\) to also compute the necessary values enabling trade-offs between an efficient \(\mathsf {Eval}\) and an inefficient \(\mathsf {Gen}\). Updates to this accumulator then still profit from the efficiency of the secret shared trapdoor. Additionally, q gives an upper bound on the size of the accumulated sets, and thus needs to be considered in the selection of the curves even though the powers of \(g_1\) are not placed in the public key.

3.2 SPDZ vs. Shamir Secret Sharing

In this section, we want to compare two MPC protocols on which our MPC-\(q\)-SDH Accumulator can be based on, namely SPDZ and Shamir secret sharing. Both protocols allow us to keep shares of the secret trapdoor and improve performance compared to the keyless \(q\)-SDH Accumulator. However, in relying on these protocols for security, the trust assumptions of the MPC-\(q\)-SDH Accumulator also have to include the underlying protocols’ trust-assumptions.

SPDZ is a full-threshold dishonest-majority protocol that protects against \(n-1\) corrupted parties. Therefore, an honest party will always detect malicious behavior. However, full-threshold schemes are not robust; if one party fails to supply its shares, the computation always fails.

On the contrary, Shamir secret sharing is an honest-majority threshold protocol. It is more robust than SPDZ since it allows \(k \le \frac{n-1}{2}\) corrupted parties while still being capable of providing correct results. This also means, if some parties (k \(\le \frac{n-1}{2}\)) fail to provide their shares, the other parties can still compute the correct results without them. Thus, no accumulator manager on its own is a single point of failure. However, if more than k parties are corrupted, the adversaries can reconstruct the secret trapdoor and, therefore, compromise the security of our MPC-\(q\)-SDH Accumulator.

4 Implementation and Performance Evaluation

We implemented the proposed dynamic (threshold) secret-shared accumulator from \(q\)-SDH and evaluated it against small to large sets.Footnote 7 Our primary implementations are based on SPDZ with OT-based preprocessing and Shamir secret sharing in the MP-SPDZ [36]Footnote 8 framework. However, to demonstrate the usability of our accumulator, we additionally build an implementation in the malicious security setting with dishonest-majority based on the FRESCO framework. We discuss the benchmarks for the MP-SPDZ implementation in this section. For a discussion of the FRESCO benchmarks we refer the reader to the full version.

Remark 3

We want to note, that in our benchmarks we test the performance of the MPC variant of \(\mathsf {WitUpdate}\) from Scheme 2, even though in practice the non-MPC variant from Scheme 1 should be used.

MP-SPDZ implements the SPDZ protocol with various extensions, as well as semi-honest and malicious variants of Shamir secret sharing [18, 19, 40]. For pairing and elliptic curve group operations, we rely on relicFootnote 9 and integrate \(\mathsf {Exp}_{\mathbb {G}}\), Output-\(\mathbb {G} \), and the corresponding operations to update the MAC described in [49] into MP-SPDZ. We use the pairing friendly BLS12-381 curve [7], which provides around 120 bit of security following recent estimates [6]. For completeness, we also implemented the q-SDH accumulator from Scheme 1 and a Merkle-tree accumulator using SHA-256. This enables us to compare the performance in cases where the secret trapdoors are available in the MPC case and when they are not. In Table 1, we present the numbers for various sizes of accumulated sets.

Table 1. Performance of the accumulator algorithms without access to the secret trapdoors. Time in milliseconds averaged over 100 executions.
Full size table

The evaluation of the MPC protocols was performed on a cluster with a Xeon E5-4669v4 CPU, where each party was assigned only 1 core. The hosts were connected via a 1 Gbit/s LAN network, and an average round-trip time of \({<}1\) ms. For the WAN setting, a network with a round-trip time of \(100\) ms and a bandwidth of 100 Mbit/s was simulated. We provide benchmarks for both preprocessing and online phases of the MPC protocols, where the cost of the preprocessing phase is determined by the number of shared multiplications, whereas the performance of the online phase is proportional to the multiplicative depth of the circuit and the number of openings.

4.1 Evaluation of MPC-\(q\)-SDH

In the offline phase of the implemented MPC protocols, the required Beaver triples [8] for shared multiplication and the pre-shared random values are generated. A shared inverse operation requires one multiplication and one shared random value. In Table 2, we list the number of triples required for each operation for the MPC-\(q\)-SDH accumulator. Except for \(\mathsf {Eval}\)  they require a constant number of multiplications and inverse operations and, therefore, a constant number of Beaver triples and shared random elements. In \(\mathsf {Eval}\), the number of required Beaver triples is determined by \(|\mathcal {X}|\). Furthermore, Table 2 lists the number of opening rounds (including openings in multiplications, excluding MAC-checks) of the online phase of the MPC-\(q\)-SDH accumulator allowing one to calculate the number of communication rounds for different sharing schemes.

As discussed in Remark 2, \(\mathsf {Gen}\) is not producing the public parameters \(h_i\). If \(\mathsf {Eval}\) without MPC is desired, the time and communication of \(\mathsf {Eval}\) for the respective set sizes should be added to the time and communication of \(\mathsf {Gen}\) to obtain an estimate of its performance.

Table 2. Number of Beaver triples, shared random values, and opening rounds required by MPC-\(q\)-SDH.
Full size table

Dishonest-Majority Based on SPDZ. Table 3 compares the offline performance of the MPC-\(q\)-SDH accumulator based on SPDZ in different settings. We give both timings for the accumulation of \(|\mathcal {X}|\) elements in \(\mathsf {Eval}\) and the necessary pre-computation for a single inversion, which is used in several other operations (e.g., \(\mathsf {WitCreate}\)). Additionally we also give the time for pre-computing a single random element, which is required to generate the authenticated share of the secret-key in \(\mathsf {Eval}\). Further note that batching the generation of many triples together like for the \(\mathsf {Eval}\) phase is more efficient in practice than producing a single triple and as these triples are not dependent on the input, all parties can continuously generate triples in the background for later use in the online phase.

Table 3. Offline phase performance of different steps of the MPC-\(q\)-SDH accumulator with access to the secret trapdoor based on MP-SPDZ. Time in milliseconds.
Full size table

In Table 4, we present the online performance of our MPC-\(q\)-SDH accumulator based on SPDZ for different set sizes, parties, security settings, and network settings. It can clearly be seen, that – except for the \(\mathsf {Eval}\) operation – the runtime of each operation is independent of the set size. In other words, after an initial accumulation of a given set, every other operation has constant time. In comparison, the runtime of the non-MPC accumulators without access to the secret trapdoor, as depicted in Table 1, depends on the size of the accumulated set. Our MPC-accumulator outperforms the non-MPC q-SDH accumulators the larger the accumulated set gets. In the LAN setting MPC-\(q\)-SDH’s \(\mathsf {Eval}\) is faster than the non-MPC version for all benchmarked players, even in the WAN settings it outperforms the non-MPC version in the two player case. For \(2^{14}\) elements, it is even faster for all benchmarked players in all settings, including the WAN setting. In any case, the witnesses have constant size contrary to the \(\log _2(|\mathcal {X}|)\) sized witnesses of the Merkle-tree accumulator.

The numbers for the evaluation of the online phase in the WAN setting are also presented in Table 4. The overhead that can be observed compared to the LAN setting is influenced by the communication cost. Since our implementation implements all multiplications in \(\mathsf {Eval}\) in a depth-optimized tree-like fashion, the overhead from switching to a WAN setting is not too severe.

On the first look, one can observe an irregularity in our benchmarks. More specifically, notice that for four or more parties, the maliciously secure evaluation of the \(\mathsf {Eval}\) online phase is consistently faster than the semi-honest evaluation of the same phase. However, this is a direct consequence of a difference in how MP-SPDZ handles the communication in those security models, where communication is handled in a non-synchronized send-to-all approach in the malicious setting and a synchronized broadcast approach in the semi-honest setting. The synchronization in the latter case scales worse for more parties and, therefore, introduces some additional delays.

Table 4. Online phase performance of the MPC-\(q\)-SDH accumulator with access to the secret trapdoor based on SPDZ implemented in MP-SPDZ, for both the LAN and WAN settings with n parties. Time in milliseconds averaged over 50 executions.
Full size table
Table 5. Communication cost (in kB per party) of the MPC-\(q\)-SDH accumulator with access to the secret trapdoor based on SPDZ implemented in MP-SPDZ.
Full size table

Finally, Table 5 depicts the size of the communication between the parties for both offline and online phases. The communication of \(\mathsf {Eval}\) has to account for a number of multiplications dependent on \(\mathcal {X}\) and therefore scales linearly with its size. As we already observed for the runtime of MPC-\(q\)-SDH, also the communication of \(\mathsf {WitCreate}\), \(\mathsf {Add}\), \(\mathsf {Delete}\) and \(\mathsf {WitUpdate}\) is independent of the size of the accumulated set, and additionally less than 200 kB for all algorithms. Combined with the analysis of the runtime, we conclude that the performance of the operations that might be performed multiple times per accumulator is very efficient in both runtime and communication. When compared to the performance of the non-MPC accumulators in Table 1, we see that the performance of operations that benefit from access to the secret trapdoor are multiple orders of magnitude faster in the MPC accumulators and, in the LAN setting, even come close to the performance of the standard Merkle-tree accumulator, for both the semi-honest and malicious variant.

Honest-Majority Threshold Sharing based on Shamir Secret Sharing. In this section, we discuss the benchmarks of our implementation based on Shamir secret sharing. MP-SPDZ implements semi-honest Shamir secret sharing based on [19] and a maliciously secure variant following [40]Footnote 10. In Table 6, we present the offline phase runtime, in Table 7 we show the runtime of the online phase, and in Table 8 we depict the size of the communication between the parties for the 3-party case.

Table 6. Offline phase performance of different steps of the MPC-\(q\)-SDH accumulator with access to the secret trapdoor in the semi-honest (SH) and malicious threshold setting implemented in MP-SPDZ. Time in milliseconds.
Full size table

The most expensive part of the SPDZ offline phase is creating the Beaver triples required for the \(\mathsf {Eval}\) operation. As Table 6 shows, this step is several orders of magnitudes cheaper in the Shamir-based implementation. This is especially true in the semi-honest setting, in which no Beaver triples are required in the Shamir-based implementation. The offline runtime of the other operations is similar to the SPDZ-based implementations.

The Shamir-based implementation’s online runtime is slightly cheaper than the runtime of the SPDZ-based implementation, except for the \(\mathsf {Eval}\) operation. However, the difference in runtime of the \(\mathsf {Eval}\) operation is also not significant, especially when considering the trade for the much cheaper offline phase.

Table 7. Online phase performance of the MPC-\(q\)-SDH accumulator with access to the secret trapdoor in the threshold setting implemented in MP-SPDZ, for both the LAN and WAN settings with n parties. Time in milliseconds averaged over 50 executions.
Full size table

Similar behavior can be seen for the communication cost, as depicted in Table 8. Offline communication is several orders of magnitude smaller in the Shamir-based implementation than in SPDZ, while online communication is similar to the SPDZ based version. Only the \(\mathsf {Eval}\) operation requires about twice as much online communication in the Shamir-based implementation. To summarize, our honest-majority threshold implementation based on Shamir secret sharing provides much better offline phase performance, with similar online performance compared to our dishonest majority full-threshold implementation.

Table 8. Communication cost (in kB per party) of the MPC-\(q\)-SDH accumulator in the 3-party threshold setting implemented in MP-SPDZ.
Full size table

4.2 Further Improvement

The maliciously secure MPC protocols we use in this work delay the MAC check to the output phase after executing the \(\mathsf {Open}\) subroutine. This means, it is possible for intermediate results to be wrong due to tampering of an attacker; however, since honest parties only reveal randomized values during the openings in a multiplication, no information about secret values can be gained by attackers.

Similar to threshold signature schemes [20, 28, 32], the protocols can be optimized by skipping the MAC checks at the end of \(\mathsf {WitCreate}\), \(\mathsf {Add}\), \(\mathsf {Delete}\), and \(\mathsf {WitUpdate}\) and use the \(\mathsf {Verify}\) step of the accumulator to check for correctness instead. The only feasible attack on this optimization is to produce invalid accumulators/witnesses without leaking information on the secret trapdoor; however, false output values can be detected during verification. Therefore, we can execute the semi-honest online phase and call \(\mathsf {Verify}\) at the end, while still protecting against malicious parties. This trades the extra round of communication in the MAC check for an evaluation of a bilinear pairing (\(\approx 10\,\)ms on our benchmark platform) which results in a further speedup, especially in the WAN-setting.

5 Applications

5.1 Credential Revocation in Distributed Credential Systems

As first application of MPC-based accumulators, we focus on distributed credential systems [31], and in particular, on the implementation in Sovrin [37]. In general, anonymous credentials provide a mechanism for making identity assertions while maintaining privacy, yet, in classical, non-distributed systems require a trusted credential issuer. This central issuer, however, is both a single point of failure and a target for compromise and can make it challenging to deploy such a system. In a distributed credential system, on the other hand, this trusted credential issuer is eliminated, e.g., by using distributed ledgers.

We shortly recall how Sovrin implements revocation. When issuing a credential, every user gets a unique revocation identifier \(i_R\). All valid revocation IDs are accumulated using a \(q\)-SDH accumulator which is published. Additionally, the users obtains a witness certifying membership of its \(i_R\) in the accumulator. Whenever a user shows their credential, they have to prove that they know this witness for their \(i_R\) with respect to the published accumulator. When a new user joins, the accumulator has to be updated. Consequently, all the witnesses have to be updated as well, as otherwise they would no longer be able to provide a valid proof. Similar, in the case that a user is revoked and thus removed from the accumulator, all other users have to update their witnesses accordingly. Also, the verifiers always have to check for updated accumulators.

Now, recall that the \(q\)-SDH accumulator supports all required operations without needing access to the trapdoor. Hence, all operations can be performed and, especially, the users can update their witnesses on their own if the corresponding \(i_R\)s are published on the ledger. While functionality-wise all operations are supported, performance-wise a large number of users becomes an issue. With potentially millions to billions of users, adding and deleting members from the accumulator becomes increasingly expensive (cf. Table 1). Hence, at a certain size, having access to the trapdoor would be beneficial. But, on the other side, generating membership witnesses for non-members would then become possible.

The latter is also an issue during the setup of the system. Trusting one third party to generate the public parameters of the accumulator might be undesired in a distributed system as in this case. The special structure of the Sovrin ecosystem with their semi-trusted foundation members, however, naturally fits to our multi-party accumulator. First, the foundation members can setup the public parameters in a distributed manner. Secondly, as all of them have shares of the trapdoor, they can also run the updates of the accumulator using the MPC-\(q\)-SDH-accumulator. Additionally, using a threshold secret sharing scheme can add robustness against foundation members failing to provide their shares for computations. The change to this accumulator is completely transparent to the clients and verifiers and no changes are required there. Furthermore, the \(\mathsf {Verify}\) step of the MPC-\(q\)-SDH-accumulator is equal to the \(\mathsf {Verify}\) operation of the non-MPC \(q\)-SDH-accumulator. Therefore, the same efficient zero-knowledge proofs [2] can be used to prove knowledge of a witness without revealing it. These proofs are significantly more efficient then proving witnesses of a Merkle-Tree-accumulator, even when SNARK-friendly hash functions are used.

5.2 Privacy-Preserving Certificate-Transparency Logs

We finally look at the application of accumulators in the CT ecosystem. Certificate Authorities request the inclusion of certificates in the log whenever they sign a new certificate. Once the certificate was included in the log, auditors can check the consistency of this log. Additionally, TLS clients also verify whether all certificates that they obtain were actually logged, thereby ensuring that log servers do not hand out promises of certificate inclusion without following through. Technically, the CT log is realized as a Merkle-tree accumulator containing all certificates. As certificates need to be added continuously, it is made dynamic by simply recalculating the root hash and all the proofs. Functionality wise, dynamic accumulators would perfectly fit this use-case. However, their real-world performance without secret trapdoors is not good enough – recalculating hash trees is just more efficient. Knowledge of the secret trapdoors would however be catastrophic for this application, as the guarantees of the whole system break down: log servers could produce witnesses for any certificate they get queried on, even if it was never submitted to the log servers for inclusion.

In the CT ecosystem, the clients need to contact the log servers for the inclusion proof, and therefore verifying certificates has negative privacy implications, as this query reveals the browsing behavior of the client to the log server. Based on previous work by Lueks and Goldberg [43], Kales et al. [35] proposed to rethink retrieval of the inclusion proofs by employing multi-server private information retrieval (PIR) to query the proofs. To further improve performance, the accumulator is split into sub-accumulators based on, e.g., time periods. All sub-accumulators are then accumulated in a top-level accumulator. Consequently, the witnesses with respect to the sub-accumulator stay constant and can be embedded in the server’s certificate and only the membership-proofs of the sub-accumulators need to be updated when new certificates are added to the log. Only these top-level proofs have to be queried using PIR, thus greatly improving the overall performance, as smaller databases are more efficient to query.

However, one drawback of this solution is the increase in certificate size if one were to include this static membership witness for the sub-accumulator in the certificate itself. Kales et al. [35] propose to build sub-accumulators per hour, which would result in sub-accumulators that hold about \(2^{16}\) certificates. A Merkle-tree membership proof for these sub-accumulators is 512 bytes in size when using SHA-256. In contrast, a membership proof for the q-SDH accumulator is only 48 bytes in size (with the curve used in our implementation). A typical DER-encoded X509 certificate using RSA-2048 as used in TLS is about 1–2 KB in size, meaning inclusion of the Merkle-tree sub-accumulator membership proof would increase the certificate size by 25–50%, whereas the q-SDH sub-accumulator membership proof only increases the size by 2.5–5%.

We can now leverage the fact that their solution already requires two non-colluding servers for the multi-server PIR. These servers hold copies of the Merkle-tree accumulator and answer private membership queries for the top-level accumulator. Switching the used accumulators to our MPC-\(q\)-SDH accumulator would give the benefit of small, constant size membership proofs, while still being performant enough to accumulate and produce witnesses for all elements of a sub-accumulator in one hour.