Keywords

19.1 Introduction

A fractal is a fragmented geometric rough shape that can be delineated into parts, each of which is a reduced-size copy of the whole structure. The characteristics, so-called symmetries, in a fractal signify invariance under contractions or dilations. The roughness and fragmentation of a natural fractal shape neither fluctuate up and down or vanish but stay unchanged at any zoom level. The key to the whole structure is still attached to the structure of every piece in a fractal. Fractals possess self-similarity in a structure across all scales. As we zoom in or zoom out a feature, the geometry and appearance of a fractal surface remain unchanged or self-similar (Mandelbrot, 1989). Self-similarity has been used under two contexts. It suggests that each part of the body/structure of a fractal is very much like a tree branch or a piece of a broccoli which is simply a linear geometric reduction of the whole body. It also expresses that not only is the reduction linearly geometric but also the ratio of reduction is the same in all directions. Self-similarity indicates that some aspect of a process or phenomena is invariant under scale-changing transformation, such as simple zooming in or out. In short, a self-similar structure repeats a unit pattern on different scale or size. Self-affine shapes and self-affinity are recent terms that are mostly used in geomorphology and relief analysis, which suggests that though the reduction is still linear, it is different in a way that, as one goes from a large piece to small piece, we must contract the vertical and horizontal coordinates in different ratios (Burrough, 1981). If a natural scene is self-similar, determination of its scale is not possible. The simplest visual test of self-similarity is to see whether any enlargement of any part of a structure remains indistinguishable from the whole or from any other part of the same body.

Since the term fractal was first coined by Benoit Mandelbrot in 1975, fractal models and related analysis techniques were matters for speculative coffee break discussions between sessions at geoscience conferences. For the first time, fractal geometry proposed by Mandelbrot (1975) has provided the possibility of precisely simulating and describing landscapes by employing a mathematical model. Fractal analysis without any question has shown to look beyond the traditional techniques to contain ‘new’ information in a phenomenon. If a landscape possesses fractal character, it should reveal statistically self-similar or statistically self-affine nature. Simulating landforms processes using Mandelbrot’s fractional Brownian motion (fBm) has gained enormous popularity in the last three decades. The application of fractal technique in geomorphology started sprouting only by the 1980s, though it was suggested that the application of fractal was always important to geomorphology, even before Mandelbrot’s coining the word ‘fractal’. Reviewing all the papers of fractal in geomorphology is beyond the scope of this paper; however, some of the most cited landmark papers that focused on different themes of geomorphology are presented here.

Goodchild (1982) presented fractal Brownian process as a terrain simulation model. Mark and Aronson (1984) studied scale-dependent fractal dimension of topographic surface: with special application in geomorphology. ‘Self-similar’ profiles of deep-sea topography were investigated by Fox (1986). Culling and Datko (1987) applied fractal geometry to soil-covered landscapes. Goodchild and Mark (1987) conducted a comprehensive review of the relevance of fractals to geography under three headings: self-similarity, the response of measure to scale and the recursive subdivision of space. The fractal geometry of the landscape was measured by Milne (1988). Gilbert, 1989 evaluated whether the topographic data sets have fractal properties or otherwise. Fractal mapping of digital images of Arizona were conducted by Huang and Turcotte (1989). Fractal sinuosity of stream channel was determined by Snow (1989). Unwin (1989) introduced fractals and geosciences to computer geosciences. The surface roughness of talus slope was studied by applying fractal techniques by Andrle and Abrahams (1989). Fingerprints and fractal terrain were assessed by Piech & Piech, 1990. Polidori et al. (1991) applied fractal technique to assess quality of digital elevation model.

In 1992, a special issue was published in the journal Geomorphology, devoted to the application of fractal geometry on landform analysis, where there are nine articles in the theme, ranging in topic including catchment evolution model, fluvial land sculpturing, tectonic, climate and lithology control, measurement of self-affinity, fractal significance of drainage basin parameters, fractal dimension of sinkholes, desert storm, etc. (Willgoose et al., 1991a; Willgoose et al., 1991b; Tarboton et al., 1992; Chase, 1992; Klinkengerg, 1992; Nathaniel & Chase, 1992; Ouchi & Matsushita, 1992; Breyer & Snow, 1992; Reams, 1992; Mayer, 1992; Snow, 1992). Whether there exists any relationship between fractals and morphometric measures has been investigated by Klinkengerg (1992) in the same issue. A review article on fractals, fractal dimensions and landscapes came out in 1993 by Xu et al. The next year, another review article was published by Jie & Haosheng (1994) on fractal geomorphology, where the authors focused on the issues of geomorphic fractals and geomorphic conditions, fractal dimensions and geomorphic processes, digital modelling of fractal landscape, range scale of geomorphic fractals and fractal characteristics of geomorphic phenomena in space and time. Gao & Xia published fractals in Physical Geography in 1996 (Gao & Xia, 1996). Chaos, fractals and self-organization in coastal geomorphology were investigated by Baas (2002). The author simulated dune landscapes in vegetated coastal environments. Hagerhalla et al. (2004) studied fractal dimension of landscape silhouette outlines as a predictor of landscape preference. Taud and Parrot (2005) measured roughness of DEM applying the local fractal dimension. Another review paper came out by Sun et al. (2006) where the scholars took a survey of several methods for fractal dimension calculation which are commonly used in many studies. Turcotte (2007) related fundamental statistical properties of landform and drainage networks that have been developed in statistical physics. Fractal dimension of a badland topography at Deccan was investigated by Joshi et al. (2009). Relationships between the fractal dimension of the drainage basins were assessed by Khanbabaei et al. (2013). A review article on the methods of fractal geometry used in the study of complex geomorphic networks was published by Kusák, 2014, where the focus was on the comparisons of the basic terms used in fractal geometry. Tectonic and lithological control on topography and their reflection in fractal dimension were presented by Liucci & Melelli (2017). Pardo-Iguzquiza et al. (2019) took a complete review of fractals in karst to demonstrate fractal behaviour of karst topography. A case study of fractal-based modelling and spatial analysis of urban form and growth of Shenzhen in China was conducted by Man & Chen, 2020. Patuano & Tara (2020) presented the summary of a literature review of the methods and interpretations of fractal geometry, currently used in landscape architecture. Over 40 studies were examined for their use of fractal concepts within the analysis of landscape-related elements.

A brief traverse through the fractal journey of the landscape from the 1980s till the present, as outlined in the previous paragraphs, revealed that the application field is widely variable, ranging from tectonics, coastal configuration, river basin geometry, landslides, soil studies and hordes of other applications. With the availability of high-resolution digital elevation data and operating GIS tools, further new interests have arisen in the technique.

Fractal geomorphology emerges as a new discipline to evaluate the origin, process and distribution of relief on the earth. Though landforms widely exhibit fractal nature, it is complex to asses it due to the non-homogeneity of relief geometry in space. The main objective of the present study is to assess the applicability of fractal dimension to identify badland locations and to understand microprocesses operating in badland topography. The significance of the study is that fractal dimension technique addresses spatial characteristics of the landform features and therefore represents a powerful method to investigate the relationships between landforms and their underlying processes.

19.2 Study Area

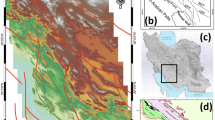
The study area selected for the study is the Tapi Basin which is the second largest west flowing peninsular river in India (Fig. 19.1). It flows through the states of Madhya Pradesh, Maharashtra and Gujarat. Its length is 724 km, and it drains an area of 64,750 km2. It rises from Satpura Ranges at an elevation of 762 m and drains into Arabian Sea. It flows through a rift valley, and its trough accommodates considerable deposits of alluvium. The area extends between 75°15′E to 75°45′E longitude and 20°25′ to 22°35’N latitude. The climate is semi-arid with the annual average rainfall between the range of 650 and 780 mm. December is the coldest month with the mean daily minimum temperature at 11.9 °C and the mean daily maximum at 29.8 °C. Temperatures begin to rise steadily from the beginning of the March, reaching its peak in May. Mean daily maximum temperature reaches 45–48 °C on the hottest day in May. Natural vegetation is mostly absent except in the form of acacia thorny plants. Deccan Trap region as a whole is rocky landscape where sediment deposits are restricted and thin, if at all they are present. River Tapi flows for a large part within a rift valley, and its trough accommodates considerable deposits of alluvium. On the right-hand bank of the river, numerous tributaries, collecting their headwaters from foot of Satpura systems, have dissected the alluvium-covered pediment surface and have caused badland formations along a stretch of 60–70 km. There has not been any document/report or research article on the origin of these badlands, though tectonics as well as climate forcing during the LGM are speculated during the scientific discussions. The focus of the present study is these badland areas.

Fig. 19.1
figure 1

Location map of the study area in general and also showing two sample basins

Full size image

19.3 Material and Methods

Fractal dimension of the entire area covered by badlands in the basin was calculated first, to assess whether there is any relation between badlands and values of fractal dimension (D). In other words, whether values of D can be used to identify and demarcate badlands in any region.

‘Viz-Morphotec’ is a new set of software application programs for morphometry developed by Dr. Prakash Joglekar (Scientist F, DRDO, Delhi) as per well-documented algorithms and procedures. Fractal dimension of landscape is one of the parameters in this software and has been used for the computation of fractal dimension indices in this study. The specification of the system and program is Turbo Pascal for Windows, 32-bit OS, 4 GB Disk Memory, 2 GB RAM, Intel Xeon 3.40 GHz. Currently there are 10–12 programs plus few more in the software. The software was designed to compute basin and topographic indices at regional scale, such as hypsometric integral, asymmetry factor, knick points, valley width–height ratio, stream profiles, stream order, bifurcation ratio, sinuosity index, circularity ratio, elongation ratio, fractal dimension (basin), iso-base, hypsometric integral, roughness index, surface index, mountain front sinuosity and rose diagram, swath profiles trend surface and fractal dimension (topography). Input DEM 3601×3601 ASTER (1×1), SRTM (3×3), Re-sampled SRTM (15×15). Output files: Compatibility with ENVI, ERDAS, Geomatica/.bmp.

The fractal dimension program in the software was used to compute the D indices in the present study. For morphometric analysis, ASTER and SRTM DEMs are mostly used in the software, since the software was mainly designed to detect morphometry at a regional scale. But the input DEM for the present study was self-generated Cartosat (10 m) for the part of the Tapi Basin where badlands are present.

To evaluate the fractal property (self-similar/self-affine) of the badland areas in the basin, fractal dimensions were calculated at micro level for two selected catchments from the area at three levels, namely, linear D (Laverty 1987), D for the basin area (Goodchild, 1982; Turcotte, 1992) and D for the surface (Mandelbrot, 1975).

Results were synthesized, and findings were presented.

19.3.1 DEM Extraction Using Cartosat-1 Stereo Imagery

Cartosat-1 , which was launched on May 5, 2005 (carrying two panchromatic sensors with 2.5-m spatial resolution and having fore-aft stereo capability), has been designed to generate DEMs and ortho-images for terrain modelling and is widely used nowadays, especially in India. Cartosat DEM of 30-m resolution is available on Bhuvan portal for free download. But the study needs a higher-resolution DEM than that; hence a DEM was self-generated for the present study using 8 Cartosat-1 stereo images taken over the badlands along Tapi River. The details of each scene of the eight Cartosat images are displayed in Table 19.1.

Table 19.1 Details of each scene of the eight Cartosat images used to create DEM
Full size table

Extraction of DEM from stereo images can be treated as a semi-automatic procedure. Leica Photogrammetry Suite (LPS) 9.2 was used for DEM generation. The first step is to identify the GCPs for each image, and for that, both the Google image and the Cartosat images were opened in ArcGIS. After the points have been identified, the images PAN-A and PAN-F were imported in Leica LPS as indicated in Fig. 19.2. Cartosat-1 images are provided with ‘rational polynomial coefficients’ (RPC). These RPCs are computed by using the available information, i.e. sensor model, sensor position and attitude data, ellipsoid parameters and map projection. Further, rational polynomial coefficients (RPC) file is attached in the block file as a part of image orientation. GCPs were collected directly from the field by using differential Global Positioning System (dGPS). Five GCPs were taken for each image. Figure 19.3 indicates the GCPs of one image actually in the field. Twenty-five GCPs were used as control points to refine orientation results (Fig. 19.4). Using the ‘bundle method’ of aerial triangulation, tie points were generated. The RMSEs of the residuals were obtained after block triangulation. Once aerial triangulation with optimum RMSE is done, the data is exported in ArcGIS 10, and DEM was extracted at 10-m resolution. Standard WGS-84 projection and datum were assigned for the Cartosat 1 photogrammetry model. The ortho-rectified image is indicated in Fig. 19.5. For accuracy checking, the Survey of India topographical maps of the area were used which revealed error-free matching with great accuracy. The flow chart in Fig. 19.6 demonstrates the entire steps of DEM creation from IRS Cartosat stereo images using LPS and ArcGIS.

Fig. 19.2
figure 2

Input GCP, classic point measurement tool in LPS

Full size image
Fig. 19.3
figure 3

Measuring ground control points in the field using dGPS

Full size image
Fig. 19.4
figure 4

Depicting the positions of the 25 GCPs as control points to refine orientation results

Full size image
Fig. 19.5
figure 5

DEM and the ortho-rectified image

Full size image
Fig. 19.6
figure 6

Flow chart demonstrating the entire steps of DEM creation from IRS Cartosat stereo images using LPS and ArcGIS

Full size image

Figure 19.7 demonstrates the Carto DEM of 10-m resolution which became the input DEM for all the further calculations.

Fig. 19.7
figure 7

Carto DEM of 10-m resolution which is the input DEM for Viz-Morphotec software

Full size image

19.3.2 Calculation of Fractal Dimension

Calculations of the fractals were computed for 137 × 77 grids cell of 100 × 100 pixel dimension. The box counting was performed by varying grid dimension from 4 to 50 cells in x, y and z axes. The fractal dimension (D) was computed for each pixel based on the slope of regression of graph of log (N) against log (r). N is the number of boxes that cover the pattern, and r is the magnification or the inverse of the box size. Density-sliced image for local D (D range 2.8–3.0) is presented in Fig. 19.8. The density-sliced image of D has been draped on Google Earth image of the area (Fig. 19.9) which reveals a remarkable match of the areas with D values above 2.8 with the location of badlands in the basin. The percentage area against the D values were obtained (Fig. 19.10) which indicates clearly that D values around 2.90–2.95 were observed over the badlands in the region. The result is showing that fractal dimension can be effectively used to delineate badlands in any basin. The software proved to be useful in determining fractal dimension on a broad scale in addition to other morphometric parameters.

Fig. 19.8
figure 8

Density-sliced image for local D, Calculated using Viz-Morphotec software (D ranges from 2.8 to 3.0)

Full size image
Fig. 19.9
figure 9

Density-sliced image of D has been draped on Google Earth image of the area, depicting the perfect coincidence of badlands with D values between 2.8 and 3

Full size image
Fig. 19.10
figure 10

Percentage area against the D values, revealing that values above 2.9 are clustered within the badlands in the area, as shown by red in the circle

Full size image

The next step is to test whether we can meaningfully apply the technique to evaluate the fractal properties of the badlands. Badlands are deeply dissected topography, with dense drainage density. Relief within a badland can be variable, such as in areas like Chambal badlands of India where relief of more than 100 m is found, but the badlands that are developed over the Deccan region are usually of a lot smaller dimension in terms of vertical relief and horizontal extent (Joshi et al., 2009). The Deccan Trap region as a whole is rocky, and sediments and soils have been formed at only restricted patches along some riverbanks and few foot slope pediment zones. The badlands in the study area have maximum relief of 10–25 m, so landform processes are operating at a much finer resolution. Hence, Cartosat DEM of 10-m resolution is believed to be a fair match with the landscape operating scale here.

19.3.2.1 Linear Fractal Dimension of the Channel

In order to evaluate the linear fractal dimension of the streams in the basin, a field survey was conducted to select a few badland catchments using the locations of badlands identified by the D values of the area (Fig. 19.9). Two sample catchments were selected in the field and demarcated them in the DEM. The locations of these two sample catchments are indicated in the location map (Fig. 19.1), and field views are shown in Fig. 19.11. They are Bhaunak Basin and Sur Basin. General geomorphometry of these two sample basins is presented in Table 19.2. There are two distinct geomorphic units within both the basins, namely, pediments and badlands. It is clearly visible in Fig. 19.12 that there is a sharp break of slope, indicated by a red line in the diagram. Figures 19.13 and 19.14 display surface and slope maps of the basins. As we can see in these maps, the upstream part is the hillslope pediment zone, and the downstream reach is the true badland alluvial zone. The fractal dimension (D), in general, ranges between 1 (indicating almost straight) and 2 (nearly filling the plane). Over a range of scales, statistically self-similar lines demonstrate constant values of D (Mandelbrot, 1967). The fractal value (D) of a curve is calculated by measuring the entire length of the curve using various step sizes . When the curve is irregular, the step size increases, leading to increase in the total length of the curve. Two stream channels were selected each from the two sample catchments, and linear fractal dimensions were computed using Eq. (19.1) in the program:

$$ \log\ L=K+B\ \log\ d $$
(19.1)
$$ D=1-B $$

where L is the length of the curve , d is the step size, B is the slope of the regression, K is a constant, and D is function of the regression slope B. The steeper the negative slope (B is negative value), the higher the fractal dimension. The results of the calculation are present in Fig. 19.15 and Table 19.3. It is clear from the table that the values are closer to 1 than 2, indicating low sinuosity of the channels in question. Variations in fractal dimensions are observed between Bhaunak and the Sur basins, but there is no significant variation within the individual basins. Bhaunak shows lower D than the Sur Basin .

Fig. 19.11
figure 11

The field views of the two sample catchments, where (a) and (b) depict parts of Bhaunak Basin and (c) and (d) capture parts of Sur Basin. What is seen in the pictures are the true badland parts of the basins

Full size image
Table 19.2 Topographical parameters of the sample basins
Full size table
Fig. 19.12
figure 12

Contour maps of Sur and Bhaunak basins and the threshold contour (in red colour), which demarcates upstream and downstream reaches

Full size image
Fig. 19.13
figure 13

Surface maps of the two sample basins, namely, Sur and Bhaunak

Full size image
Fig. 19.14
figure 14

Slope maps of the two sample basins, namely, Sur and Bhaunak

Full size image
Fig. 19.15
figure 15

Linear fractal dimensions of the channels, showing upstream and downstream curves separately

Full size image
Table 19.3 Linear fractal dimension for the sample basins
Full size table

19.3.2.2 Fractal Dimensions of the Basin Area

The catchment boundaries of Bhaunak Nadi and Sur Nadi were demarcated with the help of hydrology tool in ArcGIS 10. The fractal dimension of the basin area for the sample basins was calculated using box-counting method (Goodchild, 1982; Turcotte, 1992), for that grids of different scales were plotted on area as well as sample basin boundary, and fractal has been calculated with the help of Eq. (19.2):

$$ (D)=\frac{\ln \left({N}_n+\frac{1}{N_n}\right)}{\ln \left(\frac{r_n}{r_n}\right)+1} $$
(19.2)

where (r) is the size of the grid and (N) signifies the number of boxes to cover the entire area for each grid size. The computed D for the perimeter for the two basins is demonstrated in Table 19.4. The box-counting dimension is much more widely used than the self-similarity dimension since the box-counting dimension can measure pictures that are not self-similar (and most real-life applications are not self-similar). Due to the nearly box-shaped nature of the demarcated basins, the values are close to 2, indicating near space filling.

Table 19.4 Box sizes and the number of boxes (for box-counting method) and fractal values for the two basins
Full size table

19.3.2.3 Variograms and the Surface Fractal Dimensions

The roughness or spatial continuity in a data set is indicated by variograms. Of all the varieties of methods of computation of D for surface, variogram technique is the most widely used one. The variogram of a surface is constructed by considering the variance of its elevation as a function of its horizontal distance. For a pair of points x1, y1, z1 and x2, y2, z2 on a grid of digital topography, with x and y horizontal coordinates and ‘z’ being the elevation, the contribution to the variance is expressed as

$$ {\left({Z}_1-{Z}_2\right)}^2={\left(\Delta z\right)}^2 $$
(19.3)

and the horizontal distance is depicted as:

$$ {\left[\left({x}_1-{x}_2\right)+\left({y}_1-{y}_2\right)\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=\Delta x $$
(19.4)

It calculates these for every pair of points on the grid and plots the logarithm of the standard deviation over a binned distance interval, against the logarithm of the distance at the logarithmic midpoint of that interval. Manually it is computationally intensive operation, because n by n grid contains n2(n2 − 1)/2 points. The following equation (Eq. (19.5), Carr, 1995) has been employed in the program to calculate variograms of the sample basins, which is expressed as:

$$ y(h)=\left(1/2n\right)\sum {\left[Z\left({x}_i,{y}_i\right)-Z\left({x}_{i+h},{y}_{i+h}\right)\right]}^2 $$
(19.5)

where γ(h) = semivariance at lag distance h; Z(xi,yi) = data value at location i; Z(xi+h,yi+h) = data value at location plus distance h; and n = number of points in the data set.

19.3.2.4 Estimation of Fractal Dimension from Variograms

Fractal dimension of the landscape can be directly obtained from the variogram, assuming that land surfaces have statistical properties to those of fractional Brownian surface (Mandelbrot, 1975). The two random function of F(t) and F(rt)/rH, when properly rescaled, are statistically similar. For a surface, the single variable t is replaced by point coordinated x and y on a plane to give F(x,y) as the surface altitude z at position (x,y). The surface that consists of these F(x.y) points is usually called a fractional Brownian surface (fBm) (Mandelbrot, 1975).

On fractional Brownian surface, the variogram is described by what is expressed in Eq. (19.6), such as

$$ E\Big[F\left(x,y\right)\hbox{--} F{\left(x+\Delta x,y+\Delta y\right)}^2={\left(\Delta {x}^2+\Delta {y}^2\right)}^{2H} $$
(19.6)

The variogram takes on the form of a power function in which H (Hurst exponent) should range between 0 and 1. In case of a fractional Brownian surface, D = 3 − H. As H increases toward its upper limit (i.e. small D), the variability of the surface is locally small but rises rapidly with distance; whereas, when H is small (i.e. large D), the surface shows high local variability but a slow increase at large distance (Mandelbrot, 1975).

The slope and the trend of a variogram can be directly used to interpret the nature of fractal of the landscape. On a log plot of standard deviation v/s distance, the slope of a variogram will be indicated by (3 − D)/2, resulting into a steep variogram representing low fractal dimension, while a gentle slope implies high fractal dimension. Straight variogram represents a true fractal (self-similar). If the variogram has breaks in the slope, it indicates that each break is associated with changes in the process or lithology and represents a ‘multifractal’ landscape. In a topography where there are variations in either lithology and/or processes, a variogram shows generally a multifractal topography (Voss, 1988).

19.3.2.5 Relation Between H and Self-Similarity of the Landscape

If the relief (or variance of elevation) in a small area resembles that of the entire area, when the relief is magnified by the area factor (entire area/small area ratio), the landform is considered as self-similar, where H = 1. If relief increases, on the other hand, then the landform is considered self-affine (0 < H < 1). This is a more probable situation in real landscapes. With similar total relief, the greater the local relief, the lesser the value of H. With similar local relief, the greater the value of H, the lesser the total relief.

Texture is a word used in landform studies to indicate arrangements of topographic heights and the frequency of changes, and surface fractal dimension is simply the measure of it. The calculated D values fall within the general range of 2 (flat) to 3 (completely space filling).Using the equations cited above, variograms and the fractal dimensions were computed for the two sample basins. Both Bhaunak and Sur basins were demarcated into two sectors, namely, upstream pediment section and downstream badland section. Variograms were separately generated for all the four sections, and results are depicted in Fig. 19.16 and Table 19.5. Hurst components (H) were also calculated for the sample basins, and they are also included in Table 19.5.

Fig. 19.16
figure 16

Variograms for both the upstream and downstream sections of the sample basins. Upstream reaches of both the basins as depicted in (a) and (b) are straight lines, implying self-similarity, whereas, downstream reaches shown in (c) and (d) show slight concavity, that is deviation from self-similarity but more of self-affinity

Full size image
Table 19.5 Fractal dimension of the surface and ‘H’ values of the sample basins
Full size table

19.4 Discussions

In the present study, demarcations of badlands were done using a new software, Viz-Morphotec, which clearly reveals a strong association of D values with the occurrences of badlands. At a micro-level, the fractal calculations were done at three levels, namely, linear, perimeter and surface, for two sample basins. The data presented above reveals that in case of linear D, the low values for both the channels in Bhaunak suggest that the rivers are actively eroding, and linear erosion is predominant in the entire section being included in the analysis. They are also close to the source areas. Sinuosity will always indicate low under such conditions. The gradients of these badland gullies/streams are high that directly drain into the main streams. Hence there is rapid linear erosion resulting in low values of D. Sur is revealing higher values of D, showing more sinuosity. Minor variations prevail in the values of D between the two catchments, which could be due to the variations in their textural and stratigraphic characteristics as well as gradients of the longitudinal profiles.

The fractal dimension of the basin perimeters conducted using box-counting method yielded in the high values of D for both the basins, reaching almost 2. This is due to the nearly box-shaped nature of the demarcated basins.

In surface D, values above 2.5 are considered to be very rough surface, and the values for both the basins are more than that. Values for upstream basins are below 2. Generally, surface fractal values range between 2 and 3, but in this calculation, for the upstream reaches, the values are less than 2. This is very unusual. The surface shows high local variability. There is a slow increase in roughness with distance for the badland areas, while the hillslope areas demonstrate exactly the opposite trend. The fractal dimension (D) of a surface is a relief-independent parameter. High fractal does not necessarily mean a rough surface but rapid change in the relief in a small local area (but gradual change in a large area), and low fractal suggests slow changes in a small area but large variation over a long distance (Sung and Chen, 2004). High values of D and small H (Table 19.5) as shown in these areas are in accordance with the normal trend. Hurst exponent is useful to determine the self-similarity of the landscape and even more useful when comparisons are made of the minor variations in the surface morphology between the two sites. The upstream areas are very small in aerial extent, and hence variation in the surface relief is not significantly reflected in the analysis.

A straight variogram suggest self-similar landscape. The fractal dimension of a topography is controlled by the changes in its variability with distance but not the amplitude of that variability (Joshi et al., 2009). A topography which is uncorrelated at all length scales will indicate high fractal value, while topography that is strongly correlated at short wavelengths (but less so at long wavelengths) will reveal low fractal dimension (Mandelbrot, 1989). A true fractal must reveal a straight variogram. Departure from the straightness indicates multifractal topography, more so at lower fractal dimension, at lesser wavelength scales (Voss, 1988; Mandelbrot, 1989). Multifractal can be interpreted in two ways: that the landscape is not self-similar and also that more than one process is operating in the region.

The trend lines of the two sample basins (Fig. 19.15) do not reveal noteworthy difference with each other. The variograms of the two sample basins are smooth and slightly concave, not straight, indicating multifractal topographic distribution for this range. Sur Upper course (Fig. 19.16a) shows almost smooth and straight trend, indicating a fractal self-similar topography for a short range. Even the upstream trend of Bhaunak (Fig. 19.16b) also is straight. However, downstream for both the basins show smooth but slightly concave profile. Breaks in the variogram slopes are indicative of multifractal topography and change in the processes operating within the area. The variograms show steeper slopes at shorter length scales with D clustering around 2.2/2.3 and gentler slopes at wavelengths longer than 1 km, representing D, in the vicinity of 2.4 and above. The interpretation of the variogram slopes suggest that ‘statistical self-similarity’ is not indicated here and also that two processes are dominantly operating in the badland areas. There is no sharp break in the slope of the variograms, but smooth concave slope, indicating that one process merges into the other.

19.5 Conclusions

Along the banks of Tapi River within Maharashtra, badlands have been developed along a stretch of approximately 70 km. The exact locations of these badlands have been delineated using fractal values calculated in a new software, Viz-Morphotec. The microprocesses operating at these badlands were further attempted at finer landscape operation scale at linear, perimeter and surface levels by selecting two badland catchments and performing the fractal calculations.

Within the two catchments under review, two distinct geomorphic units could be identified: hillslope and pediment zone. The pediment zone is deeply overlain by alluvium that continues till the riverbanks of the main stream. These alluviums are severely dissected to form badlands. Fractal values of the streams (linear) show low to moderate values, indicating less sinuosity of the streams and high competence. The D values for basin perimeters are close to 2, which is nearly space filling. The trend lines of the variograms show slightly concave curve, indicating multifractal topography (not self-similar in true sense), and two processes are dominantly operating, with one merging smoothly into another. Though fractal dimension does not highlight the actual process in the area, based on the understanding of the general processes operating on the badlands and the slope of the variograms, it is very likely that in the upstream reach, which is the hillslope units of these basins, unusually low D values are found as against high values downslope. It is probably because high D values do not indicate necessarily high relief or rougher surface, but it indicates that the rate of change in relief over a small area is high but gradual at the long distance and vice versa. Surface fractal dimension indicates values higher than 2.5 implying a rough surface, which is very typical of badland topography. Marginal variations occur in the two sample basins, but not significant enough to warrant attention. The curves of the variograms indicate possible influence of erosional and diffusional processes operating on the topography, or they could be the result of tectonics or changes in the climatic conditions, which are still manifested in the landscape. In future, more data need to be generated from similar badland watersheds to make comparison and for better understanding of the landscape processes operating at micro-scale within the badland watersheds in the region.