Keywords

1 Introduction

Bank revetments at German inland waterways are mainly secured by loose or grouted armour stones on a filter layer. Their design according to BAW Code of Practice: Principles for the Design of Bank and Bottom Protection for Inland Waterways (GBB) [1] encompasses a hydraulic and a geotechnical design, where the former defines the armour stone diameter necessary to withstand waves and currents and the latter evaluates the embankment stability under a rapid water level drawdown. The presented study focuses on the geotechnical design.

The National Research Council [2, p. 2] states that “probabilistic methods, while not a substitute for traditional deterministic design methods, do offer a systematic and quantitative way of accounting for uncertainties encountered by geotechnical engineers, and they are most effective when used to organize and quantify these uncertainties for engineering designs and decisions.”

First investigations of uncertainties inherent to shore protection structures can be found in the Netherlands. Triggered by a severe storm event in 1953, van Danzig [3] presents a probabilistic approach for the geotechnical design of flood defence systems. Since then, numerous concepts for the design of sea defence structures, i. e. dikes, dunes and breakwaters, have been published, i. e. [4,5,6,7,8,9]. Approximately ten years ago, first studies of the hydraulic [10] and geotechnical stability [11, 12] of river and canal embankments were published, which focus on flood events and natural flow. So far, revetment stability under ship-induced loads has not been addressed.

The uncertainty inherent to the design of hydraulic structures is a result of aleatory and epistemic uncertainties. A third category of uncertainties are the so-called ‘unknown unknowns' which refer to unidentified aleatory and epistemic uncertainties. This work primarily deals with aleatory uncertainty by introducing load and resistance parameters as random variables.

PIANC [13] states that the effects of ship or wind-induced water motion have a random character, however, to the knowledge of the authors, the uncertainty of ship-induced drawdowns and their effect on revetment design has not been investigated yet.

Sources of uncertainty inherent to resistance parameters are natural (inherent) variability, measurement error, transformation error and statistical uncertainty [14]. The natural variability is a result of the genesis of soil. Transformation uncertainty is “related to the accuracy of physical or statistical models” [14] and a result of empirical or other correlation models. For instance, the friction angle is usually determined by direct shear tests based on the relationship between measured shear stress failure and normal stress (Mohr-Coulomb failure criterion). Statistical uncertainty arises from the choice of probability function and its parameters. For the probability function of the effective friction angle φ′, Lacasse and Nadim [15], Wolff et al. [16], Lumb [17] and JCSS [18] suggest a Gaussian distribution, whereas Schultze [19] recommends a Lognormal distribution. The hydraulic conductivity k is commonly considered as lognormally distributed [20,21,22]. This paper focuses on statistical uncertainty. So far, the effects of different probability functions and parameters on revetment design have not been studied.

2 Reliability-Based Revetment Design: Theory and Methods

2.1 Principles of the Revetment Design

In simple terms, a vessel passage in a confined waterway cross-section, i. e. canal or river, leads to changed discharge conditions, which trigger a flow around the vessel and, thereby, cause a lowering of the water level next to the vessel, referred to as drawdown [1]. If the water level is lowered faster than the hydrostatic pore pressure in the soil can adapt to, excess pore pressure may develop (Fig. 1). This process is caused by a delayed pressure equalisation due to gas bubbles in the water at shallower depth [23, 24] and influenced by the compressibility of the water-gas-mixture [25, 26]. The excess pore pressure leads to reduced effective stress, which lowers the shear strength of the soil. This may result in local slope sliding or liquefaction [1].

Fig. 1
figure 1

Hydrostatic pore water pressure and excess pore pressure during rapid drawdown [1]

Full size image

Wave-induced drawdowns can be simplified by a uniformly decreasing water level with constant drawdown rate [23, 24]. The excess pore pressure attains a maximum at the end of the drawdown za, which allows to assess the acting forces as a steady-state problem. A depth-depending excess pore pressure Δp (z) may develop:

$$\Delta p (z) ={\gamma }_{w} {z}_{a} \left(1 - {a\mathrm{e}}^{-bz}\right)$$
(1)

where \({\gamma }_{w}\) is the unit weight of water and a = 1 and b are pore pressure parameters; b describes the shape of Δp (z) as response to k and the ratio of design drawdown time \({t}_{a}^{*}\) = 5 s and drawdown time ta, Eqs. (2) and (3), for a gas content of 5–15% in the pore fluid [25].

$${\mathrm{b}}^{*} =0.166\cdot {\mathrm{k}}^{-0.327}$$
(2)
$$b = {b}^{*}\sqrt{\frac{{t}_{a}^{*}}{{t}_{a}}}$$
(3)

The excess pore pressure may cause driving forces to exceed resisting forces at the vertical slice of an infinite slope leading to local slope failure. The resisting forces are a function of buoyant unit weight of the soil \({\gamma }_{B}^{^{\prime}}\), slope inclination β and φ′, the driving forces are governed by za. The difference of resisting and driving forces reaches a minimum at a critical depth dcrit as follows:

$${d}_{crit} = \frac{1}{b}\mathrm{ln}\frac{\mathrm{tan}\;{\varphi }^{^{\prime}} {\gamma }_{w} {z}_{a} b}{\mathrm{cos}\beta {\gamma }_{B}^{^{\prime}} (\mathrm{tan}\;{\varphi }^{^{\prime}}-\mathrm{tan}\beta )} {for}\; {\varphi }^{^{\prime}}>\beta $$
(4)

If dcrit > 0, the equilibrium condition stated in Eq. (5) is used to determine the required unit weight of armour stones under buoyancy g′, which is the product of required armour layer thickness dD and buoyant unit weight of armour stones \({\gamma }_{D}^{^{\prime}}\). Furthermore, Eq. (5) encompasses the filter layer thickness dF, the buoyant unit weight of the filter layer \({\gamma }_{F}^{^{\prime}}\), the effective cohesion c′ and the shear strength \(\tau \), e.g. as a result of a toe support.

$${g}^{^{\prime}}={\gamma }_{D}^{^{\prime}} {d}_{D}= \frac{\Delta p{\mathrm{tan}}\;{\varphi }^{^{\prime}} - {c}^{^{\prime}}-\tau }{\mathrm{cos}\beta \mathrm{tan}\;{\varphi }^{^{\prime}}-\mathrm{sin}\beta }- \left( {\gamma }_{F}^{^{\prime}} {d}_{F}+{\gamma }_{B}^{^{\prime}} {d}_{crit}\right)$$
(5)

Waves and drawdown generate flow in permeable soils, which may lead to considerable vertical hydraulic gradients at bottom and bank and, thereby, liquefaction of near-surface soil layers. In the case of a toe support or a moderate slope inclination, the revetment dimensions determined in Eq. (5) may not satisfy the equilibrium of liquefaction given in Eq. (6) with the corresponding critical depth dcritB stated in Eq. (7).

$${g}^{^{\prime}}={\gamma }_{D}^{^{\prime}}{d}_{D}\ge \frac{\Delta p}{\mathrm{cos}\beta }- \left({\gamma }_{F}^{^{\prime}} {d}_{F}+{\gamma }_{B}^{^{\prime}} {d}_{critB}\right)$$
(6)
$${d}_{critB} = \frac{1}{b}\mathrm{ln}\left(\frac{{\gamma }_{w} {z}_{a} b}{{\gamma }_{B}^{^{\prime}}\mathrm{cos}\beta }\right)$$
(7)

A design according to GBB [1] fulfils the specifications, when the analyses demonstrate that the limiting equilibrium states (Eqs. 5, 6) are satisfied under the relevant combination of characteristic values. Characteristic values are “selected as a cautious estimate of the value affecting the occurrence of the limit state” [27]. Their selection is either based on expert knowledge or statistical methods. GBB [1] recommends a value at the lower end of the range of possible values for k; for the choice of φ′ no recommendations are provided; za and ta are derived from worst-case design vessel passages [28].

2.2 Reliability Analyses and Parameter Combinations

The theory of reliability-based methods and their application in geotechnical engineering is well-known. Thus, for mathematical basics reference is made to literature [29, 30]. This paper directly presents the results of the uncertainty analyses, which are conducted with the Python package OpenTURNS [30]. A minimum of 10,000 Monte Carlo simulations is run to obtain a range of possible armour layer thicknesses. Subsequently, the 95% quantiles of the random output are computed to compare the probabilistic results to deterministic benchmark solutions.

The probability functions of the soil parameters are defined as follows: The mean value is constant, while the variability of the soil properties relative to the mean is governed by the coefficient of variation (cov). Different cov are investigated as indicated by the two probability density functions shown in Fig. 2. Since GBB [1] does not states particular bounds that represent characteristic values, a range of φ′ and k are considered for a deterministic benchmark solution. The lower bound of the benchmark solution is defined as the 5% quantile of the respective distribution. The upper bound of the deterministic benchmark solution is the mean of the respective distribution. For illustrative purposes, case studies with permeable sand (SW) and with silty sand (SU) are conducted. The variability of the soil is expressed via mean and cov. The soil parameters originate from the German design standard EAU [31].

Fig. 2
figure 2

Parameter definition to compare the random analyses to deterministic benchmark solutions

Full size image

As it will be shown in Sect. 3.1, currently available data does not support an uncertainty representation of drawdown parameters. The drawdown combinations used beyond Sect. 3.1 are thus based on literature and valid for a standardised rectangular trapezoidal waterway cross-section [28]. Combining loads and soil types, four case studies are investigated (see Table 1).

Table 1: Combinations of loads and soil types with their physical properties based on literature [28, 31]
Full size table

3 Results

3.1 Uncertainty of Loads

Two field campaigns conducted by the Bundesanstalt für Wasserbau (BAW) at Rhine river and Küsten Canal were used to investigate distributions and correlations of vessel-induced drawdowns. A campaign commonly lasted between one to two weeks. The measured values encompass dimensions and draught of the vessel, vessel velocity, passing distance and resulting water level fluctuations and flow velocities. Within the scope of this study only drawdowns are evaluated, which were recorded by absolute pressure probes at a minimum of two different heights.

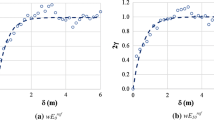
It was found that based on the existing data drawdown parameters (1) are difficult to describe by generally valid probability functions; a Lognormal distribution tends to fit the data best (see Fig. 3), although not all datasets confirm this result. (2) With a Pearson coefficient ρP = 0.2 there is no significant correlation between za and ta.

Fig. 3
figure 3

Examples of probability density functions of sternal drawdown height za and drawdown time ta. Probability density functions of bow drawdowns are similar

Full size image

Commonly, the armour layer thickness required to protect an embankment against slope sliding ranges between 0.60 and 0.80 m. The current analysis, however, results in armour layer thicknesses greater 1.00 m (see Fig. 4). It is assumed that, although, data analyses indicate a negligible correlation of za and ta, random parameter combination and large uncertainty inherent to distribution fitting results in overly large revetment dimensions. Despite this fact, the observations raise the question whether current design drawdowns represent the most critical cases. In the future, long-term observations may assist in determining distributions and correlations of the drawdown parameters as well as critical drawdown combinations.

For now, deterministic loads as proposed in MAR [28], which are obtained from conservative equations in combination with worst case design scenarios, are used for further analyses. From the available load combinations, the most unfavourable are chosen (see Sect. 2.2, Table 1).

Fig. 4
figure 4

Armour layer thickness obtained from the uncertainty analysis with random drawdown za and drawdown time ta. It is obvious that the analysis results in significantly larger revetment dimensions than usual

Full size image

3.2 Effect of Parameter Uncertainty of Random Friction Angle or Hydraulic Conductivity

Figure 5 illustrates the effects of distribution uncertainty of φ′ on the armour layer thickness for two distribution types. It is observed that neither the permeable sand (SW) nor the silty sand (SU) requires a thicker armour layer as a result of the different distribution types. Eventually, with covφ′ > 0.1, the Gaussian distribution may lead to larger armour layer thicknesses. This observation agrees with Schneider and Schneider [32], who recommend the use of Lognormal distributions in particular for larger coefficients of variation (covtotal > 0.3).

Fig. 5
figure 5

Armour layer thickness as a function of covφ′ for permeable sand (left, SW) and silty sand (right, SU). The effective friction angle is approximated by a Lognormal (LOG) and a Gaussian (GAUSS) distribution. The hatched areas indicate the deterministic benchmark solutions obtained with the 5 and 50% quantiles of φ′. The black graphs depict the 95% quantiles obtained from the uncertainty analysis with random φ′

Full size image

An increasing covφ′ leads to an increasing armour layer thickness. Depending on soil type and drawdown combination a maximum increase of 20 cm is observed for the investigated parameter range. In short, the uncertainty of covφ′ affects the uncertainty of the required armour layer thickness more than the choice of distribution. The design of less permeable soils is more strongly affected than the design of permeable soils.

The effects of the uncertainty of k on the required armour layer thickness are shown in Fig. 6. In contrast to φ′, literature clearly states that a Lognormal distribution is the most suitable choice for k. Compared to the results with random φ′, an uncertain k contributes more strongly to the uncertainty of the required armour layer thickness due to the larger variability of k. However, the required armour layer thickness does not rise linearly; the larger covk the smaller the increase of the armour layer thickness. Consequently, the variability of k affects the armour layer thickness less with increasing covk. In conclusion, the results confirm the recommendations of GBB [1] regarding the choice of the characteristic value of k as minimum observed in field or laboratory tests.

Fig. 6
figure 6

Armour layer thickness as a function of covk for permeable sand (SW) and silty sand (SU). The hydraulic conductivity is approximated by a Lognormal distribution. The hatched areas indicate the deterministic benchmark solutions obtained with the 5 and 50%quantiles of k. The black graphs depict the 95% quantiles obtained from the uncertainty analysis with random k.

Full size image

Finally, it is pointed out that for random φ′ and k the armour layer thickness in the SW cases is governed by the small ta at moderate za (SW2), whereas the armour layer thickness in the SU cases is governed by the large ta in combination with large za (SU1). This behaviour is explained by the time to reach a quasi-stationary state and, thus, the maximum excess pore pressure. In soils of smaller hydraulic conductivity it takes longer to reach a quasi-stationary state, while in permeable soils the quasi-stationary state is reached faster. In less permeable soil the maximum excess pore pressure is thus reached with large ta, whereas small ta do not allow the excess pore pressure to fully build up. As a result, the SU cases require larger armour layer thicknesses with larger, but slower drawdowns, whereas the SW cases require more armour stones with smaller, but faster drawdowns. The observation emphasises the importance of investigating different drawdown combinations to identify the most critical combination.

3.3 Effect of Parameter Uncertainty of Random Friction Angle and Hydraulic Conductivity

The armour layer thickness obtained when considering combinations of random φ′ and k is shown in Fig. 7. Again, the choice of the probability function does not significantly affect the result. As the minima of φ′ and k govern the design, there is hardly any difference between the results obtained with Lognormal (LOG) and Gaussian (GAUSS) φ′.

Compared to analyses with either random φ′ or k, the uncertainty inherent to the design increases when considering both, φ′ and k, as random. At the same time, it is observed that the random combination of φ′ and k results in smaller armour layer thicknesses than the deterministic 5% quantile result. Depending on the soil type, a maximum difference of approximately 15 cm is observed between deterministic benchmark solution and uncertainty analysis.

The analyses assume uncorrelated φ′ and k. However, in the case of the investigated parameters the correlation is slightly negative [32]. A zone that is characterised by small φ′ is more likely to be associated with high k and vice versa. Using the minima of φ′ and k as characteristic values may therefore result in a conservative design.

Fig. 7.
figure 7

Armour layer thickness as a function of covφ′,k for permeable sand (left, SW) and silty sand (right, SU). The effective friction angle is approximated by a Lognormal (LOG) and a Gaussian (GAUSS) distribution. The hatched areas indicate the deterministic benchmark solutions obtained with the 5% and 50% quantiles. The black graphs depict the 95% quantiles obtained from the uncertainty analysis with random φ′ and k.

Full size image

4 Discussion and Conclusions

The analyses demonstrate that the majority of uncertainty inherent to the geotechnical revetment design results from the employed load combinations. At present available data does not allow approximating drawdowns by means of probability functions. Long-term observations may assist in determining adequate distributions and correlations. With an increased observation period it may also be conceivable to apply extreme value theory to determine characteristic values. At present, it is recommended that a design or assessment of the geotechnical design should explore a number of drawdown combinations, e.g. obtained from field observations or from MAR [28], to identify the most relevant drawdown combination.

The analysis with random soil parameters indicates that the choice of distribution type does not affect the armour layer thickness significantly. In contrast to that, the variance of soil parameters affects the required armour layer thickness significantly; if considered separately, the minima of φ′ and k govern the design.

Considering uncorrelated or negatively correlated soil parameters, the minima φ′ and k as characteristic values may result in an overly conservative design. The presented uncorrelated reliability analyses indicate that the armour layer thickness may be reduced by a maximum of 15 cm if considering both, φ′ and k, as random variables. For practical design purposes, this means that using reliability-based methods with random soil parameters and the combined 95%-exceedance value may allow for a more economic design than using the 5%-characteristic values of φ′ and k. Further investigations regarding the required target reliability and a corresponding semi-probabilistic design approach with partial factors are required.

To conclude with, it is important to note that the stability of a slope in rapid drawdown situations depends on the local excess pore pressure and shear strength. Therefore, it may not be sufficient to examine the statistical variability of the soil parameters. Future investigations that account for the spatial variability of soil, e.g. by means of random fields, may supplement current knowledge regarding the choice of characteristic soil parameters.