Keywords

1 Introduction

By accounting uncertainty of load and material properties, civil engineering researchers like Freudenthal [1] changed the classic deterministic perspective of structural design towards a more scientific approach. Since 1950, substantial research has been done and published, e.g. refer to the CEB/FIP Bulletin No. 112 [2] or the “Probabilistic Model Code” documents [3], developed by the Joint Committee on Structural Safety. Furthermore, scientific committees provided the international code ISO 2394 “General principles on reliability for structures” [4] as a step for international standardisation of safety elements.

The goal of reliability analysis is to determinate the probability of failure with statistical methods. Safety elements can be derived by deterministic, the so-called “semi-probabilistic”, and probabilistic methods. Eurocode 0 [5] categorises such probabilistic methods into Level I (partial safety factors are assumed to achieve a certain failure probability), Level II (approximated calculation of the failure probability) and Level III (exact determination of the failure probability). The Eurocode itself uses Level I methods in the design equations and offers a generic description of Level II and Level III methods. Eurocode 0 [5] gives only a detailed view on the Mean Value First Order Second Moment Method (MVFOSM), which can be considered inconsistent regarding the reliability, as it is shown e.g. by Ricker [6].

In mathematical terms, the determination of the reliability index β is easier than the calculation of the probability of failure. Current international codes, as Eurocode 0 [5], provide different target values for the probability of failure and the respective reliability indices β, depending on certain boundary conditions, e.g. β = 3.8 is defined for a 50-year reference period. To calculate the probability of failure with Level II and Level III reliability methods, it is needed an algorithm to solve the multidimensional probability integral. In most cases, it is not possible to use analytic mathematic methods for joint density functions, depending on an arbitrary number of random variables with different distribution functions, and sophisticated limit state functions.

So far, there are few commercial software tools as well as non-commercial and open-source software tools for reliability analysis available. An example is the software tool “mistral” (Methods in Structural Reliability Analysis) that is written as a R-package [7]. The new software tool, which is described in this paper, has several more features (e.g. an algorithm for the automation of parametric studies) and more probabilistic methods are available.

2 Reliability Methods

The fundamental mathematical problem of reliability analysis is based on the assessment of the probability of failure pf by solving the following high-dimensional convolution integral:

$$ p_{f} = P\left( {g\left( {\vec{x}} \right)} \right) \le 0 = \mathop \smallint \limits_{{g\left( {\vec{x}} \right) \le 0}} F_{X} \left( {\vec{x}} \right){\text{d}}x $$
(1)

where \( g(\vec{x}) \) ≤ 0 is denoted the failure domain and fx(\( \vec{x} \)) is the joint probability density function of the basic random variables in a resistance or load function. In many cases, no analytical mathematical solution exists. Thus, only numerical methods give acceptable (or satisfactory) results. There are several reliability analysis techniques to calculate a reliability index and the respective probability of failure. Table 1 gives an overview on some common methods and their respective accuracy.

Table 1 Reliability methods
Full size table

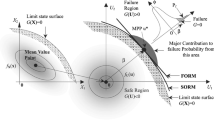
In the field reliability analysis in structural concrete members, FORM, SORM, and Monte Carlo simulation methods are the most relevant techniques. The solution of a high dimensional integral, which is the probability of failure, can be described as a (non-linear) optimisation problem with boundary conditions. Figure 1 illustrates the geometrical interpretation of the reliability index β in relation to the probability of failure and respective the safe region or the unsafe region (failure).

Fig. 1
figure 1

Fundamental mathematical problem of reliability analysis

Full size image

2.1 FORM Algorithm

The solution of a high dimensional integral can be described as a (non-linear) optimisation problem with side conditions. This optimisation problem is not simple and, therefore, leads to the development of several algorithms. One of the most relevant approximation methods, the so-called “First Order Reliability Methods” (FORM), were developed 40 years ago and are still considered as robust algorithms for the safety level assessment. In fact, the FORM methods have a great importance in civil engineering regarding code calibrating and reliability in general [8]. For an almost linear limit state function, the FORM algorithm provides satisfactory results that are comparable with the results attained with Level III methods.

The FORM algorithm is an iterative procedure and non-normal distributed random variables are approximated by the so called “Tail Approximation” whereby the density function fX(\( \vec{x} \)) and probability function FX(\( \vec{x} \)) in the point \( \vec{x}_{i}^{*} \) from the original distribution and the standard normal distribution are equalised. The Starting vector \( \vec{x}_{i = 1}^{*} \) is of great importance because it is possible that the algorithm finds local minimas.

Figure 2 shown the procedure of a common FORM algorithm.

Fig. 2
figure 2

Procedure of a FORM algorithm (adapted from [17])

Full size image

2.2 SORM Algorithm

The second-order reliability method (SORM) has been established as an attempt to improve the accuracy of the first-order methods, as the FORM. In first-order methods, since the limit state function is approximated by a linear function, accuracy problems can occur when the performance function is strongly nonlinear [9]. As opposed to the first-order methods, in the SORM, the integration boundary \( g\left( {\overrightarrow {x} } \right) \) = 0, denoted the limit-state surface, is no longer approximated by a hyperplane; instead, the boundary \( g\left( {\overrightarrow {x} } \right) \) = 0 is replaced by a paraboloid in a transformed standard normal space [10,11,12].

The requirements for this approximation are, however, that the limit state function is continuous near the approximation point and can be differentiated at least twice. Fundamentally, for convex functions \( g\left( {\overrightarrow {x} } \right) \) = 0 an approximation as a hypersphere and an approximation as a linear hyperplane represent an upper limit and a lower limit for the failure probability pf (Fig. 3).

Fig. 3
figure 3

Schematic representation of the integration areas (adapted from [18])

Full size image

It is assumed that, in the standard normal space, the reliability index β corresponds to the minimum distance from the origin of the axes to the limit state surface. The minimum distance point on the limit state surface is denoted the design point \( \vec{x}^{*} \).

In the curvature-fitting SORM, the paraboloid is defined by matching its principal curvatures to the principal curvatures of the limit state surface at the design-point \( \vec{x}^{*} \) [13]. To this end, Eq. (1) is transformed into a so-called quadric function. A quadric function depends on the number of variables and can be a curve, surface or hyper surface of second order. The basic variables Xi are converted into standard normal distributed variables Ui. The coordinate system (u1, u2, …, un) is rotated around its origin so that one of the coordinate axes coincides with the design point. In the new coordinate system, the design point has the coordinates (0, …, β). This rotation is carried out through an orthogonal transformation matrix by using, for example, the Gram-Schmidt orthogonalization algorithm. Then, at the design point, the principal curvatures of the limit-state surface are obtained as the eigenvalues of Hessian matrix [13].

The exact calculation of the probability of failure can be rather complex. Breitung [10], for example, has derived an asymptotic approximate equation that provides insight into the nature of the contribution of each curvature, where the probability of failure is expressed as:

$$ p_{f} \approx \varPhi \left( { - \beta } \right) \mathop \prod \limits_{i = 1}^{n - 1} \left( {1 - \beta \kappa_{i} } \right)^{ - 1/2} $$
(2)

in which Φ(.) is the standard normal cumulative distribution function, β is the distance from the coordinate origin (i.e. reliability index). The first term in Eq. (1) represents the first-order approximation of the failure probabilities pf, and the product term involving the quantities (1 – β ki), with β ki being the main curvatures at the design point, represents the second-order correction [13].

2.3 Monte Carlo Simulation

The Monte Carlo simulation method uses techniques of statistical calculation by generating uniform distributed (pseudo) random numbers. By generating a stochastically independent, high number of those random variables, the probability of failure can be calculated using Eq. (3):

$$ p_{F} = \frac{{n_{F} }}{N} $$
(3)

where N is the total number of realisations (or number of simulations) and nF is the number of simulations, for which the performance function is less or equal to zero: g ≤ 0).

If the number of realizations increases, the accuracy of the simulation will also increase, whereas the coefficient of variation will decrease.

For arbitrary types of distributions (e.g. lognormal, gamma, …), the generated uniformly distributed random variables have to be transformed with the probability function FX(\( \vec{x} \)), applicable for the certain distribution type (Fig. 4).

Fig. 4
figure 4

Principle of Monte Carlo simulation

Full size image

3 Implementation of Reliability Methods

Chapter 3 describes a new open-source software library for reliability analysis in civil engineering. The goal is to facilitate the adoption of reliability methods among engineers in practice as well as to provide an open platform for further scientific collaboration in software language “R” [14].

3.1 Description of Software Tool

The new library is being developed as a so-called “R package” in open-source programming software “R”. The package is capable of carrying out systematic parameter studies using different probabilistic reliability methods (e.g. FORM, SORM, Monte Carlo Simulation). Based on this, an overview on the probabilistic reliability methods implemented in the package as well as results of first parametric studies are given. The developed package allows to perform systematic and large parameter studies and provides different algorithms of reliability analysis in an effective way. The structure of the software tool is shown in Fig. 5.

Fig. 5
figure 5

Structure of the software tool

Full size image

3.2 Example of Parameter Study

As a practical example, the limit state function of the bending problem for steel reinforced concrete members is chosen. Equations (5) and (6) shows a formula of the state function g which is used for the parameter study.

$$ g = M_{R} - M_{E} $$
(4)
$$ M_{R} = \theta_{R} \cdot A_{s} \cdot f_{y} \cdot d \cdot \left( {1 - \frac{{A_{s} \cdot f_{y} }}{{2 \cdot d \cdot f_{c} }}} \right) $$
(5)
$$ M_{E} = \theta_{E} \cdot \left( {g + q} \right) \cdot \frac{{6^{2} }}{8} $$
(6)

Table 2 shows the statistical parameters of the basic variables (mean and standard deviation) and their distribution types.

Table 2 Limit state function 1
Full size table

In Fig. 6, the resulting reliability indices β are presented in dependence of the varied effective depth. For the parametric study, three different reliability methods (FORM, SORM, Monte Carlo) were used.

Fig. 6
figure 6

Results parameter study of bending problem

Full size image

It can be seen that the curvature of the limit state function shows the non-linear effect of the limit state function (Fig. 6). The results of the SORM algorithm (Level II) and the Crude Monte Carlo method (Level III) are almost the same, and therefore, it gives a first indication that the software is suitable for parametric studies with the reliability methods described in Chap. 2. The new software code is working well and this first example shows the effectiveness of the new software library, especially for large parameter studies.

4 Conclusions and Outlook

It is shown in this paper how different reliability methods can be implemented in program code. In addition, the results of a first parameter studies are presented to illustrate the correctness and functionality of the new software package.

The parametric study highlighted two important aspects. On the one hand, the implementation of reliability methods in civil engineering is an important step towards a wider application of statistical methods, to which this contribution should motivate. On the other hand, the parameter study presented shows the application of the probabilistic methods using a practical example with a nonlinear limit state function and non-normally distributed basic variables.

Furthermore, advanced reliability methods (e.g. Monte Carlo with Subset Sampling Simulation) will be implemented in the new R package. Further work will result in larger parameter studies, which will support the development of a new guideline for the application of reliability methods in civil engineering, and will continue the progress of reliability research mentioned in Chap. 1. In the project “TesiproV”, the authors will provide a new guideline, which describes certain techniques of code calibration, based on reliability methods, as well as the assessment of new partial safety factors.