On High-Precision $L^\infty$-stable IMEX Schemes for Scalar Hyperbolic Multi-scale Equations

Abstract

We present a framework to build high-accuracy IMEX schemes that fulfill the maximum principle, applied to a scalar hyperbolic multi-scale equation. Motivated by the findings in [5] that implicit R-K schemes are not $L^\infty$-stable, our scheme, for which we can prove the $L^\infty$ stability, is based on a convex combination between a first-order and a class of second-order IMEX schemes. We numerically demonstrate the advantages of our scheme, especially for discontinuous problems, and give a MOOD procedure to increase the precision.

1 Introduction

We consider the scalar multi-scale equation

$$\begin{aligned} w_t + c_e w_x + \frac{c_i}{\varepsilon } w_x = 0, \end{aligned}$$

(1)

where we set the constants $c_e, c_i > 0$ and the parameter $\varepsilon >0$. The model (1) mimics the behavior of the isentropic Euler equations with a slow speed $c_e$ and a fast speed $c_i/\varepsilon$, where $\varepsilon$ corresponds to the square of the Mach number. We treat the derivative $w_x$ associated with the slow scale $c_e$ explicitly, whereas $w_x$ associated with the fast scale $c_i/\varepsilon$ is treated implicitly in time due to the stiffness introduced by $\varepsilon < 1$. For computational efficiency, the resulting CFL condition, and therefore the time step, has to be independent of $\varepsilon$. In space, we apply an upwind discretization because, already having in mind the non-linear nature of e.g. the Euler equations, using a central scheme for the implicit part will not lead to a $L^\infty$-stable scheme, as shown in [4] for a non-linear system.

The discretization of time and space follows the usual finite difference framework. The space domain $[x_1,x_N]$ is partitioned in N uniformly spaced points $(x_j)_{j \in [1,N]}$, with the step size $\Delta x$. We discretize the time variable with $t^n = n \Delta t$, where $\Delta t$ denotes the time step. Then, the solution w(t, x) of (1) at $(t^n,x_j)$ is approximated by $w_j^n$. The first-order implicit-explicit (IMEX) discretization of (1) is given by

$$\begin{aligned} w_j^{n+1} = w_j - \lambda (w_j^n - w_{j-1}^n) - {\mu _\varepsilon }(w_j^{n+1} - w_{j-1}^{n+1}), \end{aligned}$$

(2)

where we define $\lambda = c_e \frac{\Delta t}{\Delta x}$ and ${\mu _\varepsilon }= \frac{c_i}{\varepsilon } \frac{\Delta t}{\Delta x}$ for abbreviation. Note that $\lambda , {\mu _\varepsilon }>0$.

We are interested in IMEX schemes that meet the maximum principle. Here, we focus on $L^\infty$-stable schemes, where a scheme is said to be $L^\infty$-stable if

$$\begin{aligned} \Vert w^{n+1}\Vert _\infty = \underset{ j \in \llbracket 1, N \rrbracket }{\max } |w_j^{n+1}| \le \Vert w^n\Vert _\infty . \end{aligned}$$

(3)

As proven in [3], the first-order scheme (2) is $L^\infty$-stable and TVD. Furthermore, as proven in [5], implicit Runge-Kutta schemes, and consequently second-order IMEX schemes, are not $L^\infty$-stable. Therefore, we would like to propose a convex combination of (2) with a second-order IMEX scheme and give conditions for the $L^\infty$ stability for the resulting scheme. We define the convex combination between the first-order scheme $w^{n+1,1\text {st}}_j$ and a second-order update $w^{n+1,2\text {nd}}_j$ for a parameter $\theta \in (0,1)$ as:

$$\begin{aligned} w^{n+1}_j = (1 -\theta )~ w^{n+1,1\text {st}}_j + \theta ~ w^{n+1,2\text {nd}}_j. \end{aligned}$$

(4)

2 IMEX Formulation

Generic formulations of an IMEX scheme introduce two $s\times s$ matrices $A = (a_{ij})$ and $\tilde{A}~=~(\tilde{a}_{ij})$, as well as two vectors $b,\tilde{b} \in \mathbb {R}^s$. They are regrouped in two linked Butcher tableaux

$$\begin{aligned} \begin{array}{c|c} c \, &{} A \\ \hline &{} \, b^T \end{array}, \qquad \qquad \begin{array}{c|c} \tilde{c} \, &{} \tilde{A} \\ \hline &{} \, \tilde{b}^T \end{array}. \end{aligned}$$

The coefficients $c, \tilde{c}$ are only necessary if the right hand side depends explicitly on time. In the following we will use the pairs (A, b) for the implicit and $(\tilde{A}, \tilde{b})$ for the explicit part. To reduce computational costs, we take A to be lower triangular and $\tilde{A}$ to be strictly lower triangular. Applying the IMEX formulation on (1), we obtain the following scheme:

$$\begin{aligned} w^{n+1} = w^n - c_e \Delta t \sum _{k=1}^{s} \tilde{b}_k w^{(k)}_x - \frac{c_i}{\varepsilon } \Delta t \sum _{k=1}^{s} b_k w^{(k)}_x, \end{aligned}$$

(5)

with the stages

$$\begin{aligned} w^{(k)} = w^n - c_e \Delta t \sum _{l=1}^{k-1} \tilde{a}_{kl} w^{(l)}_x - \frac{c_i}{\varepsilon }\Delta t \sum _{l=1}^{k} a_{kl} w^{(l)}_x. \end{aligned}$$

(6)

IMEX Runge-Kutta (R-K) schemes can be classified depending on the structure of the matrix A.

Definition 1

An IMEX R-K method is said to be of type CK (Carpenter and Kennedy [6]) if the matrix can be written as

where and is invertible. In the case where $a=0$, the scheme is said to be of ARS type (Asher, Ruuth and Spiteri [1]).

In the following we will consider a second-order 2-stage and a second-order 3-stage IMEX R-K method of type CK. To obtain a second-order scheme, there are the following compatibility conditions [9]:

$$\begin{aligned} \begin{aligned}&\sum _{k=1}^s \tilde{b}_k = 1 ; \quad \sum _{k=1}^s b_k = 1 ; \quad \forall k,\, \tilde{c}_k = \sum _{l=1}^{k-1} \tilde{a}_{kl} ; \quad \forall k,\, c_k = \sum _{l=1}^{k-1} a_{kl} \, ; \\&\sum _{k=1}^s \tilde{b}_k \tilde{c}_k = \frac{1}{2} ; \quad \sum _{k=1}^s \tilde{b}_k c_k = \frac{1}{2} ; \quad \sum _{k=1}^s b_k \tilde{c}_k = \frac{1}{2} ; \quad \sum _{k=1}^s b_k c_k = \frac{1}{2}. \end{aligned} \end{aligned}$$

(7)

2.1 A 2-Stage CK Type IMEX R-K Method

For a 2-stage CK type method, we have the following Butcher tableaux, with $a_{22}~\ne ~0$:

(8)

With the compatibility conditions (7), we can simplify (8) to

(9)

where $\alpha - \gamma \ne 0$ and $\alpha \ne 0$.

Using (5), (6) and (9), we can define the second-order discretization of (1) as

$$\begin{aligned} \begin{aligned} w^{(1)}_j&= w_j^n - \lambda \alpha (w_j^n - w_{j-1}^n) - \gamma {\mu _\varepsilon }(w_j^n - w_{j-1}^n) - {\mu _\varepsilon }(\alpha - \gamma ) (w_j^{(1)} - w_{j-1}^{(1)}), \\ w^{n+1}_j&= w_j^n - \left( 1 - \frac{1}{2 \alpha }\right) (\lambda + {\mu _\varepsilon }) (w_j^n - w_{j-1}^n) - \frac{1}{2\alpha }(\lambda + {\mu _\varepsilon }) (w_j^{(1)} - w_{j-1}^{(1)}). \end{aligned} \end{aligned}$$

(10)

Due to the matrix structure of the CK type R-K scheme, we have only two computational steps. The first one computes $w^{(1)}$, and the second one $w^{n+1}$. The convex combination (4) between the schemes (2) and (10), with the shorter notation $\Delta = w_j - w_{j-1}$, is given by:

(11)

We can sort (11) by grouping the $w^{n+1}$ and $w^{(1)}$ terms:

$$\begin{aligned}&\begin{aligned} (1 + {\mu _\varepsilon }(\alpha - \gamma ) )w^{(1)}_j - {\mu _\varepsilon }(\alpha - \gamma ) w_{j-1}^{(1)} = (1&- (\lambda \alpha + \gamma {\mu _\varepsilon }))w_j^n \\&+ (\lambda \alpha + \gamma {\mu _\varepsilon }) w_{j-1}^n, \end{aligned} \end{aligned}$$

(12)

$$\begin{aligned}&\begin{aligned} (1 + (1-\theta ){\mu _\varepsilon })w^{n+1}_j - (1-\theta ){\mu _\varepsilon }w_{j-1}^{n+1} = w_j^n&- \left( \lambda - \theta \frac{1}{2\alpha }(\lambda + {\mu _\varepsilon }) + \theta {\mu _\varepsilon }\right) \Delta ^n \\&- \theta \frac{1}{2\alpha }(\lambda + {\mu _\varepsilon }) \Delta ^{(1)}. \end{aligned} \end{aligned}$$

(13)

In the following, we will assume periodic boundary conditions. We will prove the $L^\infty$ stability (3) by starting with the proof of $\Vert w^{(1)}\Vert _\infty \le \Vert w^n\Vert _\infty$. For each time step, we will use the triangle inequality $|x + y| \le |x| + |y|$ and the reverse triangle inequality $|x| - |y| \le |x - y|$ for $x,y\in \mathbb {R}$. To apply use those inequalities, we require in (12)

(14)

(15)

(16)

(17)

Using equation (12), we can now write the following estimate for $\Vert w^n\Vert _\infty$:

$$\begin{aligned} \begin{aligned} \Vert w^n\Vert _\infty&= (1 -(\lambda \alpha + \gamma {\mu _\varepsilon }))\Vert w^n\Vert _\infty + ( \lambda \alpha + \gamma {\mu _\varepsilon })\Vert w^n\Vert _\infty \\&\ge \Vert (1 -(\lambda \alpha + \gamma {\mu _\varepsilon }))w^n_j + ( \lambda \alpha + \gamma {\mu _\varepsilon })w^n_{j-1}\Vert _\infty \\&= \Vert (1 + {\mu _\varepsilon }(\alpha - \gamma ) )w^{(1)}_j - {\mu _\varepsilon }(\alpha - \gamma ) w_{j-1}^{(1)}\Vert _\infty \\&\ge (1 + {\mu _\varepsilon }(\alpha - \gamma ) )\Vert w^{(1)}\Vert _\infty - {\mu _\varepsilon }(\alpha - \gamma ) \Vert w^{(1)}\Vert _\infty \\&= \Vert w^{(1)}\Vert _\infty . \end{aligned} \end{aligned}$$

From requirement (14), we get that $\alpha c_e + \gamma \frac{c_i}{\varepsilon } \ge 0$. In order to get a Butcher tableau independent of $\varepsilon$, we require $\alpha > 0$ and $\gamma \ge 0$. Relation (15) leads to a CFL condition $\frac{\Delta t}{\Delta x}(\alpha c_e + \gamma \frac{c_i}{\varepsilon }) \le 1$. Note that, due to computational efficiency, we seek a time step restriction independent of $\varepsilon$. Therefore, we must take $\gamma = 0$, which is compatible with the restriction $\gamma \ge 0$. With those settings, (16) and (17) are always fulfilled.

Let us prove now that $\Vert w^{n+1}\Vert _\infty \le \Vert w^n\Vert _\infty$. First, we rewrite (12) as follows:

$$\begin{aligned} -{\mu _\varepsilon }\Delta ^{(1)} = \frac{1}{\alpha } w_j^{(1)} - \frac{1}{\alpha } w_j^n + \lambda (w_j^n - w_{j-1}^n). \end{aligned}$$

(18)

After inserting (18) into (13), we obtain further conditions given by

$$\begin{aligned} r_1 = 1- \frac{\theta }{2 \alpha ^2} + \lambda \left( -1 + \frac{\theta }{\alpha }\right) + {\mu _\varepsilon }\theta \left( -1 + \frac{1}{2 \alpha }\right)&\ge 0, \end{aligned}$$

(19)

$$\begin{aligned} r_2 =\lambda \left( 1 - \frac{\theta }{\alpha }\right) + {\mu _\varepsilon }\theta \left( 1 - \frac{1}{2 \alpha }\right)&\ge 0, \end{aligned}$$

(20)

$$\begin{aligned} \frac{\theta }{2 \alpha ^2} - \frac{\theta \lambda }{2 \alpha }&\ge 0. \end{aligned}$$

(21)

Using (13), as well as the above conditions, we obtain the following estimate

$$\begin{aligned} \begin{aligned} \Vert w^{n+1}\Vert _\infty&= (1 + (1-\theta ){\mu _\varepsilon })\Vert w^{n+1}\Vert _\infty - (1-\theta ){\mu _\varepsilon }\Vert w^{n+1}\Vert _\infty \\&\le \Vert (1 + (1-\theta ){\mu _\varepsilon })w^{n+1}_j - (1-\theta ){\mu _\varepsilon }w^{n+1}_{j-1}\Vert _\infty \\&= \Vert r_1 w_j^n + r_2 w_{j-1}^n + ({\mu _\varepsilon }- \frac{\theta \lambda }{2 a}) w_j^{(1)} + \frac{\theta \lambda }{2 \alpha } w_{j-1}^{(1)}\Vert _\infty \\&\le \left( 1-\frac{\theta }{2 \alpha ^2} \right) \Vert w^n\Vert _\infty + \frac{\theta }{2 \alpha ^2} \Vert w^{(1)}\Vert _\infty \\&\le \Vert w^n\Vert _\infty , \end{aligned} \end{aligned}$$

which shows the $L^\infty$ stability. From the constraints (19)–(21), we can compute the final estimates for the free parameters $\alpha ,\theta ,\lambda$. The condition (21) gives a CFL restriction of $\lambda \le \frac{1}{\alpha }$. Since we want to avoid a dependence of $c_e, c_i$ or $\varepsilon$ on $\alpha$ and $\theta$, we need in (20) $1 - \frac{\theta }{\alpha } \ge 0$, that is $\alpha \ge \theta$ and $1 - \frac{1}{2 a} \ge 0$, which leads to $\alpha \ge \frac{1}{2}$. With the same motivation, we need $-1 + \frac{1}{2 \alpha } \ge 0$ in (19), that is $\alpha \le \frac{1}{2}$. Together it follows that $\alpha = \frac{1}{2}$ and we get from (19) the final CFL condition $\lambda \le 1$. With $\alpha = \frac{1}{2}$ and $\gamma = 0$ fixed, we have recovered a 2-stage ARS type method with the midpoint rule as the implicit part, given by

(22)

The above results are summed up in the following theorem:

Theorem 1

For periodic boundary conditions and under the CFL condition

$$\begin{aligned} \Delta t \le \frac{\Delta x}{c_e}, \end{aligned}$$

the scheme consisting of the convex combination of the first-order scheme (2) and the second-order scheme constructed from (22) is $L^\infty$-stable as long as $\theta \le \frac{1}{2}$.

Remark 1

In order to have the maximal input of the second-order scheme, we would want to set $\theta = \theta _{\text {opt}} = \frac{1}{2}$. With this choice of $\theta$, the restriction (19) for $\alpha = \frac{1}{2}$ is satisfied immediately and we get the less restrictive CFL condition

$$\begin{aligned} \Delta t \le 2\frac{\Delta x}{c_e}. \end{aligned}$$

Unfortunately, the midpoint rule with the above CFL condition and $\theta = \theta _{\text {opt}}$ exactly reduces to two steps of a first-order scheme. We therefore advise $\theta < \frac{1}{2}$ to get a second-order scheme.

Since $\gamma =0$, the initial CK type method (9) reduces to an ARS type method (22). This observation is summarized in the following corollary

Corollary 1

If there is a second-order CK type IMEX R-K scheme of the form (9) that is $L^\infty$-stable in the convex combination with (2) under a CFL condition independent of $\varepsilon$, then it has to be of ARS type.

2.2 A 3-Stage CK Type IMEX R-K Method

In this section, we adapt the derivation of the 2-stage case to a 3-stage CK type method. It is described by the following Butcher tableaux, with $a_{22} \ne 0$ and $a_{33} \ne 0$:

(23)

To have the same number of computational steps as in the 2-stage scheme (5), we have set $b = (a_{3j})$ and $\tilde{b} = (\tilde{a}_{3j})$.

With the second-order compatibility conditions (7) and $a_{22} = \beta$ and $a_{33} = \alpha$, we introduce $\kappa = \frac{2(\gamma + \beta )(1-\alpha )+2\alpha -1}{2(\gamma +\beta )}$ and simplify (23) to:

(24)

Analogously to (10), we can write the second-order scheme using (24) as

$$\begin{aligned}&\qquad w^{(1)}_j + {\mu _\varepsilon }\beta \Delta ^{(1)} = w^n_j - (\lambda (\gamma + \beta ) + {\mu _\varepsilon }\gamma )\Delta ^n \\&w^{n+1}_j + {\mu _\varepsilon }\alpha \Delta ^{n+1} = w_j^n - \left( \lambda \frac{2(\gamma + \beta )-1}{2(\gamma + \beta )} + \kappa {\mu _\varepsilon }\right) \Delta ^n \\&\qquad \qquad \qquad \qquad \qquad \qquad - \left( \lambda \frac{1}{2(\gamma + \beta )} + {\mu _\varepsilon }\frac{1- 2\alpha }{2(\gamma + \beta )}\right) \Delta ^{(1)}. \end{aligned}$$

We conduct an analogous analysis as in the 2-stage case, which results in the following ARS-type IMEX R-K method for $\beta \in (0,\frac{1}{2})$:

(25)

One example for (25) is the widely used ARS(2,2,2) method with $\beta = 1 - \frac{ \sqrt{2} }{2}$, see [1].

Theorem 2

For periodic boundary conditions and under the CFL condition

$$\begin{aligned} \Delta t \le \frac{\Delta x}{c_e}, \end{aligned}$$

the scheme consisting of the convex combination of the first-order scheme (2) and the second-order scheme constructed from (25) with $\beta \in (0,\frac{1}{2})$ is $L^\infty$-stable as long as $\theta \le 2 \beta (1-\beta )$.

Remark 2

In order to have the maximal input of the second-order scheme, we set

$$\begin{aligned} \theta _{\text {opt}} = 2 \beta (1-\beta ). \end{aligned}$$

(26)

With the choice $\theta = \theta _{\text {opt}}$, we get the less restrictive CFL condition

$$\begin{aligned} \Delta t \le C_{\text {opt}} \frac{\Delta x}{c_e} \text {, where } C_{\text {opt}} = \frac{1}{1-\beta }. \end{aligned}$$

(27)

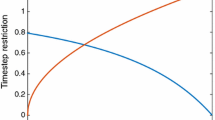
The values of $\theta _{\text {opt}}$ and $C_{\text {opt}}$ are displayed with respect to $\beta$ in Fig. 1.

/2 /2

Fig. 1

Values of the optimal convex combination parameter $\theta _{\text {opt}}$ (left panel) and the optimal CFL number $C_{\text {opt}}$ (right panel), with respect to the IMEX parameter $\beta$.

Remark 3

Allowing $\beta = \frac{1}{2}$, the 3-stage ARS type method (25) reduces to the 2-stage ARS type method using the midpoint rule (22). In addition, the choice $\beta = \frac{1}{2}$ maximizes both $\theta _{\text {opt}}$ and $\lambda$.

Corollary 2

If there is a second-order CK type IMEX R-K scheme of the form (25) that is $L^\infty$-stable in the convex combination with (2) under a CFL condition independent of $\varepsilon$, then it has to be of ARS type.

3 Numerical Results

This section is dedicated to providing numerical experiments to test the schemes introduced above:

• The first-order scheme given by (2),

• The second-order scheme given by (25),

• The $L^\infty$-stable scheme obtained via the convex combination with the parameter $\theta = \theta _{\text {opt}}$ given by (26), between the first-order scheme (2) and the second-order scheme (25),

• The MOOD scheme resulting from an optimal order detection procedure explained in Sect. 3.1 and applied to the $L^\infty$-stable scheme.

Throughout this section, the space domain is given by [0, 1] and periodic boundary conditions are prescribed. The time domain is given by $[0, t_{\text {end}}]$, where $t_{\text {end}}$ chosen such that the exact solution completes exactly one revolution of the space domain, as follows:

$$\begin{aligned} t_{\text {end}} = \frac{1}{ c_e + \frac{c_i}{\varepsilon } }. \end{aligned}$$

Unless otherwise mentioned, the space and time discretizations are linked with the optimal CFL condition defined by (27). The constants $c_e$ and $c_i$ are both taken equal to 1.

We start this section with an introduction to an order detection procedure in Sect. 3.1. Then, we provide a way to choose the parameter $\beta$ in Sect. 3.2. Finally, in Sect. 3.3, we provide several numerical tests with smooth and especially non-smooth exact solutions. The smooth exact solution is given by

(28)

and describes the transport of a sine wave of amplitude $\varepsilon$. The discontinuous exact solution is given by

(29)

which corresponds to the transport of a square wave of amplitude $\varepsilon$.

3.1 Optimal Order Detection: A MOOD-like Technique

The $L^\infty$-stable scheme is a convex combination between the diffusive first-order scheme and the oscillatory second-order scheme. Since those oscillations may violate the maximum principle, we do not wish to use the second-order scheme everywhere in the computational domain. Using the $L^\infty$-stable scheme introduces enough diffusion to get rid of the oscillations and to ensure the maximum principle. However, once the diffusion has been introduced, there is no need to add even more diffusion and the second-order scheme could be used until its result once again violates the maximum principle, at which point the $L^\infty$-stable scheme is necessary once again.

The procedure outlined above is akin to the Multidimensional Optimal-Order Detection techniques developed in the MOOD framework (see for instance [2]). It results in the MOOD scheme, given by the algorithm below:

Algorithm If the exact solution is bounded between $w_\text {min}$ and $w_\text {max}$, using the optimal CFL number (27), the MOOD scheme is given as a result of applying the following algorithm at each time step.

• 1. Compute the second-order solution.

• 2. Detect if this second-order solution breaks the maximum principle, i.e. if it oscillates below $w_\text {min}$ or above $w_\text {max}$.

• 3. If the maximum principle is violated, compute and output the solution given by the $L^\infty$-stable scheme; otherwise, output the second-order solution.

This algorithm ensures a drastic improvement in the numerical results when this procedure is used instead of using the $L^\infty$-stable scheme at each time step.

3.2 Choice of $\beta$ in the 3-Stage Method

This first set of numerical experiments is dedicated to providing a way to choose an optimal value for $\beta$. At the moment, we know that $\beta \in (0, 1/2)$ and we are able to find a non-zero value of $\theta$ for all values of $\beta$. According to Fig. 1, the optimal CFL number as well as the optimal $\theta$ increase as $\beta$ goes to 1/2. Therefore, it would be tempting to take $\beta$ as close to 1/2 as possible. To check whether this preliminary analysis is accurate, we study the CPU time and the $L^\infty$ error of the scheme with respect to $\beta$, in order to suggest an optimal value of $\beta$.

Throughout this set of numerical experiments, we consider the smooth exact solution (28) with $\varepsilon = 10^{-1}$.

Study of the CPU time. The CPU time taken by our program is influenced by $\beta$ because the CFL number $C_{\text {opt}}$, given by (27), itself depends on $\beta$. Indeed, as $\beta$ varies from 0 to 1/2, $C_{\text {opt}}$ ranges between 1 and 2, as evidenced in Fig. 1.

Fig. 2

CPU time (in milliseconds) with respect to the IMEX parameter $\beta$, using the optimal values $\theta _{\text {opt}}$ and $C_{\text {opt}}$, in the context of the test case presented in Sect. 3.2.

In Fig. 2, we note that the CPU time for the $L^\infty$-stable and MOOD schemes decreases when $\beta$ tends to 1/2. This was expected as the CFL number $C_{\text {opt}}$ is increasing with $\beta$, thus allowing for larger time steps. Let us also note that the MOOD procedure is not very costly for this smooth test case. Moreover, we remark that the second-order scheme takes twice as much CPU time as the first-order scheme, which is also expected due to the additional intermediate step.

Study of the $L^\infty$ Error. Now, we turn to the study of the $L^\infty$ error with respect to $\beta$. For $\beta \in (0,1/2)$, the $L^\infty$-stable and MOOD schemes are $L^\infty$-stable, but this property alone does not indicate their precision. From now on, we take the optimal CFL number $C_{\text {opt}}$.

Fig. 3

$L^\infty$ error with respect to the IMEX parameter $\beta$, using the optimal values $\theta _{\text {opt}}$ and $C_{\text {opt}}$, in the context of the test case presented in Sect. 3.2. The right panels contain a zoom on the left panel data.

In Fig. 3, we observe that the second-order scheme is, as expected, much more precise than the first-order one. In addition, we note that the $L^\infty$-stable scheme is more precise than the first-order one, but not by a large margin. Finally, we remark that the MOOD procedure is essential to improve the precision of the $L^\infty$-stable scheme.

Regarding the choice of $\beta$, we note on the top right panel that the $L^\infty$-stable scheme reduces to the first-order one in two cases. When $\beta = 0$, we get $\theta _{\text {opt}} = 0$, and the convex combination consists only in the first-order scheme. When $\beta = 1/2$, we get $\theta _{\text {opt}} = 0$ and $C_{\text {opt}} = 2$, and the convex combination actually coincides with the first-order scheme. Between these two values, the $L^\infty$ error produced by the $L^\infty$-stable scheme reaches a minimum. Interestingly, this minimum is close to the point where the MOOD error starts increasing (see the bottom right panel). We note that this minimum is located around $\beta \simeq 1 - \sqrt{2}/2$, which is widely used e.g. in [1, 3, 9].

Conclusion: Choice of $\beta$. In this first study, we have observed that:

• the CPU time gets smaller as $\beta$ gets larger;

• the $L^\infty$ error reaches a minimum at $\beta = 1 - \sqrt{2}/2$.

Based on this observations, we define $\beta _{\text {opt}}$, which will be used in the remainder of this article, as

$$\begin{aligned} \beta _{\text {opt}} = 1 - \frac{\sqrt{2}}{2}. \end{aligned}$$

3.3 Numerical Tests

Before we start with the numerical results, we want to remark that we do not consider an increase in space order. Such an increase, and its effect on smooth solutions, has been documented at length in [3]. Therein was concluded that, if $\varepsilon$ is close to 1, then using a second-order scheme in time and a first-order scheme in space does not provide a significant and observable gain compared to a first-order scheme in time and space. Conversely, if $\varepsilon$ is close to 0, then using a first-order scheme in time and a second-order scheme in space does not provide a significant and observable gain compared to a first-order scheme in time and space.

Therefore, we focus here only on second-order time accuracy whereas accuracy in space will be studied in forthcoming work.

3.3.1 Smooth Solution: Order of Accuracy

To demonstrate that our schemes reach the desired order of accuracy, we compute $L^\infty$ error curves with the smooth initial condition (28). In Fig. 4, we display the $L^\infty$ error with respect to the number of discretization points for the four schemes under consideration.

Fig. 4

$L^\infty$ error curves for the smooth solution (28), with $\varepsilon = 10^{-2}$.

We note, as expected, that the first- and second-order schemes are respectively first- and second-order accurate. Moreover, the $L^\infty$-stable scheme is first-order accurate, and the MOOD procedure greatly increases the precision of the $L^\infty$-stable scheme, almost bringing it to the level of the second-order scheme. The loss of precision of the MOOD scheme compared to the second-order scheme is due to the fact that the MOOD scheme is $L^\infty$-stable, contrary to the second-order scheme, and therefore it does not allow any violation of the maximum principle, even if such a violation would result in a precision increase.

As a consequence, the MOOD procedure is especially well-suited for smooth problems where the maximum principle is important. Let us now compare these approaches on a discontinuous solution, where we expect the $L^\infty$-stable scheme to be of greater interest.

3.3.2 Discontinuous Solution

We now consider the following discontinuous exact solution $w_{\text {ex}}$. In Fig. 5, we display the results of the four schemes for different values of $\varepsilon$.

Fig. 5

Approximation of the discontinuous solution (29). From left to right and top to bottom, we have taken: $\varepsilon = 1$ and $N = 40$, $\varepsilon = 10^{-1}$ and $N = 220$, $\varepsilon = 10^{-2}$ and $N = 2000$, $\varepsilon = 10^{-3}$ and $N = 20000$. These large values of N have been chosen to ensure that 20 time iterations are systematically needed to reach $t_{\text {end}}$. If smaller values are taken, the time steps are too large to visualize noticeable differences between the schemes.

We first notice in the top left panel that the approximation of the exact solution is similar for all four schemes in the case of $\varepsilon =1$.

In the other three panels, for $\varepsilon \in \{ 10^{-1}, 10^{-2}, 10^{-3} \}$, we note that the first-order scheme is always in-bounds, while the second-order scheme always violates the maximum principle. Here, we observe a clear improvement when using the $L^\infty$-stable scheme, but the result is still somewhat diffusive. The MOOD procedure allows another gain in precision compared to the first-order scheme, while still staying in-bounds.

This underlines the necessity of $L^\infty$-stable schemes when approximating discontinuous solutions. In addition, the MOOD procedure is useful when approximating continuous and discontinuous solutions with good precision, while respecting the maximum principle.

Fig. 6

$L^1$ (left panels) and $L^1_o$ (right panels) error curves for the discontinuous solution (29), for $\varepsilon = 1$ (top panels) and $\varepsilon = 10^{-2}$ (bottom panels).

The final numerical experiment consists in quantifying how much better the result of the $L^\infty$-stable scheme is, compared to both first- and second-order approximations, when considering a discontinuous solution. To address such an issue, we cannot simply compute the error in the $L^\infty$ norm. Indeed, this norm is not well-suited for measuring the errors produced when approximating a discontinuous exact solution with a diffusive approximation. Instead, we turn to the $L^1$ norm, as well as a modification, the $L^1_o$ quasinorm, which does not satisfy the triangle inequality property of a norm but enables us to measure relevant errors, defined as follows:

$$\begin{aligned} \Vert w^n \Vert _{L^1_o} = \frac{1}{\Delta x} \sum _j \left( |w_j^n| + \max _{m \le n} \left[ \left( \max _j w_j^m - \min _j w_j^m \right) - \left( \max _j w_j^0 - \min _j w_j^0 \right) \right] \right) . \end{aligned}$$

This quasinorm is the $L^1$ norm added to a quantity which has been designed to measure only overshoots and undershoots. This quantity encodes how much the numerical solution violates the maximum principle. Therefore, we expect this added term to vanish as soon as the $L^\infty$-stable scheme, with or without MOOD, is employed.

In the top panels of Fig. 6, we note that, for $\varepsilon = 1$, both errors take similar values for the four schemes under consideration. This is due to the fact that there are few spurious oscillations in this case (see Fig. 5, top left panel). In addition, we observe that the scheme is accurate up to order 1/2 which is expected when approximating discontinuous solutions, see for instance [7].

Now, looking at the bottom left panel, we note that the $L^1$ error is lower for the second-order scheme than for the other ones and that the orders of accuracy of all schemes tend to 1/2 for large enough N. However, the bottom right panel, which takes into account the over- and undershoots when computing the error, paints another picture: the second-order scheme is actually the worst of all four. In addition, the error actually stays roughly constant when the number of discretization points increases. This means that, as N increases, the gains in $L^1$ error seem to be compensated by an increase of the overshoot and undershoot amplitude.

4 Conclusions and Future Work

We have presented a way of constructing $L^\infty$-stable IMEX schemes that, combined with a MOOD procedure, yield high-precision approximate solutions for stiff and non-stiff systems. As we have demonstrated with simple numerical examples, for non-stiff systems higher order IMEX R-K schemes still give good results although violating the maximum principle, whereas for stiff systems they produce spurious oscillations and $L^\infty$-stable schemes are needed to give accurate solutions. In this work, we have mainly focused on the time accuracy and have neglected higher order space discretizations. This, together with the extension to TVD and higher order IMEX schemes, is explored in [8]. In addition, for physical applications, asymptotic preservation properties, as well as scale-independent diffusion, will be studied.