1 Introduction

In this work, our aim is to study the dynamics of a higher-order Ginzburg–Landau type equation. In particular, the model under consideration has the form of a higher-order nonlinear Schrödinger (NLS) equation incorporating gain and loss. The origin of our motivation is the following dimensionless higher-order NLS equation:

$$\displaystyle \begin{gathered} {} \partial_t u + \frac{{\mathrm{i}}s}{2} \partial_x^2 u - \mathrm{i}|u|{}^2u =\beta \partial_x^3 u+\mu \partial_x (|u|{}^2u) +\left(\nu-\mathrm{i}\sigma_R\right)u \partial_x(|u|{}^2), \end{gathered} $$
(1)

where u(x, t) is a complex field, β, μ, ν and σ R are real constants, while s = ±1 stands for normal (s = +1) or anomalous (s = −1) group-velocity dispersion. Note that Equation (1) can be viewed as a perturbed NLS equation, with the perturbation—in case of small values of relevant coefficients—appearing in the right-hand side (see, e.g., Refs. [1,2,3]).

Variants of Equation (1) appear in a variety of physical contexts, where they are derived at higher-order approximations of perturbation theory [the lowest-order nonlinear model is simply the NLS equation in the left-hand side of Equation (1)]. The most prominent example is probably that of nonlinear optics [1,2,3]. In this case, t and x denote propagation distance and retarded time (in a reference frame moving with the group velocity), respectively, while u(x, t) is the complex electric field envelope.

For β = μ = ν = σ R = 0, Equation (1) reduces to the unperturbed equation, i.e., the completely integrable NLS [4], which supports bright soliton solutions (for s = −1) [5], or dark soliton solutions (for s = +1) [6]. As concerns the origin of the higher-order terms, we mention the following. While the unperturbed NLS equation is sufficient to describe optical pulse propagation, for ultra-short pulses, third-order dispersion and self-steepening (characterized by coefficients β, μ and ν, respectively) become important and have to be incorporated in the model. Similar situations also occur in other contexts and, thus, corresponding versions of Equation (2) have been derived and used, e.g., in the context of nonlinear metamaterials [7,8,9], but also in the problem of water waves in finite depth [10,11,12]. Moreover, in the context of optics, and for relatively long propagation distances, higher-order nonlinear dissipative effects, such as the stimulated Raman scattering (SRS) effect, of strength σ R > 0, are also important [1,2,3].

In addition to the above mentioned effects, our aim is to investigate the dynamics in the framework of Equation (1), but also incorporating linear or nonlinear gain and loss. This way, we are going to analyze the following model:

$$\displaystyle \begin{gathered} {} \partial_t u + \frac{{\mathrm{i}}s}{2} \partial_x^2 u - \mathrm{i}|u|{}^2u =\gamma u+\delta|u|{}^2u + \mu \partial_x (|u|{}^2u)+\beta \partial_x^3 u +\left(\nu-\mathrm{i}\sigma_R\right)u \partial_x(|u|{}^2), \end{gathered} $$
(2)

which also incorporates dissipative effects, such as linear loss (for γ < 0) [or gain (for γ > 0)]. These effects are physically relevant in the context of nonlinear optics [1,2,3, 13]: indeed, nonlinear gain (δ > 0) [or loss (δ < 0)] may be used to counterbalance the effects from the linear loss/gain mechanisms, which may potentially lead to the stabilization of optical solitons—see, e.g., Refs. [14, 15]. Notice that it is the presence of gain/loss that renders Equation (2) a higher-order cubically nonlinear Ginzburg–Landau-type equation (see recent studies [16,17,18] on such models), featuring zero diffusion.

In this work, we will discuss various possible dynamical scenarios associated with Equation (2). In particular, the organization of the presentation and main results of this work can be described as follows.

In Section 2, first we show that the incorporation of gain and loss terms in the model gives rise to the existence of an attractor, capturing the long-time dynamics of the system. A rigorous proof is provided, based on the interpretation of the energy balance equation and properties of the functional (phase) space in which the problem defines an infinite-dimensional flow. It will also be discussed that although the gain/loss effects are pivotal for the dissipative nature of the infinite-dimensional flow that will be defined below, the structure of the attractor is basically determined by the other higher-order effects. In the same Section (Section 2), we also examine conditions for finite-time collapse of the solutions of the model. In particular, upon using energy arguments, we find that the collapse dynamics is chiefly controlled by the linear/nonlinear gain/loss strengths. We also identify a critical value of the linear gain, separating the possible decay of solutions to the trivial zero-state, from collapse.

In addition, considering the higher-order Ginzburg–Landau-type equation as a perturbed NLS equation, in Section 3 we study the dynamics of bright and dark solitons under the influence of the higher-order effects. The analysis is based on various perturbative techniques, relying on general aspects of the perturbation theory for bright and dark solitons. Specifically, we adopt the so-called adiabatic approximation, according to which the soliton form does not chance due to the (small) perturbation, but its characteristics (center, amplitude, velocity, etc.) become unknown functions of time. We derive relevant evolution equations for the soliton characteristics and describe the pertinent soliton dynamics. We also briefly discuss still another method to analyze soliton dynamics, namely a multiscale expansion technique that asymptotically reduces the model to a Korteweg-de Vries–Burgers (KdV-B) equation. This way, we discuss various other nonlinear wave structures that can be supported by the higher-order effects, namely anti-dark solitons, as well as shock waves and rarefaction waves.

2 Limit Set and Collapse

2.1 Existence of the Limit Set

Let us consider the case s = −1, and supplement Equation (2) with periodic boundary conditions for u and its spatial derivatives up to the-second order, namely:

$$\displaystyle \begin{aligned} \begin{array}{cc} u(x+2L,t)=u(x,t),\;\;\mbox{and}\\ \;\;\;\;\;\;\;\partial^j_x(x+2L,t)=\partial^j_x(x,t),\;\; j=1,2, \end{array} \end{aligned} $$
(3)

\(\forall \;\;(x,t)\in {\mathbb R}\times [0,T]\), for some T > 0, where L > 0 is given. The initial condition

$$\displaystyle \begin{aligned} u (x,0)=u_0(x),\quad \forall\,x\in{\mathbb R}, \end{aligned} $$
(4)

also satisfies the periodicity conditions (3).

As shown in Ref. [19], all possible regimes except γ > 0, δ < 0, are associated with finite-time collapse or decay. Furthermore, a critical value γ ∗ can be identified in the regime γ < 0, δ > 0, which separates finite-time collapse from the decay of solutions. On the other hand, for γ > 0, δ < 0, below we prove the existence of a limit set (attractor) \(\omega (\mathcal {B})\), attracting all bounded orbits initiating from arbitrary, appropriately smooth initial data u 0 (considered elements of a bounded set \(\mathcal {B}\) in a suitable Sobolev space). Notice that, as shown numerically in Ref. [20], the attractor \(\omega (\mathcal {B})\) captures the full route, ranging from Poincaré–Bendixson limit-cycle dynamics to quasiperiodic or chaotic dynamics.

The starting point of our proof is the power balance equation:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \frac{d}{dt}\int_{-L}^{L}|u|{}^2dx=2\gamma\int_{-L}^{L}|u|{}^2dx +2\delta\int_{-L}^{L}|u|{}^4dx, \end{array} \end{aligned} $$
(5)

satisfied by any local solution \(u\in C([0,T], H^k_{per}(\varOmega ))\), which initiates from sufficiently smooth initial data \(u_0\in H^k_{per}(\varOmega )\), for fixed k ≥ 3. Here, \(H^k_{per}(\varOmega )\) denotes the Sobolev spaces of periodic functions \(H^k_{per}\) [21], in the fundamental interval Ω = [−L, L]. Analysis of (5), results in the asymptotic estimate:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \limsup_{t\rightarrow\infty} \frac{1}{2L}\int_{-L}^{L}|u(x,t)|{}^2dx\leq-\frac{\gamma}{\delta}, \end{array} \end{aligned} $$
(6)

implying that local in time solutions \(u\in C([0,T], H^k_{per}(\varOmega ))\) are uniformly bounded in L 2(Ω). This allows for the definition of the extended dynamical system:

$$\displaystyle \begin{aligned} \varphi(t, u_0): H^k_{per}(\varOmega))\rightarrow L^2(\varOmega),~~\varphi(t, u_0)=u, \end{aligned}$$

whose orbits are bounded ∀t ≥ 0. Moreover, from the above asymptotic estimate, we derive the following: if L 2(Ω) is endowed with the equivalent averaged norm

$$\displaystyle \begin{aligned} ||u||{}^2_{\alpha}=\frac{1}{2L}\int_{-L}^{L}|u|{}^2dx, \end{aligned}$$

then its ball:

$$\displaystyle \begin{aligned}\mathcal{B}_{\alpha}(0,\rho)=\left\{u\in L^2(\varOmega)\;:\;||u||{}^2_{\alpha}\leq \rho^2, \;\;\rho^2>-\frac{\gamma}{\delta}\right\},\end{aligned}$$

attracts all bounded sets \(\mathcal {B}\in H^k_{per}(\varOmega )\). That is, there exists T ∗ > 0, such that \(\varphi (t, \mathcal {B})\subset \mathcal {B}_{\alpha }\), for all t ≥ T ∗. Thus, we may define for any bounded set \(\mathcal {B}\in H^k_{per}(\varOmega ))\), k ≥ 3, its ω-limit set in L 2(Ω),

$$\displaystyle \begin{aligned} \omega(\mathcal{B})=\bigcap_{s\geq 0}\overline{\bigcup_{t\geq s}\varphi(t ,\mathcal{B}}). \end{aligned}$$

The closures are taken with respect to the weak topology of L 2(Ω). Then, the standard (embedding) properties of Sobolev spaces imply that the attractor \(\omega (\mathcal {B})\) is at least weakly compact in L 2(Ω), or relatively compact in the dual space \(H^{-1}_{per}(\varOmega )\).

In the direct numerical simulations of Ref. [20], it was found that apart from the gain/loss parameters γ and δ, the other higher-order effects play also important role on the dynamics. In particular, the competition between the third-order dispersion (characterized by the coefficient β) and SRS effect (characterized by the coefficient σ R gives rise to rich dynamics (briefly mentioned above): indeed, the dynamics ranges from Poincaré–Bendixson-type scenarios, in the sense that bounded solutions may converge either to distinct equilibria via orbital connections or to space-time periodic solutions, to the emergence of almost periodic and chaotic behavior. A main result is that third-order dispersion has a dominant role in the development of such complex dynamics, since it can be chiefly responsible (even in the absence of other higher-order effects) for the existence of periodic, quasiperiodic, and chaotic spatiotemporal structures.

We conclude by illustrating some representative results illustrating the richness of these dynamics.

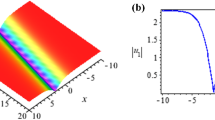
Figure 1 depicts the birth of a space time periodic solution emerging from the modulation instability of the continuous wave (cw) steady-state solution of amplitude \(|\phi _b|{ }^2=-\frac {\gamma }{\delta }\) for the choice of parameters β = 0.55, σ R = 0.01, γ = 1.5, δ = −1, σ R = 0.3, μ = ν = 0.01. The initial condition is a single-mode cw of the form

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} u_0(x)=\epsilon\, e^{-i\frac{K\pi x}{L}},\;K>0. \end{array} \end{aligned} $$
(7)

with K = 5 and 𝜖 = 0.01. This is one of the examples showing the Poincaré-Bendixson type dynamics when the instability of a steady state gives rise to the birth of a limit-cycle. The results visualise the asymptotic behavior in the 2D-finite dimensional subspace

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mathcal{P}_2{=}\{(X,Y)\in\mathbb{R}^2\;:\;(X(t),Y(t)){=}(|u(x_1,t)|{}^2,|u(x_2,t)|{}^2),\;\;x_1,\;x_2\in \varOmega,\;t\geq 0\}, \end{array} \end{aligned} $$

for some arbitrarily chosen fixed spatial coordinates x 1, x 2. In this subspace, the steady-state ϕ b is marked by the point \(\mathbf {A}=(|\phi _b|{ }^2,|\phi _b|{ }^2)=\left (-\frac {\gamma }{\delta },-\frac {\gamma }{\delta }\right )\). The 3D-counterpart is defined as

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mathcal{P}_3{=}\{(X,Y,Z)\in\mathbb{R}^3& \;:\;&\displaystyle (X(t),Y(t),Z(t)){=}(|u(x_1,t)|{}^2,|u(x_2,t)|{}^2,|u(x_3,t)|{}^2),\\ & &\displaystyle \;\;x_1,\;x_2,\;x_3\in \varOmega,\;t\geq 0\}. \end{array} \end{aligned} $$
(8)

The emergence of limit-cycles characterizing the global attractor persists up to certain thresholds for the parameter β.

Fig. 1
figure 1

(Color Online) Upper left panel: The birth of a space-time periodic solution from the instability of the cw-steady state of amplitude |ϕ b|2 = −γ∕δ, for cw-initial data (7) of K = 5 and 𝜖 = 0.01. Parameters β = 0.55, σ R = 0.01, γ = 1.5, δ = −1, σ R = 0.3, μ = ν = 0.01. Upper right panel: Integral curves X(t) = |u(x 1, t)|2 (upper fig.-purple curve) and Y (t) = |u(x 2, t)|2 (bottom fig.-red curve), for the spatial coordinates x 1 = 0 and x 2 = 5 respectively: Convergence to a periodic solution, for the set of parameters of the upper left panel. Bottom left panel: The space-time periodic solution of the left upper panel, as a limit cycle in the 2D-phase space \(\mathcal {P}_2\) for the spatial coordinates x 1 = 0 and x 2 = 5. Bottom middle panel: Convergence to the limit cycle of the bottom left panel for the cw-initial condition of K = 5 and \(\epsilon = \sqrt {3}\). Bottom right panel: The space-time periodic solution of the upper right panel as a limit cycle on the 3D-phase space \(\mathcal {P}_3\) (defined by (8)), for the choice of spatial coordinates x 1 = 0, x 2 = 5 and x 3 = 10

Full size image

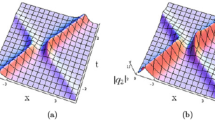
On the other hand, even when the steady state ϕ b is asymptotically stable, the convergence may include highly non-trivial transient dynamics. Figure 2 depict an example of the evolution of the initial condition

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} u_0(x)=\epsilon\, \mathrm{sech} x. \end{array} \end{aligned} $$
(9)

Such initial data correspond to the profile of a “bright soliton” as an initial state. The example is for 𝜖 = 1 and parameters σ R = μ = ν = β = 0.01. The gain/loss strengths are γ = 1.5, δ = −1. We observe formation of a “shock-wave” transitioning to an unstable periodic solution and then, the formation of a decaying travelling pulse, prior to the ultimate convergence to the asymptotically stable state ϕ b.

Fig. 2
figure 2

(Color Online) Snapshots of the evolution of the density |u|2 for initial data (9) with 𝜖 = 1, when σ R = μ = ν = β = 0.01 and γ = 1.5, δ = −1. Formation of a decaying “bright” traveling solitary pulse, prior to the ultimate convergence to the steady state ϕ b. The array indicates the direction of the travelling pulses

Full size image

2.2 Conditions for Collapse

The question of collapse concerns sufficiently smooth (weak) solutions of Equation (2). The existence of such solutions, is guaranteed by a local existence result associated with the initial-boundary value problem (2)–(4). In particular, the methods which are used in order to prove such a local existence result in the Sobolev spaces of periodic functions \(H^k_{per}\) [22, 23], are based on the lines of approach of [24,25,26,27]. The application of these methods to establish local existence for the problem (2)–(4), although involving lengthy computations, is now considered as standard. Thus, we refrain from showing the details here, and we just state it in:

Theorem 1

Let \(u_0\in H^k_{per}(\varOmega )\) for any integer k ≥ 2, and \(\beta ,\gamma ,\delta ,\mu ,\nu , \sigma _R\in \mathbb {R}.\) Then there exists T > 0, such that the problem (2)–(4), has a unique solution

$$\displaystyle \begin{aligned} u\in C([0,T], H^k_{per}(\varOmega)) \quad \mathit{\mbox{and}}\quad u_t\in C([0,T], H^{k-3}_{per}(\varOmega)). \end{aligned}$$

Moreover, the solution \(u\in H^k_{per}(\varOmega )\) depends continuously on the initial data \(u_0\in H^k_{per}(\varOmega )\) , i.e., the solution operator

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mathcal{S}(t): H^k_{per}(\varOmega)& \mapsto&\displaystyle H^k_{per}(\varOmega),\;\;\;\;t\in[0,T],\\ u_0& \mapsto&\displaystyle \mathcal{S}(t)u_0=u, \end{array} \end{aligned} $$
(10)

is continuous.

Here, for the sake of completeness, let us recall the definition of \(H^k_{per}(\varOmega )\):

$$\displaystyle \begin{gathered} {} H^k_{per}(\varOmega)=\{u:\varOmega\rightarrow \mathbb{C},\;\; u\;\mbox{and}\; \frac{\partial^ju} {\partial x^j}\in L^2(\varOmega),\;\; j=1,2,\ldots,k;\\ u(x),\;\;\mbox{and}\;\;\frac{\partial^ju}{\partial x^j}(x)\;\mbox{for }j=1,2,\ldots,k-1\mbox{, are }2L\mbox{- periodic}\}. \end{gathered} $$
(11)

Since our analytical energy arguments for examining collapse require sufficiently smoothness of local-in-time solutions, we shall implement Theorem 1 by assuming that k = 3, at least. As it follows from the definition of the Sobolev spaces (2.2), this assumption means that the initial condition u 0(x), x ∈ Ω, and its spatial (weak) derivatives, at least up to the 2nd-order, are 2L-periodic. Then, it turns out from Theorem 1, that the unique, local-in-time solution u(x, t) of (2) satisfies the periodic boundary conditions (3) for t ≥ 0, and is sufficiently (weakly) smooth. Such periodicity and smoothness properties of the local-in-time solutions are sufficient for our purposes (see Theorem 2 below).

Next, we adopt the method of deriving a differential inequality for the functional

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} M(t)=\frac{{{e}^{-2\gamma t}}}{2L }\int_{-L}^{L}|u(x,t)|{}^2dx, \end{array} \end{aligned} $$
(12)

and then, showing that its solution diverges in finite-time under appropriate assumptions on its initial value at time t = 0; see [22, 23, 28,29,30] and references therein. Note that the choice of this functional is not arbitrary; in fact, it is a direct consequence of the conservation laws of the NLS model. For a discrete counterpart of this argument applied in discrete Ginzburg–Landau-type equations, we refer to [31]. For applications of these types of arguments in the study of escape dynamics for Klein–Gordon chains, we refer to [32].

Theorem 2

For \(u_0\in H^k_{per}(\varOmega )\) , k ≥ 3, let \(\mathcal {S}(t)u_0=u\in C([0,T_{\mathrm {max}}), H^k_{per}(\varOmega ))\) be the local- in- time solution of the problem (2)–(4), with [0, T max) be its maximal interval of existence. Assume that the parameter δ > 0 and that the initial condition u 0(x) is such that M(0) > 0. Then, T max is finite, in the following cases:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} & &\displaystyle (i)\;\;\;\;\;\;\;\;\;\;\;{{T}_{\mathrm{max}}}\le \frac{1}{2\gamma }\log \left[ 1+\frac{\gamma }{\delta M\left( 0 \right)} \right], \end{array} \end{aligned} $$
(13)
$$\displaystyle \begin{aligned} \begin{array}{rcl} {} & &\displaystyle \mathit{\mbox{for}}\;\;\gamma\neq 0,\;\;\mathit{\mbox{and}}\;\;\ \gamma>-\delta M\left( 0 \right). \end{array} \end{aligned} $$
(14)
$$\displaystyle \begin{aligned} \begin{array}{rcl} {} & &\displaystyle (ii)\;\;\;\;\;\;\;\;\;\;\;{{T}_{\mathrm{max}}}\le \frac{1}{2\delta M\left( 0 \right)},\;\;\mathit{\mbox{for}}\;\;\gamma=0. \end{array} \end{aligned} $$
(15)

Proof

For any T < T max, since k ≥ 3, due to the continuous embedding [22]:

$$\displaystyle \begin{aligned} C([0,T], H^k_{per}(\varOmega))\subset C([0,T], L^2(\varOmega)), \end{aligned}$$

the solution \(\mathcal {S}(t)u_0=u\in C([0,T], L^2(\varOmega ))\). Furthermore, it follows from Theorem 1, that u t ∈ C([0, T], L 2(Ω)). Then, by differentiating M(t) with respect to time, we find that:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \frac{dM(t)}{dt}=-\gamma \frac{e^{-2\gamma t}}{L}\int_{-L}^{L}|u|{}^2dx +\frac{e^{-2\gamma t}}{L}\mathrm{Re}\int_{-L}^{L}u_t\overline{u}dx. \end{array} \end{aligned} $$
(16)

In the second term on the right-hand side of (16), we substitute u t by the right-hand side of Equation (2). Then, after some computations, Equation (16) results in:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \frac{dM(t)}{dt}=\delta \frac{e^{-2\gamma t}}{L}\int_{-L}^{L}|u|{}^4dx. \end{array} \end{aligned} $$
(17)

Next, by the Cauchy-Schwarz inequality, we have

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \int_{-L}^{L}|u|{}^2dx\leq \sqrt{2L}\left(\int_{-L}^{L}|u|{}^4dx\right)^{1/2}. \end{array} \end{aligned} $$
(18)

Therefore, for the functional M(t) defined in (12), we get the inequality

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} M(t)\leq \frac{e^{-2\gamma t}}{\sqrt{2L}}\left(\int_{-L}^{L}|u|{}^4dx\right)^{1/2}, \end{array} \end{aligned} $$
(19)

which in turns, implies the estimate

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} M(t)^2\leq \frac{e^{-4\gamma t}}{2L}\int_{-L}^{L}|u|{}^4dx, \end{array} \end{aligned} $$
(20)

for all t ∈ [0, T max). On the other hand, from (17) we have that

$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_{-L}^{L}|u|{}^4dx=e^{2\gamma t}\frac{L}{\delta}\,\frac{dM(t)}{dt}, \end{array} \end{aligned} $$

and hence, we may rewrite (20) as

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} {{\left[ M\left( t \right) \right]}^{2}}\le \frac{{{e}^{-2\gamma t}}}{2\delta }\frac{dM\left( t \right)}{dt},\;\;\mbox{or}\;\; \frac{\frac{dM\left( t \right)}{dt}}{{{\left[ M\left( t \right) \right]}^{2}}}\ge 2\delta {{e}^{2\gamma t}}. \end{array} \end{aligned} $$
(21)

Since

$$\displaystyle \begin{aligned}\frac{d}{dt}\left[ \frac{1}{M\left( t \right)} \right] =-\frac{\frac{dM\left( t \right)}{dt}}{{{\left[ M\left( t \right) \right]}^{2}}},\end{aligned}$$

we get from (21) the differential inequality

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \frac{d}{dt}\left[ \frac{1}{M\left( t \right)} \right]\le -2\delta {{e}^{2\gamma t}}. \end{array} \end{aligned} $$
(22)

Integration of (22) with respect to time, implies that

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{1}{M\left( t \right)}\le \frac{1}{M\left( 0 \right)}-2\delta \int_{0}^{t}{{{e}^{2\gamma s}}ds}, \end{array} \end{aligned} $$

and since M(t) > 0, we see that M(0) > 0 satisfies the inequality

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} 2\delta \int_{0}^{t}{{{e}^{2\gamma s}}ds}\le \frac{1}{M\left( 0 \right)}. \end{array} \end{aligned} $$
(23)

From (23), we shall distinguish between the following cases for the damping parameter γ:

  • We assume that the damping parameter γ ≠ 0. In this case, (23) implies that

    $$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{2\delta }{2\gamma }\left( {{e}^{2\gamma t}}-1 \right)\le \frac{1}{M\left( 0 \right)},\;\;\mbox{or}\;\; {{e}^{2\gamma t}}\le 1+\frac{\gamma }{\delta M\left( 0 \right)}. \end{array} \end{aligned} $$

    Thus, assuming that

    $$\displaystyle \begin{aligned} \frac{\gamma }{\delta M\left( 0 \right)}>-1, \end{aligned}$$

    we derive that the maximal time of existence is finite, since

    $$\displaystyle \begin{aligned} \begin{array}{rcl} t \le \frac{1}{2\gamma }\log \left[ 1+\frac{\gamma }{\delta M\left( 0 \right)} \right]. \end{array} \end{aligned} $$

    The inequality above, proves the estimate of the collapse time (13) under assumption (14), that is, case (i) of the Theorem.

  • Assume that the damping parameter is γ = 0. Then, Equation (23) implies that

    $$\displaystyle \begin{aligned} 2\delta t\le \frac{1}{M\left( 0 \right)}, \end{aligned}$$

    or

    $$\displaystyle \begin{aligned} \begin{array}{rcl} t\le \frac{1}{2\delta M\left( 0 \right)}. \end{array} \end{aligned} $$

    This inequality proves the estimate of the collapse time (15) in the absence of damping, that is, case (ii) of the Theorem. □

From condition (14) on the definition of the analytical upper bound of the blow-up time

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} T_{\mathrm{max}}[\gamma,\delta,M(0)]=\frac{1}{2\gamma }\log \left[ 1+\frac{\gamma }{\delta M\left( 0 \right)} \right], \end{array} \end{aligned} $$
(24)

given in (13), we define a critical value of the linear gain/loss parameter as

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \gamma^{*}=-\delta M(0). \end{array} \end{aligned} $$
(25)

We observe that

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \lim_{\gamma\rightarrow\gamma^*}T_{\mathrm{max}}[\gamma,\delta,M(0)]=+\infty, \end{array} \end{aligned} $$
(26)

while T max[γ, δ, M(0)] is finite if

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \gamma>\gamma^*, \end{array} \end{aligned} $$
(27)

according to the condition (14). Then, (26) suggests that when δ > 0, the critical value γ ∗ may act as a critical point separating the two dynamical behaviors: blow-up in finite-time for γ > γ ∗ and global existence for γ < γ ∗.

We also remark that the analytical upper bound for the blow-up time (15) in the case γ = 0,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} T_{\mathrm{max}}[\delta,M(0)]=\frac{1}{2\delta M\left( 0 \right)}, \end{array} \end{aligned} $$
(28)

is actually the limit of the analytical upper bound (24) for γ > 0 as γ → 0, e.g.,

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \lim_{\gamma\rightarrow 0}T_{\mathrm{max}}[\gamma,\delta,M(0)]=T_{\mathrm{max}}[\delta,M(0)]. \end{array} \end{aligned} $$
(29)

The analytical estimates for the blow-up time have been proved sharp with respect to their dependence on the several parameters as it was illustrated by the relevant numerical simulations [19].

3 Soliton Dynamics: Perturbative Approach

Below, our aim is to consider the higher-order Ginzburg–Landau equation (2) as a perturbed NLS equation. This can be done, upon rewriting Equation (2) in the following form,

$$\displaystyle \begin{aligned} \begin{array}{rcl} i u_t -\frac{s}{2}u_{xx} +|u|{}^2 u = \varepsilon F[u], {} \end{array} \end{aligned} $$
(30)

where subscripts denote partial derivatives, and the functional perturbation F[u] is given by:

$$\displaystyle \begin{aligned} \begin{array}{rcl} F[u]= i\gamma u+i\delta |u|{}^2u +i\beta u_{xxx} + i\mu(|u|{}^2u)_x+ (i\nu+\sigma_R)u(|u|{}^2)_x. {} \end{array} \end{aligned} $$
(31)

In other, words, we consider the situation where the coefficients of the gain/loss and higher-order terms are small, i.e., of the order of a formal small parameter ε (with 0 < ε ≪ 1). This problem finds applications in long-haul optical fiber communications, where the terms involved in F[u] can indeed be considered as small perturbations [1].

Based on the fact that, for 𝜖 = 0, Equation (30) becomes the traditional NLS model that possesses bright or dark solitons for s = −1 and s = +1 respectively, we will study separately these two cases, and investigate how the perturbation (31) alters the soliton dynamics. Our analysis relies on various perturbation techniques that have been developed in the past, both for bright [33,34,35] and dark [36,37,38], including the perturbed inverse scattering method, the variational approach (or Lagrangian method), the Lie transform method, and others (see also [1,2,3] and references therein). Among these techniques, a particularly convenient method to study the soliton dynamics is the so-called adiabatic approach. According to this, an adiabatic relation is the balance between nonlinearity and dispersion, so that (amplitude)×(width)= const. In other words, it is assumed that—in the presence of the perturbations—the functional form of the soliton remains unchanged, but the soliton parameters change (slowly) as the soliton evolves. Thus, the soliton parameters are treated as unknown functions of t, and their evolution is determined by the evolution of the conserved quantities (integrals of motion) of the unperturbed NLS. Particularly relevant such conserved quantities include the energy:

$$\displaystyle \begin{aligned} E=\int_{-\infty}^{-\infty}|u|{}^{2}{\mathrm{d}}x, \end{aligned} $$
(32)

the momentum,

$$\displaystyle \begin{aligned} P=\frac{i}{2}\int_{-\infty}^{-\infty}\left(u \bar{u}_{x} -\bar{u} u_{x} \right){\mathrm{d}}x, \end{aligned} $$
(33)

where overbar denotes complex conjugate, and the Hamiltonian:

$$\displaystyle \begin{aligned} H=\frac{1}{2}\int_{-\infty}^{-\infty} \left(s|u_{x}|{}^{2}+|u|{}^{4}\right){\mathrm{d}}x. \end{aligned} $$
(34)

In addition, for our considerations below, it is also useful to introduce still another conserved quantity, namely the central position of the soliton(s)–alias “soliton center”—given by:

$$\displaystyle \begin{aligned} \begin{array}{rcl} R_{\mathrm{bs}}= \int_{-\infty}^{+\infty} x|u|{}^2 {\mathrm{d}}x, \quad R_{\mathrm{ds}}= \int_{-\infty}^{+\infty} x \left( u_\infty^2 - |u|{}^2 \right) {\mathrm{d}}x, {} \end{array} \end{aligned} $$
(35)

for the bright and dark solitons respectively.

3.1 Perturbation Theory for Bright Solitons (s = −1)

We start with the case of s = −1, i.e., the case of bright solitons. First, using Equation (30) and its complex conjugate, it is straightforward to derive the following equations for the evolution of the NLS conserved quantities under the action of the perturbation:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{dE}{dt}& =&\displaystyle \varepsilon \int_{-\infty}^{+\infty}\left(\bar{u}F +u\bar{F}\right){\mathrm{d}}x, {} \end{array} \end{aligned} $$
(36)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{dP}{dt}& =&\displaystyle \varepsilon i \int_{-\infty}^{+\infty}\left(\bar{u}_x F - u_x\bar{F}\right){\mathrm{d}}x, {} \end{array} \end{aligned} $$
(37)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{dH}{dt}& =&\displaystyle 2 \varepsilon \int_{-\infty}^{+\infty} \left[ \left(\frac{1}{2} \bar{u}_{xx} +|u|{}^2 \bar{u} \right)F +\left( \frac{1}{2} u_{xx} +|u|{}^2 u \right)\bar{F} \right] {\mathrm{d}}x. {} \end{array} \end{aligned} $$
(38)

For sufficiently small perturbation, the form of the bright soliton solution u bs(x, t) may be assumed to have the following rather general form, where all its parameters are allowed to vary in t as

$$\displaystyle \begin{aligned} u_{\mathrm{bs}}(x,t)=\eta(t)\,{\mathrm{sech}}[\eta(t) (x-x_0(t))] \exp\left[-i\kappa(t)x + i\phi(t) \right], {} \end{aligned} $$
(39)

where the soliton’s amplitude (and inverse width) η, its central position x 0, the wavenumber κ, and phase ϕ are unknown functions of t that have to be determined. Notice that, in the absence of the perturbation, x 0 and ϕ are constants, given by:

$$\displaystyle \begin{aligned} \frac{dx_0}{dt}=-\kappa, \quad \frac{d\phi}{dt}=\frac{1}{2}\left(\eta^2-\kappa^2\right). {} \end{aligned} $$
(40)

Substituting the soliton (39) into Equations (37)–(38) [and (35)], we obtain a set of four ordinary differential equations (ODEs) for the four unknown soliton parameters:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{{d\eta }}{{dt}} & =&\displaystyle -{\mathrm{Im}} \left\{ \int_{ - \infty }^{\infty} F[u]\bar{u}{\mathrm{d}}x \right\}, {} \end{array} \end{aligned} $$
(41)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{{d\kappa}}{{dt}} & =&\displaystyle {\mathrm{Re}} \left\{ \int_{ - \infty }^\infty {F[u]\tanh [\eta (x - x_0 )]\bar{u}{\mathrm{d}}x}\right\}, {} \end{array} \end{aligned} $$
(42)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{{dt_0 }}{{dt}} & =&\displaystyle - \kappa - \frac{1}{{{\eta ^2}}}{\mathrm{Im}} \left\{\int_{ - \infty }^\infty {F[u](x - x_0)\bar{u}{\mathrm{d}}x}\right\}, {} \end{array} \end{aligned} $$
(43)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{{d\phi }}{{dt}} & =&\displaystyle \frac{1}{2}({\eta ^2} - {\kappa^2}) + x_0 \frac{{d\kappa}}{{dt}} \\ & -&\displaystyle {\mathrm{Re}}\left\{ \int_{ - \infty }^\infty {F[u]\left[ \frac{1}{\eta} - (x - x_0 ) \tanh [\eta (x - x_0)]\right] } \bar{u}{\mathrm{d}}x\right\}, {} \end{array} \end{aligned} $$
(44)

where Re and Im stand for the real and imaginary parts, respectively.

Before analyzing the full problem, where the perturbation F[u] is given by Equation (31), it is relevant to consider at first a simple example. In particular, let the linear loss/gain term be a small perturbation, i.e., F[u] = iγu, with γ ≪ 1, and assume that δ = β = ν = σ R = 0. Then, substituting this form of F[u] into Equations (41)–(44), and performing the integrations, it is found that the soliton wavenumber κ and the central position x 0 remain unaffected of the perturbation, while the soliton amplitude η and phase ϕ evolve, due to the presence of the loss/gain, as follows:

$$\displaystyle \begin{aligned} \eta(t)=\exp(2\gamma t), \quad \phi(t)=\phi(0) -\frac{1}{8\gamma} \left[1-\exp(4 \gamma t)\right]. \end{aligned} $$
(45)

To obtain the above result, it was assumed that η(0) = 1 and κ(0) = x 0(0) = 0 (hence κ(t) = x 0(t) = 0 ∀t). Thus, in the presence of loss, γ < 0 (or gain, γ > 0) the soliton amplitude decreases (or increases), while its width increases (or decreases), i.e., the soliton broadens (or is compressed) during its evolution.

We now return to the full problem, and study the effect of the perturbation (31) on the dynamics of bright solitons. Following the same procedure, i.e., substituting Equation (31) into Equations (41)–(44), and performing the integrations, we find that the soliton parameters evolve according to the following system:

$$\displaystyle \begin{aligned} \frac{{d\eta }}{{dt}} &= \frac{2}{3}\eta (3\gamma + 2\delta {\eta ^2}), {} \end{aligned} $$
(46)
$$\displaystyle \begin{aligned} \frac{{d\kappa}}{{dt}} &= - \frac{8}{{15}}{\sigma _R}{\eta ^4}, {} \end{aligned} $$
(47)
$$\displaystyle \begin{aligned} \frac{{dt_0}}{{dt}} &= - \kappa + \frac{1}{3}(3\beta - 3\mu - 2\nu )\eta + 3\beta {\kappa^2}{\eta ^2}, {} \end{aligned} $$
(48)
$$\displaystyle \begin{aligned} \frac{{d\phi }}{{dt}} &= - \kappa \left[(\mu - 3\beta ){\eta ^2} + \beta ({\eta ^2} - 2){q^2}\right] + \frac{1}{2}({\eta ^2} - {\kappa^2}) - \frac{8}{{15}}{\sigma _R}t_0 {\eta ^4}. {} \end{aligned} $$
(49)

Although the result in this case is more complicated, it is still possible to arrive at a simple analytical result. Indeed, first observe that Equation (46) can be solved analytically to provide the functional form of η(z), which is found to be:

$$\displaystyle \begin{aligned} \eta^2(t)=\frac{3C \gamma e^{4\gamma t}}{1-2C \delta e^{4\gamma t}}, \quad C=\frac{\eta^2(0)}{3\gamma+2\delta\eta^2(0)}. \end{aligned} $$
(50)

Then, the wavenumber κ(t) can be obtained from Equation (47) by simply integrating the above expression for η. Finally, having found η(t) and κ(t), integration of Equations (48) and (49) yield, respectively, the functional forms of x 0(z) and ϕ(t).

3.2 Perturbation Theory for Dark Solitons (s = +1)

In this section, we consider the case s = +1, and provide analytical results based on the perturbation theory for dark solitons devised in Ref. [38]. We start by noting that, for ε = 0, the unperturbed defocusing NLS Equation (30) possesses the following single dark soliton solution:

$$\displaystyle \begin{aligned} u_{\mathrm{ds}}(x,t)=[A+iB\tanh(BX)]]e^{i\sigma_0}, {} \end{aligned} $$
(51)

where X = x − X 0, with \(X_0=x-\int _0^t A(s)ds-x_0\) being the dark soliton center, \(A^2+B^2=u_\infty ^2\), and \(\varDelta \phi _0=2\tan ^{-1}(B/A)\) is the phase jump across the soliton. The latter, is equal to π for stationary, so-called “black” solitons with A = 0 (moving solitons with A≠0 are termed “grey”) [39, 40]; finally, A and B depict the velocity and depth of the dark soliton, respectively, while x 0 and σ 0 are real parameters. Notice that u ∞ represents the boundary condition at infinity, i.e., u ∞ = u(x →∞), and sets the amplitude of the soliton background. The dark soliton (51) is, therefore, comprised of a background of constant density, and a density dip that propagates on top, accompanied by a phase jump across the minimum density.

The effect of the perturbation of Equation (31) on the dark soliton dynamics will now be studied upon assuming that the soliton parameters are slowly varying functions of t. As shown in Ref. [38], dissipative terms—similar to the ones considered here—give rise to a shelf, which develops around the soliton; the shelf has a non-trivial contribution to the integrals employed in order to find expressions for the soliton parameters. Thus, this perturbative approach is better suited here, compared to ones merely relying on the adiabatic approximation [36, 37], as they do not take into account this important contribution.

Our analysis starts with the dynamics of the soliton background. Assuming that u(x →∞) = u 0(t), we derive from Equation (30 the equation:

$$\displaystyle \begin{aligned} iu_{0t}-|u_0|{}^2u_0=i\gamma u_0+i\delta |u_0|{}^2u_0. \end{aligned} $$
(52)

Then, employing the polar decomposition \(u_0=u_\infty (t)\exp (i\theta (t))\), we obtain:

$$\displaystyle \begin{aligned} u_\infty^{\prime}=(\gamma+\delta u_\infty^2)u_\infty, \quad \theta^{\prime}=u_\infty^2, {} \end{aligned} $$
(53)

where primes denote differentiation with respect to t. The role of the term of strength δ is now more obvious: a nontrivial equilibrium (constant solution), exists iff γδ < 0 which is \(u_\infty ^2=-\gamma /\delta \). Note the relevance of the solution \(u_{\infty }^2\) with the upper bound in the estimate (6). It is also the density of the cw steady-state solution ϕ b (see Fig. 1). We focus here on these solutions, i.e., solutions that tend to stabilize the soliton, by keeping its parameters constant. The evolution of the rest of the soliton parameters [see (51)] can be found by means of a multiscale boundary layer theory [38]; the resulting evolution equations are:

$$\displaystyle \begin{aligned} \begin{array}{rcl} 2 B A_t & =&\displaystyle \mathrm{Re}\left\{ \int_{-\infty}^{\infty} F[u_{\mathrm{ds}}](\bar{u}_{\mathrm{ds}})_t\; dx \right\}, \end{array} \end{aligned} $$
(54)
$$\displaystyle \begin{aligned} \begin{array}{rcl} B x_{0t} & =&\displaystyle \mathrm{Im}\left\{ \int_{-\infty}^{\infty} x(F[u_\infty]u_\infty - F[u_{\mathrm{ds}}]\bar{u}_{\mathrm{ds}})\; dx \right\}, \end{array} \end{aligned} $$
(55)
$$\displaystyle \begin{aligned} \begin{array}{rcl} u_\infty \sigma_{0t} & =&\displaystyle \mathrm{Im}\left\{ \int_{-\infty}^{\infty} (F[u_\infty]u_\infty - F[u_{\mathrm{ds}}]\bar{u}_{\mathrm{ds}})\; dx \right\}+ \mathrm{Re}\left\{ F[u_\infty] \right\}, \end{array} \end{aligned} $$
(56)
$$\displaystyle \begin{aligned} \begin{array}{rcl} BB_t& =&\displaystyle u_\infty u_{\infty t}-AA_t, \end{array} \end{aligned} $$
(57)
$$\displaystyle \begin{aligned} \begin{array}{rcl} u_\infty^2\varDelta\phi_{0t}& =&\displaystyle 2AB_t-2BA_t, \end{array} \end{aligned} $$
(58)
$$\displaystyle \begin{aligned} \begin{array}{rcl} q_1^{\pm} & =&\displaystyle \frac{1}{2} \frac{\sigma_{0t} \pm \varDelta\phi_{0t}}{u_\infty \mp A}, \quad \phi_{1t}^{\pm} = \mp 2q_1^{\pm}. {} \end{array} \end{aligned} $$
(59)

Here, we should mention that \(q_1^{\pm }\) and \(\phi _1^{\pm }\) in Equations (59) represent the asympotics of the shelf, induced by the perturbation F[u], as x →±∞ respectively; in fact, they are higher-order corrections to the soliton, so that the shelf amplitude is \(u_\infty +q_1^{\pm }\) and its speed u ∞. Integrating the above equations, and using Equation (53), finally yields:

$$\displaystyle \begin{aligned} u_\infty^{\prime} &= (\gamma+\delta u_\infty^2)u_\infty, {} \end{aligned} $$
(60)
$$\displaystyle \begin{aligned} A^{\prime} &= \frac{4}{{15}}{\sigma _R}{A^4} + \frac{2}{3}\delta {A^3} - \frac{8}{{15}}{\sigma _R}u_\infty ^2{A^2} + \left( {\gamma + \frac{\delta }{3}u_\infty ^2} \right)A + \frac{4}{{15}}{\sigma _R}u_\infty ^4, {} \end{aligned} $$
(61)
$$\displaystyle \begin{aligned} x_0^{\prime} &= \left( 2\beta-\mu-\frac{2\nu}{3} \right)A^2 -\left( 2\beta+2\mu+\frac{4\nu}{3} \right)u_\infty ^2, \end{aligned} $$
(62)
$$\displaystyle \begin{aligned} \sigma{{}^{\prime}_0} &= \frac{{{B_z}}}{{{u_\infty }}} - \frac{{2B}}{{3{u_\infty }}}\left( {3\gamma + 4u_\infty ^2\delta + 2\delta {A^2}} \right). \end{aligned} $$
(63)

These equations show that the evolution of the soliton center, described by the equation \(X_0^{\prime }=A+x_0^{\prime }\), is affected by all parameters of Equation (30) [directly or indirectly from A(t)]. On the other hand, the rest of the soliton characteristics, i.e., the background, the dip and the shelf, only depend on γ, δ and σ R. This implies that soliton stabilization can be targeted accordingly. Indeed, stable fixed points of this system correspond to stable solitons traveling on top of a constant background with a constant speed. It is possible to identify two such solitons, namely a grey and a black one, supported in the presence (σ R≠0) and in the absence (σ R = 0) of the SRS effect, respectively. In both cases, the background assumes the same form: this can be obtained by means of Equation (60), which depicts the nontrivial stationary solution \(u_\infty ^2=-\gamma /\delta \) for γδ < 0, i.e., for linear loss and nonlinear gain, or vice versa.

We start with the case σ R≠0. Substituting the above mentioned constant background in Equation (61), and seeking stationary solutions for the soliton velocity, we arrive at a 4th-order algebraic equation for A. Solving this equation, we find that there exists only one root, namely \(A = (4\delta \sigma _R)^{-1}(- 5\delta ^2 + \sqrt {25 \delta ^4 - 16\gamma \delta \sigma _R^2}),\) which does not violate the relationship \(A^2+B^2=u_\infty ^2\). Thus, a stable soliton exists for:

$$\displaystyle \begin{aligned} u_\infty^2=-\frac{\gamma}{\delta},\quad A = \frac{{ - 5{\delta ^2} + \sqrt {25{\delta ^4} - 16\gamma \delta \sigma _R^2} }}{{4\delta {\sigma _R}}}. {} \end{aligned} $$
(64)

Note that since γδ < 0 the quantity under the square root is always positive.

In general, the solution of Equation (60) with u ∞(0) = u 0 is:

$$\displaystyle \begin{aligned} u_\infty^2(t)=\frac{\gamma u_0^2 e^{2\gamma t}}{\gamma+\delta u_0^2-\delta u_0^2 e^{2\gamma t}}, {} \end{aligned} $$
(65)

which suggests that there is a (finite) time for which the background exhibits blow-up, as it was discussed in Theorem 2. Indeed, the denominator becomes zero when

$$\displaystyle \begin{aligned} t=t_* \equiv \frac{1}{2\gamma}\ln\left( 1+\frac{\gamma}{\delta u_0^2} \right). \end{aligned} $$
(66)

The unexpected feature here is that the addition of the term iδ|u|2 u which compensates the effect of the linear loss term iγu may result in blow-up of the background in finite time, even when the other soliton parameters remain finite. In addition, Equation (65) indicates that an equilibrium can also be reached in finite time when the denominator is a multiple of the numerator. Nevertheless, while under this requirement the background will be stabilized, this does not necessarily guarantees the stabilization of the other soliton parameters.

Next, we consider the case of σ R = 0. In this case, Equations (60) and (61) lead to the following equations for the background and soliton velocity:

$$\displaystyle \begin{aligned} u_\infty^2=-\frac{\gamma}{\delta},\quad A^{\prime}= \frac{2}{3} (\delta A^2-\gamma)A, {} \end{aligned} $$
(67)

Obviously, the above equation for the velocity depicts a stationary solution A = 0 (recall that γδ < 0), that corresponds to a black soliton. Hence, when SRS is absent (which would give a frequency downshift causing the soliton to move), a stable black soliton can exist.

An important comment is in order here. While for these specific choice of u ∞ and A the soliton gets stabilized, this does not mean that the shelf is no longer present. In fact, the shelf is always present in the perturbed NLS, even though its amplitude is small, since it appears as a higher-order correction in the perturbation theory [38]. Thus, the shelf does not affect the soliton propagation but it does, however, affect soliton interactions (see Ref. [41] for a relevant study, but in the framework of another dissipative NLS model). Notice, also, that the shelf can be suppressed with counter effect the destabilization of the soliton.

Finally, we briefly consider the case where gain/loss terms are absent, i.e., γ = δ = 0. In this particular case, the dark soliton dynamics is merely driven by the SRS effect. Indeed, now the evolution of the background and soliton velocity is described by the following equations:

$$\displaystyle \begin{aligned} u_\infty^{\prime}=0,\quad A^{\prime}=\frac{4}{15}\sigma_R(A^2-u_\infty^2)^2, {}\end{aligned} $$
(68)

which recover the results obtained in Refs. [36, 37]. The soliton dynamics in this case can be understood as follows. Since \(A^2\neq u_\infty ^2\), the right-hand-side of the second equation is always positive and, thus, the soliton becomes shallower and faster, i.e., B → 0 and A → u ∞, so that the condition \(A^2+B^2=u_\infty ^2\) is satisfied. Thus, the dark soliton eventually decays to the stationary background. It is therefore clear that no stable dark soliton (in the sense of the existence of stationary soliton parameters) exists in this case.

3.3 Solitons and Shock Waves in an Effective KdV-Burgers Picture

Finally, for completeness, it is relevant to briefly mention the following. Apart from the direct perturbation theory for solitons, there exists still another method to analyze the dynamics of dark solitons in the framework of Equation (30). Indeed, as shown in Ref. [42] for the special case of γ = δ = 0, it is possible to employ a multiscale expansion method and asymptotically reduce the higher-order NLS equation to a Korteweg-de Vries–Burgers (KdV-B) equation. This can be done upon seeking solutions of the form:

$$\displaystyle \begin{aligned} u(x,t)=[u_\infty +U(x,t)]\exp[i u_\infty^2 t + i \phi(x,t)], {} \end{aligned} $$
(69)

where U(x, t) and ϕ(x, t) are unknown real functions (to be determined) representing an amplitude and a phase modulation of the background wave \(u_b=u_\infty \exp (i u_\infty ^2 t)\). Then, it is assumed that these functions are presented in the form of formal asymptotic series,

$$\displaystyle \begin{aligned} U=\epsilon^2 U_1 + \epsilon^4 U_2 + \cdots, \quad \phi = \epsilon \phi_1 + \epsilon^3 \phi_2 +\cdots, {} \end{aligned} $$
(70)

where the unknown functions U j and ϕ j (j = 1, 2, …) depend on the slow variables X = 𝜖(x − υt) and T = 𝜖 3 t, with υ being an unknown velocity, and 𝜖 being a formal small parameter. Substituting Equations (69)–(70) into Equation (30), we obtain the following results. First, to the lowest-order of approximation in 𝜖 of the perturbation technique, we derive the unknown velocity υ and an equation connecting the functions ϕ 1T and U 1. Second, to the next order of approximation, we derive the following KdV-B equation:

$$\displaystyle \begin{aligned} U_{1T} + c_1 U_1 U_{1X} + c_2 U_{1XXX} = c_3 U_{1XX}, {} \end{aligned} $$
(71)

where, U 1 obviously represents the soliton amplitude. The coefficients of the underlying KdV equation, c 1 and c 2, depend on the coefficients of the pNLS, β and ν, as well as on the background amplitude u ∞, while the diffusion coefficient c 3 depends on the SRS parameter, σ R.

Importantly, the relevant asymptotic reduction to the KdV-B equation can be performed for both normal and anomalous dispersion cases, i.e., for both s = ±1. Of course, in the case s = −1 it is known [1,2,3] that the soliton’s background plane wave is prone to the modulational instability (MI), but this long-wavelength instability may be suppressed: indeed, in applications, one expects periodic or other boundary conditions in the x-direction, meaning that the admitted wavenumbers are quantized, hence they are limited from below by a minimum wavenumber, k min, which corresponds to the transverse size of the system. In such a case, if k min > K max (where K is the perturbation wavenumber characterizing the MI, and K max defines the width of the instability band, 0 ≤ K ≤ K max), no quantized wavenumber can get into the instability band and, hence, the MI is eliminated.

The effective KdV-B description of the soliton dynamics offers a number of interesting results. First, in the absence of the SRS effect (σ R = 0), dark solitons small-amplitude dark solitary wave solutions can exist for both the normal and anomalous dispersion regimes. This result is in sharp contrast with the conventional form and certain perturbed versions of the NLS equation, where dark solitons solely exist for the normal dispersion regime (s = +1). In addition, in this latter regime, there exists another type of solution, namely an anti-dark soliton, having the form of a hump, rather than a dip, on top of the background plane wave. Notice that the transformation from the dark to the anti-dark soliton is possible (see details in Ref. [42]).

When the SRS effect is present (σ R≠0), the soliton dynamics is governed by a KdV–B equation. In this case, the evolution of solitons can be studied by means of the perturbation theory for solitons [33, 35]. The results that can been obtained in this case show that the solitons experience a decrease in their amplitudes and/or their velocities, depending on the direction of propagation and the dispersion region (s = −1 or s = +1). In particular, right-going solitons experience a decrease in both their amplitudes and their velocities, while the evolution of left-going solitons depends on s: for s = −1, they increase their amplitudes and decrease their velocities, while for s = +1, they decrease their amplitudes and increase their velocities—in accordance with the results presented in the previous section.

Still another nonlinear wave structure that can be predicted to occur in this setting, is the one of a traveling shock wave [43]. In the effective KdV-B picture, the existence of such a structure is not surprising, because the KdV-B equation possesses stable traveling shock wave solutions. The latter, are obviously supported by the SRS effect (recall that if σ R = 0 then c 3 = 0 and the diffusion term in Equation (71) vanishes, as was also found by means of other methods in other studies [44,45,46]. Notice that, as before, shock wave type structures are possible for both normal and anomalous dispersion cases. In particular, in the case of the normal dispersion (s = +1), the structure has the usual shock wave profile, while in the case of the anomalous dispersion (s = −1 it has the form of a rarefaction wave.

Finally, based on the analysis of the shock wave structure of the KdV-B equation, one may deduce the relevant profiles in the context of the perturbed NLS equation. Thus, the structure of the front of the shock solutions may be monotonic, in the nonlinearity-dominated regime, or oscillatory in the dispersion-dominated regime. In fact, since the former regime is only accessible for s = −1 [43] the front of the rarefaction wave is monotonic. On the other hand, the profile of the front of the shock wave supported for s = +1, may be either monotonic in the nonlinearity-dominated regime (resembling the regular stationary solutions of the Burgers equation), or oscillating. It is interesting to mention that the oscillations in the kink front can be studied in the framework of the perturbation theory for solitons of the KdV equation, treating the diffusion term as a small perturbation [33, 35]. This way, it can be deduced that the oscillations of the shock front can be considered as a succession of KdV solitons, a fact that completes the connection between the soliton and shock wave solutions of the perturbed NLS model.