ϕ ⁴ Solitons in Kirchhoff Wave Equation

Abstract

We express the Kirchhoff wave equation in terms of classic field theory. This permits us to introduce the spontaneous symmetry breaking phenomenon in the study of linear structures, such as strings in order to investigate the existence of solitons solutions. We find ϕ ⁴ solitons in the space of spatial gradient of lateral displacement of a string. This helps us detect stable states in deformations of strings.

1 Introduction

In the last 30 years important progress has been made in understanding of properties of certain non-linear differential equations which arise in many different areas of Physics, e.g., physics of plasma, solid state physics, biophysics, field theory etc. [1,2,3,4,5]. A common interesting feature is the occurrence of solitons, i.e., stable, non-dissipative and localized configurations behaving in many ways like particles. In the analysis of these equations many interesting mathematical structures have been discovered which surprisingly also appear in quantum mechanics and quantum field theory [6]. From a pragmatic point of view these completely soluble non-linear equations are a substantial extension of the ‘tool kit’ of a physicist which otherwise is mainly restricted to solving linear systems. They also serve as valuable source for intuition about the behavior of non-linear systems. In Mathematics and Physics, a soliton, or solitary wave, is a self-reinforcing wave-packet that maintains its shape while it propagates at a constant velocity. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium. Solitons are the solutions of a widespread class of weakly nonlinear dispersive partial differential equations describing physical systems.

ϕ ⁴ solitons are stable solutions which appear in spontaneous symmetry breaking (SSB) in scalar field theories [7]. A category of systems for which SSB might happen are linear structures such as rob, string, needle etc. Thus, if a string is compressed by the application of a force F along its axis the obvious solution is that it stays in the configuration x = y = 0 (see Figure 1). However, if the force gets too large (F > F _cr), the string will jump into a bent position. It does this because the energy in this state is lower than in meta-stable state, where it stays aligned along the z axis. The cylindrical symmetry of the system around z axis is broken by the buckling of the string [7].

Fig. 1

The cylindrical symmetry of the system around z axis is broken by the buckling of the string

In a ϕ ⁴—scalar field the SSB is sourced from a concrete type of potential density. This SSB produces solitary waves which ensure the stable behavior of ϕ scalar field. The wave function of the lateral displacement u for a string such as the one in Figure 1 is the solution of the Kirchhoff wave equation [8]. In this work we attempt to reveal similarities between the potential density produced from Kirchhoff wave equation and ϕ ⁴—scalar field potential density. This would permit us to reveal the existence of soliton in the Kirchhoff description. This would help us in order to find stable states when the string suffers lateral deformation under the action of axial tensions. This is the main motivation of the present work.

2 SSB in ϕ ⁴ Scalar Field Theory: The Kink Solitons

The Lagrangian density of scalar field ϕ(x) with a ϕ ⁴ interaction is given as [9]:

$$\displaystyle \begin{aligned} \mathcal{L}= \frac{1}{2}(\partial_{\mu} \phi )(\partial^{\mu} \phi) - \bigg\{ \frac{1}{2} \alpha \phi^2 + \frac{1}{4} \lambda \phi^4 \bigg\} , {} \end{aligned} $$

(1)

where μ = 0, 1, 2, 3 with $\partial _0 \phi = \frac {\partial \phi }{\partial t}$, $\partial _1 \phi = - \frac {\partial \phi }{\partial x}$, $\partial _2 \phi = - \frac {\partial \phi }{\partial y}$, $\partial _3 \phi = - \frac {\partial \phi }{\partial z}$

The term of kinetic density is $\frac {1}{2}(\partial _{\mu } \phi )(\partial ^{\mu } \phi )$ and the potential density is:

$$\displaystyle \begin{aligned} U(\phi)= \frac{1}{2} \alpha \phi^2 + \frac{1}{4} \lambda \phi^4 {}\end{aligned} $$

(2)

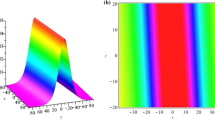
When α, λ have positive values we have the symmetric phase (green line in Figure 2). When α < 0, λ > 0 we have the phase of symmetry breaking (SB) (red line in Figure 2). Thus, the ground state of energy has shifted from ϕ = 0 to $\phi ^* = \pm \sqrt {\frac {\left |\alpha \right |}{\lambda }}$. This is the SSB phenomenon where the system should select a new vacuum. In a thermal system the parameter α is a function of $\frac {T-T_c}{T_c}$ were T is the temperature and T _c is the critical temperature. In a similar way, in a string SSB the parameter α could be a function of $\frac {F-F_c}{F_c}$. A model which demonstrates SSB is the ϕ ⁴ theory [9] where the potential has the form:

$$\displaystyle \begin{aligned} U(\phi)= \frac{\lambda}{4} \Big( \phi^2 - \frac{\alpha}{\lambda} \Big)^2 = - \frac{1}{2} \left|\alpha\right| \phi^2 + \frac{1}{4} \lambda \phi^4 + \frac{\alpha^2}{4 \lambda} {}\end{aligned} $$

(3)

Fig. 2

The SSB in scalar field theory. The critical point (0.0) behaves as a saddle-point

The above potential refers to the SB phase (α < 0, λ > 0) and a constant term has been added. So, the critical state (0, 0) is excited to $(0, \frac {\alpha ^2}{4 \lambda })$. This state describes the meta-stable state of the string, before the cylindrical symmetry of the system around z axis is broken by the buckling of the string. The potential of Equation (3) has the same minima as the potential of Equation (2) namely $\phi ^* = \pm \sqrt {\frac {\left |\alpha \right |}{\lambda }}$. This means that solitons solutions, if they exist, must asymptotically tend toward these values as x →±∞, that is:

$$\displaystyle \begin{aligned} \phi(\left|x\right| = \infty) = \pm \sqrt{\frac{\left| \alpha \right|}{\lambda}} {} \end{aligned} $$

(4)

We can integrate the ϕ ⁴ theory given by the Equation (3) to yield [9]: $x-x_0 = \pm \int _{\phi (x_0)}^{\phi (x)} \frac {d \overline {\phi }}{\sqrt {\frac {\lambda }{2}}} \frac {1}{(\overline {\phi }^2 - \frac {\alpha }{\lambda })}$ and inverting, we find that [9]:

$$\displaystyle \begin{aligned} \phi(x) = \pm \bigg(\sqrt{\frac{\left|\alpha \right|}{\lambda}} \bigg) \tanh \left( \frac{\sqrt{\alpha}}{\sqrt{2}}{(x-x_0)}\right) {}\end{aligned} $$

(5)

This is the kink soliton of ϕ ⁴ scalar field (Figure 3).

Fig. 3

The ϕ ⁴ soliton with α = λ = 1 and x ₀ = 0

The most important property of solitons, as it has already been mentioned, is that they are stable structures which behave as particles. The energy density of these solitons is [9]:

$$\displaystyle \begin{aligned} \varepsilon(x) = \bigg(\frac{\alpha^2}{2 \lambda} \bigg) sech^4 \big[ \frac{m(x-x_0)}{\sqrt{2}} \big]. {}\end{aligned} $$

(6)

The mass of particle-soliton is given by the integral over the energy density:

$$\displaystyle \begin{aligned} M = \int_{-\infty}^{\infty} \varepsilon (x)dx = \frac{2\sqrt{2}}{3} \frac{\left|\alpha\right|{}^{\frac{3}{2}}}{\lambda} {} \end{aligned} $$

(7)

3 Kirchhoff Wave Function, Energy and Potential

The Kirchhoff wave equation without damping term is defined [8, 10, 11], as:

$$\displaystyle \begin{aligned} \frac{\partial^2 u}{\partial^2 t} - (1+ \int_{\varOmega}^{} \left| \nabla u \right|{}^2 dx) \nabla^2 u = 0 {} \end{aligned} $$

(8)

Where u(t, x) is the lateral displacement of a string at the space coordinate x and the time t, while Ω is a bounded domain in $\mathbb {R}^N$ with a smooth boundary ∂Ω.

Here the energy is given as $E(t)=\int _{\varOmega }^{} \mathbb {\varepsilon } dx$ where the energy density ε is [12,13,14]:

$$\displaystyle \begin{aligned} {\varepsilon}(t) = \frac{1}{2}\left|\frac{\partial u}{\partial t}\right|{}^2 + \bigg\{\frac{1}{2}\left|\frac{\partial u}{\partial x}\right|{}^2 + \frac{1}{4}\left|\frac{\partial u}{\partial x}\right|{}^2 \left|\frac{\partial u}{\partial x}\right|{}^2 \bigg\} {} \end{aligned} $$

(9)

The first term in Equation (9) is the kinetic term and the term in the curly brackets is the Kirchhoff potential density (Kpd), U _Kirchhoff. So, we have that:

$$\displaystyle \begin{aligned} U_{Kirchhoff} = \frac{1}{2}\left|\frac{\partial u}{\partial x}\right|{}^2 + \frac{1}{4}\left|\frac{\partial u}{\partial x}\right|{}^2 \left|\frac{\partial u}{\partial x}\right|{}^2 = \frac{1}{2}\left|\frac{\partial u}{\partial x}\right|{}^2 + \frac{1}{4}\left|\frac{\partial u}{\partial x}\right|{}^4 {} \end{aligned} $$

(10)

4 The Kpd Produced from Classical Field Theory

In this section we will try to produce the Kpd through the classical field theory. Thus, the investigation of solitons in the wave equation is not just the result of comparing potentials but it has a fundamental origin. Let’s start from the classical wave equation:

$$\displaystyle \begin{aligned} \partial_\mu^2 \phi = \frac{\partial^2 \phi}{\partial^2 t} - \nabla^2 \phi = 0 {} \end{aligned} $$

(11)

Note that in Equation (11) the wave speed constant factor c ² has been omitted. This is done here since both Equation (8) and Equation (10) that represent Kirchhoff wave equation without damping term and Kpd, respectively, appear in the cited references without constant factors. However, we will restore the specific factor later, during the derivation of the complete form of Kpd (Equation (22)).

If we substitute the ∇² ϕ as $\nabla ^2 \phi (1+ \big (\frac {\partial \phi }{\partial x} \big )^2 )$, then Equation (8) is written as:

$$\displaystyle \begin{aligned} \frac{\partial^2 \phi}{\partial^2 t} - \nabla^2 \phi \bigg(1+ \Big(\frac{\partial \phi}{\partial x}\Big)^2\bigg)= 0 {}\end{aligned} $$

(12)

$$\displaystyle \begin{aligned} \partial_\mu^2 \phi = \frac{\partial^2 \phi}{\partial^2 t} - \nabla^2 \phi = - \frac{\partial U}{\partial \phi} {} \end{aligned} $$

(13)

For static solution $(\frac {\partial ^2 \phi }{\partial ^2 t})=0$ the E-L equation of Equation (13) becomes:

$$\displaystyle \begin{aligned} - \nabla^2 \phi = - \frac{\partial U}{\partial \phi} {} \end{aligned} $$

(14)

where U(ϕ) the potential density of ϕ-field. From Equation (14) we can estimate the potential density U as follows:

We multiply Equation (14) by $\frac {\partial \phi }{\partial x}$ and we take the following:

$$\displaystyle \begin{aligned} - \nabla^2 \phi \cdot \frac{\partial \phi}{\partial x} = - \frac{\partial U}{\partial\phi} \cdot \frac{\partial \phi}{\partial x}, {} \end{aligned} $$

(15)

which can be integrated over x, yielding [9]:

$$\displaystyle \begin{aligned} U(\phi) = \frac{1}{2}\Big(\frac{\partial \phi}{\partial x}\Big)^2 {} \end{aligned} $$

(16)

Following the above procedure, we estimate (see Appendix) the U ^′ for the case of the wave described by Equation (12) as:

$$\displaystyle \begin{aligned} U^{\prime}(\phi) = \frac{1}{2}\Big(\frac{\partial \phi}{\partial x}\Big)^2 + \frac{1}{4}\Big(\frac{\partial \phi}{\partial x}\Big)^4 {} \end{aligned} $$

(17)

The potential density U ^′(ϕ) has the same form with Kpd, as expressed in Equation (10).

5 SSB in the Kpd

Now we will investigate the SSB in the Kpd. If we compare the Kpd from Equation (17) and the potential density of SSB in the ϕ ⁴ theory from Equation (3), we find out that Equation (3) refers to a scalar field ϕ while Equation (17) refers to gradient of ϕ, that is $\frac {\partial \phi }{\partial x}$ (or ∇ϕ). We face this by defining a new field ξ as ξ ≡∇ϕ. Thus, we can research solitons in ξ-field. This means for the string case, that the solitons solutions exist not at the lateral displacement space but in its spatial gradient space. The next thing we have to do, is to introduce coefficients in the terms of Equation (17).

The original equation of Kirchhoff without damping is written as [8]:

$$\displaystyle \begin{aligned} \frac{\partial^2 u}{\partial^2 t} = \nabla^2 u \cdot \Big(\frac{p_0}{p_h} + \frac{Y}{p2L}\int_{0}^{L}\Big(\frac{\partial u}{\partial x}\Big)^2 dx \Big), {} \end{aligned} $$

(18)

where 0 < x < L, with L the length of string, Y  the Young modulus, p the mass density, h the cross-section area, p ₀ the initial external force. In classical wave equation Equation (11), we normally have a coefficient $c^2=\frac {p_0}{p_h}$ in front of the term ∇² ϕ. This is in agreement with Equation (18). The substitution $\nabla ^2 \phi \rightarrow \frac {p_0}{p_h}\nabla ^2 \phi$ in Equation (11) transports the coefficient $\frac {p_0}{p_h}$ in Equation (17) in front of the first term. From Equation (18), we have that the second coefficient is the quantity $\frac {Y}{p2L}>0$. Thus, the Kpd is written as:

$$\displaystyle \begin{aligned} U^{\prime}(\phi) = \frac{1}{2}\alpha\Big(\frac{\partial \phi}{\partial x}\Big)^2 + \frac{1}{4}\lambda\Big(\frac{\partial \phi}{\partial x}\Big)^4, {} \end{aligned} $$

(19)

where:

$$\displaystyle \begin{aligned} \alpha= \frac{p_0}{ph} {} \end{aligned} $$

(20)

and

$$\displaystyle \begin{aligned} \lambda= \frac{Y}{p2L} {} \end{aligned} $$

(21)

The next thing we have to do is to add the constant term in Equation (19). This quantity is $\frac {\alpha ^2}{4\lambda }= \frac {p_0^2}{2ph^2Y}L$. We consider the p ₀ as the resultant of axial forces. The quantity $\frac {p_0^2}{2ph^2Y}L>0$ expresses the excited potential of string before the cylindrical symmetry of the system around z axis is broken by the buckling of the string. This meta-stable state due to the axial compression ΔL from the external force. We have to give an explanation for the negative sign of the coefficient α, which indicates the symmetry breaking whenever the string leaves the axis and goes to the lateral positions. The symmetry breaking is accomplished when the external axial force overcomes a critical value. Then the internal elasticity forces obtain measure greater than external forces and p ₀ obtains negative sign. From Equation (20) the coefficient α becomes negative too. Therefore, the Kpd for the field ξ is written in the final form as:

$$\displaystyle \begin{aligned} U_{Kirchhoff}(\xi) = -\frac{1}{2}\left|\alpha\right|\xi^2 + \frac{1}{4}\lambda\xi^4 + \frac{\alpha^2}{4\lambda} {} \end{aligned} $$

(22)

Now the Kpd has taken the form of the potential density of SSB (see Equation (3)), which provides the theoretical basis for the formation of kink solitons. The solitons solutions from Equation (5) and (Equations (20) and (21)) is written as:

$$\displaystyle \begin{aligned} \xi(x) = \pm\sqrt{\frac{p_0 2L}{Yh}}\tanh \bigg[ \sqrt{\frac{p_0}{2ph}}(x-\varDelta L_{cr})\bigg], {} \end{aligned} $$

(23)

where ΔL _cr is the axial compression when the force overcomes its critical value.

The existence of solitons dependents from the asymptotic behavior $\xi (\pm \infty )= \pm \sqrt {\frac {p_0 2L}{Yh}}$.

The mass of Kirchhoff soliton which is given in Equation (7) has the form:

$$\displaystyle \begin{aligned} M_{Kirchhoff} = \frac{4\sqrt{2}}{3}\frac{p_0^{3/2}}{Y h^{3/2}\sqrt{p}}L {} \end{aligned} $$

(24)

The transmission length where the solitons survive is determined by their mass, according to the proportion which connects the mass of a particle and its transmission length in the field theory is:

$$\displaystyle \begin{aligned} R\sim\frac{1}{M} {} \end{aligned} $$

(25)

Thus, for materials with high Young modulus Y , such as steel, from Equation (24) we obtain that the M _Kirchhoff is small. This means from Equation (25) that transmission length R where the solitons survive is long and the range of stable state is long too. So, the steel string could be found in lateral positions (Figure 1) with greater stability and without breaking. Nevertheless, from Equation (24) one can determine values of parameters which are possible to give stable states.

6 Conclusions

In this work we have produced the potential density of Kirchhoff wave equation, for static solution without damping term, through the classical field theory. Thus, we attempt to study a linear structure such as a string, which suffers lateral deformation under the action of axial tensions through the spontaneous symmetry breaking phenomenon. The result is that ϕ ⁴ solitons in the space of gradient of lateral displacement of string, emerge. The existence of these stable solutions permits us to determine the stability of string deformation, through the extension of spatial range of solitons propagation. This approximation we applied on the issue of elasticity, is a new way to face the limits of elasticity for linear structures.

Appendix: Estimation of the Potential Density U ′(ϕ)

For the Kirchhoff wave equation $\frac {\partial ^2 \phi }{\partial ^2 t} - \nabla ^2 \phi \bigg (1+ \Big (\frac {\partial \phi }{\partial x}\Big )^2\bigg )= 0$ (Equation (12)) we initially consider that exists a potential density U ^′(ϕ) which satisfies a generalized “Euler-Lagrange” equation that could be written as:

$$\displaystyle \begin{aligned} - \nabla^2 \phi \bigg(1+ \Big(\frac{\partial \phi}{\partial x}\Big)^2\bigg)= - \frac{\partial U^{\prime}}{\partial \phi}, {} \end{aligned} $$

(26)

by proceeding to the replacement $- \nabla ^2 \phi \rightarrow - \nabla ^2 \phi \bigg (1+ \Big (\frac {\partial \phi }{\partial x}\Big )^2\bigg )$ in the E-L equation for static solution as presented in Equation (14).

We set as potential density U ^′(ϕ):

$$\displaystyle \begin{aligned} U^{\prime} (\phi) = U(\phi) + U_1 (\phi) {} \end{aligned} $$

(27)

So, Equation (26) is written as:

$$\displaystyle \begin{aligned} - \nabla^2 \phi - \nabla^2 \phi \cdot \Big(\frac{\partial \phi}{\partial x}\Big)^2= - \frac{\partial U}{\partial \phi} - \frac{\partial U_1}{\partial \phi}, {} \end{aligned} $$

(28)

and by using the E-L of Equation (14) we obtain:

$$\displaystyle \begin{aligned} \nabla^2 \phi \cdot \Big(\frac{\partial \phi}{\partial x}\Big)^2= \frac{\partial U_1}{\partial \phi} {} \end{aligned} $$

(29)

This equation tells us that the correction term in E-L equation corresponds to a potential density U ₁ as the E-L equation corresponds to the potential density U.

We multiply Equation (29) by $\frac {\partial \phi }{\partial x}$ to take:

$$\displaystyle \begin{aligned} \nabla^2 \phi \cdot \frac{\partial \phi}{\partial x}\Big(\frac{\partial \phi}{\partial x}\Big)^2= \frac{\partial U_1}{\partial \phi} \frac{\partial \phi}{\partial x} {} \end{aligned} $$

(30)

Moreover, Equation (30) can be integrated over x, yielding $\int \frac {\partial ^2 \phi }{\partial x^2} \cdot \frac {\partial \phi }{\partial x} \Big (\frac {\partial \phi }{\partial x}\Big )^2 dx = \int \frac {\partial U_1}{\partial x} \frac {\partial \phi }{\partial x} dx$.

Thus, we have that:

$$\displaystyle \begin{aligned} \int \frac{\partial}{\partial x} \Big(\frac{\partial \phi}{\partial x}\Big) \Big(\frac{\partial \phi}{\partial x}\Big)^3 dx = \int \frac{\partial U_1}{\partial x} dx = U_1(\phi) {} \end{aligned} $$

(31)

The first part of Equation (31) is estimated as:

$$\displaystyle \begin{gathered} \int \frac{\partial}{\partial x} \Big(\frac{\partial \phi}{\partial x}\Big) \Big(\frac{\partial \phi}{\partial x}\Big)^3 dx = \Big(\frac{\partial \phi}{\partial x}\Big)^4 - \int \Big(\frac{\partial \phi}{\partial x}\Big) \frac{\partial}{\partial x} \Big(\frac{\partial \phi}{\partial x}\Big)^3 dx = \Big(\frac{\partial \phi}{\partial x}\Big)^4\\ - \int \frac{\partial \phi}{\partial x} 3 \Big(\frac{\partial \phi}{\partial x}\Big)^2 \frac{\partial}{\partial x} \Big(\frac{\partial \phi}{\partial x}\Big) dx \Rightarrow \\ 4 \int \frac{\partial}{\partial x} \Big(\frac{\partial \phi}{\partial x}\Big)\Big(\frac{\partial \phi}{\partial x}\Big)^3 dx = \Big(\frac{\partial \phi}{\partial x}\Big)^4 \Rightarrow \\ \int \frac{\partial}{\partial x} \Big(\frac{\partial \phi}{\partial x}\Big) \Big(\frac{\partial \phi}{\partial x}\Big)^3 = \frac{1}{4} \Big(\frac{\partial \phi}{\partial x}\Big)^4{} \end{gathered} $$

(32)

Using Equations (16), (27), (31) and (32) we finally obtain:

$$\displaystyle \begin{aligned} U^{\prime}(\phi) = \frac{1}{2}\Big(\frac{\partial \phi}{\partial x}\Big)^2 + \frac{1}{4} \Big(\frac{\partial \phi}{\partial x}\Big)^4 {} \end{aligned} $$

(33)