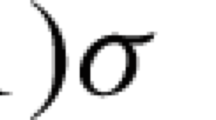Abstract
In this survey article, we discuss recent developments on the mean curvature flow of graphical submanifolds, generated by smooth maps between Riemannian manifolds. We will see interesting applications of this technique, in the understanding of the homotopy type of maps between manifolds.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Introduction
Let f : M → N be a smooth map between two manifolds M and N. It is a fundamental problem to find canonical representatives in the homotopy class of f. By a canonical representative is usually meant a map in the homotopy class of the given map f which is a critical point of a suitable functional. In the mid-1960s, Eells and Sampson [34] introduced the harmonic maps as critical points of the energy density, to attack the aforementioned problem.
One possible approach to construct harmonic maps is via the harmonic map heat flow. If M is compact and N is negatively curved, in [34] Eells and Sampson were able to prove long-time existence and convergence of the flow, showing that under these assumptions one finds harmonic representatives in a given homotopy class. In general, one can neither expect long-time existence nor convergence of this flow. For example, the situation is very complicated in the case of maps between spheres.
There is another important functional that we may consider in the space of smooth maps. Given a map f : M → N between Riemannian manifolds, let us denote its graph in the product space M × N by
Following the terminology introduced by Schoen [79], a map whose graph is minimal submanifold is called minimal map. Therefore, minimal maps are critical points of the volume functional.
In this survey, among others, we will discuss deformation of graphical submanifolds via the mean curvature flow. Before stating the problems that we would like to deal with, let us provide some basic facts and definitions. Let M be a smooth m-dimensional manifold, T > 0 a positive number and F : M × [0, T) → P a smooth time-dependent family of immersions of M into a Riemannian manifold P. We say that F evolves in time under the mean curvature flow if it satisfies the evolution equation
for any (x, t) ∈ M × [0, T), where H(x, t) stands for the mean curvature vector at the point x of the immersion F(⋅ , t) : M → P. It is a well-known fact that if M is compact and F 0 : M → P is an immersion, then the initial value problem for the mean curvature flow admits a unique smooth solution on a maximal time interval \([0,T_{\max })\), where \(0<T_{\max }\le \infty \). Suppose now that P is the product manifold M × N and F 0 is the graph of a map f : M → N. Notice that long as the submanifolds deformed under mean curvature flow remain graphical, one obtains a smooth family of maps which belong to the homotopy class of the map f. In the case of long-time existence and convergence of the flow, we obtain a smooth homotopy from f to a minimal map.
The first result regarding evolutions by mean curvature of graphical submanifolds is due to Ecker and Huisken [33]. They proved long-time existence of entire graphical hypersurfaces in \(\mathbb {R}^{n+1}\). Moreover, Ecker and Huisken proved convergence to a flat subspace, if the growth rate at infinity of the initial graphical submanifold is linear. On the other hand, in higher codimensions, the complexity of the normal bundle makes the situation more complicated. Results analogous to that of Ecker and Huisken are not available any more without further assumptions. However, the ideas developed in the paper of Ecker and Huisken opened a new era for the study of the mean curvature flow of submanifolds in Riemannian manifolds of arbitrary codimension; see for example [12, 13, 16,17,18, 60,61,62, 64, 75, 77, 78, 85, 87,88,89,90,91, 94,95,96, 98,99,100].
This new deformation of maps between Riemannian manifolds via the mean curvature flow has been used in order to have a better understanding of the relation between the k-dilation Dil k and the homotopy type of maps. In order to be precise, let us recall at first the following definition:
Definition 1
Let f : M → N be a map between two Riemannian manifolds. We say that Dil k(f) ≤ α if f maps each k-dimensional submanifold Σ ⊂ M to an image with k-dimensional volume at most \(\alpha \cdot \mathcal {H}^{k}(\varSigma )\), where \(\mathcal {H}^{k}(\varSigma )\) stands for the k-dimensional Hausdorff measure of Σ. In particular, we say that f is area decreasing if Dil 2(f) ≤ 1, strictly area decreasing if Dil 2(f) = 1, and area preserving if Dil 2(f) = 1.
Roughly speaking, the k-dilation measures how much the map f : M → N contracts k-dimensional volumes. Gromov in [38] realized that there is a close relationship between the 1-dilation of a map and its homotopy type. For instance, he proved that if f is a map from \(\mathbb {S}^m\) to \(\mathbb {S}^{m}\), then its degree is at most \({Dil}^m_1(f)\) and this bound is sharp up to a constant factor. Motivated by this result, in [40, 41] Gromov proposed the following:
Problem 1
Let \(f:\mathbb {S}^m\to \mathbb {S}^n\) be a smooth map between euclidean spheres. Is there a number ε(k, m, n) such that if Dil k(f) < ε would imply that f is null-homotopic?
Tsui and Wang in [91] proved using the mean curvature flow that smooth strictly area decreasing maps \(f:\mathbb {S}^m\to \mathbb {S}^n\) can be smoothly deformed to a constant map. Guth [42] proved this result cannot be extended in the case of maps with k-dilation strictly less than 1, if k ≥ 3. The result of Tsui and Wang was generalized by Lee and Lee in [60]. In the matter of fact, they proved that any strictly area decreasing map between compact Riemannian manifolds M and N whose sectional curvatures are bounded by secM ≥ σ 1 and σ 2 ≥secN, where σ 1, σ 2 are two real constants such that σ 1 ≥ σ 2 > 0 or σ 1 > 0 ≥ σ 2, is homotopic by mean curvature flow to a constant map. We would like to point out here that the curvature assumptions can be relaxed to
where σ is a positive constant number, as it was shown in [75] by Savas-Halilaj and Smoczyk.
In the case of a smooth area decreasing map f : M → N between two compact Riemann surfaces M and N of the same constant sectional curvature σ, we have a complete picture of the behaviour of the mean curvature flow. It turns out that, under the mean curvature flow, such a map either instantly becomes strictly area decreasing or it was and remains an area preserving map. Moreover, the mean curvature flow preserves the graphical property, exists for all time, and converges to a minimal surface Σ ∞ of the product M × N. Additionally:
-
(I)
If the evolved graphs are generated by strictly area decreasing maps then:
-
(a)
If σ > 0, then Σ ∞ is the graph of a constant map.
-
(b)
If σ = 0, then Σ ∞ is the graph of an affine minimal map.
-
(a)
-
(II)
If the evolved graphs are generated by area preserving maps then:
-
(a)
If σ > 0, then Σ ∞ is the graph of an isometry.
-
(b)
If σ = 0, then Σ ∞ is the graph of an affine minimal diffeomorphism.
-
(a)
The first steps in the proof of the above result were made in the seminal works of Smoczyk [85] and Wang [94, 95, 100], where the area preserving case was investigated. The strictly area decreasing case was first treated by Tsui and Wang [91], in the positive case, and completed recently by Savas-Halilaj and Smoczyk in [78]. The primary goal of this survey is to present a unified proof of this result, based in [78].
From the results of Wang [94, 95, 100], we get another proof of Smale’s Theorem [84] which says that any diffeomorphism of \(\mathbb {S}^2\) can be smoothly deformed into an isometry. Let us mention here that, according to a deep theorem of Hatcher [49], any diffeomorphism of \(\mathbb {S}^3\) can be deformed into an isometry of \(\mathbb {S}^3\). Such a result is not expected for spheres of dimension greater or equal than 4; see for example [28]. However, the following problem is challenging:
Problem 2
Let \(f:\mathbb {S}^m\to \mathbb {S}^m\), m ≥ 4, be a smooth diffeomorphism. Under which conditions f can be smoothly deformed into an isometry of the sphere?
Another interesting problem is the investigation of the symplectomorphism group of the complex projective space \(\mathbb {C}\mathbb {P}^m\). Gromov [39] proved that the bi-holomorphic group of \(\mathbb {C}\mathbb {P}^2\) is a deformation retract of its symplectomorphism group. A natural problem is to determine whether a similar result holds for \(\mathbb {C}\mathbb {P}^m\) with m ≥ 3. In the matter of fact, the following problem is still open:
Problem 3
Let \(f:\mathbb {C}\mathbb {P}^m\to \mathbb {C}\mathbb {P}^m\), m ≥ 3, be a smooth symplectomorphism. Is it true that the mean curvature flow deforms the graph Γ(f) of f smoothly to the graph Γ(g) of bi-holomorphic map \(g:\mathbb {C}\mathbb {P}^m\to \mathbb {C}\mathbb {P}^m\)? Is it true that any minimal symplectomorphism \(f:\mathbb {C}\mathbb {P}^m\to \mathbb {C}\mathbb {P}^m\) is a bi-holomorphic isometry?
Medoš and Wang in [64] made some contribution by giving an affirmative answer to the above problem under the additional assumption that the singular values of the differential of the symplectomorphism are close to 1.
The paper is structured as follows. In Section 2 we set up the notation and recall basic facts from submanifold geometry. In Section 3 we discuss minimal submanifolds in euclidean spaces. We introduce the generalized Gauss map and prove the Ruh-Vilms Theorem. Section 4 describes the class of graphical submanifolds and review some Bernstein-type theorems. Section 5 is devoted to the maximum principle for scalar and systems of PDEs. In Section 6, we introduce the mean curvature flow, prove short-time existence, and derive various basic evolution equations. Section 7 describes how to built smooth singularity models for the mean curvature flow. Section 8 combines results from the previous sections to prove our main result.
2 Riemannian Submanifolds
In this section we set up the notation and recall some basic facts from submanifold geometry. We closely follow the exposition in [5, 29, 55, 59, 92, 102].
2.1 Notation and Conventions
Let M be a m-dimensional manifold and (E, π, M) a vector bundle of rank k over M. We often denote the bundles only by its total space E. The fiber of E at a point x ∈ M is denoted by E x, the tangent space of M at a point x ∈ M will be denoted by T x M and the space of sections of E is denoted by Γ(E). For the tangent bundle of M, we use the symbol TM. Sections of the tangent bundle are called vector fields and usually Γ(TM) is denoted by \(\mathfrak {X}(M)\). A smooth map T : E → V between two vector bundles E and V over M which maps the fiber E x linearly to V x, for any x ∈ M is called bundle morphism. If additionally, T is bijective we call it bundle isomorphism.
Definition 2
A (linear) connection on a vector bundle E is a map \(\nabla ^E\colon \mathfrak {X}(M)\times \varGamma (E)\rightarrow \varGamma (E)\), written \( \nabla ^E(v,\phi )=\nabla ^E_v\phi , \) satisfying the properties:
-
(a)
For any \(v_1, v_2\in \mathfrak {X}(M)\) and \(\phi \in \varGamma \left (E\right )\), it holds
$$\displaystyle \begin{aligned} \nabla^E_{v_1+v_2}\phi=\nabla^E_{v_1}\phi+\nabla^E_{v_2}\phi. \end{aligned}$$ -
(b)
For any \(v\in \mathfrak {X}(M)\), \(f\in C^{\infty }\left (M\right )\) and \(\phi \in \varGamma \left (E\right )\), it holds
$$\displaystyle \begin{aligned} \nabla^E_{fv}\phi=f\nabla^E_{v}\phi. \end{aligned}$$ -
(c)
For any \(v\in \mathfrak {X}(M)\), \(f\in C^{\infty }\left (M\right )\) and \(\phi _1,\phi _2\in \varGamma \left (E\right )\), it holds
$$\displaystyle \begin{aligned} \nabla^E_{v}(\phi_1+\phi_2)=\nabla^E_{v}\phi_1+\nabla^E_{v}\phi_2. \end{aligned}$$ -
(d)
For any \(v\in \mathfrak {X}(M)\), \(\phi \in \varGamma \left (E\right )\) and \(f\in C^{\infty }\left (M\right )\), it holds
$$\displaystyle \begin{aligned} \nabla^E_{v}\left(f\phi\right)=\left(vf\right)\phi+f\nabla^E_{v}\phi. \end{aligned}$$
For any ϕ ∈ Γ(E) and x 0 ∈ M, the value \(\nabla ^E\phi _x|{ }_{x_0}\) of the quantity \(\nabla ^E_v\phi \) at x 0 ∈ M depends only on the value of v at x 0 and on the restriction of ϕ along a curve passing through x 0 with speed v. If ϕ 1, ϕ 2 ∈ Γ(E) coincide on a neighbourhood of x 0 ∈ M, then
for any pair of vector fields \(v_1,v_2\in \mathfrak {X}(M)\) with \(v_1|{ }_{x_0}=v_2|{ }_{x_0}\).
Definition 3
A section ϕ ∈ Γ(E) is said to be parallel with respect to ∇E if, for any vector field v on M, it holds \(\nabla ^E_{v}\phi =0\).
We can define higher derivatives of sections of a vector bundle over a manifold M whose tangent bundle TM is equipped with a connection.
Definition 4
Suppose that M is a smooth manifold and E a vector bundle over M. Let ∇M be a connection of TM and ∇E a connection of E. For any pair \(v_1,v_2\in \mathfrak {X}(M)\), the map \(\nabla ^{2}_{v_1,v_2}\colon \varGamma (E)\rightarrow \varGamma (E),\) given by
is called the second covariant derivative of ϕ, with respect to the directions v 1 and v 2. By coupling the connections ∇M and ∇E, one may define, the k-th derivative ∇k of a section ϕ in Γ(E).
To each connection there is associated an important operator, which measures the non commutativity of the covariant derivatiation.
Definition 5
The operator \(R^{E}:\mathfrak {X}(M)\times \mathfrak {X}(M)\times \varGamma (E)\rightarrow \varGamma (E)\), defined by
for any \(v_1,v_2 \in \mathfrak {X}(M) \) and ϕ ∈ Γ(E), is called the curvature operator of ∇E.
Now let us turn our attention to vector bundles equipped with a Riemannian metric structure.
Definition 6
A Riemannian metric on a vector bundle E of rank k over the manifold M is a smooth map g E : Γ(E) × Γ(E) → C ∞(M), such that its restriction to the fibers is a positive definite inner product.
Definition 7
A connection ∇E is called compatible with the Riemannian metric g E or metric compatible if it satisfies
for any \(v \in \mathfrak {X}(M)\) and ϕ 1, ϕ 2 ∈ Γ(E). A vector bundle E endowed with these structures is called Riemannian vector bundle endowed with a compatible linear connection.
We say that a set of sections {ϕ 1, …, ϕ k} forms an orthonormal frame, with respect to g E if and only if g E(ϕ i, ϕ j) = δ ij, for any i, j ∈{1, …, k}. In particular, around any point x 0 of M it is possible to find a local orthonormal frame {ϕ 1, …, ϕ k} such that
for any tangent vector v. Such frames are called normal or geodesic frames.
Let us restrict ourselves at the tangent bundle TM of M. Given a Riemannian metric g on M, there is a unique connection ∇, referred as the Levi-Civita connection, which is compatible with the Riemannian metric. More precisely, ∇ is given by the Koszul formula
for all \(v_1,v_2,v_3\in \frak {X}(M)\). The Levi-Civita also satisfy
for any \(v_1,v_2\in \mathfrak {X}(M)\).
Denote by R the curvature operator with respect to the connection ∇. Combining R with g we obtain a (4,0)-tensor which, for simplicity, we again denote with the letter R. More precisely,
for any \(v_1,v_2,v_3,v_4\in \mathfrak {X}(M)\). If v 1, v 2 are linearly independent vectors, then
is called the sectional curvature of the plane spanned by the vectors v 1 and v 2. By contracting the operator R with g we obtain the Ricci operator \(\operatorname {Ric}\) and the scalar curvature \(\operatorname {scal}\), i.e.,
where \(v\in \mathfrak {X}(M)\) and \(\left \{e_{1},\dots ,e_{m}\right \} \) is a local orthonormal frame on M.
Remark 1
One can use the operations of Linear Algebra to produce new vector bundles from given ones. For example, if E and V are vector bundles over a manifold M, then E ∗, E × V , E ⊗ V , E ⊕ V , \(\operatorname {Hom}(E;V)\), Λ r(V ) and \(\operatorname {Sym}^r(V)\) gives rise to new bundles over M. If M is endowed with a Riemannian metric, then this metric and its Levi-Civita connections extends in a natural way to all the aforementioned bundles; for more details see [59] or [102].
2.2 The Pull-back Bundle
Let M and N be two manifolds, (E, π, N) is a vector bundle of rank k over N and suppose that f : M → N is a smooth map. The map f induces a new vector bundle of rank k over M. Indeed, take as total space
and as projection the map π f : f ∗ E → M given by π f(x, ξ) = x. The space Γ(f ∗ E) contains all sections of E with base point at f(M) and inherit naturally a vector space structure from E f(x), given by
The triple (f ∗ E, π f, M) carries the structure of a vector bundle over M. This bundle is called the pull-back or the induced by f vector bundle on M.
Suppose that h is a Riemannian metric on E and ∇E is a metric compatible connection. The map f induces a connection \(\nabla ^{f^*E}\) on the pull-back bundle which is defined as follows: Let {𝜗 1, …, 𝜗 k} be a local orthonormal frame field of E in a neighbourhood of the point f(x) ∈ N. Then, any section ϕ ∈ Γ(f ∗ E) can be written in the form
where ϕ α, α ∈{1, …, k}, are the components of ϕ with respect to the given orthonormal frame field. Define now the induced connection by
for x ∈ M and v ∈ T x M. One can easily show that the curvature operator \(R^{f^*E}\) of \(\nabla ^{f^*E}\) is given by
for any x ∈ M, v 1, v 2 ∈ T x M and ϕ ∈ E|f(x).
Let us discuss the case where f : (M, g, ∇g) → (N, h, ∇h) is a map between Riemannian manifolds. The restriction of h on f ∗ TN, induces a Riemannian metric on f ∗ TN, which is compatible with the pull-back connection, that is
Moreover, for \(v_1,v_2\in \mathfrak {X}(M)\), it holds
Definition 8
The Hessian of a map f : (M, g, ∇g) → (N, h, ∇h) is defined to be the symmetric tensor \(B:\mathfrak {X}(M)\times \mathfrak {X}(M)\to \varGamma (f^*E)\) given by
for any \(v_1,v_2\in \mathfrak {X}(M)\). The trace of B with respect to g is denoted by Δ g,h f and is called the Laplacian of f. If the Laplacian of f is zero, then f is called a harmonic map.
2.3 The Second Fundamental Form
Consider Riemannian manifolds (M, g, ∇g) and (N, h, ∇h) of dimension m and n, respectively, with m ≤ n. A map f : M → N is called an isometric immersion if and only if f ∗ h = g. For simplicity, we often denote both metrics g and h by 〈⋅ , ⋅〉. At every x ∈ M, we have the orthogonal decomposition
where N f(x) M is the orthogonal complement of df x(T x M) with respect to h. The union NM of all normal spaces form a vector bundle of rank n − m over M which is called the normal bundle. According to the above decomposition, any section v ∈ Γ(f ∗ TN) can be decomposed in a unique way in the form
where v ⊤ is the tangent and v ⊥ is the normal part of v along the submanifold. A well known fact in submanifold theory is that
for any \(v_1,v_2\in \mathfrak {X}(M)\). In submanifold theory, the Hessian of f is denoted by the letter A, i.e., we have
The tensor A is called the second fundamental form of f. If ξ is a normal vector, then the tensor A ξ given by
for any tangent vectors v 1, v 2, is called shape operator with respect to ξ. The Weingarten operator A ξ associated with ξ is defined by
The Laplacian of f or, equivalently, the trace of A with respect to g is called the (unormalized) mean curvature and is denoted by the letter H, that is
Definition 9
A submanifold with zero mean curvature is called minimal.
The restriction of h on NM gives rise to a Riemannian metric on the normal bundle. Moreover, the restriction of ∇h on NM induces a connection ∇⊥ on NM which is compatible with the metric; i.e., just define
The curvature tensor of the normal bundle is denoted by R ⊥ and is given by
As usual, we can form from R ⊥ a C ∞(M)-valued tensor which we denote again by R ⊥, that is
The Riemann curvature operator R of M, the curvature operator \(\widetilde {R}\) of N and the normal curvature R ⊥ are related to the second fundamental form A through the Gauss-Codazzi-Ricci equations:
-
(a)
Gauss equation:
$$\displaystyle \begin{aligned} \begin{array}{rcl} \quad \,\,\,R(v_1,v_2,v_3,v_4)& =&\displaystyle {\widetilde R}\big(df(v_1),df(v_2),df(v_3),df(v_4)\big)\\ & &\displaystyle +\langle A(v_1,v_3),A(v_2,v_4)\rangle -\langle A(v_2,v_3),A(v_1,v_4)\rangle. \end{array} \end{aligned} $$ -
(b)
Codazzi equation:
$$\displaystyle \begin{aligned}\big(\nabla^{\perp}_{v_1}A\big)(v_2,v_3)-\big(\nabla^{\perp}_{v_2}A\big)(v_1,v_3)= \big(\widetilde{R}\big(df(v_1)df(v_2),df(v_3)\big)\big)^\bot.\end{aligned}$$ -
(c)
Ricci equation:
$$\displaystyle \begin{aligned} \begin{array}{rcl} R^{\perp}(v_1,v_2,\xi,\eta)& =&\displaystyle {\widetilde R}\big(df(v_1),df(v_2),\xi,\eta\big)\\ & &\displaystyle +\sum_{k}\big(A^{\xi}(v_1,e_k) A^{\eta}(v_2,e_k) - A^{\eta}(v_1,e_k) A^{\xi}(v_2,e_k)\big), \end{array} \end{aligned} $$
where \(v_1,v_2,v_3,v_4\in \mathfrak {X}(M)\), ξ, η ∈ NM and {e 1, …, e m} is a local orthonormal frame field with respect to g.
2.4 Local Representations
Let f : (M, g) → (N, h) be a smooth map between Riemannian manifolds. For computational reasons, we need expressions for components of various tensorial quantities. We can express coordinates with respect to local charts or with respect to orthonormal frames.
Let discuss at first the notation with respect to a local coordinate system. Choose a chart (U, φ) around a point x ∈ M and a chart (V, ψ) around f(x) ∈ N. Assume that \(\varphi :U\to \mathbb {R}^m\) is represented as φ = (x 1, …, x m) and suppose that \(\psi :V\to \mathbb {R}^n\) is represented as ψ = (y 1, …, y n). We use Latin indices to describe quantities on M and Greek indices for quantities on N. From the charts φ and ψ, we obtain for f the local expression expression
where
Denote now the basic vector fields associated with the charts (U, φ) and (V, ψ) by \(\{\partial _{x_i},\dots ,\partial _{x_m}\big \}\) and \(\{\partial _{y_1},\dots ,\partial _{y_n}\big \}\), respectively. Moreover, denote their corresponding dual forms by {dx 1, …, dx m} and {dy 1, …, dy n}. With respect to these conventions, the Riemannian metrics g and h can be written in the form
The Christoffel symbols \(\varGamma ^k_{ij}\) of the metric g, are defined by the formula
and they can be expressed in terms of the metric as
where g ij are the components of the inverse of the matrix of the metric g, with respect to the basis \(\{\partial _{x_1},\dots ,\partial _{x_m}\}\). Similarly, are defined the Christoffel symbols \(\varGamma ^{\alpha }_{\beta \gamma }\) of h. The differential of the map f and the pull-back via f of the metric h are given by
By a straightforward computation, we see that the Hessian B of f can be represented in the form
Suppose now that f : M → N is an isometric immersion. Then, the second fundamental form A and the mean curvature H are represented, respectively, as
and
Let us discuss now expressions of tensors in local orthonormal frames. Let {e 1, …, e m} be a local orthonormal frame of the tangent bundle and {ξ m+1, …, ξ n} a local orthonormal frame of the normal bundle. Here we use Latin indices for components on the tangent bundle and Greek indices for components on the normal bundle. For example, we write:
Now the Gauss-Codazzi-Ricci equations can be written as:
-
(a)
Gauss equation:
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} R_{ijkl}={\widetilde{R}} _{ijkl}+\sum_{\alpha} \big(A^\alpha_{ik}A^\alpha_{jl}- A^\alpha_{jk}A^\alpha_{il}\big). \end{array} \end{aligned} $$(3) -
(b)
Codazzi equation:
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \big(\nabla^{\perp}_{e_i}A\big)^{\alpha}_{jk}-\big(\nabla^{\perp}_{e_j}A\big)^{\alpha}_{ik}=-\sum_{\alpha}\widetilde{R}_{ijk\alpha}. \end{array} \end{aligned} $$(4) -
(c)
Ricci equation:
$$\displaystyle \begin{aligned} R^{\perp}_{ij\alpha\beta}=\widetilde{R}_{ij\alpha\beta}+\sum_{k}\big(A^{\alpha}_{ik}A^{\beta}_{jk}-A^{\beta}_{ik}A^{\alpha}_{jk}\big). \end{aligned} $$(5)
3 Minimal Submanifolds
The theory of minimal submanifolds is one of the most active subjects of differential geometry. There is a vast of literature, but here we will present rather basic facts concerning higher codimensional minimal submanifolds. For more details we refer to [21, 22, 70].
3.1 The Gauss Map of a Minimal Submanifold
One of the most important objects in the submanifold geometry is the Gauss map. For codimension one oriented submanifolds in the euclidean space, the Gauss map associates to every point of the hypersurface its oriented unit normal vector. This concept can be generalized to higher codimensional oriented submanifolds. Let \(f:M\to {\mathbb R^{n}}\) be an isometric immersion of a m-dimensional oriented Riemannian manifold M into the euclidean space. The image df(T x M), can be taken after a suitable parallel displacement in \(\mathbb {R}^n\), into a point \(\mathcal {G}(x)\) of the oriented Grassmann space \(\mathbb {G}_+(m,n)\) of m-dimensional oriented subspaces of \(\mathbb {R}^n\). The map \(\mathcal {G}:M\to \mathbb {G}_+(m,n)\) defined in this way, is called the generalized Gauss map.
There is a natural way to visualize the Grassmann space \(\mathbb {G}_+(m,n)\). Let us denote by \(\varLambda ^m(\mathbb {R}^n)\) the dual space of all alternative multilinear forms of degree m. Elements of \(\varLambda ^m(\mathbb {R}^n)\) are called m-vectors. Hence, given vectors v 1, …, v m on \(\mathbb {R}^n\), the exterior product v 1 ∧⋯ ∧ v m is the linear map which on an alternating form Ω of degree m takes the value
The exterior product is linear in each variable separately. Interchanging two elements the sign of the product changes and if two variables are the same the exterior product vanishes. An m-vector ξ is called simple or decomposable if it can be written as a single wedge product of vectors, that is
Note that are m-vectors which are not simple. Using standard techniques from Linear Algebra one can verify that the exterior product v 1 ∧⋯ ∧ v m is zero if and only if the vectors are linearly dependent. Moreover, if {e 1, …, e n} consists a basis for \(\mathbb {R}^n\), then the m-vectors
consists a basis of \(\varLambda ^m(\mathbb {R}^n)\). Therefore, the dimension of the vector space of m-vectors is
Each simple vector represents a unique m-dimensional subspace of \(\mathbb {R}^n\). Moreover, if ξ and η are simple vectors representing the same subspace, then there exists a non-zero real number such that ξ = λη. Therefore, there is an obvious equivalence relation on the space of simple vectors such that the space of equivalence classes is to an one to one correspondence with the space of m-dimensional subspaces of \(\mathbb {R}^n\). Additionally, we can consider the following relation on the set of non-zero simple m-vectors: ξ and η are called equivalent if and only if ξ = λη for some positive number λ. Denote by [ξ] the class containing all simple m-vectors that are equivalent to ξ. The equivalence classes now obtained are called oriented m-dimensional subspaces of \(\mathbb {R}^n\).
We can equip \(\varLambda ^m(\mathbb {R}^n)\) with a natural inner product, which for simplicity we denote again by 〈⋅ , ⋅〉. Indeed, define
on simple m-vectors and then extend linearly. Moreover, if {e 1, …, e n} is an orthonormal basis of \(\mathbb {R}^n\) then, the m-vectors
consists an orthonormal basis for the exterior power \(\varLambda ^m(\mathbb {R}^n)\). Moreover, it turns out that for vectors v 1, …, v m in \(\mathbb {R}^n\), the norm
gives the m-volume of the parallelepiped spanned by these vectors.
We can equip \(\mathbb {G}_+(m,n)\) with a natural differentiable structure. For every m-dimensional subspace V 0 of \(\mathbb {G}_+(m,n)\), consider the open neighbourhood U(V 0) of oriented m-dimensional subspaces whose orthogonal projection into V 0 is one-to-one. Let {e 1, …, e m} be an orthonormal base spanning V 0 and {η m+1, …, η n} an orthonormal base spanning its orthogonal complement \(V_0^{\perp }\) in \(\mathbb {R}^n\). Then, we may parametrize U(V 0) via \(\xi :\mathbb {R}^{m(n-m)}\to U(V_0)\) given by
Two charts U(V i), U(V j) with distinct V i, V j are analytically compatible.
Definition 10
The map \(\varPsi :\mathbb {G}_+(m,n)\to \mathbb {S}^{\binom {n}{m}-1}\) given by
is called the Plücker embedding. We regard the Grassmann space \(\mathbb {G}_+(m,n)\) as a Riemannian manifold with the induced by Ψ Riemannian metric.
Theorem 1
The Plücker embedding is minimal.
Proof
Fix a m-dimensional linear space \(V_0\in \mathbb {G}_+(m,n)\) and consider the parametrization \(\xi :\mathbb {R}^{m(n-m)}\to U(V_0)\subset \mathbb {G}_+(m,n)\) described in (6). Now
where the index α run from m + 1 to n and
Note that
and
where i, j ∈{1, …, m} and α, β ∈{m + 1, …, n}. In particular,
and
Additionally,
and
Moreover,
Hence, the vectors
form an orthonormal basis of \(T_{V_0}\mathbb {G}_+(m,n)\) with respect to the induced by Ψ Riemannian metric. Moreover, from (7), (8), and (9) we deduce that
According to (8), the second fundamental form A of the Plücker embedding at the point V 0 is equal to
and, in particular,
for any i ∈{1, …, m} and α ∈{m + 1, …, n}. Thus, the mean curvature H of the embedding Ψ at V 0 is given by
Consequently, Ψ gives rise to a minimal submanifold of the sphere. □
In 1970, Ruh and Vilms [74] obtained an important link between minimality of a submanifold and the harmonicity of its generalized Gauss map. More precisely, the following result holds:
Theorem 2
Let \(f:M\to \mathbb {R}^n\) be a minimal isometric immersion. Then, the generalized Gauss map \(\mathcal {G}\) of f is a harmonic map.
Proof
Consider the map
where Ψ is the Plücker embedding. From the composition formula, we have
for any \(v_1,v_2\in \mathfrak {X}(M)\), where B F and \(B_{\mathcal {G}}\) are the Hessians of F and \(\mathcal {G}\) and A Ψ the second fundamental form of Ψ, respectively. Fix a local orthonormal frame field {e 1, …, e m} defined on an open neighbourhood U of M and a local orthonormal frame {η m+1, …, η n} in the normal bundle of the immersion. Note that since f is isometric immersion, for any x ∈ U, we have
Fix now a point x 0 ∈ U and for simplicity suppose that the frame {e 1, …, e m} is normal at x 0. By straightforward computations we see that at x 0 we have
where A is the second fundamental form of f. Hence, in view of (7), we obtain that the differential of \(\mathcal {G}\) at x 0 is equal to
Recall that, from the Codazzi equations (4), we have at x 0 that
for any j, k, l ∈{1, …, m}. Differentiating dF and estimating at x 0 we get
Therefore, at x 0 we have the identity
Summing up and using the minimality of f, we see that at x 0 it holds
Hence, bearing in mind equation (10) which gives the formula for the second fundamental form of Ψ it follows that at x 0 we have
Combining the last equality with (12) we get the desired result. □
3.2 Weierstrass Representations
For two dimensional surfaces in the euclidean space, there is a link between minimality and holomorphicity through a general formula which express a simply-connected minimal surface in terms of complex functions with certain properties. In particular, the following result holds:
Theorem 3
Let \(\varphi _1,\dots ,\varphi _{n}:U\subset \mathbb {C}\to {\mathbb C}\) be holomorphic functions, where U is simply connected, such that \(\varphi ^2_1+\dots +\varphi ^2_{n}=0\) and |φ 1|2 + ⋯ + |φ n|2 > 0. Then, the map
where z 0 ∈ U, gives rise to minimal surface in \({\mathbb R^{n}}\) . Conversely, every minimal surface in \({\mathbb R^{n}}\) , at least locally, can be described in this form.
The idea to obtain such a parametrization is the following: Let \(f:M\to \mathbb {R}^n\) be a minimal immersion of a 2-manifold. Choose a local isothermal system of coordinates \((U\subset \mathbb {C},z=x+iy)\), where U is simply connected; see [54]. Then, the induced by f metric g on M has the form g = E|dz|2, where E is a smooth positive function. Moreover, in these coordinates, the Laplace–Beltrami operator Δ with respect to g is expressed by
With respect to such parameters, minimality is equivalent to harmonicity. Consider now the map \(\varphi =(\varphi _1,\dots ,\varphi _n):U\to \mathbb {C}^n\), φ = f x − if y. One can readily check that φ is holomorphic and its components satisfy
By fixing a point z 0 ∈ U it is clear that, up to a parallel transport,
The map φ has also a very important geometric interpretation. At first we observe that the variety
is diffeomorphic with \(\mathbb {G}_+(2,n)\). To see this, consider a 2-plane \(\varPi \subset \mathbb {R}^n\) that is spanned by u ∧ v, where the vectors u and v satisfy |u|−|v| = 0 and 〈u, v〉 = 0. Then, vector w = u + iv belongs to Q n−2. Hence, to each oriented 2-plane we associate a point in Q n−2. In fact, this correspondence actually is a diffeomorphism. Consequently, the map \(\overline \varphi :U\to Q_{n-2}\), \(\overline \varphi =f_x+if_y\), is exactly the generalized Gauss map of the minimal surface.
Let M be a manifold of dimension 2m endowed with a Riemannian metric g and a metric connection ∇. An almost complex structure on M is by definition a bundle isomorphism J : TM → TM satisfying J ∘ J = −I. The pair (M, J) is called an almost complex manifold. If J is an isometry with respect to g and parallel with respect to ∇, then the triple (M, g, J) is called Kähler manifold. In this case, the 2-form Ω given by
where \(v_1,v_2\in \frak {X}(M)\), is closed and is called the Kähler form. A smooth map f : (M, J M) → (N, J N) between Kähler manifolds is called holomorphic if df ∘ J M = J N ∘ df and anti-holomorphic if df ∘ J M = −J N ∘ df. If the map f is a holomorphic or anti-holomorphic isometric immersion, then f(M) will be called an immersed complex submanifold of N. Such immersions are automatically minimal.
With the terminology we just introduced and the discussion above, we can now state the following result which was originally proved by Chern [20].
Theorem 4
An oriented surface of the euclidean space is minimal if and only if its generalized Gauss map is anti-homolomorphic.
We will present now another interesting category of submanifolds, the so called Lagrangian submanifolds.
Definition 11
Let M m be a Riemannian manifold, (N 2m, g N, Ω) be a Kähler manifold and f : M m → N 2m an isometric immersion. The immersion f will be called Lagrangian if and only if f ∗ Ω = 0.
Let us conclude this section with the following parametrization of minimal Lagrangian surfaces in \(\mathbb {R}^4\); see Chen and Morvan [19] and Aiyama [1, 2].
Theorem 5
Suppose that \(f,g:U\to \mathbb {C}\) are two holomorphic maps defined in a simply connected domain U of the complex plane satisfying |f z|2 + |g z|2 > 0. Then the map
where β is a real number, is a minimal conformal Lagrangian immersion in \(\mathbb {C}^2\) . The generalized Gauss map \(\mathcal {G}\) takes values in \(\mathbb {S}^2\times \{(e^{i\beta },0)\}\simeq \mathbb {C}\cup \{\infty \}\) and is given by the formula
Conversely, every minimal Lagrangian immersion \(f:M\to \mathbb {C}^2\) can be, at least locally, parametrized as above.
4 Scalar and Vectorial Maximum Principles
The maximum principle is one of the most useful tools employed in the study of PDEs. All maximum principles rely on the following elementary result of calculus: Suppose that Ω is an open, bounded domain of \(\mathbb {R}^m\) and let \(u:{\overline \varOmega }\to {\mathbb R}\) be a continuous function which is C 2-smooth in Ω. If u attains its maximum at interior point x 0, then
As an immediate consequence of this fact is that any continuous and C 2-smooth up to the boundary strictly convex function must attain its maximum at the boundary of Ω. In the matter of fact, one can show a little bit more: Any continuous and C 2-smooth up to the boundary weakly convex function either attain its maximum at the boundary of Ω or otherwise is constant. The above principle holds for a large class of solutions of partial differential inequalities.
4.1 Hopf’s Maximum Principles
Suppose that Ω is a bounded, open and connected domain of \({\mathbb R^{m}}\). We wish to study operators \(\mathcal {L}\colon C^{2}(\varOmega )\to C^{0}(\varOmega )\) of the form
where here \(a_{ij}=a_{ij},\,b_{j}\colon \varOmega \to {\mathbb R}\), i, j ∈{1, …, m}, are uniformly bounded functions and \(\partial _{x_i}\), i ∈{1, …, m}, the partial derivatives with respect the cartesian coordinates of \({\mathbb R^{m}}\). The symmetric matrix \(\mathcal {A}\) with coefficients the functions a ij is called the representative matrix of \(\mathcal {L}\).
Definition 12
The operator \(\mathcal {L}\) is called elliptic if the matrix \(\mathcal {A}\) is positive at each point of Ω. Moreover, \(\mathcal {L}\) is called uniformly elliptic if the smallest eigenvalue of its matrix \(\mathcal {A}\) is a function which is bounded away from zero.
Theorem 6 (Hopf’s Strong Maximum Principle)
Let \(\varOmega \subset \mathbb {R}^m\) be an open, connected and bounded domain. Suppose that \(u\in C^2(\varOmega )\cap C^{0}(\overline {\varOmega })\) is a solution of the differential inequality
where \(\mathcal {L}\) is an uniformly elliptic differential operator with uniformly bounded coefficients and h a continuous function on \(\overline {\varOmega }\).
-
(a)
Suppose that h = 0 and that u attains its maximum at an interior point of Ω. Then, u is constant.
-
(b)
Suppose that h ≤ 0 and that u attains a non-negative maximum at an interior point of Ω. Then, u is constant.
For the proof see [35] or [72].
4.2 Maximum Principles for Systems
We would like to have a form of the maximum principle that is applicable for sections in vector bundles. To generalize, first note that Hopf’s maximum principle for functions can be re-formulated as follows:
Let Ω be an open subset of \(\mathbb {R}^m\) and \(u:\varOmega \subset \mathbb {R}^m\to [a,b]\) a C 2-smooth function satisfying the uniformly elliptic differential equation
If a point of Ω is mapped into a boundary point of [a, b], then any point of Ω is mapped into the boundary.
From this point of view of the statement of Hopf’s maximum principle, one can guess how the generalization of the maximum principle for vector valued maps should be. The interval is replaced by a convex set K and the statement reads:
Let \(\varOmega \subset \mathbb {R}^m\) be open, \(K\subset \mathbb {R}^n\) closed convex and u : Ω → K a C 2-smooth vector valued map satisfying the uniformly elliptic differential system
If a point of Ω is mapped into a boundary point of K then every point is mapped into the boundary.
4.2.1 Convexity and Distance Functions
A crucial role in the proof of the vectorial maximum principle plays the geometry of the (signed) distance function from the boundary of a convex set. In this subsection, we review the basic definitions of the geometry of convex sets in euclidean space such as supporting half-spaces, tangent cones, normal vectors and distance functions.
Definition 13
A subset K of \({\mathbb R^{n}}\) is called convex if for any pair of points z, w ∈ K, the segment
is contained in K. The set K is said to be strictly convex, if for any pair z, w ∈ K the segment \(\mathcal {E}_{z,w}\) belongs to the interior of K.
A convex set \(K\subset {\mathbb R^{n}}\) may have non-smooth boundary. It is a well-known fact in Convex Geometry that the boundary ∂K is a continuous hypersurface of \({\mathbb R^{n}}\). In fact, according to a result of Reidemeister [73], the boundary ∂K is Lipschitz continuous and so almost everywhere differentiable. In particular, there is no well-defined tangent or normal space of K in the classical sense. However, there is a way to generalize these notions for convex subsets of \({\mathbb R^{n}}\).
Definition 14
Let K be a closed convex subset of the euclidean space \({\mathbb R^{n}}\). A supporting half-space of the set K is a closed half-space of \({\mathbb R^{n}}\) which contains K and has points of K on its boundary. A supporting hyperplane of K is a hyperplane which is the boundary of a supporting half-space of K. The tangent cone \(C_{y_0}K\) of K at y 0 ∈ ∂K is defined as the intersection of all supporting half-spaces of K that contain y 0.
Definition 15
Let \(K\subset {\mathbb R^{n}}\) be a closed convex subset and y 0 ∈ ∂K. Then:
-
(a)
A non-zero vector ξ is called normal vector of ∂K at y 0, if ξ is normal to a supporting hyperplane of K passing through y 0. This normal vector is called inward pointing, if it points into the half-space containing K.
-
(b)
A vector η is called inward pointing at y 0 ∈ ∂K, if
$$\displaystyle \begin{aligned}\langle\xi,\eta\rangle\ge 0\end{aligned}$$for any inward pointing normal vector ξ at y 0.
Let \(K\subset \mathbb {R}^n\) be a closed convex set and \(d:\mathbb {R}^n\to \mathbb {R}\) the function given by
Note that for each \(x\in {\mathbb R^{n}}\) there is at least one point y ∈ ∂K such that
Moreover, the function d is Lipschitz continuous. For a better understanding of the properties of d, let us suppose that ∂K is C 2-smooth. Denote by ξ the inward pointing unit normal vector field along ∂K and by the A the corresponding Weingarten operator. Because K is convex, from Hadamard’s Theorem, A is non-negative definite. In particular, K is strictly convex if and only if A is positive definite; see for example [29]. Fix a point y 0 ∈ ∂K. In an open neighbourhood \(U\subset {\mathbb R^{n}}\) of y 0, the part U ∩ ∂K can be parametrized via an embedding \(f:\varOmega =U\cap T_{y_0}K\to {\mathbb R^{n}},\) which assigns to each point of Ω the height of ∂K from its tangent plane at y 0. Recall from multi-variable calculus that the distance of any point z ∈ K 0 to ∂K is realized as the intersection of a straight line passing through z and meeting ∂K orthogonally. Hence, the level set
of d is parametrized locally via the map \(f_t:\varOmega \to {\mathbb R^{n}}\) given by
Proposition 1
There exists a positive real number ε, such that f t is an immersion for all t ∈ (−ε, ε). Moreover, the unit normal along f t coincide with the unit normal ξ of f. Additionally, the Weingarten operator A t of f t is related to the Weingarten operator A of f by the formula
In particular, K t is strictly convex if and only if ∂K is strictly convex.
Proof
We have
Hence, ξ is a unit normal vector field along f t. Therefore,
and so
From the above formula we deduce that there exists a positive constant ε such that K t is convex for all t ∈ (−ε, ε). In addition, if ∂K is strictly convex, the level sets close to the boundary are also strictly convex. □
Proposition 2
Let K be a closed and convex set in \({\mathbb R^{n}}\).
-
(a)
For any y 0 ∈ ∂K there exists a neighbourhood \(U\subset {\mathbb R^{n}}\) containing y 0 , such that d is C 2 -smooth function on U ∩ K 0.
-
(b)
Let v, w tangent vectors of K d(z) at z ∈ K 0 . Then, the Hessian ∇2 d of d satisfies
$$\displaystyle \begin{aligned}\nabla^2d(v,w)=-\frac{A(v,w)}{1-d(z)A(v,w)},\end{aligned}$$where A is the shape operator of ∂K associated to the inward pointing unit normal, and
$$\displaystyle \begin{aligned}\nabla^2d(v,\xi)=0.\end{aligned}$$
Proof
Parametrize, locally, the boundary ∂K as the image of an embedding \(f:\varOmega \subset \mathbb {R}^{n-1}\to \mathbb {R}^n\). Define the map \(F:\varOmega \times {\mathbb R}\subset \mathbb {R}^n\to {\mathbb R^{n}}\), given by
Then, \(dF_{(y_0,t)}(\partial _t)=\xi _{y_0}\) and \(dF_{(y_0,t)}(v)=df_{x_0}(v-tAv),\) for any index i ∈{1, …, n − 1} and \(v\in T_{y_0}\varOmega \). From the inverse mapping theorem, there exists an open subset D ⊂ Ω and a positive number ε such that the map F is a C 2-diffeomorphism for any (x, t) ∈ D × (−ε, ε). Hence, under a change of coordinates, d may be regarded as a C 2-smooth function defined on D × (−ε, ε). In the matter of fact, in these coordinates, we have
Therefore, ∇d (x,t) = ξ x. Because |∇d| = 1, we deduce that ∇2 d vanishes on the normal bundle of any level set K t. Moreover, ∇2 d = −A t on the tangent space of any level set K t. Now the desired result follows from Proposition 1. This completes the proof. □
4.2.2 Weinberger’s Maximum Principle
Weinberger [101] established a strong maximum principle for C 2-smooth maps \(u:\varOmega \subset \mathbb {R}^m\to K\subset \mathbb {R}^n\) with values in a closed convex set \(K\subset {\mathbb R^{n}}\), whose boundary ∂K satisfies some regularity conditions that he called “slab conditions”. Inspired by the ideas of Weinberger, Wang [93] gave a geometric proof of the strong maximum principle, in the case where the boundary ∂K of K is of class C 2. The idea of Wang was to apply Hopf’s maximum principle to the function \(d\circ u:\varOmega \to {\mathbb R}\), whose value at x is equal to the distance of u(x) from the boundary ∂K. Later, Evans [36] removed all additional regularity requirements on the boundary of K.
Theorem 7 (Weinberger-Evans)
Let K be a closed, convex set of \({\mathbb R^{n}}\) and \(u:\varOmega \subset {\mathbb R^{m}}\to K\subset {\mathbb R^{n}}\) , u = (u 1, …, u n), a solution of the uniformly elliptic system of partial differential equations
where Ω is a connected open domain of \({\mathbb R^{m}}\) and \(\varPsi :\varOmega \times {\mathbb R^{n}}\to {\mathbb R^{n}}\) a continuous map that is Lipschitz continuous in the second variable. Suppose further that Ψ is pointing into K.
-
(a)
If there is a point x 0 ∈ Ω such that u(x 0) ∈ ∂K, then u(x) ∈ ∂K for any point x ∈ Ω.
-
(b)
Assume additionally that the boundary ∂K is strictly convex. If there is a point x 0 ∈ Ω such that u(x 0) ∈ ∂K, then u is constant.
Proof
Let us give the proof in the case where the boundary of K is smooth of class C 2, following the ideas in [93]. Consider the function \(f=d\circ u:\varOmega \to {\mathbb R}\). We compute,
and
Consider now the uniformly differential operator \(\widetilde {\mathcal {L}}\) given by
By a straightforward computation, we get
Denote the first sum in the right hand side of (15) by I and the second sum by II. Observe at first that
We restrict our selves in a sufficiently small neighbourhood \(U\subset \mathbb {R}^n\) around u(x 0) and in an neighbourhood V of x 0 such that u(V ) ⊂ U. For each x ∈ V , denote by \(\widehat u(x)\) the unique point on ∂K with the property
Recall that the integral curves ∇d are straight lines perpendicular to each level set of d. Thus, \(\nabla d_{u(x)}=\nabla d_{\widehat u(x)}.\) Since Ψ is inward pointing, we get that
Therefore, exploiting the Lipschitz property of Ψ, we get that
where h is a non-negative bounded function. Recall from Proposition 1 that U is foliated by level sets of d. Thus, we can decompose \( u_{x_i}\) in the form
where (⋅)⊤ denotes the orthogonal projection into the tangent space and (⋅)⊤ the orthogonal projection into the normal space of the foliation. Bearing in mind the conclusions of Proposition 2, we deduce that
Since, A is non-negative definite and \(\mathcal {A}=(a_{ij})\) is positive definite, we deduce that
In addition, for any x such that u(x) ∈ ∂K, we have that
Putting everything together, we get
Since f ≥ 0 and there exists a point x 0 such that f(x 0) = 0, from Hopf’s strong maximum principle we deduce that f ≡ 0. This implies now that all the values of u lie in the boundary of K. Moreover, going back to the original equation for f, we see that II ≡ 0. Consequently, if ∂K is strictly convex, from (16) it follows that u must be constant. This completes the proof. □
4.3 Maximum Principles for Bundles
To state the maximum principle for sections in vector bundles, we must introduce an appropriate notion of convexity for subsets of vector bundles. Let us recall at first the following definition of Hamilton [45]:
Definition 16 (Hamilton)
Suppose that E is a vector bundle over the manifold M and let K be a closed subset of E.
-
(a)
The set K is called fiber-convex or convex in the fiber, if for each x ∈ M, the set K x = K ∩ E x is a convex subset of the fiber E x.
-
(b)
The set K is called invariant under parallel transport, if for every smooth curve γ : [0, b] → M and any vector v ∈ K γ(0), the unique parallel section v(t) ∈ E γ(t), t ∈ [0, b], along γ(t) with v(0) = v, is contained in K.
-
(c)
A fiberwise map Ψ : E → E is a map such that π ∘ Ψ = π, where π denotes the bundle projection. We say that a fiberwise map Ψ points into K (or is inward pointing), if for any x ∈ M and any 𝜗 ∈ ∂K x the vector Ψ(𝜗) belongs to the tangent cone C 𝜗 K x of K x at 𝜗.
Let E be a Riemannian vector bundle over a manifold M equipped with a metric compatible connection. We consider uniformly elliptic operators \(\mathcal {L}\) that are given locally by
where {e 1, …, e m} is a local orthonormal frame of M, \(\mathcal {A}=(a_{ij})\) a symmetric, uniformly positive definite tensor and \(b=\sum _{i=1}^mb_ie_i\) is a smooth vector field.
For the proof of the maximum principle, we will use a result due to Böhm and Wilking [9].
Lemma 1
Let M be a Riemannian manifold and E a Riemannian vector bundle over M equipped with a metric compatible connection. Let K ⊂ E be a closed and fiber-convex subset which is invariant under parallel transport. If ϕ is a smooth section with values in K then, for any x ∈ M and v ∈ T x M, the Hessian
belongs into the tangent cone of K x at the point ϕ|x.
Proof
It suffices to prove the result in the case where there exists a point x 0 which is mapped via ϕ in the boundary of K, since otherwise the result is trivially true. Consider a unit vector \(v\in T_{x_0}M\) and an normal coordinate system (x 1 , …, x m) in an open neighbourhood U around a point x 0 such that \(\left .\partial _{x_1}\right |{ }_{x_0}=v.\) Moreover, pick a basis \(\{\phi _1|{ }_{x_0}\,,\dots ,\phi _k|{ }_{x_0}\}\) of \(E_{x_0}\) and extend it into a local geodesic orthonormal frame field. Then,
where the components \(u_i:U\to {\mathbb R}\), i ∈{1 , …, k}, are smooth functions. A simple computation shows
where γ : (−ε, ε) → U is a length minimizing geodesic such that
Define now the set
Clearly \(\mathcal {K}\) is a closed and convex subset of \({\mathbb R^{k}}\). Since ϕ ∈ K and K is invariant under parallel transport, we deduce that the curve \(\sigma :(-\varepsilon ,\varepsilon )\to {\mathbb R^{k}}\), given by
lies in \(\mathcal {K}\). It suffices to prove that σ″(0) points into \(\mathcal {K}\). Indeed, because \(\mathcal {K}\) is convex, for any unit inward pointing normal ξ of \(\mathcal {K}\) at σ(0), we have
for any t ∈ (−ε, ε). Because g attains its minimum at t = 0, from standard calculus we get that g″(0) ≥ 0, which implies 〈σ″(0), ξ〉≥ 0. This completes the proof. □
Remark 2
According to the above result, it follows that if ϕ is a section lying in a set satisfying the conditions of Lemma 1 and \(\mathcal {L}\) is a uniformly elliptic operator of second order, then section \(\mathcal {L}\phi \) always points into K.
Theorem 8 (Strong Elliptic Maximum Principle)
Suppose that M is a Riemannian manifold (without boundary) and E a vector bundle of rank k over M equipped with a Riemannian metric g E and a metric compatible connection. Let K be a closed fiber-convex subset of the bundle E that is invariant under parallel transport and ϕ ∈ Γ(E), ϕ : M → K, a smooth section such that
where \(\mathcal {L}\) is a uniformly elliptic operator of second order of the form given in (E) and Ψ is a smooth fiberwise map that points into K. If there exists a point x 0 ∈ M such that \(\phi |{ }_{x_0}\in \partial K_{x_0}\) , then ϕ|x ∈ ∂K x for any point x ∈ M. If, additionally, in a neighbourhood of \(\phi |{ }_{x_0}\) the set \(K_{x_0}\) is strictly convex and the boundary \(\partial {K}_{x_0}\) is C 2 -smooth, then ϕ is a parallel section.
Proof
We follow the exposition in [76]. Let {ϕ 1, …, ϕ k} be a geodesic orthonormal frame field defined in a neighbourhood U around x 0 ∈ M. Hence, ϕ = u 1 ϕ 1 + ⋯ + u k ϕ k, where \(u_{i}:U\to {\mathbb R}\), i ∈{1, …, k}, are smooth functions. With respect to this frame we have
Therefore, the map \(u:U\to {\mathbb R^{k}}\), u = (u 1, …, u k), satisfies a uniformly elliptic system of second order of the form
where \(\varPhi :{\mathbb R^{k}}\to {\mathbb R^{k}}\), Φ = (Φ 1, …, Φ k), is given by
for any i ∈{1, …, k}. Consider now the convex set
-
Claim1:
For any point x ∈ U we have \(u(x)\in \mathcal {K}\).
Indeed, fix a point x ∈ U and let γ : [0, 1] → U be the geodesic curve joining the points x and x 0. Denote by θ the parallel section which is obtained by the parallel transport of ϕ|x along the geodesic γ. Then,
where \(y_{i}:[0,1]\to {\mathbb R}\), i ∈{1, …, k}, are smooth functions. Because, θ and ϕ i, i ∈{1, …, k}, are parallel along γ, it follows that
Hence, y i(t) = y i(0) = u i(x), for any t ∈ [0, 1] and i ∈{1, …, k}. Therefore,
Since by our assumptions K is invariant under parallel transport, it follows that \(\theta |{ }_{x_0}\in K_{x_0}\). Hence, \(u(U)\subset \mathcal {K}\) and this proves Claim 1.
-
Claim2:
For any \(y\in \partial \mathcal {K}\) the vector Φ(y) defined in (18) points into \(\mathcal {K}\) at y.
First note that the boundary of each slice K x is invariant under parallel transport. From (18) we deduce that it suffices to prove that both terms appearing on the right hand side of (18) point into \(\mathcal {K}\). The first term points into \(\mathcal {K}\) by assumption on Ψ. The second term is inward pointing due to Lemma 1. This completes the proof of Claim 2.
Observe now that the solution of the uniformly second order elliptic partial differential system (17) satisfies all the assumptions of Theorem 7. Therefore, because \(u(x_0)\in \partial \mathcal {K}\) it follows that u(U) is contained in the boundary \(\partial \mathcal {K}\) of \(\mathcal {K}\). Consequently, ϕ|x ∈ ∂K for any x ∈ U. Since M is connected, we deduce that ϕ(M) ⊂ ∂K. Note, that if \(\mathcal {K}\) is additionally strictly convex at u(x 0), then the map u is constant. This implies that
for any x ∈ U. Thus, ϕ is a parallel section taking all its values in ∂K. □
4.3.1 Maximum Principles for Symmetric Tensors
Let (E, g E) be a Riemannian vector bundle over a manifold M. For any \(\phi \in \operatorname {Sym}(E^*\otimes E^*)\), a real number λ is called eigenvalue of ϕ with respect to \({\operatorname {g}_{E}}\) at the point x ∈ M, if there exists a non-zero vector v ∈ E x, such that
for any w ∈ E x. The linear subspace \(\operatorname {Eig}_{\lambda ,\phi }(x)\) of E x given by
is called the eigenspace of λ at x. Since ϕ is symmetric, it admits k real eigenvalues λ 1(x), …, λ k(x) at each point x ∈ M. We will always arrange the eigenvalues such that λ 1(x) ≤⋯ ≤ λ k(x). If λ 1(x) ≥ 0 (resp. > 0) we say that ϕ is non-negatively (resp. positively) definite at x.
Before stating the main results, let us recall the following definition due to Hamilton [44].
Definition 17
A fiberwise map \(\varPsi :\operatorname {Sym}(E^*\otimes E^*)\to \operatorname {Sym}(E^*\otimes E^*)\) is said to satisfy the null-eigenvector condition, if whenever 𝜗 is a non-negative symmetric 2-tensor at a point x ∈ M and if v ∈ T x M is a null-eigenvector of 𝜗, then Ψ(𝜗)(v, v) ≥ 0.
The next theorem consists the elliptic analogue of the maximum principle of Hamilton [45]. More precisely:
Theorem 9
Let (M, g) be a Riemannian manifold (without boundary) and suppose that (E, g E) is a Riemannian vector bundle over M equipped with a metric connection. Assume that \(\phi \in \operatorname {Sym}(E^*\otimes E^*)\) is non-negative definite and satisfies
where Ψ is a smooth fiberwise map satisfying the null-eigenvector condition. If there is a point of M where ϕ has a zero eigenvalue, then ϕ must have a zero eigenvalue everywhere.
Proof
Denote by K the set of non-negative definite symmetric 2-tensors, i.e.,
Each set K x is a closed and convex. Then,
The tangent cone of K x at a point 𝜗 ∈ ∂K is given by
-
Claim1.
The set K is invariant under parallel translation.
Let γ : [0, 1] → M be a geodesic, P t the parallel transport operator of vectors along γ and Π t the parallel transport operator of 2-tensors along the curve γ. Consider 𝜗 ∈ K γ(0). Then, for any v ∈ T γ(0) M, we have
Therefore, for any vector v ∈ T γ(0) M, it holds (Π t 𝜗)(P t v, P t v) = 𝜗(v, v). Consequently, for any w ∈ T γ(t) M, we obtain that
This proves the claim.
-
Claim2.
Let \(\varPsi :\operatorname {Sym}(E^*\otimes E^*)\to \operatorname {Sym}(E^*\otimes E^*)\) be a smooth fiberwise map satisfying the null-eigenvector condition. Then, for any x ∈ M and 𝜗 ∈ ∂K, the vector Ψ(x, 𝜗) points into K.
Indeed, let \(\vartheta \in \partial {K}_{x_{0}}\). Then Ψ points inwards of \({K}_{x_{0}}\) at 𝜗 if and only if
for any x in M and null-eigenvector \(v\in T_{x_0}M\) of ϕ.
This complete the proof. □
4.3.2 A Second Derivative Test for Symmetric 2-tensors
Theorem 10
Let (M, g) be a Riemannian manifold (without boundary) and (E, g E) a Riemannian vector bundle of rank k over the manifold M equipped with a metric connection ∇. Suppose that \(\phi \in \operatorname {Sym}(E^*\otimes E^*)\) is a smooth symmetric 2-tensor. If the biggest eigenvalue λ k of ϕ admits a local maximum λ at an interior point x 0 ∈ M, then
for all \(v\in \operatorname {Eig}_{\lambda ,\phi }(x_0)\) and for all uniformly elliptic second order operators \(\mathcal {L}\).
Remark 3
The above theorem is due to Hamilton [44]. Replacing ϕ by − ϕ in Theorem 10, we get a similar result for the smallest eigenvalue λ 1 of ϕ.
Proof
Let \(v\in \operatorname {Eig}_{\lambda ,\phi }(x_0)\) be a unit vector and V ∈ Γ(E) such that \(V|{ }_{x_0}=v\) and \(\nabla V|{ }_{x_0}=0.\) Define the symmetric 2-tensor S given by \(S=\phi -\lambda {\operatorname {g}_{E}}\). From our assumptions, S is non-positive definite in a small neighbourhood of x 0. Moreover, the biggest eigenvalue of S at x 0 equals 0. Consider the smooth function \(f:M\to {\mathbb R}\), given by f(x) = S(V |x, V |x). The function f is non-positive in the same neighbourhood around x 0 and attains a local maximum at x 0. In particular, f(x 0) = 0, df(x 0) = 0 and \((\mathcal {L}f)(x_0)\le 0.\) Consider a local orthonormal frame {e 1, …, e m} with respect to g defined in a neighbourhood of the point x 0. A simple calculation yields
Taking into account that \({\operatorname {g}_{E}}\) is parallel, we deduce that
Furthermore,
Bearing in mind the definition of S and using the fact that \({\operatorname {g}_{E}}\) is parallel with respect to ∇, we obtain
Estimating at x 0 and taking into account that \(V|{ }_{x_0}=v\) is a null eigenvector of S at x 0, we get
This completes the proof. □
5 Graphical Submanifolds
5.1 Definitions
Let (M, g M) and (N, g N) be Riemannian manifolds of dimension m and n, respectively. The induced metric on M × N will be denoted by \({\operatorname {g}_{M\times N}}=g_M\times g_N.\) We often denote the product metric also by 〈⋅ , ⋅〉. A smooth map f : M → N defines an embedding F : M → M × N, given by F(x) = (x, f(x)), for any x ∈ M. The graph of f is defined to be the submanifold
Since F is an embedding, it induces another Riemannian metric \(g=F^*{\operatorname {g}_{M\times N}}\) on M. The two natural projections π M : M × N → M and π N : M × N → N are submersions, that is they are smooth and have maximal rank. Note that the tangent bundle of the product manifold M × N, splits as a direct sum
The four metrics \(g_M,g_N,{\operatorname {g}_{M\times N}}\) and g are related by
The Levi-Civita connection \(\nabla ^{{\operatorname {g}_{M\times N}}}\) associated to the Riemannian metric \({\operatorname {g}_{M\times N}}\) on M × N is related to the Levi-Civita connections \(\nabla ^{g_M}\) on (M, g M) and \(\nabla ^{g_N}\) on (N, g N) by
The corresponding curvature operator \({\widetilde {R}}\) on the product M × N is related to the curvature operators on (M, g M) and R N on (N, g N) by
The map f : M → N is called minimal if Γ(f) ⊂ M × N is minimal.
5.2 Singular Value Decomposition
For any fixed point x ∈ M, let \(\lambda ^2_{1}(x)\le \cdots \le \lambda ^2_{m}(x)\) be the eigenvalues of f ∗ g N with respect to g M. The corresponding values λ i ≥ 0, i ∈{1, …, m}, are usually called singular values of the differential df of f at the point x. Let \(r=r(x)=\operatorname {rank} df(x).\) Then, \(r\le \min \{m,n\}\) and λ 1(x) = ⋯ = λ m−r(x) = 0. It is well-known that the singular values can be used to define the so-called singular decomposition of df. At the point x, consider an orthonormal basis {α 1, …, α m−r;α m−r+1, …, α m} with respect to g M which diagonalizes f ∗ g N. Moreover, at f(x) consider an orthonormal basis {β 1, …, β n−r;β n−r+1, …, β n} with respect to g N such that, for any i ∈{m − r + 1, …, m},
It is well-known fact that, with the above ordering, the singular values give rise to continuous functions. In the matter of fact, they are even smooth on an open and dense subset of M. In particular, they are smooth on open subsets where the corresponding multiplicities are constant and the corresponding eigenspaces are smooth distributions; see [83].
We may define a special basis for the tangent and the normal space of the graph in terms of the singular values. The vectors
form an orthonormal basis with respect to the metric \({\operatorname {g}_{M\times N}}\) of the tangent space \(dF\left (T_{x}M\right )\) of the graph Γ(f) at x. Moreover, the vectors
give an orthonormal basis with respect to \({\operatorname {g}_{M\times N}}\) of the normal space N x M.
5.3 Length and Area Decreasing Maps
Let (M, g M) and (N, g N) be two Riemannian manifolds of dimensions m and n respectively. For any smooth map f : M → N its differential df induces a map Λ k df : Λ k TM → Λ k TN given by
for any smooth vector fields v 1, …, v k ∈ TM. The map Λ k df is called the k-Jacobian of f. The supremum norm or the k-dilation |Λ k df|(x) of the map f at a point x ∈ M is defined as the supremum of
when {v 1, …, v m} runs over all orthonormal bases of T x M.
Definition 18
A smooth map f : (M, g M) → (N, g N) between Riemannian manifolds is called (weakly) k-volume decreasing if |Λ k df|≤ 1, strictly k-volume decreasing if |Λ k df| < 1 and k-volume preserving if |Λ k df| = 1. For k = 1 we use the term length instead of 1-volume and if k = 2 we use the term area instead of 2-volume.
There is a way to express the length and area decreasing property of a map in terms of positivity of symmetric tensors. Define on M the symmetric 2-tensors S M×N and S given by
With respect to the basis of the singular value decomposition, we have
Hence, the eigenvalues μ 1, μ 2, …, μ m of S with respect to g, are
Hence, f is length decreasing if S ≥ 0. Additionally let us mention that
and
Observe now that, for any pair of indices i, j ∈{1, …, m}, we have
Hence, the map is strictly area decreasing, if and only if the tensor S is strictly 2-positive, i.e., the sum of the two smallest eigenvalues is positive. The 2-positivity of a tensor \(T\in \operatorname {Sym}(T^*M\otimes T^*M)\) can be expressed as the positivity of another tensor \(T^{[2]}\in \operatorname {Sym}(\varLambda ^{2}T^*M\otimes \varLambda ^{2}T^*M)\). Indeed, let P and Q be two symmetric 2-tensors. Then, the Kulkarni-Nomizu product P○∧ Q given by
is an element of the vector bundle \(\operatorname {Sym}(\varLambda ^{2}T^*M\otimes \varLambda ^{2}T^*M)\). Now, to every element \(T\in \operatorname {Sym}(T^*M\otimes T^*M)\) let us assign an element T [2] of the bundle \(\operatorname {Sym}(\varLambda ^{2}T^*M\otimes \varLambda ^{2}T^*M)\), by setting
We point out that the Riemannian metric G of Λ 2 TM is given by
The relation between the eigenvalues of the tensor T and the eigenvalues of T [2] is explained in the following lemma:
Lemma 2
Let T be a symmetric 2-tensor with eigenvalues μ 1 ≤⋯ ≤ μ m and corresponding eigenvectors {v 1, …, v m} with respect to the metric g. Then the eigenvalues of the symmetric 2-tensor T [2] with respect to G are μ i + μ j, for any 1 ≤ i < j ≤ m, with corresponding eigenvectors v i ∧ v j, for any 1 ≤ i < j ≤ m.
5.4 Minimal Graphs in the Euclidean Space
Let us discuss the case of graphs generated by smooth maps \(f:\mathbb {R}^m\to \mathbb {R}^n\). The induced metric g on the graph is given in local coordinates in the form
As usual, the components of the inverse matrix of the induced metric g are denoted by g ij. It is not difficult to show that Γ(f) is minimal if and only if the components of
satisfy the following system of differential equations
The equation is known in the literature as the minimal surface equation. For graphical hypersurfaces, that is for graphs generated by functions smooth \(f:U\subset \mathbb {R}^m\to \mathbb {R}\), minimality is expressed by the equation
There is a long history of attempts to study entire solutions of the minimal surface equation. Bernstein [8] proved that the only entire minimal graphs in the \(\mathbb {R}^3\) are planes. However, there was a gap in the original proof of Bernstein which was fixed 40 years later; see [51, 65]. In the meantime, several complex analysis proofs have been obtained; for more details see the surveys of Osserman [70, 71].
It was conjectured for a long time that the theorem of Bernstein holds in any dimension for graphical hypersurfaces. For m = 3, its validity was proved by De Giorgi [30], for n = 4 by Almgren [3] and for m = 5, 6, 7 by Simons [80]. It was a big surprise when Bombieri, De Giorgi and Giusti [10] proved that, for m ≥ 8, there are entire solutions of the minimal surface equation other than the affine ones.
In higher codimensions, the situation is more complicated. There are plenty of non-flat entire minimal graphs. For example, the graph of an entire holomorphic map \(f:\mathbb {C}^m\to \mathbb {C}^n\) is minimal. Moreover, Osserman [70] has constructed examples of complete minimal two-dimensional graphs in \(\mathbb {R}^4\), which are not complex analytic with respect to any orthogonal complex structure on \(\mathbb {R}^4\). For instance, the graph Γ(f) over the map \(f :\mathbb {R}^2\to \mathbb {R}^2\), given by
for any \((x, y)\in \mathbb {R}^2\), is such an example. Now the obvious questions became:
Question 1
If entire solutions of the minimal surface equation need not be linear, do they have any other distinguishing characteristics? What additional restrictions on entire solutions would guarantee linearity in all dimensions?
The first result in this direction was obtained by Osserman [69] for two-dimensional graphs, generated by maps \(f:\mathbb {R}^2\to \mathbb {R}^n\). He proved that if the differential df of the map f is bounded, then must be a plane. In fact, he proved the following more general theorem:
Theorem 11
Suppose that Σ is a complete, oriented minimal surface (not necessarily graphical) in the euclidean space \(\mathbb {R}^n\) . Assume that the Gauss map of Σ omits an open neighbourhood in the Grassmannian. Then, Σ is flat.
Let us restrict now in two dimensional graphs in \(\mathbb {R}^4\), i.e., minimal graphs generated by maps f = (f 1, f 2). For such graphs, Simon [81] proved that if one component of f have bounded gradient, then f is affine. Later on, Schoen [79] obtained a Bernstein-type result by imposing the assumption that \(f:\mathbb {R}^2\to \mathbb {R}^2\) is a diffeomorphism. Moreover, Ni [68] has derived a result of Bernstein type under the assumption that f is an area-preserving map. In this case, area preserving is equivalent with the condition \(|\det (df)|=1.\) The function \(\operatorname {Jac}(f)=\det (df)\) is called the Jacobian determinant of f. All these result were generalized by Hasanis, Savas-Halilaj and Vlachos in [47, 48], just by assuming that \(\operatorname {Jac}(f)\) is bounded. In fact, the following result is shown:
Theorem 12
Let \(f:\mathbb {R}^2\to \mathbb {R}^2\) be an entire solution of the minimal surface equation. Assume that Γ(f) is not a plane. Then, Γ(f) is a complex analytic curve if and only if the Jacobian determinant \(\operatorname {Jac}(f)\) of f does not take every real value. In particular if Γ(f) is a complex analytic curve, then:
-
(a)
The Jacobian determinant \(\operatorname {Jac}(f)\) takes every real value in (0, +∞) or in [0, +∞) if f is holomorphic.
-
(b)
The Jacobian determinant \(\operatorname {Jac}(f)\) takes every real value in (−∞, 0) or in (−∞, 0], if f is anti-holomorphic.
All these proofs use strongly the fact that the Gauss map of a minimal surface in the euclidean space is anti-holomorphic.
The first Bernstein-type theorem which was valid for arbitrary dimension and codimension is due to Hildebrandt, Jost, and Widman [50]. They obtained such a result under the assumption of a certain quantitative bound for the slope, that is a bound on the norm of the differential of the generating map.
Let us describe here briefly their technique. Note at first that a bound on the differential of the map forces the Gauss map of the graph to lie in a bounded region of the Grassmannian manifold. In particular, the first step is to determine which bounds on the differential will force the Gauss map to have its range in a sufficiently small convex subset of the Grassmannian. The second step is to find a convex function defined on the convex set, which contains the Gauss image of the graph, and to compose it with the Gauss map. By Theorem 2 of Ruh and Vilms, the Gauss map is harmonic. Consequently, the composition of the Gauss map with the convex function will give rise to a subharmonic function defined on the graph. The third step is to show that this particular subharmonic function is constant and the Gauss map is parallel. Of course, there are many difficulties to overcome to run this program. The first problem is the complexity of the Grassmannian manifolds. For example, it is not so easy to identify which are the convex subsets of the Grassmannian and their corresponding convex supporting functions. One way is to consider distance balls. In fact, Hildebrandt, Jost, and Widman [50] identified the largest ball in the Grassmannian manifold on which the square of the distance function is convex. Another major difficulty is that an entire euclidean minimal graph is complete and non-compact. Consequently, the standard maximum principle cannot be applied directly. Let us mention here that the original assumption on the slope was obtained by Hildebrandt, Jost, and Widman in [50] was
where β 0 is a constant and \(p=\min \{m,n\}\). Over the years, the bound on E(f) was improved. Recently, Jost, Xin, and Yang [56] proved the following:
Theorem 13
Let \(f:\mathbb {R}^m\to \mathbb {R}^n\) be an entire solution of the minimal surface equation. Suppose that there exists a number β 0 such that
and
Then Γ(f) is an affine subspace of \(\mathbb {R}^m\times \mathbb {R}^n\).
Remark 4
For codimension one graphs, the above theorem was first obtained by Moser [67].
Question 2
Let \(f:{\mathbb R^{m}}\to {\mathbb R^{n}}\) be an entire solution of the minimal surface equation such that
Is it true that Γ(f) is an affine subspace of \(\mathbb {R}^m\times \mathbb {R}^n\)?
Remark 5
The number 9 in the above conjecture should be the sharp bound. The reason is that there are examples of Lipschitz minimal maps constructed by Lawson and Osserman [58] with E(f) = 9; see also [37]. These examples are generated from the map \(f:\mathbb {C}^2-\{0\}=\mathbb {R}^4-\{0\}\to \mathbb {R}\times \mathbb {C}={\mathbb R^{3}}\) given by
where \(\mathcal {H}:\mathbb {C}^2\to \mathbb {R}\times \mathbb {C}\) is the Hopf-map \(\mathcal {H}(z,w)=(|z|{ }^2-|w|{ }^2,2z\overline w)\).
Let us conclude this section by mentioning some results in special situations. The first one is due to Fischer-Colbrie [37] and it says that a 3-dimensional complete minimal graph with bounded differential is totally geodesic. In the matter of fact, the following holds:
Theorem 14
Let \(f:\mathbb {R}^3\to \mathbb {R}^n\) be an entire solution of the minimal surface equation. If |df| is uniformly bounded, then Γ(f) is flat.
In codimension two, no specific bound on the differential of f is needed. Recently, Assimos and Jost [6] obtained the following interesting theorem:
Theorem 15
Let \(f:\mathbb {R}^m\to \mathbb {R}^2\) be an entire solution of the minimal surface equation. Suppose that there exists a number β 0 such that
Then Γ(f) is an affine subspace of \(\mathbb {R}^m\times \mathbb {R}^2\).
The next result we would like to mention is due to Wang [97]. He obtained the following theorem for strictly area decreasing minimal graphs.
Theorem 16
Let \(f:{\mathbb R^{m}}\to {\mathbb R^{n}}\) be an entire solution of the minimal surface equation. Suppose that there exists numbers δ 1 ∈ (0, 1) and δ 2 > 0 such that |Λ 2 df|≤ 1 − δ 1 and E(f) ≤ δ 2 . Then Γ(f) is an affine subspace of \(\mathbb {R}^m\times \mathbb {R}^n\).
Remark 6
The above cannot be extended for k-volume decreasing minimal maps with k > 2. For example, consider \(f:\mathbb {C}^2={\mathbb R^{4}}\to \mathbb {C}^2={\mathbb R^{4}}\), given by
where \(z,w\in \mathbb {C}\), \(h:\mathbb {C}\to \mathbb {C}\) is a non-affine holomorphic map and β 0 a real number. Observe that the graph Γ(f) is a non-flat minimal submanifold of \({\mathbb R^{8}}\) and |Λ 4 df| = |β 0|. Consequently, there exists an abundance of non-flat minimal graphs in the euclidean space with arbitrary small 4-Jacobian.
6 Mean Curvature Flow
In this section, we introduce the notion of the mean curvature flow. Later, we will examine how various geometric quantities evolve under the mean curvature flow. Suppose that M is a manifold of dimension m, let T > 0 be a real number and F : M × [0, T) → N a smooth time-dependent family of immersions of M into a Riemannian manifold N of dimension n. We follow the exposition in [5, 32, 63, 86].
Definition 19
Let N be a Riemannian manifold. We say that a family of immersions F : M × [0, T) → N evolves by mean curvature flow (MCF for short) with initial data the immersion F 0: M → N if it satisfies the initial value problem
for any (x, t) ∈ M × [0, T), where H(F(x, t)) denotes the mean curvature vector of the immersion F(⋅ , t) : M → N at the point x ∈ M.
6.1 Basic Facts for Systems of Parabolic PDEs
In this section we recall basic facts about solvability of Cauchy problems; for more details see [57].
6.1.1 Differential Operators
Let M be a smooth manifold equipped with a Riemannian metric g whose associated Levi-Civita connection is ∇M. Suppose that E 1 and E 2 are two vector bundles over M and assume that E 1 is equipped with a Riemannian metric h and a compatible connection \(\nabla ^{E_1}\). As in Definition 4, from the connections ∇M and \(\nabla ^{E_1}\), one can form the k-th derivative ∇k of a section ϕ ∈ Γ(E 1).
Definition 20
A map P : Γ(E 1) → Γ(E 2) of the form
where Q is smooth in all its variables, will be called differential operator of order k. In the case where P is \(\mathbb {R}\)-linear, we say that P is a linear differential operator of order k. Otherwise, we say that P is non-linear.
Suppose that P : Γ(E 1) → Γ(E 2) is a linear differential operator of degree k. Then, in index notation, it can be written in the form
where for each x ∈ M, \(A^{i_1\dots \, i_k}(x)\colon (E_1)_x\to (E_2)_x\) is linear map. These maps are called the coefficients of the linear operator P.
Definition 21
Let P : Γ(E 1) → Γ(E 2) be a linear differential operator of order k, let x be a point in M and \(\zeta =\sum _i\zeta _idx_i\in T^*_xM\). The linear map σ ζ(P;x): (E 1)x → (E 2)x, given by
is called the principal symbol of the operator P at the point x and in the direction ζ. In particular, the operator P is called elliptic if its principal symbol is an isomorphism, for every point x and every non-zero direction ζ.
Definition 22
The differential or the linearization of P at ϕ 0, if it exists, is defined to be the linear map \(DP|{ }_{\phi _0}\colon \varGamma (E_1)\to \varGamma (E_2)\), given by the expression
for any ψ ∈ Γ(E 1).
Definition 23
Let P : Γ(E 1) → Γ(E 2) be a differential operator of order k. We say that P is elliptic, undetermined elliptic or overdetermined elliptic if its linearization is so.
Example 1
Let f : M → N be a smooth map between manifolds endowed with Riemannian metrics g M and g N, respectively, and consider the operator \(\varDelta _{g_M,g_N}\colon C^\infty (M) \to C^\infty (M)\), given by
where B stands for the Hessian of f. In local coordinates, we have
The linearization of \(\varDelta _{g_M,g_N}f\) is
Hence, for any
we have
Consequently, the Laplacian operator \(\varDelta _{g_M,g_n}\) is elliptic.
6.1.2 Time-Dependent Vector Bundles
Suppose that \(I\subset \mathbb {R}\) is an open interval and let {g(t)}t ∈ I be a smooth family of Riemannian metrics on a manifold M. This means that for any (x, t) ∈ M × I we have an inner product g (x,t) on T x M. We can regard {g(t)}t ∈ I as a metric g acting on the spatial tangent bundle \(\mathcal {H}\), defined by
where π 2 : M × I → I is given by π 2(x, t) = t. Note that each g(t) is a metric on \(\mathcal {H}\) since \(\mathcal {H}_{(x,t)}\) is isomorphic to T x M via π 2. We can even extend g into a metric on M × I, with respect to which we have the orthogonal decomposition
Since \(\mathcal {H}\) is a subbundle of T(M × I), any section of \(\mathcal {H}\) is also a section of T(M × I). Sections of \(\varGamma (\mathcal {H})\) are called spatial vector fields. There is a natural connection ∇ on M × I. Namely, define ∇ by
for any \(v,w\in \varGamma (\mathcal {H})\), where ∇g(t) stand for the Levi-Civita connection of g(t). One can readily check that ∇ is compatible with g, i.e.,
for any \(v\in \mathfrak {X}(M\times \mathbb {R})\) and \(w_1,w_2\in \varGamma (\mathcal {H})\). Moreover, for any \(w_1,w_2\in \varGamma (\mathcal {H})\),
The situation we discussed above occurs, when we have a family of immersions F : M × I → N. In this case, F ∗ h gives a family of metrics on M. Endowing M × I with the connection ∇, we have for any \(v\in \varGamma (\mathcal {H})\) that
6.1.3 Parabolic Differential Equations
Let M be a manifold equipped with a family of metrics {g(t)}[0,T). Denote by {∇g(t)}t ∈ [0,T) the corresponding Levi-Civita connections. Let E 1 and E 2 be vector bundles over M and assume that E 1 is equipped with a fixed time independent metric h and connections {∇(t)}t ∈ [0,T) that are compatible with h, i.e.,
for any tangent vector v, sections ϕ 1, ϕ 2 ∈ Γ(E) and any time t ∈ [0, T).
As in Definition 4, by coupling ∇(t) with ∇g(t) we obtain repeated covariant derivatives ∇k(t) acting on sections of E 1. Suppose now that {ϕ(t)}t ∈ [0,T) is a smooth time-dependent family of sections of E 1, where smooth means that for any fixed (x, t) ∈ M × [0, T), the time-derivative
exists. Hence, \(\{\nabla _{\partial _t}\phi \}_{t\in [0,T)}\) is another one parameter family of sections on E 1. We are interested now in expressions of the form:
where now P : Γ(E 1) → Γ(E 2) is a time-dependent differentiable operator of order k. If for each fixed t the operator P is linear elliptic, we say that (26) is a linear parabolic differential equation. We say that (26) represents a non-linear parabolic differential equation if and only if, for any ϕ ∈ Γ(E 1), its linearization is parabolic.
Theorem 17
If the differential operator P is parabolic at ϕ 0 ∈ Γ(E 1), then there exist a T > 0 and a smooth family ϕ(t) ∈ Γ(E 1), for t ∈ [0, T], such that there exists a unique smooth solution for the initial value problem
for t ∈ [0, T], where T depends on the initial data ϕ 0.
We close this section with an application of this general theory.
Definition 24
Let (M, g M) and (N, g N) be Riemannian manifolds. We say that a family of smooth maps F : M × [0, T) → N evolves by (harmonic) heat flow, with initial data F 0: M → N, if it satisfies the initial value problem
Theorem 18
Let (M, g M) be a compact Riemannian manifold and suppose that F 0: (M, g M) → (N, g N) is a smooth map into a Riemannian manifold (N, g N). Then, (27) admits a unique, smooth solution on a maximal time interval \([0,T_{\max })\) , where \(0<T_{\max }\le \infty \).
Proof
We already computed that for ζ ∈ T ∗ M, we have
Hence, the parabolic theory can be used to ensure short-time existence. □
6.2 Short-time Existence of the Mean Curvature Flow
A supposed solution F of MCF can be represented in local coordinates as
Then, from (2) we have
where
Note that g is the induced metric and it depends on F. Hence,
and consequently
Combining the formula (28) with equation (2), we obtain
By a straightforward computation, we get
Denote by π TM and π NM the projections of F ∗ TN onto dF(T x M) and NM, respectively. Then, for any \(\phi =\sum _\alpha \phi _\alpha \partial _{y_\alpha }\in \varGamma (F^*TN)\), we have
Therefore, the principal symbol is given by
Observe that the principal symbol is zero for tangent directions. Thus, MCF is degenerate and we cannot obtain information from the standard theory about short-time existence. Short-time existence and uniqueness of MCF was originally proven using results of Hamilton [43, 44] based on the Nash-Moser iteration method. We present a proof adapting a variant of the DeTurck’s trick which was first used in Ricci flow [31]; see also [7, 63, 92].
Theorem 19 (Invariance Under Tangential Variations)
Suppose that F : M × [0, T) → N is a family of immersions satisfying the system of PDEs
where (x, t) ∈ M × [0, T), the manifold M is compact and V is a time-dependent family of smooth vector fields. Then, there exists a unique family of diffeomorphisms ψ: M × [0, T) → M, such that the map \(\widehat {F}\colon M\times [0,T)\to N\) given by \(\widehat {F}(x,t)=F\big (\psi (x,t),t\big ),\) is a solution of
Conversely, if F : M × [0, T) → N is a solution of the mean curvature flow and ψ: M × [0, T) → M is a family of diffeomorphisms, then \(\widehat {F}\colon M\times [0,T)\to N\) satisfies a system of the form (29).
Proof
Consider for the moment an arbitrary family a time-dependent of diffeomorphisms ψ: M × [0, T) → M and define \(\widehat F\colon M\times [0,T)\to N\) given by \( \widehat {F}(x,t)=F\big (\psi (x,t),t\big ), \) for (x, t) ∈ M × [0, T). From the chain rule, we have
for any (x, t) ∈ M × [0, T). Hence, it suffices to find a one-parameter family of diffeomorphisms ψ: M × [0, T) → M solving the initial value problem
for any (x, t) ∈ M × [0, T), where I : M → M is the identity map. By Picard-Lindelöf theorem there exists a unique smooth solution of the above initial value problem. Moreover, because the initial data is the identity, taking T > 0 small enough we can assume that for any t ∈ [0, T] the map ψ(⋅ , t) : M → M is a diffeomorphism. The converse is straightforward. □
Theorem 20 (Short-time Existence)
Let M be a compact Riemannian manifold and F 0: M → N an immersion into a Riemannian manifold N. Then, the mean curvature flow with initial data the immersion F 0 admits a smooth solution on a maximal time interval \([0,T_{\max })\) , where \(0<T_{\max }\le \infty \).
Proof
The idea is to modify MCF by adding some tangential component in order to make it parabolic. Suppose that \(F:M\times [0,T_{\max })\to N\) solves MCF. Fix a Riemannian metric \(\widehat g\) on M, denote its Levi-Civita connection by \(\widehat {\nabla }\) and consider the vector field V DT on M given by
Note that in local coordinates, V DT has the form
where \(\varGamma ^k_{ij}\) and \(\widehat {\varGamma }^k _{ij}\) are the Christoffel symbols of the connections ∇ and \(\widehat \nabla \), respectively. Consider now the initial value problem,
The first equation of (31) in local coordinates takes the form
Since \(\widehat {\varGamma }^{k}_{ij}\) does not depend on time, the principal symbol of (31) is
Hence (31) is parabolic and has a unique solution. According to Theorem 19, from a solution of (31) we obtain a solution of the mean curvature flow. □
Definition 25
Let F : M × [0, T) → N be a solution of MCF. Fix a metric \(\widehat g\) and consider the vector field V DT. The modified flow (31) is called DeTurck mean curvature flow.
Lemma 3
The vector field V DT defined in (30) is minus the Laplacian of the identity map \(I\colon (M,g)\to (M,\widehat g).\)
Proof
The Hessian B of the map I is given by
for any \(v_1,v_2\in \mathfrak {X}(M)\). Hence, \(\varDelta _{{g},\widehat {g}}I=-V_{DT}.\) This completes the proof. □
Theorem 21 (Uniqueness)
Let M be a compact Riemannian manifold and F 0: M → N an immersion into a Riemannian manifold N. Then, the solution of MCF, with initial data the immersion F 0: M → N, is unique up to diffeomorphisms.
Proof
Suppose that \(\widetilde {F}\colon M\times [0,T_{\max })\to N\) is the maximal solution of MCF, with initial data the given immersion F 0, and denote the induced metrics by \(\widetilde {g}\). As in the existence part, fix a metric \(\widehat g\) and denote by \(\widehat \nabla \) its associated Levi-Civita connection. Consider the initial value problem
Observe that the above problem is a parabolic and thus its solution gives rise to a unique one parameter family of diffeomorphisms ϕ : M × [0, ε) → M, for at least some short time ε > 0. Denote by ψ: M × [0, ε) → M the one parameter family of diffeomorphisms with the property that, for each t, the map ψ(⋅ , t) is the inverse of ϕ(⋅ , t), i.e.,
for any (x, t) in space-time. From the chain rule, we have
Define the map F : M × [0, ε) → N given by \(F(x,t)=\widetilde {F}(\psi (x,t),t),\) for any \((x,t)\in M\times [0,T_{\max })\). The induced time-dependent metric on M is \(g=\psi ^*\widetilde g\). Moreover, the map F satisfies the evolution equation
where for any point (x, t) in space-time, we have
Taking into account (32) and the composition formula for the Laplacian (see for example [24, page 116, equation (2.56)]), we have
for any (x, t) ∈ M × [0, ε). From (33) and (34), we see that F satisfies the DeTurck mean curvature flow
with initial data the immersion F 0 : M → N.
Suppose now that \({\widetilde F}_1,{\widetilde F}_2\colon M\times [0,T_{\max })\to N\) are two solutions of the mean curvature flow, with the same initial condition F 0: M → N. As before fix a metric \(\widehat g\) on M and denote by \(\widetilde g_1\) and \(\widetilde g_2\) the induced time-dependent metrics on M by \({\widetilde F}_1\) and \({\widetilde F}_2\), respectively. Denote by
the one-parameter family of diffeomorphisms solving the initial value problem
Then, as we verified above, the maps
satisfy
for any (x, t) ∈ M × [0, ε), form solutions of the DeTurck mean curvature flow, with common initial data the immersion F 0: M → N. Since the DeTurck mean curvature flow is parabolic, it follows that its solution is unique. □
6.3 Parabolic Maximum Principles
In this subsection, we state the weak and strong version of the parabolic maximum principle for scalar functions obeying a diffusion-reaction equation on a manifold equipped with a smooth time-dependent family of Riemannian metrics. Then we also present Hamilton’s version [44, 45] of the parabolic maximum principle for arbitrary sections of a vector bundle; for detailed proofs see also the excellent monograph [26].
6.3.1 Scalar Parabolic Maximum Principle
Suppose that M is a smooth manifold, possibly with boundary ∂M, and {g(t)}t ∈ [0,T) a smooth family of Riemannian metrics. We will consider the second order time-dependent operator \(\mathcal {L}\) given by
where
Note that, for each fixed time, \(\mathcal {L}\) is an elliptic operator.
Theorem 22 (Comparison Principle)
Suppose that M is a compact, without boundary, manifold equipped with a smooth family {g(t)}t ∈ [0,T) of Riemannian metrics and \(u\colon M\times [0,T)\to \mathbb {R}\) a C 2 -smooth function, which satisfies the differential inequality
where \(\mathcal {L}\) is the (time-dependent) operator defined in (P) and \(\varPsi :\mathbb {R}\times \mathbb {R}\to \mathbb {R}\) a smooth map. Let φ be the solution of the associated ODE
Then, the solution u of the differential inequality is bounded from above by the solution φ of the ODE, that is u(x, t) ≤ φ(t), for every (x, t) ∈ M × [0, T).
As in the elliptic case, there exists a criterion which forces a solution of a parabolic differential inequality to be constant.
Theorem 23 (Strong Maximum Principle)
Suppose that M is a smooth manifold, possibly with boundary, equipped with a smooth family {g(t)}t ∈ [0,T) of Riemannian metrics. Let \(u\in C^{2}\big (M\times (0,T)\big )\cup C^0\big (\overline {M}\times [0,T]\big )\) be a solution of
where c is a non-negative constant.
-
(a)
If c = 0 and u attains a maximum at point (x 0, t 0) ∈ M × (0, T) then u is constant on M × [0, t 0].
-
(b)
If c < 0 and the function u attains a non-negative maximum at a point (x 0, t 0) ∈ M × (0, T), then u is constant on M × [0, t 0].
By reversing both inequalities we obtain the corresponding minimum version of the comparison and strong principle; for the proofs see [5, 35] or [72].
6.3.2 Vectorial Parabolic Maximum Principle
Let M be a smooth manifold, possibly with boundary ∂M, equipped with a smooth family of metrics {g(t)}t ∈ [0,T) and associated Levi-Civita connections ∇g(t). Let E be a vector bundle over M equipped with a time-independent metric h and a family {∇(t)}t ∈ [0,T) of connections that are compatible with h. The time-dependent Laplacian acting on smooth sections of E is defined by
where {v 1, …, v m} is an orthonormal basis of g(t).
Following the same lines as in the elliptic case, we can derive Weinberger-Hamilton’s versions of the parabolic maximum principle.
Theorem 24 (Weak Vectorial Maximum Principle)
Suppose that M is a compact manifold, possibly with boundary ∂K, equipped with a smooth family {g(t)}t ∈ [0,T) of Riemannian metrics. Let E be a vector bundle over M endowed with time independent bundle metric h and a family {∇(t)}t ∈ [0,T) of connections that are compatible with h. Let K be a closed fiber-convex subset of E that is invariant under parallel transport with respect to each connection ∇(t), t ∈ [0, T), and let {ϕ(t)}t ∈ [0,T) be a smooth family of sections such that
where X is a smooth time dependent vector field and Ψ is a smooth fiberwise map that points into K. If ϕ (x,t) ∈ K for any (x, t) in the parabolic boundary of M × [0, T), i.e., for any (x, t) ∈(M ×{0})∪(∂M × [0, T)), then ϕ (x,t) ∈ K for any (x, t) ∈ M × [0, T).
Theorem 25 (Strong Vectorial Maximum Principle)
Suppose that M is a smooth, not necessarily compact, manifold equipped with a smooth family {g(t)}t ∈ [0,T) of Riemannian metrics. Moreover, let E be a vector bundle over M endowed with time independent metric h and a family {∇(t)}t ∈ [0,T) of connections that are compatible with h. Assume that K is a closed fiber-convex subset of the vector bundle E that is invariant under parallel transport with respect to each connection ∇(t), t ∈ [0, T), and let {ϕ(t)}t ∈ [0,T) be a smooth family of sections such that
where X is a smooth time dependent vector field and Ψ is a smooth fiberwise map that points into K. If there exists a point (x 0, t 0) ∈ M × (0, T) such that \(\phi _{(x_0,t_0)}\in \partial K\) , then ϕ (x,t) ∈ ∂K for any (x, t) ∈ M × [0, t 0].
Let us describe now the parabolic maximum principle in the special case where as vector bundle we consider the space of symmetric 2-tensors.
Theorem 26
Let M be a compact manifold equipped with a smooth family {g(t)}t ∈ [0,T) of Riemannian metrics. Suppose that {ϕ(t)}t ∈ [0,T) is smooth family of symmetric 2-tensors on M such that
where \(\varPsi :\operatorname {Sym}(T^*M\otimes T^*M)\to \operatorname {Sym}(T^*M\otimes T^*M)\) is a smooth fiberwise map satisfying the null-eigenvector condition and X is a smooth time dependent vector field. If ϕ(0) ≥ 0, then ϕ(t) ≥ 0 for all t ∈ [0, T). Additionally, if there is a point (x 0, t 0) ∈ M × (0, T) where ϕ(t 0) has a zero eigenvalue then ϕ(t) has a zero eigenvalue for any t ∈ (0, t 0).
6.4 Evolution Equations
We will compute the evolution of some important quantities. In order to simplify the notation, we omit upper or lower indices on connections and Laplacians which identify the corresponding bundles where they are defined. Most of these computations can be found in [4, 75,76,77,78, 86, 94, 96].
Lemma 4
Suppose that F : M × [0, T) → N is a solution of the mean curvature flow. Then, the following facts are true:
-
(a)
The induced metrics g evolve in time under the equation
$$\displaystyle \begin{aligned}\big(\nabla_{\partial_t}g\big)(v_1,v_2)=-2\langle H,A(v_1,v_2 )\rangle=-2A^H(v_1,v_2),\end{aligned}$$for any \(v_1,v_2\in \frak {X}(M)\).
-
(b)
The induced volume form Ω on (M, g) evolves according to the equation
$$\displaystyle \begin{aligned}\nabla_{\partial_t}\varOmega=-|H|{}^2\varOmega.\end{aligned}$$Moreover, the volume of the evolved submanifolds satisfy
$$\displaystyle \begin{aligned}\partial_t{Vo\quad l}=-\int_M|H|{}^2\varOmega. \end{aligned}$$ -
(c)
There exists a local smooth time-dependent tangent orthonormal frame field and a local smooth time-dependent orthonormal frame field along the normal bundle of the evolving submanifolds.
Proof
-
(a)
Let v 1, …, v m be time-independent tangent vector fields. Keeping in mind the notation introduced in Section 6.1.2, we have
$$\displaystyle \begin{aligned}\nabla_{\partial_t}dF(v_i)=\nabla_{v_i}dF(\partial_t)+dF\big([\partial_t,v_i]\big)=\nabla_{v_i}H,\end{aligned}$$for any i ∈{1, …, m}. Therefore, for any i, j ∈{1, …, m}, we deduce that
$$\displaystyle \begin{aligned} \begin{array}{rcl} (\nabla_{\partial_t}g)(v_i,v_j)& =&\displaystyle \partial_t(g(v_i,v_j))-g(\nabla_{\partial_t}v_i,v_j)- g(v_i,\nabla_{\partial_t}v_j)\\ & =&\displaystyle \partial_t\langle dF(v_i),dF(v_j)\rangle=\langle\nabla_{v_i}H,dF(v_j)\rangle+\langle\nabla_{v_j}H,dF(v_i)\rangle\\ & =&\displaystyle -\langle H,\nabla_{v_i}dF(v_j)\rangle-\langle H,\nabla_{v_j}dF(v_i)\rangle\\ & =&\displaystyle -2\langle H,A(v_i,v_j)\rangle. \end{array} \end{aligned} $$ -
(b)
We compute
$$\displaystyle \begin{aligned} \begin{array}{rcl} \partial_t \sqrt{\det g_{ij}} & =&\displaystyle \sum_{k,l}\frac{\big(g^{kl}\partial_t g_{kl}\big) \det g_{ij}}{2\sqrt{\det g_{ij}}} =-\sum_{k,l} \langle H,g^{kl} A_{kl}\rangle \sqrt{\det g_{ij}}\\ & =&\displaystyle -|H|{}^2\sqrt{\det g_{ij}}. \end{array} \end{aligned} $$ -
(c)
The associated adjoint operator P : (TM, g) → (TM, g) of A H satisfies
$$\displaystyle \begin{aligned} A^H(v_1,v_2)=g(Pv_1,v_2)=g(v_1,Pv_2), \end{aligned} $$(35)for any \(v_1,v_2\in \mathfrak {X}(M)\). Consider now the family of bundle isomorphism U(t) : (TM, g(0)) →(TM, g(t)), given as the solution of the initial value problem
$$\displaystyle \begin{aligned} \left\{ \begin{array}{lll} \nabla_{\partial_t} U(t)=P\circ U(t), &\\ \,\, U(0)=I. & \end{array} \right. \end{aligned} $$(36)By a straightforward computation, we can show that U ∗(t)g(t) = g(0). Hence, if {e 1(0), …, e m(0)} is a local orthonormal frame with respect to g(0), then {e 1(t) = U(t)e 1(0), …, e m(t) = U(t)e m(0)} is a local orthonormal frame of g(t). By taking the complement of {e 1, …, e m}, we get a time-dependent frame field on the normal bundles of the evolving submanifolds.
□
Lemma 5
The time-derivative of the second fundamental form is given by
where the indices are with respect to a local orthonormal frame.
Proof
Suppose that {e 1, …, e m;ξ m+1, …, ξ n} is a local adapted orthonormal frame field around a fixed point (x 0, t 0). Recall that
In order to simplify the computations, we may assume that {e 1, …, e m} is normal frame at (x 0, t 0). Under these considerations, we have that at (x 0, t 0)
Hence,
and so
where R ∇ is the curvature operator of ∇ on T(M × (0, T)). Consequently, at (x 0, t 0) we have
On the other hand,
Combining the last two equalities we obtain the result. □
Lemma 6
The mean curvature H evolves in time under the equation
Moreover,
where the indices are with respect to a local orthonormal frame.
Proof
Let (x 0, t 0) ∈ M × (0, T) and {e 1, …, e m;ξ m+1, …, ξ n} be a local orthonormal frame field around of (x 0, t 0). From (37) and Lemma 5, we have
from where we deduce the evolution equation for H. Moreover
On the other hand
Combining the last two identities we obtain the desired identity. □
6.5 Evolution Equations of Parallel Forms
Let F : M × [0, T) → N be a solution of the mean curvature flow and suppose that Φ is a parallel k-tensor on N. Then, the pullback via F of Φ gives rise to a time-dependent k-form on M. For example, the volume form of N is such a tensor. As we will see in the next section, interesting situations occurs when N is a Riemannian product N 1 × N 2 and we consider the volume forms Ω 1 and Ω 2 of N 1 and N 2, respectively.
In the next lemmata, we will compute how these pullback tensors evolve under the mean curvature flow.
Lemma 7
The covariant derivative of the tensor F ∗ Φ is given by
for any adapted orthonormal frame field {e 1, …, e m;ξ m+1, …, ξ n−m}.
Proof
As usually let us suppose that {e 1, …, e m} is a normal frame at a fixed point (x 0, t 0) in space-time. By a direct computation, we get that at (x 0, t 0) we have
This completes the proof. □
By a direct computation we can derive the expression for the Laplacian of the pullback of a parallel k-tensor on N.
Lemma 8
The Laplacian of the k-tensor F ∗ Φ is given by
for any adapted orthonormal frame field {e 1, …, e m;ξ m+1, …, ξ n−m}.
Proof
Let {e 1, …, e m;ξ m+1, …, ξ n−m} be an adapted normal frame at the point (x 0, t 0) in space-time. We compute,
Summing over k and using the Codazzi equation (4), we get the result. □
Lemma 9
Suppose that F : M × [0, T) → N is a solution of the mean curvature flow and let Φ be a parallel m-form on N. Then, u = ∗(F ∗ Φ), where ∗ is the Hodge star operator with respect to the induced Riemannian metric g, evolves in time under the equation
for any adapted orthonormal frame field {e 1, …, e m;ξ m+1, …, ξ n−m}.
Proof
Let us make our computations again, with respect to a time-dependent orthonormal frame field as in Lemma 4. We compute,
Taking into account the formulas (37), we have
for any i ∈{1, …, m}. Hence, putting everything together, we deduce that
Combining with Lemma 8 we obtain the result. □
7 Formation of Singularities Under Mean Curvature Flow
In this section, we present how one can build smooth singularity models for the mean curvature flow by rescaling properly around points, where the second fundamental form attains its maximum. The proof relies heavily on a compactness theorem of Cheeger-Gromov-Taylor [14] for pointed Riemannian manifolds and on the standard compactness theorem for immersions; see for example [27].
7.1 Characterization of the Maximal Time of Existence
In the following theorem, we give a characterization of the maximal time of solutions of the mean curvature flow. Its proof has been done by Huisken in [52, 53] and is based on the parabolic maximum principle. The key observation is that all higher derivatives ∇k A, \(k\in {\mathbb N}\), of the second fundamental tensor are uniformly bounded, once A is uniformly bounded. More precisely, the following result holds:
Theorem 27
Let M be a compact manifold and let F 0: M → N a smooth immersion into a complete Riemannian manifold N. Then, the maximal time \(T_{\max }\) of the solution of the mean curvature flow, with initial data F 0 , is finite if and only if
An immediate consequence of the above result is the following theorem.
Theorem 28
Let M be a compact manifold and \(F:M\to [0,T_{\max })\to N\) a solution of the mean curvature flow on a maximal time interval in a complete Riemannian manifold N. If the norm |A| of the second fundamental form is uniformly bounded, then the maximal time of solution of the flow is infinite.
Remark 7
When the target space N is compact and the maximal time of solution of the flow is infinite, due to a deep result of Simon [82], it follows that the flow converges smoothly and uniformly to a minimal submanifold. However, long-time existence does not automatically imply convergence. For instance, start with a latitude circle \(\mathbb {S}^1\) on a complete surface of revolution that does not admit closed embedded curves as geodesics. Then the flow with initial that particular circle will run forever, but it will not converge.
Remark 8
Due to a recent result of Cooper [27], it is not necessary to have boundedness on the full norm of the second fundamental form in order to get long-time existence of the flow. In the matter of fact, he showed that uniform boundedness of the second fundamental form only in the direction of the mean curvature also leads to long-time existence.
7.2 Cheeger-Gromov Compactness for Metrics
Let us recall here the basic notions and definitions. For more details, see [5, 25] and [66]. We closely follow the exposition in [78].
Definition 26
Let (E, π, Σ) be a vector bundle endowed with a Riemannian metric g and a metric connection ∇ and suppose that \(\{\xi _k\}_{k\in \mathbb {N}}\) is a sequence of sections of E. Let U be an open subset of Σ with compact closure \(\bar {U}\) in Σ. Fix a natural number p ≥ 0. We say that \(\{\xi _k\}_{k\in \mathbb {N}}\) converges C p-smoothly to \(\xi _\infty \in \varGamma (E|{ }_{\overline {U}})\), if for every ε > 0, there exists k 0 = k 0(ε), such that
where k ≥ k 0. We say that \(\{\xi _k\}_{k\in \mathbb {N}}\) C ∞-smoothly converges to \(\xi _{\infty }\in \varGamma (E|{ }_{\bar {U}})\) if \(\{\xi _k\}_{k\in \mathbb {N}}\) converges in C p to \(\xi _{\infty }\in \varGamma (E|{ }_{\overline {U}})\), for any p ≥ 0.
Definition 27
Let (E, π, Σ) be a vector bundle endowed with a Riemannian metric g and a metric connection ∇. Let \(\{U_n\}_{n\in \mathbb {N}}\) be an exhaustion of Σ and \(\{\xi _k\}_{k\in \mathbb {N}}\) be a sequence of sections of E defined on open sets A k of Σ. We say that \(\{\xi _k\}_{k\in \mathbb {N}}\) converges smoothly on compact sets to ξ ∞∈ Γ(E) if:
-
(a)
For every \(n\in \mathbb {N}\) there exists k 0 such that \(\overline {U}_n\subset A_k\), for all natural numbers k ≥ k 0.
-
(b)
The sequence \(\{\xi |{ }_{\overline {U}_k}\}_{k\ge k_0}\) converges in C ∞ to the restriction of the section ξ ∞ on \(\overline {U}_n\).
In the next definitions, we recall the notion of the smooth Cheeger-Gromov convergence of sequences of Riemannian manifolds.
Definition 28
A pointed Riemannian manifold (Σ, g, x) is a Riemannian manifold (Σ, g) with a choice of origin or base point x ∈ Σ. If the metric g is complete, we say that (Σ, g, x) is a complete pointed Riemannian manifold.
Definition 29
We will say that a sequence \(\{( \varSigma _k,g_k,x_k)\}_{k\in \mathbb {N}}\) of complete, pointed Riemannian manifolds smoothly converges in the sense of Cheeger-Gromov to a complete pointed Riemannian manifold (Σ ∞, g ∞, x ∞), if there exists:
-
(a)
An exhaustion \(\{U_k\}_{k\in \mathbb {N}}\) of Σ ∞ with x ∞∈ U k, for all \(k\in \mathbb {N}\).
-
(b)
A sequence of diffeomorphisms Φ k: U k → Φ k(U k) ⊂ Σ k, with
$$\displaystyle \begin{aligned}\varPhi_k(x_{\infty})=x_k\end{aligned}$$and such that the sequence \(\{\varPhi ^*_k g_k\}_{k\in \mathbb {N}}\) smoothly converges in C ∞ to g ∞ on compact sets in Σ ∞.
The sequence \(\{(U_k,\varPhi _k)\}_{k\in \mathbb {N}}\) is called a family of convergence pairs of the sequence \(\{(\varSigma _k,g_k,x_k)\}_{k\in \mathbb {N}}\), with respect to the limit (Σ ∞, g ∞, x ∞).
When we say smooth convergence, we always mean smooth convergence in the sense of Cheeger-Gromov. The family of convergence pairs is not unique. Two such families \(\{(U_k,\varPhi _k)\}_{k\in \mathbb {N}}\),\(\{(W_k,\varPsi _k)\}_{k\in \mathbb {N}}\) are equivalent in the sense that there exists an isometry I of the limit (Σ ∞, g ∞, x ∞), such that for every compact subset K of Σ ∞, there exists a natural number k 0, such that for any natural k ≥ k 0:
-
(a)
The mapping \(\varPhi ^{-1}_k\circ \varPsi _k\) is well defined over K.
-
(b)
The sequence \(\{\varPhi ^{-1}_k\circ \varPsi _k\}_{k\ge k_0}\) smoothly converges to I on K.
The limiting pointed Riemannian manifold (Σ ∞, g ∞, x ∞) of the Definition 29 is unique up to isometries.
Definition 30
Let M be a Riemannian manifold. The injectivity radius at x ∈ M is the supremum of all values r, such that the expotential map from the unit ball B r(x) in T x M, to the manifold M, is injective.
Definition 31
A complete Riemannian manifold (Σ, g) is said to have bounded geometry, if the following conditions are satisfied:
-
(a)
For any integer j ≥ 0, there exists a uniform positive constant C j, such that |∇j R|≤ C j.
-
(b)
The injectivity radius satisfies inj g(Σ) > 0.
The following proposition is standard and will be useful in the proof of the long-time existence of the mean curvature flow.
Proposition 3
Suppose (Σ, g) is a complete Riemannian manifold with bounded geometry. Suppose that \(\{\alpha _k\}_{k\in \mathbb {N}}\) is an increasing sequence of real numbers that tends to + ∞ and let \(\{x_k\}_{k\in \mathbb {N}}\) be a sequence of points on Σ. Then, the sequence \(\{(\varSigma ,\alpha ^2 _k g,x_k)\}_{k\in {\mathbb N}}\) smoothly subconverges to the euclidean space \((\mathbb {R}^m,g_{euc},0)\).
We will use the following definition of uniformly bounded geometry for a sequence of pointed Riemannian manifolds.
Definition 32
We say that a sequence \(\{(\varSigma _k,g_k,x_k)\}_{k\in \mathbb {N}}\) of complete pointed Riemannian manifolds has uniformly bounded geometry, if the following two conditions are satisfied:
-
(a)
For any integer j ≥ 0, there exists a uniform constant C j, such that for each \(k\in \mathbb {N}\) it holds |∇j R k|≤ C j, where R k is the curvature operator of the metric g k.
-
(b)
There exists a uniform constant c 0, such that \(inj_{g_k} (\varSigma _k)\ge c_0>0\).
In the next result, we state the Cheeger-Gromov compactness theorem for sequences of complete pointed Riemannian manifolds. The version that we present here is due to Hamilton [46].
Theorem 29
Let \(\{(\varSigma _k,g_k,x_k)\}_{k\in \mathbb {N}}\) be a sequence of complete pointed Riemannian manifolds with uniformly bounded geometry. Then, the sequence \(\{(\varSigma _k,g_k,x_k)\}_{k\in \mathbb {N}}\) subconverges smoothly to a complete pointed Riemannian manifold (Σ ∞, g ∞, x ∞).
Remark 9
We would like to mention here that due to an estimate from Cheeger, Gromov and Taylor [14], the above compactness theorem still holds under the weaker assumption that the injectivity radius is uniformly bounded from below by a positive constant, only along the base points \(\{x_k\}_{k\in \mathbb {N}}\), thereby avoiding the assumption of the uniform lower bound for \(inj_{g_k}(\varSigma _k)\).
7.3 Convergence of Immersions
Definition 33
Let F k: (Σ k, g k, x k) → (P k, h k, y k) be a sequence of isometric immersions, such that F(x k) = y k, for any \(k\in \mathbb {N}\). We say that the sequence \(\{F_k\}_{k\in \mathbb {N}}\) converges smoothly to an isometric immersion
if the following conditions are satisfied:
-
(a)
The sequence \(\{(\varSigma _k,g_k,x_k)\}_{k\in \mathbb {N}}\) smoothly converges to (Σ ∞, g ∞, x ∞).
-
(b)
The sequence \(\{(P_k,h_k,y_k)\}_{k\in \mathbb {N}}\) smoothly converges to (P ∞, h ∞, y ∞).
-
(c)
If \(\{(U_k,\varPhi _k)\}_{k\in \mathbb {N}}\) is a family of convergence pairs of \(\{(\varSigma _k,g_k,x_k)\}_{k\in \mathbb {N}}\) and \(\{(W_k,\varPsi _k)\}_{k\in \mathbb {N}}\) is a family of convergence pairs of \(\{(P_k,h_k,y_k)\}_{k\in \mathbb {N}}\), then for each \(k\in \mathbb {N}\), we have F k ∘ Φ k(U k) ⊂ Ψ k(W k) and \(\varPsi ^{-1}_k\circ F\circ \varPhi _k\) smoothly converges to F ∞ on compact sets.
Lemma 10
Suppose that (P, h) is a complete Riemannian manifold with bounded geometry. Then, for any C > 0, there exists a positive constant r > 0, such that inj g(Σ) > r, for any isometric immersion F : (Σ, g) → (P, h) such that the norm |A F| of its second fundamental form satisfies |A F|≤ C.
The last lemma and the Cheeger-Gromov compactness theorem allow us to deduce a compactness theorem in the category of sequences of immersions; see for example [27].
Theorem 30
Let \(\{(\varSigma _k,g_k,x_k)\}_{k\in \mathbb {N}}\) and \(\{(P_k,h_k,y_k)\}_{k\in \mathbb {N}}\) be two sequences of complete Riemannian manifolds with dimensions m and l, respectively. Suppose that F k: (Σ k, g k, x k) → (P k, h k, y k) is a family of isometric immersions, where F k(x k) = y k . Assume that:
-
(a)
Each Σ k is compact.
-
(b)
The sequence \(\{(P_k,h_k,y_k)\}_{k\in \mathbb {N}}\) has uniformly bounded geometry.
-
(c)
For any integer j ≥ 0, there exists a uniform constant C j , such that
$$\displaystyle \begin{aligned}|(\nabla^{F_k})^j A_{F_k}|\le C_j,\end{aligned}$$for any \(k\in \mathbb {N}\) . Here, \(A_{F_k}\) stands for the second fundamental form of F k.
Then, the sequence \(\{F_k\}_{k\in \mathbb {N}}\) subconverges smoothly to a complete isometric immersion F ∞: (Σ ∞, g ∞, x ∞) → (P ∞, h ∞, y ∞).
7.4 Modeling the Singularities
In the following theorem, we describe a method of rescaling around points, where the second fundamental form attains its maximum.
Theorem 31
Let Σ be a compact manifold and let \(F\colon \varSigma \times [0,T_{\max })\to (P,h)\) be a solution of mean curvature flow, where P is a Riemannian manifold with bounded geometry and \(T_{\max }\le \infty \) is the maximal time of existence of a smooth solution. Suppose that there exists a point x ∞∈ Σ and a sequence of points \(\{(x_k,t_k)\}_{k\in \mathbb {N}}\) in Σ × [0, T) with \(\lim x_k=x_{\infty }\), \(\lim t_k=T_{\max }\) such that
Then:
-
(a)
The family of maps \(F_k\colon \varSigma \times [-a_k ^2 t_k,0]\to (P,a_k ^2 h)\),\(k\in \mathbb {N}\) , given by
$$\displaystyle \begin{aligned}F_k (x,s)=F_{k,s}(x)=F(x,s/a_k ^2 +t_k),\end{aligned}$$form a sequence of mean curvature flow solutions. The mean curvature \(H_{F_k}\) and the norm \(|A_{F_k}|\) of the second fundamental form of F k satisfy the equation
$$\displaystyle \begin{aligned}H_{F_k}=\frac{1}{a^{2}_k}H(x,s/a^2_k+t_k)\quad \mathit{\text{and}}\quad |A_{F_k}(x,s)|=\frac{1}{a_k}|A(x,s/a^2_k+t_k)|. \end{aligned}$$Moreover, for any s ≤ 0 we have
$$\displaystyle \begin{aligned}|A_{F_k}(x,s)|\le 1\quad \mathit{\text{and}}\quad |A_{F_k}(x_k,0)|=1,\end{aligned}$$for any \(k\in \mathbb {N}.\)
-
(b)
For any fixed s ≤ 0, the sequence \(\{(\varSigma ,F^*_{k,s}(a_k ^2 h),x_k)\}_{k\in \mathbb {N}}\) smoothly subconverges in the Cheeger-Gromov sense to a connected complete pointed Riemannian manifold (Σ ∞, g ∞(s), x ∞), where Σ ∞ does not depend on the choice of s. Moreover, the sequence \(\big \{\big (P,a_k ^2 h,F_k(x_k,s)\big )\big \}_{k\in \mathbb {N}}\) smoothly subconverges in the Cheeger-Gromov sense to the standard Euclidean space \((\mathbb {R}^l,g_{euc},0)\).
-
(c)
There is an ancient smooth solution \(F_{\infty }\colon \varSigma _{\infty }\times (-\infty ,0]\to \mathbb {R}^l\) of the mean curvature flow, such that for each fixed time s ≤ 0, the sequence \(\{F_{k,s}\}_{k\in \mathbb {N}}\) smoothly subconverges in the Cheeger-Gromov sense to F ∞,s . Additionally,
$$\displaystyle \begin{aligned}|A_{F_{\infty}}|\le 1\quad \mathit{\text{and}}\quad |A_{F_{\infty}}(x_{\infty},0)|=1.\end{aligned}$$ -
(d)
If \(\dim \varSigma =2\) and \(H_{F_{\infty }}=0\) , then the limiting Riemann surface Σ ∞ has finite total curvature. In the matter of fact, the limiting surface Σ ∞ is conformally diffeomorphic to a compact Riemann surface minus a finite number of points and is of parabolic type.
8 Graphical MCF of Surfaces in Four Manifolds
Let (M, g M) and (N, g N) be compact Riemann surfaces. Recall that a smooth map f : M → N is called area decreasing if |Λ 2 df|≤ 1, where Λ 2 df is the 2-Jacobian of f. Being area decreasing means that the map f contracts 2-dimensional regions of M. If |Λ 2 df| < 1 the map is called strictly area decreasing and if |Λ 2 df|≡ 1 the map is said area preserving.
We will deform area decreasing maps f by evolving their corresponding graphs
under the mean curvature flow in the Riemannian product 4-manifold
where π M : M × N → M and π N : M × N → N are the natural projection maps.
Our goal is to give a detailed, unified proof of the following theorem, which was shown in [78, 85, 95, 100]. For the strictly area decreasing case, we closely follow the presentation in [78].
Theorem 32
Let (M, g M) and (N, g N) be compact Riemann surfaces and f : M → N be a smooth area decreasing map. Suppose that the curvatures σ M of g M and σ N of g N are related by
Then there exists a family of smooth area decreasing maps f t : M → N, t ∈ [0, ∞), f 0 = f, such that the graphs Γ(f t) of f t move by mean curvature flow in \((M\times N,{\operatorname {g}_{M\times N}})\) . Furthermore, there exist only two possible categories of initial data sets and corresponding solutions:
-
(I)
The curvatures σ M and σ N are constant and equal and the map f 0 is area preserving. In this category, each f t is area preserving and Γ(f t) smoothly converges to a minimal Lagrangian graph Γ(f ∞) in M × N, with respect to the symplectic form
$$\displaystyle \begin{aligned}\varOmega_{M\times N}=\pi^*_M\varOmega_M\mp\pi^*_N\varOmega_N,\end{aligned}$$depending on whether the map f 0 is orientation preserving or reversing, respectively. Here Ω M and Ω N are the positively oriented volume forms of M and N, respectively.
-
(II)
All other possible cases. In this category, for t > 0 each map f t is strictly area decreasing. Moreover, depending on the sign of \(\sigma =\min \sigma _M\) we have the following behavior:
-
(a)
If σ > 0, then the family Γ(f t) smoothly converges to the graph of a constant map.
-
(b)
If σ = 0, then Γ(f t) smoothly converges to a totally geodesic graph Γ(f ∞) of M × N.
-
(c)
If σ < 0, then Γ(f t) smoothly converges to a minimal surface M ∞ of the product manifold M × N.
-
(a)
8.1 Jacobians of the Projection Maps
Let Ω M denote the Kähler form of the Riemann surface (M, g M) and Ω N the Kähler form of (N, g N). We can extend Ω M and Ω N to two parallel 2-forms on the product manifold M × N by pulling them back via the projection maps π M and π N. That is we may define the parallel forms \(\varOmega _1=\pi ^*_M\varOmega _M\) and \(\varOmega _2=\pi ^*_N\varOmega _N.\) Define now two smooth functions u 1 and u 2 given by
and
where here ∗ stands for the Hodge star operator with respect to the metric g. Note that u 1 is the Jacobian of the projection map from Γ(f) to the first factor of M × N and u 2 is the Jacobian of the projection map of Γ(f) to the second factor of M × N. With respect to the basis {e 1, e 2;ξ 3, ξ 4} of the singular decomposition, we can write
Another important quantity that plays a crucial role in the case of maps between equi-dimensional manifolds is the Jacobian determinant, i.e., the map given by
Moreover, the difference between u 1 and |u 2| measures how far f is from being area preserving. In particular:
8.2 The Kähler Angles
There are two natural complex structures associated to the product space \((M\times N,{\operatorname {g}_{M\times N}})\), namely \(J_1=\pi ^*_MJ_M-\pi ^*_NJ_N\) and \(J_2=\pi ^*_MJ_M+\pi ^*_NJ_N,\) where J M and J N are the complex structures on M and N defined by
Chern and Wolfson [23] introduced a function which measures the deviation of the tangent plane dF(T x M) from a complex line of the space T F(x)(M × N). More precisely, if we consider \((M\times N,{\operatorname {g}_{M\times N}})\) as a complex manifold with respect to J 1 then its corresponding Kähler angle a 1 is given by the formula
For our convenience we require that a 1 ∈ [0, π]. Note that in general a 1 is not smooth at points where φ = ±1. If there exists a point x ∈ M such that a 1(x) = 0 then dF(T x M) is a complex line of T F(x)(M × N) and x is called a complex point of F. If a 1(x) = π then dF(T x M) is an anti-complex line of T F(x)(M × N) and x is said anti-complex point of F. In the case where a 1(x) = π∕2, the point x is called Lagrangian point of the map F. In this case u 1 = u 2. Similarly, if we regard the product manifold \((M\times N,{\operatorname {g}_{M\times N}})\) as a Kähler manifold with respect to the complex structure J 2, then its corresponding Kähler angle a 2 is defined by the formula
The graph Γ(f) in the product Kähler manifold \((M\times N,{\operatorname {g}_{M\times N}},J_i)\) is called symplectic with respect to the Kähler form related to J i, if the corresponding Kähler angle satisfies \(\cos a_i>0\). Therefore a map f is strictly area decreasing if and only if its graph Γ(f) is symplectic with respect to both Kähler forms.
8.3 Structure Equations
Around each point x ∈ Γ(f) we choose an adapted local orthonormal frame {e 1, e 2;ξ 3, ξ 4} along the graph. In this special case the Gauss equation reads
where here σ g is the Gauss curvature of the induced metric. From the Ricci equation we see that the curvature σ n of the normal bundle of Γ(f) is given by the formula
The sum of the last four terms in the above formula is equal to minus the commutator σ ⊥ of the matrices \(A^3=(A^3_{ij})\) and \(A^4=(A^4_{ij}),\) that is
In the case where u 1 = u 2 and σ M = σ = σ n, it turns out that the immersion F is Lagrangian and σ g = σ n. In this case, the following algebraic equality holds
8.4 Estimates for the Jacobians and the Kähler Angles
Let us evolve now by mean curvature flow the graph Γ(f). Denote by \(T_{\max }\) the maximal time of solution of the flow and by T Γ the time until graphical property is preserved. Of course, \(0<T_{\varGamma }\le T_{\max }.\) We will give here several a priori estimates for the Jacobians u 1 and u 2 and the Kähler angles. The proofs are straightforward and follow directly as special cases of the general formulas of Section 6.5.
Lemma 11
The gradients of the functions φ, 𝜗 at a point x ∈ M satisfy the equations
As long the mean curvature flow remains graphical, the Jacobians u 1 and u 2 satisfy the following coupled system of parabolic equations
Moreover, φ and 𝜗 satisfy the following system of equations
Lemma 12
Let f : (M, g M) → (N, g N) be an area decreasing map between compact Riemann surfaces. Suppose that the curvatures of g M and g N satisfy \(\sigma =\min \sigma _M\ge \max \sigma _N.\) Then the following statements hold.
-
(a)
The conditions \(\operatorname {Jac}(f)\le 1\) or \(\operatorname {Jac}(f)\ge -1\) are both preserved as long as the flow remains graphical. In particular, the area decreasing property is preserved as long as the flow remains graphical.
-
(b)
If there is a point (x 0, t 0) ∈ M × (0, T Γ) where \(\operatorname {Jac}^2(f)(x_0,t_0)=1\) , then \(\operatorname {Jac}^2(f)\equiv 1\) in space and time and σ M ≡ σ ≡ σ N.
-
(c)
The flow remains graphical as long as it exists, that is \(T_{\varGamma }=T_{\max }\).
Proof
-
(a)
From Lemma 11, we deduce that
$$\displaystyle \begin{aligned} \begin{array}{rcl} {\partial_t}\varphi-\varDelta \varphi& =&\displaystyle \big(|A|{}^2-2\sigma^{\perp}+\sigma_N(1-\varphi^2)\big)\varphi+\frac{1}{2}(\sigma_M-\sigma_N)(\varphi+\vartheta)(1-\varphi^2). \end{array} \end{aligned} $$Note that the quantities 1 − φ 2 and φ + 𝜗 are non-negative. Hence, because of our curvature assumptions, the last line of the above equality is positive. Thus, there exists a time dependent function h such that
$$\displaystyle \begin{aligned}\partial_t \varphi-\varDelta \varphi\ge h\,\varphi.\end{aligned}$$From the maximum principle we deduce that φ stays non-negative in time.
-
(b)
From the strong maximum principle it follows that if φ vanishes at a point (x 0, t 0) ∈ M × (0, T Γ), then it vanishes identically in space and time. In this case, 𝜗 is positive. Going back to the evolution equation of φ, we see that σ M and σ N must be constant equal to σ. Similarly, we prove the results concerning 𝜗.
-
(c)
By compactness, initially, we have that minx ∈ M u 1(x, 0) = ε > 0. By continuity, the minimum of u 1 stays positive for small values of t. However, we will show that the flow remains graphical as long as it exists. As a matter of fact, we will show that
$$\displaystyle \begin{aligned}\min_{x\in M} u_1(x,t)>0,\end{aligned}$$as long as the flow exists. Suppose to the contrary, that there exists a first time where the graphical property does not hold. This means that there exists a point (x 0, t 0) in space-time with t 0 < T, such that u 1(x 0, t 0) = 0 and u 1(x, t) > 0, for all (x, t) ∈ M × [0, t 0). Since the area decreasing property is preserved by the flow and |A|2 is bounded on M × [0, t 0], there exists a constant \(c(t_0)\in \mathbb {R}\), such that
$$\displaystyle \begin{aligned}\partial_t u_1-\varDelta u_1\ge c(t_0)u_1,\end{aligned}$$for all (x, t) ∈ M × [0, t 0). From the parabolic maximum principle, we get \(u_1(x,t)\ge e^{c(t_0)t},\) for all (x, t) ∈ M × [0, t 0). Passing to the limit as t approaches t 0, we obtain
$$\displaystyle \begin{aligned}u_1(x_0,t_0)=\lim_{t\to t_0} u_1(x_0,t)\ge e^{c(t_0)t_0}>0,\end{aligned}$$which leads to a contradiction.
This completes the proof. □
From the Lemma 12 we see that, under our assumptions, the evolved maps \(\{f_t\}_{t\in (0,T_{\max })}\) are either strictly area decreasing or area preserving. This fact leads us to investigate these two cases separately.
8.4.1 Strictly Area Decreasing Case
We will explore the behaviour of \(\rho :M\times [0,T_{\max })\to \mathbb {R}\) given by ρ = φ 𝜗 under the graphical mean curvature flow.
Lemma 13
Let (M, g M) and (N, g N) be compact Riemann surfaces such that their curvatures σ M and σ N are related by \(\sigma =\min \sigma _M\ge \max \sigma _N.\) The following hold true:
-
(a)
If σ ≥ 0, then there exists a positive constant c 0 such that
$$\displaystyle \begin{aligned}\rho\ge\frac{c_0e^{\sigma t}}{\sqrt{1+c^2_0e^{2\sigma t}}},\end{aligned}$$for any (x, t) in space-time.
-
(b)
If σ < 0, then there exists a positive constant c 0 such that
$$\displaystyle \begin{aligned}\rho\ge\frac{c_0e^{2\sigma t}}{\sqrt{1+c^2_0e^{4\sigma t}}},\end{aligned}$$for any (x, t) in space-time.
Proof
From Lemma 11 we get,
Note that
Since by assumption σ M ≥ σ ≥ σ N, we deduce that
One can algebraically check that
-
(a)
Suppose at first that σ ≥ 0. Then
$$\displaystyle \begin{aligned}\partial_t\rho-\varDelta\rho\ge-\frac{1}{2\rho}|\nabla\rho|{}^2+\sigma\rho(1-\rho^2).\end{aligned}$$From the comparison maximum principle we obtain
$$\displaystyle \begin{aligned}\rho\ge\frac{c_0e^{\sigma t}}{\sqrt{1+c^2_0e^{2\sigma t}}},\end{aligned}$$where c 0 is a positive constant.
-
(b)
In the case where σ < 0, from the Equation (40) we deduce that
$$\displaystyle \begin{aligned}\partial_t\rho-\varDelta\rho\ge-\frac{1}{2\rho}|\nabla\rho|{}^2+2\sigma\rho(1-\rho^2),\end{aligned}$$from where we get the desired estimate.
This completes the proof. □
8.4.2 Area Preserving Case
Suppose that the family of the graphs is generated orientation preserving by area decreasing maps. This means that φ is identically zero. In the next lemma we derive an estimate for the Kähler angle 𝜗.
Lemma 14
Suppose that M and N are compact with the same constant sectional curvature σ and that f : M → N is an area preserving map. Then, there exists a positive real number c 0 such that
for any point (x, t) in space-time.
Proof
Since |A|2 + 2σ ⊥≥ 0, from the evolution equation of 𝜗, we get
According to the parabolic maximum principle, there exist a positive real number c 0 such that
for any (x, t) in space-time. This completes the proof. □
8.5 Curvature Decay Estimates
8.5.1 Strictly Area Decreasing Case
Lemma 15
Let f : (M, g M) → (N, g N) be a strictly area decreasing map. Suppose that the curvatures of M and N satisfy \(\sigma =\min \sigma _M\ge \max \sigma _N.\) Let \(\delta :[0,T)\to {\mathbb R}\) be a positive increasing real function and τ the time dependent function given by \(\tau =\log \big (\delta |H|{ }^2+\varepsilon \big ),\) where ε is a non-negative number. Then,
Proof
Recall from Lemma 6 that |H|2 evolves in time under the equation
where {e 1, e 2} is a local orthonormal frame with respect to g. Using the special frames of the singular value decomposition we see that
Note that from Cauchy–Schwarz inequality |A H|≤|A|⋅|H|. Moreover, observe that at points where the mean curvature vector is non-zero, from Kato’s inequality, we have that
Consequently, at points where the norm |H| of the mean curvature is not zero the following inequality holds
Now let us compute the evolution equation of the function τ. We have,
Note that
Therefore,
and this completes the proof. □
Theorem 33
Let f : (M, g M) → (N, g N) be an area decreasing map, where M and N are compact Riemann surfaces. Suppose that the curvatures of M and N satisfy \(\sigma =\min \sigma _M\ge \sup \sigma _N.\) Then the following statements hold:
-
(a)
There exist a positive time independent constant C such that |H|2 ≤ C.
-
(b)
If σ ≥ 0, there exist a time independent constant C so that |H|2 ≤ Ct −1.
Proof
Consider the time dependent function \(\varTheta =\log (\delta |H|{ }^2+\varepsilon )-\log \rho ,\) where δ is a positive increasing function. From Lemmas 6 and 13 and |H|2 ≤ 2|A|2, we deduce that
Choosing δ = 1 and ε = 0, we obtain that
From the maximum principle the norm |H| remains uniformly bounded in time regardless of the sign of the constant σ. In the case where σ ≥ 0, choosing ε = 1 and δ = t, we deduce that Θ remains uniformly bounded in time which gives the desired decay estimate for H. □
8.5.2 Area Preserving Case
In the sequel, we provide a very important decay estimate due to Wang [91] for the mean curvature in the area preserving case.
Theorem 34
Suppose that M and N are compact Riemannian manifolds with the same constant sectional curvature σ and that f : M → N is an area preserving map. Then, the following decay estimate holds:
where Ω is the volume element of the induced metric.
Proof
The idea is to compare |H| with 𝜗. We compute
But from the evolution equation of 𝜗 and |H|2, we obtain
Using the Equation (39) and the formula
the identity (41) becomes
Integrating and using Stokes’ theorem, we have
Using
in the first term on the right hand side of the above equation and completing the square, we have
Moreover, from Lemma 4, we have \(\nabla _{\partial _t} \varOmega =-|H|{ }^2 \varOmega .\) Also, by Cauchy–Schwarz inequality, we get
Therefore, putting everything together, we get
and by integration, we obtain the result. □
8.6 Long-time Existence
We will show now that the graphical MCF exists for all times.
Theorem 35
Let (M, g M) and (N, g N) be compact Riemann surfaces such that their curvatures σ M and σ N are related by \(\sigma =\min \sigma _M\ge \max \sigma _N.\) Also, let f : M → N be an area preserving map. Evolve the graph off under the mean curvature flow. Then, the norm of the second fundamental form of the evolved graphs stays uniformly bounded in time and so the graphical mean curvature flow exists for all times.
Proof
Suppose that |A| is not uniformly bounded. Then, there exists a sequence \(\{(x_k,t_k)\}_{k\in \mathbb {N}}\) in \(M\times [0,T_{\max })\) with \(\lim t_k=T_{\max }\le \infty ,\) and such that
Let \(F_k\colon M\times [-a_k ^2 t_k,0]\to (N,a_k ^2 g_N)\) be the graph of the “rescaled map”
-
Claim:
The singular values are invariant under parabolic rescalings.
Let {α 1, α 2} and {β 1, β 2} orthonormal frames of the singular value decomposition of f. Then \(\{\widetilde {\alpha }_1={\alpha _1}/{a_k},\widetilde {\alpha }_2={\alpha _2}/{a_k}\}\) is an orthonormal frame with respect to \(a_k ^2g_M\) and \(\{\widetilde {\beta }_1={\beta _1}/{\alpha _k},\widetilde {\beta }_2={\beta _2}/{\alpha _k}\}\) is orthonormal with respect to g N. Therefore, the singular values of the rescaled map f are given by
and
This completes the proof of the claim.
Thus, \(\varphi _{F_k}=\varphi \) and \(\vartheta _{F_k}=\vartheta \). Also, from Theorem 31(a) we have
for any \((x,s)\in M\times [-a_k ^2 t_k,0]\).
CASE 1 Suppose that the evolved graphs are generated by strictly area decreasing maps. Since from the estimate of Lemma 15 the norm |H| of the mean curvature is uniformly bounded and the convergence is smooth, it follows that \(F_{\infty }:\varSigma _{\infty }\to \mathbb {R}^{4}\) is a complete minimal immersion of parabolic type. Hence, any non-negative superharmonic function must be constant. Since the convergence is smooth, the corresponding Kähler angles φ ∞, 𝜗 ∞ of F ∞ with respect to the complex structures \(J=(J_{\mathbb {R}^2},-J_{\mathbb {R}^2})\) and \(J_2=(J_{\mathbb {R}^2},J_{\mathbb {R}^2})\) of \(\mathbb {R}^{4}\) are non-negative. As in Lemma 11 we get that
where \(-\sigma ^{\perp }_{F_{\infty }}\) is the normal curvature of F ∞. Moreover,
Note that from (38) one can easily derive the inequalities
From (43) and (44) we deduce that φ ∞ and 𝜗 ∞ are superharmonic and consequently they must be constants. Thus, the functions (u 1)∞ and (u 2)∞ are also constants. We will distinguish three subcases:
Sub-case A Suppose at first that φ ∞ > 0 and 𝜗 ∞ > 0. Then from (43) and (44) we deduce that
which implies that \(|A_{F_{\infty }}|=0\). This contradicts the fact that there is a point where \(|A_{F_{\infty }}|=1\).
Sub-case B Suppose that both constants φ ∞ and 𝜗 ∞ are zero. Then from the Equations (45) and (46) we obtain that \(A_{F_\infty }\) vanishes identically, which is a again a contradiction.
Sub-case C Suppose now that only one of the constants φ ∞, 𝜗 ∞ is zero. Let us assume that φ ∞ = 0 and 𝜗 ∞ > 0. The case φ ∞ > 0 and 𝜗 ∞ = 0 is treated in a similar way. Since φ ∞ = 0, \(F_\infty :\varSigma _\infty \to \mathbb {R}^{4}\) must be a minimal Lagrangian immersion. Note that in this case necessarily (u 1)∞ = (u 2)∞ = const > 0. Recall from Theorem 5 that the minimal Lagrangian F ∞ can be locally reparametrized in the form
where β is a constant and \(\mathcal {F}_1\), \(\mathcal {F}_2:\mathbb {D}\subset \mathbb {C}\to \mathbb {C}\) are holomorphic functions defined in a simply connected domain \(\mathbb {D}\) such that
The Gauss map of F ∞ is described by \(\mathcal {G}:\mathbb {D}\to \mathbb {S}^{2}=\mathbb {C}\cup \{\infty \}\) given by
Because (u 1)∞ = const > 0 we get that F ∞ is the graph of an area preserving map h. Then
Therefore
A straightforward computation shows that
Hence, the image of \(\mathcal {G}\) is contained in a bounded subset of \(\mathbb {C}\cup \{\infty \}\). But then, due to Theorem 11 the immersion F ∞ must be flat, which is a contradiction.
CASE 2 Let us treat now the area preserving case. In this situation, we have that
We distinguish two subcases:
Sub-case A Let us suppose that σ ≤ 0. Using Lemma 34, we have
where c > 0. Since the convergence is smooth, we have
Therefore, \(H_{F_{\infty }}=0.\) Proceeding exactly in the same way as in CASE 1 we can prove that F ∞ is flat, something which leads to a contradiction.
Sub-case B Let us treat now the case σ > 0. We will show at first that \(T_{\max }=\infty \). To show this, assume in contrary that \(T_{\max }<+\infty \). Then,
As in the previous case, we deduce that \(H_{F_{\infty }}=0.\) Performing exactly the same procedure as above, we get a contradiction. Therefore, there is no finite time singularity and the flow exists for all times. It remains to show that |A|2 ≤ C, where C is time independent. Indeed, since λμ = 1, we obtain
On the other hand, from Lemma 14, we have
which tends to 1 as t →∞. Therefore, 𝜗 ∞ = 1 and λ ∞ = 1. Therefore, f ∞ is an isometry and, thus, F ∞ must be totally geodesic. The latter implies \(|A_{F_{\infty }}|=0\) and this is again a contradiction.
This completes the proof. □
8.7 Convergence and Proof of Theorem 32
We are ready to prove the main theorem stated in the introduction of this section. We will show that the graphical mean curvature flow of an area preserving map converges to an isometry in the positive case, to an affine map in the zero case, and to a minimal surface in the negative case. Recall that from Theorem 35, we already know that the norm of the second fundamental form stays uniformly bounded in time. Since
and since the graphical flow exists for all time we have that there exists a time-independent constant C, such that
Therefore, there exists a sequence \(\{t_k\}_{k\in \mathbb {N}}\), such that
From Theorem 35, the norms of the second fundamental forms of the evolving submanifolds and their derivatives are uniformly bounded in time. Since the product manifold M × N is compact, after passing to a subsequence of \(\{t_k\}_{k\in \mathbb {N}}\) if necessary, we deduce that the flow subconverges smoothly to a smooth surface M ∞ of M × N; see for example [11, Theorem 1.1]. From (47) M ∞ should be minimal. Due to a deep result of Simon [82], it follows that the flow converges smoothly and uniformly to a minimal surface M ∞⊂ M × N. Additionally, we have the following situations:
Area Preserving Case
Let us treat the case where the evolving maps are area preserving.
-
(a)
If σ > 0, then from Lemma 14(c), we have 𝜗 → 1, as t →∞. Therefore, M ∞ is the graph of an isometry f ∞: M → N.
-
(b)
If σ = 0, then from Lemma 14(c), we have that 𝜗 ≥ c 0 > 0. Hence, the surface M ∞ is the graph of a map f ∞: M → N. From Lemma 11 and the fact that \(2\sigma _\infty ^\bot =|A_\infty |{ }^2,\) we have
$$\displaystyle \begin{aligned}-\varDelta\vartheta_\infty=2|A_\infty|{}^2\vartheta_\infty\ge 0.\end{aligned}$$By the strong maximum principle, we get |A ∞|2 = 0. Hence, M ∞ is totally geodesic.
Strictly Area Decreasing Case
Assume that our maps are area decreasing.
-
(a)
Suppose that σ > 0. In this case the flow is smoothly converging to a graphical minimal surface M ∞ = Γ(f ∞) of M × N. Due to Theorem 13(a), the biggest singular value tends to zero as time goes to infinity. Hence, M ∞ must be totally geodesic and f ∞ is a constant map.
-
(b)
Assume that σ = 0. As in the previous case, we have smooth convergence of the flow to a minimal graphical surface M ∞ = Γ(f ∞) of M × N, where f ∞ is a strictly area decreasing map. Because of the formula
$$\displaystyle \begin{aligned}\partial_t\int_{M}\varOmega=-\int_{M} |H|{}^2\varOmega\le 0,\end{aligned}$$we obtain that
$$\displaystyle \begin{aligned}\int_M\varOmega\le \int_M\varOmega_M=\operatorname{constant}.\end{aligned}$$From Theorem 33(b), there is a non-negative constant C such that
$$\displaystyle \begin{aligned}\int_M |H|{}^2\varOmega\le\frac{C}{t}\int_M\varOmega \le\frac{C}{t}\int_M\varOmega.\end{aligned}$$Due to our assumptions we have \(u^2_2\le u^2_1\le 1\) and \(\min \sigma _M\ge 0\ge \sup \sigma _N.\) Moreover, recall that
$$\displaystyle \begin{aligned}\varOmega=\sqrt{(1+\lambda^2)(1+\mu^2)}\varOmega_M=u^{-1}_1\varOmega_M.\end{aligned}$$From the Gauss equation (8.3) and the Gauss-Bonnet formula we get
$$\displaystyle \begin{aligned} \begin{array}{rcl} \int_M|A|{}^2\varOmega & =&\displaystyle \int_M|H|{}^2\varOmega+2\int_M\big(\sigma_Mu^2_1+\sigma_Nu^2_2\big)\varOmega -2\int_M \sigma_{g(t)}\varOmega\\ & \le&\displaystyle 2\int_M\sigma_Mu^2_1\varOmega-2\int_M \sigma_{g(t)}\varOmega +\int_M|H|{}^2\varOmega\\ & \le&\displaystyle 2\int_M\sigma_Mu_1\varOmega-2\int_M \sigma_{g(t)}\varOmega+\int_M|H|{}^2\varOmega\\ & \le&\displaystyle 2\int_M\sigma_M\varOmega_M -2\int_M \sigma_{g(t)}\varOmega +\int_M|H|{}^2\varOmega=\int_M|H|{}^2\varOmega\\ & \le&\displaystyle Ct^{-1}, \end{array} \end{aligned} $$where C is a non-negative constant. Passing to the limit, we deduce that
$$\displaystyle \begin{aligned}\int_M|A_{\infty}|{}^2\varOmega_{\infty}=0.\end{aligned}$$Thus, M ∞ = F ∞(M) must be a totally geodesic graphical surface.
This completes the proof. □
Notes
- 1.
These notes are based partly on a series of lectures delivered by the author at the Chern Institute of Mathematics held in Tianjin-China in November 2019.
- 2.
The author would like to acknowledge support by the General Secretariat for Research and Technology (GSRT) and the Hellenic Foundation for Research and Innovation (HFRI) Grant No:133.
References
R. Aiyama, Totally real surfaces in the complex 2-space, in Steps in Differential Geometry (Debrecen, 2000). Institute of Mathematical Information, Debrecen (2001), pp. 15–22
R. Aiyama, Lagrangian surfaces with circle symmetry in the complex two-space. Michigan Math. J. 52, 491–506 (2004)
F. Almgren, Some interior regularity theorems for minimal surfaces and an extension of Bernstein’s theorem. Ann. Math. 84, 277–292 (1966)
B. Andrews, C. Baker, Mean curvature flow of pinched submanifolds to spheres. J. Differ. Geom. 85, 357–395 (2010)
B. Andrews, C. Hopper, The Ricci flow in Riemannian geometry, A complete proof of the differentiable 1/4-pinching sphere theorem. Lecture Notes in Mathematics, vol. 2011 (Springer, Heidelberg, 2011)
R. Assimos, J. Jost, The geometry of maximum principles and a Bernstein theorem in codimension 2. arXiv:1811.09869 (2018)
C. Baker, The mean curvature flow of submanifolds of high codimension, PhD Thesis (Australian National University, Mathematical Sciences Institute, Australia, 2010). https://arxiv.org/abs/1104.4409
S. Bernstein, Über ein geometrisches Theorem und seine Anwendung auf die partiellen Differentialgleichungen yom elliptischen Typus. Math. Z. 26, 551–558 (1927). (translation of the original version in Comm. Soc. Math. Kharkov 2-‘eme sér. 15, 38–45 (1915-1917))
C. Böhm, B. Wilking, Nonnegatively curved manifolds with finite fundamental groups admit metrics with positive Ricci curvature. Geom. Funct. Anal. 17, 665–681 (2007)
E. Bombieri, E. De Giorgi, E. Giusti, Minimal cones and the Bernstein conjecture. Invent. Math. 7, 243–268 (1969)
P. Breuning, Immersions with bounded second fundamental form. J. Geom. Anal. 25, 1344–1386 (2015)
A. Chau, J. Chen, W. He, Lagrangian mean curvature flow for entire Lipschitz graphs. Calc. Var. Partial Differ. Equations 44, 199–220 (2012)
A. Chau, J. Chen, Y. Yuan, Lagrangian mean curvature flow for entire Lipschitz graphs II. Math. Ann., 357, 165–183 (2013)
J. Cheeger, M. Gromov, M. Taylor, Finite propagation speed, kernel estimates for functions of the Laplace operator, and the geometry of complete Riemannian manifolds. J. Differ. Geom. 17, 15–53 (1982)
J. Chen, W. He, A note on singular time of mean curvature flow. Math. Z., 266, 921–931 (2010)
J. Chen, J. Li, Mean curvature flow of surface in 4-manifolds. Adv. Math. 163, 287–309 (2001)
J. Chen, J. Li, Singularity of mean curvature flow of Lagrangian submanifolds. Invent. Math. 156, 25–51 (2004)
J. Chen, G. Tian, Moving symplectic curves in Kähler-Einstein surfaces. Acta Math. Sin. (Engl. Ser.) 16, 541–548 (2000)
B.-Y. Chen, J.-M. Morvan, Géométrie des surfaces lagrangiennes de C 2. J. Math. Pures Appl. 66, 321–325 (1987)
S.-S. Chern, Minimal surfaces in an euclidean space of N dimensions, in Differential and Combinatorial Topology (Princeton University, Princeton, 1965), pp. 187–198
S.-S. Chern, Minimal submanifolds in a Riemannian manifold, in University of Kansas, Department of Mathematics Technical Report, vol. 19 (New Series) (University of Kansas Lawrence, Lawrence, 1968)
S.S. Chern, R. Osserman, Complete minimal surfaces in Euclidean n-space. J. Anal. Math. 19, 15–34 (1967)
S.-S. Chern, J.G. Wolfson, Minimal surfaces by moving frames. Am. J. Math. 105, 59–83 (1983)
B. Chow, P. Lu, L. Ni, Hamilton’s Ricci Flow (American Mathematical Society/Science Press Beijing, Providence/New York, 2006)
B. Chow, S.-C. Chu, D. Glickenstein, C. Guenther, J. Isenberg, T. Ivey, D. Knopf, P. Lu, F. Luo, L. Ni, The Ricci flow: techniques and applications. Geometric aspects. Part I, in Mathematical Surveys and Monographs, vol. 135 (American Mathematical Society, Providence, RI, 2007)
B. Chow, S.-C. Chu, D. Glickenstein, C. Guenther, J. Isenberg, T. Ivey, D. Knopf, P. Lu, F. Luo, L. Ni, The Ricci flow: techniques and applications. Part II, in Mathematical Surveys and Monographs, vol. 144 (American Mathematical Society, Providence RI, 2008)
A. Cooper, Mean Curvature Flow in Higher Codimension, Thesis (Ph.D.) (Michigan State University, Michigan, 2011)
D. Crowley, T. Schick, The Gromoll filtration, KO-characteristic classes and metrics of positive scalar curvature. Geom. Topol. 17, 1773–1789 (2013)
M. Dajczer, R. Tojeiro, Submanifold Theory Beyond an Introduction (Springer, New York, 2019)
E. De Giorgi, Una extensione del teorema di Bernstein. Ann. Sci. Norm. Super. Pisa 19, 79–85 (1965)
D. DeTurck, Deforming metrics in the direction of their Ricci tensors. J. Differ. Geom. 18, 157–162 (1983)
K. Ecker, Regularity Theory for Mean Curvature Flow (Birkhäuser Boston Inc., Boston, 2004)
K. Ecker, G. Huisken, Mean curvature evolution of entire graphs. Ann. Math. 130, 453–471 (1989)
J. Eells, J. Sampson, Harmonic mappings of Riemannian manifolds. Am. J. Math. 86, 109–160 (1964)
L.C. Evans, Partial differential equations, in Graduate Studies in Mathematics, vol. 19 (2010)
L.C. Evans, A strong maximum principle for parabolic systems in a convex set with arbitrary boundary. Proc. Am. Math. Soc. 138, 3179–3185 (2010)
D. Fischer-Colbrie, Some rigidity theorems for minimal submanifolds of the sphere. Acta Math. 145, 29–46 (1980)
M. Gromov, Homotopical effects of dilatation. J. Differ. Geom. 13, 303–310 (1978)
M. Gromov, Pseudoholomorphic curves in symplectic manifolds. Invent. Math. 82, 307–347 (1985)
M. Gromov, Carnot-Carathéodory spaces seen from within, in Sub-Riemannian Geometry. Program of Mathematical, vol. 144 (Birkhäuser, Basel, 1996), pp. 79–323
M. Gromov, Quantitative homotopy theory, in Prospects in Mathematics (American Mathematical Society, Providence, 1999), pp. 45–49
L. Guth, Contraction of areas vs. topology of mappings. Geom. Funct. Anal. 23, 1804–1902 (2013)
R. Hamilton, The inverse function theorem of Nash and Moser. Bull. Am. Math. Soc. (N.S.) 7, 65–222 (1982)
R. Hamilton, Three-manifolds with positive Ricci curvature. J. Differ. Geom. 17, 255–306 (1982)
R. Hamilton, Four-manifolds with positive curvature operator. J. Differ. Geom. 24, 153–179 (1986)
R. Hamilton, A compactness property for solutions of the Ricci flow. Am. J. Math. 117, 545–572 (1995)
T. Hasanis, A. Savas-Halilaj, T. Vlachos, Minimal graphs in \(\mathbb {R}^4\) with bounded Jacobians. Proc. Am. Math. Soc. 137, 3463–3471 (2009)
T. Hasanis, A. Savas-Halilaj, T. Vlachos, On the Jacobian of minimal graphs in \(\mathbb {R}^4\). Bull. Lond. Math. Soc. 43, 321–327 (2011)
A. Hatcher, A proof of the Smale conjecture, \(\operatorname {Diff}(\mathbb {S}^3)\simeq \mathbb {O}(4)\). Ann. Math. 117, 553–607 (1983)
S. Hildebrandt, J. Jost, K.O. Widman, Harmonic mappings and minimal submanifolds. Invent. Math. 62, 269–298 (1980)
E. Hopf, On S. Bernstein’s theorem on surfaces z(x, y) of nonpositive curvature. Proc. Am. Math. Soc. 1, 80–85 (1950)
G. Huisken, Flow by mean curvature of convex surfaces into spheres. J. Differ. Geom. 20, 237–266 (1984)
G. Huisken, Asymptotic behavior for singularities of the mean curvature flow. J. Differ. Geom. 31, 285–299 (1990)
J. Jost, Compact Riemann Surfaces: An Introduction to Contemporary Mathematics (Springer, Berlin, 2006)
J. Jost, Riemannian Geometry and Geometric Analysis Universitext edn., vol. 7 (Springer, Cham, 2017)
J. Jost, Y.-L. Xin, L. Yang, The Geometry of Grassmannian manifolds and Bernstein type theorems for higher codimension. Ann. Sci. Norm. Super. Pisa Cl. Sci. 16, 1–39 (2016)
J. Kazdan, Applications of Partial Differential Equations to Problems in Differential Geometry (1983). http://www.math.upenn.edu/~kazdan/japan/japan.pdf
H.-B. Lawson, R. Osserman, Non-existence, non-uniqueness and irregularity of solutions to the minimal surface system. Acta Math. 139, 1–17 (1977)
J.M. Lee, Riemannian manifolds, in Graduate Texts in Mathematical, vol. 176 (Springer, Berlin, 1997)
K.-W. Lee, Y.-I. Lee, Mean curvature flow of the graphs of maps between compact manifolds. Trans. Am. Math. Soc. 363, 5745–5759 (2011)
J. Li, L. Yang, Symplectic mean curvature flows in Kähler surfaces with positive holomorphic sectional curvatures. Geom. Dedicata 170, 63–69 (2014)
F. Lubbe, Curvature estimates for graphical mean curvature flow in higher codimension, in Technische Informationsbibliothek und Universitätsbibliothek Hannover (TIB), Hannover (2015)
C. Mantegazza, Lecture Notes on Mean Curvature Flow (Birkhäuser/Springer, Basel, 2011)
I. Medoš, M.-T. Wang, Deforming symplectomorphisms of complex projective spaces by the mean curvature flow. J. Differ. Geom. 87, 309–341 (2011)
E.J. Mickle, A remark on a theorem of Serge Bernstein. Proc. Am. Math. Soc. 1, 86–89 (1950)
J. Morgan, G. Tian, Ricci flow and the Poincaré conjecture, in Clay Mathematics Monographs, vol. 3 (American Mathematical Society/Clay Mathematics Institute, Providence/Cambridge, 2007)
J. Moser, On Harnack’s theorem for elliptic differential equations. Comm. Pure Appl. Math. 14, 577–591 (1961)
L. Ni, A Bernstein type theorem for minimal volume preserving maps. Proc. Am. Math. Soc. 130, 1207–1210 (2002)
R. Osserman, Global properties of minimal surfaces in E 3 and E n. Ann. Math. (2) 80, 340–364 (1964)
R. Osserman, A Survey of Minimal Surfaces (Van Nostrand-Reinhold, New York, 1969)
R. Osserman, The minimal surface equation, in Seminar on Nonlinear Partial Differential Equations, Berkeley, California (1983), pp. 237–259
M.H. Protter, H.F. Weinberger, Maximum Principles in Differential Equations (Springer, New York, 1984)
K. Reidemeister, Uber die singulären Randpunkte eines konvexen Körpers. Math. Ann. 83, 116–118 (1921)
E.A. Ruh, J. Vilms, The tension field of the Gauss map. Trans. Am. Math. Soc. 149, 569–573 (1970)
A. Savas-Halilaj, K. Smoczyk, Homotopy of area decreasing maps by mean curvature flow. Adv. Math. 255, 455–473 (2014)
A. Savas-Halilaj, K. Smoczyk, Bernstein theorems for length and area decreasing minimal maps. Calc. Var. Partial Differ. Equations 50, 549–577 (2014)
A. Savas-Halilaj, K. Smoczyk, Evolution of contractions by mean curvature flow. Math. Ann. 361, 725–740 (2015)
A. Savas-Halilaj, K. Smoczyk, Mean curvature flow of area decreasing maps between Riemann surfaces. Ann. Global Anal. Geom. 53, 11–37 (2018)
R. Schoen, The role of harmonic mappings in rigidity and deformation problems. Lecture Notes in Pure and Application Mathematical, vol. 143 (Dekker, New York, 1993), pp. 179–200
J. Simons, Minimal varieties in Riemannian manifolds. Ann. Math. (2) 88, 62–105 (1968)
L. Simon, A Hölder estimate for quasiconformal maps between surfaces in euclidean space. Acta Math. 139, 19–51 (1977)
L. Simon, Asymptotics for a class of nonlinear evolution equations, with applications to geometric problems. Ann. Math. (2) 118, 525–571 (1983)
D. Singley, Smoothness theorems for the principal curvatures and principal vectors of a hypersurface. Rocky Mountain J. Math. 5, 135–144 (1975)
S. Smale, Diffeomorphisms of the 2-sphere. Proc. Am. Math. Soc. 10, 621–626 (1959)
K. Smoczyk, Angle theorems for the Lagrangian mean curvature flow. Math. Z. 240, 849–883 (2002)
K. Smoczyk, Mean curvature flow in higher codimension: introduction and survey, in Global Differential Geometry, Springer Proceedings of the Mathematical, vol. 17 (Springer, Heidelberg, 2012), pp. 231–274
K. Smoczyk, M.-T. Wang, Mean curvature flows of Lagrangians submanifolds with convex potentials. J. Differ. Geom. 62, 243–257 (2002)
K. Smoczyk, M.-T. Wang, Generalized Lagrangian mean curvature flows in symplectic manifolds. Asian J. Math. 15, 129–140 (2011)
K. Smoczyk, M.-P. Tsui, M.-T. Wang, Curvature decay estimates for mean curvature flow in higher codimensions. Trans. Am. Math. Soc. 368, 7763–7775 (2016)
K. Smoczyk, M.-P. Tsui, M.-T. Wang, Generalized Lagrangian mean curvature flows: the cotangent bundle case. J. Reine Angew. Math. 750, 97–121 (2019)
M.-P. Tsui, M.-T. Wang, Mean curvature flows and isotopy of maps between spheres. Comm. Pure Appl. Math. 57, 1110–1126 (2004)
A. Vogiatzi, Mean Curvature Flow and Isotopy of Problems, M.S. Thesis (University of Ioannina, Ioannina, 2020), pp. 1–91
X. Wang, A remark on strong maximum principle for parabolic and elliptic systems. Proc. Am. Math. Soc. 109, 343–348 (1990)
M.-T. Wang, Mean curvature flow of surfaces in Einstein four-manifolds. J. Differ. Geom. 57, 301–338 (2001)
M.-T. Wang, Deforming area preserving diffeomorphism of surfaces by mean curvature flow. Math. Res. Lett. 8, 651–661 (2001)
M.-T. Wang, Long-time existence and convergence of graphic mean curvature flow in arbitrary codimension. Invent. Math. 148, 525–543 (2002)
M.-T. Wang, On graphic Bernstein type results in higher codimension. Trans. Am. Math. Soc. 355, 265–271 (2003)
M.-T. Wang, Subsets of Grassmannians preserved by mean curvature flow. Comm. Anal. Geom. 13, 981–998 (2005)
M.-T. Wang, Lectures on mean curvature flows in higher codimensions. Handbook of Geometric Analysis, vol. 1 (2008), pp. 525–543
M.-T. Wang, Mean curvature flows and isotopy problems, in Surveys in Differential Geometry. Geometry and Topology (International Press, Somerville, 2013), pp. 227–235
H.F. Weinberger, Invariant sets for weakly coupled parabolic and elliptic systems. Rend. Mat. (6) 8, 295–310 (1975)
Y.-L. Xin, Geometry of harmonic maps, in Progress in Nonlinear Differential Equations and their Applications, vol. 23 (Birkhäuser Boston, Inc., Boston, 1996)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Savas-Halilaj, A. (2021). Graphical Mean Curvature Flow. In: Rassias, T.M. (eds) Nonlinear Analysis, Differential Equations, and Applications. Springer Optimization and Its Applications, vol 173. Springer, Cham. https://doi.org/10.1007/978-3-030-72563-1_20
Download citation
DOI: https://doi.org/10.1007/978-3-030-72563-1_20
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-72562-4
Online ISBN: 978-3-030-72563-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)