Financial Contagion in Interbank Networks: The Case of Erdős–Rényi Network Model

Abstract

In this study, we extend the model developed in Leventides et al. (J Econ Behav Organ 158:500–525, 2019) to include a wide variety of network topologies and provide a better understanding of the relation between network structure, banks’ characteristics and interbank contagion. While the focus of this paper is on the various factors that affect interbank contagion such as bank capital ratios, leverage, interconnectedness and homogeneity across banks’ sizes, the model lacks flexibility as far as the variability of the networks links is concerned. In order to circumvent this problem, we introduce the Erdős–Rényi probabilistic network model in our study to provide a wider vicinity of scenarios concerning the network structure of the interbank system and study how homogeneity within the interbank network affects the propagation of financial distress from one institution to the other parts of the system through bilateral exposures.

1 Introduction

Meeting the SDGs has currently secured prior importance for both businesses’ and nations’ socio-economic-environmental transformation to achieving sustainable development. More than 10,000 companies around the world have already signed up to the principles of sustainable business behavior and an adequate number of special toolkits has been developed to assist them towards this transformation. As explicitly stated in [1] “Achieving the Global Goals would create a world that is comprehensively sustainable: socially fair; environmentally secure; economically prosperous; inclusive; and more predictable”. According to Oxford Analytica Foundation [2], “companies that see the business case – as well as the moral imperative – for achieving all the Global Goals will take a ‘Global Goals lens’ to every aspect of their business strategy to change the way they operate and put more focus on inclusion”. Accordingly, Weber [3] underlined that “the banking sector became aware of the opportunity to finance the change to more sustainable development instead of just focusing on risks for their lending business”. Alves et al. [4] debated that “EU aid policy evolved over the last fifteen years in accordance to the notion of financial liberalization and to the importance of private initiative and combined with the SDGs increased the promotion of the financial sector as engine of growth and development in the developing countries’ and that “the New International Financial architecture assigns new roles for developing nations in the global financial markets”. Achieving the Agenda 2030 depends on aligning the entire global chain of the financial and the banking system with sustainability and long-term outcomes therefore delineating of interbank linkages network structure becomes of outmost importance.

Furthermore, in the wake of the aftermaths of global financial crisis of 2007–2009 and the European sovereign debt crisis, there is a lot of attention of systemic risk, interconnectedness and contagious effects. Thus, there is a critical need for a better understanding of the fragility of the financial systems, their inner interconnections, their interaction with real economy and the conditions that can drive them from stability to instability and complete breakdown. In recent years, both academics and regulators has started to study various architectures of the financial system in order to assess certain risks within the system that potentially lead to huge losses for the overall economy.

The global financial system can be represented as a large complex network in which banks, hedge funds and other financial institutions are interconnected to each other through various forms of financial linkages. For example, in the banking sector, banks can be interconnected through direct and indirect links. Direct interconnectedness arises from bilateral transactions; borrowing or lending relationships between banks. A default by one bank, for example, can impose distress on other entities that hold significant liabilities of the defaulting bank. Thus, the failure of a bank can jeopardize the ability of its creditors banks to meet their obligations to their interbank creditors which may lead to a domino effect. There are also indirect ways that banks can be interconnected, since they invest in common securities, namely portfolio overlap. If, for example, a bank holds identical assets with other banks the correlation between their portfolios can cause fire sales in the market during a crisis period depressing thus overall prices in the market, ultimately leading to downward spirals for asset sales and inducing significant losses for all the participants in the market. The complexity of the financial system led many academics to utilize the network theory to study the effects of the interconnectedness and network topology on financial stability. Studying the financial system as a network is one of the methods to investigate the emergence of systemic risk through the connections of banks. In such a network structure every node represents a bank, the connections between banks are represented by edges where edge’s weight represents the magnitude of exposure between the two parties and edge directionality allows one to determine who is the creditor and who is the lender. A robust interbank market plays an important role on the stability of the financial system. Through the interbank market, banks which suffer a liquidity shortage can borrow from banks with liquidity surpluses. The interbank market can stabilize the financial system, by redistributing the funds in a effective way among the banks but at the same time can make the system prone to contagion of financial trouble from one bank to another (linkages).

In this paper, we focus our attention on the direct contagion channel and aim to identify the main drivers that affect interbank contagion. The flourishing literature which ensued in recent years has developed both theoretical models and empirical applications aimed at addressing the various issues concerning systemic risk. Counterfactual simulations on data have been extensively employed to study interbank contagion under different scenarios related to the topology of the interbank network, the size of interbank exposures and the degree of heterogeneity and interconnectedness within the network. In our assessment of the various drivers that affect interbank contagion, we extend the model developed in Leventides et al. [5] to include a wide variety of network topologies and provide a better understanding of the relation between network structure, banks’ characteristics and interbank contagion. While the focus of this paper is on the various factors that affect interbank contagion such as bank capital ratios, leverage, interconnectedness and homogeneity across banks’ sizes, the model lacks flexibility as far as the variability of the networks links is concerned. In this effort, interbank exposure and capital equity among banks displayed a stochasticness and the ability to construct a wide range of scenarios regarding connective links among banks is limited.

The introduction of the Erdős–Rényi probabilistic network model provides us with a wider vicinity of scenarios concerning the network structure of the interbank system. Under this framework, we build up multiple scenarios of various network structures that include a satisfactory number of cases via Monte Carlo simulations. In every single network that we construct, we investigate the dynamics of cascading defaults from an initial random shock that hits the system. Erdős–Rényi random graph model is one of the earliest theoretical network models and was introduced in the early 1960s by the Hungarian mathematicians Paul Erdős and Alfréd Rényi. In this random graph, each possible link between any two nodes can occur with a certain independent and identical probability, the Erdős and Rényi probability.

The Erdős and Rényi random graph model is a model in which has been extensively applied for the study of contagion in financial networks, e.g. [23, 24]. However, a number of alternatives have been recently developed that differ in the probability law governing the distribution of links between nodes. Using the Erdős–Rényi network structure, the degree distribution or the connectivity among banks can vary with respect to the chosen probability p. Thus, each random network generated with the same parameters N, p looks slightly different. Not only the detailed wiring network graph changes between realizations, but so does the number of links. Random graphs or Erdős–Rényi graphs are useful for modeling, analysis, and solving of structural and algorithmic problems arising in mathematics, theoretical computer science, statistical mechanics, natural sciences, and even in social sciences. However, the utility of an Erdős–Rényi model lies mainly in its mathematical simplicity, not in its realism. Virtually, the comparison with real-world networks indicates that the random network model does not capture the degree distribution of real networks but it provides a useful baseline for more complicated network models.

The remainder of the paper is organized as follows. The following section discusses briefly the recent literature that has addressed on the topic of interbank contagion. Various aspects of systemic risk and network structures that are either found in real-world data or used in some theoretical studies of interbank contagion are addressed before we introduce the model investigated in Section 3. In Section 4 we describe the variables, considered in our subsequent analysis, provide in full detail the computer experiments conducted and discuss our simulations results. Summary and concluding remarks are drawn in the final section.

2 Related Literature

According to Upper [11], the channels through which a shock spreads can be broken down into two groups: indirect and direct contagion channels. A direct contagion channel results from the direct interbank linkages among banks and can take effect when an idiosyncratic shock travels through the network. This shock can be due to the inability of some banks to meet their financial obligations or due to interbank exposures that are quite large relative to the lender’s capital. The possibility of the occurrence and transmission of direct contagion depends mainly on the structure and size of the interbank market. On the other hand, indirect contagion is created by indirect linkages among banks such as identical assets, portfolio returns and overlapping portfolios. If, for example, a bank holds identical assets with other banks, the correlation between their portfolios can cause fire sales in the market during a crisis period, thus depressing overall prices in the market and inducing significant losses for all participants [12]. Distinguishing among the various contagion channels is crucial for understanding financial contagion and the mechanisms through which it spreads and evolves.

There are a number of recent studies that have dealt with the issue of interbank contagion. Memmel and Sachs [13] simulate interbank contagion effects for the German banking sector and find that bank capital ratios, the share of interbank assets in the system and the degree of equality in the distribution of interbank exposures are the most important determinants for financial stability. Georgescu [14] compares the contagion potential of accounting induced regulatory constraints to that of funding constraints in a bank network and concludes that the interplay between illiquidity and solvency can lead to bank failures which are manifested by the vulnerable funding structure of banks during a crisis. Tonzer [15] examines the relationship between cross-border bank linkages and financial stability and show that larger cross-border exposures increase bank risks, however, when bilateral interbank linkages exist there is a shift toward a more stable banking system. Fink et al. [16] model contagion in the German interbank market via the credit quality channel and propose a novel metric which estimates the potential regulatory capital loss to a banking system due to contagion via interbank loans. They show that contagion effects can be reduced if banks alter their lending and borrowing habits in response to policy interventions.

Our analysis also relates to the role of heterogeneity in the structure of interbank networks and how this characteristic affect systemic risk. Iori et al. [6] use an Erdős–Rényi network model of 400 banks comprising the interbank market in which the lending and borrowing functions are endogenously generated. The authors find that the likelihood of contagion is lowered in case the interconnected institutions are homogeneous, i.e. they have similar characteristics such as size or investment opportunities and thus, no institution becomes significant for either borrowing or lending. The authors also suggest, in line with Allen and Gale [17], that as connectivity increases the system becomes more stable. In a related study, Caccioli et al. [18] study the role of heterogeneity in degree distributions (the number of incoming and outgoing links), balance sheet size and degree correlations between banks. They find that networks with heterogeneous degree distributions are shown to be more resilient to contagion triggered by the failure of a random bank, but more fragile with respect to contagion triggered by the failure of highly connected nodes. The authors also provide evidence that when the average degree of connectivity is low, the probability of contagion due to failure of highly connected banks is higher than that due to the failure of large banks. However, when the average degree of connectivity is high, the opposite holds. Since the second scenario seems to be more realistic (networks with high connectivity), having “too big to fail” banks is more effective in eliminating a shock. Ladley [19] develops a partial equilibrium model of a closed economy in which heterogeneous banks interact with borrowers and depositors through the interbank market. Banks in the model are subject to regulation and the aim of the model is to qualitatively show how regulation and network structure can constrain or enhance the risk of contagion. The results show that for high levels of connectivity the system is more stable when the shock is small, while the contagion effects are amplified in case of larger initial shocks. Chinazzi et al. [20] explore the interplay between heterogeneity, network structure and balance sheet composition in the transmission of contagion. They argue that heterogeneity in connectivity provides additional resiliency to the system when the initial default is random and also show that ‘too-connected-to-fail’ banks are more dangerous than ‘too-big-to-fail’ ones and should be the primary concern of policy makers since their failure can trigger systemic breakdowns. Amini et al. [10] focus on bank heterogeneity in terms of the number of banks included in the network and the magnitude of their interconnections with other banks. They conclude that the more heterogeneity is introduced, the less resilient the network becomes. Contrary to these findings, the study of Georg and Poschmann [21] finds no significant evidence that the heterogeneity of the financial system has a negative impact on financial stability.

Finally, as far as the structure of an interbank system is concerned, the most common network structures that are either found in real-world data or used in some theoretical studies of interbank contagion are the Erdős–Rényi random network structure, introduced in Erdős and Rényi (1960), the small-world structure, introduced in Watts and Strogatz (1998) and the scale-free structure, introduced in Barabasi and Albert (1999).

The Erdős–Rényi network structure, which is applied in our study, can be obtained by connecting any two nodes with a fixed and independent probability p. Thus, in an Erdős–Rényi network structure the degree or the number of links of a node is p(n-1). The expected degree distribution for such networks is Binomial, converging to Poisson for large n. The Erdős and Rényi (1960) random graph model is a model in which has been extensively applied for the study of contagion in financial networks, e.g. in the contributions from Iori et al. [6], Nier et al. [7], Gai and Kapadia [8], May and Arinaminpathy[9] and Amini et al. [10]. A number of alternatives models have been recently developed that differ in the probability law governing the distribution of links between nodes. Nier et al. [7] study the extent to which the resilience of an interbank network depends on a combination of variables characterizing the network topology, banks’ characteristics in terms of net worth and interbank exposures, and market concentration. Using Monte Carlo simulation experiments in Erdős–Rényi random graphs, they find that the effect of the degree of connectivity is non-monotonic. Specifically, a small initial increase in connectivity increases the chance of contagion defaults. However, after a certain threshold value, connectivity improves the capacity of a banking system to withstand shocks. In addition, the authors find that the banking system is more resilient to contagious defaults if its banks are better capitalized and this effect is non-linear. Finally, the size of interbank liabilities tends to increase the risk of default cascades, even if banks hold capital against such exposures and more concentrated banking systems are shown to be prone to larger systemic risk. Gai and Kapadia [8] using a network model of a banking system study how the probability and potential impact of contagion is influenced by aggregate and idiosyncratic shocks, network structure and liquidity. The authors agree with Haldane (2009) concerning the “robust-yet-fragile” property that the financial system exhibit. Even when the probability of contagion is very low, its effects can have tremendous consequences to the financial system. Higher connectivity may reduce the probability of default when contagion has not started yet but it may also increase the probability of having large default cascades when contagion begins. May and Arinaminpathy [9] apply an Erdos–Renyi network structure of which they build on the models of Nier et al. [7] and Gai and Kapadia [8] and study the interplay between the characteristics of individual banks and the overall behavior of the network. The authors consider that banks interact through different asset classes and study contagion between those asset classes. May and Arinaminpathy [9] find that increasing the level of connectivity is beneficial only when the initial shock has been caused by a default on interbank loans. However, by contrast, the opposite holds in case of liquidity shocks since they do not experience attenuation and for a given asset class, they tend to grow as more and more banks hold the failing asset. Finally, the authors emphasize the importance of having large capital buffers that will make for greater robustness both of individual banks and of the system as a whole. Finally, Amini et al. [10] test the impact of heterogeneity in an interbank network structure and the relation between resilience and connectivity using three different network models; a scale-free network with equal and heterogeneous weights and an Erdős–Rényi network with equal weights. The main result of this study is that the most heterogeneity is introduced, the least the resilience of the network.

3 Erdős–Rényi Random Graph Model

The random graph model which is one of the earliest theoretical network models was introduced by Erdős and Rényi (1960). In this random graph, each possible link between any two nodes can occur with a certain independent and identical probability, p. This model is typically denoted G(n, p) and has two parameters: n the number of vertices and p, the probability that each simple edge (i, j) exists, which is constant for each pair nodes.

The adjacency matrix of a random graph is given by

$$ \forall i>j,{A}_{ij}={A}_{ji}=\left\{\begin{array}{c}1,\kern3em \mathrm{edge}\ \left(\mathrm{i},\mathrm{j}\ \right)\mathrm{exists};\mathrm{prob}\ \left(\mathrm{p}\right)\\ {}0,\mathrm{edge}\ \left(\mathrm{i},\mathrm{j}\ \right)\ \mathrm{does}\ \mathrm{not}\ \mathrm{exist};\mathrm{prob}\ \left(1-\mathrm{p}\right)\end{array}\right. $$

In other words, each edge is included in the graph with probability p, independent from every other edge. The probability to create randomly a graph with n nodes and m edges is given by ${p}^m{\left(1-p\right)}^{\left(\begin{array}{c}n\\ {}2\end{array}\right)-m}$. Furthermore, the probability p serves as the parameter of our model and as p increases, the graph is more likely to have more edges.

The restriction of i > j appears because edges are undirected or to put it differently, the adjacency matrix is symmetric across the diagonal, and there are no self loops. In the network there are n (n − 1) possible links to be created, resulting in an expected number of edges in the network equal to pn (n − 1), so that the (expected) average degree is p(n − 1). Thus, the degree distribution of such a graph is given by

$$ p(k)=\left(\begin{array}{c}n-1\\ {}k\end{array}\right){p}^k{\left(1-p\right)}^{n-1-k} $$

(1)

The mean degree, c, in the G(n,p) graph model is given by

$$ c=\left(n-1\right)p $$

(2)

In other words, each vertex has (n-1) possible partners and each of these exist with the same independent probability p. Asymptotically, as n → ∞, the degree distribution of a random graph converges to a Poisson (c) distribution

$$ p(k)=\frac{e^{-c}{c}^k}{k!} $$

(3)

Due to the above property, the Erdős–Rényi random graph model is sometimes referred as Poisson random graph or random graph. The Erdős and Rényi (1960) graph model results in networks with small diameters and short average path lengths, capturing very well the “small-world” property, observed in many real networks. The clustering coefficient of an Erdős–Rényi graph model is equal to the probability of an edge’s existence between two nodes, p. The Erdős and Rényi (1960) random graph model is a model in which has been extensively applied for the study of contagion in financial networks, e.g. in the contributions from Iori et al. [6], Nier et al. [7], Gai and Kapadia [8] and Montagna and Kok (2013).

In an Erdős –Rényi model we begin with n isolated nodes as presented in the first snapshot in Figure 1. Then, with probability p > 0 each pair of nodes is connected by a link. Therefore, in this model the network is determined only by the number of nodes, n, and edges, m, and usually an Erdős–Rényi random graph is written as G(n, m) or G(n, p). In Figure 1 we present some examples of Erdős–Rényi random graphs with the same number of nodes and different linking probabilities. It is easy to understand that if we repeat the process for the same number of nodes and the same probability, we will not necessarily get the same network.

Figure 1

Erdős–Rényi random networks: Erdős–Rényi random networks with ten nodes and different probabilities of connecting a pair of nodes

However, a number of alternatives models have been recently developed that differ in the probability law governing the distribution of links between nodes. Since, the Erdős–Rényi probability, p, is assumed to be equal and constant across all pairs of nodes, the resulting network structure does not present marked heterogeneity. Thus, modeling interbank networks using the Erdős–Rényi structure fails to mimic the heterogeneity observed in real interbank network systems.

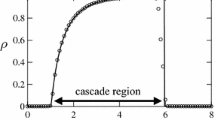
In order to fully understand the heterogeneity of an Erdős–Rényi random network, we now consider one particular random realization of an Erdős–Rényi random network with 1000 nodes and p = 0.04, that is G(n = 1000, p = 0.04) and plot the probability p(k) of finding a node of degree k, versus the degree, we obtain Figure 2, where it can be seen that the maximum of the distribution is about the value k = (n − 1) p = 39. Obviously, the probability p(k)follows a binomial distribution of the form represented in Equation (1). As we explained above, for large values of n, the degree distribution of a random graph converges to a Poisson (c) distribution. Figure 2 displays the heterogeneity plot for G(1000, 0.04), where two characteristic features of the Erdős–Rényi networks are observed. The first is a typical dispersion of the points around the value x = 0, and the second is the very small value of ρ(G), which in this case is 0.0066.

Figure 2

Heterogeneity of Erdős–Rényi random networks. A typical Poisson degree distribution of an Erdős–Rényi random network with 1000 nodes and p = 0.04 (left), and the characteristic heterogeneity plot for the same network. (Source: Estrada [22])

3.1 The Mathematical Description of the Contagion Model

In this section we study the case of an Erdős–Rényi network model in which, as we stated earlier, all nodes have the same probability of being connected to another node in the network. Our model is tailored to simulate default cascades triggered by an exogenous shock in an interbank network as in Leventides et al. [5]. We first introduce the interbank network model, describe the default cascades initiated by a random negative shock on this network and analyze the parameters that affect interbank contagion.

3.2 The Interbank Network

As in Leventides et al. [5], we assume that the banking system contains i = 1,..., N banks. Every bank has its own balance sheet and the accounting equation holds at all times. Total assets are divided in three categories: interbank assets ${A}_i^{IB}$, other assets ${A}_i^{OT}$ and cash reserves C _i. On the liabilities side of the balance sheet we have included: interbank liabilities ${L}_i^{IB}$, other liabilities ${L}_i^{OT}$ and equity capital E _i. A schematic overview of the balance sheet is given in Table 1. Although the proposed balance sheet structure does not capture all elements of a bank balance sheet, it includes all those positions that are relevant to our study.

Table 1 Stylized Balance sheet structure

We introduce a standard notation for our model and we define a simple interbank network as G = (V, E), where V represents the nodes of the graph while E represents the edges. We further consider Α, the adjacency matrix of the graph, defined as

$$ \forall i>j,{A}_{ij}={A}_{ji}=\left\{\begin{array}{c}1,\kern2.75em \mathrm{edge}\ \left(\mathrm{i},\mathrm{j}\ \right)\mathrm{exists}\\ {}0,\mathrm{edge}\ \left(\mathrm{i},\mathrm{j}\ \right)\ \mathrm{does}\ \mathrm{not}\ \mathrm{exist}\end{array}\right. $$

The uth row or column of A has k _u entries, where k _u is the degree of the node u, which is simply the number of nearest neighbours that u has. Denoting by 1 a |V| × 1vector, the column vector of node degrees κis given by

$$ \kappa ={\left({1}^T\mathrm{A}\right)}^T={\mathrm{A}}^T1 $$

(4)

We define the indegree as the number of links pointing toward a given node, and the outdegree as the number of links departing from the corresponding node. Specifically:

$$ {\kappa}^{in}={\left({1}^T\mathrm{A}\right)}^T={\mathrm{A}}^T1 $$

(5)

$$ {\kappa}^{out}=\mathrm{A}1 $$

(6)

Thus, our interbank network of credit exposures between n banks can be visualized by a graph G = (V, E) where V represents the set of financial institutions—nodes, and E is the set of the edges linking the banks, that is, the set of ordered couples(i, j) ∈ V × V indicating the presence of a loan made by bank i to bank j. The number of nodes defines the size of the interbank network. Every edge (i, j) is weighted by the face value of the interbank claim and the representation of interbank claims is made by a single weighted N × N matrix Χ:

$$ \mathrm{X}=\left[\begin{array}{ccccc}0& \cdots & {x}_{1j}& \cdots & {x}_{1N}\\ {}\vdots & \ddots & \vdots & \cdots & \vdots \\ {}{x}_{i1}& \cdots & 0& \cdots & {x}_{iN}\\ {}\vdots & \cdots & \vdots & \ddots & \vdots \\ {}{x}_{N1}& \cdots & {x}_{Nj}& \cdots & 0\end{array}\right] $$

where x _ij is the credit exposure of bank i vis-à-vis bank j and N is the number of banks in the network. Interbank assets are represented along the rows while columns represent interbank liabilities. Once X is in place, the interbank entries of each bank are given according to the following rules:

• (i) ${A}_i=\sum \limits_{j=1}^N{x}_{ij}$ (horizontal summation), where A _i is the total interbank assets of bank i.

• (ii) ${L}_i=\sum \limits_{i=1}^N{x}_{ij}$ (vertical summation), where L _i is the summation of the total interbank liabilities of bank j.

One can observe that the diagonal line contains zeros due to the fact that banks do not lend to themselves. In this framework, a random network is generated based on two parameters, the size of the network (number of nodes/banks) and the probability p_ij that there is a lending/borrowing link between two nodes/banks. Thus, each possible link between two nodes exists with an independent and identical probability, which is often called the Erdős–Rényi probability.

Although, we have undirected edges in this framework, we cannot really speak of undirected links, since the two directions of the same link are given different weights.

3.3 Shock Propagation and Contagion Dynamics

The failure of a bank can affect other banks through their interbank connections. Below, we describe the mechanism through which an initial shock affecting a bank propagates onto its counterparties along the network. Contrary to the recent literature, the term contagion here translates into total capital losses due to multiple default cascades. The cascade dynamics we use in this study are straightforward to implement and enable us to run a great number of simulations on a variety of different scenarios (Table 2).

Table 2 OLS regression analysis for Scenario 1 (Heterogeneous banks with homogeneous exposures)

The default procedure starts with an exogenous shock being simulated, typically by setting to zero the equity of one randomly chosen bank i and the cascade of defaults proceeds on a timestep-by-timestep basis, assuming zero recovery for shock transmissions. The zero recovery assumption, which is a realistic one in the short run, is often used in the literature to analyze worst case scenarios and refers to a situation where creditor banks lose all of their interbank assets held against a defaulting bank [8, 20]. A bank’s default implies that it is no longer able to meet its interbank liabilities to its counterparties. Since these liabilities constitute other banks’ assets, the banks that get into trouble affect simultaneously their counterparties, leading to write-downs in their balance sheets. The interbank asset loss due to failure of bank i is subtracted from the bank’s j capital. Bank j will fail if its exposure against bank i exceeds its equity. A second round of bank failure occurs if bank creditors cannot withstand the losses realized due to its default and eventually, contagion stops if no additional bank goes bankrupt, otherwise a third round of contagion takes place. An initial shock can be amplified through banks’ interconnections and further transmitted to other institutions, such that the overall effect on the system goes largely beyond the original shock. As Upper and Worms (2004) demonstrate, in response to a liquidity shock banks prefer to withdraw their deposits at other banks instead of liquidating their long-term assets, creating further instability and liquidity dry-ups in the financial system.

A general mathematical description of the dynamical system expressing the shock propagation mechanism is presented hereafter. We consider a network consisting of N banks numbered from 1 to N. We define b_i as the capital possessed by bank i in the network and

$$ {\displaystyle \begin{array}{l}{b}_0=\left({b}_1,{b}_2,\dots, {b}_N\right)\\ {}\end{array}} $$

(7)

stands for the initial vector of bank capital. X is defined as a N × N matrix with entries:

x _i j= the credit exposure of bank i vis-à-vis bank j in the network

$$ {x}_{i\;i}={b}_i $$

(8)

We consider the case where some of the banks (one or more) collapse. We wish to study how the crisis travels through the bank network and when exactly it comes to a fixed point. The collapse of banks i ₁ , i ₂ , ..., i _k (where k ≤ N), can be described in the following way. Consider the element ${x}_0\in {Z}_N^2={\left\{0,1\right\}}^N$ which has zero entries everywhere except the positions i ₁ , i ₂ , ..., i _k where x ₀ takes on the value 1. Then,

$$ {b}_1={b}_0-\mathrm{X}\cdotp {x}_0 $$

(9)

is the new vector of capital of the N banks. We now take

$$ {x}_1(i)=\left\{\begin{array}{l}1,{b}_1(i)\le 0;\\ {}0,{b}_1(i)>0.\end{array}\right. $$

(10)

Then ${x}_1\in {Z}_2^N$ and x ₁ indicates the banks that have collapsed after the bankruptcy of the first k banks. The vector x ₁ takes on the value 1 in the positions i ₁ , i ₂ , ..., i _k . If x ₁ ≠ x ₀, this indicates that the collapse of the first k banks has adversely affected other banks leading them to bankruptcy. Similarly, from x ₁ we take:

$$ {b}_1={b}_0-\mathrm{X}\cdotp {x}_1 $$

(11)

and then

$$ {x}_2(i)=\left\{\begin{array}{l}1,{b}_2(i)\le 0;\\ {}0,{b}_2(i)>0.\end{array}\right. $$

(12)

The vector x ₂ indicates the banks that collapse after the bankruptcy of the banks of x ₁. Therefore, we have a map:

$$ F:Z{\displaystyle \begin{array}{c}\mathrm{N}\\ {}2\end{array}}\to Z{\displaystyle \begin{array}{c}\mathrm{N}\\ {}2\end{array}} $$

(13)

$$ x\to \mathrm{F}(x)=f\left({b}_0-\mathrm{X}\cdotp x\right) $$

(14)

The map F(x) defines a dynamical system x _n + 1 = F(x _n) which describes the evolution of contagion in the interbank network.

3.4 Monte Carlo simulations

In this section we apply Monte Carlo simulations in four different stages. As in Leventides et al. [5], we introduce randomness in three areas: amount of capital, interbank claims and network structure. The stochasticness introduced in our model provides us with a wide vicinity of scenarios that may come across in real world. Using the Erdős–Rényi network structure, the degree distribution or the connectivity among banks can vary with respect to the chosen probability p. Thus, each random network generated with the same parameters N, p looks slightly different.

The second stage involves estimating the parameters of interest, i.e. the value of the coefficients in the regression model. In the third stage the test statistics of interest are saved, while in the fourth stage we go back to the first stage and repeat N times. The quantity N is the number of replications which should be as large as is feasible. As Monte Carlo is based on random sampling from a given distribution (with results equal to their analytical counterparts asymptotically), setting a small number of replications will yield results that are sensitive to odd combinations of random number draws. Generally speaking, the sampling variation is measured by the standard error estimate, denoted ${S}_x=\sqrt{\operatorname{var}(x)/N}$, where x denotes the value of the parameter of interest and var(x) is the variance of the estimates of the quantity of interest over the N replications.

Similar to Leventides et al. [5], we consider four different scenarios, in line with Chinazzi et al. [20], where we let vary the balance sheet composition, the size of the network and the link probability among banks which is held constant for each pair of nodes. The four scenarios tested are as follows:

Scenario 1:	• Heterogeneous banks with homogeneous exposures. In this scenario, we construct interbank networks where banks have different equity size and their interbank claims are evenly distributed across the outgoing links
Scenario 2:	• Heterogeneous banks with heterogeneous exposures. In this scenario, the interbank networks allow for heterogeneous bank sizes and heterogeneous interbank claims among banks.
Scenario 3:	• Homogeneous banks with heterogeneous exposures. In this scenario, we construct interbank networks where banks have the same equity size and unevenly distribute their exposures across creditor banks
Scenario 4:	• Homogeneous banks with homogeneous exposures. In this last scenario, we construct interbank networks where banks have the same equity size and interbank claims are evenly distributed across creditor banks

In each case, we do not control the number of outgoing links as in Leventides et al. [5] but for each network that is generated a random probability, which is constant for each pair of nodes, defines the lending/borrowing relation of each bank. The probability p_ij is assumed to be equal and constant across all pairs (i,j). For simplicity, we denote the probability, termed as the Erdős–Rényi probability, by p. Since the probability of forming a link is homogeneous, the resulting network structure does not present marked heterogeneity.

We examine banking systems consisting of small banks with low, medium and large interbank exposures, as well as systems of large banks with corresponding exposure levels. We consider a basic model that uses only two components from a bank’s balance sheet, that is, equity and interbank loans–in the words of May and Arinaminpathy [9] ‘a caricature for banking ecosystems’. We generate our model in two separate steps. First, we construct a model structure of N nodes representing the banks in our system and randomly choose the probability p of forming a link between each of the $\left(\begin{array}{l}N\\ {}2\end{array}\right)$ possible links.

For all the possible couples of nodes, a link is created with probability p which represent lending/borrowing relationship, while in a second step, we assign each node to a stylized balance sheet structure. Once the banking networks are created, the default propagation dynamics are implemented to examine the effects of an idiosyncratic shock hitting one bank. The effect of a shock is simulated, typically by setting to zero the equity of the affected bank. We estimate the initial loss of capital by letting the first bank default and subsequently record the loss as percentage of the total capital in the system. Consequently, the defaulted bank will be unable to repay its creditors and the interbank loans that were granted will be written-off, as we have selected to work under a zero recovery assumption. This bad debt will be recorded and expressed as percentage of the total capital in the system. Moreover, the creditors of the defaulted bank will experience a shock on their balance sheets and the recorded losses will be subtracted from their equity.

If at any time the total losses realized by a bank exceed its net worth, the bank is deemed in default and is removed from the network. Note that time steps are modeled as being discrete and there is the possibility that many banks default simultaneously in each timestep. These shocks propagate to their creditors and take effect in the next timestep. When no further failures are observed, the default procedure terminates and various contagion indicators¹ are calculated based on the contagion map as described in Subsection 3.3.

4 Main Findings

This section discusses the main findings of this study. Subsection 4.1 describes in full detail the computer experiments conducted while Subsection 4.2 discusses the simulation results of all four scenarios considered.

4.1 Computer Experiments

Having generated banking systems via an Erdős–Rényi network structure framework and balance sheet allocation, the dynamics of an initial shock affecting a bank within the interbank network can be investigated. Given the complexity of the interbank network outlined above, it is extremely difficult to derive analytical solutions. In order to obtain data to describe the variables that affect contagion, we employ several Monte Carlo simulations. In each realization, we construct an interbank network with N ∈ [20, 50, 80, 100] nodes under the rewiring process of the Erdős–Rényi methodology. In a second step, we test the four scenarios mentioned before by varying the equity size of banks and the interbank exposure structure across creditor banks. For each scenario tested we check a wide range of link probabilities, such that we can observe dense or sparse interbank network systems. Since the probability of forming a link is homogeneous, the resulting network structure does not present marked heterogeneity.

When homogeneity across bank sizes is considered, all banks are assumed to have the same equity size and thus, each bank is endowed with a balance sheet that consists of 100 units of equity. On the other hand, when homogeneity is present with respect to interbank exposures, interbank claims are randomly allocated within the interbank network and are categorized as follows: small loans granted (4 units), medium loans (8 units) and large loans (14 units). With respect to scenarios tested where heterogeneity of bank size is introduced, the amount of equity of each bank is drawn from a uniform distribution in the range: b _i ∈ [0, 100], whereas when heterogeneity is introduced with respect to interbank claims, credit is allocated in the following ranges: a _ij ∈ [0, 4], a _ij ∈ [0, 8], a _ij ∈ [0, 14]_. ² Interbank exposures are set 60% lower than these in Leventides et al. [5]. This is due to the fact that we cannot control the connectivity across banks since the link probability in randomly selected. The interbank exposure decrease was set by trial and error in order not to observe enormous high leveraged systems. In addition, we control the leverage of the system by setting the rule that the maximum leverage ratio of each network system cannot exceed five. Then, balance sheets are assigned to each node, consistent with each specific scenario tested. We randomly choose a single bank in the system to default due to an exogenous shock and the default cascades proceed sequentially, assuming zero recovery. When no further failures are observed results are recorded before another realization begins. We then impose another shock on the second bank in the network and this procedure continues until all banks in the interbank network are hit by an exogenous shock.

For each scenario tested and for each network size we have three cases in which we allow the weight of outgoing links (small, medium and large interbank claims)to vary among banks. Each case gives us 6000 realizations or, to put it differently, 6000 banking crises. We deem that 6000 realizations provide a satisfactory number of runs and robustness to our analysis. Thus, for each scenario tested and each network size we employ 6000 × 3 = 18,000 realizations using the following variables in each realization:

• Total loss of capital due to contagion as percentage of total capital in the system (CATEND)

• Initial loss of capital by defaulting bank i as percentage of total capital in the system (CATIN1), i.e. bank’s i depleted equity divided by the total equity in the network

• Loss of capital at the first stage (interbank loans that cannot be repaid) by defaulting bank i as percentage of total capital in the system (CATIN2), i.e. total amount of loans granted to bank i that cannot be repaid divided by the total equity in the network

• Leverage of the interbank network(LEVIN), i.e. total interbank exposures as measured by the sum of matrix’s A elements, divided by the total capital in the network

• Number of outgoing links of bank i (NOUTGOING), i.e. the outdegree of a bank i which corresponds to the number of creditors in the network. It is defined as the summation of the ith column of the adjacency matrix A.

• Shock propagation variable (COUNT) which measures the number of rounds needed until no further bank defaults

• Variance of capital (equity) (VARCAP) used in those scenarios tested where only heterogeneous bank sizes are considered

• Variance of interbank loans (VARLOANS) used in those scenarios tested where only heterogeneous interbank loan exposures are considered

• Erdős–Rényi probability p_ij (p) that there is a lending/borrowing link between two nodes/banks.

Our selection of variables is motivated by economic intuition and by the findings of previous studies on the dynamics of systemic risks [7] and Leventides et al. [5]. Table 3 presents summary statistics on these variables. In order to study the effect the aforementioned variables have on contagion risk, we estimate the following ordinary least squares (OLS) models:

$$ {\displaystyle \begin{array}{ll} CATEND & ={\beta}_1 CATIN1+{\beta}_2 CATIN2+{\beta}_3 LEVIN+{\beta}_4 NOUTGOING\\ {}&+{\beta}_5 COUNT +{\beta}_6 VARCAP+{\beta}_7p\end{array}} $$

(15)

$$ {\displaystyle \begin{array}{ll} CATEND ={\beta}_1 CATIN1+{\beta}_2 CATIN2+{\beta}_3 LEVIN+{\beta}_4 NOUTGOING\\ {} +{\beta}_5 COUNT +{\beta}_6 VARCAP+{\beta}_7 VARLOANS+{\beta}_8p\end{array}} $$

(16)

$$ {\displaystyle \begin{array}{ll}CATEND ={\beta}_1 CATIN2+{\beta}_2 LEVIN+{\beta}_3 NOUTGOING+{\beta}_4 COUNT\\{}+{\beta}_5 VARLOANS+{\beta}_6p\end{array}} $$

(17)

$$ {\displaystyle \begin{array}{ll} CATEND& ={\beta}_1 CATIN2+{\beta}_2 LEVIN+{\beta}_3\\& NOUTGOING+{\beta}_4 COUNT+{\beta}_5p \end{array}}$$

(18)

Table 3 Summary statistics

The model described in Equation (15) is applied to scenarios involving heterogeneous bank sizes with homogeneous exposures in the network structure, Equation (15) refers to a situation where emphasis is placed on heterogeneous interbank loan exposures combined with heterogeneous bank sizes, Equation (17) takes into account homogeneous banks with heterogeneous exposures while Equation (18) considers only homogeneous bank sizes and interbank claims. The variable CATIN1 has been omitted from Eqs. (17) and (18) due to the fact that banks in the interbank system are homogeneous, i.e. we keep constant the equity of each bank and thus CATIN1 remains stable during our simulation runs. There is an explanation in the next subsection concerning the fact that in our experiments we have selected to work with standardized variables—both dependent and independent variables—and have not included the intercept term in the regression models as it will be zero. Our concern is to measure effects not in terms of the original units of the dependent variable or the independent variables, but in standard deviation units.³

4.2 Simulation Results

In this section, we discuss the regression results of all four scenarios. Since our variables are measured on different scales, we cannot directly infer which independent variable has the largest effect on the dependent variable. In order to circumvent this problem we standardize our series to have zero mean and unit variance. Table 2 presents the regression results of the first scenario using the OLS model described in Equation (15), where heterogeneous banks distribute evenly their interbank claims across the outgoing links of a network consisting of N = 20, 50, 80 and 100 banks. Almost all regressor coefficients are found to be statistically significant for all the sizes of the network. We discern only two cases where regressor coefficients are found to be statistically insignificant and has to do with CATIN1 variable and one case that has to do with CATIN2. R-squared coefficients take on large values ranging from 74.9 to 80% and highlight the ability of our selected variables to explain financial distress in interbank networks.

The variable CATIN1 captures the initial effect defaulting bank i exerts on the network, whereas the magnitude of interconnectedness across the banks that comprise the interbank network is measured through parameter CATIN2. As we observe from Table 1, variable CATIN1 does not seem to affect much the dependent variable, whereas two regressor coefficients are found to be insignificant. Financial shocks will propagate into the defaulting bank’s counterparties along the network, erode their capital and make them more vulnerable to subsequent shocks. The magnitude of the positive relationship between CATIN2 and CATEND – the dependent variable - seems to increase as the size of the interbank network increases with the only exception being the N = 50 bank network segment which follows an autonomous path (although statistically insignificant). The increasing magnitude of the above relationship seems to cease as we move from the case of n = 80 banks to the case of n = 100 banks. This finding implies that as we move from smaller to larger network settings, systemic risk and the likelihood of contagion increases. However, when we move from the case of n = 80 banks to the case of n = 100 banks the likelihood of contagion seems to decreases. Figure 3 visually illustrates the extent of contagion as a function of the percentage loss of capital due to bank’s i default. It is shown that as the network size increases from small to medium sized networks, we observe that capital losses rises, confirming the findings from the regression model. As we can observe from Figure 3, as we move from the n = 80 interbank network scheme to n = 100 the likelihood of contagion seems to decrease since we have very few cases that cause systemic break downs and defaults.

Figure 3

Scenario 1: Heterogeneous Banks with homogeneous exposures. Extent of contagion (expressed as the total capital lost from the banking system due to the failure of at least one bank) as a function of the % initial loss of capital due to default of the first bank. Panels (a–d) show the relation between the % initial loss of capital due to default of the first bank and the extent of contagion across interbank networks with different number of banks

As expected, we also find that there is a positive relationship between the leverage of the network and the capital losses due to contagion, which is depicted by Figure 4. This result is in line with the findings of Nier et al. [7] who provide evidence that systemic risk increases when system-wide leverage increases. Highly leveraged banks in the interbank network are clearly more exposed to the risk of default on interbank loans. The greater the size of default on debt is, the larger the losses are that banks transmit to their neighbors, other things being equal. Thus, highly leveraged banks contribute more to systemic risk as they become a vehicle for transmitting shocks within the network. Moreover, it is shown that the magnitude of the positive relationship between the network’s leverage and contagion risk increases as we move from smaller to larger interbank networks (illustrated in Table 2) with the only exception being the n = 80 bank network scheme where the magnitude of the standardized coefficients seems to decrease.

Figure 4

Scenario 1: Heterogeneous Banks with homogeneous exposures. Extent of contagion (expressed as the total capital lost from the banking system due to the failure of at least one bank) as a function of the leverage of the system. Panels (a–d) show the relation between the leverage of the system and the extent of contagion across interbank networks with different number of banks

Our results also suggest that connectivity, expressed in our experiments as the outgoing⁴ of the first bank that defaults, has a negative effect on interbank contagion with the only exception being the case of n = 50 banks where we can observe a positive relationship between contagious defaults and connectivity.

Interestingly, as we move from small networks consisted of twenty banks to networks consisted of 50 banks the effect of connectivity to interbank contagion turns from negative to positive and after then connectivity keeps affect negatively the systemic risk of the network. Thus, as we move from network systems consisted of fifty banks to networks consisted of 100 banks this negative relationship seems to decrease. In relatively small interbank networks, a high level of connectivity will allow an efficient absorption of shocks, whereas in medium size networks the increased connectivity will spread the shock throughout the system, potentially leading to many default cascades. The link probability, that is assumed to be equal across all pairs, seems to contribute to the resilience of the system for small and medium size networks. However, as we move from medium to large size networks this effect turns negative to the resilience of the system as it seems to contribute positively to systemic risk.

Our regression analysis also shows that the COUNT variable which measures the number of rounds until no further bank defaults, has a positive impact on interbank contagion. Heterogeneity expressed as the variance of capital exhibits a negative and statistically significant relationship with interbank contagion, showing that size heterogeneity can have positive effects on the stability of an interbank network.

However, the positive magnitude seems to decrease as we move from small to large interbank networks. An interbank network consisting of banks of various sizes can more easily withstand a negative shock, therefore no institution becomes significant for either borrowing or lending. Furthermore, in such network both smaller and larger banks can act as shock absorbers when an initial shock hits the banking system, making contagion a less likely phenomenon. This finding is in line with the results of Iori et al. [6] concerning bank size heterogeneity.

Table 4 presents the regression results of the second scenario using the model described in Equation (16), where banking institutions with heterogeneous bank sizes are linked to one another via heterogeneous interbank claims. The regressor coefficients are statistically significant in almost all cases and the R-squared values are quite high and lie in the vicinity of 75–83%, highlighting the good explanatory power of the model.

Table 4 OLS regression analysis for Scenario 2 (Heterogeneous banks with heterogeneous exposures)

CATIN1 does not seem to impact much the dependent variable in all network segments and the regressor coefficients in the relatively large interbank networks becomes statistically insignificant. The magnitude of standardized coefficients is almost the same with the corresponding magnitude of those derived from the first scenario. In other words, an initial shock from defaulting bank i will spill over more easily in the network. Thus, the first bank defaulting has the dynamics to spread the initial shock and contaminate the entire interbank network. CATIN2 has a large positive impact on contagion risk, however, its magnitude fades away as we move from smaller to larger networks. It should also be highlighted that the CATIN2 coefficients are much larger than those recorded in the first scenario in all network sizes. An initial shock following the default of bank i seems to contribute much to a banking crisis scenario within small and medium-sized networks and the size of total capital losses is smaller than that documented in the first scenario. Figure 5 depicts the extent of contagion as a function of the percentage loss of capital due to default of the first bank and confirms the results recorded in Table 5.

Figure 5

Scenario 2: Heterogeneous Banks with heterogeneous exposures. Extent of contagion (expressed as the total capital lost from the banking system due to the failure of at least one bank) as a function of the % initial loss of capital due to default of the first bank. Panels (a–d) show the relation between the % initial loss of capital due to default of the first bank and the extent of contagion across interbank networks with different number of banks

Table 5 OLS regression analysis for Scenario 3 (Homogeneous banks with heterogeneous exposures)

The results also show that there still exists a positive relationship between leverage and contagion (illustrated in Figure 6); however, the coefficient estimates are larger in almost all cases than those recorded in the previous scenario. Moreover, the magnitude of the leverage coefficients decreases as the number of banks in the interbank network increases, with the only exception being the 100 bank network segment where one can observe a slight increase compared to the 80 bank network segment.

Figure 6

Scenario 2: Heterogeneous Banks with heterogeneous exposures. Extent of contagion (expressed as the total capital lost from the banking system due to the failure of at least one bank) as a function of the leverage of the system. Panels (a–d) show the relation between the leverage of the system and the extent of contagion across interbank networks with different number of banks

Results on connectivity are qualitatively similar to those of the first scenario, showing that connectivity negatively impacts contagion risk especially in small and medium interbank networks with the only exception being the 100 bank network segment which follows an autonomous path and is positively related to contagion (although statistically insignificant).

As far as the link probability is concerned, we can observe a different pattern from that of the first scenario. For small and large sized networks, link probability seems to contribute negatively to systemic risk while for medium sized networks there is a positive relationship between link probability and contagion. The number of rounds until no further bank defaults positively impacts contagion risk and contributes the most to total capital losses in the banking system when medium and large interbank networks are formed. Under this scenario, the heterogeneity allowed on both bank sizes and interbank exposures has had a great impact on the resilience of the network system. Heterogeneity impacts negatively on interbank contagion although its intensity decreases as the size of the network increases. Moreover, as we can see from the Table 4 heterogeneity of bank size contributes less to the resilience of the interbank network than heterogeneity of interbank exposures when it comes to small and medium sized networks.

The heterogeneity of interbank exposures acts as a diversification tool and contributes to a smaller extent to an unfolding crisis compared to the scenario where homogeneous banks are interconnected via heterogeneous exposures (shown in Table 4).

Table 5 depicts the results of the third scenario as described in Equation (17). In this scenario, we construct network systems where banks have the same equity size and unevenly distribute their exposures across creditor banks. We note that an initial shock fades away with the failure of the first bank and does not spillover to other banks within the network. This is mainly due to our choice of parameters regarding the equity of each bank, the links among banks and the interbank claims among creditor banks. In order to observe default cascades we relax our initial assumptions and lower the equity of each bank in the network system.

Specifically, each bank is now endowed with a balance sheet that consists of 25 units of equity and interbank claims among creditor banks are distributed in the following ranges: a _ij ∈ [0, 10], a _ij ∈ [0, 20], a _ij ∈ [0, 35]. Interbank exposures levels were kept the same as in Leventides et al. (2018). Moreover, we control the leverage of the system by setting the rule that the maximum leverage ratio of each network system cannot exceed seven. Similar to the previous scenarios, the regressor coefficients are statistically significant in all cases and the R-squared values are still large, in fact the largest of all three scenarios tested. Variable CATIN2 has a highly significant positive impact on systemic risk that fades away as the network system gets larger. The same observation holds for the level of connectivity in the banking system i.e. a strong negative impact on contagion risk that dissipates as N increases.

The leverage of the system has a positive impact on systemic risk and its magnitude decreases as the size of the network increases. Figures 7 and 8 illustrate the third scenario as a function of the percentage loss of capital due to default of the first bank in the network and as a function of leverage in the banking system, respectively. As in the previous cases, we find the number of rounds until no further bank defaults to affect contagion risk positively and statistically significantly, and such impact is magnified in relatively larger interbank networks. The heterogeneity of interbank exposures plays a significant role in the stability of the financial network especially in the medium sized interbank networks.

Figure 7

Scenario 3: Homogeneous banks with heterogeneous exposures (expressed as the total capital lost from the banking system due to the failure of at least one bank) as a function of the % initial loss of capital due to default of the first bank. Panels (a–d) show the relation between the % initial loss of capital due to default of the first bank and the extent of contagion across interbank networks with different number of banks

Figure 8

Scenario 3: Homogeneous banks with heterogeneous exposures. Extent of contagion (expressed as the total capital lost from the banking system due to the failure of at least one bank) as a function of the leverage of the system. Panels (a–d) show the relation between the leverage of the system and the extent of contagion across interbank networks with different number of banks

Finally, Table 6 depicts the results of the fourth scenario as described in Equation (18). In this scenario, we construct network systems where banks have the same equity size and interbank claims are evenly distributed across creditor banks. We acknowledge the fact that this scenario is a bit unrealistic as banks in real-world interbank networks do not have the same equity size and do not necessarily distribute their interbank claims evenly across their creditors. However, by testing a wide range of link probabilities between any two nodes, we are in a position to effectively examine the effect of different calibrations on systemic risk. Thus, although this scenario can be regarded as a special case with magnifying effects, it provides useful insights on interbank market resiliency during periods of stress.

Table 6 OLS regression analysis for Scenario 4 (Homogeneous banks with homogeneous exposures)

The variable CATIN2 has a strong positive impact on systemic risk that dissipates as the network system gets larger. Simulations show that this scenario yields qualitatively similar results with the previous three scenarios in relation to the leverage of the network, that is, leverage positively and significantly affects contagion risk (illustrated in Figure 10). However, in this scenario, we observe that this effect becomes stronger progressively when the number of constituent banks in the network increases. Figure 9 confirms the results recorded in the Table 6 concerning the relationship between the extent of contagion and the percentage loss of capital in the network. For instance, the likelihood of systemic breakdowns seems to decrease as we move from smaller to larger network systems since we have very few cases that cause large capital losses. Connectivity impacts negatively on interbank contagion, although this negative impact dissipates as the number of banks in the interbank networks increases. As expected, the link probability has the same negative impact as connectivity on the interbank contagion. Contrary to the previous findings concerning connectivity, the negative impact of the link probability on interbank contagion seems to scale up as we move from smaller to larger interbank networks (Figure 10).

Figure 9

Scenario 4: Homogeneous banks with homogeneous exposures (expressed as the total capital lost from the banking system due to the failure of at least one bank) as a function of the % initial loss of capital due to default of the first bank. Panels (a–d) show the relation between the % initial loss of capital due to default of the first bank and the extent of contagion across interbank networks with different number of banks

Figure 10

Scenario 4: Homogeneous banks with homogeneous exposures. Extent of contagion (expressed as the total capital lost from the banking system due to the failure of at least one bank) as a function of the leverage of the system. Panels (a–d) show the relation between the leverage of the system and the extent of contagion across interbank networks with different number of banks

Finally, the number of rounds until no further bank defaults affects contagion risk in a statistically significant manner especially when small interbank networks are considered.

The main intuition behind these results is that increasing connectivity on a homogeneous interbank network can reduce the frequency of contagion in case the first bank that defaults is less leveraged as the interbank network has the dynamics to absorb more easily the shock and thus the initial shock is dissipated at a faster rate. This is the case for small network systems. As the size of the network increase and the system gets more leveraged, the stabilizing force of connectivity weakens and default cascades prevail.

Tables 7, 8, 9, and 10 depict robustness tests on all four scenarios based on random sampling. We have performed second run Monte Carlo simulations in order to examine whether the new results differ from the previous ones, thus checking how random sampling affects our main conclusions. We observe qualitatively similar results in all four cases to those from the first run providing evidence that our findings are stable across different simulation scenarios.

Table 7 Robustness tests: OLS regression analysis for Scenario 1 (Heterogeneous banks with homogeneous exposures)

Table 8 Robustness tests: OLS regression analysis for Scenario 2 (Heterogeneous banks with heterogeneous exposures)

Table 9 Robustness tests: OLS regression analysis for Scenario 3 (Homogeneous banks with heterogeneous exposures)

Table 10 Robustness tests: OLS regression analysis for Scenario4 (Homogeneous banks with homogeneous exposures)

5 Conclusions

This paper investigates how complexity under a specific network structure, that has been extensively applied for the study of contagion in financial networks, affects interbank contagion. Similar to Leventides et al. [5], we explore the interplay between heterogeneity, balance sheet composition in the spreading of contagion using four basic scenarios, under an Erdős–Rényi network structure using a wide range of link probabilities between any two banks.

Our findings indicate a non-monotonic relation between diversification and interbank contagion across the different sizes of interbank networks for all scenarios tested. While for small or medium interbank networks, connectivity can act as an absorbing barrier, such that interbank systems of these sizes can withstand the initial shock, for large network systems connectivity does not seem to provide an effective shield against capital losses. Our results, for the four scenarios tested, indicate that small and thus more concentrated interbank network systems are more prone to contagion. In these cases, we observe that the size of total capital losses is, in most cases, larger than that documented in medium and large sized systems, which is in line with the findings of Nier et al. [7].

As far as heterogeneity is concerned, this enters in our experiments in the form of interbank claims and bank sizes. Our results clearly suggests that heterogeneity plays a significant role in the stability of the financial system. Similar to Leventides et al. [5], we still find that when heterogeneity is introduced with respect to the size of each bank, the system’s shock absorption capacity is enhanced. In addition, when we allow for heterogeneity on interbank exposures in our model, we observe additional resilience to the interbank network as an initial shock dissipates more easily than in the case of homogeneous interbank claims.

Finally, we should also justify the fact that we choose to work under an Erdős–Rényi network structure even if this network framework is not very realistic. In an such a network framework, where the probability of forming a link is homogeneous, the resulting network structure does not present marked heterogeneity. As we observed from all the four scenarios tested, the initial shock that hits the system seems to propagates into the system jeopardizing thus the stability of the entire system. This strengthens even more our arguments concerning the critical role that heterogeneity plays in the resilience of the financial system.