Keywords

1 Introduction

Big data has widely appeared in various fields, such as pattern recognition and machine learning [1, 2]. A common problem in data processing is that the data often contains some unimportant features [3, 4], which will increase the calculation cost and affect the effectiveness of model training [5, 6]. Therefore, feature selection has become one of the important research fields of machine learning in recent years.

Feature selection is used to delete redundant features for conducting dimensionality reduction [1], which can help model training and reduce the impact of “dimension disaster” [7]. Depending on the availability of sample labels, feature selection is divided into supervised, semi-supervised and unsupervised. Supervised feature selection [8] only uses labeled samples to train the model, and takes the structural relationship between labels and features to choose the important features, so as to explores the result of feature subset with the highest relevance to the label. Unsupervised feature selection [9,10,11] uses unlabeled sample training model, which selects the most representative features from the original feature set according to certain evaluation criteria. Semi-supervised feature selection [12, 13] uses a small number of labeled samples and a lot of unlabeled samples to achieve the optimal feature subset. These types of methods are efficient, because they can not only mine the global and local structure of all samples, but also utilize the small number of labels that providing category information. Therefore, this paper focus on research on semi-supervised feature selection.

Various semi-supervised feature selection methods have been proposed recently. For example, the typical feature selection based on classifier [14] (semi-supervised support vector machine, S3VM), it uses support vector machine (SVM) to tag no label samples, and then fused the “soft” label samples for model training. Zhao and Liu [15] proposed a semi-supervised regularized feature selection framework based on spectral learning to evaluate the correlation of features. In addition, Ren et al. [16] proposed a forward semi-supervised feature selection framework based on wrapper type, which combines forward selection with wrapper type to obtain the optimal feature subset. Chen et al. [17] combined the traditional fisher-score method to obtain the global optimal feature subset by the “soft" label of unlabeled samples with label propagation technology.

However, the existing semi-supervised feature selection methods have some defects. First, many semi-supervised feature selection researches focus on the lowest classification error rate without considering the misclassification cost. It has assumed that different misclassifications owning the equal costs [18], which may lead the model pays attention to samples which causes high misclassification losses, resulting in biases in the features selected by the learning model. Second, some advanced semi-supervised feature selection algorithms do not consider the structural information of the paired samples in each feature dimension, which can improve the performance of feature selection [19]. In addition, researchers believe that the correlation of a single candidate features is equal to the correlation of selected features, without considering the joint correlation of a pair of features, which will regard low-relevance features as salient features. Therefore, some low-correlation features are regarded as salient features.

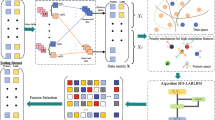
To solve the above problems, we propose semi-supervised feature selection based on cost-sensitive and structural information (SF_CSSI). The contributions of this paper are as follows:

  • In practical applications, misclassification has always existed, however, the cost of misclassification is always ignored by researchers. The proposed method considers the misclassification cost and sets different penalty costs for different categories samples. In contrast to conventional feature selection methods, we try to minimize the total cost rather than the total error rate, aiming to prevent disasters caused by mistakes with high costs.

  • In this paper, the proposed method converts each original feature vector into a structure-based feature graph representation, which contains structural information between sample pairs in each feature dimension, in order to preserve more meaningful information. Furthermore, the proposed method constructs feature information matrix to simultaneously maximize joint relevancy of different pairwise feature combinations in relation to the target feature graphs and minimize redundancy among selected features, so as to obtain feature subset with high correlation and low redundancy.

  • The method proposed in this paper has rarely been studied, because it considers misclassification cost, structural information and information measurement of paired features. Experiments prove that the proposed method in this paper can achieve better feature selection results on real datasets.

2 Approach

2.1 Notations

In this paper, matrices are written as boldface uppercase letters, vectors are written as boldface lowercase letters and scalars are written as normal italic letters. For matrix \(\mathbf{{X}}\), \({x_{i,j}}\) represents the element in the i-th row and j-th column of \(\mathbf{{X}}\). The Frobenius norm of matrix \(\mathbf{{X}} \in \mathbb {R}^{n \times d}\) is defined as \({\left\| \mathbf{{X}} \right\| _F} = \sqrt{\sum \nolimits _{i,j} {x_{_{i,j}}^2} } \). The \({l_{2,1}}\)-norm of matrix \(\mathbf{{X}}\) is defined as \({\left\| \mathbf{{X}} \right\| _{2,1}} = \sum \nolimits _{i = 1}^n {\sqrt{\sum \nolimits _{j = 1}^d {x_{_{ij}}^2} } }\). For vector \(\mathbf{{x}}\), its \({l_1}\)-norm is defined \({\left\| \mathbf{{x}} \right\| _1} = \sum \nolimits _{i = 1}^n {\left| {{x_i}} \right| }\). The symbol \( \odot \) denotes multiplication of corresponding elements and \(tr\left( \mathbf{{X}} \right) \) represents the trace of matrix \(\mathbf{{X}}\).

In semi-supervised learning, the data set consists of two parts: labeled data \({\mathbf{{X}}_L} = \left( {x{}_1,{x_2}, \ldots ,{x_l}} \right) \) and unlabeled data \({\mathbf{{X}}_U} = \left( {x{}_{l+1},{x_{l+2}}, \ldots ,{x_{l + u}}} \right) \), \(u = n - l\), n represents the number of samples, l represents the number of labeled samples, u represents the number of unlabeled samples. The corresponding labels is \({\mathbf{{Y}}_L} = {\left( {y{}_1,{y_2}, \ldots ,{y_l}} \right) ^T}\) and the label of \({\mathbf{{Y}}_U} = {\left( {y{}_{l + 1},{y_{l + 2}}, \ldots ,{y_{l + u}}} \right) ^T}\) is unknown.

2.2 Cost-Sensitive Feature Selection

Given data set \(\mathbf{{X}} = \left[ {{\mathbf{{x}}_1},{\mathbf{{x}}_2}, \cdots ,{\mathbf{{x}}_n}} \right] \in \mathbb {R}^{n \times d}\), n represents the number of samples, d represents the features of each sample. The traditional feature selection imposes a sparsity penalty in the objective function, which makes the selected features more sparse and more discriminative. The objective function of traditional feature selection [9] is defined as:

$$\begin{aligned} \mathop {\mathrm{{min}}}\limits _\mathbf{{W}} \left\| {\mathbf{{Y}} - \mathbf{{XW}}} \right\| _F^2 + \lambda {\left\| \mathbf{{W}} \right\| _{2,1}} \end{aligned}$$
(1)

However, cost-sensitive learning is embedded into feature selection framework because the misclassification problem often occurs in practical applications. Cost-sensitive learning assigns different cost parameters to different types of samples, without loss of generality, so the specified cost matrix is introduced into the feature selection framework. The traditional cost-sensitive feature selection objective function [20] is defined as:

$$\begin{aligned} \mathop {\mathrm{{min}}}\limits _\mathbf{{W}} {\left\| {\mathbf{{(}}{\mathbf{{X}}^T}{} \mathbf{{W - Y)}} \odot \mathbf{{C}}} \right\| _{2,1}} + \lambda {\left\| \mathbf{{W}} \right\| _{2,1}}, \end{aligned}$$
(2)

where \(\mathbf{{W}} \in {\mathbb {R}^{d \times m}}\) represents the feature weight matrix, \(\mathbf{{Y}} \in {\mathbb {R}^{n \times m}}\) represents labels, \(\mathbf{{C}} \in {{\mathbb {R}}^{n \times m}}\) represents cost matrix, \({\lambda }\) represents the penalty coefficient.

2.3 Feature Selection with Graph Structural Information

The structural information can provide more abundant representation but few researchers pay attention to these between the features in each pairs of samples.

Therefore, each feature vector is transformed into a feature graph structure, which encapsulates the pairwise relationship between samples. In addition, the information theory criterion of Jensen-Shannon divergence is used to measure the joint correlation between different paired feature combinations and target labels. The specific process is as follows.

Let \(\mathbf{{X}} = \left\{ {{{\mathbf{{f}}_1}}\mathrm{{,}} \ldots \mathrm{{,}}{{{\mathbf{{f}}_i}}}\mathrm{{,}} \ldots \mathrm{{,}}{\mathbf{{f}}_N}} \right\} \in {\mathbb {R}^{{M} \times {N}}}\) represents a data set of M samples and N features. Each original feature vector \({{\mathbf{{f}}_i}} = {\left( {{f_{i1}}\mathrm{{,}} \ldots \mathrm{{,}}{f_{ia}}\mathrm{{,}} \ldots \mathrm{{,}}{f_{ib}}\mathrm{{,}} \ldots \mathrm{{,}}{f_{iM}}} \right) ^T}\)is transformed into a feature graph \({\mathbf{{G}}_i}\left( {{V_i}\mathrm{{,}}{E_i}} \right) \), where vertex \({v_{ia}} \in {V_i}\) represents the a-th sample \({f_{ia}}\) in feature \({{\mathbf{{f}}_i}}\) (i.e., each vertex represents a sample), edge \(\left( {{v_{ia}}\mathrm{{,}}{v_{ib}}} \right) \in {E_i}\) represents the weight of the a-th sample and the b-th sample (i.e., the edge represents the correlation between a pair of samples in the corresponding feature dimension). In addition, we also construct a graph structure for the target feature \(\mathbf{{Y}}\). For classification problems, \(\mathbf{{Y}}\) are discrete value \(c \in \left\{ {\mathrm{{1,2,}} \ldots \mathrm{{,}}m} \right\} \). Therefore, we calculate the continuous value of each discrete target feature \({{\mathbf{{f}}_i}}\) as \(\mathop {{\mathbf{{f}}_i}}\limits ^ \wedge = {\left( {\mathop {{f_{i1}}}\limits ^ \wedge \mathrm{{,}} \ldots \mathrm{{,}}\mathop {{f_{ia}}}\limits ^ \wedge \mathrm{{,}} \ldots \mathrm{{,}}\mathop {{f_{ib}}}\limits ^ \wedge \mathrm{{,}} \ldots \mathrm{{,}}\mathop {{f_{iM}}}\limits ^ \wedge } \right) ^{T}}\), \(\mathop {{f_{ia}}}\limits ^ \wedge \) represents the a-th sample in \(\mathop {{\mathbf{{f}}_i}}\limits ^ \wedge \). When the \({f_{ia}}\) in \({{\mathbf{{f}}_i}}\) belongs to class m, \(\mathop {{f_{ia}}}\limits ^ \wedge \) is the mean value of all class m samples in \({{\mathbf{{f}}_i}}\). Similarly, we construct the graph structure of the target feature \(\mathop {{\mathbf{{f}}_i}}\limits ^ \wedge \) as \(\mathop {{\mathbf{{G}}_i}}\limits ^ \wedge \left( {{{\mathop V\limits ^ \wedge }_i}\mathrm{{,}}\mathop {{E_i}}\limits ^ \wedge } \right) \). \(\mathop {{v_{ia}}}\limits ^ \wedge \in \mathop {{V_i}}\limits ^ \wedge \) represents the a-th sample in target feature \(\mathop {{\mathbf{{f}}_i}}\limits ^ \wedge \), \( \left( {\mathop {{v_{ia}}}\limits ^ \wedge \mathrm{{,}}\mathop {{v_{ib}}}\limits ^ \wedge } \right) \in \mathop {{E_i}}\limits ^ \wedge \) is the weighted edge connecting the a-th sample and the b-th sample of \(\mathop {{\mathbf{{f}}_i}}\limits ^ \wedge \). This paper uses Euclidean distance to calculate the relationship between pairs of feature samples, that is, the weight of \({f_{ia}}\) and \({f_{ib}}\) can be expressed as:

$$\begin{aligned} \omega \left( {{v_{ia}}\mathrm{{,}}{v_{ib}}} \right) = \sqrt{{{\left( {{f_{ia}} - {f_{ib}}} \right) }^2}} \end{aligned}$$
(3)

Similiarly, the weight of edge \( \left( {\mathop {{v_{ia}}}\limits ^ \wedge \mathrm{{,}}\mathop {{v_{ib}}}\limits ^ \wedge } \right) \in \mathop {{E_i}}\limits ^ \wedge \) in \(\mathop {{\mathbf{{G}}_i}}\limits ^ \wedge \left( {{{\mathop V\limits ^ \wedge }_i}\mathrm{{,}}\mathop {{E_i}}\limits ^ \wedge } \right) \) is expressed as follows:

$$\begin{aligned} \omega \left( {\mathop {{v_{ia}}}\limits ^ \wedge \mathrm{{,}}\mathop {{v_{ib}}}\limits ^ \wedge } \right) = \sqrt{{{\left( {{\mu _{ia}} - {\mu _{ib}}} \right) }^2}}, \end{aligned}$$
(4)

where \({\mu _{ia}}\) is the mean value of all samples in \({{\mathbf{{f}}_i}}\) from the same class m.

Jensen Shannon divergence (JSD) is used to measure the divergence between two probability distributions [21]. Give two (discrete) probability distributions \({\mathcal{P}} = \left( {{p_1}\mathrm{{,}} \ldots \mathrm{{,}}{p_a}\mathrm{{,}} \ldots {p_A}} \right) \) and \({\mathcal{K}} = \left( {{k_1}\mathrm{{,}} \ldots \mathrm{{,}}{k_b}\mathrm{{,}} \ldots {k_B}} \right) \). The JSD between \({\mathcal{P}}\) and \({\mathcal{K}}\) is defined as:

$$\begin{aligned} {D_{\mathrm{{JS}}}}\left( {{{\mathcal{P}}},{{\mathcal{K}}}} \right) = {H_S}\left( {\frac{{{\mathcal{P}} + {\mathcal{K}}}}{2}} \right) - \frac{1}{2}{H_S}\left( {\mathcal{P}} \right) - \frac{1}{2}{H_S}\left( {\mathcal{K}} \right) , \end{aligned}$$
(5)

where \({H_S}\left( {\mathcal{P}} \right) = \sum \nolimits _{i = 1}^A {{p_i}\log {p_i}} \) is the Shannon entropy of probability distribution \({\mathcal{P}}\). In the literature [22], the JSD has been used as a means of measuring the information theoretic dissimilarity between graphs associated with their probability distributions. In this paper, we focus on the similarity between graph-based feature representations. We use the negative exponent of \({D_{\mathrm{{JS}}}}\left( {{{\mathcal{P}}},{{\mathcal{K}}}} \right) \) to calculate the similarity \({I_S}\) between probability distributions \({\mathcal{P}}\) and \({\mathcal{K}}\), so:

$$\begin{aligned} {I_S}\left( {{\mathcal{P}},{\mathcal{K}}} \right) = \mathrm{{exp}}\left\{ { - {D_{\mathrm{{JS}}}}\left( {{\mathcal{P}},{\mathcal{K}}} \right) } \right\} \end{aligned}$$
(6)

The information theoretic function is used to evaluate the relevance between different feature combination and target labels to achieve the maximum correlation and minimum redundancy standards. For a set of N features \( {{{\mathbf{{f}}_1}}\mathrm{{,}} \ldots \mathrm{{,}}{{{\mathbf{{f}}_i}}}\mathrm{{,}} \ldots \mathrm{{,}}{\mathbf{{f}}_N}} \) and related continuous target feature \(\mathbf{{Y}}\), the correlation degree of feature pair \(\left\{ {{\mathbf{{f}}_i},{\mathbf{{f}}_j}} \right\} \) is expressed as follows:

$$\begin{aligned} {U_{{f_i},{f_j}}}= \frac{{{I_s}\left( {{\mathbf{{G}}_i}{} \mathbf{{,}}\mathop {{\mathbf{{G}}}}\limits ^ \wedge } \right) + {I_s}\left( {{\mathbf{{G}}_j}{} \mathbf{{,}}\mathop {{\mathbf{{G}}}}\limits ^ \wedge } \right) }}{{{I_s}\left( {{\mathbf{{G}}_i}{} \mathbf{{,}}{\mathbf{{G}}_j}} \right) }}, \end{aligned}$$
(7)

where \({{I_s}}\) is the JSD based similarity measure of information theory defined in Eq. 6. \({{I_s}\left( {{\mathbf{{G}}_i}{} \mathbf{{,}}\mathop {{\mathbf{{G}}}}\limits ^ \wedge } \right) }\) represents the correlation measures of feature \({\mathbf{{f}}_i}\) with target feature \(\mathbf{{Y}}\). \({{I_s}\left( {{\mathbf{{G}}_j}{} \mathbf{{,}}\mathop {{\mathbf{{G}}}}\limits ^ \wedge } \right) }\) represents the correlation measures of feature \({\mathbf{{f}}_j}\) with target feature \(\mathbf{{Y}}\). \({I_s}\left( {{\mathbf{{G}}_i}{} \mathbf{{,}}{\mathbf{{G}}_j}} \right) \) denotes the redundancy of paired feature \(\left\{ {{\mathbf{{f}}_i},{\mathbf{{f}}_j}} \right\} \). Therefore, \({U_{{f_i},{f_j}}}\) is large if and only if \({{I_s}\left( {{\mathbf{{G}}_i}{} \mathbf{{,}}\mathop {{\mathbf{{G}}}}\limits ^ \wedge } \right) }\) \(+\) \({{I_s}\left( {{\mathbf{{G}}_j}{} \mathbf{{,}}\mathop {{\mathbf{{G}}}}\limits ^ \wedge } \right) }\) is large and \({I_s}\left( {{\mathbf{{G}}_i}{} \mathbf{{,}}{\mathbf{{G}}_j}} \right) \) is small. This indicates that the pairwise feature \(\left\{ {{\mathbf{{f}}_i},{\mathbf{{f}}_j}} \right\} \) is informative and less redundant.

Given the feature information matrix \(\mathbf{{U}}\) and d-dimensional feature vector \(\mathbf{{w}}\). The feature subset is identified by solving the maximization problem of the following formula:

$$\begin{aligned} \mathrm{{max }}~f\mathrm{{(}}{} \mathbf{{w}}\mathrm{{) = }}\mathop {\mathrm{{max}}}\limits _{\mathbf{{w}} \in \mathbb {R}^d} {\mathbf{{w}}^T}{} \mathbf{{Uw}}, \end{aligned}$$
(8)

where \(\mathbf{{w}} \in \mathbb {R}^d\), \(\mathbf{{w}} = {\left( {{{w}_1},{w_2}, \cdots , {{w_i}}, \cdots , {{w_n}}} \right) ^T}\), \({{w_i}} > 0\), \({{w_i}}\) represents the correlation coefficient of the i-th feature.

2.4 Mathematical Formulation

The purpose of our proposed method is to improve the performance of feature selection through structural information and misclassification costs when the data does not have a large number of labels. Therefore, we combine cost-sensitive and Eq. 8 to propose semi-supervised feature selection based on cost-sensitive and structural information. The specific mathematical expression is as follows:

$$\begin{aligned} \mathop {\min }\limits _\mathbf{{w}} {\alpha _1}tr({\mathbf{{w}}^T}{\mathbf{{X}}^T}{} \mathbf{{LXw}}) + \sum \limits _{i = 1}^l {\left\| {{x_i}{} \mathbf{{w}} - {y_i}} \right\| _\mathrm{{2}}^2} {c_i} + {\alpha _2}||\mathbf{{w}}|{|_1} - {\alpha _3}{\mathbf{{w}}^T}{} \mathbf{{Uw}} \end{aligned}$$
(9)

The first term represents the learning of local proximity structure, which helps the model to select a representative feature subset by maintaining the local structure of the samples. \(\mathbf{{w}}\) represents the feature coefficient vector, \(\mathbf{{L}}\) is the Laplacian matrix, \(\mathbf{{L}} = \mathbf{{D}} - \mathbf{{A}}\), where \(\mathbf{{D}}\) is a diagonal matrix, the diagonal element satisfies \({D_{ii}} = \sum \nolimits _{j = 1}^n {{A_{ij}}} \) and \(\mathbf{{A}}\) is the affinity matrix, if \(i \ne j\), \({A_{ij}} = \exp ( - \frac{{||{x_{^i}} - {x_{^j}}||_2^2}}{{2{\sigma ^2}}})\); otherwise, \({A_{ij}} = 0\). The cost \({c_i}\) represents the cost, the second term indicates that the loss of the original feature is combined with the cost to obtain the misclassification cost loss. Since we judge the misclassification result based on the label sample, we only use the labeled sample to calculate the misclassification loss. The third term \({\left\| \mathbf{{w}} \right\| _1}\) represents the sparse regular term, which uses the \({l_1}\)-norm to shrink some coefficients to zero. The fourth term encourages the selected features to be jointly more relevant with the target while maintaining less redundancy between features, \({\alpha _1}\), \({\alpha _2}\) and \({\alpha _3}\) are the penalty coefficients.

2.5 Optimization

In order to optimize, Eq. 9 can be rewritten as follows:

$$\begin{aligned} \begin{aligned} \mathop {\mathrm{{min}}}\limits _\mathbf{{w},\mathbf{{Q}}} {\alpha _1}tr\left( {{\mathbf{{w}}^T}{\mathbf{{X}}^T}{} \mathbf{{LXw}}} \right) + tr\left( {{{\left( {{\mathbf{{X}}_L}{} \mathbf{{w}} - {\mathbf{{Y}}_L}} \right) }^T}{} \mathbf{{C}}\left( {{\mathbf{{X}}_L}{} \mathbf{{w}} - {\mathbf{{Y}}_L}} \right) } \right) \\ +\,\,{\alpha _2}tr\left( {{\mathbf{{w}}^T}{} \mathbf{{Qw}}} \right) - {\alpha _3}{\mathbf{{w}}^T}{} \mathbf{{Uw}}, \end{aligned} \end{aligned}$$
(10)

where \(\mathbf{{Q}}\) is the diagonal matrix. We use the idea of iterative learning to optimize the objective function, that is, update \(\mathbf{{w}}\) by fixing \(\mathbf{{Q}}\) and update \(\mathbf{{Q}}\) by fixing \(\mathbf{{w}}\), until Eq. 9 converges, so that the optimal solution of weight vector \(\mathbf{{w}}\) can be obtained.

  • Update \(\mathbf{{w}}\) by fixing \(\mathbf{{Q}}\)

When \(\mathbf{{Q}}\) is fixed, Eq. 10 can be regarded as a function of \(\mathbf{{w}}\):

$$\begin{aligned} \begin{aligned} L\left( \mathbf{{w}} \right) = {\alpha _1}tr\left( {{\mathbf{{w}}^T}{\mathbf{{X}}^T}{} \mathbf{{LXw}}} \right) + tr\left( {{{\left( {{\mathbf{{X}}_L}{} \mathbf{{w}} - {\mathbf{{Y}}_L}} \right) }^T}{} \mathbf{{C}}\left( {{\mathbf{{X}}_L}{} \mathbf{{w}} - {\mathbf{{Y}}_L}} \right) } \right) \\+\,\,{\alpha _2}tr\left( {{\mathbf{{w}}^T}{} \mathbf{{Qw}}} \right) - {\alpha _3}{\mathbf{{w}}^T}{} \mathbf{{Uw}} \end{aligned} \end{aligned}$$
(11)

We take the derivative of \(\mathbf{{w}}\) in Eq. 11 and make it equal to zero:

$$\begin{aligned} \frac{{\partial L}}{{\partial \mathbf{{w}}}} = 2{\alpha _1}{\mathbf{{X}}^T}{} \mathbf{{LXw}} + 2{\mathbf{{X}}_L}^T\mathbf{{C}}{\mathbf{{X}}_L}{} \mathbf{{w}} - 2{\mathbf{{X}}_L}^T\mathbf{{C}}{\mathbf{{Y}}_L} + 2{\alpha _2}{} \mathbf{{Qw}} - 2{\alpha _3}{} \mathbf{{Uw}} = 0 \end{aligned}$$
(12)

According to Eq. 12, it is solved as follows:

$$\begin{aligned} \mathbf{{w}} = {\left( {2{\alpha _1}{\mathbf{{X}}^T}{} \mathbf{{LX}} + 2{\mathbf{{X}}_L}^T\mathbf{{C}}{\mathbf{{X}}_L} + 2{\alpha _2}{} \mathbf{{Q}} - 2{\alpha _3}{} \mathbf{{U}}} \right) ^{ - 1}}2{\mathbf{{X}}_L}^T\mathbf{{C}}{\mathbf{{Y}}_L} \end{aligned}$$
(13)

  • Update \(\mathbf{{Q}}\) by fixing \(\mathbf{{w}}\)

When \(\mathbf{{w}}\) is fixed, Eq. 10 can be regarded as:

$$\begin{aligned} \mathop {\mathrm{{min}}}\limits _\mathbf{{Q}} {\alpha _2}tr\left( {{\mathbf{{w}}^T}{} \mathbf{{Qw}}} \right) \end{aligned}$$
(14)

By setting the partial derivative of the above function with respect to \(\mathbf{{Q}}\) as 0 and according to the article [23], it is solved as follows:

$$\begin{aligned} {Q_{ii}} = \frac{1}{{2\left| {{w_i}} \right| }}, \end{aligned}$$
(15)

where \(\mathbf{{Q}}\) is a diagonal matrix and \({Q_{ii}} = \frac{1}{{2\left| {{w_i}} \right| }}\) is the diagonal element.

figure a

2.6 Convergence Analysis

Let \(\mathbf{{w}}\) and \(\mathbf{{Q}}\) be \({\mathbf{{w}}^{\left( \mathrm{{t}} \right) }}\) and \({\mathbf{{Q}}^{\left( \mathrm{{t}} \right) }}\) in the t-th iteration, and Eq. 10 can be rewritten as:

$$\begin{aligned} \begin{aligned} {E}\left( {{\mathbf{{w}}^{\left( t \right) }}{} \mathbf{{,}}{\mathbf{{Q}}^{\left( t \right) }}} \right) \,=\,{\alpha _1}tr\left( {{{\left( {{\mathbf{{w}}^{\left( t \right) }}} \right) }^T}{\mathbf{{X}}^T}{} \mathbf{{LX}}{\mathbf{{w}}^{\left( t \right) }}} \right) + tr\left( {{{\left( {{\mathbf{{X}}_L}{\mathbf{{w}}^{\left( t \right) }} - {\mathbf{{Y}}_L}} \right) }^T}{} \mathbf{{C}}\left( {{\mathbf{{X}}_L}{\mathbf{{w}}^{\left( t \right) }} - {\mathbf{{Y}}_L}} \right) } \right) \\+\,\,{\alpha _2}tr\left( {{{\left( {{\mathbf{{w}}^{\left( t \right) }}} \right) }^{T}}{\mathbf{{Q}}^{\left( t \right) }}{\mathbf{{w}}^{\left( t \right) }}} \right) - {\alpha _3}{\left( {{\mathbf{{w}}^{\left( t \right) }}} \right) ^{T}}{} \mathbf{{U}}{\mathbf{{w}}^{\left( t \right) }} \end{aligned} \end{aligned}$$
(16)

Because the objective function \({E}\left( {{\mathbf{{w}}^{\left( t \right) }}{} \mathbf{{,}}{\mathbf{{Q}}^{\left( t \right) }}} \right) \) is a convex optimization problem about \(\mathbf{{w}}\), we have the following inequality:

$$\begin{aligned} {E}\left( {{\mathbf{{w}}^{\left( t+1 \right) }}{} \mathbf{{,}}{\mathbf{{Q}}^{\left( {t} \right) }}} \right) \le {E}\left( {{\mathbf{{w}}^{\left( t \right) }}{} \mathbf{{,}}{\mathbf{{Q}}^{\left( t \right) }}} \right) \end{aligned}$$
(17)

According to the article [23], we know that Eq. 14 is convergent, so we can deduce that Eq. 10 is convergent about \(\mathbf{{Q}}\), so we express the convergence as the following inequality:

$$\begin{aligned} {E}\left( {{\mathbf{{w}}^{\left( {t + 1} \right) }}{} \mathbf{{,}}{\mathbf{{Q}}^{\left( {t+1 } \right) }}} \right) \le {E}\left( {{\mathbf{{w}}^{\left( t+1 \right) }}{} \mathbf{{,}}{\mathbf{{Q}}^{\left( {t} \right) }}} \right) \end{aligned}$$
(18)

Combining Eq. 17 and Eq. 18, we can get the inequality:

$$\begin{aligned} {E}\left( {{\mathbf{{w}}^{\left( {t + 1} \right) }}{} \mathbf{{,}}{\mathbf{{Q}}^{\left( {t + 1} \right) }}} \right) \le {E}\left( {{\mathbf{{w}}^{\left( t \right) }}{} \mathbf{{,}}{\mathbf{{Q}}^{\left( t \right) }}} \right) \end{aligned}$$
(19)

Equation 16 is non-increasing at each iteration according to Eq. 19. Therefore, the proposed Algorithm 1 is convergence.

3 Experiments

In this section, we evaluated our proposed SF_CSSI and other six comparison methods on eight data sets. Specially, we first employed each feature selection method to choose the new feature subsets from original data sets, and then utilized support vector machine classification to evaluate the selected subsets.

3.1 Datasets and Comparison Methods

The data sets (i.e., madelon, SECOM, chess, isolet, Hill-with, Hill-without, musk and sonar) are from UCI Machine Learning RepositoryFootnote 1. We summarized the detail of all data sets in Table 1.

Table 1. Summarization of data sets.
Full size table

We compared our proposed method with six comparison methods and the details of them are listed as follow:

  • Cost-Sensitive Laplacian Score (CSLS [24]) uses Laplacian graphs and the cost of misclassification between classes to score each feature individually.

  • Semi-supervised feature selection based on joint mutual information (Semi-JMI [25]) uses the redundancy between features and the correlation between features and labels to complete feature selection.

  • Semi-supervised feature selection based on information theory method (Semi-IMIM [25]) only uses the correlation between features and labels to complete feature selection.

  • Cost-Sensitive Feature Selection via F-Measure Optimization Reduction (CSFS [20]) introduces cost sensitivity to select features, which optimizes F-measure instead of accuracy to take class imbalance issue into account.

  • Cost-sensitive feature selection via the \({l_{2,1}}\)-norm (CSEFS [26]) combines \({l_{2,1}}\)-norm minimization regularization and loss term of embedding misclassification cost to select feature subset.

  • Semi-supervised Feature Selection via Rescaled Linear Regression (RLSR [17]) uses a set of scale factors to adjust regression coefficients, then uses regression coefficients to rank features.

Table 2. Total cost (cost ± std) of misclassification on eight data sets. Bold numbers indicate the best results.
Full size table

3.2 Experimental Settings

The experiment of this paper is implemented with the MATLAB 2018a under Windows 10 system. Referring to [27] article’s method, we can divide the data set into three parts: labeled sample set (L), unlabeled sample set (U), and test sample set (T). For each of data sets, the labeled samples were randomly selected with the given ratio \(\left\{ {\mathrm{{10}}\%,20\%,30\% } \right\} \).

Table 3. The value of specificity on eight data sets. Bold numbers indicate the best results.
Full size table

We use 10-fold cross-validation to generate training sample set and test sample set, then randomly select \(\mathrm {L}\) and \(\mathrm {U}\) from the training sample set for training, and finally use \(\mathrm {T}\) to test the performance of different methods. All algorithms perform 10 times 10-fold cross-validation and take the average of the 10 experimental results as the final total cost, which reduce the accidental occurrence. We set the parameters \(\alpha _1\), \(\alpha _2\) and \(\alpha _3\) in Eq. 9 in range of \(\left\{ {{{10}^{ - 3}},{{10}^{ - 1}},\mathrm{{ }}...\mathrm{{ }},\mathrm{{ 1}}{\mathrm{{0}}^1},{{10}^3}} \right\} \). For other comparison methods, we set these according to their corresponding literature.

Table 4. The value of sensitivity on eight data sets. Bold numbers indicate the best results.
Full size table

The total cost, specificity and sensitivity are used as evaluation indicators to evaluate the performance of all methods on eight data sets.

The total cost is calculated as follows:

$$\begin{aligned} {Total~~Cost} = \mathrm{{sum}}\left( {c_{i}} \right) , \end{aligned}$$
(20)
Fig. 1.
figure 1

The total cost of different methods under different labeled samples, at eight data sets while \(cos{t_1}\) = 10, \(cos{t_2}\) = 25.

Full size image
$$\begin{aligned} {c_{i}} = \left\{ \begin{array}{l} {{cos}}{{{t}}_1} \quad \mathrm{{or}\quad {cos}}{{{t}}_2}\qquad \mathrm{{,~predicted~~label}} \ne \mathrm{{true~~label}}\\ 0\qquad \qquad \qquad \qquad \,\,\,\, \mathrm{{, \,\, otherwise}} \end{array} \right. , \end{aligned}$$
(21)

where \({c_{i}}\) represents the misclassification cost of a sample. If the predicted label is equal to the true label, the cost of \({c_{i}}\) is 0, otherwise, the cost of \({c_{i}}\) is equal to \(cos{t_1}\) or \(cos{t_2}\) (\(cos{t_1}\) and \(cos{t_2}\) represent the costs of being judged as positive and negative samples, respectively).

For a binary classification, there are four possible results: TP (True Positive) is positive instances correctly classified and TN (True Negative) is negative instances correctly classified. FP (False Positive) is negative instances incorrectly classified and FN (False Negative) is positive instances misclassified.

Specificity refers to the proportion of samples that are actually negative which are judged to be negative. It can be calculated by the following formula:

$$\begin{aligned} {specificity} = \frac{{{{TN}}}}{{{{FP}} + {{TN}}}} \end{aligned}$$
(22)

Sensitivity refers to the proportion of samples that are actually positive which are judged to be positive. It can be calculated by the following formula:

$$\begin{aligned} {sensitivity} = \frac{{{{TP}}}}{{{{TP}} + {{FN}}}} \end{aligned}$$
(23)

3.3 Experiment Results and Analysis

In this experiment, we reported the cost, specificity and sensitivity of all methods on eight UCI datasets in Table 2, Table 3 and Table 4 under different cost value settings and listed our observations as follows. In addition, we use a line chart to show the changing trend of the total cost under different proportions of labeled samples. It can be seen from Fig. 1.

From Table 2, we can know that the proposed SF_CSSI method outperformed other methods on most cases. Especially, on the chess data set, the total cost of SF_CSSI has reduced by 75\(\%\) compared with the second best approach Semi-JMI, when \(cos{t_1}\) = 10 and \(cos{t_2}\) = 25. When \(cos{t_1}\) = 25 and \(cos{t_2}\) = 10, 31\(\%\) reduction was achieved by the proposed method SF_CSSI on the Hill-without data set, compared to the second best approach CSFS.

From Table 3 and Table 4, the proposed model has high specificity and sensitivity. The highest specificity was obtained on SECOM and Hill-without data sets. The highest sensitivity was obtained on isolet and Hill-without data sets compared with other methods. In addition, specificity and sensitivity are commonly used diagnostic methods in clinical practice. The higher the value is, the more real, reliable and practical the diagnosis result will be.

From Fig. 1, the more labeled data we have, the lower cost we can achieve, in most cases. We also notice that SF_CSSI outperformed other CSLS, CSFS and CSEFS methods on almost all cases, which indicates that CSLS, CSFS and CSEFS can be improved with unlabeled data. This verifies the effectiveness of the semi-supervised feature selection method. In addition, the proposed method has the minimum total cost on most cases, especially in Hill-without data set.

3.4 Conclusion

This paper considers the misclassification and the structural information of the paired samples on each feature dimension. In addition, the information theory method is used to introduce a feature information matrix to simultaneously maximize joint relevancy of different pairwise feature combinations in relation to the target feature graphs and minimize redundancy among selected features. Compared with previous research on semi-supervised feature selection, this paper comprehensively considers the cost of misclassification, the structure information of paired samples on the feature dimension, and the information relationship of paired features. In general, it is more interpretable and generalizable for our method than others in this paper. Experiments on 8 real data sets show that the proposed method has better feature selection results.

In future work, we will try to extend our method to conduct a cost-sensitive multi-class classification.