Keywords

1 Introduction

A water supply network is an infrastructure responsible for bringing drinking water to consumers. Currently, the population is growing, specifically in urban areas. This causes new challenges regarding the construction and enlargement of this utility. The design and building of extensions of such water supply networks is a hard and expensive task. Therefore, efficient planning may result in substantial cost reduction.

The optimal design of a water supply network is a problem in which the demand of a set of consumer points must be covered with specific conditions of pressure and flow. Generally, network characteristics are previously established as well as consumers’ geographical locations and the connections between them, representing the future pipes’ settlement. Moreover, the demand of each consumer area is usually estimated using the population growing estimation and the per capita consumption. Consequently, the problem is the election of the pipes’ diameters, which have to be chosen among a commercially available set, while technical and demand requirements are fulfilled.

2 State of the Art

As previously stated, the intrinsic characteristics of hydraulic systems and the discrete nature of some of their variables make this problem a non-linear mixed-integer problem. One of the first attempts to solve it was by implementing a method named linear programming gradient (LPG) which decomposes the original problem into two subproblems, one linear and another one non-linear [1, 2]. It is an iterative process in which the flows are fixed and then, the pipes are divided into various segments with different diameters. The main problem of this methodology is that some segments take a diameter in more than 95% of their lengths and a different one to the rest, which is unrealistic. The other approach is to use linear programming taking the diameters as continuous variables. Once the problem is solved, they are transformed into similar commercial diameters [3]. However, these transformations could suppose the loss of the optimum.

To face this challenge, metaheuristics emerged as methods capable of treating diameters as discrete variables and working with non-linear constraints. For this reason, they can solve this non-linear mixed-integer problem more realistically. Metaheuristics are iterative processes that explore the search space to find the global optimum. Although it is not always found, satisfactory solutions are usually achieved in a short time. These methods try to emulate phenomena as behaviors of humans or animals or other natural processes. They can be classified according to their basis. Some of them are based on populations, as the genetic algorithm (GA), the particular swam optimisation (PSO), or the memetic algorithm (MA). While others are based on solutions and their trajectories, as the simulated annealing (SA) or the tabu search (TS).

Recently, several authors have applied metaheuristics to plan the design of water supply networks. For instance, SA and GA are used to solve the problem achieving significant improvement in the quality of the solution and the resolution time [4]. PSO was chosen to address the problem using a model whose objective function included penalty costs [5]. Meirelles et al. [6] have recently used the same algorithm but adding to the general objective of minimizing total costs, the benefits of energy production that would involve the installation of recuperators in the network. This makes sense when the study network is located in an area with large slopes.

Another option is to solve a model which includes penalization costs for reliability. The solutions reached by these models are, in general, branched networks that are a bit more expensive but much more reliable. GA [7] and a metaheuristic based on the behavior of ant colonies [8] have been used to assess the aforementioned model.

To the best of the authors’ knowledge, the resolution of this problem using tabu search has been treated in the scientific literature only by Cunha and Ribeiro [9]. In our study, new criteria, as the use of different initial solutions or the neighborhood generation process, are applied to improve the previously achieved results.

3 Mathematical Model

Water distribution network design models seek to minimize the network deployment costs. A common strategy is to add penalty terms in the objective function or constraints for non-compliance with certain network requirements as pressure drop, water velocity, or reliability.

In this study, the traditional model, which does not include any penalty terms, is chosen and some requirements are included as constraints. The sets, the data, and the variables are defined in Tables 1, 2, and 3. The pipes are represented by arcs and the consumer points by nodes.

Table 1 Sets of the model
Full size table
Table 2 Data of the model
Full size table
Table 3 Variables of the model
Full size table

The complete model is detailed below.

$${\text{Min}}\,{\text{Total}}\,{\text{costs}} = f\left( {\emptyset _{{1k}} ,\emptyset _{{2k}} , \ldots ,\emptyset _{{Ak}} } \right) = \sum\limits_{{j \in A}} C \left( {\emptyset _{{jk}} } \right) \cdot L_{j}$$
(1)
$$\sum_{\forall j\in {I}_{i}}{q}_{j}-\sum_{\forall j\in {O}_{i}}{q}_{j}={d}_{i} \forall i=1\dots N$$
(2)
$$\sum_{\forall j\in M}{H}_{jk}=0 \forall m=1\dots M$$
(3)
$${h}_{i}={h}_{i-1}-{H}_{jk} \forall i=2\dots N, j\in {I}_{i}$$
(4)
$${h}_{i}\ge {h}_{i}^{\min} \forall i=2\dots N$$
(5)
$${\varnothing }_{jk}\in K ; {q}_{j}\in R ; {h}_{i}\in R$$
(6)

The final objective of the model is to find the optimal diameters of each network pipe that minimizes the total costs (1) while satisfying a series of technical limitations [5]. Furthermore, the diameters, which are the main variables, are discrete because they have to be chosen from a set of commercial ones. The network performance is subject to laws of flow balance (2) and energy conservation (3). The pressure of each node is calculated by the pressure of a linked node less the pressure drop in the arc which connects both nodes (4). Moreover, they all must be equal or higher than a minimum operating pressure, \({h}_{i}^{\min}\) (5). The pressure drops are calculated using the Hazen–Williams Eq. (7) where C is the roughness coefficient depending on the pipe material, α is a parameter which depends on the measurement units, and p and γ are empirical constants whose values are 1.852 and 4.87, respectively. It must be noted that the Hazen–Williams equation is utilized once the diameter has been assigned to the arc j, connecting this variable to the technical pressure equations.

$$H_{{jk}} = \alpha \cdot \frac{{L_{j} \cdot q_{j} ^{p} }}{{C^{p} \cdot \emptyset _{{jk}} ^{\gamma } }}$$
(7)

Finally, the nature of variables is established in Eq. (6), with R being the set of real numbers.

4 Tabu Search Algorithm

Tabu search (TS) is a metaheuristic firstly introduced by Glover in 1986 [10]. The main characteristic that differences it from other metaheuristics is the use of short-term memory. The search space is created by possible changes or movements of the current solution. When a new solution is achieved, the movement that caused it takes the attribute “tabu”, being a prohibited movement during a certain number of iterations. This process tries to avoid solutions being trapped in local optima, which is one of the major challenges of metaheuristics, by allowing the temporary worsening of the solutions.

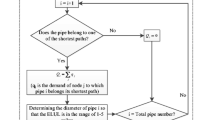
The algorithm works with solutions in the form of lists. Each element represents the diameter assigned to each arc. The neighborhood structure is built through the decrease of one diameter unit to the next one in the commercial catalog. It also includes short-term memory and an aspiration criterion which allows attaining a new solution despite taking a tabu movement if this new solution improves the best attained solution. The problm studied in this work requires two different evaluation functions. The first one performs the hydraulic simulation of the network. If a solution is hydraulically non-valid, it is rejected and saved in a list in order to avoid checking the same solution more than once. Additionally, a mechanism that generates new solutions when a neighborhood is full of non-valid solutions is included.

The second function evaluates the total cost of the hydraulically valid solutions. The whole process is summarized in Fig. 1, and the number of iterations of the process is previously set to a maximum.

Fig. 1
figure 1

Designed tabu search algorithm

Full size image

5 Case Study: Alperovits and Shamir’s Network

The designed methodology has been tested in Alperovits and Shamir’s [1] network. It has been considered as a relevant case study to analyze the optimal water network design from the beginning to nowadays. This network consists of 2 loops, 7 nodes, and 8 arcs (see Fig. 2). The water is supplied by a single source node and the circulation is entirely done by gravity, which means no impulsion is required. Figure 2 also shows the data which define the network. Elevation (Ei) is in metres and demand (di) in m3/s. The elevation of the source node corresponds to its pressure (h1). Finally, the length of every arc is 1,000 m.

Fig. 2
figure 2

Layout and data of the water supply network

Full size image

In addition, 14 diameters are available, each one with a specific unit cost (see Table 4). The acronyms m.u. represents monetary units which are arbitrarily created. Measurement units of pipe length are in inches, as in the original paper, and its corresponding value in SI units, metres.

Table 4 Catalog of diameters and their unit costs
Full size table

The number of arcs together with the number of available diameters generates a search space composed of 148 = 1,475,789,056 \({14}^{8}=\mathrm{1,475,789,056}\) possible solutions. The minimum operating pressure in every node has been fixed to 30 m, and it is a constraint of the model.

6 Results

Python is the software used to develop the algorithm and test its results. In order to simulate the network and to analyze if the hydraulic requirements are reached, the WNTR library [11] was employed. This Python package allows defining water networks as well as simulating their performance. The non-linear problem is internally solved by the Newton–Rapson method. The use of this library has made it possible to explore different solutions iteratively in a short time.

The algorithm has been implemented from two different initial solutions. Solution A is the worst possible solution whose cost is 4,400,000 m.u. and all pipes have the biggest available diameter. This is an unacceptable solution because the pressure in the nodes would be insufficient. Solution B is a hydraulically valid solution with a cost of 498,000 m.u.

Once the algorithm is calibrated (the initial solution, the tabu size, and the stop criterion), multiple simulations are made, reaching, in most cases, a solution whose cost is 420,000 m.u. The characteristics of this best attained solution are presented in Table 5. The pressure requirement is achieved in all nodes, except in node 1 that is the source node, a reservoir (and it is not required). Moreover, it can be noted that two arcs have almost no flow.

Table 5 The best attained solution
Full size table

The use of metaheuristics has made discrete solutions to prevail over continuous ones. Table 6 shows several results attained by different authors and the solution type. The solution obtained in this study does not improve GA results but resolution times and procedure complexity are considerably reduced. It is expecting that this approach will attain better results for bigger networks.

Table 6 Solutions of Alperovits and Shamir’s network found by other authors
Full size table

7 Conclusions

The purpose of this study was the design, development, and validation of a tabu search algorithm to solve the water distribution network design problem. The optimization of this design is sought by adding new criteria to the metaheuristic. Obtained results are clearly in line (error equal to 0.2%) to the ones attained by other authors for Alperovits and Shamir’s network. Furthermore, using the designed tabu search together with the WNTR library, the problem is solved in a very short time. Hence, this library has fully demonstrated to be a really useful tool to solve the non-linear mixed-integer problem iteratively. This has allowed testing different configurations and conditions of the hydraulic system.

Future work may include the resolution of larger and more realistic networks using this tool in order to demonstrate the good performance of the designed methodology in these cases.