Abstract
We consider the problem of automatically checking safety properties of fault-tolerant distributed algorithms. We express the considered class of distributed algorithms in terms of the Heard-Of Model where arbitrary many processes proceed in infinite rounds in the presence of failures such as message losses or message corruptions. We propose, for the considered class, a sound but (in general) incomplete procedure that is guaranteed to terminate even in the presence of unbounded numbers of processes. In addition, we report on preliminary experiments for which either correctness is proved by our approach or a concrete trace violating the considered safety property is automatically found.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Fault-tolerant distributed algorithms are difficult to prove correct. Such algorithms are meant to operate in the presence of faults ranging from process crashes to message losses or corruption. We consider the parameterized case where arbitrarily many identical processes participate in running the distributed algorithm. We adopt the popular Heard-Of model [3, 4]. This model uniformly describes distributed algorithms in the presence of transmission-based failures whether static or dynamic, permanent or transient. Algorithms proceed in rounds where, at each round, each process sends a message to other processes, hears from some of them, and updates its state. Hence, at each round, a process “hears” from a set of other processes. Fault descriptions are captured by stating constraints on the possible sets of processes and messages each process hears from (e.g. each process hears from at least half the processes or at most a third of the sent messages have been corrupted).
We consider the problem of automatically establishing the correctness of safety properties for parameterized distributed algorithms expressed in the Heard-Of model. The safety properties we consider concern checking state reachability, i.e., reachability of configurations where a given number of processes are in some forbidden combination of states. Observe that we do not check whether the algorithms make progress. This would require us to account for communication predicates that ensure the processes eventually hear from enough other processes. We need however to constrain, depending on the environment we want to capture, that messages may be lost (benign crashes or transmission failures) or altered (corruption failure). For consensus protocols, this is enough to capture all executions that violate agreement (two processes decide on different values), validity (a value is decided although no process proposed it) or irrevocability (a decided value is revoked). The verification problem is made difficult by the parameterization in the number of processes and by the allowed faults. Parameterization requires us to verify infinite families of algorithms, one for each number of participating processes. The transmission model allows each process to receive a subset of the sent messages (benign failures) in addition to a number of altered messages (corrupted communication), making this information local to the processes.
Related work. Abstractions for threshold-based fault-tolerant distributed systems were introduced in [11, 12]. The work is extended to synchronous round-based semantics in [17]. These works can handle interesting fault-tolerant algorithms in presence of different faults such as Byzantine faults, but have the limitation of requiring the user to encode the distributed system in terms of threshold automata and propose interval-based over-approximations or bounded-model checking based under-approximations for the parameterized verification problem. The models we consider directly target al.gorithms expressed in the Heard-Of model with a sound over-approximation and can account for message losses (omission fault) and message alteration (corruption fault). The work in [14] has the merit of proposing cutoffs for a syntactically restricted class of consensus algorithms. The class is also expressed in the Heard-Of model. While we do not provide such cutoffs, our work can afford to check correctness for richer fragments that can more faithfully capture constructs such as “the number of received messages with value \(v_0\) is at least two thirds the number of processes” as opposed to “the number of received messages is at least two thirds the number of processes, and all of them have value \(v_0\)”. The approach in [14] can verify Heard-Of algorithms such as Paxos that we cannot verify in our current approach. Because in our current setting, we have only many-to-many transmissions, while we need to account for one-to-many and many-to-one transmissions to be able to capture those algorithms. However, they only consider benign faults for the algorithms, but our approach can handle both benign and corruption faults. To the best of our knowledge, we are the first ones to verify Heard-of algorithms in presence of corruption faults.
Ongoing works [1, 13] study automatizing deciding satisfiability of constraints involving arbitrarily many processes and cardinality constraints over sets of received messages with specific properties. Such constraints naturally arise when verifying fault-tolerant distributed algorithms. For instance, [7, 15] consider a rich class of algorithms but require the user to supply such constraints in order to automatically establish correctness. The work in [15] abstracts the quorum of threads in the Paxos algorithm by introducing a new sort for quorum and adding an axiom to capture the fact that the intersection of two quorums is non-empty. While this abstraction is enough for verifying Paxos, it is too coarse for the algorithms we consider, since the size of the intersection of quorums are essential for proving the correctness of them. Other approaches [6, 8,9,10] can tackle wider classes of systems but adopt an interactive approach to verification, while our approach is fully automatic.
Contributions. We propose a sound and automatic approach to check safety properties. More specifically:
-
1.
We identify a subclass of fault-tolerant distributed algorithms in terms of the Heard-Of model and describe the considered safety properties.
-
2.
We introduce a symbolic representation where we capture cardinality constraints on multisets (formed by values of variables or heard-of sets) using integer counters, hence avoiding the challenge of implementing quantifier elimination for theories with cardinality constraints.
-
3.
We show how to use the symbolic representation in a sound but (in general) incomplete procedure for checking state reachability in the presence of lossy or corrupt communication.
-
4.
We show termination of the procedure even in the presence of arbitrarily many processes.
-
5.
We report on preliminary experiments with correct and buggy examples.
Outline. We describe the challenges of the verification problem using a motivating example in Sect. 2. We then introduce the class of distributed algorithms and the properties we aim to verify in Sect. 3. We formalize the symbolic representations in Sect. 4 and use them in Sect. 5 in a sound (but in general incomplete) verification algorithm for which we show termination. We describe preliminary experiments in Sect. 6 and conclude in Sect. 7.
The One-Third-Rule consensus algorithm. An arbitrary number of processes synchronize in rounds and try to choose the same value for res. \(\mathtt {HO^{}_{}}\) is the multiset of values received from other processes and \(|{\mathtt {HO^{\mathtt {d}}_{}}}|\) is the number of those messages equal to \(\mathtt {d}\).
2 Motivating Example
The One-Third-Rule algorithm listed in Fig. 1 is a simple consensus protocol that can tolerate benign transmission failures such as process crashes and message losses. Each process \(\mathtt {p}\) has two local variables \(\mathtt {x_p}\) and \(\mathtt {res_p}\) ranging over finite domains. The values of each variable \(\mathtt {x_p}\) range over the set \(\{0,1\}\). They are used to capture the candidate of process \(\mathtt {p}\) in the consensus algorithm. The values of each variable \(\mathtt {res_p}\) range over  and are used to capture the decisions of the process. The initial value
and are used to capture the decisions of the process. The initial value  captures that the process did not decide yet. The example is formalized in the Heard-Of model where n processes operate in infinite rounds in lock-step. The goal of the protocol is for the processes to agree on one of the initial values as a common output.
captures that the process did not decide yet. The example is formalized in the Heard-Of model where n processes operate in infinite rounds in lock-step. The goal of the protocol is for the processes to agree on one of the initial values as a common output.
In each round, a process first sends its local candidate value \(\mathtt {x}_\mathtt {p}\) to all other processes and receives values sent by other processes. Then, it executes one of the guarded commands that follow the send operation and whose guard is satisfied. In the original HO model [4] it is assumed that process ids of those processes a process \(\mathtt {p}\) hears from is stored in the set \(\mathtt {HO^{}_{p}}\). We make a small modification and assume that the values received from those processes by process \(\mathtt {p}\) are stored in a local multiset \(\mathtt {HO^{}_{p}}\) called the heard-of multiset of \(\mathtt {p}\). At each round, there are as many \(\mathtt {HO^{}_{p}}\) multisets as there are processes. These are used to uniformly capture different failures (e.g., delays, losses, crashes, corruption). For instance, if \(\overline{\mathtt {x}}\) is the multiset obtained by collecting the values of all variables \(\mathtt {x}_\mathtt {p}\) just sent by all processes, and in case of benign transmission failures (e.g. process crashes or message losses), each \(\mathtt {HO^{}_{p}}\) will be smaller than \(\overline{\mathtt {x}}\) for each value, written \(\mathtt {HO^{}_{p}} \preceq \overline{\mathtt {x}}\). For a multiset \(\overline{\mathtt {m}}\), we write \(|{\overline{\mathtt {m}}}|\) to mean the cardinality of \(\overline{\mathtt {m}}\). For instance, \(|{\overline{\mathtt {x}}}|\) is the number n of processes running the algorithm while \(|{\mathtt {HO^{}_{p}}}|\) captures the total number of messages received by process \(\mathtt {p}\) (i.e. the total number of processes that \(\mathtt {p}\) heard from). Moreover, for any value \(\mathtt {d}\) in the domain of the sent variables, we write \(|{\mathtt {HO^{\mathtt {d}}_{p}}}|\) to mean the number of those messages that are equal to \(\mathtt {d}\).
In Fig. 1, a process \(\mathtt {p}\) that receives more messages than two-thirds of the total number of processes (i.e. \(|{\mathtt {HO^{}_{p}}}|>2n/3\)) will update the value of its local candidate \(\mathtt {x_\mathtt {p}}\) with the smallest most often received value (lines 1 to 4). Besides, if among the received messages, more than two-thirds of the number of processes have the same value (here \(|{\mathtt {HO^{0}_{p}}}|>2n/3\) or \(|{\mathtt {HO^{1}_{p}}}|>2n/3\)), then both variables \(\mathtt {x_p}\) and \(\mathtt {res_p}\) are updated to the said value (lines 3 and 4). The process is then said to have decided on the value of \(\mathtt {res_p}\). Observe that if a process does not receive its candidate value \(\mathtt {x}_\mathtt {p}\) from more than 2n/3 processes, then it will not decide on it (lines 1 and 2). Furthermore, if a process has only heard from less than 2n/3 processes then it will not update its local variables (line 5).
Typical safety properties for such consensus protocols include:
-
Agreement: whenever two processes have reached a decision, the values they have decided on must be equal.
-
Validity: if all processes propose the same initial value, then the processes who have reached a decision must have decided on that initial value.
-
Irrevocability: if a process has decided on a value, it does not revoke its decision later.
Detecting violations of the above properties boils down to checking reachability of sets of configurations for unbounded numbers of processes. However, the correctness of the One-Third-Rule algorithm is independent of the number of processes. In fact, its correctness lies in the fact that: (1) in each round, \(\mathtt {HO^{}_{p}} \preceq \overline{\mathtt {x}}\) for each process \(\mathtt {p}\), (2) only those processes can update their \(\mathtt {x}\) who have heard from more than two thirds of the total number of processes and (3) only those can decide who have heard the same value from more than two thirds of the processes.
A run of the One-Third-Rule algorithm by two process groups \(\mathtt {i}\) and \(\mathtt {j}\) in backward from configurations with processes having decided on different values of \(\mathtt {res}\). The widths of the bars model the size of the corresponding multisets. Different colors correspond to different rounds.
In order to capture unbounded numbers of processes, we use constraints that group the processes based on the valuations of their local variables. Observe there are finitely many such valuations. We then describe bad configurations using such constraints. For instance, in order to check the agreement property for the One-Third-Rule algorithm, we need to check reachability of all constraints capturing all configurations where at least two groups of processes, namely \(\mathtt {i}\) and \(\mathtt {j}\) have \(\mathtt {res_{i}}=0\) and \(\mathtt {res_{j}}=1\). Assume this constraint had been reached after \(\mathtt {r}\) rounds. It is not difficult to see that process groups \(\mathtt {i}\) and \(\mathtt {j}\) could not have executed the guarded commands 3 and 4 during the same round \(\mathtt {r}\) and assign 0 and 1 to \(\mathtt {res_{i}}\) and \(\mathtt {res_{j}}\) respectively. This is because they would have had to satisfy both of the guards \(|{\mathtt {HO^{0}_{i}}}|>2n/3\) and \(|{\mathtt {HO^{1}_{j}}}|>2n/3\). Combined with \(\mathtt {HO^{}_{p}} \preceq \overline{\mathtt {x}}\) for each process \(\mathtt {p}\) (since message loss is the only fault), we get \(|{\overline{\mathtt {x}}^{0}}|>2n/3\) and \(|{\overline{\mathtt {x}}^{1}}|>2n/3\). This would give \(|{\overline{\mathtt {x}}}|>4n/3\), which contradicts the assumption that the number of processes in the system is n. Thus, we should look for runs in which \(\mathtt {res_{i}}\) and \(\mathtt {res_{j}}\) are set to 0 and 1 in separate rounds.
A possible run in backwards is shown in Fig. 2 in which each group of processes in each round is represented by its valuation, its heard-of multiset and the weakest predicate on its local variables that needs to be satisfied to make the run possible. In this description, we do not account for corruption or duplication of messages and therefore assume heard-of multisets are smaller (because of message loss) than the multiset of sent values \(\overline{\mathtt {x}}\). Accounting for corruption or duplication of messages is a matter of assuming other relations between \(\overline{\mathtt {x}}\) and the heard-of multisets. A key to the correctness of the algorithm is the fact that the fraction 2n/3 used in the guards ensures local heard-of multisets of participating processes (i.e. not executing the \(\mathtt {skip}\) command because they did not receive enough messages) have large intersections (in fact larger than n/3 for any pair of such multisets).
We start the run without any assumption on \(\overline{\mathtt {x}}\), therefore it satisfies \(\mathtt {true}\). If all processes in group \(\mathtt {i}\) and all those in group \(\mathtt {j}\) had executed the commands 1 and 3 respectively during round \(\mathtt {r}\) (note that each group could have also executed more commands, and we might need to split groups), one of the possible predecessors would be that the same process groups i and j existed with valuations \(\mathtt {res_{i}}=-1\) and \(\mathtt {res_{j}}=0\). Moreover, the predicate \(|{\overline{\mathtt {x}}^{0}}|>2n/3\) needs to hold at the beginning of round \(\mathtt {r}\). This is implied by the guards of the commands 1 and 3, \(|{\mathtt {HO^{}_{i}}}|>2n/3 ~\wedge ~ |{\mathtt {HO^{1}_{i}}}|\le |{\mathtt {HO^{0}_{i}}}|\le 2n/3\) and \(|{\mathtt {HO^{0}_{j}}}|>2n/3\), as well as the invariant \(\mathtt {HO^{}_{p}} \preceq \overline{\mathtt {x}}\) for each process \(\mathtt {p}\). We could unroll the loop once more, assuming that in round \(\mathtt {r}-1\) the two process groups had executed commands 1 and 2 respectively and assigned different values to their variables \(\mathtt {x_{i}}\) and \(\mathtt {x_{j}}\) (this does not contradict \(|{\overline{\mathtt {x}}^{0}}|>2n/3\)). The guards of the corresponding commands together with the invariant \(\mathtt {HO^{}_{p}} \preceq \overline{\mathtt {x}}\) for each process \(\mathtt {p}\) entail that the predicate \(|{\overline{\mathtt {x}}^{0}}|>n/3\) held at the beginning of the round \(\mathtt {r}-1\). Further unrollings of the loop in backward for any number of times will maintain \(|{\overline{\mathtt {x}}^{0}}|>n/3\). As a result, firing command 4 in some previous iteration would have been impossible as it requires \(|{\mathtt {HO^{1}_{}}}|>2n/3\). This command is however needed to reach to the initial state. A systematic exploration of similar constraints allows us to conclude the impossibility of deciding on different values.
The \(\mathcal {A}_{E,T}\) consensus algorithm [3]. An arbitrary number of processes synchronize in rounds and try to choose the same value for res. The messages might get lost or corrupted. Per each round, process, and data value, there will be at most \(\alpha \) corrupted messages. T is the threshold on the number of received messages and E is enough number of received messages with a certain value. According to [3], for correctness of the algorithm, it is sufficient that \(T\ge 2(n+2\alpha -E)\), \(E\ge \frac{n}{2}+\alpha \) and \(n>T\ge E\). We check correctness by adding these predicates as invariants.
The work in [3] introduced algorithms in Heard-Of model where received messages might be corrupted. One such algorithm is demonstrated in Fig. 3. We can handle such algorithms and the analysis is similar to the case where we have omission faults. The only difference is that the invariant in presence of corruption faults is that no more than \(\alpha \) messages received per round, per process and per data value will be corrupted. Therefore, the invariant is that \(|{\mathtt {HO^{\mathtt {d}}_{p}}}|\le |{\overline{\mathtt {x}}^{\mathtt {d}}}|+\alpha \).
Our work proposes a sound but (in general) incomplete algorithm for checking control state reachability for unbounded number of processes. The algorithm is guaranteed to terminate and starts from a symbolic representation of all bad configurations. It successively computes representations of over-approximations of predecessor configurations.
3 Heard-Of Programs
To simplify the presentation, we use a unique domain for all local variables and assume programs to proceed in infinite rounds where the state of each process is captured by the local variables. Introducing specific data domains for each variable or explicit local states in the transitions is straightforward. We use valuations (i.e., mapping from the set of local variables of a process to its domain) to capture the values of process variables. We define the syntax and semantics of a language to capture a class of heard-of programs. A heard-of program \(\mathtt {prg}=\left( {\mathtt {V},\mathtt {D},\mathtt {Init},\mathtt {Tr}}\right) \) involves:
-
A set \(\mathtt {V}\) of variables local to each process.
-
A finite set \(\mathtt {D}\subset \mathbb {Z}\) of possible data values,
-
An initial set of valuations \(\mathtt {Init}\) sending local variables \(\mathtt {V}\) to \(\mathtt {D}\),
-
A set of transitions \(\mathtt {Tr}\).
The syntax of such programs is as follows.
Each process starts by setting the initial values to its local variables. Then, all processes execute the transitions in a lock-step manner. Each program consists of a macro-round which is a sequence of \(|\mathtt {Tr}|\) consecutive rounds \((\mathtt {r}\mod |\mathtt {Tr}|)=0,\ldots ,(\mathtt {r}\mod |\mathtt {Tr}|)=|\mathtt {Tr}|-1\). The program starts in round \(\mathtt {r}=0\) and at each round \(\mathtt {r}\), all the processes will execute the transition designated with (\(\mathtt {r}\mod |\mathtt {Tr}|\)). \(\mathtt {r}\) is incremented after each transition.
In each transition \(\left( {\mathtt {r}\!\!\mod |\mathtt {Tr}|=\mathtt {e}:\mathtt {send}~\mathtt {v};~ \mathtt {cmd}_1,\ldots \mathtt {cmd}_K}\right) \), first, all processes send the value of their local variable \(\mathtt {v}\). After \(\mathtt {send}\), there is an implicit receive step in which the processes receive the values sent by others. Between the send and receive of the messages, an adversarial environment can choose to drop or alter messages. The received values are stored in a \(\mathtt {HO}\) (heard-of) multiset that is local to each process. The impact of the environment is captured by the heard-of multiset.
After send and receive, each process \(\mathtt {p}\) with heard-of multiset \(\mathtt {HO^{}_{p}}\) executes a guarded command \(\mathtt {cmd}_k=\left( {\mathtt {guard}_k:\mathtt {val}^1_k\rightarrow \mathtt {val}^2_k}\right) \) where \(\mathtt {HO^{}_{p}}\models \mathtt {guard}_k\). A \(\mathtt {guard}\) mainly focuses on capturing cardinality of some \(\mathtt {HO}\) multiset(s). This cardinality is in many cases compared to a fraction of the total number of processes, i.e. \(\mathtt {c.n}\). In order to simplify the presentation, we consider each \(\mathtt {cmd}\) to be a change in the local valuation of a process . A \(\mathtt {skip}\) command can easily be transformed to this format by choosing identical values for the command. Introducing explicit local states is simple but would not improve readability.
Configurations. Configurations of a heard-of program describe the round number, as well as the local state of the processes, i.e. their valuations and heard-of multisets. More formally, a configuration of \(\mathtt {prg}=\left( {\mathtt {V},\mathtt {D},\mathtt {Init},\mathtt {Tr}}\right) \) is a tuple \(\left( {\mathtt {r}^{},\left[ {\mathtt {p}^{}_1,\ldots ,\mathtt {p}^{}_a}\right] }\right) \) where:
-
\(\mathtt {r}\) is the round number.
-
for all i in \(0\le i\le a\), \(\mathtt {p}_i=\left( {\mathtt {val}_i,\mathtt {HO}_i}\right) \) is a process where:
-
\(\mathtt {val}_i\) is a mapping \(\mathtt {V}\rightarrow \mathtt {D}\). In other words, the valuation \(\mathtt {val}_i\) maps each local variable of the process to a value in the domain.
-
\(\mathtt {HO}_i :\mathtt {D}\rightarrow \mathbb {N}\) is a multiset of integer values.
-
Values of a configuration. For a configuration \(\mathtt {c}=\left( {\mathtt {r}^{},\left[ {\mathtt {p}^{}_1,\ldots ,\mathtt {p}^{}_a}\right] }\right) \) and for any variable \(\mathtt {v}\in \mathtt {V}\) we define \(\mathtt {valuesOf}(\mathtt {c},\mathtt {v})\) to be a multiset containing all the local values of \(\mathtt {v}\) in all the processes. More formally, for all \(\mathtt {d}\in \mathtt {D}\), \(\mathtt {valuesOf}(\mathtt {c},\mathtt {v})(\mathtt {d})=|\left\{ {\mathtt {p}_i|\mathtt {p}_i=(\mathtt {val}_i,\mathtt {HO}_i) \text { with } \mathtt {val}_i(\mathtt {v})=\mathtt {d}}\right\} |\).
Example 1
For the program in Fig. 1, consider the following processes at round \(\mathtt {r}=0\).
-
 , \(\varnothing )\)
, \(\varnothing )\) -
 , \(\varnothing )\)
, \(\varnothing )\) -
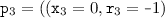 , \(\varnothing )\)
, \(\varnothing )\) -
 , \(\varnothing )\)
, \(\varnothing )\)
The configuration \(\mathtt {c}= (0,\left[ {\mathtt {p}_1,\mathtt {p}_2,\mathtt {p}_3,\mathtt {p}_4}\right] )\) captures initial configuration. The heard-of multisets of the processes are empty initially. The values of variable \(\mathtt {x}\) are captured by the multiset \(\mathtt {valuesOf}(\mathtt {c},\mathtt {x})=\left[ {0,1,1,1}\right] \).
Semantics. Given a program \(\mathtt {prg}=\left( {\mathtt {V},\mathtt {D},\mathtt {Init},\mathtt {Tr}}\right) \), the processes start executing \(\mathtt {Tr}\) from an initial configuration \(\mathtt {c}_{init} = \left( {\mathtt {r}^{init},\left[ {\mathtt {p}^{init}_1,\ldots ,\mathtt {p}^{init}_a}\right] }\right) \) where \(\mathtt {r}^{init}=0\), and for all \(1\le i\le a\), \(\mathtt {p}^{init}_i = \left( {\mathtt {val}_i,\emptyset }\right) \), and \(\mathtt {val}_i \in \mathtt {Init}\). Suppose configurations \(\mathtt {c}\) and \(\mathtt {c}'\) can be written (up to a renaming of the processes) as \(\mathtt {c}=(\mathtt {r},\left[ {(\mathtt {val}_1,\mathtt {HO}_1), \ldots (\mathtt {val}_a,\mathtt {HO}_a)}\right] )\), \(\mathtt {c}'=(\mathtt {r}',\left[ {(\mathtt {val}_1',\mathtt {HO}_1'), \ldots (\mathtt {val}_a',\mathtt {HO}_a')}\right] )\), and \(\mathtt {tr}=\left( {\mathtt {r}\!\!\mod |\mathtt {Tr}|=\mathtt {e}:\mathtt {send}~\mathtt {v};~ \mathtt {cmd}_1,\ldots \mathtt {cmd}_K}\right) \) with \(\mathtt {cmd}_k = \left( {\mathtt {guard}_{k},\mathtt {val}^1_{k}\rightarrow \mathtt {val}^2_{k}}\right) \) for each \(k:1\le k\le K\). We write \(\mathtt {c}\xrightarrow []{\mathtt {tr}}\mathtt {c}'\) to mean that \(\mathtt {r}'=\mathtt {r}+1\) and there is a total function \(\mathtt {F}:\left\{ {1,\ldots a}\right\} \rightarrow \left\{ {1,\ldots K}\right\} \) where for each \(i:1\le i \le a\), \(\mathtt {val}_i=\mathtt {val}^{1}_{\mathtt {F}(i)}\), \(\mathtt {val}_i'=\mathtt {val}^{2}_{\mathtt {F}(i)}\) and \(\mathtt {HO}_i\models \mathtt {guard}_{\mathtt {F}(i)}\). Note that the numbers of processes in \(\mathtt {c}\) and \(\mathtt {c}'\) are finite, arbitrary large and equal.
Example 2
Consider Example 1 and \(\mathtt {tr}\) being the transition \(\mathtt {tr}\) in Fig. 1. Processes 1 to 4 can take guarded commands 2, 2, 5 and 4 respectively and result in the configuration \(\mathtt {c}'=(1,\left[ {\mathtt {p}_1',\mathtt {p}_2',\mathtt {p}_3',\mathtt {p}_4'}\right] )\) where:
-
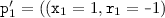 , \(\left[ {1,0,1}\right] )\)
, \(\left[ {1,0,1}\right] )\) -
 , \(\left[ {1,1,0}\right] )\)
, \(\left[ {1,1,0}\right] )\) -
 , \(\left[ {0,1}\right] )\)
, \(\left[ {0,1}\right] )\) -
\(\mathtt {p}_4'=((\mathtt {x}_4=1,\mathtt {r}_4=1)\), \(\left[ {1,1,1}\right] )\)
Here \(\mathtt {F}=\left\{ {(1,2),(2,2),(3,5),(4,4)}\right\} \) witnesses \(\mathtt {c}\xrightarrow []{\mathtt {tr}}\mathtt {c}'\).
4 Symbolic Representation
In this section, we formally define our symbolic representation and describe a corresponding entailment relation. We assume a program \(\mathtt {prg}= \left( {\mathtt {V},\mathtt {D},\mathtt {Init},\mathtt {Tr}}\right) \).
Constraints. A constraint \(\mathtt {\phi }\) is a tuple \(\left( {\mathtt {e},\mathtt {gl}^{},\left\{ {\mathtt {val}^{}_1,\ldots ,\mathtt {val}^{}_b}\right\} }\right) \) that denotes a possibly infinite set of configurations such that:
-
An integer \(\mathtt {e}\) in
 capturing the control location of the execution.
capturing the control location of the execution. -
A global condition \(\mathtt {gl}\) in the form of a Presburger predicate with a free variable n (for the number of processes) and a set of \(|{\mathtt {V}}|\times |{\mathtt {D}}|\) free variables \({{^\#}{\mathtt {V}}^{}}=\left\{ {{{^\#}{\mathtt {v}}^{\mathtt {d}}} ~|~\mathtt {v}\in \mathtt {V}\text { and } \mathtt {d}\in \mathtt {D} }\right\} \), where each \({{^\#}{\mathtt {v}}^{\mathtt {d}}}\) accounts for the number of occurrences of value \(\mathtt {d}\) among variables \(\mathtt {v}\) of all processes.
-
A base formed by a set of valuations \(\left\{ {\mathtt {val}_1, \ldots \mathtt {val}_b}\right\} \). The valuations are similar to those used by the configurations and represent groups of processes with the same valuations.
Each valuation in the base of a constraint corresponds to one or more processes with that valuation in a denoted configuration. Besides, a constraint does not explicitly represent conditions on heard-of multisets; instead, we maintain a global condition \(\mathtt {gl}\) which is a predicate on the number of occurrences of values in program variables of all processes (i.e.g.lobal state). The intuition is that heard-of sets ultimately originate from the global state. Hence constraining their values (to satisfy some guarded commands) is a matter of constraining the global state and accounting for possible faults (see Sect. 5). For a predicate p that might depend on a set of integer variables \(X=\left\{ {x_1,\ldots ,x_q}\right\} \), we write p(X) to clarify that p might have a subset of X as free variables. To simplify the presentation, we typically omit to mention that a predicate might have n (for the number of processes) as a free variable. For instance, we write \(\mathtt {gl}({{^\#}{\mathtt {V}}^{}})\) to clarify that \(\mathtt {gl}\) might have as free variables a subset of \({{^\#}{\mathtt {V}}^{}}\) in addition to the variable n.
Denotations. For a constraint \(\mathtt {\phi }= \left( {\mathtt {e},\mathtt {gl}^{\mathtt {\phi }},\left\{ {\mathtt {val}^{\mathtt {\phi }}_1,\ldots ,\mathtt {val}^{\mathtt {\phi }}_b}\right\} }\right) \) we write \(\mathtt {c}\models \mathtt {\phi }\) to mean \(\mathtt {\phi }\) denotes the configuration \(\mathtt {c}=(\mathtt {r},(\mathtt {val}^\mathtt {c}_1,\mathtt {HO}^\mathtt {c}_1), \ldots , (\mathtt {val}^\mathtt {c}_a,\mathtt {HO}^\mathtt {c}_a))\). Intuitively, \(\mathtt {\phi }\) should account for all local valuations in \(\mathtt {c}\) (captured by a surjection from \(\left\{ {1,\ldots a }\right\} \) to \(\left\{ {1,\ldots b}\right\} \)). Moreover, the predicate \(\mathtt {gl}^\mathtt {\phi }\) must be compatible with the multiset of all local valuations of the processes. More formally:
-
1.
\(\mathtt {r}\mod |\mathtt {Tr}|=\mathtt {e}\).
-
2.
Replacing in the global condition \(\mathtt {gl}\) each occurrence of \({{^\#}{\mathtt {v}}^{\mathtt {d}}}\) by the number of occurrences of \(\mathtt {d}\) in \(\mathtt {c}\) (i.e., \(\mathtt {valuesOf}(\mathtt {c},\mathtt {v})(\mathtt {d})\)) and each occurrence of n by the number of processes in \(\mathtt {c}\) (i.e., a) results in a valid formula.
-
3.
There is a surjection \(\mathtt {S}::\left\{ {1,\ldots a }\right\} \rightarrow \left\{ {1,\ldots b}\right\} \) such that for all \(1\le i \le a\), \(\mathtt {val}^{\mathtt {c}}_{i}=\mathtt {val}^{\mathtt {\phi }}_{\mathtt {S}(i)}\)
Observe that a constraint \(\left( {\mathtt {e},\mathtt {gl}^{},\left\{ {\mathtt {val}^{}_1,\ldots ,\mathtt {val}^{}_b}\right\} }\right) \) will have an empty denotation if its base requires the presence of valuations forbidden by the global condition, or if the global condition requires valuations forbidden by the base (since we require a surjection). It is safe to systematically discard such constraints in our analysis presented in Sect. 5.
Example 3
The configuration \(\mathtt {c}'\) in Example 2 is in the denotation of the constraint  with \(\mathtt {S}\) being \(\left\{ {(1,1),(2,1),(3,2),(4,3)}\right\} \).
with \(\mathtt {S}\) being \(\left\{ {(1,1),(2,1),(3,2),(4,3)}\right\} \).
Entailment. We write \(\mathtt {\phi }_1\sqsubseteq \mathtt {\phi }_2\) to mean \(\mathtt {\phi }_1=\left( {\mathtt {e},\mathtt {gl}^1,\left\{ {\mathtt {val}^1_1,\ldots ,\mathtt {val}^1_{b_1}}\right\} }\right) \) is entailed by \(\mathtt {\phi }_2=\left( {\mathtt {e},\mathtt {gl}^2,\left\{ {\mathtt {val}^2_1,\ldots ,\mathtt {val}^2_{b_2}}\right\} }\right) \). This will ensure that configurations denoted by \(\mathtt {\phi }_2\) are also denoted by \(\mathtt {\phi }_1\). Intuitively, \(\mathtt {\phi }_1\) and \(\mathtt {\phi }_2\) must have the same round number modulo \(|\mathtt {Tr}|\), and
-
There is a bijection \(\mathtt {Y}::\left\{ {1,\ldots b_2}\right\} \rightarrow \left\{ {1,\dots b_1}\right\} \) with \(\mathtt {val}^2_j=\mathtt {val}^1_{\mathtt {Y}(j)}\) for all \(1\le j\le b_2\).
-
\(\mathtt {gl}^{2}\Rightarrow \mathtt {gl}^{1}\).
5 A Symbolic Verification Procedure
We use the constraints defined in Sect. 4 as a symbolic representation to denote sets of configurations. We adopt a working-list procedure that checks reachability of a \(\sqsubseteq \)-minimal set \(\varPhi \) of target constraints by a program \(\mathtt {prg}=\left( {\mathtt {V},\mathtt {D},\mathtt {Init},\mathtt {Tr}}\right) \). For a bad set \(\mathtt {B}=\left\{ {\mathtt {val}_1,\ldots \mathtt {val}_x}\right\} \) of valuations, the set of target constraints \(\varPhi _\mathtt {B}\) contains each \(\left( {\mathtt {e},\mathtt {true},\mathtt {val}_1,\ldots ,\mathtt {val}_x}\right) \) where \(\mathtt {e}\) is a value in  . In addition, it contains each constraint obtained from such a constraint by adding some unique valuations that were not in its base (since we require surjections for the denotations in Sect. 4).
. In addition, it contains each constraint obtained from such a constraint by adding some unique valuations that were not in its base (since we require surjections for the denotations in Sect. 4).
The procedure computes a fixpoint using the entailment relation \(\sqsubseteq \) and a predecessor computation that results, for a constraint \(\mathtt {\phi }\) and a transition \(\mathtt {tr}\), in a finite set \(\mathtt {pre_\mathtt {tr}}(\mathtt {\phi })\). In fact, \(\mathtt {pre_\mathtt {tr}}(\mathtt {\phi })\) is the set of constraints that capture an over-approximation of all the configurations that might reach in one round a configuration denoted by \(\mathtt {\phi }\). Figure 4 captures this computations and uses several sets of integer variables. The variables \({{^\#}{\mathtt {V}}^{}}=\left\{ {{{^\#}{\mathtt {v}}^{\mathtt {d}}} ~|~\mathtt {v}\in \mathtt {V}\text { and } \mathtt {d}\in \mathtt {D} }\right\} \) (resp. \({{^\#}{\mathtt {V}'}^{}}=\left\{ {{{^\#}{\mathtt {v}'}^{\mathtt {d}}} ~|~\mathtt {v}\in \mathtt {V}\text { and } \mathtt {d}\in \mathtt {D} }\right\} \)) are used to constrain values of process variables in the successor constraint \(\mathtt {\phi }\) (resp. predecessor constraint \(\mathtt {\phi }'\)). The variables \({{^\#}{\mathtt {HO}_k}^{}}=\left\{ {\mathtt {{^\#}ho_{{k}}^{\mathtt {d}}} ~|~\mathtt {d}\in \mathtt {D} }\right\} \) are used to constrain values in the heard-of multisets of processes taking a guarded command \(\mathtt {cmd}_k\) in \(\mathtt {tr}\). The remaining text in this Section describes the over-approximation.
Choice of guarded commands and resulting bases. Intuitively, the set \(\mathtt {I}\) corresponds to combinations of processes in the successors (i.e., \(\mathtt {\phi }\)) and guarded commands in the transition (i.e., \(\mathtt {tr}\)). Each pair \((k,j)\in \mathtt {I}\) corresponds to a group of processes with the same valuation \(\mathtt {val}_{H^{-1}((k,j))}'\) in the predecessors (i.e., \(\mathtt {\phi }'\)) that took the guarded command \(\mathtt {cmd}_k\) in the transition \(\mathtt {tr}\) resulting in a valuations \(\mathtt {val}_j\) in \(\mathtt {\phi }\). Observe there are finitely many such combinations, and hence finitely many such sets \(\mathtt {I}\). The definition of \(\mathtt {I}\) ensures that the set \(\left\{ {1,\ldots b}\right\} \) of process groups of \(\mathtt {\phi }\) is covered. In addition, two pairs \((k_1,j_1)\) and \((k_2,j_2)\) may result in equal valuations \(\mathtt {val}_{H^{-1}((k_1,j_1))}'\)and \(\mathtt {val}_{H^{-1}((k_2,j_2))}'\). We keep only one representative in \(\mathtt {\phi }'\) by making a set \(\mathtt {setOf}({\mathtt {val}'_1,\ldots ,\mathtt {val}'_{|\mathtt {I}|}})\) of the multiset \([\mathtt {val}'_1,\ldots ,\mathtt {val}'_{|\mathtt {I}|}]\)
Constraints imposed by the guards. Given a guarded command \(\mathtt {cmd}_k\), we use the predicate \(\xi (\mathtt {guard}_k)\) to encode the fact that the heard-of multisets of predecessor configurations denoted by \(\mathtt {\phi }'\) satisfy the guard \(\mathtt {guard}_k\) of \(\mathtt {cmd}_k\). For this, we use an integer variable \(\mathtt {{^\#}ho_{{k}}^{\mathtt {d}}}\) for each value \(\mathtt {d}\) and index \(k:1\le k\le K\) to count the occurrences of \(\mathtt {d}\) in the heard-of multiset of the processes taking \(\mathtt {cmd}_k\). We write \({{^\#}{\mathtt {HO}_k}^{}}=\left\{ {\mathtt {{^\#}ho_{{k}}^{\mathtt {d}}} ~|~\mathtt {d}\in \mathtt {D} }\right\} \) to mean the set of all such variables for all values in \(\mathtt {D}\). For instance, \(\mathtt {guard}_3\) is \(|{\mathtt {HO}^{0}}|>2n/3\) in Fig. 1 and is encoded with the predicate \((\mathtt {{^\#}ho_{{3}}^{0}} > 2n/3)\). We also need to relate the constraints on the heard-of multisets to the constraints on the variables values in the predecessor constraint \(\mathtt {\phi }'\). Assume \(\mathtt {\phi }'\) denotes a configuration \(\mathtt {c}'\) resulting, via \(\mathtt {tr}\), in a configuration \(\mathtt {c}\) denoted by \(\mathtt {\phi }\). Suppose \(\mathtt {tr}\) sends values of variable \(\mathtt {v}\). In the case of benign failures (e.g., message losses), any heard-of multiset \(\mathtt {HO}_{k}\) of some process that took a guarded command \(\mathtt {cmd}_k\) in \(\mathtt {tr}\) needs to get its values from the multiset \(\mathtt {valuesOf}(\mathtt {c}',\mathtt {v})\) of values of \(\mathtt {v}\) in \(\mathtt {c}'\). We therefore enforce \(\mathtt {HO}_{k} \preceq \mathtt {valuesOf}(\mathtt {c}',\mathtt {v})\). This is captured by \(\mathtt {HAX}_k({{^\#}{\mathtt {HO}_k}^{}},{{^\#}{\mathtt {V}'}^{}})=\bigwedge \limits _{\mathtt {d}\in \mathtt {D}}0\le \mathtt {{^\#}ho_{{k}}^{\mathtt {d}}} \le {{^\#}{\mathtt {v}'}^{\mathtt {d}}}\). For each guarded command \(\mathtt {cmd}_k\), the predicate \( \gamma _k({{^\#}{\mathtt {V}'}^{}})=\exists {{^\#}{\mathtt {HO}_k}^{}}. \left( \begin{array}{l} \xi (\mathtt {guard}_k)({{^\#}{\mathtt {HO}_k}^{}}) \wedge \mathtt {HAX}_k({{^\#}{\mathtt {HO}_k}^{}},{{^\#}{\mathtt {V}'}^{}}) \end{array} \right) \) captures the strongest constraints imposed, in the predecessor processes, by the guard of \(\mathtt {cmd}_k\) on values of the variable that was sent (here \(\mathtt {v}\)). We explain later in this section how we handle corrupt communication. These predicates are only dependent on the chosen guarded commands and the sent variables. We collect them in a set \(\varGamma =\left\{ {\gamma _k ~|~k:1\le k\le K }\right\} \). Observe the set \(\varGamma \) is finite.
Constraints imposed by the commands. Each time a process takes a chosen guarded command \(\mathtt {cmd}_k = \left( {\mathtt {guard}_{k},\mathtt {val}^1_{k}\rightarrow \mathtt {val}^2_{k}}\right) \) with (k, j) in \(\mathtt {I}\) for some j, it transforms its valuation from \(\mathtt {val}^1_{k}\) to \(\mathtt {val}^2_{k}\). This affects the relation between \(\mathtt {gl}({{^\#}{\mathtt {V}}^{}})\) and \(\mathtt {gl}'({{^\#}{\mathtt {V}'}^{}})\) as the number of occurrences of a variable with a given value depends on the proportions of processes that take each guarded command. We first illustrate how this relation can be captured exactly by introducing auxiliary variables to represent the number of processes that took each one of the chosen guarded commands. Then we describe how we can over-approximate this relation and avoid the introduction of the variables.
First, we introduce an integer variable \(\delta _{k}\), for each \(k\in \left\{ {1,\ldots , K}\right\} \), to capture the number of processes in some configuration \(\mathtt {c}'\) denoted by \(\mathtt {\phi }'\) that executed the guarded command \(\mathtt {cmd}_k =\left( {\mathtt {guard}_{k},\mathtt {val}^1_{k}\rightarrow \mathtt {val}^2_{k}}\right) \). If \(\mathtt {d}_1=\mathtt {val}^1_{k}(\mathtt {v})\) and \(\mathtt {d}_2=\mathtt {val}^2_{k}(\mathtt {v})\), then each process taking the guarded command \(\mathtt {cmd}_k\) will decrease the number of occurrences of \(\mathtt {d}_1\) and increase the number of occurrences of \(\mathtt {d}_2\). More precisely, for each variable \(\mathtt {v}\), the following relation holds:
The relation \(\mathtt {DAX}_{e}\) is expensive to compute. Instead, we over-approximate it with \(\mathtt {DAX}\) (see below) where we identify two cases in which we can relate variables in \({{^\#}{\mathtt {V}}^{}}\) and \({{^\#}{\mathtt {V}'}^{}}\). For each variable \(\mathtt {v}\in \mathtt {V}\), the first case (captured with the predicate \(\mathtt {preserved}_\mathtt {I}(\mathtt {v})\)) is true when each chosen guarded command \(\left( {\mathtt {guard}_{k},\mathtt {val}^1_{k}\rightarrow \mathtt {val}^2_{k}}\right) \) with \((k,\_)\in \mathtt {I}\) preserves the variable \(\mathtt {v}\) (i.e., \(\mathtt {val}^1_k(\mathtt {v})=\mathtt {val}^2_k(\mathtt {v})\)). The second (captured with the predicate \(\mathtt {uniqueChange}_\mathtt {I}(\mathtt {v},\mathtt {d})\)) corresponds to the situation when the only allowed changes for variable \(\mathtt {v}\) are to some value \(\mathtt {d}\) (i.e., for all \(k,k'\) with \((k,\_),(k',\_)\in \mathtt {I}\), if \(\mathtt {val}^1_k(\mathtt {v}) \ne \mathtt {val}^2_k(\mathtt {v})\) and \(\mathtt {val}^1_{k'}(\mathtt {v}) \ne \mathtt {val}^2_{k'}(\mathtt {v})\) then \(\mathtt {val}^2_k(\mathtt {v}) = \mathtt {val}^2_{k'}(\mathtt {v}) = \mathtt {d}\)). The over-approximation \(\mathtt {DAX}\) of \(\mathtt {DAX}_e\) is defined as:
To achieve the computation of \(\mathtt {gl}'({{^\#}{\mathtt {V}'}^{}})\), we account for the global condition of the successor constraint (using \(\mathtt {gl}({{^\#}{\mathtt {V}}^{}})\)) and deduce constraints on \(\mathtt {V}'\) via the relation \(\mathtt {DAX}({{^\#}{\mathtt {V}}^{}}, {{^\#}{\mathtt {V}'}^{}})\). More precisely, we compute: \(\pi ({{^\#}{\mathtt {V}'}^{}})=\exists {{^\#}{\mathtt {V}}^{}}.~\mathtt {DAX}({{^\#}{\mathtt {V}}^{}},{{^\#}{\mathtt {V}'}^{}}) \wedge \mathtt {gl}({{^\#}{\mathtt {V}}^{}})\). In general, arbitrarily many different such predicates may be generated in the fixpoint iteration. To help termination, we use the abstraction \(\mathtt {PrAbs}_{[\varGamma ]}(\pi )\) of \(\pi \) with respect to the predicates \(\varGamma =\left\{ {\gamma _k ~|~k:1\le k\le K }\right\} \) obtained from all the guards.
Example 4
Consider the configurations \(\mathtt {c}\), \(\mathtt {c}'\) and the constraint \(\mathtt {\phi }'\) in the Examples 1, 2 and 3. We have shown \(\mathtt {c}\xrightarrow []{\mathtt {tr}}\mathtt {c}'\) using \(\mathtt {F}\) and \(\mathtt {c}'\models \mathtt {\phi }'\) using \(\mathtt {S}\). Consider now the constraint  . We define \(\mathtt {H}= \left\{ {(1,(2,1)),(2,(5,2)),(1,(4,3))}\right\} \) to show \(\mathtt {\phi }'\in \mathtt {pre_\mathtt {tr}}(\mathtt {\phi })\). Moreover, there is a surjection \(\mathtt {S}'=\left\{ {(1,1),(2,1),(3,2),(4,1)}\right\} \) that witnesses \(\mathtt {c}\models \mathtt {\phi }\).
. We define \(\mathtt {H}= \left\{ {(1,(2,1)),(2,(5,2)),(1,(4,3))}\right\} \) to show \(\mathtt {\phi }'\in \mathtt {pre_\mathtt {tr}}(\mathtt {\phi })\). Moreover, there is a surjection \(\mathtt {S}'=\left\{ {(1,1),(2,1),(3,2),(4,1)}\right\} \) that witnesses \(\mathtt {c}\models \mathtt {\phi }\).
Corrupted communications. As in [3], corrupted communications or value faults are related to the classical Byzantine Faults in which a portion of the received messages are corrupted. Note that in the classical Byzantine setting, also the state of a process can be corrupted, which is not the case in this model. All processes follow the algorithm but may receive a number of corrupted messages (whether accidental or malicious). We weaken this assumption so that in each round, for each process and for each data value, no more than \(\alpha \) (given as a fraction of n) messages received by a process may have been corrupted. This assumption is weaker than the one in [14]. We model this by enforcing the following invariants. \(\mathtt {DAX}\) remains unchanged because of the assumption that states of processes are not corrupted. It is the relation between the heard-of multisets and process variables that change: \(\mathtt {HAX}_k=\bigwedge \limits _{\mathtt {d}\in \mathtt {D}}(0\le \mathtt {{^\#}ho_{{k}}^{\mathtt {d}}}\le {{^\#}{\mathtt {v}'}^{\mathtt {d}}}+\alpha )\). The rest of the computation of predecessors remains unchanged.
Theorem 1
The proposed predecessor computation method introduced in Fig. 4 is a sound over-approximation for parameterized Heard-Of programs.
Proof
Sketch. Assume configurations \(\mathtt {c}, \mathtt {c}'\) and constraint \(\mathtt {\phi }\) as described in Fig. 5. The total function \(\mathtt {F}\) witnesses \(\mathtt {c}'\rightarrow \mathtt {c}\) and surjection \(\mathtt {S}\) witnesses \(\mathtt {c}\models \mathtt {\phi }\). We show a constraint \(\mathtt {\phi }'\) that denotes \(\mathtt {c}'\) is generated by the procedure. All generated \(\mathtt {e}'\) capture \(\mathtt {r}'\) if \(\mathtt {c}'\rightarrow \mathtt {c}\) and \(\mathtt {c}\models \mathtt {\phi }\). Observe each \(\mathtt {val}^\mathtt {\phi }_j\) is mapped to (via \(\mathtt {S}\)) at least some \(\mathtt {val}^\mathtt {\phi }_i\). By choosing \(\mathtt {I}=\left\{ {(\mathtt {F}(i),\mathtt {S}(i)) ~|~i:1\le i \le a }\right\} \) we ensure the existence of a surjection \(\mathtt {S}'\) that maps each \(\mathtt {val}^{\mathtt {c}'}_i\) to some \(\mathtt {val}^{\mathtt {\phi }'}_{j'}\). In addition, the values \(\mathtt {valuesOf}(\mathtt {c}',\mathtt {v})\), for each \(\mathtt {v}\in \mathtt {V}\), resulted in heard-of multisets that satisfied the guarded commands \(\left\{ {\mathtt {cmd}_{\mathtt {F}(i)} ~|~i:1\le i \le a }\right\} \). Moreover, \(\mathtt {valuesOf}(\mathtt {c}',\mathtt {v})\) satisfies \(\mathtt {gl}'\) because of the following. Indeed, \(\mathtt {valuesOf}(\mathtt {c},\mathtt {v})\) satisfy \(\mathtt {gl}\) and are related to \(\mathtt {valuesOf}(\mathtt {c}',\mathtt {v})\) with \(\mathtt {DAX}_e\) and its over-approximations \(\mathtt {DAX}\) and its predicate abstraction with respect to some predicates. Finally, \(\mathtt {Inv}\) restricts \(\mathtt {valuesOf}(\mathtt {c}',\mathtt {v})\) to possible values (e.g., sum of all occurrences per variable should be n) or relevant values (e.g., enforcing invariants under which correctness is checked).
Theorem 2
The proposed procedure terminates.
Termination is obtained by the fact that at most a finite number of constraints might be generated. To see this, observe that constraints consist of an integer capturing control location, a predicate (the global condition), and a set of local valuations of processes (the base). The number of control locations and that of the local valuations of processes is finite. In addition, the number of combinations of subsets of guarded commands is finite and the strengthening invariants do not change.
6 Experimental Results
We report on experiments with our open-source prototype SyncV which is publically available online at https://gitlab.liu.se/live/syncv for the verification of a class of HO algorithms. The experiments were conducted on a 2.9 GHz processor with 8 GB of memory. We conducted experiments on several variations of the One-Third-Rule and \(\mathcal {A}_{E,T}\) algorithms. In fact, these variations correspond to checking the correctness properties of agreement, validity, and irrevocability for correct and buggy versions of the considered algorithms and for an unbounded number of processes. For each property, a correct version and a buggy version were tested. The buggy versions differ from the correct ones by the considered guards in the commands. For verification of the \(\mathcal {A}_{E,T}\) algorithm, we strengthened our invariant \(\mathtt {Inv}\) in Fig. 4 with the invariants represented in Fig. 3 that according [3] are essential for correctness of the algorithm.
For all the correct versions, our tool reported that the program is safe and for all the buggy ones, it presented a valid trace violating the considered property. Our implemented procedure does not eagerly concretize local valuations of processes. Instead, we concretize on demand. All benchmarks are available on the tool homepage.
Checking different correctness properties. We discussed in depth checking the agreement correctness property in Sects. 2 and 5. Checking the validity property is similar in the sense that it also uses a finite set of forbidden valuations to characterize the set of bad constraints. In order to check irrevocability, one needs to see if a process can make a decision and revoke it later. In order to make such checks, we take into account a history of the changes. We do that by augmenting each process group in a constraint by a list of possible decisions as its history. This list is empty by default. A bad constraint that violates irrevocability has at least one process group with a minimum of two different values in its history.
7 Conclusion and Future Work
We have studied a subclass of fault-tolerant distributed algorithms in terms of the Heard-Of model and proposed a symbolic representation using cardinality constraints on multisets to model sets of configurations generated during the analysis of such programs. We have also introduced a sound procedure for checking state reachability to check various correctness properties for consensus programs such as agreement, validity, and irrevocability in the presence of lossy or corrupt communications. We showed that the introduced procedure terminates even for an unbounded number of processes. To the best of our knowledge, this is the first fully-automatic approach to verify Heard-Of protocols in the presence of corrupt communication. We reported on preliminary experiments with correct and buggy variations of the protocols (Table 1).
Future Work. Future work can consider improving the scalability of the tool, and also extending the presented technique to more general models and more sophisticated faults such as Byzantine faults. Besides, the current technique assumes symmetric processes in the sense that all of them execute the same operation in each round. One can extend the model to non-symmetric processes as in the Heard-Of examples having coordinators, for instance in CoordUniformVoting and LastVoting algorithms in [4], or the Phase King and Phase Queen algorithms introduced in [2] in which a King or Queen is distinguished in each round, or the reliable broadcast algorithm in [16]. It will also be interesting to combine the approach with abstract interpretation for loops to be able to capture the distributed algorithms in which the number of iterations is crucial for the correctness of the algorithm, for example, the FloodMin algorithm in [5]. Moreover, identification of conditions for completeness of the approach, automatic refinement of the over-approximation and combination with richer theories are interesting directions for future work.
References
Alberti, F., Ghilardi, S., Pagani, E.: Cardinality constraints for arrays (decidability results and applications). Form. Methods Syst. Des. 51(3), 545–574 (2017). https://doi.org/10.1007/s10703-017-0279-6
Berman, P., Garay, J.A., Perry, K.J.: Optimal early stopping in distributed consensus. In: Segall, A., Zaks, S. (eds.) WDAG 1992. LNCS, vol. 647, pp. 221–237. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-56188-9_15
Biely, M., Widder, J., Charron-Bost, B., Gaillard, A., Hutle, M., Schiper, A.: Tolerating corrupted communication. In: Proceedings of the Twenty-sixth Annual ACM Symposium on Principles of Distributed Computing - PODC 2007. ACM Press (2007). https://doi.org/10.1145/1281100.1281136
Charron-Bost, B., Schiper, A.: The heard-of model: computing in distributed systems with benign faults. Distrib. Comput. 22(1), 49–71 (2009). https://doi.org/10.1007/s00446-009-0084-6
Chaudhuri, S., Erlihy, M., Lynch, N.A., Tuttle, M.R.: Tight bounds for k-set agreement. J. ACM (JACM) 47(5), 912–943 (2000)
Debrat, H., Merz, S.: Verifying fault-tolerant distributed algorithms in the heard-of model. Archive of Formal Proofs (2012) https://www.isa-afp.org/entries/Heard_Of.shtml
Drăgoi, C., Henzinger, T.A., Zufferey, D.: PSync: a partially synchronous language for fault-tolerant distributed algorithms. In: Proceedings of the 43rd Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages - POPL 2016. ACM Press (2016). https://doi.org/10.1145/2837614.2837650
Gleissenthall, K.v., Bjørner, N., Rybalchenko, A.: Cardinalities and universal quantifiers for verifying parameterized systems. In: Proceedings of the 37th ACM SIGPLAN Conference on Programming Language Design and Implementation, pp. 599–613 (2016)
Hawblitzel, C., Howell, J., Kapritsos, M., Lorch, J.R., Parno, B., Roberts, M.L., Setty, S., Zill, B.: IronFleet. In: Proceedings of the 25th Symposium on Operating Systems Principles - SOSP 2015. ACM Press (2015). https://doi.org/10.1145/2815400.2815428
Jaskelioff, M., Merz, S.: Proving the correctness of disk paxos. Archive of Formal Proofs (2005). https://www.isa-afp.org/entries/DiskPaxos.shtml
John, A., Konnov, I., Schmid, U., Veith, H., Widder, J.: Parameterized model checking of fault-tolerant distributed algorithms by abstraction. In: 2013 Formal Methods in Computer-Aided Design. IEEE (2013). https://doi.org/10.1109/fmcad.2013.6679411
Konnov, I., Veith, H., Widder, J.: On the completeness of bounded model checking for threshold-based distributed algorithms: reachability. Inform.Comput. 252, 95–109 (2017). https://doi.org/10.1016/j.ic.2016.03.006
Kuncak, V., Nguyen, H.H., Rinard, M.: An algorithm for deciding BAPA: Boolean algebra with presburger arithmetic. In: Nieuwenhuis, R. (ed.) CADE 2005. LNCS (LNAI), vol. 3632, pp. 260–277. Springer, Heidelberg (2005). https://doi.org/10.1007/11532231_20
Marić, O., Sprenger, C., Basin, D.: Cutoff bounds for consensus algorithms. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10427, pp. 217–237. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63390-9_12
Padon, O., Losa, G., Sagiv, M., Shoham, S.: Paxos made EPR: decidable reasoning about distributed protocols. In: Proceedings of the ACM on Programming Languages 1(OOPSLA), pp. 1–31 (2017). https://doi.org/10.1145/3140568
Srikanth, T., Toueg, S.: Simulating authenticated broadcasts to derive simple fault-tolerant algorithms. Distrib. Comput. 2(2), 80–94 (1987)
Stoilkovska, I., Konnov, I., Widder, J., Zuleger, F.: Verifying safety of synchronous fault-tolerant algorithms by bounded model checking. In: Vojnar, T., Zhang, L. (eds.) TACAS 2019. LNCS, vol. 11428, pp. 357–374. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17465-1_20
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Ganjei, Z., Rezine, A., Eles, P., Peng, Z. (2021). Verifying Safety of Parameterized Heard-Of Algorithms. In: Georgiou, C., Majumdar, R. (eds) Networked Systems. NETYS 2020. Lecture Notes in Computer Science(), vol 12129. Springer, Cham. https://doi.org/10.1007/978-3-030-67087-0_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-67087-0_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-67086-3
Online ISBN: 978-3-030-67087-0
eBook Packages: Computer ScienceComputer Science (R0)








 ,
,  ,
, 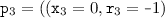 ,
,  ,
, 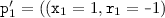 ,
,  ,
,  ,
,  capturing the control location of the execution.
capturing the control location of the execution.
