Igusa’s Conjecture on Exponential Sums Modulo p ^m and the Local-Global Principle

Abstract

In this survey we discuss the conjecture of Igusa on exponential sums modulo p ^m and some progress of this conjecture. We also present a connection between this conjecture and the local-global principle for forms of higher degree.

3.1 Introduction

Exponential sums play an important role in number theory with many deep applications. One of which is the use of the quadratic Gauss sums in Gauss’s proof of the law of quadratic reciprocity that is the first example of reciprocity laws (see [Ire90, Chapters 5 and 6]). Exponential sums modulo p have a deep connection with the Riemann hypothesis over finite fields by the works of Weil, Deligne, Katz, Laumon among others (see for example [Del77, Del74, Del80, Kat85, Kat99, Kat89, Wei48]).

This survey aims to introduce Igusa’s conjecture on exponential sums modulo p ^m. We report the progress made towards its resolution and its connection with the local-global principle for forms which was indeed one of the initial goals of Igusa.

We begin with one important class of exponential sums depending on a non-constant polynomial f in n variables with integer coefficients. Let N be a positive integer. We define the exponential sum modulo N associated to f by

$$\displaystyle \begin{aligned} E_N(f):=\dfrac{1}{N^n}\sum_{\overline{x}\in(\mathbb{Z}/N \mathbb{Z})^{n}}\exp(\frac{2\pi if(x)}{N}). \end{aligned} $$

(3.1)

Our goal is to look for good upper bounds of these sums. The Chinese remainder theorem allows us to simplify slightly the previous problem. In fact, we can express

$$\displaystyle \begin{aligned} \dfrac{1}{N}=\sum_{i=1}^{k}\dfrac{a_i}{p_i^{m_i}} \end{aligned}$$

where p ₁, …, p _k are distinct primes, a ₁, …, a _k and m ₁, …, m _k are integers such that (a _i, p _i) = 1 and m _i ≥ 1 for all 1 ≤ i ≤ k. It follows that

$$\displaystyle \begin{aligned} E_N(f)=\prod_{i=1}^{k}E_{p_i^{m_i}}(a_if). \end{aligned} $$

(3.2)

Thus it is sufficient to find good estimates of the exponential sums

$$\displaystyle \begin{aligned} E_{p,m}(f):=E_{p^m}(f) = \dfrac{1}{p^{mn}}\sum_{\overline{x}\in(\mathbb{Z}/p^m \mathbb{Z})^{n}}\exp(\frac{2\pi if(x)}{p^m}) \end{aligned}$$

for all primes p and all m ≥ 1.

Example 3.1.1

We consider the simplest example where f(x) = x. We see easily that for N > 1, we have

$$\displaystyle \begin{aligned} E_N(f)=0. \end{aligned}$$

Example 3.1.2

We now consider a more complicated polynomial by taking f(x) = x ². Let p be a prime and m be a positive integer. We write m = 2k + r where k ≥ 1 and r ∈{0, 1}. We calculate directly $E_{p^m}(f)$ by distinguishing two cases.

Case 1: p is an odd prime. We see that if (a, p) = 1 and 0 ≤ α ≤ k − 1, then

$$\displaystyle \begin{aligned} \sum_{b=1}^{p^{\alpha+1}}\exp(\frac{2\pi i(p^{\alpha}a+p^{m-1-\alpha}b)^2}{p^m})=0. \end{aligned}$$

Thus we get

$$\displaystyle \begin{aligned}E_{p^{2k}}(f)=\frac{1}{p^{2k}}\sum_{a=1}^{p^k}\exp(\frac{2\pi i(p^{k}a)^2}{p^{2k}})=\frac{1}{p^{k}}. \end{aligned}$$

We also have

$$\displaystyle \begin{aligned}E_{p^{2k+1}}(f)=\frac{1}{p^{2k+1}}\sum_{a=1}^{p^{k+1}}\exp(\frac{2\pi i(p^{k}a)^2}{p^{2k+1}})=\frac{1}{p^{k+1}}\sum_{a=1}^p\exp(\frac{2\pi ia^2}{p}). \end{aligned}$$

Thus

$$\displaystyle \begin{aligned} |E_{p^{2k+1}}(f)|=\frac{1}{p^{k+\frac{1}{2}}}. \end{aligned}$$

Here the above equality is a consequence of the following fact about quadratic Gauss sums (see for example [Ire90, Chapter 6])

$$\displaystyle \begin{aligned}(\sum_{a=1}^p\exp(\frac{2\pi ia^2}{p}))^2=p. \end{aligned}$$

Case 2: p = 2. It is still true that if (a, 2) = 1 and 0 ≤ α ≤ k − 2, then

$$\displaystyle \begin{aligned}\sum_{b=1}^{2^{\alpha+2}}\exp(\frac{2\pi i(2^{\alpha}a+2^{m-2-\alpha}b)^2}{2^{m}})=0. \end{aligned}$$

Thus

$$\displaystyle \begin{aligned}E_{2^{2k}}(f)=\frac{1}{2^{2k}}\sum_{a=1}^{2^{k+1}}\exp(\frac{2\pi i(2^{k-1}a)^2}{2^{2k}})=\frac{1}{2^{k+1}}\sum_{a=1}^4\exp(\frac{2\pi ia^2}{4})=\frac{1+i}{2^k}. \end{aligned}$$

Further, we have

$$\displaystyle \begin{aligned}E_{2^{2k+1}}(f)=\frac{1}{2^{2k+1}}\sum_{a=1}^{2^{k+2}}\exp(\frac{2\pi i(2^{k-1}a)^2}{2^{2k+1}})=\frac{1}{2^{k+2}}\sum_{a=1}^8\exp(\frac{2\pi ia^2}{8})=\frac{1+i}{2^{\frac{2k+1}{2}}}.\end{aligned}$$

By the same calculation, for all primes p, all positive integers m and all non-zero integers A such that (A, p) = 1, we have

$$\displaystyle \begin{aligned}|E_{p^m}(Ax^2)|\leq c_p \, p^{-\frac{m}{2}},\end{aligned}$$

where

$$\displaystyle \begin{aligned} c_p=\begin{cases} 1 & \text{ if } p\neq 2, \\ \sqrt{2} & \text{ otherwise}. \end{cases} \end{aligned} $$

(3.3)

Hence by (3.2) we conclude that for all non-zero integers N,

$$\displaystyle \begin{aligned} |E_{N}(f)|\leq \sqrt{2} N^{-\frac{1}{2}}. \end{aligned}$$

The equality holds if N > 1 is a square number.

In the case where f is a polynomial in one variable, exponential sums modulo p ^m have been studied by many mathematicians and we refer the reader to [Coc99] for more details.

For polynomials f in n variables, Igusa showed that for each prime p, there exist a constant σ _p ≤ +∞ and a positive constant c _p such that for all σ < σ _p and all m ≥ 1, we have

$$\displaystyle \begin{aligned} |E_{p^m}(f)|\leq c_p \, p^{-m\sigma}. \end{aligned} $$

(3.4)

Furthermore, either σ _p = +∞ or − σ _p is the real part of a pole of the Igusa local zeta function associated to f. Thus we would like to know how to obtain a global information from the local information for each prime p, i.e. the dependence of c _p and σ _p in p.

Example 3.1.3

In Example 3.1.1, for each prime p we can take σ _p = +∞ and an arbitrary positive constant c _p > 0.

In Example 3.1.2 we can take $\sigma _p=\frac {1}{2}$ for all primes p and

$$\displaystyle \begin{aligned} c_p=\begin{cases} 1 & \text{ if } p\neq 2, \\ \sqrt{2} & \text{ otherwise}. \end{cases} \end{aligned} $$

(3.5)

In order to prove (3.4), Igusa found a way to understand exponential sums via singularity theory. In fact, exponential sums $E_{p^m}(f)$ modulo p ^m can be computed by certain Igusa local zeta functions (see Sect. 3.2 for more details). As a consequence, the asymptotic expansion of $E_{p^m}(f)$ for m > 1 could be given in terms of poles of these Igusa local zeta functions.

We now give more details about the above discussion. First we recall some basic facts about p-adic fields and then express exponential sums modulo p ^m as p-adic integrals. Letting p be a prime, we define the p-adic norm |.|_p on the field of rational numbers ${\mathbb Q}$ as follows. We set |0|_p := 0 and for all integers a, b, k with (a, p) = (b, p) = 1,

$$\displaystyle \begin{aligned}|\dfrac{a}{b}p^k|{}_p:=p^{-k}\end{aligned}$$

We denote by ${\mathbb Q}_p$ the completion of ${\mathbb Q}$ with respect to this norm and by ${\mathbb Z}_p$ the closure of ${\mathbb Z}$ in ${\mathbb Q}_p$. Then ${\mathbb Q}_p$ is a locally compact field equipped with the norm |.|_p which extends |.|_p over ${\mathbb Q}$. Further, ${\mathbb Z}_p$ is a closed and open subring of ${\mathbb Q}_p$ and

$$\displaystyle \begin{aligned} {\mathbb Z}_{p}=\{x\in {\mathbb Q}_p \ | \ |x|{}_p\leq 1\}. \end{aligned}$$

It is a discrete valuation ring with the unique maximal ideal

$$\displaystyle \begin{aligned} {\mathscr M}_p=p{\mathbb Z}_p=\{x\in{\mathbb Q}_p| |x|{}_p<1\}. \end{aligned}$$

Let x be an element of ${\mathbb Q}_p$. We can write

$$\displaystyle \begin{aligned}x=\sum_{i\geq k}a_ip^i\end{aligned}$$

for some integers k and a _i with 0 ≤ a _i ≤ p − 1. If x = 0, then we set $\operatorname {ord}_p(x):=+\infty$. Otherwise, we can suppose that a _k ≠ 0 and set $\operatorname {ord}_p(x):=k$. Then it is clear that

$$\displaystyle \begin{aligned} |x|{}_p=p^{-\operatorname{ord}_p(x)}. \end{aligned}$$

Here we take the convention that p ^−∞ = 0. We note that $x\in {\mathbb Z}_p$ if and only if $\operatorname {ord}_p(x)\geq 0$ and $x\in {\mathscr M}_p$ if and only if $\operatorname {ord}_p(x)>0$.

The standard additive character of ${\mathbb Q}_p$ is the homomorphism of abelian groups

$$\displaystyle \begin{aligned}\psi_1:=\exp: ({\mathbb Q}_p,+)\to({\mathbb C}^*,\times)\end{aligned}$$

which sends x to $\exp (2\pi ix')$ with $x'\in {\mathbb Z}[\frac {1}{p}]\cap (x+{\mathbb Z}_p)$. It is well-defined since the value $\exp (2\pi ix')$ does not depend on the choice of $x'\in {\mathbb Z}[\frac {1}{p}]\cap (x+{\mathbb Z}_p)$. An additive character ψ of ${\mathbb Q}_p$ is defined to be a continuous homomorphism from $({\mathbb Q}_p,+)$ to $({\mathbb C}^*,\times )$ with compact image. For such an additive character ψ there exists a unique $z\in {\mathbb Q}_p$ such that

$$\displaystyle \begin{aligned} \psi_z(x):=\psi_1(xz)=\psi(x). \end{aligned}$$

Since ${\mathbb Q}_p$ is locally compact, we can endow ${\mathbb Q}_p^n$ with the Haar measure |dx| normalized such that ${\mathbb Z}_p^n$ has volume 1. It follows immediately that

$$\displaystyle \begin{aligned}E_{p^m}(f)=\int_{{\mathbb Z}_p^n}\psi_{p^{-m}}(f(x))|dx|.\end{aligned}$$

This suggests that to any additive character ψ of ${\mathbb Q}_p$ we can associate an exponential sum by

$$\displaystyle \begin{aligned}E_{\psi}(f):=\int_{{\mathbb Z}_p^n}\psi(f(x))|dx|. \end{aligned}$$

This integral is an example of Igusa local zeta functions.

More generally, letting L be a non-Archimedean local field which is a finite extension of either the p-adic field ${\mathbb Q}_p$ or the field of Laurent series ${\mathbb F}_q((t))$ with coefficients in a finite field ${\mathbb F}_q$, we can associate an exponential sum E _ψ(f) to any polynomial f ∈ L[x ₁, …, x _n] and any additive character ψ of L.

As mentioned earlier, the asymptotic expansion of $E_{p^m}(f)$ for m > 1 could be given in terms of poles of the associated Igusa local zeta function. To determine the poles of Igusa local zeta functions, Igusa formulated the so-called strong monodromy conjecture which relates these poles to eigenvalues of monodromy and roots of Bernstein-Sato polynomials (see Sect. 3.2.3). As a consequence, if the strong monodromy conjecture holds for f, then the size of $E_{p^m}(f)$ can be bounded in terms of the biggest non-trivial root of the Bernstein-Sato polynomial b _f of f.

We now state a coarse form of Igusa’s conjecture for a uniform bound of exponential sums modulo p ^m when p and m go to infinity.

Conjecture 3.1.4

Let f be a non-constant polynomial in n variables with coefficients in ${\mathbb Z}$ and σ be a positive real number. Suppose that for all primes p large enough, there exists a constant c _p > 0 such that we have

$$\displaystyle \begin{aligned}|E_{p^m}(f)|\leq c_p \, p^{-m\sigma}\end{aligned}$$

for all m ≥ 2. Then there exists a constant C > 0 such that

$$\displaystyle \begin{aligned}|E_{p^m}(f)|\leq C \, p^{-m\sigma}\end{aligned}$$

for all primes p large enough and all m ≥ 2.

Remark 3.1.5

We rediscover the original conjecture of Igusa for homogeneous polynomials f. We refer the reader to Sect. 3.4.2 for a discussion about this conjecture as well as a variant of this conjecture due to Cluckers [Clu08a] and Cluckers and Veys [Clu16].

Remark 3.1.6

The condition m ≥ 2 in Conjecture 3.1.4 can be replaced by a weaker condition m ≥ 1 in many cases (see Example 3.1.2). However, in general, we have to treat separately the case m = 1 as explained below.

Let us consider the polynomial $f=x_1-x_1^2x_2$. We show that $E_{p^m}(f)=0$ for all primes p and all m > 1 (see Remark 3.3.3 for more details). But for all primes p we have

$$\displaystyle \begin{aligned} E_{p}(f)=&\frac{1}{p^2}(\sum_{x_1 \neq 0\mod p}\sum_{x_2\in {\mathbb Z}/p{\mathbb Z}}\exp(\frac{2\pi i (x_1-x_1^2x_2)}{p})+\sum_{x_2\in {\mathbb Z}/p{\mathbb Z}}1) =\frac{1}{p}. \end{aligned} $$

Let σ > 1 then

$$\displaystyle \begin{aligned}|E_{p^m}(f)|\leq p^{\sigma-1} p^{-m\sigma}\end{aligned}$$

for all primes p and all m ≥ 1 but we cannot find a constant C such that

$$\displaystyle \begin{aligned}|E_{p^m}(f)|\leq C \, p^{-m\sigma}\end{aligned}$$

for all primes p large enough and all m ≥ 1.

Remark 3.1.7

We keep the notation of Conjecture 3.1.4. Suppose that there exist a positive integer M and a constant C ≤ 1 such that

$$\displaystyle \begin{aligned}|E_{p^m}(af)|\leq C \, p^{-m\sigma}\end{aligned}$$

for all primes p > M, all integers a with (a, p) = 1 and all m ≥ 1. Moreover, for each prime p ≤ M there exists a constant c _p such that

$$\displaystyle \begin{aligned}|E_{p^m}(af)|\leq c_p \, p^{-m\sigma}\end{aligned}$$

for all integers a with (a, p) = 1 and all m ≥ 1. Thus (3.2) implies immediately

$$\displaystyle \begin{aligned}|E_{N}(f)|\leq C'N^{-\sigma}\end{aligned}$$

for some constant C′ > 0 and all N ≥ 1.

Remark 3.1.8

The statement of Conjecture 3.1.4 extends without difficulty to an arbitrary global field K (i.e a finite extension of ${\mathbb Q}$ or a function field of an algebraic curve over a finite field) and a non-constant polynomial $f\in \mathscr {O}_K[x_1,\dots ,x_n]$ where $\mathscr {O}_K$ is the ring of integers of K.

In fact, for any finite place v of K, we denote by K _v the completion of K at v equipped with the norm $|.|:K_v\to {\mathbb R}$ and by $\mathscr {O}_v$ the ring of integers of K _v. Let π _v be a uniformizer of $\mathscr {O}_v$. We fix an additive character ψ ₁ of K _v such that $\psi _1|{ }_{\mathscr {O}_v}=1$ but $\psi _1|\pi _v^{-1}\mathscr {O}_v\neq 1$ (see Sects. 3.2 and 3.3 for more details). Let σ be a positive real number such that for all but finitely many finite places v of K and all $z\in K_v\setminus \pi _v^{-1}\mathscr {O}_v$, we have

$$\displaystyle \begin{aligned}|E_{\psi_z}(f)|=|\int_{\mathscr{O}_v^n}\psi_1(zf(x))|dx||\leq c_v|z|{}^{-\sigma}. \end{aligned}$$

Then we can ask whether there exists a constant C such that c _v ≤ C for all but finitely many finite places v.

In Sect. 3.4 we give an overview of progress on this conjecture due to many mathematicians. We begin with the work of Igusa in the non-degenerate case and end with the most recent result of Cluckers, Mustaţă and the author in case of non-rational singularities.

We should mention that Igusa’s work [Igu78] around exponential sums modulo p ^m was motivated by his ultimate hope to extend the local-global principle to forms of higher degree (i.e. homogeneous polynomials of degree at least 3). Recall that for a form $f \in {\mathbb Z}[x_1,\dots ,x_n]$ of degree d, we say that the local-global principle holds for f if the following assertion is true: f represents zero in ${\mathbb Q}$ if and only if it represents zero in ${\mathbb R}$ and in all fields ${\mathbb Q}_p$. The Hasse-Minkowski theorem states that the local-global principle holds for quadratic forms. The idea of Igusa to generalize the Hasse-Minkowski theorem to forms of higher degree is divided into two steps. First, a good uniform bound of exponential sums modulo p ^m in p and m together with some extra conditions would imply the existence of a certain Poisson formula (see Sect. 3.3.2 and Proposition 3.3.7). Second, one derives the local-global principle from this Poisson formula (see Sect. 3.5).

The above discussion illustrates one of the common approaches of this volume which is to apply analytic techniques in the study of arithmetic geometry. The reader is strongly encouraged to read other chapters for “further examples” in different settings, in particular, the lecture of Poineau and Turchetti [Poi20a, Poi20b] and to discover possible connections among them.

We close this section by saying some words about function fields. In this lecture we only consider Conjecture 3.1.4 for number fields K but it is natural to ask whether one could extend the results in Sects. 3.2, 3.3 and 3.4 to the case where K is a function field which means the function field of an algebraic curve over a finite field ${\mathbb F}_q$. The answer is yes for non-constant polynomials f ∈ K[x ₁, …, x _n] such that for all critical values a of f, f ⁻¹(a) admits an embedded resolution with good reduction at all but finitely many places v of K (see Sect. 3.2 for the definition of such a resolution). For number fields the existence of an embedded resolution for all polynomials f is guaranteed by Hironaka’s theorem in [Hir64]. However, the resolution of singularities in positive characteristic is more complicated and the existence of such a resolution for general f is still unknown. Hence we hope that some young mathematicians could attack this challenging question in the future.

3.2 Igusa Local Zeta Functions and Exponential Sums Modulo p ^m

In this section we review the notion of Igusa local zeta functions and exponential sums modulo p ^m over an arbitrary non-Archimedean local field of characteristic 0. We refer the reader to the excellent survey of Denef [Den91] and the work of Igusa [Igu78] for more details.

3.2.1 Local Fields

For the rest of this paper we fix a positive integer n ≥ 1.

In what follows, we consider a non-Archimedean local field L of characteristic 0. It means that L is a finite extension of ${\mathbb Q}_p$ defined as in Sect. 3.1 for some prime p. To simplify, we will say that L is a p-adic field and we set p _L := p.

We remark that the norm |.|_p on ${\mathbb Q}_p$ extends uniquely to a norm |.|_L in L. We will write |.| instead of |.|_L if no confusion results. Let $\mathscr {O}_L$ be the ring of integers in L. Then

$$\displaystyle \begin{aligned} \mathscr{O}_L=\{x\in L \ | \ |x|\leq 1\}. \end{aligned}$$

It is a discrete valuation ring with the maximal ideal ${\mathscr M}_L$ given by

$$\displaystyle \begin{aligned} {\mathscr M}_L=\{x\in L \ | \ |x| < 1\}. \end{aligned}$$

We denote by $k_L=\mathscr {O}_L/{\mathscr M}_L$ the residue field of L. This field is a finite extension of ${\mathbb F}_p$ and we denote by q _L the cardinality of k _L. Let ϖ be a uniformizer of L, i.e. ϖ is a generator of ${\mathscr M}_L$. For each non-zero element x ∈ L, we can write in a unique way x = λϖ ^α where $\lambda \in \mathscr {O}_L^*$ and $\alpha \in {\mathbb Z}$. We set

$$\displaystyle \begin{aligned} \text{ac}(x):=\lambda, \quad \operatorname{ord}(x):=\alpha, \end{aligned}$$

and

$$\displaystyle \begin{aligned} \overline{\text{ac}}(x):=\text{ac}(x) \mbox{ mod } {\mathscr M}_L. \end{aligned}$$

We can extend the maps ac and $\operatorname {ord}$ to L by setting ac(0) = 0 and $\operatorname {ord}(0)=+\infty$.

We introduce the following three functions which will play an important role in the sequel. First, the standard additive character of L is the homomorphism $\psi _1:L \to {\mathbb C}^*$ given by

$$\displaystyle \begin{aligned} \psi_1:=\exp(\operatorname{Tr}_{L/{\mathbb Q}_p}(x)) \end{aligned}$$

where $\exp (.)$ is the map given in Sect. 3.1. Any additive character ψ of L can be written in the form ψ(x) := ψ _z(x) = ψ(zx) for some element z ∈ L. We put

$$\displaystyle \begin{aligned} m(\psi):=-\operatorname{ord}(z). \end{aligned}$$

Second, a multiplicative character χ of $\mathscr {O}_L^*$ is defined to be a continuous homomorphism from $(\mathscr {O}_L^*,\times )$ to $({\mathbb C}^*,\times )$ with finite image. For a multiplicative character χ, let c(χ) be the smallest integer such that $\chi |{ }_{1+{\mathscr M}_L^{c(\chi )}}$ is trivial. It is called the conductor of χ. We set χ(0) := 0. It is clear that χ induces a character of $\mathscr {O}_L^{*}/(1+{\mathscr M}_L^{c(\chi )})$. In particular, if c(χ) = 1, then χ induces a character of $k_L^*$ which is still denoted by χ and we extend χ to k _L by setting χ(0) = 0.

Third, a Schwartz-Bruhat function $\Phi :L^n \to {\mathbb C}$ is a locally constant function with compact support, denoted by $\operatorname {Supp}(\Phi )$. We say that Φ is residual if $\operatorname {Supp}(\Phi )\subset \mathscr {O}_L^n$ and if Φ(x) only depends on $x \mbox{ mod } {\mathscr M}_L$. If Φ is residual, then Φ induces a function $\overline {\Phi }:k_L^n\to {\mathbb C}$.

As in case of ${\mathbb Q}_p^n$, we will endow L ⁿ with a Haar measure |dx| such that the volume of $\mathscr {O}_L^n$ is 1.

3.2.2 Embedded Resolutions

Let K be a field of characteristic 0. Let f ∈ K[x ₁, …, x _n] be a non-constant polynomial in n variables. We set

$$\displaystyle \begin{aligned} X=\mathbb A^n_K=\operatorname*{\mathrm{Spec}} K[x_1,\dots,x_n], \end{aligned}$$

and

$$\displaystyle \begin{aligned} D=f^{-1}(0)=\operatorname*{\mathrm{Spec}} K[x_1,\dots,x_n]/(f). \end{aligned}$$

An embedded resolution (Y, h) of D in X is a closed smooth subscheme Y  of the projective space ${\mathbb P}^m_X$ over X for some m such that the restriction h to Y  of the projection ${\mathbb P}^m_X \to X$ has the following properties:

• (i) h : Y ∖h ⁻¹(D) → X∖D is an isomorphism,

• (ii) the reduced scheme (h ⁻¹(D))_red associated to h ⁻¹(D) has simple normal crossings as a subscheme of Y  (i.e. its irreducible components are smooth and intersect transversally).

Let $E_{i}, i\in \mathscr {T}$, be the irreducible components of (h ⁻¹(D))_red. For each $i\in \mathscr {T}$, let N _i be the multiplicity of E _i in the divisor of f ∘ h on Y  and let ν _i − 1 be the multiplicity of E _i in the divisor of h ^∗(dx ₁ ∧… ∧ dx _n). The set $\{(N_{i},\nu _{i})_{i \in \mathscr {T}} \}$ are called the numerical data of the resolution.

Further, for each subset $I\subset \mathscr {T}$, we define

$$\displaystyle \begin{aligned} E_{I}:=\cap_{i\in I} E_{i} \qquad \text{and} \qquad \overset{\circ}{E_{I}}:=E_{I}\backslash\cup_{j\in \mathscr{T}\backslash I}E_{j}. \end{aligned}$$

In particular, when I = ∅ we have E _∅ = Y .

We also denote by C _f ⊂ X be the critical locus of $f:X \to \mathbb A^1_K$.

We remark that such a resolution exists by the seminal work of Hironaka [Hir64, Main Theorem II]. It can be obtained from a series of blow-ups with smooth centers.

Remark 3.2.1

Let K′ be a field extension of K. By the functoriality of embedded resolutions, h induces an embedded resolution $h: Y_{K'}\to {\mathbb A}^n_{K'}=X_{K'}$ of $D_{K'}$ in $X_{K'}$. We remark that each blow-up center C of h may be written as a union of finitely many irreducible components C _i over K′ and we can replace the blow-up with center C by the composition of blow-ups with center C _i. If K′ is an algebraically closed field, then h induces an embedded resolution which can be obtained by successive blow-ups at irreducible smooth varieties. Similarly, each irreducible component E _i can be split into a disjoint union of finitely many irreducible components E _ij over K′. But we always have N _i = N _ij, ν _i = ν _ij.

In what follows, let K be a number field, $\mathscr {O}_K$ be its ring of integers and $f\in \mathscr {O}_K[x_1,\dots ,x_n]$ be a non-constant polynomial in n variables. Let (Y, h) be an embedded resolution of D in X. If Z is a closed subscheme of Y  and $\mathfrak {p}$ is a prime ideal of $\mathscr {O}_K$, we denote by $\overline {Z}$ the reduction modulo $\mathfrak {p}$ of Z (see [Shi55]). We say that the embedded resolution (Y, h) of D in X has good reduction modulo $\mathfrak {p}$ if the following conditions are satisfied:

• (i) $\overline {Y}$ and $\overline {E}_{i}$ are smooth for all $i \in \mathscr {T}$,

• (ii) $\cup _{i\in \mathscr {T}}\overline {E}_{i}$ has simple normal crossings,

• (iii) the schemes $\overline {E}_{i}$ and $\overline {E}_{j}$ have no common components for all $i,j \in \mathscr {T}$ with i ≠ j.

One can show that there exists a finite subset S of $\operatorname *{\mathrm {Spec}}\mathscr {O}_K$, such that for all $\mathfrak {p}\notin S$, we have $f\in \mathscr {O}_{\mathfrak {p}}[x]$, $f\not \equiv 0 \bmod \mathfrak {p}$ and that the resolution (Y, h) for f has good reduction mod $\mathfrak {p}$ (see [Den87, Theorem 2.4]). Then for $\mathfrak {p}\notin S$ and $I\subset \mathscr {T}$, one can show that $\overline {E}_{I}=\cap _{i\in I}\overline {E}_{i}$. We set

$$\displaystyle \begin{aligned} \overset{\circ}{\overline{E}}_{I}:=\overline{E}_{I}\backslash\cup_{j\notin I}\overline{E}_{j}. \end{aligned}$$

Letting a be a closed point of $\overline {Y}$, we put $\mathscr {T}_{a}:=\{i\in \mathscr {T}| a\in \overline {E}_{i}\}$. In the local ring of $\overline {Y}$ at a, we can write

$$\displaystyle \begin{aligned} \overline{f}\circ\overline{h}=\overline{u}\prod_{i\in \mathscr{T}_{a}}\overline{g}_{i}^{N_{i}}, \end{aligned}$$

where $\overline {u}$ is a unit, $(\overline {g}_{i})_{i\in \mathscr {T}_{a}}$ is a part of a regular system of parameters and N _i is the corresponding multiplicity defined as above.

3.2.3 Igusa Local Zeta Functions and the Monodromy Conjecture

Recall that L is a p-adic field. Let f ∈ L[x ₁, …, x _n] be a non-constant polynomial in n variables with coefficients in L. Let χ be a multiplicative character of $\mathscr {O}_L^*$ and Φ be a Schwartz-Bruhat function on L ⁿ. Following Weil we associate to the data (L, f, χ,  Φ) an Igusa local zeta function

$$\displaystyle \begin{aligned}Z_{L,\Phi,f}(s,\chi):=\int_{L^n}\Phi(x) \, \chi(\text{ac}(f(x)) \, |f(x)|{}^s \, |dx|,\end{aligned}$$

for $s\in {\mathbb C}$ with $\Re (s)>0$. One can see that Z _L,Φ,f(s, χ) is holomorphic in this region and extends to a meromorphic function on ${\mathbb C}$. The following theorem gives basic properties of these zeta functions Z _L,Φ,f(s, χ).

Theorem 3.2.2 (Igusa [Igu74] and [Igu78])

We keep the previous notation. Then we have

• (i) Z _L,Φ,f(s, χ) is a rational function of $q_L^{-s}$.

• (ii) If (Y, h) is an embedded resolution of f ⁻¹(0) in ${\mathbb A}^n_L$ with the numerical data $\{(N_i,\nu _i)_{i\in \mathscr {T}}\}$ , then the poles of Z _L,Φ,f(s, χ) are among the values

  $$\displaystyle \begin{aligned} s=-\frac{\nu_i}{N_i}+\frac{2\pi ik}{\log_e{q_L}} \end{aligned}$$

  with $k\in {\mathbb Z}$ and $i\in \mathscr {T}$ such that $\chi ^{N_i}=1$.

• (iii) If $\operatorname {Supp}(\Phi )\cap C_f\subset f^{-1}(0)$ , then Z _L,Φ,f(s, χ) = 0 for all but finitely many χ. Here recall that C _f ⊂ X denotes the singular locus of $f:X \to \mathbb A^1_L$.

In the case where we have an embedded resolution having good reduction modulo ${\mathscr M}_L$, the above results could be improved as follows.

Theorem 3.2.3 (Denef [Den91] and [Den87])

Suppose that there exists an embedded resolution (Y, h) of f ⁻¹(0) having good reduction modulo ${\mathscr M}_L$ and $f\neq 0 \mathit{\mbox{ mod }} {\mathscr M}_L$ . We suppose further that Φ is a residual Schwartz-Bruhat function on L ⁿ . Then we have

• (i) If the conductor c(χ) of χ is at least 2 and that the numerical data $\{(N_i,\nu _i)_{i\in \mathscr {T}}\}$ of (Y, h) satisfying $N_i\notin {\mathscr M}_L$ for all $i\in \mathscr {T}$ , then Z _L,Φ,f(s, χ) is constant as a function of s. Moreover, if $C_{\overline {f}}\cap \operatorname {Supp}(\overline {\Phi })\subset \overline {f}^{-1}(0)$ , then Z _L,Φ,f(s, χ) = 0.

• (ii) If c(χ) = 1 and χ is of order d, let $\mathscr {T}_d=\{I \subset \mathscr {T} \mid \forall i\in I: d\mid N_{i}\}$ . Then

  $$\displaystyle \begin{aligned} Z_{L,\Phi,f}(s,\chi)=q_L^{-n}\sum_{I \in \mathscr{T}_d} c_{I,\Phi,\chi}\prod_{i\in I}\frac{(q_L-1)q_L^{-N_{i}s-\nu_{i}}}{1-q_L^{-N_{i}s-\nu_{i}}}, \end{aligned}$$

  where

  

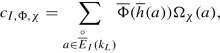
  and

  $$\displaystyle \begin{aligned}\Omega_{\chi}(a)=\chi(\overline{u}(a))\end{aligned}$$

  for any choice of $\overline {u}$ in the local ring of $\overline {Y}$ at $\overline {a}$ as in Sect. 3.2.1.

□

In many known examples, many of the possible poles are false poles of the zeta function (even if we take the intersection of the sets of possible poles over all embedded resolutions). The monodromy conjecture suggests an explanation for this phenomenon.

Now let us recall some notions about monodromy and Bernstein-Sato polynomials.

Let $f\in {\mathbb C}[x_1,\dots ,x_n]$ be a non-constant polynomial with coefficients in ${\mathbb C}$ and P be a point in ${\mathbb C}^n$ such that f(P) = a. Let B be a sufficiently small ball with center P. In [Mil68] Milnor proved that f|_B is a locally trivial C ^∞ fibration over a small enough punctured disc $A\subset {\mathbb C}\setminus \{a\}$. Thus the diffeomorphism type of F _P = f ⁻¹(t) ∩ B of f around P does not depend on t ∈ A. The counter clockwise generator of the fundamental group of A induces an automorphism T of $H^*(F_P,{\mathbb C})$. We call F _P and T the Milnor fiber and the local monodromy of f at P, respectively.

Let K be a field of characteristic 0 and f ∈ K[x ₁, …, x _n] be a polynomial. Bernstein [Ber72] proved that there exist $P\in K[x,\dfrac {\partial }{\partial x},s]$ and a polynomial b(s) ∈ K[s] ∖{0} such that Pf ^s+1 = b(s)f ^s. The monic polynomial of smallest degree satisfying this functional equation is called the Bernstein-Sato polynomial of f, denoted by b _f. One can show that (s + 1)∣b _f(s) if f is non-constant. Furthermore, Kashiwara claimed in [Kas76] that all roots of b _f are negative rational numbers. Moreover, Malgrange [Mal83] proved that if α is a root of b _f, then $\exp (2\pi i\alpha )$ is an eigenvalue of the local monodromy of f at some point of f ⁻¹(0) and all eigenvalues are obtained in this way.

Igusa suggested that the poles of the Igusa local zeta function associated to f should be described by the roots of the associated Bernstern-Sato polynomial or the eigenvalues of the local monodromy of f.

Conjecture 3.2.4 (Igusa, Monodromy Conjecture)

Let K be a number field and f be a non-constant polynomial in K[x ₁, …, x _n]. For all but finitely many primes p, if s is a pole of Z _L,Φ,f(s, χ) where L is a p-adic field containing K, then $\exp (2\pi i\Re (s))$ is an eigenvalue of the local monodromy of f at some complex point of f ⁻¹(0).

Conjecture 3.2.5 (Strong Monodromy Conjecture)

Let K be a number field and f be a non-constant polynomial in K[x ₁, …, x _n]. For all but finitely many primes p, if s is a pole of Z _L,Φ,f(s, χ) where L is a p-adic field containing K, then $\Re (s)$ is a root of b _f.

By the above discussion, if α is a root of b _f, then $\exp (2\pi i\alpha )$ is an eigenvalue of the local monodromy of f at some point. Thus Conjecture 3.2.5 implies Conjecture 3.2.4. Note that Conjecture 3.2.4 only implies that if s is pole of Z _L,Φ,f(s, χ), then $\Re (s)+a$ is a root of b _f for some integer a.

Both conjectures might be true for all p-adic fields. But it seems very hard for primes for which we cannot find an embedded resolution with good reduction. Although both conjectures have been checked in many cases (see for example [Loe88] for polynomials in two variables), to our knowledge, they are widely open in general.

3.2.4 Exponential Sums and Fiber Integration

In this section we introduce a general form of exponential sums modulo p ^m and its relation with Igusa local zeta functions.

Recall that L is a p-adic field. Let f be a non-constant polynomial in L[x ₁, …, x _n], Φ be a Schwartz-Bruhat function on L ⁿ and z be an element of L. To this data we associate the exponential sum E _L,Φ,z(f) by

$$\displaystyle \begin{aligned}E_{L,\Phi,z}(f):=\int_{L^n} \Phi(x) \, \psi_1(zf(x)) \, |dx|.\end{aligned}$$

It is clear that if $L={\mathbb Q}_p$, z = p ^−m, $\Phi ={\mathbf 1}_{{\mathbb Z}_p}$, then E _L,Φ,z(f) is equal to $E_{p^m}(f)$ introduced in Sect. 3.1.

To describe the relation between exponential sums modulo p ^m and Igusa local zeta functions, we need to recall the notion of fiber integration. For each y ∈ L, we set U _y := f ⁻¹(y) ∖ C _f. Since f(x) = y on U _y, we get

$$\displaystyle \begin{aligned} \dfrac{\partial f}{\partial x_1}dx_1+\dots+\dfrac{\partial f}{\partial x_n}dx_n=0 \end{aligned} $$

(3.6)

on U _y. Let a ∈ U _y. Since a∉C _f, there exists 1 ≤ ℓ ≤ n such that $\dfrac {\partial f}{\partial x_\ell }(a)\neq 0$. If j ≠ ℓ and 1 ≤ j ≤ n such that $\dfrac {\partial f}{\partial x_j}(a)\neq 0$, taking the exterior product on both sides of (3.6) with ∧_{i ≠ j,i ≠ ℓ} dx _i yields

$$\displaystyle \begin{aligned}(-1)^{j-1}\dfrac{\partial f}{\partial x_j}(a)\bigwedge_{i\neq \ell}dx_i=(-1)^{\ell-1}\dfrac{\partial f}{\partial x_\ell}(a)\bigwedge_{i\neq j}dx_i.\end{aligned} $$

Thus $d_{f,y}:=(-1)^{\ell -1}(\dfrac {\partial f}{\partial x_\ell })^{-1}\bigwedge _{i\neq \ell }dx_i|{ }_{U_y}$ is a well-defined non-vanishing regular (n − 1)-form around a ∈ U _y. For each Schwartz-Bruhat function Φ on L ⁿ, we set

$$\displaystyle \begin{aligned}F_{f,y}(\Phi):=\int_{f^{-1}(y)}\Phi \, |d_{f,y}|.\end{aligned} $$

We can show that

$$\displaystyle \begin{aligned}E_{L,\Phi,z}(f)=\int_LF_{f,y}(\Phi) \, \psi_1(zy) \, |dy|\end{aligned}$$

is the Fourier transform of F _f,y( Φ) and

$$\displaystyle \begin{aligned}Z_{L,\Phi,f}(s,\chi)=\int_LF_{f,y}(\Phi) \, \omega_{\chi,s}(y) \, |dy|\end{aligned}$$

is the Mellin transform of $(1-q_L^{-1})q_L^{-\operatorname {ord}(y)}F_{f,y}(\Phi )$ where the quasi-character ω _χ,s is given by $\omega _{\chi ,s}(y)=\chi (\text{ac}(y))q_L^{-\operatorname {ord}(y)s}$.

On the other hand, using Fourier transform we can compute E _L,Φ,z(f) by Igusa local zeta functions.

Proposition 3.2.6 ([Den91], Proposition 1.4.4)

Let $u\in \mathscr {O}_{L}^{\times }$ , ϖ be a uniformiser of L and $m\in {\mathbb Z}$ . Then $E_{L,\Phi ,u\varpi ^{-m}}(f)$ is equal to

$$\displaystyle \begin{aligned} Z_{L,\Phi,f}(0,\chi_{\mathrm{triv}})&+\mathrm{Coeff}_{t^{m-1}}\Big( \dfrac{(t-q_L)Z_{L,\Phi,f}(s,\chi_{\mathrm{triv}})}{(q_L-1)(1-t)}\Big)\\ &+\sum_{\chi\neq\chi_{\mathrm{triv}}}g_{\chi^{-1}}\chi(u)\mathrm{Coeff}_{t^{m-c(\chi)}} \big(Z_{L,\Phi,f}(s,\chi)\big), \end{aligned} $$

where g _χ is the Gauss sum given by

$$\displaystyle \begin{aligned} g_{\chi}=\frac{q_L^{1-c(\chi)}}{q_L-1}\sum_{\overline{v}\in(\mathscr{O}_{L}/{\mathscr M}_L^{c(\chi)})^{*}}\chi(v)\psi_1(v/\varpi^{c(\chi)}). \end{aligned}$$

As a consequence, we obtain the following asymptotic expansion of exponential sums.

Corollary 3.2.7

Suppose that $C_f\cap \operatorname {Supp}(\Phi )\subset f^{-1}(0)$ . Then E _L,Φ,z(f) is a finite ${\mathbb C}$ -linear combination of functions of the form

$$\displaystyle \begin{aligned}\chi(\mathrm{ac}(z))|z|{}^{\lambda}(\log_{q_L}|z|)^{\beta}\end{aligned}$$

with coefficients independent of z, and with $\lambda \in {\mathbb C}$ a pole of

$$\displaystyle \begin{aligned} H(L,\chi,s)Z_{L,\Phi,f}(s,\chi)\end{aligned}$$

where

$$\displaystyle \begin{aligned} H(L,\chi,s)=\begin{cases} q_L^{s+1}-1 & \mathrm{ if } \chi=\chi_{\mathrm{triv}}, \\ 1 & \mathrm{ otherwise}. \end{cases} \end{aligned} $$

and with $\beta \in {\mathbb N}$ , β ≤ (multiplicity of pole λ) − 1, provided that |z| is large enough. Moreover, all poles λ appear effectively in this linear combination.

A pole λ appearing in Corollary 3.2.7 will be called a non-trivial pole of the Igusa local zeta function associated to f and Φ. We will denote the set of such poles by $\operatorname {Pol}(f,\Phi )$. For $\lambda \in \operatorname {Pol}(f,\Phi )$ we set

$$\displaystyle \begin{aligned}m_{f,\Phi}(\lambda):=\max\{m_{f,\Phi,\chi}(\lambda) \mid \lambda \mathrm{ is a pole of }H(L,\chi,s)Z_{L,\Phi,f}(s,\chi)\}\end{aligned}$$

where m _f,Φ,χ(λ) is the multiplicity of the pole λ of H(L, χ, s)Z _L,Φ,f(s, χ). Moreover, we set

$$\displaystyle \begin{aligned}\sigma_{f,\Phi}:=\min\{-\Re(\lambda) \mid \lambda\in\operatorname{Pol}(f,\Phi)\}\end{aligned}$$

and

$$\displaystyle \begin{aligned}\beta_{f,\Phi}:=\max\{m_{f,\Phi}(\lambda) \mid \lambda\in \operatorname{Pol}(f,\Phi), \ \Re(\lambda)=-\sigma_{f,\Phi} \}.\end{aligned}$$

It is very useful that the previous asymptotic expansion of exponential sums gives us all the important information about the poles of the Igusa local zeta function associated to f and Φ. If the strong monodromy conjecture (Conjecture 3.2.5) holds, then we would obtain a very deep and mysterious connection between the arithmetic side, the geometric side and the topological side of f.

3.3 Igusa’s Conjecture on Exponential Sums Modulo p ^m

This section aims to state a general conjecture on exponential sums modulo p ^m in spirit of Igusa as we mentioned in Sect. 3.1. To do so we review the notion of a certain Poisson formula (see [Igu78, Igu76] for more details).

3.3.1 Adèles

In what follows, K denotes a number field. Let $\mathscr {O}_K$ be its ring of integers. For each place v of K, we denote by |.|_v the associated absolute value of K and K _v be the completion of K by |.|_v. By Ostrowski’s theorem, K _v is either ${\mathbb R}$, ${\mathbb C}$ or a p-adic field. We normalize the norms |.|_v where v runs through the set of places of K such that the product formula holds. This formula says that for all x ∈ K ^∗, |x|_v = 1 for all but finitely many places v and we have

$$\displaystyle \begin{aligned} \prod_{v} |x|{}_v=1 \end{aligned}$$

where v runs through the set of places of K.

We say that v is an Archimedean place of K if $K_v={\mathbb R}$ or $K_v={\mathbb C}$. Otherwise, we say that v is a non-Archimedean place of K. We denote by S _∞ the set of all Archimedean places of K

$$\displaystyle \begin{aligned} S_{\infty}:=\{ v \mid v \text{ is Archimedean} \}. \end{aligned} $$

(3.7)

With the notation as in Sect. 3.2, for each non-Archimedean place v, we denote by $\mathscr {O}_v$ the ring of integers of the local field K _v, ${\mathscr M}_v$ the maximal ideal of $\mathscr {O}_v$, k _v the residue field of K _v and p _v the characteristic of K _v. Finally, we fix a uniformizer ϖ _v of K _v and denote by $\operatorname {ord}_v$ and ac_v the associated valuation map and the angular component map of K _v, respectively.

Let $X={\mathbb A}_K^n$ the affine space of dimension n. A subvariety U of X is locally K-closed if we can write U = V ∖ W where V  and W are closed subvarieties of X defined over K.

Let U be such a subvariety of X. If we write I(V ) = (f ₁, …, f _ℓ) and I(W) = (g ₁, …, g _r) with polynomials f _i, g _j ∈ K[x ₁, …, x _n], then a ∈ U if and only if f _i(a) = 0 for all 1 ≤ i ≤ ℓ and g _j(a) ≠ 0 for some 1 ≤ j ≤ r. For each place v of K, we put

$$\displaystyle \begin{aligned} U_v:=\{x\in K_v^n \mid (\forall i, f_i(x)=0)\wedge(\exists j,g_j(x)\neq 0)\}. \end{aligned}$$

It is clear that U _v is locally compact. Moreover, if v is non-Archimedean, we set

$$\displaystyle \begin{aligned} U_v^0:=\{x\in \mathscr{O}_v^n \mid (\forall i, f_i(x)=0)\wedge(\exists g\in I(W)\cap \mathscr{O}_K[x_1,\dots,x_n],g(x)\in\mathscr{O}_v^{*})\}, \end{aligned}$$

then $U_v^0$ is compact. Let S be a finite set of places of K such that S contains S _∞ defined as in (3.7). Then ∏_{v ∈ S} U _v is locally compact and $\prod _{v\notin S}U_v^0$ is compact. It implies that

$$\displaystyle \begin{aligned}U_S=\prod_{v\in S}U_v\times \prod_{v\notin S}U_v^0\end{aligned}$$

is also locally compact. It is clear that if S ⊂ S′, then $U_S\subset U_{S'}$. Thus we can take the inductive limit $U_{A}=\xrightarrow [S]{\lim }U_S$ which is called the adelization of U. The set U(K) of K-points of U can be viewed as a discrete subset of U _A by the diagonal embedding. Note that this construction is functorial.

We suppose further that U is smooth and that there exists an everywhere regular differential form ω of the highest degree on U vanishing nowhere and defined over K. Let Ψ be a non-trivial character of K _A∕K, i.e. a homomorphism from K _A to the unit circle which is trivial on K. For each place v of K, there exists a natural embedding K _v↪K _A which sends x to the adèle whose v-th coordinate is x and others coordinates are 0. Via this embedding Ψ induces a character ψ _v on K _v. We can associate a measure |dx|_v on $K_v^n$ which is the n-fold product of the self-dual measure relative to ψ _v on K _v. We observe that for all but finitely many non-Archimedean places v, the character ψ _v is trivial on $\mathscr {O}_v$ but non-trivial on ${\mathscr M}_v^{-1}$, and the measure of $\mathscr {O}_v^n$ is equal to 1. Next, we endow the set U _v with the Borel measure |ω|_v associated with ω and the measure |dx|_v. For each finite set S of places of K such that S contains S _∞ defined as in (3.7), we define the measure |ω|_A on U _S to be the product of measures

$$\displaystyle \begin{aligned} |\omega|{}_A:=\bigotimes_{v\in S}|\omega|{}_v\otimes\bigotimes_{v\notin S}|\omega|{}_v\end{aligned}$$

under the assumption that the product measure ⊗_v∉S|ω|_v exists on $\prod _{v\notin S}U_v^0$. We will call |ω|_A the Tamagawa measure on U _A. In particular, the Tamagawa measure exists on X _A by taking U = X.

Recall that S _∞ is the set of all Archimedean places of K as in (3.7). We set

$$\displaystyle \begin{aligned}X_{\infty}:=\prod_{v\in S_\infty}X_v,\end{aligned}$$

and

$$\displaystyle \begin{aligned}X_0:=\lim_{\to S}\prod_{v\in S\setminus S_\infty}X_v^0.\end{aligned}$$

Viewing X _∞ as a finite product of copies of ${\mathbb R}$, we consider the space ${\mathscr S}(X_{\infty })$ of Schwartz-Bruhat functions on X _∞. Since X ₀ is a locally compact abelian group with arbitrary large and small compact open subgroups, we can define the space ${\mathscr S}(X_0)$ of Schwartz-Bruhat functions on X ₀. The Schwartz-Bruhat functions on X _A is defined to be the tensor product

$$\displaystyle \begin{aligned} {\mathscr S}(X_A):={\mathscr S}(X_\infty)\otimes_{{\mathbb C}}{\mathscr S}(X_0). \end{aligned}$$

Each element of ${\mathscr S}(X_A)$ is a ${\mathbb C}$-linear combination of elements of the form Φ_∞⊗ Φ₀ with $\Phi _\infty \in {\mathscr S}(X_\infty )$ and $\Phi _0\in {\mathscr S}(X_0)$. A tempered distribution T on X _A is a ${\mathbb C}$-linear form on ${\mathscr S}(X_A)$ such that for all fixed functions $\Phi _0\in {\mathscr S}(X_0)$, T( Φ_∞⊗ Φ₀) depends continuously on Φ_∞ in ${\mathscr S}(X_\infty )$. We denote by ${\mathscr S}(X_A)'$ the ${\mathbb C}$-vector space of all tempered distributions on X _A.

3.3.2 Poisson Formulas and Formulas of Siegel Type

We continue with the notation of the previous section. Recall that K is a number field and $X={\mathbb A}_K^n$ is the affine space of dimension n. Let $f \in \mathscr {O}_K[x_1,\dots ,x_n]$ be a non-constant polynomial. We fix a non-trivial character Ψ of K _A∕K. For any z ∈ K we define a tempered distribution Ψ(zf(x)) on X _A given by

$$\displaystyle \begin{aligned}\Psi(zf(x))(\Phi):=\int_{X_A} \Phi(x) \, \Psi(zf(x)) \, |dx|{}_A.\end{aligned}$$

Note that this integral is absolutely convergent.

We say that the Poisson formula holds for f if the following conditions hold:

• (i) The infinite sum

  $$\displaystyle \begin{aligned}\sum_{z\in K}\Psi(zf(x))\end{aligned}$$

  belongs to ${\mathscr S}(X_A)'$. It is equivalent to the fact that the Eisenstein-Siegel series

  $$\displaystyle \begin{aligned}\sum_{z\in K}\int_{X_A} \Phi(x) \, \Psi(zf(x)) \, |dx|{}_A\end{aligned}$$

  converges absolutely for every $\Phi \in {\mathscr S}(X_A)$.

• (ii) For all y ∈ K, the measure |d _f,y|_A exists on U _y,A.

• (iii) If j : U _y,A → X _A is the induced map by U _y → X, then the global singular series j _∗(|d _f,y|_A) (or simply |d _f,y|_A) exists in ${\mathscr S}(X_A)'$ or equivalently, the integral

  $$\displaystyle \begin{aligned}\int_{U_{y,A}}\Phi \, |d_{f,y}|{}_A\end{aligned}$$

  is absolutely convergent for every $\Phi \in {\mathscr S}(X_A)$.

• (iv) The infinite sum

  $$\displaystyle \begin{aligned}\sum_{y\in K}|d_{f,y}|{}_A\end{aligned}$$

  belongs to ${\mathscr S}(X_A)'$.

• (v) We have the following equality

  $$\displaystyle \begin{aligned}\sum_{z\in K}\Psi(zf(x))=\sum_{y\in K}|d_{f,y}|{}_A\end{aligned}$$

  in ${\mathscr S}(X_A)'$.

Igusa gave a criterion for the existence of Poisson formulas based on his conjecture on exponential sums modulo p ^m.

Proposition 3.3.1 (See [Igu78])

Let f be a form of degree d in $\mathscr {O}_K[x_1,\dots ,x_n]$ (i.e $f \in \mathscr {O}_K[x_1,\dots ,x_n]$ is a homogeneous polynomial of degree d).

Then the Poisson formula holds for f if the following conditions hold:

• (i) $\operatorname {codim}(C_f)\geq 3$ , i.e. the affine hypersurface defined by f is irreducible and normal.

• (ii) There exist a constant σ > 2 and a positive constant c such that for all but finitely many non-Archimedean places v and all $z\in K_v\setminus \mathscr {O}_v$ , we have

  $$\displaystyle \begin{aligned} |E_{K_v,{\mathbf 1}_{\mathscr{O}_v^n},z}(f)|\leq c \, |z|{}_v^{-\sigma}. \end{aligned} $$

  (3.8)

There is no reason to restrict (3.8) to homogeneous polynomials and to the condition σ > 2. Thus we could relax these restrictions to obtain a more general statement. For the constant σ, by Corollary 3.2.7, we should choose

$$\displaystyle \begin{aligned}\sigma<\liminf_{p_v\to +\infty}\sigma_{f,{\mathbf 1}_{\mathscr{O}_v^n}}.\end{aligned}$$

We should mention that it may be interesting to investigate (3.8) for families of Schwartz-Bruhat functions $(\Phi _v)_{v\notin S_\infty }$ in the case where there exists a closed subset W defined over $\mathscr {O}_K$ of the affine space ${\mathbb A}_K^n$ such that Φ_v = Φ_W,v is the characteristic function of the set $\{x\in \mathscr {O}_v^n \mid x \mod {\mathscr M}_v\in W(k_v)\}$ for each place v∉S _∞.

We are ready to state a general form of Igusa’s conjecture on exponential sums.

Conjecture 3.3.2

Let K be a number field and f be a non-constant polynomial in $\mathscr {O}_K[x_1,\dots ,x_n]$ . Let W be a closed subset defined over $\mathscr {O}_K$ of the affine space ${\mathbb A}^n$ such that $f(W({\mathbb C}))$ contains at most one critical value of f. Let Φ _W,v be the characteristic function of the set $\{x\in \mathscr {O}_v^n \mid x \mod {\mathscr M}_v\in W(k_v)\}$ for each place v∉S _∞ . We set

$$\displaystyle \begin{aligned}\sigma:=\liminf_{p_v\to +\infty}\sigma_{f,\Phi_{W,v}}\end{aligned}$$

and

$$\displaystyle \begin{aligned}\beta:=\limsup_{p_v\to +\infty} \beta_{f,\Phi_{W,v}} \end{aligned}$$

as in Sect. 3.2.

Then there exists a positive constant c such that for all but finitely many places v, all z ∈ K _v with $\operatorname {ord}_v(z)\leq -2$ , we have

$$\displaystyle \begin{aligned} |E_{K_v,\Phi_{W,v},z}(f)|\leq c \, |\operatorname{ord}_v(z)|{}^{\beta-1} \, |z|{}_v^{-\sigma}. \end{aligned} $$

(3.9)

Remark 3.3.3

If $f(W({\mathbb C}))$ contains no critical values of f, then

$$\displaystyle \begin{aligned}E_{K_v,\Phi_{W,v},z}(f)=0\end{aligned}$$

provided that k _v has large enough characteristic and $\operatorname {ord}_v(z)\leq -2$ (see [Den91, Remark 4.5.3]). Hence Conjecture 3.3.2 holds in this case.

Remark 3.3.4

We note that in the original statement of Igusa in [Igu78], he only considered the case where f is homogeneous, $W={\mathbb A}_K^n$ (i.e. $\Phi _{W,v}={\mathbf {1}}_{\mathscr {O}_v^n}$ for all finite places v). Further, there are some extra conditions. The first one is that f has an embedded resolution such that ν _i > N _i for all exceptional divisors E _i. In this case Igusa chose β = 1 and an arbitrary real number σ such that

$$\displaystyle \begin{aligned}\sigma<\min\{\dfrac{\nu_i}{N_i} \mid E_i \mbox{ is an exceptional divisor}\}.\end{aligned}$$

The second one is that $\operatorname {ord}_v(z)\leq -1$. When $\operatorname {ord}_v(z)=-1$, the corresponding exponential sums become exponential sums over finite fields and we can apply the method of Deligne and Katz (see for example [Del77, Del74, Del80, Kat89]).

By Remark 3.1.6, the condition $\operatorname {ord}_v(z)\leq -2$ in Conjecture 3.3.2 is necessary.

3.3.3 Some Expected Results

Let $f \in \mathscr {O}_K[x_1,\dots ,x_n]$ be a homogeneous polynomial of degree d ≥ 2. Suppose that Conjecture 3.3.2 holds for f and $W={\mathbb A}_K^n$. Further, we suppose that

$$\displaystyle \begin{aligned}\liminf_{p_v\to +\infty}\sigma_{f,{\mathbf{1}}_{\mathscr{O}_v^n}}>1.\end{aligned}$$

It follows that f has only rational singularities (see [Clu19, Proposition 3.10]). As a consequence, if we denote by − α _f the biggest root of (s + 1)⁻¹ b _f(s), then α _f > 1.

If the strong monodromy conjecture (Conjecture 3.2.5) also holds for f, then we obtain an upper bound for α _f

$$\displaystyle \begin{aligned} \alpha_f \leq \liminf_{p_v\to +\infty}(\inf_{\Phi_v\in{\mathscr S}(K_v^n)}\sigma_{f,\Phi_v}). \end{aligned} $$

(3.10)

A lower bound for this quantity was due to Mustaţă and Popa. In fact, their result holds for any field K of characteristic 0.

Proposition 3.3.5 (Mustaţă and Popa [Mus20])

With the above notation, we have

$$\displaystyle \begin{aligned}\alpha_f\geq \dfrac{\operatorname{codim}(C_f)}{d}.\end{aligned}$$

On the other hand, we have to deal with the case where $\operatorname {ord}(z)=-1$. One of the key ingredients is to have good estimates of exponential sums over finite fields. In this case we have the following result due to Cluckers.

Proposition 3.3.6 (Cluckers [Clu08a])

Recall that K is a number field and f is a homogeneous polynomial in $\mathscr {O}_K[x_1,\dots ,x_n]$ of degree d ≥ 2. Then there exists a constant c > 0 such that for all places v of K and all z ∈ K _v with $\operatorname {ord}_v(z)=-1$ , we have

$$\displaystyle \begin{aligned}|E_{K_v,{\mathbf 1}_{\mathscr{O}_v^n},z}(f)|\leq c \, |z|{}^{-\sigma_f}\end{aligned}$$

where

$$\displaystyle \begin{aligned}\sigma_f=\liminf_{p_v\to +\infty}(\inf_{\Phi_v\in{\mathscr S}(K_v^n)}\sigma_{f,\Phi_v}).\end{aligned}$$

As a consequence, we deduce the Poisson formula for f under some conditions.

Proposition 3.3.7

Let K be a number field and f be a homogeneous polynomial in $\mathscr {O}_K[x_1,\dots ,x_n]$ of degree d ≥ 2. Suppose that Conjectures 3.2.5 and 3.3.2 hold for f. If $\operatorname {codim}(C_f)\geq 3$ and α _f > 2, then the Poisson formula holds for f.

In particular, if $\operatorname {codim}(C_f)\geq 2d+1$ , then the Poisson formula holds for f.

Proof

The proof follows immediately from (3.10) and Propositions 3.3.1, 3.3.5, 3.3.6. □

Remark 3.3.8

It is quite tempting to study Conjecture 3.3.2 for σ = α _f.

3.4 Progress on Igusa’s Conjecture

In what follows, let K be a number field with the ring of integers $\mathscr {O}_K$ and let $f \in \mathscr {O}_K[x_1,\dots ,x_n]$ be a non-constant polynomial in n variables. Recall that f is said to be a form of degree d if f is a homogeneous polynomial of degree d.

3.4.1 The Non-degenerate Case

Igusa proved his conjecture for strong non-degenerate forms, i.e. homogeneous polynomials with a unique critical point {0}.

Theorem 3.4.1 (Igusa [Igu78])

Suppose that f is a form of degree d with C _f = {0}. Then there exists a positive constant c such that for all non-Archimedean places v of K and all $z\in K_v\setminus \mathscr {O}_v$,

$$\displaystyle \begin{aligned}|E_{K_v,{\mathbf 1}_{\mathscr{O}_v^n},z}|\leq c \, |z|{}^{-\frac{n}{d}}.\end{aligned}$$

In particular, if n ≥ 2d + 1, then the Poisson formula holds for f.

Denef and Sperber investigated Conjecture 3.3.2 for non-degenerate polynomials (not necessarily homogeneous). We recall first the notion of non-degenerate polynomials.

Let k be a field and $\bar k$ be an algebraic closure of k. Let

$$\displaystyle \begin{aligned} f = f(0)+\sum_{i \in {\mathbb Z}_{\geq 0}^n} c_i x^i \in k[x_1,\dots,x_n] \end{aligned}$$

where we set x := (x ₁, …, x _n) and $x^i:=x_1^{i_1} \cdots x_n^{i_n}$ with i = (i ₁, …, i _n). The Newton polyhedron of f at the origin is defined by

$$\displaystyle \begin{aligned} \Delta_0(f) = \operatorname{Conv} \operatorname{Supp} f + {\mathbb R}_{\geq 0}^n, \end{aligned}$$

where $\operatorname {Supp} f = \left \{ \left . i \in {\mathbb Z}_{\geq 0}^n \, \right | \, c_i \neq 0 \right \}$ denotes the support of f. For all non-empty faces τ ⊆ Δ₀(f) of any dimension, ranging from vertices to Δ₀(f) itself, we write

$$\displaystyle \begin{aligned} f_\tau = \sum_{i \in \tau \cap {\mathbb Z}_{\geq 0}^n} c_i x^i. \end{aligned}$$

We say that f is non-degenerate with respect to τ if the system of equations

$$\displaystyle \begin{aligned} \frac{\partial f_\tau}{\partial x_1} = \ldots = \frac{\partial f_\tau}{\partial x_n} = 0 \end{aligned}$$

has no solutions in ${\overline {k}^*}^n$. It is equivalent to require that the map $\overline {k}^{\ast n} \rightarrow \overline {k}$ given by α↦f _τ(α) has no critical values. We say that f is non-degenerate with respect to the faces of Δ₀(f) if it is non-degenerate with respect to all possible choices of τ.

Let σ _0,f be the biggest real number t such that $(\frac {1}{t},\dots ,\frac {1}{t})\in \Delta _0(f)$ and β _0,f be the codimension of the smallest face τ ₀(f) of Δ₀(f) containing $(\frac {1}{\sigma _{0,f}},\dots ,\frac {1}{\sigma _{0,f}})$. Denef and Sperber suggested that certain estimates of exponential sums modulo p ^m of a non-degenerate polynomial can follow from those of exponential sums over finite fields. More precisely, they used the work of Adolphson-Sperber (see [Ado89]) on exponential sums over finite fields to obtain the first remarkable result after Igusa’s work.

Theorem 3.4.2 (See [Den01])

Suppose that f is non-degenerate with respect to the faces of its Newton polyhedron Δ ₀(f) at the origin and that {0, 1}ⁿ ∩ τ ₀(f) = ∅. Then there exists a positive constant c which depends only on Δ ₀ such that for all but finitely many non-Archimedean places v of K and all $z \in K_v\setminus \mathscr {O}_v$ , we have

$$\displaystyle \begin{aligned} |E_{K_v,{\mathbf 1}_{{\mathscr M}_v^n},z}|\leq c \, |\operatorname{ord}_v(z)|{}^{\beta_{0,f}-1} \, |z|{}^{-\sigma_{0,f}}. \end{aligned} $$

(3.11)

Moreover, if f is homogeneous, then

$$\displaystyle \begin{aligned} |E_{K_v,{\mathbf 1}_{\mathscr{O}_v^n},z}|\leq c \, |\operatorname{ord}_v(z)|{}^{\beta_{0,f}-1} \, |z|{}^{-\sigma_{0,f}}. \end{aligned} $$

(3.12)

Using the approach of Denef-Sperber, Cluckers replaced the work of Adonphson-Sperber by that of Katz (see [Kat99]) to obtain the same bound as in (3.12) (resp. (3.11)) but for non-degenerate quasi-homogeneous polynomials (resp. all non-degenerate polynomials) without the technical condition {0, 1}ⁿ ∩ τ ₀(f) = ∅ (see [Clu08b] and [Clu10]). Recently, Castryck and the author extended Cluckers’ results to all non-degenerate polynomials under the condition $\operatorname {ord}_v(z)\leq -2$ (see [Cas19]).

3.4.2 Beyond the Non-degenerate Case

Conjecture 3.3.2 becomes more difficult if we remove non-degenerate conditions for f. Let us mention some results in this direction. On the one hand, Wright proved some results for quasi-homogeneous polynomials in two variables (see [Wri20]). Lichtin rediscovered the results of Wright by another method and extended them to homogeneous polynomials in three variables (see [Lic13], [Lic16]). On the other hand, Cluckers proved some results in the case where $\operatorname {ord}_v(z)=-1$ or $\operatorname {ord}_v(z)=-2$ (see [Clu08a]).

In [Clu16] Cluckers and Veys stated Conjecture 3.3.2 for polynomials f and the function ${\mathbf 1}_{\mathscr {O}_v^n}$ (resp. ${\mathbf 1}_{{\mathscr M}_v^n}$), $\tilde {\sigma }_f$ (resp. $\sigma =\operatorname {lct}_0(f)$) and β = n. Here $\operatorname {lct}_0(f)$ denotes the log-canonical threshold of f at 0 and $\tilde {\sigma }_f=\min \{\operatorname {lct}_b(f-f(b)) \mid b\in {\mathbb C}^n\}$. Recall that the log-canonical threshold $\operatorname {lct}_0(f)$ of f at 0 is defined to be the minimum over all the values $\dfrac {\nu _i}{N_i}$ as in Sect. 3.2.1 with 0 ∈ h(E _i). We refer the reader to [Mus12] for an introduction to log canonical thresholds. Theorem 3.2.2 and the definition of $\tilde {\sigma }_f$ imply

$$\displaystyle \begin{aligned} \tilde{\sigma}_f\leq \liminf_{p_v\to +\infty}\sigma_{f-a,\Phi_{W,v}} \end{aligned} $$

(3.13)

for all $a\in {\mathbb C}$ and all choices of W as in the statement of Conjecture 3.3.2 with $f(W({\mathbb C}))=a$ . The above inequality (3.13) becomes an equality for a certain set W if f has non-rational singularities (see [Clu19, Proposition 3.10]). Hence the conjecture of Cluckers and Veys is sharp in case of non-rational singularities.

We mention some results toward the conjecture of Cluckers and Veys. Cluckers and Veys proved their conjecture for some small values of $|\operatorname {ord}_v(z)|$. In [Cha20] Chambille and the author proved this conjecture in the case where $\operatorname {lct}(f)$ (resp. $\operatorname {lct}_0(f)$) is at most 1∕2. Their proof suggested that Conjecture 3.3.2 may hold if we can prove it for each given value of $\operatorname {ord}_v(z)$.

Recently, Cluckers, Mustaţă and the author [Clu19] used a geometric method and proved that the conjecture of Cluckers and Veys holds for all non-constant polynomials f. Moreover, Conjecture 3.3.2 holds fully in the non-rational singularities case. Here are some ideas of the proof. They first gave a so-called power condition for resolutions of singularities to characterize the possible obstruction for Cluckers-Veys’ conjecture. If the power condition holds, then they deduce an inequality associated to the numerical data of this resolution which allows to remove the above obstruction. One key ingredient is the existence of some models in the Minimal Model Program. We strongly believe that further developments of the Minimal Model Program could lead to the full resolution of Conjecture 3.3.2 in case of rational singularities. Finally, we mention that Veys obtained a proof of Conjecture 3.3.2 in case of polynomials in two variables in the same line with that of [Clu19]. But he did not use the technique from the Minimal Model Program (see [Vey20]).

To end this section, we state the main result of Cluckers-Mustaţă-Nguyen [Clu19].

Theorem 3.4.3

Let K be a number field and $f\in \mathscr {O}_K[x_1,\ldots ,x_n]$ be a non-constant polynomial, and W be any closed subscheme of ${\mathbb A}_{\mathscr {O}_K}^n$ , then there exist c > 0 and M > 0 such that

$$\displaystyle \begin{aligned} |E_{K_v,\Phi_{W,v},z}| < c \, |\operatorname{ord}_v(z)|{}^{n-1} \, |z|{}^{-\tilde{\sigma}_{W,f}} \end{aligned} $$

(3.14)

for all finite places v of K with p _v > M and all z with $\operatorname {ord}_v(z)\leq -2$ , where $\tilde {\sigma }_{W,f}=\min \{\operatorname {lct}_b(f-f(b)) \mid b\in W\}$ . Moreover, c can be chosen to be independent of the number field K containing the coefficients of f.

3.5 A Long History of the Local-Global Principle

3.5.1 The Local-Global Principle

One of the most important techniques in arithmetic geometry is the local-global principle (also known as the Hasse principle). This principle asserts that a certain property is true globally if and only if it is true everywhere locally. This principle reduces certain difficult problems in global fields to those in local fields in which we have more tools. The most famous example of the local-global principle is the Hasse-Minkowski theorem. Minkowski proved that a quadratic form over ${\mathbb Q}$ represents 0 if and only if it represents 0 in any local field containing ${\mathbb Q}$. Hasse generalized Minkowski’s theorem to number fields. In fact, the local-global principle for quadratic forms holds for all global fields.

For forms of higher degree (i.e homogeneous polynomials of degree at least 3), the local-global principle does not hold in general and many counterexamples were already constructed (see for example [Mor37, Sel51]). So the question for forms of higher degree is:

How can one characterize forms for which the local-global principle holds?

3.5.2 Progress on the Local-Global Principle

In the case where f is a cubic form in n variables over ${\mathbb Q}$, it is conjectured that f has a non-trivial rational zero as soon as n ≥ 10. Using the Hardy-Littlewood circle method, Davenport showed in [Dav63] that a cubic form over ${\mathbb Q}$ in at least 16 variables represents 0, so the local-global principle holds trivially in this case. Heath-Brown improved the result of Davenport to cubic forms in at least 14 variables (see [Hea07]) and non-singular cubic forms in at least 10 variables (see [Hea84]). Davenport also proved that cubic forms in at least 10 variables over ${\mathbb Q}$ represent 0 in all p-adic fields (see [Dav05]). Moreover, it is clear that a cubic form over ${\mathbb Q}$ has a non-trivial solution in ${\mathbb R}$. Hence we may ask whether it is possible to remove the non-singular condition in Heath-Brown’s work.

There are also results for cubic forms in fewer variables. Hooley proved in [Hoo88] that the local-global principle holds for non-singular cubic forms in at least 9 variables. Recently, Hooley showed that under the validity of the Riemann hypothesis for certain Hasse-Weil L-functions, the local-global principle holds for all non-singular forms in 8 variables (see [Hoo14]). In another approach, Manin suggested that the obstruction of the local-global principle for cubic forms may be explained by the theory of Brauer groups (the so-called Brauer-Manin obstruction) but Skorobogatov showed that the Brauer-Manin obstruction cannot fully explain the failure of the local-global principle in the general case (see [Sko99]). Further, such an obstruction is known to be empty for non-singular cubic forms in at least 5 variables.

For forms of arbitrary degree, by generalizing the method of Davenport, Birch showed in [Bir61] that a form f of degree d > 2 in n variables over ${\mathbb Q}$ represents 0 if f ⁻¹(0) has a non-singular point over all local fields containing ${\mathbb Q}$ and $n-\dim (C_f)\geq (d-1)2^d$. Recently, Browning and Prendiville improved the second condition of Birch to $n-\dim (C_f)\geq (d-\frac {1}{2}\sqrt {d})2^d$ (see [Bro17b]). In the case where C _f = {0}, Browning and Heath-Brown conjectured that the local-global principle holds for a form f of degree d in n variables if n ≥ 2d + 1 (see [Bro17a]). We will see below that this conjecture agrees with the prediction of Igusa. On the other hand, a remarkable result of Birch in [Bir57] stated that for each odd integer d ≥ 1, there exists a positive integer N(d) such that all forms of degree d in n variables with n > N(d) represent 0. It follows that the local-global principle holds trivially if n > N(d). However, to our knowledge, we do not know any quantitative results in this direction.

We now review basic ideas of the Hardy-Littlewood circle method. Let f be a homogeneous polynomial of degree d > 1 in ${\mathbb Z}[x_1,\dots ,x_n]$. Let $\omega :{\mathbb R}^n\to [0,+\infty )$ be a suitable weight function. Our goal is to obtain an asymptotic formula of the function

$$\displaystyle \begin{aligned}N_{\omega}(f,B)=\sum_{x\in{\mathbb Z}^n, f(x)=0}\omega(x/B)\end{aligned}$$

when B → +∞. Let us use the identity

$$\displaystyle \begin{aligned} N_{\omega}(f,B)=\int_{{\mathbb T}}S(\alpha,B)d\alpha \end{aligned} $$

(3.15)

where ${\mathbb T}={\mathbb R}/{\mathbb Z}$ and

$$\displaystyle \begin{aligned}S(\alpha,B)=\sum_{x\in{\mathbb Z}^n}\omega(x/B)e^{2\pi i\alpha f(x)}\end{aligned}$$

if ω has certain good analytic properties. The Hardy-Littlewood circle method consists of dividing the torus ${\mathbb T}$ into major arcs $\mathfrak {M}$ and minor arcs $\mathfrak {m}$ where for each δ > 0, we set

$$\displaystyle \begin{aligned}\mathfrak{M}(\delta):=\cup_{q\leq B^{\delta}}\cup_{0\leq a\leq q, (a,q)=1}\{\alpha\in {\mathbb T} \mid |\alpha-\frac{a}{q}|\leq B^{\delta-d}\} \end{aligned}$$

and

$$\displaystyle \begin{aligned}\mathfrak{m}(\delta):={\mathbb T}\setminus\mathfrak{M}(\delta). \end{aligned}$$

Note that if 3δ < d, then $\mathfrak {M}(\delta )$ is in fact a disjoint union of the above arcs provided B is sufficiently large.

To investigate the local-global principle for f, we would like to obtain the following asymptotic formulas

$$\displaystyle \begin{aligned} \int_{\mathfrak{M}}S(\alpha,B)d\alpha\sim c_fB^{n-d} \end{aligned} $$

(3.16)

and

$$\displaystyle \begin{aligned} \int_{\mathfrak{m}}S(\alpha,B)d\alpha=o(B^{n-d}) \end{aligned} $$

(3.17)

where the constant c _f is positive under some good conditions on f and such that f has a smooth solution over every completion of ${\mathbb Q}$ (i.e. f admits a non-singular point of f ⁻¹(0) over every completion of ${\mathbb Q}$).

A common way to work with Eq. (3.17) is to use Weyl’s bound for S(α, B) and Dirichlet’s approximation theorem to control minor arcs (see [Bir61, Bro17b] for more details). Equation (3.17) is in fact very hard to achieve. But the conjecture on exponential sums modulo p ^m could improve Eq. (3.16). More precisely, Eq. (3.16) is related to the convergence of certain singular series given by (see [Bir61, Bro17b])

$$\displaystyle \begin{aligned}\mathfrak{S}=\sum_{1\leq N}N^{-n}\sum_{a\in ({\mathbb Z}/N{\mathbb Z})^{*}}S_N(a)\end{aligned}$$

where

$$\displaystyle \begin{aligned}S_N(a)=\sum_{y\in ({\mathbb Z}/N{\mathbb Z})^n}e^{\frac{2\pi iaf(y)}{N}}.\end{aligned}$$

With the assumption of Remark 3.1.7 we would have

$$\displaystyle \begin{aligned}|S_N(a)|\leq CN^{-\sigma}\end{aligned}$$

for a positive constant C and all N ≥ 1. A direct calculation implies that $\mathfrak {S}$ converges absolutely for σ > 2.

3.5.3 Igusa’s Approach

Now we sketch another approach given by Igusa to attack the above problem (see [Igu78] and [Har80]). We first recall the idea of Weil on quadratic forms. From the work of Siegel on quadratic forms, Weil gave a general formula called Siegel’s formula (see [Wei65]) which relates a theta series to an Eisenstein series. As a consequence, the Hasse-Minkowski theorem follows from Siegel’s formula. For forms of higher degree, Igusa expected that we could derive a similar formula and use it to prove the local-global principle for these forms. Inspired by the work of Weil such a formula of Siegel type would follow from a Poisson formula. In fact, Igusa succeeded in proving the following assertion:

For forms of higher degree, if we have a good uniform bound in p and m of exponential sums modulo p ^m, then we have a Poisson formula.

Hence the strategy of Igusa breaks into two parts. The first part is to find a good uniform bound in p and m of exponential sums modulo p ^m so that we could deduce a Poisson formula. This is exactly the material presented in Sects. 3.2, 3.3 and 3.4. The second part is to use the Poisson formula to derive formulas of Siegel type and then the desired local-global principle.

Let us explain a little bit more about formulas of Siegel type. A formula of Siegel type is an equality between Eisenstein-Siegel series and the integral of a theta series in the space of tempered distributions. In the case of quadratic forms, Weil introduced the notion of metaplectic groups and used their action on the space of Schwartz-Bruhat functions ${\mathscr S}(X_A)$ to construct a theta series and compared its integral with Eisenstein-Siegel series. For forms of higher degree, Igusa pointed out that a good theory of metaplectic groups associated with these forms would be very useful although such a theory is not yet known. But he also remarked that we could use a certain smaller group to obtain similar results. More precisely, let K be a number field and let f be a non-singular form of degree d in n variables with coefficients in $\mathscr {O}_K$. Igusa introduced the group $P={\mathbb G}_a\times {\mathbb G}_m$ equipped with the law

$$\displaystyle \begin{aligned}(u,t)(u',t')=(u+t^du',tt')\end{aligned}$$

The action of P _A on ${\mathscr S}(X_A)$ is given by

$$\displaystyle \begin{aligned}((u,t)(\Phi))(x)=|t|{}_A^{\frac{n}{2}}\Psi(uf(x))\Phi(tx)\end{aligned}$$

where |t|_A =∏_v|t _v|_v is the usual norm of t. We consider the tempered distributions E and I ₀ given by

$$\displaystyle \begin{aligned}E(\Phi)=\Phi(0)+\sum_{z\in K}\Psi(zf(x))(\Phi)\end{aligned}$$

and

$$\displaystyle \begin{aligned}I_0(\Phi)=\sum_{\xi\in X_K}\Phi(\xi).\end{aligned}$$

If n ≥ 2d + 1, then Igusa showed that the Poisson formula holds for f (see Theorem 3.4.1). In particular, if |t|_A > 1, he proved in [Igu76] that

$$\displaystyle \begin{aligned} (I_0-E)((u,t)(\Phi))=O(|t|{}_A^{1-\frac{n}{2d}}) \end{aligned} $$

(3.18)

as |t|_A → +∞ and furthermore, if |t|_A < 1 but (u + z)t ^−d remains in a compact subset of K _A for some z ∈ K, then

$$\displaystyle \begin{aligned} (I_0-E)((u,t)(\Phi))=O(|t|{}_A^{\frac{n}{2d}-1}) \end{aligned} $$

(3.19)

as |t|_A → 0. Igusa conjectured that (3.19) is still true without the compactness assumption (or at least we could find some conditions of n and d such that (3.19) holds without compactness). In particular, this conjecture would imply the local-global principle for f (see [Igu76, Har80]). To summarize, under the validity of Igusa’s approach, we could prove that the local-global principle holds for any non-singular form of degree d in at least 2d + 1 variables. This agrees with the conjecture of Browning and Heath-Brown that we mentioned earlier.

Unfortunately, we are in a similar situation as that of (3.17). To our knowledge, (3.19) is out of reach. Even it is not clear that there is a connection between them by looking at the adelic circle method (see [Lac82, Mar73]). Both of them would require a lot of efforts and many new ideas but we can always hope that Igusa’s ideas could be realized in the future.

We end this survey with the case of singular forms. If f is a singular form of degree d ≥ 3, from an observation of Igusa on the work of Birch, the Poisson formula also holds for f if $\operatorname {codim}(C_f)\geq (d-1)2^d$. Moreover, Birch showed that this condition is sufficient to prove the local-global principle for f as we mentioned above. In Proposition 3.3.7, we predicted that the Poisson formula holds for f if $\operatorname {codim}(C_f)\geq 2d+1$. Hence it is tempting to ask whether we could replace the sufficient condition $\operatorname {codim}(C_f)\geq (d-1)2^d$ in the result of Birch by $\operatorname {codim}(C_f)\geq 2d+1$.