Improvement of the Power Quality in Single Phase Grid Connected Photovoltaic System Supplying Nonlinear Load

Abstract

This chapter is focused on the improvement of the grid current quality at the Point of Common Coupling (PCC) of a Single-Phase Grid-Connected Photovoltaic System (GCPVS) supplying the nonlinear load. Thus, with the implementation of a specific control strategy applied to the PV inverter which is used essentially to inject the solar power into the grid, the compensation of the disturbing current introduced by the nonlinear load can be performed. Furthermore, the efficiency of this control strategy is related to an algorithm aimed to extract the correct disturbing currents and to the performance of the used current controllers. Consequently, two methods of control strategy of the PV inverter are investigated and compared in this chapter. The first method comes from those found in the bibliography and the second is original due to use simple PI controllers. The effectiveness of each control strategy is verified by simulation using Matlab/Simulink and validated experimentally through an experimental platform. Therefore, basing on simulation and experimental results, the comparative study shows better performances of the second proposed methods.

1 Introduction

Continuously rising demand for electric power in the world and environmental pollution problems of fossil energy has been conducted to increasing the penetration of renewable energy sources (RES) into power distribution systems [1]. The Photovoltaic (PV) source is one of the RES that provides a reliable, sustainable, and clean energy supply [2]. Nowadays, due to their cost-effective application, the PV systems are largely operated as connected to the grid. Single-phase Grid-Connected Photovoltaic systems (GCPVS) are widely used since they can be installed on the building roofs to supply residential loads and inject the surplus of the PV generated power to the grid. However, with the intensive use of nonlinear loads, different disturbances caused by the injection of harmonic and reactive current affect the grid current quality at the Point of Common Coupling (PCC). This introduces negative effects on the efficiency of the power distribution system. Therefore, Power Quality (PQ) problems caused by these disturbing currents appear as important as environmental problems of fossil sources. Consequently, it is mandatory to limit the injection of this disturbing current as well as their negative effects.

Therefore, to cancel the disturbing grid current in the PCC, and in the aim to ensure a better optimization, several proposed works are focused on the use of the PV inverter as a shunt active filter in addition to its main role of power injection. This is can be achieved due to a specific control strategy applied to the PV inverter [3, 4].

The efficiency of this control strategy to mitigate disturbing grid current introduced by a nonlinear load is related to the algorithm used to extract this correct disturbing current. Several algorithms are proposed in the literature. Due to their efficiency and simplicity, Instantaneous Reactive Power (IRP) theory [5, 6] and the Synchronous Reference Frame (SRF) theory [7, 8] are the most widely used since they were adapted to be applied in single-phase systems by including some proposed techniques able to produce an imaginary axis in order to obtain a virtual orthogonal frame. This solution has a problem with a significant delay time which can affect the dynamic response of the system.

Many adaptive techniques are also proposed for disturbing current compensation such as the LMS (Least Mean Square) method [9], the LMMN (Least Mean Mixed-Norm) method [10], the DNLMS method (Decorrelation Normalized Least Mean Square) [11]. Although these techniques are efficient for estimating the grid current harmonics, their concepts remain complicated and require significant computing time. In [12], an improved method for harmonic identification based on the adaptive noise cancellation principle is proposed. This technique using a variable step is able to overcome the problem of traditional adaptive techniques which is the conflict between the steady-state accuracy and the convergence speed.

Some of Phase-Locked Loop (PLL) techniques are also extended to detect harmonic current components. Authors of [13] are used a cascaded association of a Second Order Generalized Integrators (SOGI) and a Synchronous Reference Frame PLL (SRF-PLL) structure to identify current harmonics to subtract them from the total grid current. This detection technique can be used for both single and three-phase systems to compensate selected highest harmonic current components.

Consequently, in this chapter, two new algorithms aimed to extract the correct disturbing currents are exposed and their performances are compared. Therefore, the first algorithm is based on the use of the FFT technique to detect the fundamental grid current component which is subtracted subsequently from the total grid current [12]. The Proportional-Resonant (PR) controller is used to control the detected current [4, 10, 13]. On the other hand, the principle of the mitigation of the disturbing current in the second algorithm is based on the extraction of the most predominant disturbing grid current by identifying, each active and reactive grid current amplitude to be regulated then to a null signal using a PI controller. In this case, the use of simple PI controllers is sufficient since reference signals are dc components. The effectiveness of these two control strategies is verified through the good simulation results obtained using Matlab/Simulink and validated experimentally through an experimental platform. Then, a comparative study between these two methods will be presented in this chapter to highlight the originality of the algorithm of the second method comparing to the first method which is based on the use of multiple PR controllers. This control method is frequently used in recent various algorithms and techniques of literature such as in [12, 13], which employs multiple PR controllers to control the extracted harmonic current components [4, 10, 13].

2 Description of the Grid Connected Photovoltaic System (GCPVS)

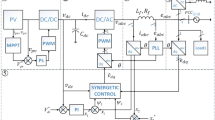
The global structure of the GCPVS considered in this work is illustrated in Fig. 1. It consists of a PV generator connected to a single-phase grid-tied inverter via a dc-dc boost converter. The connection of the PV inverter to the grid is performed by the intermediate of an inductive filter L_F to eliminate the high-frequency grid current components.

Fig. 1

General structure of the considered Grid Connected PV System (GCPVS)

To guarantee the operation of the PV generator at its maximum power point, the dc-dc boost inverter is controlled by the Maximum Power Point Tracking (MPPT) algorithm based on the Perturb and Observe (P&O) method due to its simplicity and its ability to reach the exact point of maximum power in a short time [14,15,16].

The dc-link between the boost converter and the PV inverter is performed through the capacitor C_dc which is used to create a constant voltage source useful for supplying the photovoltaic inverter and controlling the power flow between the grid and the photovoltaic system.

The considered GCPVS is simulated according to the parameters showed in Table 1.

Table 1 Parameters of the simulated grid-connected photovoltaic system (GCPVS)

As it is presented in Fig. 1, the nonlinear load L_NL is modeled as a single-phase full wave rectifier L₁ connected in parallel to an inductive load L₂ to conceive a load with spectral content rich in harmonics. The GCPVS is simulated with two cases of load (L_NL1 and L_NL2) composed by (L₁₁, L₂) and (L₁₂, L₂) respectively, to investigate the impact of the load variation. Each rectifier (L₁₁ and L₁₂) supplies an inductive load (L_R1, R_R1) and (L_R2, R_R2) respectively. The active and reactive powers of the simulated loads (L_NL1 and L_NL2) are presented in Table 2.

Table 2 Active and reactive powers of the simulated nonlinear loads

The frequency spectra of the conceived nonlinear loads are also observed in order to investigate their effect on the spectral content of the grid current. As it is depicted in Fig. 2, for the two cases of the nonlinear loads, the absorbed currents are significantly distorted. They present an important level of THD equal to 32.33% with the load L_NL1 and 29.05% with the load L_NL2. In addition, the frequency representations of these two load currents are composed of odd harmonic components of which the most dominant components are limited to the 13th order as it is shown in Fig. 2.

Fig. 2

Spectrum of the load current i_L (a) in the case of L_NL1

The study of the simulated system consists to evaluate the quality of the grid current under load condition variation (two considered nonlinear loads) and under different cases of the generated PV power which depends on the climatic conditions. Therefore, three levels of the PV inverter power (P_inv) have been fixed according to a chosen solar irradiance (G) profile presented in Fig. 3. Thus three modes are considered. Mode 1 corresponds to solar irradiance (G) equal to 100 W/m² for a period of time “t” between 0 s and 2 s. In mode 2, G increases to 230 W/m² for “t” between 2 s and 4 s and in mode 3, G decreases to 170 W/m² when “t” is between 4 s and 6 s.

Fig. 3

Simulated profile of the solar irradiance (G)

In this chapter, a detailed comparative study of the grid current quality without and with the implementation of the two proposed harmonic compensating algorithms is performed. This comparative study is aimed to evaluate the effectiveness of the two proposed algorithms to improve the grid current quality which is affected by nonlinear load. Thereafter, the following part of this paragraph will be focused on the investigation of the quality of the grid current simulated without the proposed algorithms. Consequently, the time and the frequency representations as well as the THD index of the grid current simulated without the two proposed algorithms for the two loads under the three levels of the fixed solar irradiance (G) are presented in Fig. 4. It is worth noting that without a harmonic compensating algorithm, the grid current simulated with each considered nonlinear load is highly distorted for the three levels of the solar irradiance (G). This explains the significant THD obtained in any case of operating mode (mode 1, 2, or 3) of the photovoltaic system. Comparing Fig. 2, 3 and 4, for a specific nonlinear load, the obtained spectra of the grid current under the three chosen solar irradiance (G) are constituted of the same harmonic content. They have the same orders of harmonic. The most dominants of these harmonic components are limited to the 13th order. Thus, it can be concluded that the harmonic components of the grid current are provided from the used load current.

Fig. 4

Time and frequency representations of the simulated grid current (i_g) without the proposed algorithm (a) in mode 1 with the load L_NL1, (b) in mode 2 with the load L_NL1 (c) in mode 3 with the load L_NL1, (d) in mode 1 with the load L_NL2, (e) in mode 2 with the load L_NL2, (f) in mode 3 with the load L_NL2

Furthermore, it can be noted from Fig. 4a–f that for each case of the simulated load, the magnitudes of the harmonic components remain unchanged under the three chosen levels of the solar irradiance (G), but it is only the fundamental components which are affected by the variation of G. Consequently, for a specific nonlinear load, the variation of the THD of the grid current is basically due to the variation of the fundamental component magnitude. If the magnitude of the fundamental component decreases, the THD value will increases, and vice versa.

Thereafter, a detailed theoretical study on the principle of the PV inverter control strategy based on disturbing grid current extraction methods will be presented.

3 Proposed Methods Used for the Improvement of the Power Quality at the PCC of the GCPVS

The grid-tied inverter which is a single-phase voltage source inverter is used in the PV system mainly to control the power flow between the PV system, the utility grid, and the nonlinear load connected to the PCC. In addition to this main function, the PV inverter is used as a shunt active filter in order to attenuate disturbing grid currents introduced by nonlinear loads and then guarantee a grid current with a sinusoidal form and low THD value.

To perform these two functions, the PV inverter is properly controlled. The principle of the control scheme of the PV inverter is shown in Fig. 5. It is based on two parallel control loops aimed to generate two signals c₁ and c₂. The sum of these signals represents the reference signal useful to generate the PWM signal to control the switched devices of the PV inverter. The first loop is aimed to create the first signal c₁ representing the dc voltage loop. This loop has the task to maintain the dc voltage to the desired value equal to 350 V in this work. To do that, a PI regulator is used since the input signal is a continuous one. Furthermore, the output signal of the PI regulator will be multiplied by a unitary sinusoidal signal which is synchronized with the frequency of the grid voltage. To obtain this frequency, the PLL technique was then applied.

Fig. 5

The considered control scheme of the PV inverter

On the other hand, as it is showed in Fig. 5, the second loop aims to control the disturbing grid current which is obtained from the disturbing current extraction block. This is performed by comparing the extracted disturbing grid currents introduced by the nonlinear load to a zero signal to cancel them from the total grid current to obtain a sinusoidal form with good quality. According to Fig. 5, the current control loop is composed of two main blocks. The first one is the disturbing grid current extracting block which consists of the proposed algorithm useful to extract accurately the disturbing current and the second block represents the disturbing grid current controller.

In this chapter, we propose two methods for controlling the disturbing grid current. Each method is specified by its own disturbing-current extraction algorithm and disturbing-current controller.

3.1 Investigation of the First Proposed Method of the PV Inverter Control

This paragraph is focused on the investigation of the first algorithm proposed to improve the grid current quality affected by the nonlinear load. The PV inverter control scheme based on the first method is presented in Fig. 6. The principle of each block of the current controller will be explained in the following subsections.

Fig. 6

The first proposed control strategy of the PV inverter

3.1.1 The Proposed Algorithm for the Extraction of the Disturbing Grid Current with the First Method

With the first method, the principle of the proposed algorithm is demonstrated as follows.

The distorted grid current expressed by (1) is composed of the sum of the fundamental component i_g1 and harmonic components i_gh according to (2) and (3).

$$i_{g} (t) = \sum\limits_{h = 1}^{\infty } {I_{gh} \sin (h\omega t + \theta_{h} )}$$

(1)

$$i_{g} (t) = I_{g1} \sin (\omega t + \theta_{1} ) + \sum\limits_{h = 2}^{\infty } {I_{gh} \sin (h\omega t + \theta_{h} )}$$

(2)

$$i_{g} (t) = i{}_{g1}(t) + i_{gh} (t)$$

(3)

On the other hand, according to (4), the fundamental component of the grid current can be expressed as the sum of the active and reactive components.

$$i_{g1} (t) = i{}_{g1a}(t) + i_{g1r} (t)$$

(4)

Therefore, (3) can be expressed as follows.

$$i_{g} (t) = i{}_{g1a}(t) + i{}_{gd}(t)$$

(5)

where $i{}_{gd}(t)$ is the disturbing grid current which represents the sum of the reactive fundamental component and harmonic components of the grid current as indicated by (6).

$$i_{gd} (t) = i{}_{g1r}(t) + i_{gh} (t)$$

(6)

Consequently, referring to (5), the disturbing grid current $i{}_{gd}(t)$ can be obtained by subtracting the total grid current $i{}_{g}(t)$ from the active grid current $i{}_{1ga}(t)$. Based on this principle, the algorithm for the extraction of the disturbing grid current illustrated in Fig. 7 was implemented. This algorithm is then based on the calculation of the active grid current to subtract it thereafter from the total grid current.

Fig. 7

Principe of harmonic grid current (i_gd) extraction block

From Eq. (7) which illustrates the expression of the fundamental grid current $i{}_{g1}(t)$, the active grid current $i{}_{g1a}(t)$ and reactive grid current $i{}_{g1r}(t)$ can be identified according to (8) and (9).

$$\begin{aligned} i_{g1} (t) &= I_{g1} \sin (\omega t + \theta_{1} ) \hfill \\& =\, I_{g1} \cos (\theta_{1} )\sin (\omega t) + I_{g1} \sin (\theta_{1} )\cos (\omega t) \, \hfill \\ \end{aligned}$$

(7)

$$i_{g1a} (t) = I_{g1} \cos (\theta_{1} )\sin (\omega t)$$

(8)

$$i_{g1r} (t) = I_{g1} \sin (\theta_{1} )\cos (\omega t) \,$$

(9)

Basing on (8), the active grid current $i{}_{g1a}(t)$ is then calculated. It requires the amplitude $I{}_{g1}$ and the phase angle $\theta {}_{1}$ of the fundamental grid current. To extract them, the FFT method was applied on the grid current at the fundamental frequency of the grid using the PLL technique as it is showed in Fig. 7.

3.1.2 Description of the Current Regulation Loop

As it has been mentioned above, the disturbing grid current is regulated by comparing it to a zero signal. In this work, the Proportional Resonant (PR) controller is then used to set the error of this comparison to zero. Consequently, the PV inverter is able to force the disturbing grid current to zero.

The choice of the PR controller is explained by its effectiveness to track a reference signal having a sinusoidal form. Therefore, by implementing several blocks of cascading PR controllers adjusted to the low frequencies of the harmonic components of the current, selective harmonic compensation can be obtained since the disturbing current is considered as the sum of sinusoidal currents with different frequencies. In this work, the transfer function implemented by the PR controller which is expressed by (10), is designed to attenuate the harmonic components of the grid current of order 2–13. The choice of 13th order is explained by the fact that the order harmonic components of the nonlinear load current considered in this work are limited to 13 as it is explained in the previous paragraph.

$$G_{S} (s) = \sum\limits_{13}^{h = 1} {\frac{{2K_{ih} \omega_{cut} s}}{{s^{2} + 2\omega_{cut} s + (h\omega_{0}^{{}} )^{2} }}}$$

(10)

where, $\omega_{cut}$ is the cutoff frequency, $\omega_{0}^{{}}$ is the grid angular frequency, h is the harmonic order of the grid current to be controlled, $K_{ih}$ is a constant gain.

Figure 8 shows the implemented structure of the multiple PR controllers in this work.

Fig. 8

Structure of the multiple PR controllers implemented in the first method

3.1.3 Simulation Results Obtained Using the First Method

The considered GCPVS was simulated using the proposed first method under the two considered nonlinear loads (L_NL1 and L_NL2) and with the chosen solar irradiance (G) profile presented in Fig. 3. The transfer of the power flow between the three main elements of the considered PV system: the PV inverter, the grid, and the user load are investigated in order to study the behavior of the considered GCPVS.

Figure 9a, b show the active power of these three elements simulated with the loads L_NL1 and L_NL2 respectively, under the three operating modes given by the solar irradiance (G) profile. In each mode, Table 3 represents the values of the three active powers. It can be noted from the corresponding power flow that with the two used loads, the sum of the PV inverter and the grid active powers represent the load active power for any case of the used load and the operating mode of the PV system. This means that the supply of each load is correctly ensured by both the utility grid and the PV inverter.

Fig. 9

Active grid power (P_g), active load power (P_NL1 and P_NL2), and active PV inverter power (P_inv) simulated in the three operating modes of the PV (a) with L_NL1 and (b) with L_NL2

Table 3 Simulated active powers of the grid, the PV inverter and the two used loads L_NL1 and L_NL2 with the first method

After verifying the operation of the designed GCPVS with the proposed first method, the quality of the grid current was then evaluated for the two cases of load conditions considering the solar irradiance (G) profile shown in Fig. 3. Therefore, the time and the frequency representations of the grid current as well as the THD simulated in the three operation modes of the PV inverter with two cases of load (L_NL1 and L_NL2) are presented in Fig. 10. The values of the obtained THD are indicated in Table 4.

Fig. 10

Time and frequency spectrum representations of the simulated grid current (i_g) with the first proposed algorithm (a) in mode 1 with the load L_NL1, (b) in mode 2 with the load L_NL1, (c) in mode 3 with the load L_NL1, (d) in mode 1 with the load L_NL2, (e) in mode 2 with the load L_NL2, (f) in mode 3 with the load L_NL2

Table 4 THD values obtained with the first method and without improvement

Comparing Fig. 10 that shows the simulated grid current with the proposed algorithm to Fig. 4, the quality of the waveform of the grid current was significantly improved and the THD values were attenuated in any case of operating mode of the GCPVS and under the two cases of nonlinear loads. It is worth noting that for the three cases of (Fig. 10b, e, f), although the simulated grid current has undergone an important attenuation of the THD, the waveform is yet distorted. However, the quality of the grid current remains acceptable since the amplitude of the fundamental component is low.

Comparing the simulation results to those obtained without the proposed algorithm, we can conclude that the proposed technique is efficient to compensate the harmonic current introduced by the nonlinear load and to obtain a grid current with a low THD even under a variation of the PV power and the load conditions (see Table 4).

3.2 Investigation of the Second Proposed Method of the PV Inverter Control

The control strategy of the PV inverter based on the second method of disturbing current control is showed in Fig. 11.

Fig. 11

The second proposed control strategy of the PV inverter

3.2.1 Proposed Algorithm in the Second Method for the Extraction of the Disturbing Grid Current

The principle of the second algorithm aimed to extract the disturbing grid current is essentially based on the extraction of each active and reactive disturbing current vector from the total grid current, except the vector of the active component of the fundamental current. Referring to (8) and (9), the amplitudes of active $I_{g1a}$ and reactive $I_{g1r}$ grid currents of the fundamental component can be expressed respectively by (11) and (12).

$$I_{g1a} = I_{g1} \cos (\theta_{1} )$$

(11)

$$I_{g1r} = I_{g1} \sin (\theta_{1} )$$

(12)

Similarly, each harmonic component of the grid current can be decomposed on active and reactive components as showed by (13) and (14). The expressions of the active $I_{gna}$ and reactive $I_{gnr}$ harmonic components of the grid current of order n are defined respectively by (15) and (16).

$$i_{gh} (t) = \sum\limits_{n = 2}^{\infty } {\left[ {I_{gn} .\cos (\theta_{n} ).\sin (n\omega t) + I_{gn} .\sin (\theta_{n} ).\cos (n\omega t)} \right]}$$

(13)

$$i_{gh} (t) = \sum\limits_{n = 2}^{\infty } {\left[ {i_{gna} (t) + i_{gnr} (t)} \right]}$$

(14)

With

$$I_{gna} = I_{gn} \cos (\theta_{n} )$$

(15)

$$I_{gnr} = I_{gn} \sin (\theta_{n} )$$

(16)

Therefore, the disturbing grid current $i_{gd} (t)$ expressed by (6) can be reformulated as follows

$$\begin{aligned} i_{gd} (t) &= i_{g1r} (t) + i_{gh} (t) \hfill \\& = i_{g1r} (t) + \sum\limits_{n = 2}^{\infty } {\left[ {i_{gna} (t) + i_{gnr} (t)} \right]} \hfill \\& = \sum\limits_{n = 2}^{\infty } {I_{gna} \, \sin (n\theta )} + \sum\limits_{n = 1}^{\infty } {I_{gnr} \cos (n\theta )} \hfill \\& = i_{ga - d} (t) + i_{gr - d} (t) \hfill \\ \end{aligned}$$

(17)

Thus, according to (5), to obtain a grid current with a sinusoidal form composed only by the active current $i{}_{g1a}(t)$, the disturbing grid current $i_{gd} (t)$ must be set to zero. This means that the amplitudes of all disturbing components of the grid current ($I_{g1r}$, $I_{gna}$, $I_{gnr}$) expressed by (12), (14) and (16) must be set to zero using a current regulation loop. In this aim, the amplitudes (I_g2a, …, I_gna) and (I_g1r,…, I_gnr) of different disturbing grid current components must be extracted.

In this work, an efficient algorithm having the task to extract the amplitudes of active and reactive disturbing components of the grid current is proposed. The principle of this method is illustrated in Fig. 12. As showed in this figure, to extract an amplitude of a component with order “n” among the different reactive components (I_g1r,…, I_gnr) or the different active components (I_g2a,…, I_gna) of the total grid current, the grid current expressed by (2) is multiplied respectively by $y_{n} (t) = \cos (n\theta )$(for I_g1r,…, I_gnr extraction) or $x_{n} (t) = \sin (n\theta )$ (for I_g2a,…, I_gna extraction) with a phase angle which has the same order “n” of the extracted considered component. As a result, a corresponding dc component equal to I_g1r/2,…, I_gnr/2 (for I_g1r,…, I_gnr extraction) and I_g2a/2,…, I_gna/2 (for I_g2a,…, I_gna extraction) are obtained as well as a variable term. This result is demonstrated by (18) and (19) to extract respectively the amplitude of the reactive current component and the active current component of order 2.

Fig. 12

Second algorithm scheme used to extract the amplitudes of different active and reactive components of the harmonic grid currents

$$\begin{aligned} i_{g} (t).\sin (2\omega t) =& I_{g1} \sin (\omega t + \theta_{1} ).\sin (2\omega t) + I_{g2} \sin (2\omega t + \theta_{2} ).\sin (2\omega t)) \\ & + \sum\limits_{n = 3}^{\infty } {(I_{gn} \sin (n\omega t + \theta_{n} ).\sin (2\omega t))} \\ & = \frac{{I_{g2} }}{2}.\cos (\theta_{2} ) - \frac{{I_{g2} }}{2}.\cos (4\omega t + \theta_{2} ) + I_{g1} \sin (\omega t + \theta_{1} ) \times \sin (2\omega t) \\ & + \sum\limits_{n = 3}^{\infty } {(I_{gn} .\sin (n\omega t + \theta_{n} ).\sin (2\omega t))} \\ & = \frac{{I_{g2a} }}{2} - \frac{{I_{g2} }}{2}.\cos (4\omega t + \theta_{2} ) + I_{g1} \sin (\omega t + \theta_{1} ) \times \sin (2\omega t) \\ & + \sum\limits_{n = 3}^{\infty } {(I_{gn} .\sin (n\omega t + \theta_{n} ).\sin (2\omega t))} \, \\ \end{aligned}$$

(18)

$$\begin{aligned} i_{g} (t).\cos (\omega t) & = I_{g1} .\sin (\omega t + \theta_{1} ).\cos (\omega t) + \sum\limits_{n = 2}^{\infty } {(I_{gn} \sin (n\omega t + \theta_{n} ).\cos (\omega t))} \\ & = \frac{{I_{g1} }}{2}.\sin (\theta_{1} ) + \frac{{I_{g1} }}{2}.(\sin (2\omega t + \theta_{1} ) \\ & + \sum\limits_{n = 2}^{\infty } {(I_{gn} \sin (n\omega t + \theta_{n} ) \times \cos (\omega t))} \\ & = \frac{{I_{g1r} }}{2} + \left[ {\frac{{I_{g1} }}{2}.\sin (2\omega t + \theta_{1} ) + \sum\limits_{n = 2}^{\infty } {(I_{gn} \sin (n\omega t + \theta_{n} ) \times \cos (\omega t))} } \right] \\ \end{aligned}$$

(19)

Consequently, to extract each dc component I_g1r/2,…, I_gnr/2 and I_g2a/2,…, I_gna/2, a low pass filter is used. This leads to obtaining each amplitude of the reactive components I_g1r,…, I_gnr, and the active components I_g1a,…, I_gna after multiplying the output component of the low pass filter by again equal to 2.

3.2.2 Description of the Current Regulation Loop Used in the Second Method

As it is mentioned, to improve the grid current quality at the PCC of the considered GCPVS, the active current must be isolated from the total grid current. This is performed by canceling all the dominant components of the disturbing grid current. In this work, once the amplitudes of these components I_g1r,…, I_gnr and I_g1a,…, I_gna are extracted using the appropriate algorithm described above, they are compared to a reference signal equal to zero. To regulate each amplitude to zero, the result of each comparison is then presented to a PI regulator, as shown in Fig. 13. The choice of the PI regulator is justified by the fact that it is more efficient and gives a zero steady-state error in case of dc component regulation. Thereafter, each output signal of the PI regulator is multiplied by $y_{n} (t) = \cos (n\theta )$ in case of the control of (I_g1r,…, I_gnr) and $x_{n} (t) = \sin (n\theta )$ case of the control of (I_g2a,…, I_gna), having a phase angle with the same order “n” of the controlled considered component. The sum of the obtained signals represents the reference signal c₂ generated by the current control loops as illustrated in Fig. 13.

Fig. 13

The current control block scheme used for the cancellation of selected harmonic components

3.2.3 Simulation Results Obtained Using the Second Method

The second proposed method was implemented with the GCPVS simulated according to the parameters presented in Table 1, in order to investigate its effectiveness for disturbing grid current compensation using the second algorithm. Furthermore, the two nonlinear loads (L_NL1 and L_NL2) as well as the solar irradiance (G) profile presented in Fig. 3 are considered to compare the performances of the proposed first and second methods.

As mentioned, to examine the behavior of the simulated GCPVS system, the power flow between the PV inverter, the utility grid, and each used load must be investigated. Thus, the active power of each element is simulated with the second proposed method and showed in Fig. 14a, b. Comparing this simulation curves to that obtained with the first proposed method, it can be noted that the dynamic response of these elements is slower since the active power of each element takes an important time to reach its steady-state. On the other hand, referring to Table 5 indicating the values of their steady-state active power, the GCPVS has the same behavior as in the case of the first method. This proves the good operation of the GCPVs system with the second proposed method but with rather significant response time.

Fig. 14

Active grid power (P_g), active load power (P_NL1 and P_NL2) and active PV inverter power (P_inv) simulated in the three operating modes of the PV (a) with (a) and (b) in the case of L_NL2

Table 5 Active powers of the grid, the PV inverter and the two used loads L_NL1 and L_NL2 simulated with the second method

Now, to evaluate the performance of the second proposed method for the grid current quality improvement, the time and the frequency representations, as well as the THD of the grid current obtained for the three levels of solar irradiation (G) and under the two nonlinear load conditions, are shown in Fig. 15. Comparing this figure to Fig. 10, it can be noted that the quality of the grid current was improved with the second proposed method since the waveform of the grid current has a sinusoidal shape for any case of operating mode of the GCPVS. In addition, from the THD values obtained with the first and the second methods in the three operating modes of the GCPVS using the two cases of loads (L_NL1 and L_NL2), we can conclude that the second control method is more efficient for disturbing grid current mitigation than the first method. The THD values are lower than those obtained with the first method. Therefore, for any case of GCPVS operating mode, with the second method, the THD value did not exceed 8% contrary to the first method in which the THD value remains important and the waveform of the grid current has not a sinusoidal form in some cases (Fig. 10b, e, f).

Fig. 15

Time representation and frequency spectrum of the simulated grid current (i_g) with the second proposed algorithm (a) in mode 1 with the load L_NL1, (b) in mode 2 with the load L_NL1, (c) in mode 3 with the load L_NL1, (d) in mode 1 with the load L_NL2, (e) in mode 2 with the load L_NL2, (f) in mode 3 with the load L_NL2

Furthermore, referring to Fig. 16 that shows the THD curves as a function of fundamental grid current for the two proposed methods and with the two used loads, note that the THD value decreases when the fundamental grid current increases. This is explained by the fact that the harmonic components have the same amplitudes for any case of the operating mode of the PV system with the same nonlinear load. Then, it can be concluded that the THD value is related only to the fundamental grid current amplitude for a considered load.

Fig. 16

Simulated THD as a function of the fundamental grid current obtained with the two proposed methods

We can conclude then, that the proposed second algorithm is more efficient than the first algorithm since it has successfully compensated the disturbing grid current at any operating point of the PV system even under the variation of the load conditions. But it has a slower dynamic response and requires more computing time.

3.3 Experimental Results of the Two Used Methods

To validate the obtained simulation results of the two proposed algorithms, experimental tests have been achieved on a testbed presented in Fig. 17. This testbed is composed of a Chroma 62020H-150 s programmable power supply used to model the PV generator and thus to provide a variable power to a dc-dc boost converter which is connected then to a voltage inverter. This voltage inverter is connected to an autotransformer via an inductive filter L_F equal to 20 mH to deliver a single-phase voltage with an amplitude equal to 260 V. On the other hand, two parallel loads having the task to cause a problem of power quality are installed at the PCC. The first load is a single phase full wave rectifier supplying a variable inductive load with a maximum power P equal to 656 W. Therefore, two values of this loaded power were considered during the experimental tests. The first one is equal to P_L1 = 656 W while the second value is equal to P_L2 = 492 W. On the other hand, the second load is considered as an inductive load with R = 2 Ω and L = 0.5 H.

Fig. 17

Experimental testbed

Furthermore, the P&O algorithm which is used to control the dc-dc boost converter and the two proposed algorithms to compensate disturbing current introduced by nonlinear load were implemented on the dSPACE card under the Simulink/Matlab environment.

During all the experimental tests of the control algorithms, samples of voltage and current are acquired with a sample step of 1.1e-4 s.

3.3.1 Experimental Results During the P&O Algorithm Test

As first step, the P&O algorithm which is aimed to control the dc-dc boost converter was tested and validated. Table 6 presents the electrical power parameters of a PV module at the Standard Test Conditions (STC), which are fixed using the Chroma 62020H-150 s graphic interface. Consequently, the two characteristics of I_PV−V_PV and P_PV−V_PV are obtained by the Chroma 62020H-150 s programmable power supply as showed in Fig. 18. This P_PV-V_PV curve represents a maximum power point equal to P_mpp = 335,3 W corresponding to an optimum voltage equal to V_mpp = 144,31 V. While the corresponding optimum current is equal to I_mpp = 2.324A, referring to the I_PV−V_PV curve shown in Fig. 18.

Table 6 Electrical parameters of a PV module set in the Chroma 62020H-150 s programmable power supply

Fig. 18

I_PV-V_PV and P_PV-V_PV caracteristics programed in the Chroma 62020H-150 s programmable power supply

To validate the two proposed control algorithms of the voltage inverter with variable power, the Chroma 62020H-150 s programmable power supply was programmed to generate a sequential three levels of optimal maximum power (P_mpp). Figure 19 illustrates the three cases of the active power injected by the voltage inverter called as the three experimental modes. In experimental mode 1 (Mode1_exp), the active power of the voltage inverter P₁ is equal to 165 W. Then, in the second experimental model 2 (Mode2_exp), P₂ is raised to 500 W, while in the third experimental mode 3 (Mode3_exp), the power is decreased to P₃ equal to 335 W.

Fig. 19

Experimental active power of the PV inverter

3.3.2 Experimental Results During the Two Proposed Algorithms Test

The performances of the two proposed control algorithms are verified experimentally using the same testbed presented in Fig. 17. The time and the frequency representations obtained with the two proposed algorithms according to the experimental PV inverter power showed in Fig. 19 and under the two considered load conditions (L_{NL1_exp} and L_{NL2_exp}) are presented in Fig. 20 (for the first method) and 21 (for the second method). Consequently, it can be noted that for each case of both the inverter power and the used experimental load, the grid current represents a sinusoidal form with a low THD value between 3.5 and 11.6% for the first method and 1.88 and 6.94% for the second method. In addition, Fig. 22 presents the experimental THD curves as a function of the fundamental grid current. As can be noticed from simulation results, the THD level raises when the fundamental grid current decreases for a used nonlinear load. This proves that the THD depend only on the fundamental grid current. Moreover, compared to simulation results, the second control method is also more efficient for disturbing grid current compensation since the experimental THD values are lower, for all fundamental grid current than the first method. Therefore, the experimental results validate the obtained simulated results and prove that the proposed second method is more efficient to ensure good grid current quality for different PV inverter power even with the presence of a nonlinear load.

Fig. 20

Time and frequency representations of the grid current with the first control method in (a) Mode1_exp with the load L_{NL1_exp}, (b) Mode2_exp with the load L_{LN1_exp}, (c) Mode3_exp with the load L_{NL1_exp}, (d) Mode1_exp with the load L_{NL2_exp}, (e) Mode2_exp with the load L_{NL2_exp}, (c) Mode3_exp with the load L_{NL2_exp}

Fig. 21

Time and frequency representations of the grid current with the second control method in (a) Mode1_exp with the load L_{NL1_exp}, (b) Mode2_exp with the load L_{LN1_exp}, (c) Mode3_exp with the load L_{NL1_exp}, (d) Mode1_exp with the load L_{NL2_exp}, (e) Mode2_exp with the load L_{NL2_exp}, (c) Mode3_exp with the load L_{NL2_exp}

Fig. 22

Experimental THD as a function of fundamental grid current obtained with the two proposed methods

4 Conclusion

In this chapter, two new efficient current control techniques are proposed for the control strategy of the voltage inverter connected in a single-phase grid-connected PV system supplying nonlinear load. Each technique is based on a novel algorithm aimed to extract the disturbing grid current introduced by a nonlinear load at the point of common coupling. To cancel the disturbing current, the resonant controller is used in the first method while the second method is based on the use of several PI controllers. The performances of the two proposed techniques were studied by simulation for two different load cases and with a variable PV inverter power. Thus, it has been proved that with the two proposed techniques, the PV inverter is able to inject the solar power into the grid and to improve the grid current quality simultaneously, even under the variation of the load and climatic conditions. The effectiveness of the two proposed methods have also been verified and validated experimentally on an experimental platform. It has been shown from the simulation and the experimental results that the second algorithm is more efficient in improving the quality of the grid current.