The Processes of Heat and Mass Transfer in the Earth’s Mantle

Abstract

The processes of global heat and mass transfer in the Earth are manifested in the form of thermo-compositional convection in the mantle, which is the driving force of global geodynamics. The feature of this convection is that it is accompanied by very large changes in the properties of the material. The paper presents an overview of numerical models of the authors that reproduce the main global geodynamic processes. Presented models are as follow: the splitting of the lithosphere into separate rigid plates in thermal convection with viscoplastic rheology; the model of vigorous thermal convection with generation of mantle plumes; the model of quasi-rigid continents floating on the convective viscous mantle; the model of thermal convection complicated by phase transitions; the models of thermo-compositional convection, in which massive piles of heavy material are formed at the bottom of the mantle. A schematic geodynamic model of the global heat and mass transfer in the modern Earth is presented, which is consistent at a first approximation with the currently available observational data of geophysics, geochemistry, geology and numerical modeling.

1 Introduction

The Earth is a heat engine in which the heat of decay of radioactive isotopes and the primordial heat of gravitational differentiation is converted into the energy of convective flows in the core and mantle. In the liquid outer core quasi-turbulent convection occurs with the velocities of about 0.05 cm/s or 15 km/year [1], while the convection in the high-viscosity mantle is in the plume mode with the velocities of about 10 cm/year. Convective currents in the mantle determine the global geodynamics of the Earth and are manifested in its relief, surface movements, volcanism and earthquakes.

According to the data of measurements [2] the total surface heat loss of the Earth is equal to Q_t = 47 TW ±2 TW. Accordingly, the average density of the surface heat flux is q = 92 mW/m². The heat coming out through the continents equals 15 TW with a heat flux density of 71 mW/m². The heat coming out through the oceans equals 32 TW with a density of 105 mW/m².

The sources of the Earth’s heat are the decay of radioactive elements and the primordial heat. In the process of evolution and cooling of the Earth both sources are reduced. The relationship between them for the modern Earth is not yet known. According to [3] various estimates give 15 to 41 TW for radiogenic heat and 12 to 30 TW for primordial heat.

In this paper we consider the processes of heat transfer only for the mantle of the modern Earth. The temperature difference across the mantle is supported by the heat flux coming from the core, the heat of decay of mantle radioactive isotopes and the residual primordial heat. Denote the radiogenic heat flux generated in the continental crust by Q_rc. In the model of the Earth’s composition [4] this flux equals Q_rс = 7 TW [5,6,7]. It is 15% of the total heat flux of the Earth Q_t. Thus the mantle heat flux (minus the radioactive heat of the crust) will be equal to Q_m = Q_t – Q_rc = 47–7 = 40 TW = 0.85Q_t with a heat flux density of 77 mW/m². This flux is created by flow from the core Q_сor, heat of radioactive decay in the mantle Q_rm and the heat flow due to secular cooling of the mantle Q_coolm.

The silicate mantle and the crust (after segregation of the core, but without separation of the continental crust) produce a heat flux up to 20 TW [8] or 42% of Q_t. Subtracting the radioactive heat of the crust, we find the power of the radioactive heat of the mantle, equal to Q_rm = 13 TW or 0.275Q_t.

The secular cooling rate of the mantle is estimated within a large range, from 50–70 K/Ga to 100 K/Ga [9]. With the mass of the Earth’s mantle M = 4∙10²⁴ kg and heat capacity of c_p = 1.2∙10³ J/(kgK) and dT/dt = 90 K/Gyr the heat flux due to secular cooling of mantle is equal Q_coolm = c_pM dT/dt = 14 TW.

Subtracting the cooling heat and the radioactive heat of the mantle from the mantle heat flux, we find the heat flux from the core equal to Q_cor = Q_m – Q_coolm – Q_rm = 40–14–13 = 13 TW. This value of heat flux from the core is in accordance with available estimations as 27.5% of Q_t [10, 11] (Fig. 1).

Fig. 1

The thermal balance of the Earth’s mantle

Thermal convection in the mantle occurs due to the temperature gradient, which is supported by its heating from below due to the heat flow from the core Q_cor = 13 TW, and by the total internal heating of the mantle (radiogenic heating and the heat released during secular cooling), i.e. by effective internal heat sources with a power of Q_int = Q_rm + Q_cool = 27 TW. Thus the mantle heating from inside Q_int is about 1.8 times more than the bottom heating Q_cor. So the mantle is heated as 70% from inside and 30% from below. This is consistent with the results of numerical models [10, 11] which demonstrated that the internal heating rate of the Earth’s mantle is constrained to be ≈70% by inferred plume heat flux and plume excess temperature.

Due to sphericity of the mantle, the heat flux density in the mantle decreases with radius about (r/R)² = 3.4 times. However, due to the internal heat sources, the density of the heat flux in the mantle should increase with radius. It is equal to q_cor = Q_cor/(4πr²) = 85 mWT/m² at the core-mantle boundary and q_m = Q_m/(4πR²) = 78 mWT/m² at the upper mantle surface (under the crust). As a result, despite of internal heating the heat flux density in the mantle does not significantly changes with the radius.

The temperature on the Earth’s surface is approximately T = 300 K, and at the core-mantle boundary it is less than the melting temperature of silicates and more than the melting temperature of iron being estimated at about 4000 K [12].

For mantle thickness D = 3000 km the average temperature gradient gradT is equal to 23 K/km. With q = 90 mW/m² and k = 4 Wm⁻¹ K⁻¹ the temperature at the core-mantle boundary would be equal to T = 70,000 K if the removal of heat from the Earth’s interior occurred only due to thermal conductivity q = k gradT. However, due to the fact that the hot silicate material of the mantle can flow, thermal convection occurs in the mantle which accelerates the removal of heat, and as a result the temperature at the core-mantle boundary becomes equal to 4000 K.

The feature of mantle convection is that the parameters of the mantle vary over a large range. Due to the compressibility of the material it is necessary to take into account the effects of adiabatic heating and cooling. The mantle viscosity changes with depth by 4 to 6 orders of magnitude. In this case, near the cold surface there is a strong lithospheric layer with a viscosity of up to 10²⁶ Pa s.

However, the long-acting shear stresses create zones of micro-destruction in the lithosphere. In these local zones there is a brittle plastic flow with reduced effective viscosity. As a result, the lithosphere splits into separate plates. Plates with continents float on the convecting mantle, and oceanic plates without continents take part in the convective circulation of material throughout the mantle. As a result, the Earth’s lithosphere inhibits convection and prevents heat from escaping the mantle much less than if it were continuous.

Solid-state phase transformations have a significant effect on mantle convection. In addition to convective mixing of multicomponent material, its differentiation takes place in the mantle. Due to the difference between the components in density and viscosity, the changing distribution of the components affects the convective flows. As effects of chemical reactions can be neglected, convection in the mantle can be called thermo-compositional rather than thermo-chemical one.

2 Equations of Mantle Convection

Convection is described by the equations of mass, momentum and energy transfer. Currently, the extended Boussinesq approximation (EBA) is widely used in the numerical models of mantle convection. With hydrostatic reference state the density of the mantle material is taken in the form.

$$ \uprho ={\uprho}_0\left[1\hbox{--} \upalpha T+\left(\delta {\rho}_{\mathrm{p}}/{\uprho}_0\right)\Gamma +\left(\delta {\rho}_{\mathtt{\mathrm{c}}}/{\uprho}_0\right)C\right] $$

(1)

where ρ₀ is the average density of the mantle, T is the absolute temperature, α is the coefficient of thermal expansion, δρ_p is the density jump at the phase transition boundary, Γ is the phase function that takes a value of 0 or 1 for different phases, C is the concentration of the chemical component, δρ_c is the difference in the density of the chemical component.

To nondimensionalize the equations for spherical models we use the following scaling factors with characteristic values of the corresponding parameters: the Earth‘s radius R for length, V₀ = κ₀/R for velocity, t₀ = R²/κ₀ for time, ΔT for temperature, η₀ for viscosity, k₀ for thermal conductivity, κ₀ = k₀/(ρ₀c_p) for thermal diffusivity, α₀ for the thermal expansivity, q₀ = k₀T₀/R for heat flux, σ₀ = η₀κ₀/R² for dynamic pressure and stress, p₀ = ρ₀gR for static pressure, H₀ = c_pκ ₀ΔT/R² for the density of heat sources.

In the considered EBA approximation [13, 14] the mass transfer equation is written in a simplified form as a continuity equation.

$$ \partial {V}_j/\partial {x}_j=0. $$

(2)

In the Stokes momentum transfer equation the inertial terms are neglected:

$$ 0=\hbox{--} \partial p/\partial {x}_i+\partial {\uptau}_{ij}/\partial {x}_j+\left[{\mathrm{Ra}}_R\left(\upalpha T\hbox{--} \upbeta C\right)\hbox{--} Rb\varGamma \right]{\updelta}_{ir} $$

(3)

The heat transfer equation takes into account conductive transfer, adiabatic heating and cooling, dissipative heating, heat release at phase transitions and heat release from internal sources.

$$ {\displaystyle \begin{array}{l}\mathrm{D}T/\mathrm{D}t=\partial \left(\kappa \partial T/\partial {x}_j\right)/\partial {x}_j-{\mathrm{Di}}_R\upalpha \left(T+{T}_s\right){V}_r+\left(\mathrm{Di}/\mathrm{Ra}\right){\uptau}_{ij}\partial {V}_i/\partial {x}_j\\ {}+{\upgamma}_k\left(\mathrm{Rb}/\mathrm{Ra}\right){\mathrm{Di}}_R\upalpha \left(d\Gamma /d\uppi \right)\left(T+{T}_s\right){V}_r+H,\end{array}} $$

(4)

where H = Q_int/M_m is the density of internal heat sources (radiogenic heating and the heat released during secular cooling), M_m is the mass of the mantle.

The transport equation of a chemical component is written as a continuity condition for the impurity component.

$$ \partial C/\partial t+{V}_j\partial C/\partial {x}_j=0, $$

(5)

where τ_ij = 2ηe_ij = η (∂V_i/∂x_j + ∂V_j /∂x_i) is the tensor of viscous stresses.

The parameters of the material and the model are included in the Eqs. (2–4) in the form of dimensionless combinations. Here β = (δρ_c/ρ₀)/α₀∆T, Γ = 0.5[1 + tanh(π/w)] is the phase function, π = (r–r_p)–γ(T–T_p) = −(h–h_p)– γ(T–T_p), dΓ/dπ = (2/w)(Γ–Γ²), w is the half-width of the phase transition, γ = dh/dT = (1/ρg)dP/dT is the slope of the curve of phase equilibrium, Ra_R = (R/D)³Ra, where Ra = (ρ₀α₀g∆TD³)/(κ₀η₀) is the Rayleigh number, Rb_R = (R/D)³Rb, where Rb = (δρgD³)/(κ₀η₀) is the phase Rayleigh number, Di_R = (R/D)Di, where Di = α₀gD/C_p is the dissipative number, H_R = (R/D)²H, where H is thermometric density of heat sources, ∆T = T_cmb–T_s, T_s = 273 K is the surface temperature.

3 The Parameters of the Earth’s Mantle

The characteristic values of parameters of the Earth’s mantle [12] are the following: D = 2890 km, M_m = 4.0·10²⁴ kg, ρ₀ = 4.5·10³ kg m⁻³, c_p = 1.25·10³ J/(kg K), η₀ = 10²¹ Pa s, the mean value of the thermal diffusivity κ₀ = 10⁻⁶ m²/s, the coefficient of thermal expansion α₀ = 2·10⁻⁵ K⁻¹, the temperature difference ΔT = 3700 K. As noted above, the effective internal heating of the mantle equals 24 TW, so the density of mantle heat sources will be 6·10⁻¹² W/kg.

At these values of parameters for the compressible mantle, the scaling factors for velocity and time will be κ₀/D = 1.1·10⁻³ cm/yr., D²/κ₀ = 2.6·10¹¹ y, and for the density of radioactive heat sources will be 0.55·10⁻¹² W/kg. The dimensionless parameters included in the convection equations are Ra = 4.5·10⁷, Di = α₀Dg/c_p = 0.45, H=H_r + cool = 11.

The parameters of the mantle, the viscosity η, the thermal expansion coefficients α and the thermal diffusivity κ, included in the convection equations in the form of coefficients should be set as functions of depth and temperature.

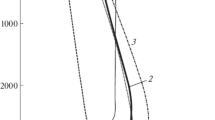
The dependences of the dimensional coefficient of thermal expansion α and thermal conductivity k (as well as the thermal diffusivity κ) on the dimensionless depth x = 1–z given in [15], can be approximated as (see Fig. 2).

Fig. 2

Depth dependence for the coefficient of thermal expansion α and thermal conductivity k with two variants for the lower mantle [15]. Their simplified dependences approximated as (6) are shown by thick lines. The right panel shows the depth distribution of viscosity obtained from postglacial rebound data [17], and the distribution calculated according to (1–6) (thick line)

$$ {\displaystyle \begin{array}{l}\upalpha =42\cdot {10}^{\hbox{--} 5}{\left(2.3+x\right)}^{\hbox{--} 3}{\mathrm{K}}^{\hbox{--} 1},\kern2.5em k=3\cdot \left[\left.1+3.3x\right)\right]\;\mathrm{W}/\mathrm{mK},\\ {}\upkappa =k/\left(\rho {c}_{\mathrm{p}}\right)=1.8\cdot \left[\left.1+3.3x\right)\right]{10}^{\hbox{--} 6}{\mathrm{m}}^2{\mathrm{c}}^{\hbox{--} 1}.\end{array}} $$

(6)

The most important parameter of the mantle is its viscosity. Viscosity is determined by the competition of diffusion and dislocation creep processes in the mantle and brittle plastic deformation in the lithosphere. Parameters included in the dependence of viscosity on temperature and pressure are found according to laboratory measurements and extrapolated to the mantle conditions. Such extrapolation leads to very high viscosity for lower mantle. Therefore, in this paper, we use the effective dependence of viscosity on temperature and pressure [16]. It was chosen as a common formula for diffusion creep with effective parameters which were selected from the condition of optimal agreement with the data of laboratory measurements and the results of solving the inverse problem for post-glacial uplifts [17].

$$ \upeta \left(\mathrm{p},\mathrm{T}\right)=A\;\exp \left[\left({E}_0+p{V}_0\right)/\left(T+{T}_s\right)\right], $$

(7)

where E₀ is the activation energy, and V₀ is the volume of activation.

The activation energy value for the entire mantle is taken from the data for olivine E₀ = 350 kJ/mol. The piecewise constant coefficient A for the lower mantle was found from the condition of normalization to the viscosity η(p,T) = A = 3·10²¹ Pa s at a depth of 700 km. The coefficient A for the upper mantle was found from the condition of viscosity jump by the factor 30 on the phase boundary 660 km. The value of the activation volume for the upper mantle V₀ = 4 cm³/mol was taken according to the measurements for olivine, and the corresponding value for the lower mantle was taken two times smaller, V₀ = 2 cm³/mol.

To obtain the spatial distribution of viscosity in the mantle η(x, y, z), we need to substitute the pressure and temperature of the mantle as a function of coordinates in the expression (7). Since the pressure can be considered hydrostatic, the dependence on the radius r will have the form p = ρ₀g(D–r). The temperature distribution in the mantle is not known in advance and can be founded only after solving the equations of convection (1–4) with the equation for viscosity η(p, T) in the form (7).

Figure 2 (right) shows the calculated laterally averaged depth viscosity distribution along with the viscosity distribution obtained from of the post-glacial uplift data [17].

The dependence (7) describes only the Newtonian viscosity η_d for diffusion creep, which occurs in the lower mantle. In the upper mantle at depths of less than 200 km, the material can also flow through the dislocation creep mechanism, in which the viscosity also depends on the strain rates in the form of a power function. The calculation of convection at the top of the upper mantle in an area where viscosity is determined by dislocation creep and has large variations requires considerable computing time. Therefore, the dislocation viscosity is often neglected, and the viscosity dependence (7) is considered as effective.

In the lithosphere at depths of less than 20 km and at temperatures below 600 K, the diffusion viscosity η_d (7), as well as the dislocation viscosity, are very high. However, in very slow processes brittle-plastic flow takes place with effective viscosity.

$$ {\upeta}_{\mathrm{y}}={\uptau}_{\mathrm{y}}/2\upvarepsilon, {\uptau}_{\mathrm{y}}={\mathtt{\mathrm{C}}}_0+\upmu P,{\upeta}_{\mathrm{y}}>{\upeta}_{\mathrm{max}} $$

(8)

where P = ρgz is the lithostatic pressure, С₀ is the cohesive strength, μ is the friction coefficient, ρ is the density, z is the depth. For the mantle the parameters С₀ and μ depend little on the kind of material and have values of the order С₀ ≈ 10 MPa and μ = 0.7 [18].

The distribution of the effective viscosity in the entire mantle, taking into account the processes of high-temperature diffusion and brittle microfractures, under the condition of the additivity of the strain rates ε = ε_d + ε_y can be described by a single formula.

$$ \upeta =1/\left(1/{\upeta}_{\mathrm{d}}+1/{\upeta}_{\mathrm{y}}\right). $$

(9)

With rise of pressure and temperature the mantle material undergoes the phase transformations with jumps in density. The main ones are the olivine-wadsleyite transition at a depth of 420 km, with the slope of the curve of phase equilibrium γ₄₁₀ = 3 Pa/K (Clapeyron slope) and the density jump δρ₄₁₀ = 0.96ρ, the ringwoodite-perovskite transition at a depth of 660 km with the Clapeyron slope γ₆₆₀ = −2.5 Pa/K and the density jump δρ₆₆₀ = 0.08ρ, and the perovskite-postperovskite transition at a depth of 2750 km with the Clapeyron slope γ₂₇₅₀ = 13 Pa/K and the density jump δρ₂₇₅₀ = 0.015ρ. With a positive slope γ a phase transition slightly accelerates convection, and with a negative slope γ it slows down convection.

4 Numerical Models of Vigorous Thermal Convection in the Regime of Pulsating Mantle Plumes

The structure of thermal convection depends fundamentally on its vigor, which in turn is determined by the values of the parameters of the mantle material and the conditions of its heating. With the parameters corresponding to the material and conditions in the modern Earth’s mantle mentioned above, the Rayleigh number Ra characterizing the convection vigor is approximately 10⁷. With its secular evolution, the Earth cools down. Since the viscosity depends exponentially on the temperature, the Rayleigh number for the mantle of the early Earth was probably an order of magnitude greater, and for the future Earth it will be several orders of magnitude smaller.

The character of mantle convective flows is usually considered in models that do not take into account the lithosphere. The viscosity in the upper cold lithospheric layer is also described by the effective viscosity, replacing in (7) the surface temperature T_s by its average mantle value [19]. Figure 3 shows the calculated structure of convection for Rayleigh numbers equal to 10⁵ and 10⁶. Such Rayleigh numbers correspond to the future colder Earth, which has an average viscosity about 100 and 10 times greater than the present one. At Ra = 10⁵ thermal convection with the viscosity depending on pressure and temperature (7) still remains almost stationary with regular cells.

Fig. 3

Calculated thermal structure in a mantle with variable viscosity at low convective vigor for the cooling future Earth. The temperature is shown in gray scale; the flow velocities are shown by arrows. The deformed phase boundaries at depths 420 km, 660 km and 2750 km are shown with white lines

With increasing Rayleigh number, ascending and descending convective flows become narrower. At Ra = 10⁶ convection becomes unsteady and its structure begins to rearrange in shape and the number of flows. New ascending flows emerging at the bottom of the mantle gradually take a mushroom shape with a head and a tail and are called plumes. When plumes reach and breakthrough the surface they create large igneous provinces on continents and basalt plateaus at the bottom of the oceans.

The hot stream of a plume tail continues to rise and burns the moving lithosphere. At Ra = 10⁶ the hot material of a plume tail rises uninterruptedly. So in this model a continuous ridge of volcanoes would appear on the surface of the moving lithospheric plate. It is shown [20] that life time of each plume is several hundred million years. The plumes die by pairwise association.

Figure 4 shows the calculated convection structure at higher vigor for Rayleigh numbers Ra = 10⁷ and Ra = 10⁸. Such Rayleigh numbers can correspond to the modern and early hotter Earth.

Fig. 4

Calculated thermal structure in a mantle with variable viscosity at high convective vigor for the modern and early hotter Earth. The temperature is shown in gray scale, the flow velocities are shown by arrows

As seen in Fig. 4, at Ra = 10⁷ the mantle plumes become unstable. The heads of plumes are more pronounced, and most importantly, inside the plume tails, the hot material from the bottom of the mantle begins to rise not continuously, but in separate portions. Therefore, thermal mantle plumes should generate on the surface of a moving plate not a continuous ridge of volcanoes, but a chain of individual volcanoes. At the bottom of the ocean, each portion of hot material of thermal plumes generates a separate large island. This phenomenon for mantle plumes can be called pulsations. It should be noted that in the literature, the pulsations of plumes are often called not the pulsating rise of hot material in the tile of each individual plume, but a simple periodic disappearance and birth of new plumes.

The physical meaning of such pulsation of mantle plumes can be understood by comparing the structure of thermal convection at the Rayleigh number Ra = 10⁷ and at even greater vigor. As seen in Fig. 4, at Ra = 10⁸, the tails of the mantle plumes are broken, and a conveyor of rising portions of the hot material along the direction of the former plume is formed. Thus, it is necessary to distinct the modes of thermal convection with quasi-stationary plumes, with pulsating plume tails and with conveyors of rising portions of the hot material called thermals. Convection calculations at even higher Rayleigh numbers show that the ascending portions of hot material (thermals) become increasingly independent, and convection goes into a turbulent regime.

The above model of convection without taking into account the lithosphere can explain only the main dominant period of eruption in hot spots of the order of 10 million years. However, the intervals between volcanic eruptions in hot spots constitute a large spectrum (for example, the Hawaiian chain in the Pacific or a chain of volcanoes ending with a Yellowstone volcano). The whole range of hot spot chain eruptions is explained by the fact that the hot material supplied by the plume first accumulates under a moving lithospheric plate in the form of a sublithospheric hot anomaly. In this hot anomaly, small-scale convection occurs during partial melting of the material. As a result, magma breaks from this anomaly to the surface occur periodically, forming chains of volcanoes [21].

5 Models of Thermal Convection that Include Plates

The process of splitting the Earth’s lithosphere into separate plates was understood and began to be modeled after it was found that, with slow processes, shear stresses generate microcracks that can be healed in dynamic equilibrium. As a result, the process of long-term shear deformation can be mathematically written as a flow with effective viscosity depending not only on temperature and pressure, but also on shear stress [12]. In last decade, the problem of plate tectonics has been principally solved and the models show how plates can naturally and self-consistently form during thermal convection in a viscous fluid with the properties of the Earth’s mantle [22].

Numerical experiments make it possible to show how the lithosphere is divided into separate rigid plates, see for example [18]. A heated fluid layer with temperature and pressure dependent diffusion viscosity that corresponds to silicate material of the mantle was considered. By the formula (7) the viscosity of the upper colder layer turns out very high, about 10²⁶ Ps. As a result, a continuous layer of the lithosphere occurs at the surface of the mantle, and mantle convection occurs only under the lithosphere. Next, effective plasticity of the real Earth’s material (allowing for microcracks and water content) was taken into account, when the viscosity depends not only on temperature and pressure, but also on stresses. This leads to the fact that in area of maximal shear stress the concentration of microcracks increase, and the effective viscosity drops sharply. The greatest stresses at convection arise over the descending convective flows. As a result, the rigid lithosphere is divided into separate rigid plates. These plates immerse to the mantle in the subduction zones, and a new material comes instead from the mantle to the surface in the mid-ocean ridges. Then it moves horizontally and cools. Accordingly, the plates thicken as they move away from the ridges. The simulation automatically reproduces the whole process.

Figure 5 shows that the horizontal velocities of all points inside each plate are identical and change abruptly at the joints of the plates in the ridges and subduction zones. Each plate moves at its own speed, thickens as it moves away from the ridge and sinks into the mantle in subduction zones. At the 660 km phase boundary the plates are bent and partially torn. The calculated fields of temperatures, viscosity, convective velocities, plate velocities and ocean floor relief with deep depressions in subduction zones and mid-ocean ridges correspond to the observed manifestations of lithospheric plate tectonics on the Earth.

Fig. 5

The numerical model of convection in a heated layer with a viscoplastic rheology corresponding to the material of the Earth’s mantle. The viscosity distribution is shown by the color scale (on the right). Flow velocities are indicated by arrows with a maximum value of 15 cm/year. Above are the distribution of the horizontal velocities of the resulting plates and the calculated relief of the ocean floor

Figure 6 shows the evolution of oceanic lithospheric plates . Plates participate in the convective circulation of the mantle material and immerse to the mantle in subduction zones. The ringwood-perovskite phase transition at a depth of 660 km slows down plates. They bend and partially break. The configurations of submerged plates near the 660 km boundary for different sites observed by tomography data can correspond to different stages of the calculated evolution of convection [22].

Fig. 6

The calculated evolution of configurations of submerged plates over time, with an interval of 3 my. Below, for comparison, the tomography data are shown [23,24,25], where low seismic velocities correspond to cold plates (blue)

Despite the fact that the problem of splitting into separate plates has now been solved in principle, and this process can be reproduced in mathematical models, there are still problems of a more detailed study of the interaction of plates, in particular at the junctions of two oceanic plates in the subduction zone. According to observations, the subduction is usually one-sided, in which only one oceanic plate is submerged into the subduction zone. However, Fig. 5 shows that in the considered model of convection with a non-deformable upper boundary there is a two-sided subduction. Crameri et al. [26] showed that it is necessary to use more real boundary conditions. Under the oceans the lithosphere is covered with a layer of water. In this case, the upper boundary of the lithosphere can be deformed. Under such conditions, if one of the plates begins to bend and sink into the mantle at the junction, it will be below the other plate. As a result, only one of the plates begins to sink into the mantle, and the subduction becomes one-sided.

To complement the theory of lithospheric plate tectonics, it is necessary to construct three-dimensional spherical convection models that take into account the self-consistent interaction of many plates.

6 Mantle Convection with Floating Continents

The oceans cover only about three-quarters of the Earth’s surface are separated by continents that can drift on a viscous mantle and change the configuration of the oceans. Numerical simulations of tectonics of floating continents were studied intensively in IFZ RAS in the 2000s, e.g [27,28,29]. To describe the interaction of convective flows with continents and to identify the characteristic features of continental drift, we solved a system of convection equations in a fluid along with Euler’s equations of motion of solids.

A numerical experiment makes it possible to understand the basic physical processes manifested in the interaction of convective flows with floating continents [28]. A layer of viscous heated fluid was considered, on which two continents in the form of light rigid plates were superimposed (see Fig. 7). Thermal convection occurs in the fluid with several convective cells. Convective currents drive the superimposed plates. Since the plates inhibit heat removal from the mantle, they change the temperature distribution in the mantle and cause changes in the entire structure of the mantle flows. The plates (continents) first combine over a downward convective flow and assemble into a supercontinent. Due to thermal blanket effect the mantle under the supercontinent gradually heats up, the supercontinent rises and breaks up. The entire cycle takes about 0.5 billion years.

Fig. 7

Calculated evolution of thermal convection in a fluid layer with two floating plates (black color). The dimensionless temperature is indicated by the color scale. The red line is the dimensionless heat flux Nu, green line is the elevation h in km. The time is in million years

The results of this numerical experiment on the simplest model confirm and illustrate the laws of continental drift discovered by A. Wegener and then developed by T. Wilson and reveal a number of new details.

To simulate the future drift of continents, a spherical convection model was considered, which was as close as possible to the modern mantle [29]. Seismic tomography gives the spatial distribution of seismic wave velocities in the mantle. It is known how these velocities depend on temperature. The spatial distribution of temperature in the real modern Earth was found by recalculation. This temperature distribution was taken as the initial state. So in this case we deal with the convective model that corresponds to the real modern Earth. Six heat-conducting rigid floating plates were superimposed on the fluid surface, corresponding by form to modern continents, with eight smaller plates, corresponding by form to large islands, taken from geographical maps (see Fig. 8). Further, a nonlinear system of thermal convection equations was numerically solved together with a system of Euler equations for the movement and rotation of continents under the action of viscous coupling forces with mantle flows, taking into account the inverse thermal and mechanical influence of continents on convection. The cold zones of the initial mantle temperature field began to descent, and the hot ones began to rise. As a result, thermal convection developed in the mantle. Due to mechanical coupling the convective currents set in motion all the continents and islands. However, due to the thermal interaction, the continents constantly influence the temperature field in the mantle. Since the model is constructed taking into account mechanical and thermal interactions of the viscous mantle and solid continents and also the parameters of the material corresponding to the real modern Earth, it allowed to calculate the possible future drift of the continents.

Fig. 8

A numerical model of the future of the continental drift. The time is shown in million years, the maximum length of the arrow corresponds to the speed of 12 cm/year. The contours show the calculated positions of continents and islands, and the arrows show the velocity of mantle flows in successive time intervals into the future for 100 my. According to the model, America will move to Antarctica, and Eurasia, Australia and Africa will assemble into a supercontinent

This numerical model shows the evolution of mantle convection taking into account its real interaction with six continents and large islands. Already in the 2000s, there were opportunities to calculate models of thermal convection with floating continents. However, most researchers were engaged in the construction of the theory of tectonics of oceanic plates, since it was more relevant and it was clear that rigid plates can arise self-consistently within thermal convection with viscoplastic rheology. Recently, interest in modeling the interaction of continents with convection has increased [30,31,32]. At the same time, the main attention is currently paid to the refinement of the properties of the mantle material and the initial temperature distribution, while modeling the shapes of continents as simple squares.

7 Global Thermo-Chemical Model of the Earth with Accumulation of Heavy Components at the Bottom of the Mantle

Important for understanding structure of the Earth and global geodynamics in the last decade was the discovery of giant piles of heavy material at the bottom of the mantle. According to seismic tomography, there are two anomalous regions at the bottom of the mantle under Africa with an average height of up to 1500 km and under the South Pacific with a height of up to 1000 km. In these regions the shear seismic velocities are reduced by 2% to 3% [33].

These piles are called Large Low Shear Velocity Provinces (LLSVP). The pile under Africa is called Tuzo in honor of T. Wilson, and the pile under the Pacific is called Jason in honor of J. Morgan. It is assumed that previously the mantle primary material enriched with iron and containing He₃ descended to the bottom of the mantle. Hereafter the oceanic crust began to go down into the mantle together with plates. At depths of about 80 km the basalt crust turns into eclogite, which is heavier than the mantle material. This eclogite accumulated as a heavy layer at the bottom of the mantle. Mantle currents have raked this material into two large piles.

This process can be illustrated by a simplified model of thermo-compositional convection in a heated spherical region (spherical axisymmetric annulus) at the Rayleigh number Ra = 2·10⁷ [34]. The even layer of a chemically different material with an increased density of 3% was placed at the bottom of the mantle. The calculations have shown that in the absence of continents and oceanic plates the descending mantle flows deform the layer of heavy material, and it decomposes into several small evenly spaced clusters.

Then the continent (as a region with the increased viscosity by four orders of magnitude) was incorporated in the model. Accumulation of heat under the continent leads to the rebuilding of convection pattern, and a large pile arises at the bottom of the mantle. Further two plates moving in different directions were added to the model. They were simulated by the prescribed surface velocity. As a result, the second large pile arises at the mantle bottom. Figure 9 shows the steady-state structure of mantle flows and temperature distribution for this case. It also demonstrates that all the heavy material at the bottom of the mantle was grouped into two large piles. The location of these piles is in good agreement with the tomography data [33].

Fig. 9

Numerical model of thermal convection in the mantle taking into account the large fixed continent (Africa) and oceanic plates of the Pacific type. The temperature distribution is shown by color scale; the velocities of the mantle flows are shown by arrows. The diamonds indicate two piles under the Pacific (Tuso) and under the Africa (Jason). White lines in the form of deformed circles show the phase boundaries at the average depths of 420 km and 660 km. The postperovskite phase is inside the lenses at the bottom of the mantle

This arrangement of piles is explained by the fact that the descending mantle currents drag the heavy material to the bottom of the mantle in different directions under the fixed continent (Africa) and under the large oceanic plate (Pacific).

At high pressures the mantle material turns into the postperovskite phase. In the absence of convection, the phase boundary of the perovskite-postperovskite transition is at a depth of 2750 km. In convection, lateral variations of the depth of this boundary occur, and their value is proportional to the Clapeyron slope of the phase change. The slope for the perovskite-postperovskite transition is very large. Therefore, in hot regions the equilibrium pressure of the phase transition increases so much (above the pressure at the bottom of the mantle) that the phase boundary falls outside the mantle. As a result, the phase of postperovskite in the mantle is not in a layer lying below the border of 2750 km, but, similar to the piles of heavy material, is located in two areas at the bottom of the mantle, where cold downward flows come. Figure 9 delineates these areas by a white line. It is noteworthy that the postperovskite regions are located at the bottom of the mantle just between eclogite piles.

As partially seen in Fig. 9 and as other more detailed models show, the mantle plumes of hot spots originate predominantly at the edges of heavy piles at the bottom of the mantle. Figure 9 also shows that the piles resting on the hot iron core are not only heavy, but also abnormally hot.

8 Conclusion

To date, the theory of global tectonics of the Earth is basically built. In its creation, the data of geophysical, geological and geochemical observations, data of laboratory studies of materials, as well as numerical modeling of heat and mass transfer processes were used.

Now it is clear why convection is possible in the mantle at a temperature below solidus, why cold “stone” plates with a thickness of more than 50 km can bend and not break when sink into the mantle. It turned out that this is due to the long duration of the processes in which diffusion has time to give the solids locally effective viscous properties.

On the long road to theory of Earth’s global tectonics there were periods of acceptance of erroneous hypotheses. For example, long time it was believed that convection in the mantle can be two-layer, and plumes rise independently of the thermal convection due to light chemical impurities.

The plumes are ascending convection jets that can occur both during thermal and thermochemical convection. At low vigor convection is laminar, at very large vigor it is turbulent, and in the intermediate case convection is in transition plume mode. The vigor of convection is determined by lateral variations in density, depending on the degree of heating and chemical impurities, as well as by the viscosity and thickness of the layer.

Deep mantle plumes cause catastrophic eruptions, and give rise to Large Igneous Provinces and hot spots on the Earth’s surface. By analogy with thermochemical subduction plumes, which arise due to chemical impurities, it was initially believed that the deep mantle plumes of hot spots also have a chemical nature. However, it turned out that they have a thermal nature. The high vigor of convection required for plumes is provided not by chemical impurities, but by a large temperature difference and low viscosity. These plumes originate at the boundary with a liquid, highly heat-conducting iron core, which constantly compensates for the removal of heat carried away by plumes from the place of their formation. Chemical impurities can only to change a little the properties of these plumes. Mantle plumes originate at the bottom of the mantle mainly at the edges of piles of heavy material, which is partially captured and reduces the buoyancy of plumes.

Due to the phase transition at a depth of 660 km, cold descending convective flows are inhibited, but convection remains a whole mantle one. The cold high-viscosity slabs descending to the bottom of the mantle (and somewhat the hot narrow plumes rising to the surface) set all the mantle material in circulation motion and interact with each other.

Figure 10 shows a schematic of the global thermochemical model of heat and mass transfer in a modern world.

Fig. 10

Schematic thermochemical geodynamic model of the modern Earth in the equatorial section, supplemented by [35]. Continents are shown in dark brown, oceanic plates are in blue, the postperovskite (ppv) phase on the mantle bottom is in green, hot piles (Tuzo and Jason) are in brown, mantle plumes are in red, convective flows are lines with arrows, PGZ are zones of preferential plume generation, ULVZ are zones of ultra-low velocities, interpreted as zones with high iron content at a high degree of partial melting

This scheme of global thermochemical convection is still simplified. It shows the basic fundamental structures formed in the process of heat and mass transfer. The whole pattern of all currents is not yet known. In reality, due to convective mixing and separation, there are many geochemical reservoirs in the mantle. In this scheme, the formation of only the two most important ones is considered.

The construction of a complete three-dimensional picture of convective flows in the mantle, explaining the evolution of the distribution of chemical isotopes in the mantle, is the next problem of global geodynamics.