Keywords

1 Introduction

Sectorization is generally related to geographical aspects and has many applications in dividing a large political territory or districts of sales, airspace, municipality, healthcare, electric power, emergency service, internet networking, police patrol, public transportation network, social facilities, collection and transportation of solid waste in municipalities, etc., into smaller regions [2, 4, 5, 11, 12]. The equilibrium of load, distance, client, contiguity, and compactness are the criteria which are generally considered in sectorization [14]. The concept of sectorization, is similar to clustering though have significant differences. Clustering strives for inner homogeneity of data while sectorization aims at the outer similarity. Therefore models for solving both problems are in general not compatible [6].

One of the problems that is related to territorial design is the location-routing problem (LRP). In the literature, it is stated that LRP consists of two difficult problems as the facility location problem (FLP) and also the vehicle routing problem (VRP) [7]. Many methods have been proposed to solve different types of LRP, which is an NP-hard problem [13]. In this work, we deal with a multi-objective location-routing problem (MO-LRP), where there are a set of potential DCs and also a set of customers in different geographical locations with known demands. Unlike previous studies, we model it as a problem consisting of sectorization, sub-sectorization, and routing sub-problems. In the sectorization stage, a subset of potential DCs is selected to be opened and customers are divided among them. Each DC and its assigned customers form a sector. In the sub-sectorization stage the customers of each DC are divided into sub-sectors. To meet their demands a fleet is considered. Starting from and returning to a DC, a route is defined for each sub-sector [8, 14,15,16].

Previously MO-LRP has been solved based on sectorization concept; for example, Barreto et al. [1] integrate some hierarchical and non-hierarchical clustering techniques into a sequential heuristic algorithm to solve this problem. Martinho et al. [8] propose a method consisting of pre-sectorization, sectorization, routing, and multi-criteria evaluation phases to deal with multi-criteria and large dimensions of the capacitated location-routing problem (CLRP). Different from these studies, we design two new approaches adapting the non-dominated sorting genetic algorithm (NSGA-II) with sectorization, sub-sectorization and routing sub-problems and solve MO-LRP by them. In the first one, all sub-problems are solved simultaneously with NSGA-II. The second approach is similar to the first one however, it has a hierarchical structure such that after creation of sectors and sub-sectors with NSGA-II, routes are defined using a binary integer programming solver for the obtained Pareto solutions. It should be noted that the operators of NSGA-II used in both approaches are the same as in the algorithm proposed by Deb et al. [3]. Also, in this study, new chromosome representation, crossover and mutation operators are designed and used in NSGA-II to solve MO-LRP, which comprise sectorization, sub-sectorization and routing stages. The operators can be used in similar evolutionary algorithms to solve the problem based on the sectorization concept.

A comparison is made over four benchmarks, based on the number of non-dominated solutions acquired by the approaches. The results show that the first approach is able to find more non-dominated solutions.

The other sections of the study are such that the problem and proposed approaches are described in Sects. 2 and 3. The experimental results, conclusion and future works are the last two sections of the work.

2 Problem Description

In this section, we describe the problem, which is solved by both approaches. In the problem, there are some potential DCs and also some customers. A subset of DCs is opened and a subset of customers is assigned to each of them. Then routes are defined to meet the demands of customers. Each route starts from a DC and returns to the same DC by visiting a subset of the assigned customers. There is a cost to open each DC and it is desired to minimize the total cost of opening DCs. As described in Sect. 1, we name each opened DC and the customers assigned to it a sector. The resulting sectors are desired to be balanced both in terms of customers’ demands and distance on routes, which are defined as the standard deviations of demands and distances in sub-sectors. In addition, in the formed sub-sectors, customers are desired to be quite close to the center, which is defined as the compactness of sub-sectors.

In Fig. 1, an illustrative example is presented, where DCs and customers are shown with squares and circles, respectively. The squares shown in green and blue are the opened ones. Each DC and the assigned customers form a sector, which are shown with the same color. In this example, each sector is divided into two sub-sectors, and a route is defined for each one. For instance, the routes denoted by dark and light green, are determined for the sub-sectors with green DC.

Fig. 1
figure 1

An illustrative example

Full size image

Some of the terminology and notations used in the paper are summarized in Table 1.

Table 1 Used notations
Full size table

As defined in Eq. 1, f 1 is the total cost of opening DCs.

$$\displaystyle \begin{aligned} f_1=\sum_{l=1}^{L} CO_{k} \times x_{k} \end{aligned} $$
(1)

where

For each sector, the sub-problems of sub-sectorization and routing are solved. Sectors and sub-sectors are expected to be balanced in terms of demand and distance. So, the objective functions of sub-sectorization and routing sub-problems are the standard deviations of demands, distances and compactness in sub-sectors, defined as in Eqs. 2, 4 and 3.

$$\displaystyle \begin{aligned} f_2 = \sqrt{\frac{1}{M-1} \sum_{m=1}^{M} (DE^m-\bar{DE})^2} \end{aligned} $$
(2)

where \(DE^m=\sum _{i=1}^{I} DE_i \times y_{i}^m\) and \(\bar {DE}=\frac {\sum _{m=1}^{M} DE^m}{M}\) and

$$\displaystyle \begin{aligned} f_3 = \sqrt{\frac{1}{M-1} \sum_{m=1}^{M} (CP^m-\bar{CP})^2} \end{aligned} $$
(3)

where \(CP^m = \frac {CE^m}{CE_{max}^m}\) and \(\bar {CP}=\frac {\sum _{m=1}^{M} CP^m}{M}\).

To calculate \(CE_{max}^m\) the coordinates of the centre point of each sub-sector are considered as the average of the coordinates of the customers in the sub-sector.

$$\displaystyle \begin{aligned} f_4 = \sqrt{\frac{1}{M-1} \sum_{m=1}^{M} (DS^m-\bar{DS})^2} \end{aligned} $$
(4)

\(DS^m=\sum _{m=1}^{M}\sum _{i=1}^{I}\sum _{j}^{I} DS_{ij} \times z_{ij}^m\) and \(\bar {DS}=\frac {\sum _{m=1}^{M} DS^m}{M}\).

It is assumed that all customers are connected with each other.

There are also some constraints; each customer must be only assigned to one sector, which is imposed by Constraint 5.

(5)

One vehicle is allocated to a sub-sector. It is assumed that the eets are homogeneous, i.e. the capacity of the vehicles is the same. Therefore, there is no need for a decision variable for assigning the vehicles. However, the total demand of customers in each sector must be less than or equal to the capacity of each vehicle, which is imposed by Constraint 6.

(6)

In addition, the number of sub-sectors must be less than or equal to the number of vehicles.

3 Solution Approaches and Algorithms

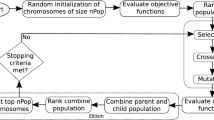
In this section, the solution approaches are described, which are also summarized in Fig. 2. In both approaches, sectorization, sub-sectorization and routing sub-problems are solved sequentially, and in this sense, both have a hierarchical structure. But in the first approach, Pareto optimality is evaluated inside of NSGA-II considering all objective functions, simultaneously. However, in the second approach, sectorization and sub-sectorization sub-problems are solved with NSGA-II and Pareto optimality is evaluated considering the total cost to open DCs, the standard deviations of demands and compactness in sub-sectors. For the non-dominated solutions obtained in this way, the routing sub-problem is solved with a solver to minimize the standard deviation of distance in sub-sectors. In the second approach, since the problem is solved in two different stages, it is called as a hierarchical approach.

Fig. 2
figure 2

General steps of the approaches

Full size image

At first, using the weighted sum method the problem is transformed to a single-objective one and it is solved with a single-objective genetic algorithm (SOGA). The purpose is to make comparison with the multi-objective one and also to create the initial populations of NSGA-II in the two approaches. Using weights w i, the objective function of the single-objective problem is defined as in Eq. 7.

(7)

To generate initial population of the SOGA, randomly a subset of potential DCs is opened and the corresponding objective function is calculated. Each customer is assigned to the nearest open DC and in this way sectors are formed. If no customer is assigned to a DC, it is removed from the opened DCs. The sectors are divided into sub-sectors, taking the constraints of capacity and number of vehicles into account. It is supposed that a vehicle is allocated to each sub-sector and the fleets are homogeneous.

During iterations, new individuals of the SOGA are derived using crossover and mutation operators. The objective functions of the new individuals formed in this process may change, in which case they must be recalculated. The used chromosome structure is seen in Fig. 3, where each column represents a DC and the subjacent rows, shows the related sectors and sub-sectors. Figure 3a and b show an example chromosome before and after sub-sectorization. In Fig. 3, ‘{}’ is used to show that the corresponding DC is not open and therefore no customer is assigned to it. Using the nearest neighbor heuristic, a traveling salesman problem (TSP) is solved for each sub-sectors. A route is defined starting from a DC, visiting the nearest customer at each stage, repeating this process until all customers are visited, and returning to the DC. After solving TSP for each sub-sector, the customers in the second line are written sequentially.

Fig. 3
figure 3

Information about DCs, assigned customers (a) before and (b) after sub-sectorization

Full size image

In the designed crossover operator, which is seen in Fig. 4, a subset of customers is selected and is replaced in sectors of children according to the parents. For example, as shown in red in Fig. 4, customers 1, 3 and 9 are selected. In parent 2, customer 3 is in the sector related to DC 1 and customers 1 and 9 are in the sector related to DC 4. Therefore, in child 1, these customers are placed in the sectors related to DCs 1 and 4. A similar process is done for child 2 considering parent 1. In children, customers are placed in random positions. The order of customers in the representation of sectors in chromosomes affects the formation of sub-sectors.

Fig. 4
figure 4

The used crossover

Full size image

As seen in Fig. 5, three types of mutations are used. The operator seen in Fig. 5a is similar to the single-point crossover but it is a mutation because it is applied to a single chromosome. In this operator, two sectors of a chromosome are selected and a process similar to single-point crossover is performed. Using the mutation operator shown in Fig. 5b, an open DC is randomly selected to close and its customers are assigned to another DC, which is randomly selected to open. If all DCs are open, one of them is closed randomly and its customers are added to another DC, which is also chosen randomly. As mentioned before, the order of customers in the representation of sectors in chromosomes is important and affects the formation of sub-sectors’. In the mutation operation shown in Fig. 5c a sector is selected randomly, and the order of customers in the representation of sectors in the chromosome is changed randomly. To apply the mutation, one of these three operations is randomly selected and performed.

Fig. 5
figure 5

The used mutations

Full size image

Both crossover and mutation operators are applied to the part of chromosomes that represents sectors. Sub-sectors are created from sectors, taking into account the constraints of the number and capacity of vehicles.

The final population obtained after finishing the SOGA iterations is used as the initial population of NSGA-II in both approaches. NSGA-II applies the same crossover and mutation operators with SOGA. In NSGA-II, during iterations, the parent and offspring populations are selected and merged. Using the non-dominated sorting and crowding distance calculation, Pareto fronts are formed and then the new population is chosen using the selection operator. The general steps of the implemented NSGA-II can also be found in [17].

As seen in Fig. 2, the two approaches are similar, and in both the sectorization and sub-sectorization steps are done with NSGA-II. In the first approach, routing is also done in NSGA-II. For this aim, using the nearest neighbor heuristic, a TSP is solved for each sub-sectors. But in the second approach the routing problem is solved outside of NSGA-II. It is performed when the iterations of the algorithm are finished. This process is done once and only for non-dominated solutions obtained by NSGA-II. For this aim, a TSP is solved for each formed sub-sectors using the intlinprog function, which is a binary integer linear programming solver in MATLAB optimization toolbox.

We suppose that each sub-sector is a complete graph, whose vertices are the DC and customers. A directional link between vertices is named a trip. Tours consist of a combination of trips. If there is a trip between two vertices on a route, the corresponding binary variable equals 1 and in otherwise it is 0. In this way, the binary decision variables of the model are defined as all possible trips. The distance of each trip is calculated and to be minimized, the objective function of the routing problem is the total distance of the resulting trips, which is also defined as in Eq. 4.

The intlinprog function can deal with both equality and inequality linear constraints. In the applied routing problem there are two types of linear equality constraints. The first one ensures that in each sub-sector the total number of trips is equal to the number of vertices, while the second one makes certain that each vertex has connected to two trips [10].

During the routing, sub-tours may occur, which are disconnected loops instead of a continuous path. In the applied method, iteratively, sub-tours are detected for each obtained solution and inequality constraints are used to prevent them. This process can be summarized as: suppose that s vertices create a sub-tour. In this case, there are s links that connect them to each other. The corresponding constraint provides that the number of links between the vertices is less than or equal to s − 1. A more detailed description of the used routing method at this stage can be found in [10].

4 Experimental Results

We implement the approaches described in Sect. 3 in MATLAB R2019b environment on an Intel Core i7 processor, 1.8 GHz with 16 GB of RAM. The parameters used in both NSGA-II and also SOGA are: population size =  200, number of iterations =  300, crossover rate =  0.6 and mutation rate =  0.1. The weights defined in Eq. 7 are: w 1 = w 2 = 1, w 3 = 20, to generate initial populations of NSGA-II in the first and second approached w 4 = 1 and w 4 = o, respectively. The reason to choose f 3 = 20 is that in some trial runs, values were generally as 20 times less than the others. Equal weights are given for the other objective-functions.

Indicating as Number of customers ×Number of vehicles ×Number of possible DCs, four benchmarks are generated as 15 × 5 × 3, 30 × 10 × 6, 60 × 20 × 12 and 120 × 40 × 24. We use the discrete uniform distributions as U(10, 100) to create customers’ demands. After defining the demands of customers, the total demand is calculated and then the capacity of each vehicle is defined as 1.3 ×round (total demand/number of vehicles). Furthermore, the coordinates of both customers and DCs in two dimensions are generated according to the normal distribution as N(50, 10). The opening cost of each DC is created according to U(10, 15).

For each benchmark, when the solutions achieved by two approaches are compared with each other, some of them dominate others. So, for each benchmark, we again do a domination check between solutions that two approaches get. To do a comparison, we divide the number of non-dominated solutions (NC) obtained by each of the approaches into the number of all non-dominated solutions. The acquired value is shown by e. Related results are presented in Table 2.

Table 2 Comparison between the approaches
Full size table

As shown in Table 2, the first approach in all of the benchmarks achieves significantly better results than the second one according to the value of e. Therefore, it can be considered as an efficient approach to solving all stages of MO-LRP simultaneously with an effective algorithm as NSGA-II.

Excluding benchmark 1, in the other ones, the best solution found by SOGA is among the non-dominated solutions obtained NSGA-II. Similar results are obtained when the initial solution is not taken from SOGA and is derived in NSGA-II. But, in this case, more non-dominated solutions are found. For example, in this way, 81 more non-dominated solutions are found applying the first approach for benchmark 1, however, the variance of the value of the objective functions increases. Even in this case, the best solution found with SOGA is among the non-dominated solutions.

All details about the benchmark and the obtained non-dominated solutions are accessible via the corresponding author’s email address.

5 Conclusion and Future Work

In this paper, we designed two approaches to solve MO-LRP. The problem consists of four objective functions, which are the total cost of opening DCs, the standard deviations of demands, distances and compactness in sub-sectors. Unlike previous studies, to solve the problem, we adapted sub-problems of sectorization, sub-sectorization and routing into two approaches. In the first approach, sectorization, sub-sectorization and routing sub-problems were solved simultaneously with NSGA-II. But in the second approach, there was a hierarchical structure such that the routing problem was solved for non-dominated solutions obtained after performing sectorization and sub-sectorization with NSGA-II. For this aim, a TSP solved using a function in the MATLAB optimization toolbox for each formed sub-sector.

The approaches are applied for four benchmarks and the achieved results are compared based on the number of non-dominated solutions. According to the acquired results, the most important outcome of this study can be summarized like this: the simultaneous approach for this problem is more effective in terms of finding more non-dominated solutions.

The sectorization and sub-sectorization stages in both approaches are mixed-integer quadratic programming optimization problems. As in many other softwares, it is also possible to solve such models in MATLAB. For example, qpprob function is one of the options that can be used for this aim but in case of using this function the nonlinear part of the objective function must be added as a constraint. The reason is that MATLAB, currently, does not have a solver for non-linear objective functions [9]. In future studies, it is planned to propose new methods by using linearization techniques as well as using the non-linear part of the objective functions as the constraints.

In this study, new chromosome representation, crossover and mutation operators designed to use in NSGA-II, which can be applied in similar algorithms. In future studies, more effective operators will be proposed.

The weights used to transform the multi-objective problem into a single-objective one affect the results. In further studies, more detailed works will be carried out on this matter.

Sectorization is more appropriate for solving large-scale problems. In future studies, larger benchmarks will be derived and solved.