Keywords

1 Introduction

The notion of classic graph coloring deals with finding the smallest integer k such that the vertices of an undirected graph can be colored with k colors, where no two adjacent vertices share the same color. The chromatic polynomial counts those proper colorings a graph admits, subject to the number of colors. William T. Tutte developed a dual concept [17], namely his nowhere-zero flows (NZ-flows), which build a polynomial, the flow polynomial, too.

We turn our attention to directed graphs, or digraphs for short. In 1982 Víctor Neumann-Lara [12] introduced the dichromatic number of a digraph D as the smallest integer k such that the vertices of D can be colored with k colors and each color class induces an acyclic digraph. This seems to be a reasonable generalization of the chromatic number since both numbers coincide in the symmetric case, where we have all arcs in both directions.

Moreover Neumann-Lara conjectured in 1985, that every orientation of a simple planar graph can be acyclically colored with two colors [13]. Regarding the dichromatic number this is not the only conjecture remaining widely open. Up to some relaxations, for instance Mohar and Li [10] affirmed the two-color-conjecture for planar digraphs of digirth four, it is known [4], that deciding whether an arbitrary digraph has dichromatic number at most two is NP-complete.

Although some progress has been made according thresholds (see e.g. [8]), even the complete case seems to be quite hard. To our knowledge it is not known how many vertices suffice to build a tournament which has dichromatic number five [14].

Nevertheless, Ellis and Soukup determined [6] thresholds for the minimum number of cycles, where reversing their orientation yields a digraph resp. tournament that has dichromatic number at most two.

Comparing the chromatic and the dichromatic number Erdős and Neumann-Lara conjectured [7] in 1979 that if the dichromatic number of a class of graphs is bounded, so is their chromatic number. While Mohar and Wu [11] considered the fractional chromatic number of linear programming proving a fractional version, this is another conjecture remaining unsolved.

With our work we hope to contribute to a better understanding of the dichromatic number. W. Hochstättler [9] developed a flow theory for the dichromatic number transferring Tutte’s theory of NZ-flows from classic graph colorings. Together with B. Altenbokum [2] we pursued this analogy by introducing algebraic Neumann-Lara-flows (NL-flows) as well as a polynomial counting these flows. The formula we derived contains the Möbius function of a certain poset. Here, we will derive the values of the Möbius function by showing that the poset correlates to the face lattice of a polyhedral cone.

Probably, the chromatic polynomial of a graph is better known than the flow polynomial. Therefore, in this paper we consider the dual case of our NL-flow polynomial, the NL-coflow polynomial which equals the chromatic polynomial for the dichromatic number divided by the number of colors if the digraph is connected. We will present a representation using totally cyclic subdigraphs and decompose them to obtain an even simpler representation. In particular, it will suffice to consider certain subsets of edges of the underlying undirected graph.

Our notation is fairly standard and, if not explicitly defined, should follow the books of Bondy and Murty [5] for digraphs and Beck and Sanyal [3] for polyhedral geometry. Note that all our digraphs may have parallel and antiparallel arcs as well as loops if not explicitly excluded.

2 Definitions and Tools

Let G be a finite Abelian group and D = (V, A) a digraph. Recall that a map f : A→G is a flow in D, if it satisfies Kirchhoff’s law of flow conservation

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \sum_{a \in \partial^+(v)}f(a) =\sum_{a \in \partial^-(v)}f(a) \end{array} \end{aligned} $$
(1)

in every vertex v ∈ V , where ∂+(v) and ∂−(v) denote the set of outgoing resp. incoming arcs at v.

Analogously, a map g : A→G is a coflow in D, if it satisfies Kirchhoff’s law for (weak) cycles C ⊆ A

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \sum_{a \in C^+}g(a)=\sum_{a \in C^-}g(a), \end{array} \end{aligned} $$
(2)

where C+ and C− denote the set of arcs in C that are traversed in forward resp. in backward direction.

Now let n be the number of vertices, m be the number of arcs and let M denote the totally unimodular (n × m)-incidence matrix of D. While condition (1) is equivalent to the condition that the vector f = (f(a1), …, f(am))⊤ is an element of the null space of M, that is Mf = 0, condition (2) is equivalent to the condition that the vector g = (g(a1), …, g(am)) is an element of the row space of M, that is g = pM, for some (1 × n)-vector p ∈ G|V |.

Definition 1

A digraph D = (V, A) is called totally cyclic, if every component is strongly connected. A feedback arc set of a digraph is a set S ⊆ A such that D − S is acyclic.

Definition 2

Let D = (V, A) be a digraph and G a finite Abelian group. An NL-G-coflow in D is a coflow g : A→G in D whose support contains a feedback arc set. For \(k \in \mathbb {Z}\) and \(G=\mathbb {Z}\), a coflow g is an NL-k-coflow, if

$$\displaystyle \begin{aligned} g(a) \in \lbrace 0,\pm 1,\ldots ,\pm (k-1) \rbrace \text{ , for all } a \in A,\end{aligned} $$

such that its support contains a feedback arc set.

In order to develop a closed formula for the number of NL-G-coflows we use a generalization of the well-known inclusion-exclusion formula, the Möbius inversion.

Definition 3 (See e.g. [1])

Let (P, ≤) be a finite poset, then the Möbius function is defined as follows

$$\displaystyle \begin{aligned} \mu: P \times P \rightarrow \mathbb{Z},\; \mu(x,y):= \begin{cases} 0 &\; ,\text{ if } x\nleq y \\ 1 &\; ,\text{ if } x=y\\ -\sum_{x \leq z < y} \mu(x,z) &\; ,\text{ otherwise }. \end{cases} \end{aligned}$$

Proposition 1 (See [1, 15])

Let (P, ≤) be a finite poset,\(f,g : P \longrightarrow \mathbb {K}\)functions and μ the Möbius function. Then the following equivalence holds

$$\displaystyle \begin{aligned} f(x)=\sum_{y \geq x}g(y) , \mathit{\text{ for all }} x \in P \Longleftrightarrow g(x)=\sum_{y \geq x}\mu(x,y)f(y), \mathit{\text{ for all }} x \in P. \end{aligned}$$

With this so called Möbius inversion from above it will suffice to compute the number of G-coflows in some given minors B, which is \(\vert G \vert ^{ \operatorname {\mathrm {rk}}(B)}\), where \( \operatorname {\mathrm {rk}}(B)\) is the rank of the incidence matrix of G[B] which equals |V (B)|− c(B), i.e. the number of vertices minus the number of connected components of G[B].

3 The NL-Coflow Polynomial

In this chapter we will define the NL-coflow polynomial, which counts the number of NL-G-coflows, using Möbius inversion. Therefor we need a specific partially ordered set. The following poset \((\mathscr {C},\geq )\) with

$$\displaystyle \begin{aligned} \mathscr{C}:= \big \lbrace A / C \; \vert \; \exists \; C_1,\ldots ,C_r \text{ directed cycles, such that } C=\bigcup_{i=1}^r C_i \big \rbrace\end{aligned} $$

and

$$\displaystyle \begin{aligned} A/\bigcup_{j\in J}C_j \geq A/\bigcup_{i \in I}C_i :\Leftrightarrow \bigcup_{j \in J} C_j \subseteq \bigcup_{i \in I} C_i,\end{aligned} $$

will serve our purpose. Note that in case D is strongly connected, A is the unique minimum of this poset.

Definition 4

Let D = (V, A) be a digraph and μ the Möbius function of \(\mathscr {C}\). Then the NL-Coflow Polynomial of D is defined as

$$\displaystyle \begin{aligned} \psi_{NL}^D(x):= \sum_{Y \in \mathscr{C}}\mu(A,Y)x^{\operatorname{\mathrm{rk}}(Y)}. \end{aligned}$$

The dual version of Theorem 3.5 in [2] reveals the following.

Theorem 1

The number of NL-G-coflows of a digraph D depends only on the order k of G and is given by\(\psi _{NL}^D(k)\).

Proof

Using Proposition 1 with \(f_k,g_k: \mathscr {C} \rightarrow \mathbb {Z}\), such that fk(Y ) indicates all G-coflows and gk(Y ) all NL-G-coflows in D[Y ], it suffices to show that

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} f_k(Z)=\sum_{\substack{Y \leq Z\\Y \in \mathscr{C}}}g_k(Y) \end{array} \end{aligned} $$
(3)

holds for all \(Z \in \mathscr {C}\). Then we obtain

$$\displaystyle \begin{aligned} \begin{array}{rcl} \psi_{NL}^D(k)=g_k(A) = \sum_{\substack{Y \leq A\\Y\in \mathscr{C}}} \mu(A,Y)f_k(Y) = \sum_{Y \in \mathscr{C}}\mu(A,Y)k^{\operatorname{\mathrm{rk}}(Y)}, \end{array} \end{aligned} $$

since the number of G-coflows on D[Y ] is given by \(k^{ \operatorname {\mathrm {rk}}(Y)}\).

Concerning (3) let \(Z \in \mathscr {C}\) and φ be a G-coflow on D[Z]. With d we denote the number of directed cycles in D[Z] and set

$$\displaystyle \begin{aligned} Y := Z / \bigcup_{i=1}^d \left\lbrace C_i \; \vert \; C_i \text{ is a directed cycle in }D[Z]\text{ and } \forall c \in C_i : \varphi(c)=0 \right\rbrace. \end{aligned}$$

Then clearly \(Y \in \mathscr {C}\) and φ|Y is an NL-G-coflow on D[Y ].

The other direction is obvious since every NL-G-coflow g on D[Y ] with \(Y \in \mathscr {C}\) can be extended to a G-coflow \(\tilde {g}\) on D[Z], setting \(\tilde {g}(a):= 0_G\) for all a ∈ Z − Y . □

3.1 Totally Cyclic Subdigraphs

Since many unions of directed cycles determine the same strongly connected subdigraph it suffices to consider all totally cyclic subdigraphs which turn out to form a graded poset.

Lemma 1

The poset

$$\displaystyle \begin{aligned} Q:=\lbrace B \subseteq A \; \vert \; D[B] \mathit{\text{ is totally cyclic subdigraph of }} D \rbrace, \end{aligned}$$

ordered by inclusion, is a graded poset with rank function \( \operatorname {\mathrm {rk}}_Q\) and its Möbius function alternates in the following fashion:

$$\displaystyle \begin{aligned} \mu_Q(\emptyset,B)=(-1)^{\operatorname{\mathrm{rk}}_Q(B)}. \end{aligned}$$

Proof

Let M be the totally unimodular (n × m)-incidence matrix of D. We will show that the face lattice of the polyhedral cone PC described by

$$\displaystyle \begin{aligned} \begin{pmatrix} M \\ -M \\ -I \end{pmatrix}x \leq 0, \end{aligned}$$

corresponds to Q.

Since M is totally unimodular all extreme rays of PC are spanned by integral points. It follows that every totally cyclic subdigraph can be represented by a face of PC, where an arc 1 ≤ i ≤ m exists iff for the corresponding entry xi > 0 holds.

Thus the elements of the face lattice of PC coincide with the elements of our poset and so do the Möbius functions. Well-known facts from topological geometry which can be found for instance in Corollary 3.3.3 and Theorem 3.5.1 in [3] yield that Q is a graded poset and

$$\displaystyle \begin{aligned} \mu_Q(\emptyset,B)=(-1)^{\dim(B)+1}\chi(B)=(-1)^{\operatorname{\mathrm{rk}}_Q(B)}\chi(B), \end{aligned}$$

where χ denotes the reduced Euler characteristic, which equals one in this case, since the faces of PC build non-empty closed polytopes (see e.g. Thm. 3.4.1 in [3]). □

Theorem 2

Let D be a digraph and (Q, ⊆) the poset defined above. Then the NL-coflow polynomial of D is given by

$$\displaystyle \begin{aligned} \psi_{NL}^D(x)=\sum_{B \in Q} (-1)^{\operatorname{\mathrm{rk}}_Q(B)}x^{\operatorname{\mathrm{rk}}(A/B)}. \end{aligned}$$

Proof

With Lemma 1 we immediately obtain:

$$\displaystyle \begin{aligned} \psi_{NL}^D(x) = \sum_{Y \in \mathscr{C}}\mu(A,Y)x^{\operatorname{\mathrm{rk}}(Y)}=\sum_{B \in Q} \mu_Q(\emptyset,B) x^{\operatorname{\mathrm{rk}}(A/B)} =\sum_{B \in Q} (-1)^{\operatorname{\mathrm{rk}}_Q(B)} x^{\operatorname{\mathrm{rk}}(A/B)}.\end{aligned} $$

□

It is well known that coflows and colorings are in bijection, once the color of some vertex in each connected component has been chosen. As a consequence we have the following corollary, where c(D) denotes the number of connected components in D.

Corollary 1

The chromatic polynomial of a digraph D is given as

$$\displaystyle \begin{aligned}\chi(D,x)=x^{c(D)}\cdot \psi^D_{NL}(x)=\sum_{B \in Q} (-1)^{\operatorname{\mathrm{rk}}_Q(B)}x^{\operatorname{\mathrm{rk}}(A/B)+c(D)}.\end{aligned}$$

4 Decomposing the NL-Coflow Polynomial

In the following we will put our previous results into the setting of polyhedral geometry. There we will find a way to compound some of the objects considered, which will, going back to graph theory, decompose the NL-coflow polynomial such that only certain subsets of edges of the underlying undirected graph need to be considered.

More precisely, fixing the support, implying a fixed exponent in our polynomial, we will show that all existing totally cyclic orientations correlate to the face lattice of some usually unbounded polyhedron. This will yield a relation between the above mentioned poset Q and the maximal faces of a class of polyhedra to be defined in the following. Using the geometric structure of those polyhedra we can contract the corresponding order complex and, by correlating the corresponding Möbius functions, obtain an even simpler representation of the NL-coflow polynomial and therefore of the chromatic polynomial of arbitrary digraphs.

Let D = (V, A) be a digraph, G = (V, E) its underlying undirected graph with |V | = n and |E| = m. For ∅ ≠ B ⊆ E a partial orientation\(\mathscr {O}(B)\) is an orientation of a subset B′⊆ B of the edges, where the remaining edges in B ∖ B′ are considered as pair of antiparallel arcs, called digons. We say a partial orientation is totally cyclic if the corresponding induced digraph is. Once the support is fixed, there is a unique inclusionwise maximal partial orientation, denoted with \(\bar {\mathscr {O}}(B)\), where we have as many digons as possible.

A flow on D is related to a partial orientation \(\mathscr {O}(B)\) by orienting only the edges with xi ≠ 0.

Let M be the totally unimodular incidence (n × m)-matrix of the subgraph induced by ∅ ≠ B ⊆ E. Then \(x \in \mathbb {R}^{2m}\) is a flow iff (M, −M)x = 0 holds.

Now, consider the following system

We denote the polyhedron described above with P and take a look at its vertices, which are the solutions of the program (P), in the first place.

Lemma 2

Letbe a solution of (P). Then a solutionof (P) exists with\( \operatorname {\mathrm {supp}}(y)\subseteq\operatorname {\mathrm {supp}}(x)\)and, if a is a bridge and, otherwise.

Proof

Let y be a solution with minimal support such that the corresponding partial orientation contains a minimum number of directed cycles.

Let . If a is a bridge, then has to hold since otherwise the flow condition would be violated. In the other case assume that . Let and be a directed cycle. After reassigning

the flow condition still holds in v:

as well as in w:

Thus the solution \(\tilde {y}\) yields a contradiction to y having minimal support. □

As a result of the preceding lemma, the vertices \(\mathscr {V}\) of P are totally cyclic subdigraphs, where the only remaining digons are bridges.

To describe the polyhedron completely we take a look at the recession cone

$$\displaystyle \begin{aligned} \begin{array}{rcl} rec(P) & =&\displaystyle \lbrace y \in \mathbb{R}^{2m} \mid \forall c \in P,\; \forall \lambda \geq 0 : c+\lambda y \in P \rbrace\\ & =&\displaystyle P(A,0)\\ & =&\displaystyle Cone \left(\lbrace y \in \mathbb{R}^{2m} \mid y \text{ is directed cycle} \rbrace \right). \end{array} \end{aligned} $$

Thus we have \(P= Conv(\mathscr {V})+Cone\left (\lbrace y \in \mathbb {R}^{2m} \mid y \text{ is directed cycle} \rbrace \right ).\)

In the following we would like to correlate the elements of our poset Q to the face lattice of P, where maximal and minimal elements, \(\hat {1}\) and \(\hat {0}\), are adjoined and the corresponding Möbius function is denoted with μP.

Since there may be several faces corresponding to the same element of Q we define a closure operator on the set of faces \(cl:\mathscr {F} \rightarrow \overline {\mathscr {F}}\) as follows, where \( \operatorname {\mathrm {eq}}(F)\) is the set of constraints in (P) where equality holds:

$$\displaystyle \begin{aligned} \begin{array}{rcl} cl(F)& =&\displaystyle F_{max}:=\bigvee \lbrace \tilde{F} \mid \operatorname{\mathrm{supp}}(\tilde{F})=\operatorname{\mathrm{supp}}(F)\rbrace\\ & =&\displaystyle \lbrace x \in P \mid \operatorname{\mathrm{supp}}(F_{max})=\operatorname{\mathrm{supp}}(F), \operatorname{\mathrm{eq}}(F_{max}) \text{ is minimal} \rbrace, \end{array} \end{aligned} $$

where ∨ is the join of all faces with equal support in the face lattice.

This function is well-defined since the dimension of every face is bounded by 2m and Fmax is uniquely determined since the join is. It is also easy to check that cl is indeed a closure operator.

Now we can identify the maximal faces with the elements of Q by either forgetting the values of a flow or by first taking an arbitrary flow \(x \in \mathbb {R}^{2m}_+\) satisfying , that lives on some face Fx and then taking its closure operator cl(Fx).

As a result the Möbius function of \(\mathscr {F}\) behaves for x, y ∈ P as follows (see Prop. 2 on p. 349 in [15]):

$$\displaystyle \begin{aligned} \sum_{\substack{z \in P\\operatorname{\mathrm{cl}}(F_z)=cl(F_y)}}\mu_P(F_x,F_z)=\begin{cases} \mu_{\bar{\mathscr{F}}}(cl(F_x),cl(F_y)) &\text{ , if } F_x=cl(F_x)\\ 0 &\text{ , if }F_x\subset cl(F_x) \end{cases}. \end{aligned}$$

This is why we will simply write μP(B, B′) instead of \(\mu _{\bar {\mathscr {F}}}(cl(F_x),cl(F_y))\) for flows x, y on B, B′∈ Q. Also we identify \(\hat {0}\) with ∅ and \(\hat {1}\) with \(\bar {\mathscr {O}}(B)\), respectively.

Examining the polyhedron P we find three cases which determine the structure and therefore the Möbius function of the face lattice:

  1. 1.

    There is exactly one vertex v in P.

    1. 1.1

      There are no further faces in P including v, i.e. \(\dim (P)=0\).

    2. 1.2

      There are further faces in P including v, so P is a pointed cone and \(\dim (P)\geq 1\).

  2. 2.

    There are at least two vertices in P.

Note that all cases are mutually exclusive and complete since every P has at least one vertex.

Lemma 3

Let \(\emptyset \neq X \in \mathscr {F}\) be a face of P. Then

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mu_P(\emptyset,X)=\begin{cases} -1 \quad& \mathit{\text{ if }}\dim(X)= 0,\\(-1)^{\operatorname{\mathrm{rk}}_P(X)} \quad& \mathit{\text{ in cases }} 1.1 \mathit{\text{ and }} 2, \\ 0 \quad& \mathit{\text{ in case }} 1.2.\end{cases}\end{array} \end{aligned} $$

Proof

If X is a vertex, then \(\dim (X)=0\) and

$$\displaystyle \begin{aligned} \mu_P(\emptyset,X)=-\mu_P(\emptyset,\emptyset)=-1=(-1)^{\operatorname{\mathrm{rk}}_P(X)}. \end{aligned}$$

For the other cases we will use Theorem 3.5.1 and Corollary 3.3.3 in [3]:

$$\displaystyle \begin{aligned} \mu_P(\emptyset,X)=(-1)^{\dim(X)+1}\chi(X)=(-1)^{\operatorname{\mathrm{rk}}_P(X)}\chi(X), \end{aligned}$$

where χ denotes the reduced Euler characteristic.

  1. 1.2

    Since there is only one vertex, every face of dimension greater 0 builds a pointed cone. Proposition 3.4.9 in [3] yields that χ(X) = 0.

  2. 2.

    Since there are at least two vertices, there are also some faces including them. Those form non-empty closed polytopes with χ(X) = 1 (see Thm. 3.4.1 in [3]).

□

Comparing the Möbius functions of P and Q we find the following relation, where cr(B) = |B|−|V (B)| + c(B) denotes the corank and β(B) the number of bridges in the graph induced by B ⊆ E.

Lemma 4

Let ∅ ≠ B ⊆ E and\(\mathscr {O}(B)\)be a totally cyclic partial orientation of B, then

$$\displaystyle \begin{aligned} \mu_Q(\emptyset,\mathscr{O}(B))=(-1)^{cr(B)+\beta(B)+1}\mu_P(\emptyset,\mathscr{O}(B)) \end{aligned}$$

holds, if μ P(∅, X) alternates, i.e. in cases 1.1, 2 and if\(\dim (X)=0\), where\(X\in \mathscr {F}\)is the maximal face corresponding to\(\mathscr {O}(B)\). Otherwise (in case 1.2) we find

$$\displaystyle \begin{aligned} \sum_{\substack{\mathscr{O}(B)\subseteq A\\tot.cyclic}}\mu_Q(\emptyset, \mathscr{O}(B))=0. \end{aligned}$$

Proof

If both Möbius functions alternate it suffices to consider elements \(\mathscr {O}(B)\subseteq A\) where \( \operatorname {\mathrm {rk}}_P(\mathscr {O}(B))\) is minimal. In this case \(\mu _P(\emptyset ,\mathscr {O}(B))=-1\) and we are left to verify

$$\displaystyle \begin{aligned} \mu_Q(\emptyset,\mathscr{O}(B))=(-1)^{cr(B)+\beta(B)}. \end{aligned}$$

We prove the statement by induction over the number of edges in B. The base cases can be easily checked. Deleting one edge d ∈ B yields the following two cases:

  1. 1.

    d is a bridge.

    Then \( \operatorname {\mathrm {rk}}_Q(B-d)= \operatorname {\mathrm {rk}}_Q(B)-1, cr(B-d)=cr(B)\) and β(B − d) = β(B) − 1.

  2. 2.

    d is not a bridge.

    Then \( \operatorname {\mathrm {rk}}_Q(B-d)= \operatorname {\mathrm {rk}}_Q(B)-1, cr(B-d)=cr(B)-1\) and β(B − d) = β(B).

Using the induction hypothesis we find in both cases

$$\displaystyle \begin{aligned} (-1)^{\operatorname{\mathrm{rk}}_Q(B)}=(-1)^{\operatorname{\mathrm{rk}}_Q(B-d)+1} \overset{IH}{=} (-1)^{cr(B-d)+\beta(B-d)+1}=(-1)^{cr(B)+\beta(B)}. \end{aligned}$$

Otherwise, i.e. case 1.2 due to Lemma 3, we have exactly one vertex and some faces containing it. The number of these faces is determined by the number of digons in \(\bar {\mathscr {O}}(B)\), which we denote with d. Then we have

$$\displaystyle \begin{aligned} \begin{array}{rcl} \sum_{\substack{\mathscr{O}(B)\subseteq A\\tot.cyclic}}\mu_Q(\emptyset, \mathscr{O}(B))& =&\displaystyle - \binom{d}{0}+ \binom{d}{1} - \binom{d}{2} +\ldots \pm \binom{d}{d} = -\sum_{k=0}^d (-1)^k \binom{d}{k}=0. \end{array} \end{aligned} $$

□

The key point is the following lemma, where the contraction finally takes place.

Lemma 5

Let ∅ ≠ B ⊆ E. Then

$$\displaystyle \begin{aligned} \sum_{\emptyset\neq X \subseteq \bar{\mathscr{O}}(B)}\mu_P(\emptyset,X)=-1. \end{aligned}$$

Proof

Since P is obviously unbounded and has at least one vertex, Corollary 3.4.10 in [3] yields that P has reduced Euler characteristic zero. Consequently the corresponding Möbius function \(\mu _P(\emptyset ,\bar {\mathscr {O}}(B))\), which is the reduced Euler characteristic (see Prop. 3.8.6 in [16]), equals zero, too. As a result,

$$\displaystyle \begin{aligned} \begin{array}{rcl} 0= \mu_P(\emptyset,\bar{\mathscr{O}}(B))=-\sum_{\emptyset \subseteq X \neq \bar{\mathscr{O}}(B)}\mu_P(\emptyset,X)= -1-\sum_{\emptyset \neq X \subseteq \bar{\mathscr{O}}(B)} \mu_P(\emptyset,X) \end{array} \end{aligned} $$

holds. □

Combining the last two lemmas we find two different kinds of compression: In cases 1.1 and 2 it suffices to count the element having minimal support due to Lemma 5 and in case 1.2 all totally cyclic partial orientations sum up to zero due to Lemma 4. The following observation translates these cases from polyhedral language into graph theoretical properties.

Definition 5

Let D = (V, A) be a totally cyclic digraph. A digon d ⊆ A is called redundant for cyclicity if D − d is still totally cyclic.

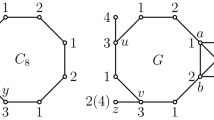
Note that every bridge is redundant for cyclicity. Fig. 1 shows a digon that is redundant but not a bridge.

Fig. 1
figure 1

A digon that is redundant for cyclicity

Full size image

Lemma 6

Case 1.2 does not hold true if and only if there exists a digon in \(\bar {\mathscr {O}}(B)\) that is redundant for cyclicity but not a bridge, or every digon in \(\bar {\mathscr {O}}(B)\) is a bridge.

Proof

First we proof the following equivalence:

There are at least two vertices in P if and only if there is a digon in \(\bar {\mathscr {O}}(B)\) that is redundant for cyclicity but not a bridge.

Let e be a digon in \(\bar {\mathscr {O}}(B)\) that is redundant but not a bridge, then and contain vertices including , resp. which hence are two different vertices in P. For the other direction take vertices v ≠ w in P. Then v ∪ w is a face in P including a digon e that is no bridge. Assume e is not redundant, then or could not have been totally cyclic and so one of the vertices v or w.

Consequently case 1.2 does not hold true iff there is a digon that is redundant but not a bridge (case 2) or, if there is only one vertex in P, then there are no further faces including it, which means that every digon in \(\bar {\mathscr {O}}(B)\) is a bridge (case 1.1). □

This leads to the following main result of this paper, a representation of the NL-coflow polynomial for arbitrary digraphs, where we sum only over certain subsets of the edges of the underlying undirected graph.

Theorem 3

Let D = (V, A) be a digraph and G = (V, E) its underlying undirected graph. Then

$$\displaystyle \begin{aligned} \psi_{NL}^D(x)= \sum_{B \in TC}(-1)^{|B|}x^{\tilde{c}(B)-c(D)} \end{aligned}$$

holds, where\(\tilde {c}(B)\)counts the components in the spanning subgraph of G with edge set B and TC includes all B ⊆ E which admit a totally cyclic partial orientation\(\mathscr {O}(B)\)in A such that\(\bar {\mathscr {O}}(B)\)has no digons but bridges or\(\bar {\mathscr {O}}(B)\)has a digon that is redundant but not a bridge.

Proof

Instead of counting totally cyclic subdigraphs one can count totally cyclic partial orientations of a fixed underlying subgraph. Thus the preceding lemmas yield

$$\displaystyle \begin{aligned} \begin{array}{rcl} \psi_{NL}^D(x) & =&\displaystyle \sum_{\substack{X\subseteq A \\ tot.cyclic}}\mu_Q(\emptyset,X)x^{\operatorname{\mathrm{rk}}(A/X)}\\ & =&\displaystyle \sum_{B\subseteq E} \sum_{\substack{\mathscr{O}(B) \\ tot.cyclic}}\mu_Q(\emptyset,\mathscr{O}(B))x^{\operatorname{\mathrm{rk}}(A/B)} \end{array} \end{aligned} $$
$$\displaystyle \begin{aligned} \begin{array}{rcl} & =&\displaystyle \sum_{\emptyset \neq B\subseteq E} \sum_{\substack{\mathscr{O}(B) \\ tot.cyclic}}\mu_Q(\emptyset,\mathscr{O}(B))x^{\operatorname{\mathrm{rk}}(A/B)}+x^{-c(D)}\\ & \overset{\mbox{Lemma 4}}{=}&\displaystyle \sum_{\substack{\emptyset \neq B\subseteq E\\(\ast)}} \sum_{\substack{\mathscr{O}(B) \\ tot.cyclic}}(-1)^{cr(B)+\beta(B)+1}\mu_P(\emptyset,\mathscr{O}(B))x^{\operatorname{\mathrm{rk}}(A/B)}+x^{-c(D)}\\ & \overset{\mbox{Lemma 5}}{=}&\displaystyle \sum_{\substack{\emptyset \neq B\subseteq E\\(\ast)}}(-1)^{cr(B)+\beta(B)}x^{\operatorname{\mathrm{rk}}(A/B)}+x^{-c(D)}\\ & =&\displaystyle \sum_{\substack{B\subseteq E\\ (\ast)}}(-1)^{cr(B)+\beta(B)}x^{n-|V(B)|+c(B)-c(D)}. \end{array} \end{aligned} $$

Condition (∗) means, that we sum over all B ⊆ E having a totally cyclic partial orientation \(\mathscr {O}(B)\subseteq A\), where case 1.2 is not true. Due to Lemma 6 this situation occurs if and only if \(\bar {\mathscr {O}}(B)\) has no digons but bridges, or there exists a digon that is redundant but not a bridge. Clearly, \(n-|V(B)|+c(B)=\tilde {c}(B)\) holds, and we are left to verify

$$\displaystyle \begin{aligned} (-1)^{cr(B)+\beta(B)}=(-1)^{|B|}. \end{aligned}$$

This can be done by induction. Deleting a bridge d ∈ B yields cr(B − d) = cr(B) and β(B − d) = β(B) − 1 while deleting a non-bridge yields cr(B − d) = cr(B) − 1 and β(B − d) = β(B). In both cases we find

$$\displaystyle \begin{aligned} (-1)^{cr(B)+\beta(B)}=(-1)^{cr(B-d)+\beta(B-d)+1}\overset{IH}{=}(-1)^{|B-d|+1}=(-1)^{|B|}. \end{aligned}$$

□

Note that TC includes all B ⊆ E which admit a totally cyclic partial orientation \(\mathscr {O}(B)\) in A, but not those, where \(\bar {\mathscr {O}}(B)\) includes a digon that is no bridge and no digon is redundant unless it is a bridge in \(\bar {\mathscr {O}}(B)\) (Fig. 2).

Fig. 2
figure 2

A totally cyclic orientation that is not considered in TC

Full size image

5 Symmetric Digraphs

Considering symmetric digraphs D = (V, A), it is obvious that the NL-coflow polynomial equals the chromatic polynomial χ(G, x) of the underlying undirected graph G = (V, E) divided by the number of colors since both polynomials count the same objects. Using Theorem 3 we find an alternative proof of this fact, where the chromatic polynomial is represented by (see [5])

$$\displaystyle \begin{aligned} \chi (G,x)= \sum_{B \subseteq E} (-1)^{|B|}x^{\tilde{c}(B)}. \end{aligned}$$

Corollary 2

Let D = (V, A) be a symmetric digraph and G = (V, E) its underlying undirected graph. Then the following holds

$$\displaystyle \begin{aligned} \psi_{NL}^D(x)= \chi(G,x)\cdot x^{-c(G)}. \end{aligned}$$

Proof

In a symmetric digraph every edge is a digon, so for every subset B ⊆ E there exists a totally cyclic partial orientation \(\mathscr {O}(B)\). Furthermore, if cr(D) = 0, every digon is a bridge and if cr(D) ≥ 1 there exists a cycle of length ≥ 3 in D where every digon is redundant but no bridge. □