Applying the Knowledge Quartet to Mathematics Teacher Educators: A Case Study Undertaken in a Co-teaching Context

Abstract

As mathematics teacher educators (MTEs), our teaching and research is informed by frameworks and explanations of terms to guide our thinking about the knowledge an effective mathematics teacher might use. This chapter investigates whether or not the Knowledge Quartet (KQ) framework can be applied to the work of MTEs. Using the context of a co-teaching situation, whereby the second author co-taught pre-service teachers (PSTs) with a practicing primary classroom teacher, we examined the types of knowledge required by the MTE and whether or not it was different from that required of a classroom teacher. Data were collected from lesson observations and interviews with PSTs, the MTE and co-teacher. The results show the KQ was transferable for describing the MTE’s knowledge; however an MTE would require a deeper and broader understanding of theoretical knowledge when teaching appropriate pedagogical practices with PSTs when compared to the foundation knowledge needed by teachers.

1 Introduction

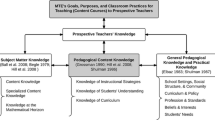
As mathematics teacher educators (MTEs), our teaching and research is informed by frameworks and explanations of terms to guide our thinking about the knowledge an effective mathematics teacher might use. For example, Shulman’s (1987) seminal study has guided many researchers as they consider important categories of a teacher’s knowledge base such as knowledge of content, pedagogical knowledge and knowledge of learners. Others have elaborated by describing specialised content knowledge when referring to a unique kind of knowledge that mathematics teachers demonstrate (Ball, Thames, & Phelps, 2008). Rowland, Turner, Thwaites and Huckstep (2009) used the term Knowledge Quartet (KQ) to describe four categories of teacher knowledge: foundation knowledge (including knowledge of content and pedagogical knowledge); transformation (representing the mathematics); connection (e.g. coherence of planning, sequencing of instruction); and contingency (when the teacher responds to classroom events). The framework has been used elsewhere to investigate classroom practice (e.g. Livy, 2010), but its use has primarily been restricted to pre-service teachers (PSTs) and primary school teachers.

This chapter investigates whether or not the KQ framework can be applied to the work of MTEs. Using the context of a co-teaching situation, whereby an MTE taught a cohort of PSTs with a practicing primary school teacher, we examine the type of knowledge required by an MTE and whether or not it is different from that required by a primary school teacher. We then use the KQ to interpret the work of the MTE, using data collected from lesson observations, and interviews conducted with PSTs, the MTE and the co-teacher.

Our research questions for guiding our study are as follows:

• How does the knowledge needed by mathematics teacher educators differ from that required by primary school teachers?

• To what extent is the KQ applicable/transferable in describing the work of mathematics teacher educators?

In seeking to answer these questions, we are responding to Rowland’s (2013) question of whether or not a framework for knowledge-in-teaching developed in one subject discipline can be legitimately adopted in another and, if so, what the conceptualisations of the dimensions would look like. As it is debatable whether or not mathematics teacher education could be considered a discipline, we have adapted the question to determine whether or not the KQ that was originally designed to examine the work of classroom mathematics teachers could be legitimately applied to the work of mathematics teacher educators.

2 Review of Literature

2.1 Mathematical Knowledge for Teaching

Research into the different types of knowledge required for teaching has been well documented (e.g. Chick, Pham, & Baker, 2006; Hill, Ball, & Schilling, 2008; Ma, 1999; Rowland et al., 2009; Shulman, 1986). Shulman’s (1987) theoretical framework described seven categories of teacher knowledge, which became the foundation for describing the knowledge base for teaching. His conceptualisation of pedagogical content knowledge (PCK) is not subject-specific and is described as

the blending of content and pedagogy into an understanding of how topics, problems, or issues are organized, represented, and adapted to the diverse interests and abilities of learners, and presented for instruction. Pedagogical content knowledge is the category [of teacher knowledge] most likely to distinguish the understanding of the content specialist from that of the pedagogue. (Shulman, 1987, p. 8)

In terms of mathematics teaching, PCK is needed for teaching different mathematical topics, in order to make these topics comprehensible to learners. This knowledge includes understanding student misconceptions; knowing how topics are organised and taught; having a repertoire of representations, explanations, and examples that illustrate concepts; and having the ability to adjust lessons to cater for all learners (Shulman, 1986). Ball et al. (2008) used the term ‘mathematics knowledge for teaching’ (MKT) to refer to the knowledge ‘needed to perform the recurrent tasks of teaching mathematics to students’ (p. 399). Their model distinguishes between subject matter knowledge; common content knowledge (CCK); specialised content knowledge (SCK); horizon knowledge and PCK; knowledge of content and teaching (KCT); knowledge of content and students (KCS); and knowledge of the curriculum (KCC). While it is beyond the scope of this chapter to discuss this model in detail, it is useful for considering the different types of knowledge required for teaching. In the model, CCK refers to common mathematical knowledge, which we would expect the ‘average’ person to possess, such as being able to correctly solve mathematical problems. SCK, on the other hand, refers to mathematical knowledge that is unique to teaching. It is knowledge that the ‘average’ person is not expected to have and refers to the knowledge required to unpack mathematics content in order to make it accessible to students. This knowledge is similar in nature to what Ma (1999) termed ‘a profound understanding of fundamental mathematics’ (PUFM) to describe understanding a topic with depth and breadth (p. 120). This involves connecting a topic with more conceptually powerful ideas of the subject, together with connecting it with those of similar or less conceptual power. For a primary school teacher, teaching the subject of subtraction, breadth would be demonstrated through connecting subtraction, including regrouping and renaming, with the topics of addition and associated regrouping and renaming, and subtraction without regrouping and renaming, and addition without regrouping and renaming. Connecting subtraction with concepts such as the rate of composing or decomposing a higher value unit, or the notion that addition and subtraction are inverse operations, is a matter of depth (Ma, 1999). Together with this knowledge, a primary school teacher would also be expected to know what representations and examples would be useful in teaching about this topic, which is all part of PCK (KCS, KCT, KCC). It is evident, therefore, in teaching primary mathematics to students that a teacher does require a specialised form of content knowledge, along with PCK to make the knowledge accessible to students. Does an MTE, who is required to teach PSTs how to teach subtraction, for example, therefore require additional knowledge to that required by a primary teacher?

Many teacher educators (TEs) transition into their role from a school teacher, but becoming a TE ‘involves much more than applying the skills of school teaching in a new (and different) context’ (Loughran, 2014, p. 272). Instead what is required is a form of ‘meta-knowledge’, which could be described as ‘knowledge for teaching knowledge for teaching mathematics’ (Beswick & Chapman, 2012, p. 2). Just like school teachers, MTEs need to study, for example, student misconceptions, analyse concepts and engage their students (Beswick & Chapman, 2012), but they also have to teach their adult students how to teach students in schools. This suggests that additional knowledge is required, beyond the knowledge previously required in their role as a mathematics school teacher. Interestingly, Beswick and Chapman (2012) also make the point that there may be elements of school teachers’ knowledge that MTEs either do not need to know or need to know differently (e.g. detailed knowledge of how to assess according to the school curriculum).

Like Loughran (2014), Murray and Male (2005) claimed that TEs’ work demanded new and different types of professional knowledge and understanding from that required of school teachers. Referring to the Standards for Dutch TEs, they list five inter-related competencies needed for the role of educating teachers: content competencies, pedagogical competencies, group dynamic and communicative competencies and developmental and personal growth competencies for working with adult learners. Although they do not explicitly answer the questions of ‘what professional knowledge TEs need, what pedagogical understanding and skills they require, and about how these things differ from the knowledge, skills and understanding of school teachers’ (Murray & Male, 2005, p. 136), they did identify that the development of pedagogy for teaching teachers and the generation of research and scholarship were key areas of development for beginning TEs.

Beyond an acknowledgement that TEs require an understanding of adult learning principles that school teachers do not (e.g. Murray & Male, 2005), we did not find compelling evidence in the literature that the (content) knowledge required by TEs is substantially different from that required by an experienced, competent school teacher. Chick and Beswick (2013, 2018) expanded an earlier PCK framework developed by Chick et al. (2006) to include mathematics teacher educator PCK (MTEPCK). Within the framework, examples are given as to how MTEPCK might be enacted for each element. As an example of profound understanding of mathematical content, the MTE might demonstrate PCK through ‘identif[ying] and explain[ing] the importance of identifying and addressing student misconceptions evident in a teaching episode’ (Chick & Beswick, 2018). This element for school teachers was exemplified by understanding why we invert and multiply when dividing fractions. The authors argued that in addition to the school mathematics knowledge required, MTEPCK is enacted in additional ways. Rather than demonstrating or providing examples of MTE knowledge in relation to mathematical content, the framework identifies aspects of MTE work (pedagogy), which proved to be useful in terms of analysing the moment-by-moment application of knowledge in the work of mathematics education (Chick & Beswick, 2018). We used a similar strategy to align elements of the KQ to the work of MTEs (see Table 3.2).

Returning to the subtraction example discussed earlier, does teaching PSTs how to teach a topic such as subtraction require knowledge beyond the depth and breadth of knowledge required by a school teacher? Chick and Beswick (2018) provided some examples of how school teaching can be transferred to teaching PSTs through replacing ‘students’ in their framework with ‘PSTs’, but most of the examples given in relation to MTEPCK could reasonably form part of a competent school teacher’s knowledge (e.g. ‘Contrasts different representations (e.g. MAB (multi-based arithmetic blocks) and LAB (linear-arithmetic blocks)) and what they offer for mathematics teaching’ (representation of concepts)) (Chick & Beswick, 2018). With this particular example, it could be argued that it would be reasonable to expect the school teacher to be aware of the affordances of both representations, how to use them and in what context. An MTE also needs to know this but arguably should also be cognizant of the theoretical underpinnings and current research behind the adoption of particular representations and use of manipulatives in order to convince their PSTs of the merits of using such representations and models. Similarly, with the subtraction example, like a school teacher, an MTE might be expected to know how to use appropriate materials such as MAB to demonstrate why the vertical subtraction algorithm ‘works’ but, in addition, be able to explain the theoretical underpinnings and research behind the use and appropriateness of the materials.

3 Theoretical Framework

3.1 The Knowledge Quartet

Developed from observations of 24 mathematics lessons by Rowland and colleagues, (Rowland et al., 2009), the Knowledge Quartet contains four ‘units’ or dimensions which describe teacher knowledge. Each dimension contains a number of elements that could be used to interpret classroom practice, including that as undertaken by PSTs. An overview of the framework is presented in Table 3.1.

Table 3.1 Overview of Knowledge Quartet and its elements

The KQ was designed to be used as a framework for identifying and discussing the ways in which the use of mathematics content knowledge was observed in teaching. In the research reported in this chapter, the authors utilised this framework, not with a focus on school mathematics teaching per se but rather the knowledge required by an MTE when teaching PSTs how to teach primary mathematics. We were motivated to select this framework as Rowland et al. (2009) had developed a range of resources to assist with interpreting the various elements.¹ The framework has been adopted and reported on by other researchers (e.g. Livy, 2010; Muir, Wells, & Chick, 2017), and we wanted to determine whether or not it was appropriate for interpreting the work of experienced MTEs, rather than PSTs or in-service mathematics teachers. An earlier study by Muir et al. (2017) used aspects of the framework to interpret the work of two teacher educators but was limited in terms of providing examples of evidence across all the elements. The study discussed in this chapter adds to this research through providing corresponding examples of MTE knowledge, aligned with school teachers’ knowledge (see Table 3.2) and through applying the KQ in practice in the context of a co-teaching arrangement.

Table 3.2 Examples of primary teacher and MTE evidence for categories of KQ

Table 3.2 shows examples of evidence related to the work of an MTE. The examples have been drawn from our own experiences as MTEs and as a result of the observations and interviews conducted with the MTE discussed in this chapter.

4 Methodology

A case study was used to investigate an MTE’s knowledge for teaching mathematics education to a cohort of PSTs. Case study was considered as a preferred methodology given that ‘how’ questions were being posed, with a focus on a contemporary phenomenon within a real-life context (Yin, 2009).

The participants in the study were an MTE, a primary school teacher and a cohort of third-year PSTs enrolled in a primary mathematics pedagogy unit. The MTE was an Early Career Researcher having worked at the university for the past 4 years since completing her doctoral studies. Prior to working in university settings, the MTE had worked as a mathematics consultant and also as a primary mathematics teacher. The primary school teacher had taught at a local school for the past 10 years and was now a leading teacher and numeracy coach. She shared a Year 4 class with another teacher and was also responsible for providing support to all teachers as a mathematics leader in her school. This included helping teachers to plan and implement their programs, as well as providing professional advice to guide their teaching.

Through a university initiative, Sarah (pseudonyms are used throughout this chapter for all participants), the MTE, had invited a practicing primary school teacher, Melissa, to co-teach her class of PSTs. Melissa was released for 1 day a week from her school to enable her to co-teach the weekly tutorials with Sarah throughout the semester. Each week Sarah and Melissa shared the teaching and after class reflected on their experience before planning the activities for the following week. As the lecturer, Sarah was responsible for assessment and marking of assignments.

As Sarah was interested in researching her own practice, she invited two colleagues (also authors) to observe her teaching. Both Julie and Mary were research colleagues of Sarah’s, with a shared interest in PST mathematics education, and were happy to participate in the study. Mary taught in the same university as Sarah and had taught the same primary mathematics pedagogy unit in the past. Julie was from a different university where she taught a similar subject. Sarah invited each colleague/researcher to observe her teaching in weeks 7 (Julie) and 8 (Mary) of semester 1, 2018. Julie and Mary collected the data from the lesson observations and conducted the interviews. Table 3.3 provides a summary of the participants and the data collected.

Table 3.3 Participants and data

Semi-structured interview schedules were used to guide the interviews, and for the PSTs included questions as follows: What do you think an observer would take away from having observed your class? Can you tell me what experiences and teaching approaches in class today assisted with your learning? For the co-teacher and MTE, the questions were similar and included, for example: What experiences and/or activities do you think were most effective today? Which ones had most impact on their learning? How did you personally contribute to their learning today? The PSTs’ post-lesson reflections included responses to questions related to how they learnt the content, describing an activity or mathematical understanding they needed help with and who helped them, and how their learning was facilitated in the lesson.

For the purpose of this chapter, two vignettes were composed from field notes taken from observations of two lessons. Post-lesson interviews conducted with all participants were fully transcribed, along with the post-lesson reflection conversation. The two researchers independently coded the data to find evidence of the categories and codes of the KQ, for example, use of balance beams to demonstrate equality, transformation (choice of representation); planning a micro lesson, making connections (decisions about sequencing); and providing definitions for area and perimeter, foundation knowledge (use of terminology). Open coding techniques were also used to identify instances relevant to the study that were not evident within the KQ. For example, when Sarah asked the PSTs to consider more than one strategy, this was coded as questioning; discussion related to assignment expectations was coded as assessment.

5 Results and Discussion

In this section, we illustrate the application of the KQ in the analysis of lesson excerpts from two lessons observed by the researchers, which provide typical examples of how Sarah taught her lessons and explored key content of the unit. They also illustrate how different aspects of the framework occurred in the lessons. Although the focus is on Sarah as the MTE, the lessons were co-taught, so sometimes incidental reference is made throughout the lesson episodes to both teachers’ roles in order to accurately represent what occurred in the lesson.

5.1 Lesson Episode 1: Algebraic Thinking

5.1.1 Lesson Observations

The lesson began with Sarah welcoming the PSTs (there were 12 students sitting at 3 tables, 1 male and 11 female). She then asked them to reflect on the prescribed reading and to discuss their experiences with learning algebra at school. Sarah then directed the PSTs to discuss what algebraic thinking would mean for primary students, to post their thoughts on sticky notes and then to place them on the board at the front of the classroom. Sarah and Melissa both facilitated discussion around particular algebraic terms such as patterning and relationships.

The PSTs were then asked to explore ways the balance scales on their tables could be used to teach algebraic concepts (see Fig. 3.1). After some exploration, some PSTs volunteered to share their thinking, drawing diagrams on the board to show how the two sides balanced (see Fig. 3.2). During the sharing, Sarah referred to a poster in the room that explained ‘talk moves’ and cited how a PST was using one of the moves (revoicing) when explaining another PST’s strategy. When asked what grade level the activity would be suitable for, Sarah deferred to Melissa and also stated that it could be appropriate for any grade level if suitably contextualised.

Fig. 3.1

Balance scales

Fig. 3.2

Balance scale drawings

Following this, Sarah shared a work sample from one of Melissa’s students who was demonstrating a common misconception of seeing the equals sign as a place to put the answer and referred them back to a similar example that was shared in last week’s tutorial. Melissa had provided a number of other examples from her primary school classroom to also demonstrate this tendency, and these were also shared. Sarah encouraged the PSTs to discuss at their tables what the samples revealed about the students’ thinking, with the general consensus being that they did not see the equations as being equal but were putting an answer in the box. They were also encouraged to think about what they would do to help students make connections, and one PST volunteered that using the dot patterns on a dice might be helpful. Sarah took this opportunity to remind them that this was called subitising.

During the next part of the lesson, growing patterns were explored. There was no explanation given as to what a growing pattern was or how it differed from a repeating pattern. PSTs used counters at their table to create growing patterns and were then directed to pair up and ask their partner to continue their patterns (see Fig. 3.3). Sarah then took the PSTs on a ‘numeracy walk’ to look at others’ patterns and to verbally describe them. At one point, one of the PSTs had difficulty explaining what their pattern was, and there was general confusion as to whether or not it was a growing pattern. Sarah asked questions about the pattern but did not attempt to explain what the pattern might be. Melissa then read the story Two of Everything (Hong, 1993) and described how it could be used as a stimulus for students to invent their own function machines. Due to time constraints, the PSTs did not get to participate in the planned activity of making their own function machines. The lesson concluded with the PSTs completing their post-lesson reflections.

Fig. 3.3

Growing patterns

5.1.2 Post-lesson Data

The PSTs’ post-lesson reflection data showed that they identified a number of strategies that assisted their learning. Frequent mention was made of the use of manipulatives, particularly the balance beams (e.g. ‘[My learning was helped] through explaining, modelling, questioning, and facilitating learning through the use of manipulatives’) and student work samples that provided examples of children’s algebraic thinking and misconceptions (e.g. ‘lots of student examples to assist us in understanding about misconceptions’). Mention was also made of the opportunities to contribute to discussions and to explain and justify their thinking (e.g. ‘asking us to explain how we would explain to students’).

The post-lesson interview conducted with the PSTs reinforced the practices mentioned in the post-lesson reflections. PSTs also had the opportunity to explicitly comment on the links they were able to make between theory and practice, for instance:

I realised that algebraic thinking is at all stages of the curriculum. [Jill]

I could see all the activities being used within a classroom and what terms we can use to explain the concepts. [Frida]

I thought it was great how she showed us that the curriculum linked to the early ones because you don’t ever think of it like that necessarily even though you may have seen it on placement [Sue]

By actually physically doing the activity [balance beams], we’ve got more chance of remembering that…when we actually get in a classroom…because we actually participated, and we can say you could use balance scales to teach it but because we actually physically did it [Scott]

Although not asked to specifically comment on Sarah’s knowledge, three of the PSTs interviewed said that they particularly valued Melissa’s current experience as a teacher and would direct practically based questions to her. Fiona noted, for example:

I probably would go to Melissa first because she’s the in-service teacher. There’s nothing wrong with Sarah but Melissa knows exactly what happens in schools. [Fiona]

5.1.3 Post-lesson Reflections: Co-teachers

Post-lesson reflective notes and discussion transcripts showed that the co-teachers were satisfied that the lesson had been effective. Again, mention was made of the effectiveness of the balance beams, for example:

I liked exploring the number balances, even though it took some time, it was really good to connect a material to a concept, how you can use it, get them to explore different ways and explain that to other people is really good, and then making sense of it in the traditional way of learning about algebra, having things balanced on either side of the equation. So it’s really nice to see that connect as they were working on it. [Melissa]

Post-lesson reflections also provided an opportunity for Sarah to reflect on her PCK and content knowledge:

Normally I would do more on the growing patterns... So we did that briefly but I was still pretty happy that we showed them growing patterns and repeating patterns…probably we could’ve unpacked the mathematics in that a bit more but we’ve only got two hours.

I’ve taught that [algebra] but when you start to think about the functions and the relationships and the groups and all that – well, see, I’ve never taught this before. So this was the first time I’ve done or taught all this. I’ve talked about different patterns and things but I’ve never taken it up to this level, but I’d done proportion and ratio which links to it - I try to then get on top of it … and I probably haven’t got my roots in it … like all that proportional reasoning that I’ve done days and days of and could just talk about. Depending on what you are researching sometimes becomes your strength.

Melissa was also able to comment on Sarah’s PCK in her post-lesson reflections and discussions:

You’re [Sarah] very good at unpacking thinking, the thinking done by teachers and the learning that needs to happen. You’re very good at pulling it apart and building their knowledge up again which is really, really good and you pose really great questions that challenges thinking…so I really like your technique when it comes to questioning and really extending them and thinking of it this way, what’s another way of doing it, now you explain, that type of thing.

I believe it was a very practical lesson. The PSTs can take away a lot of tips, techniques and ideas to use in their classroom. Made references to the Talk Moves and Knowledge Quartet; making connections to learning that has occurred in previous tutorials.

5.2 Lesson Episode 2: Measurement

Sarah welcomed the 17 PSTs (2 male, 15 female) who were seated at 5 tables, then explained the outline of the lesson, which included reference to enabling and extending prompts and use of talk moves.

The PSTs had been introduced to the KQ in week 1 and Sarah asked them what foundation knowledge would be required to teach perimeter, area and volume. After recording some ideas, Sarah invited the PSTs to turn and talk to the person beside them (modelling a talk move). During this time Sarah and Melissa roved, then Melissa led a discussion and recorded PSTs’ responses on the board (see Fig. 3.4). Sarah then asked about appropriate measuring tools, and one PST used the term ‘inches’ in her response. Sarah asked Melissa if she used the term ‘inches’ with her class, and she indicated that it was not something her students could relate to. Sarah encouraged the discussion as it was of interest.

Fig. 3.4

Recording of PSTs’ foundation knowledge

In order to focus on measurement terminology, Sarah asked, ‘is area a measurement?’ This question led to a discussion about the correct terminology to use when interpreting the symbolic representation of square units. Sarah further challenged the PSTs’ thinking of area by linking it to the surface area of a cube. She asked the PSTs to use the blocks on their tables to make a two by two by two cube and record the surface area of the construction. She left this for a moment and asked them how many cubic centimetres altogether, and they said eight. When asked how they worked it out, a PST replied length by width by height. Sarah stressed the importance of unpacking this rule with their own students to develop their conceptual knowledge, not just their procedural knowledge. One PST said she had no idea how to find the surface area. Sarah used the following prompts: ‘How many faces do you see? What is the shape of each face?’ Sarah asked them to work out the area of each face. She also drew a net, helping to unpack their thinking to find the answer of 24 square centimetres (Fig. 3.5). The PST who struggled initially said that she now got it.

Fig. 3.5

Finding the surface area of a cube

Revisiting the discussion of formula, Sarah said that primary school students should understand why the rule works. She illustrated this by using a scenario of a Year 6 class who were going to explore the area of a triangle using an online learning object (ABC Splash: Maths). PSTs were encouraged to explore this resource and consider if this program would assist students to understand the rule ‘half base by height’. Some PSTs thought that getting the students to estimate what the area might be was good. Sarah mentioned Maths 300 lesson 44 (area of a triangle) provided a good hands-on approach with grid paper. The discussion included how to calculate the area of a parallelogram with understanding (see Fig. 3.6).

Fig. 3.6

Finding the area of a parallelogram

Finally, the PSTs used matchsticks to construct rectangles to compare their perimeters and areas. Sarah posed the following questions to prompt PSTs’ thinking: Are the perimeters of the different rectangles the same? Why? Are the areas of the different rectangles the same? What is the smallest area? What is the largest area? There was also a discussion about whether a square was a rectangle, and some said no. Again, this was a situation in the lesson where the PSTs’ foundation knowledge was being tested, with some saying it was a quadrilateral. The workshop concluded with PSTs completing their post-lesson reflections.

5.2.1 Post-lesson Data

The PSTs’ post-lesson data showed that they valued the depth of discussion and choice of examples. Some PSTs mentioned the use of the open tasks and the ‘talk moves’ questioning, while others indicated the discussion helped with their foundation knowledge (e.g. ‘being able to show the connections I made on the board about calculating the area of a parallelogram’; ‘by providing explanation and working through step by step to get an understanding of the area of a triangle and time to explore with materials’).

Several mentioned connections to primary school classroom practice through the use of photographs and work samples (e.g. ‘using real examples of student learning from the classroom and Sarah backing this up with further practical tasks’). For others, it was clarification of the mathematics and terminology, such as 1cm³ is equal to 1 mL of water, and recognising misconceptions that they held. Some commented on the supportive environment in which they feel free to express their thinking while supporting each other (e.g. ‘the way they scaffolded our learning by posing questions and challenging our thinking’).

These comments were reinforced in the post-lesson PST focus interview when the PSTs were asked to comment on what helped their learning. They responded:

There was a lot of discussion or a lot of time for discussion, and flexibility in the lesson. [Carol]

I feel like there’s a lot of hands-on activities always, especially in mathematics where there’s always activities that we can do with hands-on materials. [Sam]

And they are so practical and classroom ready, like Melissa comes in and shows us things she’s already done which I think is really valuable because we know that it works. [Bob]

There’re a lot of opportunities where Sarah gets a few people up to show their examples on the board and so you see different people’s thinking and how that was different from yours and how… I may have done it more complex and just how easy it could’ve been. [Katie]

In her post-lesson reflection Melissa observed that:

Some pre-service teachers were challenged today as they were taught these concepts differently when they were in primary school. I hope they understood the importance of unpacking the concept with the students… building up their knowledge from the foundation.

I thought the lesson was effective in that it highlighted the problems associated with learning the content based only on formulae.

[What could we do differently?] Unpack the conceptual understandings with every activity would have been good. Showing them the sequence of learning involved.

5.2.2 Links to the Knowledge Quartet

There were applications of the KQ dimensions throughout the lessons. While most of these applications were evident in the descriptions of the lesson episodes, the post-lesson data were useful in terms of considering the effectiveness and/or impact of the elements.

5.2.3 Foundation

This category includes subject knowledge as well as beliefs about mathematics and mathematics pedagogy, which could be evident in both planning and teaching (Rowland et al., 2009). The data suggest that examples of evidence could be identified for each code of this category. For example, PSTs were allocated readings from the textbook Helping Children Learn Mathematics (Reys et al., 2012), and Sarah referred to the prescribed reading in both lessons observed (adheres to textbook). Overt subject knowledge was explicitly referred to when Sarah talked about algebraic thinking and how she felt more confident and prepared to teach proportional reasoning. This may have influenced her decision not to expand more on the growing patterns aspect of the lesson. Sarah’s knowledge of subject knowledge and use of terminology was enacted in the first episode in relation to algebraic terms and in the second episode in the discussion about how to calculate and record the area of shapes. In much the same way as school teachers would identify student misconceptions, Sarah, as an MTE, also recognised that her PSTs may also hold algebraic, area/perimeter and volume/capacity misconceptions (identifying errors) and would also benefit from studying student misconceptions as demonstrated in the algebraic work samples shared. Previous experience with delivering the unit also meant that Sarah was able to anticipate that the PSTs were likely to believe that algebra was not relevant for young children and used her knowledge of curriculum to address this perception. This clearly had an impact on PSTs as evidenced by their post-lesson feedback. Sarah explicitly referred to particular practices and theoretical frameworks such as ‘talk moves’ and the KQ (theoretical underpinnings). Melissa was unfamiliar with these terms, indicating an example of MTE knowledge that was not part of a school teacher’s knowledge.

It could also be expected that part of Sarah’s foundation knowledge would include knowledge of the primary curriculum and actual primary teaching. Sarah was an experienced primary school teacher and maintained an active teaching role in primary school classrooms through modelling lessons and professional learning with teachers. In the lessons observed, however, and commented on by the PSTs, she often referred to Melissa when questions were asked about curriculum or implementation in the classroom. This seemed to create the impression that Melissa held greater expertise in this area and that Sarah’s foundation knowledge in this area may be limited. We suspect, however, that this is more an indication of Sarah providing opportunity for Melissa to contribute, rather than an indication that Sarah lacked the foundation knowledge necessary to respond to PSTs’ questions directly related to primary school classroom practice.

5.2.4 Transformation

When examining the work of trainee teachers, Rowland et al. (2009) looked for instances where teachers transformed what they knew in ways that made the knowledge accessible to students. This dimension included the codes choice of examples, choice of representation and demonstration and in the context of an MTE’s work required Sarah to transform her knowledge of teaching mathematics in a way that developed her PSTs’ understanding. As the post-lesson data showed, one of the representations and demonstrations that was emphasised as being particularly effective was the use of the balance beams to model equality. Sarah was able to transform her knowledge of common algebra misconceptions through the use of this model, the use of student work samples (e.g. incorrect interpretation of the equals sign) and interactive teaching techniques such as actively involving the PSTs in balancing equations and constructing growing patterns. The use of these techniques and others such as talk moves, sticky notes and table discussions were features of Sarah’s practice. The use of the recording of diagrams on the board to work out the area of a parallelogram also illustrated a way to transform the PSTs’ understanding. The post-lesson data showed that these techniques had a positive impact upon the PSTs as evidenced, for example, by Carol and Katie’s comments.

Questioning and promoting classroom discussion was a critical aspect of Sarah’s practice. Some of her questions served to challenge the PSTs’ thinking, while others prompted them to think about their own future practice, facilitating connection. Questioning was not named as an element in the KQ but helped to demonstrate elements from the transformation and connection categories such as demonstrations and making connections between concepts and procedures.

5.2.5 Connection

Connection concerns the coherence of planning and teaching across an episode and includes the sequencing of topics of instruction within and between lessons (Rowland et al., 2009). Similar to the planning and sequencing of instruction that is undertaken by a school teacher, the MTE also has to make decisions about which tasks to use, in what order to present them and how to help her students (i.e. PSTs) make appropriate conceptual connections within the subject matter. When planning, for example, Sarah anticipated the complexity associated with understanding algebra and perimeter, area and volume. Decisions were made about sequencing that were particularly evident in the measurement episode where area and surface area were discussed before volume. During this same episode, Sarah also demonstrated the elements of making connections between procedures and between concepts in the discussion about area, calculation of area and its relationship with perimeter and volume.

A particularly important connection an MTE has to make that is not relevant to a school teacher is to link the ‘theory’ with the practice; the co-teaching arrangement facilitated the enactment of this as the PSTs had direct contact with an in-service practicing teacher. These connections were clearly made for the PSTs as evidenced in comments such as the following: ‘I could see all the experiences being used in a classroom’ (Pseudonym). Links were also made with previous lessons and experiences, including the consistent use of talk moves and reference to the KQ.

5.2.6 Contingency

This category concerns the teacher’s response to unplanned or unexpected classroom events (Rowland et al., 2009). Although there were limited examples of deviating from the agenda, there was evidence of contingency moments, and at least one student gave feedback on Sarah’s response to her ideas. Finding the surface area of a cube was one such instance. Sarah saw it as an opportunity to deepen the PSTs’ foundation knowledge and to illustrate the importance of making connections to other mathematics concepts. Another example occurred when she referred to subitising in a discussion about patterning in the first lesson episode. It seemed that the co-teaching situation, along with the course structure of teaching a designated weekly topic, meant that contingency moments might not always be acted upon, even when they were recognised. Sarah later expressed in her interview that ‘you can’t take those teachable moments and go off on a tangent’ as it may have resulted in not getting through the planned activities, which she was keen to do, particularly if Melissa had prepared them.

6 Conclusions and Implications

The work of the MTE is complex as it involves both the teaching of subject matter and appropriate pedagogical content knowledge. In addressing the first research question, it is evident that similar types of knowledge are required by MTEs and primary school teachers, such as knowing the appropriate representations and examples to use when teaching particular concepts or anticipating complexities and addressing student misconceptions. However, the MTE requires a deeper and broader understanding of the theoretical underpinnings behind the use of appropriate pedagogical practices (e.g. why we use MAB to teach place value) than arguably a school teacher needs to know. In addition, the MTE is required to justify the use of these practices to PSTs and to respond to their questions about them. Ongoing modelling of appropriate pedagogical practices, along with the accompanying commentary of why and how these practices can be used in a primary classroom, adds another layer to the knowledge MTEs require for teaching PSTs. In contrast, school teachers require a good understanding of each child’s mathematics learning and how to respond to their needs on a daily basis and detailed knowledge of assessing and reporting student learning to parents, neither of which is an aspect of knowledge MTEs require. It could be argued that MTEs respond to PSTs’ misconceptions; however, addressing specific needs within such a limited time frame of a semester is not possible. The knowledge of the co-teacher is invaluable in providing such specialised knowledge of planning, assessment and reporting practices. Both classroom teachers and MTEs require ongoing professional learning. In summary, while there are similarities in knowledge required by school teachers and MTEs, there are also differences as identified in this study.

As evident in the results and subsequent discussion, it was possible to identify elements from the KQ in the work of an MTE, indicating that it is transferable and applicable for describing MTE knowledge. As found by Muir et al. (2017), the framework proved useful in unpacking the complexity of the work of the MTE and in highlighting the somewhat subtle differences between being an MTE and a classroom teacher. Through providing examples of evidence from an MTE context, we have highlighted the similarities between classroom teaching and teaching teachers how to teach, acknowledging the ‘meta-knowledge’ (Beswick & Chapman, 2012) required by a teacher educator. Just as the KQ framework has been applied to interpret the work of classroom teachers, we can also see it being applied to interpret the work of teachers in a variety of contexts, including tertiary education. As Rowland (2013) intended, it provides a means of reflecting on teaching and teacher knowledge, with a view to developing both. Future studies could look at applying the KQ to other disciplines to further demonstrate its transferability.