Keywords

Introduction

Disasters of natural and artificial slopes around roads, railways and residential area are caused by heavy rains. Furthermore, in construction sites, slope failures occur by the destabilisation of the ground owing to change in stress caused by the embankment and cut earth. Time prediction methods based on monitoring the displacement of a slope using sensors are effective at preventing sediment-related disasters.

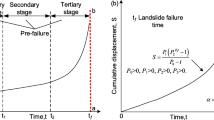
Several methods have been proposed to predict slope failure using the surface displacement of a slope. The formulae proposed by Fukuzono (1985) have been widely adopted in practice because of their simplicity. These models were proposed to predict the failure time of a slope based on the creep theory of soil, which is divided into three stages: primary creep (decreasing velocity), secondary creep (constant velocity) and tertiary creep (increasing velocity).

Fukuzono’s model formulates the relationship between the velocity of the surface displacement and the acceleration in the tertiary creep stage. Fukuzono found that the logarithm of the acceleration of the surface displacement is proportional to the logarithm of the velocity in model slope experiments. Time integration of this relationship leads to the typical trends of the time variation in the inverse-velocity of the surface displacement before failure. The failure time of a slope can be predicted when the extrapolation curves approach zero. Fukuzono’s method has been widely applied because of its simplicity and convenience of use.

His method can only be applied to the period when the surface displacement accelerates. However, the actual displacement of the slope is complicated owing to variations in the rainfall intensity and the inhomogeneity of the surface layer, and it is not easy to specify the period when the surface displacement accelerates. Moreover, the observed displacement appears to increase monotonically, slightly repeating the increase and decrease, the acceleration varies widely and some data points become negative. These results decrease the accuracy of the predicted failure time. Thinning out the observed data is effective for minimising the influence of fluctuations.

In this study, we predicted the failure time of a sandy model slope under artificial rainfall with constant rainfall conditions using four methods based on Fukuzono’s model to extract data at difference time intervals. We compared the prediction accuracy of each method and examined the influence of measurement intervals on the predicted failure time.

Methods for Predicting the Failure Time

Fundamental Equation of Fukuzono’s Model

Fukuzono (1985) proposed that the logarithm of the velocity of the surface displacement is proportional to the logarithm of the acceleration in the tertiary creep stage, which describes the accelerating surface displacement before slope failure, given as

$$ \frac{{d^{2} {\text{x}}}}{{d{\text{t}}^{2} }} = {\text{a}}\left( {\frac{{d{\text{x}}}}{{d{\text{t}}}}} \right)^{\alpha } $$
(1)

where x is the downward surface displacement along the slope, t is the time, dx/dt is the velocity, dx2/dt2 is the acceleration, and a and α are constants. α is greater than 1 in the period during which the surface displacement accelerates.

After integrating Eq. (1), the inverse-velocity of the surface displacement can be written as follows:

$$ \frac{{d{\text{t}}}}{{d{\text{x}}}} = \frac{1}{{\text{v}}} = \left\{ { - {\text{a}}({\text{a}} - 1)} \right\}^{1/(\alpha - 1)} \left( {{\text{t}}_{{\text{r}}} - {\text{t}}} \right)^{{\frac{1}{{\left( {\alpha - 1} \right)}}}} $$
(2)

where v is the velocity of the surface displacement and tr is the failure time. Eq. (2) shows a downward slope; further, the time approaches the time immediately prior to slope failure as the inverse-velocity of the surface displacement, 1/v, approaches zero. The curve is linear for α = 2, convex for α > 2 and concave for 1 < α < 2. The value of α for actual slope failure ranges from 1.5 to 2.2.

Precise Prediction Method Using Inverse-Velocity

As Eq. (2 becomes linear for α = 2, the failure time is calculated easily using two inverse-velocity values at different times. However, when α ≠ 2, it is difficult to predict it accurately using two values owing to the curvature of the inverse-velocity curve. Therefore, Fukuzono (1985) proposed the time-prediction method expressed in Eq. (3) by a time differential in Eq. (2).

$$ {\raise0.7ex\hbox{${\left( {1/{\text{v}}} \right)}$} \!\mathord{\left/ {\vphantom {{\left( {1/{\text{v}}} \right)} {\frac{{d(1/{\text{v}})}}{{d{\text{t}}}}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\frac{{d(1/{\text{v}})}}{{d{\text{t}}}}}$}} = - ({\text{a}} - 1) \times \left( {{\text{t}}_{{\text{r}}} - {\text{t}}} \right) $$
(3)

The curve of Eq. (3) is linear; the failure time, tr, is predicted by inserting two inverse-velocity values (1/vi-1, 1/vi) and two inclination values (d(1/vi-1)/dt, d(1/vi)/dt) at two different times (ti-1, ti) into Eq. (4) as follows:

$$ {\text{t}}_{{\text{r}}} = \frac{{{\text{t}}_{i} \times \left( {1/{\text{v}}_{i - 1} } \right)/\left( {\frac{{d\left( {1/{\text{v}}_{i - 1} } \right)}}{{d{\text{t}}}}} \right) - {\text{t}}_{i - 1} \times \left( {1/{\text{v}}_{i} } \right)/\left( {\frac{{d(1/{\text{v}}_{i} )}}{{d{\text{t}}}}} \right)}}{{\left( {1/{\text{v}}_{i - 1} } \right)/\left( {\frac{{d\left( {1/{\text{v}}_{i - 1} } \right)}}{{d{\text{t}}}}} \right) - \left( {1/{\text{v}}_{i} } \right)/\left( {\frac{{d(1/{\text{v}}_{i} )}}{{d{\text{t}}}}} \right)}} $$
(4)

Three Data Prediction Method

Tsuchiya and Omura (1989) proposed the time-prediction method using time–velocity relationship in Eq.[2] and time–displacement relationship by time integral in Eq. (2) from three surface displacement values at equal time intervals. We improved this method to be applicable to different time intervals. The failure time, tr, is predicted by inserting three displacement values (xi-2, xi-1, xi) at three different times (ti-2, ti-1, ti) as follows:

$$ {\text{t}}_{{\text{r}}} = \frac{{\left( {{\text{t}}_{i - 1} + {\text{t}}_{i} } \right) \times \left( {\frac{{{\text{x}}_{i} - {\text{x}}_{i - 1} }}{{{\text{x}}_{i - 1} - {\text{x}}_{i - 2} }} \times \frac{{{\text{t}}_{i - 1} - {\text{t}}_{i - 2} }}{{{\text{t}}_{i} - {\text{t}}_{i - 1} }}} \right)^{\alpha - 1} - \left( {{\text{t}}_{i - 1} - {\text{t}}_{i - 2} } \right)}}{{2 \times \left\{ {\left( {\frac{{{\text{x}}_{i} - {\text{x}}_{i - 1} }}{{{\text{x}}_{i - 1} - {\text{x}}_{i - 2} }} \times \frac{{{\text{t}}_{i - 1} - {\text{t}}_{i - 2} }}{{{\text{t}}_{i} - {\text{t}}_{i - 1} }}} \right)^{\alpha - 1} - 1} \right\}}} $$
(5)
$$ \alpha = 2 - \frac{{\log \left( {\frac{{{\text{x}}_{i - 2} - {\text{x}}_{i - 1} }}{{{\text{x}}_{i - 1} - {\text{x}}_{i} }}} \right)}}{{\log \left( {\frac{{{\text{x}}_{i - 1} - {\text{x}}_{i - 2} }}{{{\text{x}}_{i} - {\text{x}}_{i - 1} }} \cdot \frac{{{\text{t}}_{i} - {\text{t}}_{i - 1} }}{{{\text{t}}_{i - 1} - {\text{t}}_{i - 2} }}} \right)}} $$
(6)

Least Squares Prediction Method

Assuming the curve of Eq. (2) to be linear (α = 2), the relationship between the inverse-velocity and time is calculated via the least squares method using all previous inverse-velocity values from the start of the measurement. The failure time, tr, corresponds to the intercept of the straight line with the time axis.

Nonlinear Regression Prediction Method

The constants a and α in Eq. (1) are calculated by the least squares methods using velocity and acceleration data plotted in a double logarithmic chart. The failure time, tr, is predicted by inserting the constants a and α into Eq. (7) as follows:

$$ {\text{t}}_{{\text{r}}} = \frac{{{\text{v}}^{1 - \alpha } }}{{{\text{a}}({\text{a}} - 1)}} + {\text{t}} $$
(7)

Experimental Set-up and Observed Data

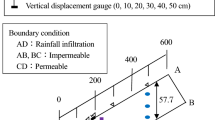
In this study, we used the observed surface displacement of a slope failure experiment that was conducted using the large-scale rainfall simulator at the National Research Institute for Earth Science and Disaster Prevention (Sasahara and Ishizawa 2016). Figure 1 shows a photograph of the model slope. The model was 300 cm long and 150 cm wide in the horizontal section and 600 cm long and 150 cm wide in the slope section with an inclination of 30°. The soil layer was 50 cm thick and composed of granitic soil. The surface of the slope was parallel to the base of the slope.

Fig. 1
figure 1

Overview of the model slope

Full size image

The surface displacement was measured using an extensometer with a non-linearity of approximately 0.1 mm; it was fixed at the upper boundary of the flume. The surface displacement was defined as the distance between the upper boundary of the flume and the moving pole at the surface of the slope at 160 cm from the toe of the slope. The surface displacement was measured every 10 s.

The rainfall had an intensity of 50 mm/h and continued until the onset of the failure of the model slope. Slope failure occurred at 9,220 s, and the surface displacement just before the slope failure was 1.27 cm.

As the extensometer has an accuracy of 0.1 mm, data were extracted to be greater than 0.1 mm between the two measurements of the surface displacement. Figure 2 shows the time variation of the surface displacement and the inverse-velocity of the surface displacement. The slope of the inverse-velocity curve before 7,500 s suddenly increases and decreases and displays a uniform downward slope afterwards.

Fig. 2
figure 2

Time variation of the surface displacement and inverse-velocity of the surface displacement

Full size image

Data for the Prediction

The time-prediction methods based on Fukuzono’s model are applied to the tertiary creep stage. However, a curve of the inverse-velocity has fluctuations and it is difficult to predict the time of onset of the tertiary creep in actual practice. Therefore, in this study, all data from the start of monitoring onwards are used to examine the influence of measurement intervals of surface displacement, Δx, and predict the failure time. The data were extracted to be greater than difference Δx from previous extracted data of the surface displacement: 0.01, 0.05, 0.1 and 0.2 cm.

The velocity of the surface displacement, vi, is calculated from vi = (xi–xi−1)/(ti–ti−1), where xi and xi−1 are the surface displacements at times ti and ti−1. Because vi is the average velocity between ti−1 and ti, the time against vi, t’i, is set as the mid of ti and ti−1, specifically t’i = (ti–ti−1)/2. The acceleration of the surface displacement, (dv/dt)i, is calculated from (dv/dt)i = (vi–vi−1)/(t’i–t’i−1), where vi and vi−1 are the velocities at times t’i and t’i−1. The time against (dv/dt)i, t’’i, is to set to the middle of t’i and t’i−1, i.e. t’’i = (t’i–t’i−1)/2.

The failure time is inferred via four prediction methods: (1) Precise prediction method, (2) Three data prediction method, (3) Least squares prediction method and (4) Nonlinear regression prediction method, using the extracted data from the start of monitoring and onwards. We compare the prediction accuracy of each method and examine the influence of measurement intervals on the predicted failure time.

Variation of the Extracted Data

Figure 3 shows the time variation of the displacement and inverse-velocity for different Δx and the relationship between velocity and acceleration. The time variation of the displacement, shown in Fig. 3a, demonstrates behaviour similar to that of tertiary creep after approximately 6500 s. When Δx = 0.1 cm or less, the measurement value of Δx = 0.01 cm is usually reproducible. However, when Δx ≥ 0.1 cm, the data could not be extracted at the initial stage of the tertiary creep and the deviation of the data at the initial stage increased at 8000 s and earlier. The time variation of the inverse-velocity, shown in Fig. 3b, significantly varied at 7500 s and earlier for Δx = 0.01 cm; however, this variation was eliminated by increasing the Δx. When Δx increases, the number of displacement data to be extracted decreases, and there are no data at the initial stage of the tertiary creep; therefore, it is impossible to predict until immediately before the failure.

Fig. 3
figure 3

Comparison of the extracted data: a time variation of displacement; b time variation of inverse-velocity; c velocity–acceleration relationship

Full size image

As shown in Fig. 3c, the velocity–acceleration relationship originally showed displacement behaviour similar to that of the tertiary creep stage, and the variation was small. The larger the Δx, the smaller the number of the data and the smaller the variation. When the variation decreases, it is assumed that applicability to Fukuzono’s prediction formula increases, whereas the previously mentioned issues will exist.

Results of Time-Prediction of Slope Failure

Figure 4 shows the comparison of the time variation of difference between the predicted failure time and the elapsed time, tr–t, obtained using the different prediction methods. The tr–t implies the time interval for the slope failure. When the accuracy of prediction is high, tr–t values are plotted in the positive domain of the graph and tend to zero as the time approaches the slope failure time (i.e. the time variation of tr–t has a downward slope). When tr–t values appear in the negative domain of the graph, the predicted failure time precedes the elapsed time and the slope failure time is thus unpredictable.

Fig. 4
figure 4

Comparison of the time variation of the predicted failure time according to the different prediction methods using the extracted data at different measurement intervals: a precise prediction method; b three data prediction method; c least squares prediction method; d nonlinear regression prediction method

Full size image

Using the precise prediction method, when Δx = 0.01 cm, tr–t is nearly 0, i.e. the current time is predicted as the precise prediction time, indicating that the failure time is unpredictable. Further, when Δx = 0.05 cm, tr–t significantly fluctuates, indicating that the prediction accuracy is poor. However, when Δx ≥ 0.1 cm, the prediction result is close to the black broken line, indicating high prediction accuracy. This result is caused by the precise prediction method, which predicts using the displacement velocity data at two different times. If Δx is small, the prediction accuracy will decrease because of the increasing and decreasing of the surface displacement even if the data exhibit a behaviour resembling the tertiary creep.

Based on the three-data prediction method, tr–t significantly increases or decreases for both Δx = 0.01 and 0.05 cm, after 8700 s at Δx = 0.05 cm, the prediction result is close to the black broken line with improved accuracy. When Δx = 0.1 cm, a table prediction result was obtained using the precise rediction method; however the accuracy before 8800 s was reduced by the three-data prediction method. This demonstrates that the predicted value can considerably vary depending on the data to be extracted.

As the least squares prediction method predicts using all data from the start of monitoring onwards, the variation is limited and shows a right-downward tendency. The predicted value is plotted below the black dashed line and is negative near the failure time, resulting in low prediction accuracy. As Δx increases, the results approach the black broken line with improved prediction accuracy. This is because of data in the initial stage of measurement, showing that the inverse-velocity is very large. As Δx increases, the number of data and the value of inverse-velocity in the initial stage decrease, thus improving the prediction accuracy.

The non-linear regression prediction method is close to the black dashed line after 8700 s, even when Δx = 0.01 cm, and comparatively high prediction accuracy results are obtained. When Δx ≥ 0.05 cm, good prediction accuracy is obtained because the variation in velocity–acceleration is small, as seen in Fig. 3c. When Δx = 0.01 cm, the constants are a = 1.32 and α = 1.79 and the correlation coefficient is 0.94. When Δx ≥ 0.05 cm, the constant a increases from 2.0 to 5.0 and α increase from 1.8 to 2.0. However, the prediction accuracy is high because the correlation coefficient is around 0.99 and the curve between inverse-velocity and time is almost linear (i.e. α is around 2.0).

Discussion

As shown in Fig. 3a, as Δx increases, the discrepancy between measured and extracted data increases. This discrepancy is evaluated using the root mean square error (RMSE), which is a method for evaluating the variation in data given by Eq.[8].

$$ {\text{RMSE } = \text{ }}\sqrt {\frac{1}{{\text{N}}}\mathop \sum \limits_{i = 1}^{{\text{N}}} \left( {{\text{F}}_{i} { - } A_{i} } \right)^{2} } $$
(8)

where N is number of target data, Fi is the measured displacement at time ti, Ai is the extracted displacement at time ti and Fi-Ai indicates an error. If there are no data at the time ti among the extracted data, the datum for ti is projected by a proportional distribution of the extracted data before and after time ti. In the RMSE, the smaller the value, the smaller the variation of the extracted data group, i.e. the greater the reproducibility.

Figure 5 shows a comparison between the RMSE and the correlation coefficient of the nonlinear regression equation for the velocity–acceleration relationship when Δx is 1/5000, 1/2500, 1/1670, 1/1000, 1/500 and 1/250 of soil layer thickness T (0.01, 0.02, 0.03, 0.05, 0.1 and 0.2 cm, respectively). When Δx/T exceeds 1/1670–1/1000, the RMSE rapidly increases and the reproducibility of measurement data decreases; however, the correlation coefficient exceeds 0.98, indicating a very high correlation. Moreover, the correlation decreases when the Δx/T is less than 1/1670–1/1000. These results imply that the appropriate interval for achieving high prediction accuracy in this study is 1/1670–1/1000.

Fig. 5
figure 5

Comparison between the RMSE and correlation coefficient for the velocity–displacement relationship with the change in measurement interval

Full size image

In the least squares prediction method and nonlinear regression prediction method, it was found that the prediction accuracy tended to improve upon increasing Δx. This suggests that additional improvement in the accuracy of prediction is possible by rejecting the data at the initial stage when the velocity is low (i.e. 1/v is very large). Therefore, the method based on the moving average acceleration (i.e. extracting the period where the average acceleration of the five preceding steps is continuously positive) performed by Iwata et al. (2017) was used to extract the time after 7600 s at the tertiary creep stage. The failure time was predicted using the least squares prediction method and nonlinear regression prediction method for this period.

Figure 6 shows a comparison of the time variation of tr–t with the tertiary creep stage. The prediction accuracy of the least squares prediction method is significantly improved in comparison with Fig. 4c. Consequently, it can be seen that to improve the prediction accuracy, rejecting data at the initial stage is very effective. Furthermore, the influence of the difference of Δx is not significant because the variation in data was small, as seen in Fig. 3c.

Fig. 6
figure 6

Comparison of the time variation of the predicted failure time in the tertiary creep stage at different measurement intervals: a least squares prediction method; b nonlinear regression prediction method

Full size image

In comparison with Fig. 4d, the non-linear regression prediction method shows a slight improvement in the prediction accuracy above 9000 s at Δx = 0.01 cm but no improvement at 9000 s or less. However, when Δx = 0.05 cm, the prediction accuracy for 8700 s or less declines because the quantity of the data used in the regression analysis is small, and the coefficient obtained in the regression analysis significantly differs owing to the slight changes in the data.

Conclusion

We predicted the failure time of a sandy model slope using four methods based on Fukuzono’s model and examined the influence of measurement intervals on the predicted failure time. The findings obtained from this study can be summarised as follows:

  1. 1.

    The prediction accuracy decreases owing to the fluctuations of the surface displacement even if the data exhibit a behaviour resembling the tertiary creep.

  2. 2.

    As the measurement intervals of displacement increase, the number of the extracted data decreases, the variation of the extracted data group decreases, thus improving the prediction accuracy.

  3. 3.

    The prediction accuracy using the precise prediction method and three-data prediction method is inferior to other methods because a small number of data are used to predict the failure time and these methods are susceptible to fluctuations.

  4. 4.

    The least squares prediction method and non-linear regression prediction method give relatively stable prediction results. However, when the data in the initial stage where the velocity is low are included in the used data, the prediction accuracy decreases.

  5. 5.

    The appropriate measurement interval to achieve high prediction accuracy in this study is 1/1670–1/1000 of soil layer thickness.

  6. 6.

    If the surface displacement data in the tertiary creep stage can be extracted, the prediction accuracy of the least squares prediction method and non-linear regression can be significantly improved.

In this study, one problem was that the quantity of the extracted data decreases as Δx increases because the measurement data are for a small model slope. However, as the displacement just before the slope failure is large at the actual slope, it is assumed that even if Δx is increased, there is no problem with the number of acquired data being reduced.