Keywords

1 Introduction

Steiner Minimum Tree (SMT) is the best connection model for multi-terminal nets in global routing of Very Large Scale Integration (VLSI). The SMT problem is to find a routing tree with the least cost to connect all given pins by introducing additional points (Steiner points). Therefore, SMT construction is one of the most important issues in VLSI routing.

Most current researches on routing algorithms are based on the Manhattan structure [6, 7], which can only routing in horizontal and vertical directions. In order to make fuller use of routing resources, the scholars are gradually shifting their focus to non-Manhattan structures, thereby improving routing quality and chip performance.

Therefore, the construction of Steiner minimum tree based on non-Manhattan structure becomes a critical step in VLSI routing. In the early years, scholars use precise algorithms [2, 14] to construct a non-Manhattan structure routing tree, which can obtain a shorter wirelength than the Manhattan structure, but the complexity is too high. So some heuristic algorithms [4, 17, 20] are proposed to solve larger-scale SMT problems. However, these traditional heuristics are prone to fall into local extrema. In recent years, evolutionary computing has developed rapidly in many fields, especially Swarm Intelligence (SI) technology [1, 3, 12, 19]. Some routing algorithms [5, 8, 13] consider important optimization goals such as wirelength, obstacles, delay and bends based on Particle Swarm Optimization (PSO) technique. In [10], a hybrid transformation strategy is proposed to expand the search space based on self-adapting PSO. And an unified algorithm for constructing Rectilinear Steiner Minimum Tree (RSMT) and XSMT is proposed in [11], which can obtain multiple topologies of SMT to optimize the congestion in global routing. It can be seen that PSO technique is indeed a powerful tool to solve SMT problems.

Based on the analysis of the above related research work, this paper designs and implements an effective algorithm to solve the XSMT construction problem using Social Learning PSO (SLPSO), called SLPSO-XSMT. The contributions of this paper are as follows:

  • A novel SLPSO approach based on the learning mechanism of example pool is proposed to enable particles to learn from different and better particles in each iteration, and enhance the diversity of population evolution.

  • Mutation and crossover operators are integrated into the update formula of the particles to achieve the discretization of SLPSO, which can well balance the exploration and exploitation capabilities, thereby better solving the XSMT construction problem.

The rest of this paper is organized as follows. Section 2 presents the problem formulation. And the SLPSO method with example pool mechanism is introduced in Sect. 3. Section 4 describes the XSMT construction using SLPSO method in details. In order to verify the good performance of the proposed SLPSO-XSMT algorithm, the experimental comparisons are given in Sect. 5. Section 6 concludes this paper.

2 Problem Formulation

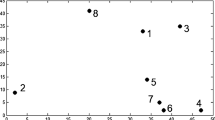
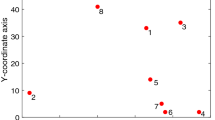
The XSMT problem can be described as follows: Given a set of pins \(P=\{P_1,P_2,...,P_3\}\), each pin is represented by a coordinate pair \((x_i,y_i)\). Then connect all pins in P through some Steiner points to construct an XSMT, where the direction of routing path can be \(45^\circ \) and \(135^\circ \), in addition to the traditional horizontal and vertical directions. Taking a routing net with 10 pins as an example, Table 1 shows the input information of the pins. The layout distribution of the given pins is shown in Fig. 1(a).

Table 1. The input information for the pins of a net
Full size table
Fig. 1.
figure 1

Routing graph corresponding to Table 1: (a) the layout distribution of pins; (b) an X-architecture Steiner tree with the given pin set.

Full size image

Definition 1

Pseudo-Steiner point. In addition to original points formed by given pins, the final XMST can be constructed by introducing additional points called pseudo-Steiner points (PSP). In Fig. 2, the point S is PSP, and PSP contains the Steiner point.

Definition 2

Choice 0 (as shown in Fig. 2(b)). The Choice 0 of PSP corresponding to edge L is defined as leading rectilinear side first from A to PSP S, and then leading non-rectilinear side to B.

Definition 3

Choice 1 (as shown in Fig. 2(c)). The Choice 1 of PSP corresponding to edge L is defined as leading non-rectilinear side first from A to PSP S, and then leading rectilinear side to B.

Definition 4

Choice 2 (as shown in Fig. 2(d)). The Choice 2 of PSP corresponding to edge L is defined as leading vertical side first from A to PSP S, and then leading horizontal side to B.

Definition 5

Choice 3 (as shown in Fig. 2(e)). The Choice 3 of PSP corresponding to edge L is defined as leading horizontal side first from A to PSP S, and then leading vertical side to B.

Fig. 2.
figure 2

Four choices of Steiner point for the given segment: (a) line segment L; (b) Choice 0; (c) Choice 1; (d) Choice 2; (e) Choice 3.

Full size image

3 SLPSO

Social learning plays an important role in the learning behavior of swarm intelligence, which helps individuals in the population to learn from other individuals without increasing the cost of their own trials and errors. In SLPSO [18], each particle learns from better individuals (called examples) in the current population, while each particle in PSO only learns from its pbest and gbest.

Definition 6

Example Pool. All particles in the swarm \(S\,\mathrm{{ = }}\,\{ {X_i}|1 \le i \le M\}\) are arranged in ascending order according to the fitness: \(S=\{X_1,...,X_{i - 1},X_i,X_{i + 1},\) \(...,X_M\}\), and then \(EP\,\mathrm{{ = }}\,\{ {X_1},...,{X_{i - 1}}\mathrm{{\} }}\) constitutes the example pool of particle \(X_i\).

Based on the example learning mechanism, the new formulas for updating particles are proposed as follows:

$$\begin{aligned} V_i^{t + 1} = \omega \cdot V_i^t + {c_1} \cdot {r_1} \cdot (P_i^t - X_i^t) + {c_2} \cdot {r_2} \cdot (K_i^t - X_i^t) \end{aligned}$$
(1)
$$\begin{aligned} X_i^{t + 1} = V_i^{t + 1} + X_i^t \end{aligned}$$
(2)

where \(P_i\) is the personal historical best position of particle i, \(K_i\) is the historical best position of the Kth particle in the example pool, which is the social learning object for particle i. \(\omega \) is the inertia weight. \({c_1}\) and \({c_2}\) are acceleration coefficients, which respectively adjust the step size of the particle flying to personal historical best position (\(P_i\)) and its social learning object (\(K_i\)). \({r_1}\) and \({r_2}\) are mutually independent random numbers uniformly distributed in the interval (0, 1).

Fig. 3.
figure 3

Example pool of particle \(X_i\)

Full size image

Figure 3 shows the example pool of a particle. For particle \(X_i\), the particles with better fitness values than it including the global optimal solution \(X_G\) constitute its example pool. \(X_i\) randomly selects any particle in the example pool at each iteration, and learns the historical experience of this particle to complete its own social learning process. This social learning mechanism allows particles to improve themselves through continuous learning from different excellent individuals during the evolution process, which is conducive to the diversified development of the population.

4 XSMT Construction Using SLPSO

4.1 Particle Encoding

The edge-vertex encoding strategy [11] is adopted in this paper, which is more suitable for evolutionary algorithms, especially PSO. For a net with n pins, the corresponding spanning tree has n-1 edges and one extra digit that is the fitness value of particle. Thus the length of a particle encoding is \(3\times (n-1)+1\).

For example, Fig. 1(b) shows an X-architecture routing tree (n = 10) corresponding to the layout distribution of pins given in Fig. 1(a), where the symbol ‘\(\times \)’ represents PSP. And this routing tree can be expressed as the particle whose encoding is the following numeric string:

$$\begin{aligned} 9\ 3\ 2 \ 3\ 7\ 0 \ 7\ 6\ 1 \ 3\ 1\ 1 \ 1\ 5\ 2 \ 9\ 10\ 1 \ 10\ 8\ 0 \ 5\ 4\ 0 \ 4\ 2\ 0 \ \mathbf {108.6686} \end{aligned}$$

where the length of the particle is \(3\times (10-1)+1=28\), the last bold number 108.6686 is the fitness of the particle and each italic number represents the choice of PSP for each edge. The first substring (9, 3, 2) represents that Pin 9 and Pin 3 of the spanning tree in Fig. 1(a) are connected through Choice 2.

4.2 Fitness Function

The length of an X-architecture Steiner tree is the sum of the lengths of all the edge segments in the tree, which is calculated as follows:

$$\begin{aligned} L({T_x}) = \sum \limits _{{e_i} \in {T_x}} {l({e_i})} \end{aligned}$$
(3)

where \(l({e_i})\) represents the length of each segment \(e_i\) in the tree \(T_x\).

The smaller the fitness value, the better the particle is represented. Thus the particle fitness function is designed as follows.

$$\begin{aligned} fitness = L({T_x}) \end{aligned}$$
(4)

4.3 Particle Update Formula

In order to better solve the XSMT problem, a new particle update method with mutation and crossover operators is proposed. The specific formula is as follows:

$$\begin{aligned} X_i^t = {F_3}({F_2}({F_1}(X_i^{t\mathrm{{ - }}1},\omega ),{c_1}),{c_2}) \end{aligned}$$
(5)

where \(\omega \) is the mutation probability, \(c_1\) and \(c_2\) are crossover probability. \(F_1\) is the mutation operator, which corresponds to the inertia component of PSO. \(F_2\) and \(F_3\) are crossover operators, corresponding to the individual cognition and social cognition, respectively.

Inertia Component. The particle velocity of SLPSO-XSMT is updated through \(F_1\), which is expressed as follows:

$$\begin{aligned} W_i^t = {F_1}(X_i^{t - 1},\omega ) = \left\{ \begin{array}{l} M(X_i^{t - 1}),\mathrm{{ }}{r_\mathrm{{1}}} < \omega \\ X_i^{t - 1},\mathrm{{ \qquad otherwise}} \end{array} \right. \end{aligned}$$
(6)

where \(\omega \) is the probability of mutation operation, and \(r_1\) is a random number in [0,1].

Fig. 4.
figure 4

Mutation operator of SLPSO-XSMT

Full size image

The proposed algorithm uses two-point mutation. If the generated random number \(r_1<\omega \), the algorithm will randomly replace the PSP choices of any two edges. Otherwise, keep the routing tree unchanged. Figure 4 gives a routing tree with 6 pins. It can be seen that after \(F_1\), the PSP choices of \(m_1\) and \(m_2\) are replaced to Choice 2 and Choice 0, respectively.

Individual Cognition. The SLPSO-XSMT algorithm uses \(F_2\) to complete the individual cognition of particles, which is expressed as follows:

$$\begin{aligned} S_i^t = {F_2}(W_i^t,{c_1}) = \left\{ \begin{array}{l} {C_p}(W_i^t),\mathrm{{ }}{r_\mathrm{{2}}} < {c_1}\\ W_i^t,\mathrm{{ \qquad otherwise}} \end{array} \right. \end{aligned}$$
(7)

where \(c_1\) represents the probability that the particle crosses with its personal historical optimum (\(X_i^P\)), and \(r_2\) is a random number in [0, 1).

Social Cognition. The SLPSO-XSMT algorithm uses \(F_3\) to complete the social cognition of particles, which is expressed as follows:

$$\begin{aligned} X_i^t = {F_3}(S_i^t,{c_2}) = \left\{ \begin{array}{l} {C_p}(S_i^t),\mathrm{{ }}{r_3} < {c_2}\\ S_i^t,\mathrm{{\qquad otherwise}} \end{array} \right. \end{aligned}$$
(8)

where \(c_2\) represents the probability that the particle crosses with the historical optimum of any particle \(X_k^P\) in the example pool, and \(r_3\) is a random number in [0, 1).

Fig. 5.
figure 5

Crossover operator of SLPSO-XSMT

Full size image

Figure 5 shows the crossover operation in individual cognition and social cognition of a particle. \(X_i\) is the particle to be crossed, and its learning object is \(X_i^P\) or \(X_k^P\). The proposed algorithm firstly selects a continuous interval of the encoding, like the corresponding edges to be crossed \(e_1\), \(e_2\), and \(e_3\). Then, replace the encoding on this interval of particle \(X_i\) with the encoding string of its learning object. After the crossover operation, the PSP choices of edges \(e_1\), \(e_2\), and \(e_3\) in \(X_i\) are respectively changed from Choice 2, Choice 3, and Choice 3 to Choice 1, Choice 0, and Choice 3, while the topology of the remaining edges remains unchanged.

Repeated iterative learning can gradually make particle \(X_i\) move closer to the global optimal position. Moreover, the acceleration coefficient \(c_1\) is set to decrease linearly and \(c_2\) is set to increase linearly, so that the algorithm has a higher probability to learn its own historical experience in the early iteration to enhance global search ability. While it has a higher probability to learn outstanding particles in the later iteration to enhance exploitation ability, so as to quickly converge to a position close to the global optimum.

4.4 Overall Procedure

Property 1

The proposed SLPSO-XSMT algorithm with example pool learning mechanism has a good balance between global exploration and local exploitation ability so as to effectively solve the XSMT problem.

The steps for SLPSO-XSMT can be summarized as follows.

  • Step 1. Initialize the population and PSO parameters, where the minimum spanning tree method is utilized to construct initial routing tree.

  • Step 2. Calculate the fitness value of each particle according to Eq. (4), and sort them in ascending order: \(S\,\mathrm{{ = }}\,\{ {X_1},...,{X_{i - 1}},{X_i},{X_{i + 1}},...,{X_M}\} \).

  • Step 3. Initialize pbest of each particle and its learning example pool \(EP=\{ X_1,...,X_{i - 1}\}\), and initialize gbest.

  • Step 4. Update the velocity and position of each particle according to Eqs. (5)–(8).

  • Step 5. Calculate the fitness value of each particle.

  • Step 6. Update pbest of each particle and its example pool EP, as well as gbest.

  • Step 7. If the termination condition is met (the set maximum number of iterations is reached), end the algorithm. Otherwise, return to step 4.

4.5 Complexity Analysis

Lemma 1

Assuming the population size is M, the number of iterations is T, the number of pins is n, and then the complexity of SLPSO-XSMT algorithm is \(O(MT \cdot n{\log _2}n)\).

Proof

The time complexity of mutation and crossover operations are both linear time O(n). As for the calculation of fitness value, its complexity is mainly determined by the complexity of the sorting method \(O(n{\log _2}n)\). Since the example pool of each particle would change at the end of each iteration, the time for updating example pool is mainly spent on sorting, that is, its time complexity is also \(O(n{\log _2}n)\). Therefore, the complexity of the internal loop of the SLPSO-XSMT algorithm is \(O(n{\log _2}n)\). At the same time, the complexity of the external loop of the algorithm is mainly related to the size of the population and the number of iterations. Therefore, the complexity of proposed SLPSO-XSMT algorithm is \(O(MT \cdot n{\log _2}n)\).

5 Experiment Results

In order to verify the performance and effectiveness of the proposed algorithm in this paper, experiments are performed on the benchmark circuit suite [15]. The parameter settings in this paper are consistent with [8]. Considering the randomness of the PSO algorithm, the mean values in all experiments are obtained by independent run 20 times.

5.1 Validation of Social Learning Mechanism

In order to verify the effectiveness of proposed social learning mechanism based on example pool, this section applies PSO [8] and the proposed SLPSO method to seek the solution of XSMT, in which the social cognition of PSO is achieved through crossing with the global optimal solution (gbest). The experiments compare the wirelength optimization capabilities and stability of the two methods, as shown in Table 2. In all test cases, the SLPSO method can achieve shorter wirelength and lower standard deviation than the PSO method. On the three evaluation indicators (best wirelength, mean wirelength and standard deviation), the SLPSO method can achieve optimization rates of 0.171%, 0.289%, and 35.881%, respectively. The experimental data show that SLPSO method has better exploration and exploitation capability than PSO method.

Table 2. Comparison between PSO and the proposed SLPSO method
Full size table

5.2 Validation of SLPSO-Based XSMT Construction Algorithm

In order to verify the good performance of proposed SLPSO-XSMT algorithm, this section gives a comparison between SLPSO-XSMT and two SMT algorithms which are traditional RSMT (R) [9] and DDE-based XSMT (DDE) [16] algorithms. As shown in Table 3, ours performs well in wirelength optimization, and can reduce the average wirelength by 8.76% and 1.81%, respectively. It can be found from the comparison with DDE-based XSMT algorithm that our algorithm is more conducive to the construction of large-scale Steiner trees.

Additionally, SLPSO-XSMT algorithm has an overwhelming advantage in stability. It can be seen that ours is far superior to the two algorithms and can greatly reduce the standard deviation of the algorithm. Among them, the DDE-based algorithm has the worst stability, and ours can reduce the standard deviation by 97.39% on average.

Table 3. Comparison between SLPSO-XSMT and other SMT algorithms
Full size table

6 Conclusion

Aiming at the XSMT construction problem in VLSI routing, this paper proposes the SLPSO-based XSMT algorithm with the goal of optimizing the total wirelength. The algorithm adopts a novel social learning mechanism based on the example pool, so that particles can learn from different and better particles in each iteration, which expands searching range and helps to break through local extremes. At the same time, mutation and crossover operators are integrated into the update formula of particles to better solve the discrete XSMT problem.

The experimental results show that the proposed SLPSO-XSMT algorithm has obvious advantages in reducing wirelength and enhancing the stability of the algorithm, especially for large-scale Steiner trees. In future work, we will continue to improve this high-performance SLPSO to better solve various problems in the field of VLSI routing.