Hyperbolic Embeddings for Hierarchical Multi-label Classification

Abstract

Hierarchical multi-label classification (HMC) is a practically relevant machine learning task with applications ranging from text categorization, image annotation and up to functional genomics. State of the art results for HMC are obtained with ensembles of predictive models, especially ensembles of predictive clustering trees. Predictive clustering trees (PCTs) generalize decision trees towards HMC and can be combined into ensembles using techniques such as bagging and random forests. There are two major issues that influence the performance of HMC methods: (1) the computational bottleneck imposed by the size of the label hierarchy that can easily reach tens of thousands of labels, and (2) the sparsity of annotations in the label/output space. To address these limitations, we propose an approach that combines graph node embeddings and a specific property of PCTs (descriptive, clustering and target attributes can be specified arbitrarily). We adapt Poincaré hyperbolic node embeddings to obtain low dimensional label set embeddings, which are then used to guide PCT construction instead of the original label space. This greatly reduces the time needed to construct a tree due to the difference in dimensionality. The input and output space remain the same: the tests in the tree use original attributes, and in the leaves the original labels are predicted directly. We empirically evaluate the proposed approach on 9 datasets. The results show that our approach dramatically reduces the computational cost of learning and can lead to improved predictive performance.

1 Introduction

In the typical supervised learning setting the goal is to predict the value of a single target variable. The tasks differ by the type of the target variable: binary classification deals with predicting a discrete variable with two possible values, multi-class classification deals with predicting a discrete variable with several possible values and regression deals with predicting a continuous variable. In many real life problems of predictive modelling the target variable is structured. Examples can be labelled with multiple labels simultaneously and some dependencies (e.g., tree-shaped or directed acyclic graph hierarchy) among labels may exist. The former task is called multi-label classification (MLC), while the latter is called hierarchical multi-label classification (HMC). These types of problems occur in domains such as life sciences (finding the most important genes for a given disease, predicting toxicity of molecules, etc.), ecology (analysis of remotely sensed data, habitat modelling), multimedia (annotation and retrieval of images and videos) and the semantic web (categorization and analysis of text and web pages). The most prominent area in a need of efficient HMC models with premium predictive performance is gene function prediction, where the goal is to predict the functions of a given gene. Gene Ontology [3] organizes 45.000 gene functions into a directed acyclic graph. Hence, the task of gene function prediction can be naturally viewed as a task of HMC.

A significant amount of research effort has been dedicated to developing methods for predicting structured outputs. In this sense, the methods for MLC [5] are the most prominent. The methods that consider hierarchical dependencies among the labels during model learning are less abundant. In two overviews of the HMC task [9, 13], several methods are analyzed based on the amount of information they exploit from the hierarchy of labels during the learning of the models. The main conclusion is that global models (predicting the complete structure as a whole) generally have better predictive performance than the local models (predicting components of the output and then combining them). The success of the HMC methods is limited by two major factors: computational cost and sparsity of the output space. The number of labels (as well as the number of examples and features) for many domains presents a major computational bottleneck for all of the HMC methods and various methods cope differently with this. The sparsity of the output space pertains to the fact that the number of labels per example as well as the number of examples per label is very small.

We propose to address the two performance limiting issues by embedding the large hierarchical label space to a smaller space. Learning embeddings of complex data such as text, images, graphs and multi-relational data is currently a highly researched topic in artificial intelligence. Related to HMC are the embeddings of graph nodes (e.g., Poincaré embeddings [10], latent space embeddings [7], NODE2VEC [4]), as well as the embeddings for multi-relational data for information extraction and completion of knowledge graphs (e.g., RESCAL, TRANSE, Universal Schema). We exploit the learned embeddings within the learning of predictive clustering trees (PCTs) – a generalization of decision trees. They support different heuristic functions that guide the tree construction, and different prototype functions that make predictions in the leaves. With different choices of heuristic and prototype functions, they have been used for structured output predictions tasks [8], including HMC [14]. Additionally, PCTs yield state of the art predictive performance for the HMC task [2, 6, 11] and have been extensively used for gene function prediction [11, 12].

The main contributions of this paper are as follows. First, we learn new embeddings for HMC by adapting the Poincaré node embeddings to get low dimensional embeddings of label sets assigned to individual examples. Second, we extend PCTs so that the heuristic function guiding the tree construction only looks at the embeddings and ignores the original high dimensional label space. This significantly reduces the time needed to construct the trees. The prototype function in the leaves is the same as for standard PCTs when used for HMC and predicts the original labels directly. A mapping from embeddings back to labels or decoding of the embeddings is not needed. Third, we empirically evaluate our approach on 9 datasets for gene function prediction. The evaluation reveals that it drastically reduces the computational cost compared to standard PCTs and, given equal time budget, yields models with superior predictive performance.

The remainder of this paper is organized as follows. In Sect. 2, we present our approach and theoretically analyze the reduction in computational cost it offers. Next, we outline the experimental design used to evaluate the performance of the obtained predictive models and discuss the obtained results in Sect. 3. Finally, we conclude and provide directions for further work in Sect. 4.

2 Method Description and Analysis

In this section, we briefly describe the calculation of the HMC embeddings by using the Poincaré hyperbolic node embeddings. We then describe PCTs and their extension so they use the label set embeddings to guide the tree construction.

2.1 Hyperbolic Embedding of Label Sets

A recently proposed approach based on the Poincaré ball model of hyperbolic space was shown to be very successful at embedding hierarchical data into low dimensions [10]. The points in the d-dimensional Poincaré ball correspond to the open d-dimensional unit ball $\mathbb {B}^d = \{x \in \mathbb {R}^d ; \; \Vert x \Vert < 1\}$, and the distance between them is given as

$$d(x,y) = \text {arcosh}\left( 1+2\frac{\Vert x - y \Vert ^2}{(1-\Vert x \Vert ^2)(1 - \Vert y \Vert ^2)}\right) .$$

This means that points close to the center have a relatively small distance to all other points in the ball, whereas the distances between points close to the border (as the denominator approaches 0) is much greater compared to its Euclidean counterpart). This property makes the space well suited for representing hierarchical data, as the norm of the embedding vector can naturally represent the depth of the node in the hierarchy. For example, the root of a tree hierarchy is an ancestor to all other nodes, and as such can be placed near the center, where the distance to all other points is relatively small. On the other hand, leaves of the tree can be placed close to the boundary.

In the HMC task, labels are organized in a hierarchy, which can consist of thousands of nodes. First, we embed the hierarchy into the Poincaré ball, following the proposed method for embedding taxonomies [10]. This way we obtain vectors representing individual labels in the hierarchy. However, each example in a HMC dataset is associated with a set of labels. To get a vector representing the set of labels assigned to an example, we aggregate the vectors representing the individual labels. For the aggregation we have multiple options, for example calculating the component-wise mean vector or the medoid vector.

2.2 Predictive Clustering Trees

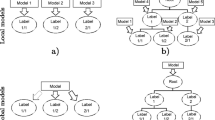
Predictive clustering trees (PCTs) are a generalization of decision trees towards predicting structured outputs including hierarchies of labels. In this work, we exploit a unique property of PCTs that allows arbitrary use of the various attributes. Specifically, for the learning of tree models there are three attribute types: descriptive, clustering and target (as illustrated in Fig. 1). The descriptive attributes are used to divide the space of examples; these are the variables encountered in the test nodes. The clustering attributes are used to guide the heuristic search of the best split at a given node. The target attributes are the ones we predict in the leaves.

Fig. 1.

An overview of our approach. We first calculate the embedding of label sets and add this information to our data. The embeddings are used for the clustering space, which guides the PCT construction, while the input and target space remain the same.

PCTs are induced with a top-down induction of decision trees algorithm. outlined in Algorithm 1 that takes as input a set of examples and indices of descriptive, clustering and target attributes (can overlap). It goes through all descriptive attributes and searches for a test that maximizes the heuristic score. The heuristic that is used to evaluate the tests is the reduction of impurity caused by splitting the data according to a test. It is calculated on the clustering attributes. If no acceptable test is found (e.g., no test reduces the variance significantly, or the number of examples in a node is below a user-specified threshold), then the algorithm creates a leaf and computes the prototype of the target attributes of the instances that were sorted to the leaf. The selection of the impurity and prototype functions depends on the types of clustering and target attributes (e.g., variance and mean for regression, entropy and majority class for classification). The support of multiple target and clustering attributes allows PCTs to be used for structured target prediction [8].

In existing uses of PCTs, clustering attributes include target attributes, i.e., the splits minimize the impurity of the target attributes. In this work, we take the attribute differentiation a step further and decouple the clustering and target attributes completely. We propose to use the learned embeddings as clustering attributes to guide the model learning and keep the original label vectors as the target attributes. This reduces the dimensionality and sparsity of the clustering space, which makes split evaluation and therefore tree construction faster. Additionally, we do not need to convert the embeddings to the original label space, since the predictions are already calculated in the label space.

We calculate the prototype in each leaf node as the mean of the label vectors (target variables) of the examples belonging to that leaf [14]. The prototype vectors present label probabilities in the corresponding leaves. The variance function is the same as for learning PCTs for multi-target regression (embeddings are continuous vectors), i.e., the weighted mean of variances of clustering attributes.

Like standard decision trees, the predictive performance of PCTs is typically much improved when used in an ensemble setting. Bagging is an ensemble method that constructs base classifiers by making bootstrap replicates of the training set and using each of these replicates to construct a predictive model. Bagging can give substantial gains in predictive performance when applied to an unstable learner, such as tree learners [1]. It reduces the variance component of the generalization error linearly with the number of ensemble members. This means that there is a limit to how much ensembles can improve the performance (the bias component of the error). At a point the ensemble is saturated, and adding additional trees no longer makes a notable difference [8].

The computational cost of learning a PCT is $\mathcal {O}(DN \log ^2 N)+\mathcal {O}(CDN \log N)$, where N is the number of examples, D is the number of descriptive attributes and C is the number of clustering attributes [8]. For standard PCTs, C is the number of labels in the hierarchy (L), which in hierarchical classification is typically much greater than $\log N$, making the second term the main contributor.

In our approach, C is instead the dimensionality of the embeddings (E), which can be only a fraction of the number of labels. We must also take into account the time needed to calculate the embeddings. They are optimized with stochastic gradient descent with time complexity $\mathcal {O}(EL)$ [10].

Therefore, we have reduced the time complexity from $\mathcal {O}(LDN \log N)$ using the standard approach, to $\mathcal {O}(EDN \log N) + \mathcal {O}(EL)$ using our approach. For larger datasets with thousands of examples and/or labels in the hierarchy, using our approach with low dimensional embeddings will offer significant speed gains.

3 Evaluation and Discussion

3.1 Experimental Design

For the evaluation of our approach we use 9 benchmark HMC datasets [14], in which examples are yeast genes. In different datasets, different features are used to describe the genes. The goal is to predict gene functions as represented by gene ontology terms. Basic properties of the datasets can be found in Table 1.

Table 1. Properties of the datasets used for the evaluation. The columns show the name of the dataset, the number of examples, the number of attributes describing the examples, and the number of labels in the target hierarchy.

We optimize the embeddings using a variant of stochastic gradient descent as recommended in [10]. The only difference is that we do not use the burn-in period, as it did not affect our results. We ran the optimization for 100 epochs with batch size 100, which took approximately 10–20 s per dataset using a single Nvidia Titan V graphics card.

In our first set of experiments, we aim to determine the best hyperparameters of our approach: the dimensionality of the embedding vectors and the aggregation function used to combine the embedding vectors of all the labels of an example. Embedding into higher dimensional space makes it easier for the optimization algorithm to find good embeddings, but increases the time required to learn them and learn PCTs on them. We consider dimensionalities from the set $\{2, 5, 10, 25, 50, 100\}$. We also consider three aggregation functions. The simplest one is to calculate the component-wise mean. The other approach is to select the medoid, i.e. the label embedding that is closest to all other label embeddings. Here, we examine both the Euclidean distance and the Poincaré distance as distance between the vectors. Note that the distances discussed here are only used to calculate the medoid of label embeddings. The embeddings themselves are always calculated and optimized in the hyperbolic space. We compare the performance of our approach to two methods: 1) the standard bagging of PCTs and 2) bagging of random PCTs, where at each step a random test to split the data is selected. Bagging of standard PCTs offer state of the art predictive performance for HMC tasks: It is what we would like to achieve or even exceed with our approach, but to learn the trees much faster. For this set of experiments, all ensembles consisted of 50 trees. We used 7 datasets, all but the largest two (hom and struc).

Fig. 2.

Performance achieved using different aggregations of label embeddings. For brevity, only three datasets are shown; the results on the other datasets are very similar.

In the second set of experiments, we compare our approach to standard PCTs in a time budgeted manner. We add trees to an ensemble and record the performance and time needed after every couple of trees added. The ensemble is built for one hour or until 250 trees are built (at that point the performance gains are negligible). This evaluation compares our approach to ensembles of standard PCTs given equal time budget. We use the hyperparameters that worked well in the first set of experiments. For all experiments, we use area under the average precision-recall curve ($AU\overline{PRC}$) [14] to measure the predictive performance. Higher values indicate better performance. To estimate $AU\overline{PRC}$ we use 10-fold cross validation and report mean and standard deviation over folds. The entire experimental pipeline required to reproduce our experiments is available online at http://kt.ijs.si/dragikocev/ISMIS2020/ISMIS2020code.zip.

3.2 Results and Discussion

Fig. 3.

The comparison of learning time (seconds) and performance of ensembles of standard PCTs, ensembles of random PCTs, and ensembles of PCTs learned on the embeddings. Vertical lines show standard deviation over folds.

Figure 2 compares the results using different aggregation functions in the first set of experiments. Both Euclidean and Poincaré distances seem to work equally well for calculating the medoid embedding, in terms of the predictive performance achieved. However, mean aggregation typically offered better performance. Given that mean is also faster to calculate than medoid, especially when examples have many labels, we decided to proceed using mean aggregation.

Figure 3 shows the results obtained with mean aggregation and different embedding dimensionalities. Additionally, it shows the performance of ensembles of standard PCTs and ensembles of random PCTs. First thing to note is that our approach noticeably outperformed ensembles of random PCTs on all datasets. This means that the label set embeddings contain useful information about the label hierarchy. We can also see that with enough dimensions, our approach achieves performance that is on par with or exceeds the performance of standard PCTs. Increasing the dimensionality of the embeddings usually improves the performance of the ensemble, but increases the time needed to learn the trees. However, the performance seems to saturate rather quickly, and using more than 25 dimensions rarely results in significant improvement. Most importantly, our approach achieves the performance similar to that of ensembles of standard PCTs in barely a fraction of the time needed to construct them.

Considering the results in Fig. 3, we decided to use the 25-dimensional embeddings for the time-budgeted experiments. The performance improvements with higher dimensions were usually small, whereas the time complexity scales linearly. Figure 4 shows the results of the second set of experiments. On the struc dataset, our approach learned 250 trees well before the hour expired, and on the hom dataset, it learned  225 trees. With the standard approach, we managed to learn only  50 and  20 trees on these datasets, respectively. As discussed in Sect. 2.2, given a high enough time budget, the difference in the number of trees would not make much difference as both ensembles would be saturated. However, the results clearly show that our approach achieves significantly better results much faster. This is especially important when working with large datasets.

Fig. 4.

The relationship between the performance and time (seconds) needed to build the ensemble. With the same time budget, our approach significantly outperforms ensembles of standard PCTs.

4 Conclusions

In this paper, we propose a new approach for solving the HMC task that combines Poincaré hyperbolic node embeddings and PCTs. We aggregate the embeddings of all the labels assigned to an example to obtain low dimensional label set embeddings. We then exploit the property of PCTs that allows us to use the label set embeddings to guide the tree construction, but still predict the original labels directly. Due to the difference in dimensionality between the embeddings and standard vector representations of label sets, our approach constructs PCTs much faster. Because we still predict the original labels directly, we do not need a mapping from the embeddings back to the labels.

We empirically evaluate our approach on 9 benchmark datasets for gene function prediction. First, we compare the aggregation functions used to combine the label-wise embeddings and show that aggregation with mean works better than the medoid aggregation. Second, we show that the models learned with our approach are much more efficient: the learning time is 5 or more folds faster than learning in the original space. In some cases they even achieve better predictive performance. Third, in time budgeted experiments we show that our approach achieves premium predictive performance much sooner than standard ensembles of PCTs. In applications with limited computational resources, it is clear that the models learned on the embeddings should be preferred.

We plan to extend the work along several dimensions. First, we will look into other node embeddings to compare them to the Poincaré variant. Next, we plan to investigate the effect of different optimization criteria on the performance. For example, we could try optimizing embeddings so that the distance between them is similar to the distance between the labels in the graph. Finally, we will investigate the influence of the embeddings on a wider set of domains.