Keywords

1 Introduction

Most conflict-driven processes in real life evolve continuously in time, and their participants continuously receive updated information and adapt accordingly. The principal models considered in classical differential game theory are associated with problems defined for a fixed time interval (players have all the information for a closed time interval) [10], problems defined for an infinite time interval with discounting (players have all information specified for an infinite time interval) [1], problems defined for a random time interval (players have information for a given time interval, but the duration of this interval is a random variable) [27]. One of the first works in the theory of differential games was devoted to a differential pursuit game (a player’s payoff depends on when the opponent gets captured) [23]. In all the above models and approaches it is assumed that at the onset players process all information about the game dynamics (equations of motion) and about players’ preferences (cost functions). However, these approaches do not take into account the fact that many real-life conflict-controlled processes are characterized by the fact that players at the initial time instant do not have all the information about the game. Therefore such classical approaches for defining optimal strategies as the Nash equilibrium, the Hamilton-Jacobi-Bellman equation [2], or the Pontryagin maximum principle [24], for example, cannot be directly used to construct a large range of real game-theoretic models. Another interesting application of dynamic and differential games is for networks, [5].

Most real conflict-driven processes continuously evolve over time, and their participants constantly adapt. This paper presents the approach of constructing a Nash equilibrium for game models with continuous updating using a modernized version of Pontryagin’s maximum principle. In game models with continuous updating, it is assumed that

  1. 1.

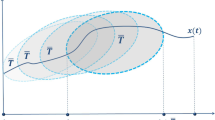
    at each current time \(t\in [t_0, +\infty )\), players only have or use information on the interval \([t, t+\overline{T}]\), where \(0<\overline{T}<\infty \) is the length of the information horizon,

  2. 2.

    as time \(t\in [t_0, +\infty )\) goes by, information related to the game continues to update and players can receive this updated information.

In the framework of the dynamic updating approach, the following papers were published [17], [18], [20], [21], [22], [29]. Their authors set the foundations for further study of a class of games with dynamic updating. It is assumed that information about motion equations and payoff functions is updated in discrete time instants and the interval for which players know information is defined by the value of the information horizon. A non-cooperative setting with dynamic updating was examined along with the concept of the Nash equilibrium with dynamic updating. Also in the papers above cooperative cases of game models with dynamic updating were considered and the Shapely value for this setting was constructed. However, the class of games with continuous updating provides new theoretical results. The class of differential games with continuous updating was considered in the papers [11], [19], here it is supposed that the updating process evolves continuously in time. In the paper [19], the system of Hamilton-Jacobi-Bellman equations are derived for the Nash equilibrium in a game with continuous updating. In the paper [11] the class of linear-quadratic differential games with continuous updating is considered and the explicit form of the Nash equilibrium is obtained.

The approach of continuous updating has some similarities with Model Predictive Control (MPC) theory which is worked out within the framework of numerical optimal control [6], [14], [26], [28], and which has also been used as a human behavior model in [25]. In the MPC approach, the current control action is achieved by solving a finite-horizon open-loop optimal control problem at each sampling instant. For linear systems there exists a solution in explicit form [3, 7]. However, in general, the MPC approach demands the solution of several optimization problems. Another related series of papers corresponds to the class of stabilizing control [12, 13, 16], here similar approaches were considered for the class of linear quadratic optimal control problems. But in the current paper and in papers about the continuous updating approach, the main goal is different: to model players’ behavior when information about the course of the game updates continuously in time.

In this paper the optimality conditions for the Nash equilibrium in the form of Pontryagin’s maximum principle are derived for a class of non-cooperative game models with continuous updating. In the previous papers on this topic, [11, 19] the optimality conditions were formulated in the form of the Hamilton-Jacobi-Bellman equation and for the special case of a linear quadratic model. From the authors’ point of view, formulating Pontryagin’s maximum principle for the continuous updating case is the final step for the Nash equilibrium’s range of optimality conditions under continuous updating. In future the authors will focus on convex differential games with continuous updating and on the uniqueness of the Nash equilibrium with continuous updating. The concept of the Nash equilibrium for the class of games with continuous updating is defined in the paper [19], and constructed here using open-loop controls and the Pontryagin maximum principle with continuous updating. The corresponding trajectory is also derived. The approach here presented is tested with the advertising game model consisting of two firms. It is interesting to note that in this particular game model the equilibrium strategies are constant functions of time t, unlike the equilibrium strategies in the initial game model.

The paper is organized as follows. Section 2 starts by describing the initial differential game model. Section 3 demonstrates the game model with continuous updating and also defines a strategy for it. In Sect. 4, the classical optimality principle Nash equilibrium is adapted for the class of games with continuous updating. In Sect. 5, a new type of Pontryagin’s maximum principle for a class of games with continuous updating is presented. Section 6 presents results of the proposed modeling approach based on continuous updating, such as a logarithmic advertising game model. Finally, we draw conclusions in Sect. 7.

2 Initial Game Model

Consider differential n-player game with prescribed duration \(\varGamma (x_0, T - t_0)\) defined on the interval \([t_0, T]\).

The state variable evolves according to the dynamics:

$$\begin{aligned} \begin{array}{l} \dot{x}(t)=f(t,x,u), \quad x(t_0)=x_0, \end{array}\end{aligned}$$
(1)

where \(x\in \mathbb {R}^l\) denotes the state variables of the game, \( u=(u_1, \ldots , u_n)\), \(u_i=u_i(t,x_0) \in U_i \subset \text {comp} \mathbb {R}^k, \ t\in [t_0,T]\), is the control of player i.

The payoff of player i is then defined as

$$\begin{aligned} K_i(x_0, T - t_0; u) = \int \limits _{t_0}^{T}g^i[t, x(t),u(t,x_0)]dt, \ i \in N, \end{aligned}$$
(2)

where \(g^i[t, x,u]\), f(t, x, u) are the integrable functions, x(t) is the solution of Cauchy problem (1) with fixed \(u(t,x_0)=(u_1(t,x_0),\ldots ,\) \(u_n(t,x_0))\). The strategy profile \(u(t,x_0)=(u_1(t,x_0),\ldots ,\) \(u_n(t,x_0))\) is called admissible if the problem (1) has a unique and continuable solution. The existence and global asymptotic stability of the open-loop equilibrium for a game with strictly convex adjustment costs was dealt with by Fershtman and Muller [4].

Using the initial differential game with prescribed duration of T, we construct the corresponding differential game with continuous updating.

3 Differential Game Model with Continuous Updating

In differential games with continuous updating players do not have information about the motion equations and payoff functions for the whole period of the game. Instead at each moment t players get information at the interval \([t,t+\overline{T}]\), where \(0< \overline{T} < +\infty \). When choosing a strategy at moment t, this is the only information they can use. Therefore, we consider subgames \(\varGamma (x, t, t+\overline{T})\) in which players find themselves at each moment t.

Let us start with the subgame \(\varGamma (x_0, t_0, t_0+\overline{T})\) defined on the interval \([t_0, t_0 + \overline{T}]\). The initial conditions in this subgame coincide with the starting point of the initial game.

Furthermore, assume that the evolution of the state can be described by the ordinary differential equation:

$$\begin{aligned} \begin{array}{l} \dot{x}^{t_0}(s)=f(s,x^{t_0},u^{t_0}), \quad x^{t_0}(t_0) = x_0, \end{array}\end{aligned}$$
(3)

where \(x^{t_0} \in \mathbb {R}^l\) denotes the state variables of the game that starts from the initial time \(t_0\), \(u^{t_0} = (u^{t_0}_1, \ldots , u^{t_0}_n), \ u_i^{t_0}=u_i^{t_0}(s,x_0) \in U_i \subset \text {comp} \mathbb {R}^k\) is the vector of actions chosen by the player i at the instant time s.

The payoff function of player i is defined in the following way:

$$\begin{aligned} K^{t_0}_i(x_0, t_0, \overline{T}; u^{t_0}) = \int \limits _{t_0}^{t_0 + \overline{T}} g^i[s, x^{t_0}(s),u^{t_0}(s,x_0)]ds, \ i \in N, \end{aligned}$$
(4)

where \(x^{t_0}(s)\), \(u^{t_0}(s,x_0)\) are trajectory and strategies in the game \(\varGamma (x_0, t_0,t_0+ \overline{T})\), \(\dot{x}^{t_0}(s)\) is the derivative of s.

Now let us give a description of subgame \(\varGamma (x, t, t+\overline{T})\) starting at an arbitrary time \(t>t_0\) from the situation x.

The motion equation for the subgame \(\varGamma (x, t, t+\overline{T})\) has the form:

$$\begin{aligned} \begin{array}{l} \dot{x}^t(s) = f(s,x^t,u^t), \quad x^t(t)=x, \\ \end{array}\end{aligned}$$
(5)

where \(\dot{x}^{t}(s)\) is the derivative of s, \(x^t \in \mathbb {R}^l\) is the state variables of the subgame that starts from time t, \(u^t=(u^t_1, \ldots , u^t_n), \ u_i^t=u_i^t(s,x) \in U_i \subset \text {comp} \mathbb {R}^k, \ s \in [t, t + \overline{T}]\), denotes the control vector of the subgame that starts from time t at the current time s.

The payoff function of player i for the subgame \(\varGamma (x, t, t+\overline{T})\) has the form:

$$\begin{aligned} K^t_i(x, t,\overline{T} ; u^t) = \int \limits _{t}^{t + \overline{T}}g^i[s, x^t(s),u^t(s,x)]ds, \ i \in N, \end{aligned}$$
(6)

where \(x^{t}(s)\), \(u^{t}(s,x)\) are the trajectories and strategies in the game \(\varGamma (x, t, t+\overline{T})\).

A differential game with continuous updating is developed according to the following rule:

Current time \(t \in [t_0, +\infty )\) evolves continuously and as a result players continuously obtain new information about motion equations and payoff functions in the game \(\varGamma (x, t, t+\overline{T})\).

The strategy profile u(t, x) in a differential game with continuous updating has the form:

$$\begin{aligned} u(t,x) = u^t(s,x)|_{s = t}, \ t \in [t_0, +\infty ), \end{aligned}$$
(7)

where \(u^t(s,x)\), \(s \in [t, t + \overline{T}]\) are strategies in the subgame \(\varGamma (x, t, t+\overline{T})\).

The trajectory x(t) in a differential game with continuous updating is determined in accordance with

$$\begin{aligned} \begin{array}{l} \dot{x}(t) = f(t,x,u), \\ x(t_0)=x_0, \\ x \in \mathbb {R}^l, \end{array} \end{aligned}$$
(8)

where \(u = u(t,x)\) are strategies in the game with continuous updating (7) and \(\dot{x}(t)\) is the derivative of t. We suppose that the strategy with continuous updating obtained using (7) is admissible, or that the problem (8) has a unique and continuable solution. The conditions of existence, uniqueness and continuability of open-loop Nash equilibrium for differential games with continuous updating are presented as follows, for every \(t\in [t_0, +\infty )\)

  1. 1.

    right-hand side of motion equations \(f(s,x^t,u^{t})\) (5) is continuous on the set \([t,t+\overline{T}] \times X^t \times U_1^{t} \times \cdots \times U_n^{t}\)

  2. 2.

    right-hand side of motion equations \(f(s,x^t,u^{t})\) satisfies the Lipschitz conditions for \(x^t\) with the constant \(k_1^{t} > 0\) uniformly regarding to \(u^t\):

    $$\begin{aligned} \begin{aligned}&|| f(s,(x^t)',u^{t}) - f(s,(x^t)'',u^{t}) || \le k_1^{t} || (x^t)' - (x^t)'' ||, \ \forall \ s \in [t,t+\overline{T}], \\&(x^t)', (x^t)'' \in X^t, u^{t} \in U^{t} \end{aligned} \end{aligned}$$
  3. 3.

    exists such a constant \(k_2^{t}\) that function \(f(s,x^t,u^{t})\) satisfies the condition:

    $$\begin{aligned} || f(s,x^t,u^{t}) || \le k_2^{t} (1 + || x||), \ \forall \ s \in [t,t+\overline{T}], \ x^t \in X^t, u^{t} \in U^{t} \end{aligned}$$
  4. 4.

    for any \(s \in [t,t+\overline{T}]\) and \(x_t \in X_t\) set

    $$\begin{aligned} G(x^t) = \{ f(s,x^t,u^{t})| u^{t} \in U^{t} \} \end{aligned}$$

    is a convex compact from \(R^l\).

The essential difference between the game model with continuous updating and a classic differential game with prescribed duration \(\varGamma (x_0, T - t_0)\) is that players in the initial game are guided by the payoffs that they will eventually obtain on the interval \([t_0, T]\), but in the case of a game with continuous updating, at the time instant t they orient themselves on the expected payoffs (6), which are calculated based on the information defined for interval \([t, t + \overline{T}]\) or the information that they have at the instant t.

4 Nash Equilibrium in a Game with Continuous Updating

In the framework of continuously updated information, it is important to model players’ behavior. To do this, we use the Nash equilibrium concept in open-loop strategies. However, for the class of differential games with continuous updating, modeling will take the following form:

For any fixed \(t\in [t_0,+\infty )\), \(u^{NE}(t,x)=(u_1^{NE}(t,x),...,u_n^{NE}(t,x))\) coincides with the Nash equilibrium in game (5), (6) defined for the interval \([t,t+\overline{T}]\) at instant t.

However, direct application of classical approaches for the definition of the Nash equilibrium in open-loop strategies is not possible, consider two intervals \([t,t+\overline{T}],\)   \([t+\epsilon ,t+\overline{T}+\epsilon ]\),   \(\epsilon<<\overline{T}\). Then according to the problem statement:

–\(u^{NE}(t)\) at instant t coincides with the open-loop Nash equilibrium in the game defined for interval \([t,t+\overline{T}]\),

–\(u^{NE}(t+\epsilon )\) at instant \(t+\epsilon \) coincides with the open-loop Nash equilibrium in the game defined for interval \([t+\epsilon ,t+\overline{T}+\epsilon ]\).

In order to construct such strategies, we consider the concept of generalized Nash equilibrium in open-loop strategies as the principle of optimality

$$\begin{aligned} \widetilde{u}^{NE}(t,s,x)=(\widetilde{u}_1^{NE}(t,s,x),...,\widetilde{u}_n^{NE}(t,s,x)), t\in [t_0,+\infty ),s\in [t,t+\overline{T}], \end{aligned}$$
(9)

which we are going to use further for construction of strategies \(u^{NE}(t,x)\).

Definition 1

Strategy profile \(\widetilde{u}^{NE}(t,s,x)=(\widetilde{u}_1^{NE}(t,s,x),...,\widetilde{u}_n^{NE}(t,s,x))\) is a generalized Nash equilibrium in the game with continuous updating, if for any fixed \(t\in [t_0,+\infty )\), strategy profile \(\widetilde{u}^{NE}(t,s,x)\) is the open-loop Nash equilibrium in game \(\varGamma (x,t,t+\overline{T})\).

Using a generalized open-loop Nash equilibrium, it is possible to define a solution concept for a game model with continuous updating.

Definition 2

Strategy profile \(u^{NE}(t,x)=(u_1^{NE}(t,x),...,u_n^{NE}(t,x))\) is called an open-loop-based Nash equilibrium with continuous updating if it is defined in the following way:

$$\begin{aligned} \begin{aligned} u^{NE}(t,x)=\,&\widetilde{u}^{NE}(t,s,x)|_{s=t}\\ =\,&(\widetilde{u}_1^{NE}(t,s,x)|_{s=t},...,\widetilde{u}_n^{NE}(t,s,x)|_{s=t}), \quad t\in [t_0,+\infty ), \end{aligned} \end{aligned}$$
(10)

where \(\widetilde{u}^{NE}(t,s,x)\) is the generalized open-loop Nash equilibrium defined in Definition 1.

Strategy profile \(u^{NE}(t,x)\) will be used as a solution concept in a game with continuous updating.

5 Pontryagin’s Maximum Principle with Continuous Updating

In order to define strategy profile \(u^{NE}(t,x)\), it is necessary to determine the generalized Nash equilibrium in open-loop strategies \(\widetilde{u}^{NE}(t,s,x)\) of a game with continuous updating. To do this, we will use a modernized version of Pontryagin’s maximum principle. Let us start by defining a real-valued function \(H^t_i\) by

$$\begin{aligned} H^t_i(\tau ,x^t,u^t,\lambda ^t)=\overline{T}g^i(\overline{T}\tau +t,x^t,u^t)+\lambda ^t_i\overline{T} f(\overline{T}\tau +t,x^t,u^t). \end{aligned}$$
(11)

The function \(H^t_i, i\in N\) is called the (current-value) Hamiltonian function and plays a prominent role in Pontryagin’s Maximum Principle. The variable \(\lambda ^t_i\) is called the (current-value) costate variable associated with the state variable \(x^t\), or the (current-value) adjoint variable.

The following theorem is applied:

Theorem 1

Let \(f(s,\cdot ,u^t)\) be continuously differentiable on \(R^l\), \(\forall s \in [t,t+\overline{T}]\) and \(g^i(s,\cdot ,u^t)\) be continuously differentiable on \(R^l\), \(\forall s \in [t,t+\overline{T}]\), \(i\in N\). Then, if \(\widetilde{u}^{NE}(t,s,x)\) provides generalized open-loop Nash equilibrium in a differential game with continuous updating, and for all \(t\in [t_0,+\infty )\) \(\widetilde{x}^t(s),\) with \( s \in [t,t+\overline{T}]\), is the corresponding state trajectory in the game \(\varGamma (x, t, t+\overline{T})\), then for all \(t\in [t_0,+\infty )\) exist n costate functions \(\lambda ^t_i(\tau ,x),\) where \( \tau \in [0,1],\ i\in N\), such that the following relations are satisfied:

  1. 1.

    for all \(\tau \in [0,1]\)

    $$\begin{aligned} H^t_i(\tau ,\widetilde{x}^t,\widetilde{u}^{NE}(t,\tau ,x),\lambda ^t) = \max \limits _{\phi _i}\{H^t_i(\tau ,\widetilde{x}^t,\widetilde{u}_{-i}^{NE}(t,\tau ,x),\lambda ^t)\}, i\in N, \end{aligned}$$
    (12)

    where \(\widetilde{u}_{-i}^{NE}=(\widetilde{u}_1^{NE},...,\phi _i,...,\widetilde{u}_n^{NE}),\)

  2. 2.

    \(\lambda ^t_i(\tau ,x)\) is a decision of the system of adjoint equations

    $$\begin{aligned}&\frac{d\lambda ^t_i(\tau ,x)}{d\tau }=-\frac{\partial H^t_i(\tau ,\widetilde{x}^t(\tau ),\widetilde{u}^{NE}(t,\tau ,x),\lambda ^t)}{\partial x^t}= \nonumber \\&=-\overline{T}\frac{\partial g^i(\overline{T}\tau +t,\widetilde{x}^t,\widetilde{u}^{NE})}{\partial x^t}-\lambda ^t_i(\tau ,x)\overline{T} \frac{\partial f(\overline{T}\tau +t,\widetilde{x}^t,\widetilde{u}^{NE})}{\partial x_t}, \ i\in N, \end{aligned}$$
    (13)

    where the transversality conditions are

    $$\begin{aligned} \lambda ^t_i(1,x)=0, \ i\in N \end{aligned}$$
    (14)
  3. 3.

    for all \(t\in [t_0,+\infty )\)

    $$\begin{aligned} \begin{array}{l} \dot{\widetilde{x}^t}(\tau ) = \overline{T}f(\overline{T}\tau +t,\widetilde{x}^t,\widetilde{u}^{NE}), \quad \widetilde{x}^t(0)=x, \ \tau \in [0,1]. \\ \end{array}\end{aligned}$$
    (15)

Proof: Let fix \(t\ge t_0\) and consider game \(\varGamma (x, t, t+\overline{T})\).

Using following substitution

$$\begin{aligned} \tau =\frac{s-t}{\overline{T}}, \end{aligned}$$
(16)

we get the motion equation (5) in the form:

$$\begin{aligned} \begin{array}{l} \dot{x}^t(\tau ) = \overline{T}f(\overline{T}\tau +t,x^t,u^t), \quad x^t(0)=x, \quad \tau \in [0,1]. \\ \end{array}\end{aligned}$$
(17)

And payoff function of player \(i \in N\) has the form

$$\begin{aligned} K^t_i(x, t,\overline{T} ; u^t) = \int \limits _{0}^{1}\overline{T}g^i[\overline{T}\tau +t, x^t(\tau ),u^t(\tau ,x)]d\tau , \ i \in N. \end{aligned}$$
(18)

For the optimization problem (17)–(18) Hamiltonian has the form

$$\begin{aligned} H^t_i(\tau ,x^t,u^t,\lambda ^t)=\overline{T}g^i(\overline{T}\tau +t,x^t(\tau ),u^t(\tau ,x))+\lambda ^t_i(\tau ,x)\overline{T} f(\overline{T}\tau +t,x^t(\tau ),u^t(\tau ,x)). \end{aligned}$$
(19)

If \(\widetilde{u}^{NE}(t,\tau ,x)\) – generalized open-loop Nash equilibrium in the differential game with continuous updating, then, according to Definition 1, for every fixed \(t\ge t_0\), \(\widetilde{u}^{NE}(t,\tau ,x)\) is an open-loop Nash equilibrium in the game \(\varGamma (x, t,t+ \overline{T})\). Therefore for any fixed \(t\ge t_0\) conditions 1–3 of the theorem are satisfied as necessary conditions for Nash equilibrium in open-loop strategies (see [1]). The Theorem is proved.

It can been mentioned also that if for every \(t\ge t_0\) functions \(H^t_i\) are concave in \((x_t,u_t)\) for all \(i\in N\), then the conditions of the theorem are sufficient for a Nash open-loop solution [15].

6 Differential Game of Logarithmic Advertising Game Model with Continuous Updating

As an illustrative example, we consider a logarithmic excess-advertising model of a duopoly proposed by Jørgensen in [8]. There are two firms operating in a market. It is assumed that market potential is constant over time. The only marketing instrument used by the firms is advertising. Advertising has diminishing returns since it suffers from increasing marginal costs. Nash optimal open-loop advertising strategies are determined in [8]. Here we obtain open-loop Nash equilibrium with continuous updating by means of Theorem 1.

6.1 Initial Game Model

Consider the model investigated in [8]. Let \(x_i(t)\) denote the rate of sales of firm i at the instant time t, (\(i = 1,2\)) and assume that \(x_1+x_2=M\), implying that the market potential is fully exhausted at each instant of time. The game is played on interval [0, T], where T is an arbitrary but fixed positive number. Because of the assumption \(x_1+x_2=M\), so . The state equation is

(20)

where k is a positive constant, \(x_i(0)\) is a given initial rate of sales of firm i. The state equation (20) model describes a market where buyers are perfectly mobile and switch instantaneously to the firm which has the largest rate of advertising expenditure, that is, advertises in excess of the other. In the model, market share increases linearly according to the amount of excess advertising. Performance indices are given by

$$\begin{aligned} K_i=\int _{0}^{T}(\varphi _i x_i-u_i)\exp \{-r_it\}dt,\quad i=1,2, \end{aligned}$$
(21)

where \(x_2=M-x_1\). Assume that \(r_i> 0,\quad i=1,2\). The open-loop Nash equilibrium in its explicit form was constructed in [8]:

$$\begin{aligned} u_i^{initial,NE}=\frac{k\varphi _i}{r_i}[1-exp\{-r_i(T-t)\}]. \end{aligned}$$
(22)

For the case \(r_1=r_2\), the optimal trajectories are given by

$$\begin{aligned} \begin{aligned} x_1(t)&=(k\log \frac{\varphi _1}{\varphi _2})t+x_1(0),\\ x_2(t)&=M-(k\log \frac{\varphi _1}{\varphi _2})t-x_1(0). \end{aligned} \end{aligned}$$
(23)

If \(r_1\not =r_2\), then trajectory \(x_1\) is the solution of

$$\begin{aligned} \dot{x_1}=k\log \frac{\varphi _1 r_2[1-exp\{-r_1(T-t)\}]}{\varphi _2 r_1[1-exp\{-r_2(T-t)\}]}. \end{aligned}$$
(24)

The solution of Eq. (24) is given by

$$x_1(t)=x_1(0)+k\log \frac{\varphi _1 r_2}{\varphi _2 r_1}t+k\int _{0}^{t}\log \frac{1-exp\{-r_1(T-s)\}}{1-exp\{-r_2(T-s)\}}ds.$$

6.2 Game Model with Continuous Updating

Now consider this model as a game with continuous updating. It is assumed that information about motion equations and payoff functions is updated continuously in time. At every instant \(t\in [0,+\infty )\), players have information only at interval \([t,t+\overline{T}]\).

Therefore, for every time instant t, we can get the payoff function of player i for the interval \([t,t+\overline{T}]\). The payoff functions are given as follows:

$$K^t_i=\int _{t}^{t+\overline{T}}(\varphi _i x^t_i-u^t_i)\exp (-r_is)ds,\quad i=1,2.$$

In order to simplify the problem that we desire to solve, we can do a transfer \(\tau =\frac{s-t}{\overline{T}}\). Furthermore, restate the problem to be solved:

(25)

The Hamiltonian functions are given by

$$\begin{aligned} H^t_1(t,\tau ,x,u^t,\lambda ^t)=(\varphi _1 x^t_1-u^t_1)\overline{T}+\lambda ^t_1(\tau ,x)\overline{T}k(\log u^t_1-\log u^t_2),\end{aligned}$$
(26)
$$\begin{aligned} H^t_2(t,\tau ,x,u^t,\lambda ^t)=(\varphi _2 x^t_2-u^t_2)\overline{T}-\lambda ^t_2(\tau ,x)\overline{T}k(\log u^t_1-\log u^t_2). \end{aligned}$$
(27)

Note that the current-value Hamiltonian is simply \(exp(r_i(\overline{T}\tau +t))\) times the conventional Hamiltonian. Necessary conditions for the maximization of \(H^t_i\), for \(u^t_i \in (0,+\infty )\) are given by

$$\frac{\partial H^t_1}{\partial u^t_1}=-\overline{T}+\lambda ^t_1(\tau ,x)\overline{T}k\frac{1}{u^t_1}=0,$$
$$\frac{\partial H^t_2}{\partial u^t_2}=-\overline{T}+\lambda ^t_2(\tau ,x)\overline{T}k\frac{1}{u^t_2}=0.$$

Therefore, the optimal control \(u^t_i\) is given by

$$\begin{aligned} u^t_1(\tau ,x)=\lambda ^t_1(\tau ,x)k, \quad u^t_2(\tau ,x)=\lambda ^t_2(\tau ,x)k. \end{aligned}$$
(28)

The adjoint variables \(\lambda ^t_i(\tau )\) should satisfy the following equations

$$\begin{aligned} \begin{aligned} \dot{\lambda }^t_1(\tau ,x)=-\frac{\partial H^t_1}{\partial x^t_1}+&\overline{T}r_1\lambda ^t_1(\tau ,x)=-\varphi _1 \overline{T}+\overline{T}r_1\lambda ^t_1(\tau ,x),\\ \dot{\lambda }^t_2(\tau ,x)=-\frac{\partial H^t_2}{\partial x^t_2}+&\overline{T}r_2\lambda ^t_2(\tau ,x)=-\varphi _2 \overline{T}+\overline{T}r_2\lambda ^t_2(\tau ,x). \end{aligned} \end{aligned}$$
(29)

Note that these equations are uncoupled. The transversality conditions are

$$\lambda ^t_i(1,x)=0, \quad i=1,2.$$

By solving the above differential equations about the adjoint variables, the solutions are given by

$$\begin{aligned} \begin{aligned} \lambda ^t_1(\tau ,x)&=\frac{\varphi _1}{r_1}[1-exp\{\overline{T}r_1(\tau -1)\}],\\ \lambda ^t_2(\tau ,x)&=\frac{\varphi _2}{r_2}[1-exp\{\overline{T}r_2(\tau -1)\}]. \end{aligned} \end{aligned}$$
(30)

Substituting (30) into (28) yields

$$\begin{aligned} u_i^{tNE}(\tau ,x)=\frac{k\varphi _i}{r_i}[1-exp\{\overline{T}r_i(\tau -1)]\}. \end{aligned}$$
(31)

Note that x is the initial state in the subgame \(\varGamma (x, t,t+ \overline{T})\). The open-loop strategies \(u_i^{tNE}(\tau ,x)\) in our example in fact do not depend on initial state x.

Let us show that the solution obtained satisfies sufficiency conditions. Since\(\frac{\partial ^2 H^t_i}{\partial x^t\partial x^t}=0,\) \(\frac{\partial ^2 H^t_i}{\partial x^t \partial u^t_i}=0,\) \(\frac{\partial ^2 H^t_i}{\partial u^t_i \partial u^t_i}=-\lambda ^t_i(\tau )\overline{T}k\frac{1}{(u^t_i)^2}\le 0 \), then, according to [9], \(u^{tNE}(\tau ,x)\) is indeed a Nash equilibrium in the subgame \(\varGamma (x, t, t+\overline{T})\).

Finally, we convert \(\tau \) to t, s. Then the generalized open-loop Nash equilibrium strategies have the following form:

$$\begin{aligned} \begin{aligned} \widetilde{u}^{NE}_1(t,s,x)&=\frac{k\varphi _1}{r_1}[1-exp\{r_1(s-t-\overline{T})\}],\\ \widetilde{u}^{NE}_2(t,s,x)&=\frac{k\varphi _2}{r_2}[1-exp\{r_2(s-t-\overline{T})\}]. \end{aligned} \end{aligned}$$
(32)

According to Definition 2, we construct an open-loop-based Nash equilibrium with continuous updating :

$$\begin{aligned} u_i^{NE}(t,x)=\widetilde{u}^{NE}_i(t,s,x)|_{s=t}=\frac{k\varphi _i}{r_i}[1-exp\{-r_i\overline{T}\}]\quad i=1,2. \end{aligned}$$
(33)

Note that in the example under consideration, strategies \(u_i^{tNE}\) are independent of the initial values of the state variables of subgame \(\varGamma (x, t, t+\overline{T})\), so strategies \(u_i^{NE}(t,x)\) in fact do not depend on x.

Consider the difference between optimal strategies in the initial game and in a game with continuous updating:

$$u_i^{initial,NE}-u_i^{NE}=\frac{k\varphi _i}{r_i}exp\{-r_i\overline{T}\}[1-exp\{-r_i(T-t-\overline{T})\}]$$

We can see that the amounts of players’ advertising expenditure is less in a game with continuous updating for \(t<T-\overline{T}\).

The optimal trajectories \(x^{NE}_1(t), \ x^{NE}_2(t)\) in a game with continuous updating are the solutions of

$$\begin{aligned} \begin{aligned} \dot{x}_1(t)&=k\log (\frac{\varphi _1r_2}{r_1\varphi _2}\frac{[1-exp\{-r_1\overline{T}\}]}{[1-exp\{-r_2\overline{T}\}]}),\\ \dot{x}_2(t)&=-\dot{x}_1(t),\\ x_1(0)&=x_1^{0},\\ x_2(0)&=x_2^{0}, \end{aligned} \end{aligned}$$
(34)

where \(r_i>0, i=1,2\). Therefore, the state dynamics of the system are given as follows:

$$\begin{aligned} \begin{aligned} x^{NE}_1(t)&=x_1^{0}+k\log (\frac{\varphi _1r_2[1-exp\{-r_1\overline{T}\}]}{r_1\varphi _2[1-exp\{-r_2\overline{T}\}]})t,\\ x_2^{NE}(t)&=M-x_1^{0}-k\log (\frac{\varphi _2r_1[1-exp\{-r_2\overline{T}\}]}{r_2\varphi _1[1-exp\{-r_1\overline{T}\}]})t. \end{aligned} \end{aligned}$$
(35)

It can be noted, that if \(r_1=r_2\), then optimal trajectories in initial model and in the game with continuous updating are the same.

Figures 1, 2 represent a comparison of results obtained in the initial model and in the model with continuous updating for the following parameters:\(\frac{\varphi _1}{r1}=0.1,\quad \frac{\varphi _2}{r_2}=0.5, \quad k=1,\quad T=10,\quad \overline{T}=0.2\), \(r_1=5,\quad r_2=3,\quad x_1^{0}=8,\quad x_2^{0}=10.\)

Fig. 1.
figure 1

Comparison of Nash equilibrium strategies in the initial model and in the game with continuous updating

Full size image
Fig. 2.
figure 2

Comparison of optimal trajectories in the initial model and in the game with continuous updating

Full size image

We see that the rate of sales for player 1 in the game with continuous updating is less than in the initial model.

7 Conclusion

A differential game model with continuous updating is presented and described. The definition of the Nash equilibrium concept for a class of games with continuous updating is given. Optimality conditions on the form of Pontryagin’s maximum principle for the class of games with continuous updating are presented for the first time and the technique for finding the Nash equilibrium is described. The theory of differential games with continuous updating is demonstrated by means of an advertising model with a logarithmic state dynamic. Ultimately, we present a comparison of the Nash equilibrium and the corresponding trajectory in both the initial game model as well as in the game model with continuous updating and conclusions are drawn.