Keywords

1 Introduction

Machine learning, especially deep learning, has shown great power over the past few years. Deep learning systems have dramatically improved the state-of-the-art standards of many tasks across domains, such as computer vision, natural language processing, speech recognition and drug discovery [15]. The tremendous success of deep learning has also inspired us to apply learning-based approaches to solve constraint satisfiability problems (CSPs). There is an interesting prospect that the end-to-end neural network models may have the ability to capture the specific structures of the problem from a certain distribution, so that some effective implicit heuristics may be learned automatically. Some previous works have implemented different (deep) neural network architectures to represent such problems and try to learn full-stack solvers [23, 26]. Thanks to the latest progress in graph representation learning, it is promising to apply graph neural networks to solve CSPs, because many of them have topology characteristics, which can be naturally represented as graphs. There have been recent efforts trying to set up end-to-end GNN models to solve the Boolean Satisfiability Problem (SAT), one of the most fundamental problems of computer science [22], and the Traveling Salesman Problem (TSP), an important \(\mathcal {NP}\)-Hard problem [20]. Experiments suggest that the GNN-based models can effectively learn the structural features of these problems, thereby obtain pretty high accuracy in predicting the satisfiability. Although such models are not yet comparable with the traditional search-based solvers, it may also be useful to combine them with traditional approaches to improve the solving performance. For instance, the GNN-based classifier for the SAT problem NeuroSAT has been further explored and observed to have some ability in finding unsatisfiable cores, which has been used to improve the efficiency of modern SAT solvers such as Glucose and Z3 [21]. We believe that, the GNN-based models also have great potential in improving the efficiency of solving CSPs with numerical constraints.

As a natural and efficient mathematical programming model, pseudo-Boolean (PB) problem, which is also known as 0–1 integer programming, has received much attention in a large number of real-world applications for a long time. Nowadays, techniques related to PB problem are crucial in many fields, such as networked data mining, planning, scheduling, transportation, management and engineering [8, 11]. However, research in complexity theory indicates even solving the satisfiability of PB constraints is an \(\mathcal {NP}\)-complete problem [12], which means it is hard to find sufficiently effective algorithms on various distributions. The mainstream approaches for PB problem benefit from the development of both Boolean Satisfiability (SAT) and Integer Programming solving techniques [6, 25]. It can be found that fundamentally they are based on the backtracking search frameworks, and largely rely on the heuristic strategies designed by experts in specific domains. It is highly probable that PB solving techniques would also benefit from heuristics learned automatically. For the aforementioned reasons, PB problem provides an important setting for investigating the capability of GNN in extracting features of numerical constraints.

In this paper, we investigate the question that whether an end-to-end GNN model can be trained to solve the satisfiability of pseudo-Boolean problem as a classification task. Other than the previous works, our setting is more universally applicable, because various \(\mathcal {NP}\)-Hard CSPs can be easily formulated as PB constraints. At first, we adopt some normalization rules to transform different kinds of constraints into normalized form in order to build a weighted bipartite graph, which can be accepted as the input of GNN. The constructed model is basically a concrete implementation of the Message Passing Neural Network [9]. The revised message passing process is applied to update the node embedding vectors involving edge weights iteratively. Finally, the classification result is produced after a readout phase. Experiments on two well-known \(\mathcal {NP}\)-Hard CSPs, 0–1 knapsack and weighted independent set, demonstrate that our model can well converge on different PB problems under some certain distributions, and predict the satisfiability with high accuracy. The trained model can also be extended to predict the problem instances of larger size than those appeared in training set, which indicates that it has some generalization capability. We can summarize our contribution in the following two points:

  • We propose a GNN-based model to solve the decision pseudo-Boolean problem. To the best of our knowledge, it is the first end-to-end GNN model for predicting the satisfiability of a general representation of CSPs with numerical constraints. It has been experimentally confirmed to achieve high accuracy on different benchmarks.

  • Compared with another GNN model NeuroSAT that intends to solve the SAT problem, our model can be seen as a generalization of it. This is because our model not only achieves the same performance on the SAT problem, but also has ability to solve more general PB problems.

The remainder of this paper proceeds by the following parts. Section 2 summarizes some related work. The problem definition and model architecture are introduced in Sect. 3. The data generation method and training configuration are detailed in Sect. 4, with some analysis about the experimental results. Finally, conclusion and future work are discussed in Sect. 5.

2 Related Work

Although the mainstream algorithms for constraint satisfaction and combinatorial optimization problems are based on reasoning and searching algorithms from symbolism, there have always been attempts trying to solve these problems through machine learning techniques. A class of research is aiming to learn effective heuristics under the backtracking search framework and has achieved progress such as [3, 14, 17]. Here, we concentrate on another route: building end-to-end neural network models which directly learn CSP solvers. The earliest research work can be traced back to the Hopfield network [10], which has made progress in solving TSP. It is guaranteed to converge to a local minimum, but the computational power is quite limited. Recently, a series of efforts have attempted to train deep learning models with different representations. [26] proposes CSP-cNN, a convolutional neural network model, to solve binary CSPs in matrix form. However, the majority of CSPs are non-binary. [23] introduces a sequence-to-sequence neural network called Ptr-Net. [4, 18] further review and extend the model. However, the structural information of CSPs may be partially lost when represented as sequential input. Structure2vec [13] adds graph embedding technique to the model, while it is still a sequential model which can only output greedy-like solutions. In summary, it is necessary to find more powerful representation models to solve various CSPs.

Fig. 1.
figure 1

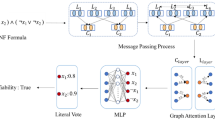
The model for solving decision pseudo-Boolean problem based on graph neural network. The pipeline is as follows: (a) A set of constraints is given as input in which all variables can be assigned True or False, then (b) some normalization rules are applied to transform the constraints into normalized form, which is done by equivalent transformation and removing tautologies. From the normalized constraints we can (c) construct a weighted bipartite graph to represent the topological relationship between variables and constraints. Each node in the graph is represented as an embedding vector, which is updated iteratively through (d) the message passing mechanism. Finally, the model (e) outputs prediction about the satisfiability.

Full size image

Graph neural network has been considered as a promising deep learning technique operating on graphs. Because of its powerful characterization capability for non-Euclidean structure data, the GNN models have made ground-breaking performance on many difficult tasks such as text classification, relation extraction, object detection, semantic segmentation and knowledge graph mining in recent years [27]. We believe graph is a suitable representation for CSPs. A basic fact is that many of the famous \(\mathcal {NP}\)-Hard problems are directly defined on graphs such as TSP, Maximum Clique and Minimum Vertex Cover. There have been some works trying to set up GNN-based models to solve SAT [1, 2, 5, 22], Graph Coloring Problem [16] and TSP [20]. Our model is distinct from the previous works in many ways. First, PB problem has the capability to conveniently formulate a larger number of CSPs compared with SAT, GCP and TSP. Although SAT is also a well-known meta-problem, it is not intuitive to translate the problem with numerical constraints into conjunction normal form. Second, PB constraints involve integer coefficients and constant items, while TSP has only one kind of numerical information (edge weights) that needs to be processed. Third, [20] introduces edge embeddings to represent the information about edge weights, which may lead to larger parameter space. Actually it takes around 2,000 epochs to converge on the dataset of graphs while \(n \sim \mathcal {U}(20, 40)\) as reported. However, the edge weights are considered in the updating process of node embeddings in our model, therefore the required parameter space and training epochs are relatively reduced.

3 Model Architecture

In this section, we first give a brief introduction to the pseudo-Boolean problem. Next, components of the model are illustrated in detail, including the graph construction, the message passing and the readout phase. The whole pipeline of the model is illustrated in Fig. 1.

3.1 Pseudo-Boolean Problem

Pseudo-Boolean problem is one of the most fundamental problems in mathematical programming. Generally, a PB problem should contain a set of pseudo-Boolean constraints. According to whether there is an objective function to optimize, it may vary slightly in definition, which can be divided into the decision problem and the optimization problem. In this paper, we focus on the decision version, in which all the variables are restricted to True or False, and all the constraints must be satisfied, with no optimization target given. Here is the formal definition: Given m constraints \(C_1, C_2, \dots , C_m\) in the form of \(C_i\): \(\sum _{j=1}^{n}{c_{ij}x_j} \ge b_i\) where \(c_{ij}, b_i \in \mathbb {Z}\), decide if a set of assignment to \(x_i \in \{0,1\}\) (\(1 \le i \le n\)) exists so that all the constraints are satisfied.

The decision PB problem is worthy of investigation for many reasons. Firstly, the bounded integer variables in linear programming can always be expressed as a combination of 0–1 variables by [24]. Moreover, the decision problem can be extended to the optimization version through simple binary search. In terms of complexity, actually it has been proven to be a famous \(\mathcal {NP}\)-Complete problem.

3.2 Graph Construction

There have been a series of works trying to apply GNN models to solve constraint satisfaction and combinatorial optimization problems. A critical step is to set up appropriate graph structures for them. [22] characterizes SAT formulas through undirected bipartite graphs, where each literal and clause corresponds to a node and each affiliation relation between literal and clause corresponds to an edge. This kind of representation is quite intuitive and reasonable with at least two justifications. First, it holds the invariance of problem in permutation and negation through graph isomorphism. Second, it imitates the order of reasoning in traditional solving techniques through the message passing process.

For PB problem, we would like to propose a bipartite graph structure which is similar to the previous work. However, the problem structure of PB is quite different from that of SAT in many ways. For instance, the coefficients of PB constraint are arbitrary integers, which cannot be represented in unweighted bipartite graph like NeuroSAT does. Besides, non-zero constant terms \(b_i\) may exist in PB problem. A question is how to deal with these constant terms in graph construction. Considering the differences above, we propose a two-stage graph construction method.

Constraint Normalization. Given a set of PB constraints, where each constraint \(C_i\): \(\sum _{j=1}^{n}{c_{ij}x_j} \ge b_i\) where \(c_{ij}, b_i \in \mathbb {Z}\), the goal is to transform them into a canonical expression. To achieve this, for a constraint \(C_i\) we first replace \(c_{ij}x_i\) with \(c_{ij}(1-\overline{x_i})\) when \(c_{ij}<0\), and move the constant item to the right side. We denote the resulting constraint \(C''_i\): \(\sum _{j=1}^{n}{|c_{ij}|l_{x_j}} \ge b'_i\), where \(l_{x_j} \in \{x_j, \overline{x_j}\}\). Later we check if the constant item \(b'_i > 0\), otherwise the constraint can be removed without changing the satisfiability. Finally we divide both sides of the constraint by \(b'_i\). After the process, all constraints are in normalized form

$$\begin{aligned} C'_i:\ \sum _{j=1}^{n}{c'_{ij}l_{x_j}} \ge 1 \end{aligned}$$
(1)

where \(c'_{ij} \in \mathbb {R^+}\) and \(l_{x_j} \in \{x_j, \overline{x_j}\}\).

Graph Generation. After the normalization stage above, every constraint \(C_i\) (\(1 \le i \le m\)) in a PB problem is turned into normalized form \(C'_i\) or removed from the problem. For each variable \(x_j\) (\(1 \le j \le n\)), we set up a pair of nodes to represent \(x_j\) and \(\overline{x_j}\) respectively, so we have a total of 2n nodes for variables. Then we set up m nodes for constraints. Suppose a constraint \(C'_i\) contains \(l_{x_j}\) with the coefficient \(c'_{ij}\), an edge connecting the nodes for \(C'_i\) and \(l_{x_j}\) is set up if \(c'_{ij} \ge 0\) with the weight of \(c'_{ij}\).

3.3 Message Passing

Now a PB problem has been represented as a weighted bipartite graph. The next step is to construct a learning model. We consider the Message Passing Neural Network (MPNN) [9] as the framework. Recently, MPNN has shown its effectiveness in solving some famous combinatorial problems, such as SAT [22] and TSP [20]. In this paper, we propose an MPNN-based model which is fit for PB problem. The forward pass of the model has two phases, a message passing phase and a readout phase.

Message Passing Phase. In the beginning, we parameterize each node in the graph randomly as a d-dimensional vector \(E_{init} \sim \mathcal {U}(0,1)\) which represents the hidden state. We note the initial hidden states of variables and constraints as \(V^{(0)}\) and \(C^{(0)}\) respectively. Let M be the adjacency matrix of the bipartite graph defined in the graph generation paragraph above. S is a transformed representation of the relevant nodes which aims to keep the consistency of node embeddings representing the same variable. In this phase, the message passing process runs for T time steps and the hidden states are updated iteratively according to:

$$\begin{aligned} \begin{aligned} C^{(t+1)}, C_h^{(t+1)}&= \mathrm{\mathbf {C_u}}(M\mathrm{\mathbf {V_{msg}}}(V^{(t)}), C_h^{(t)}) \\ V^{(t+1)}, V_h^{(t+1)}&= \mathrm{\mathbf {V_u}}(M^{\top } \mathrm{\mathbf {C_{msg}}}(C^{(t)}), V_h^{(t)}, S^{(t)}) \end{aligned} \end{aligned}$$
(2)

In the above rules, \(\mathbf {C_{msg}}\) and \(\mathbf {V_{msg}}\) are two message functions implemented with multilayer perceptrons (MLP). Besides, \(\mathbf {C_u}\) and \(\mathbf {V_u}\) are two updating functions implemented with LSTM networks, where all \(C_h^{(t)}\) and \(V_h^{(t)}\) are the hidden cell states of LSTM.

Readout Phase. After T iterations of message passing, we apply a readout function \(\mathbf {V_{vote}}: \mathbb {R}^d \rightarrow \mathbb {R}^1\) (implemented with MLP) to compute the score that every variable node votes for the satisfiability of the problem instance. Then we average all the scores to obtain the final result:

$$\begin{aligned} \hat{y} = mean(\mathrm{\mathbf {V_{vote}}}(V^{(T)})) \end{aligned}$$
(3)

The model is trained to minimize the sigmoid binary cross-entropy loss between \(\hat{y}\) and the real satisfiability of the problem instance \(\phi (P) \in \{0, 1\}\).

4 Experimental Evaluation

In order to evaluate the performance of our GNN-based model on PB problem, we prepare two different problems for the experiments: 0–1 knapsack problem (0–1KP) and weighted independent set problem (WIS). The above two problems have exceedingly different structures when expressed as PB formulas, whether in terms of the number or the average length of constraints. We generate random datasets for these problems, and train the model on them respectively.

4.1 Data Generation

There are three steps for generating the datasets:

  • Step 1. Original instances are randomly created following some certain distributions. The number of items in 0–1KP and the number of nodes in WIS are denoted as n. For each problem we uniformly generate several subsets as training sets, each of which contains 100 K instances, with different range of n. Then two datasets are generated in the same way as validation and testing sets, each of which has 10 K instances. Therefore the size ratio of training, validation and testing set is 10:1:1.

  • Step 2. Because the generated instances are all optimization problems, for each instance we first call CPLEX to obtain its optimal solution \(\phi \), and then randomly choose an integer offset \(\delta \) from \([-R/10,R/10]\) (R is an integer representing the range of coefficients, and we set \(R=100\) in all experiments). Finally, let \(\phi +\delta \) be a bound (i.e. the constant V in 0–1KP and W in WIS) to completely transform the original instance into a decision problem. It is easy to find that satisfiable and unsatisfiable instances should account for about half of each.

  • Step 3. The instances are formulated as PB constraints, normalized and turned into graphs through the rules described in Sect. 3. After that the datasets can be fed into the neural network as input for training.

0–1 Knapsack Problem. The 0–1 knapsack problem (KP) is well-known in combinatorial optimization field with a very simple structure: Given a group of items, each with a weight \(w_i\) and a value \(v_i\). There is also a backpack with a total weight limit C. The goal is to choose some items to put into the backpack, so that the sum of their values is maximized, and the sum of their weights is not exceeding the given limit of the knapsack. It is proved that the decision problem of 0–1KP is \(\mathcal {NP}\)-Complete, so there is no known polynomial-time solving algorithm. It can be naturally represented by the following PB formulas:

$$\begin{aligned} \begin{aligned} \sum _{i=1}^{n}{w_ix_i}&\le C \\ \sum _{i=1}^{n}{v_ix_i}&\ge V \end{aligned} \end{aligned}$$
(4)

The constant V represents a bound of the optimal objective. Variable \(x_i\in \{0,1\}\) indicates if an item is put into the backpack.

There have been some research works on generating difficult benchmarks of 0–1KP. Pisinger [19] proposes some randomly generated instances with multiple distributions to demonstrate that the existing heuristics can not find good solutions on all kinds of instances. The four kinds of distributions are named as:

  • Uncorrelated: \(w_i\) and \(v_i\) are randomly chosen in [1, R].

  • Weakly correlated: \(w_i\) is randomly chosen in [1, R], and \(v_i\) in \([w_i-R/10,w_i+R/10]\) such that \(v_i\ge 1\).

  • Strongly correlated: \(w_i\) is randomly chosen in [1, R], and \(v_i=w_i+R/10\).

  • Subset sum: \(w_i\) is randomly chosen in [1, R], and \(v_i=w_i\).

We generate the datasets of 0–1KP under the above distributions with equal probability. As for the capacity of knapsack C, it is also randomly selected in range \([1,\sum _{i=1}^{n}{w_i}]\) independently in each instance, in order to ensure sufficient data diversity.

Weighted Independent Set Problem. Given an undirected graph with a weight for each node, an independent set is defined as a set of nodes where any two of them are not connected with an edge. Then the maximum weighted independent set (MWIS) requires the total weights of the selected nodes to be maximized. We can model the decision problem of MWIS as PB formulas:

$$\begin{aligned} \begin{aligned} \sum _{i=1}^{n}{w_ix_i}&\ge W \\ x_i + x_j&\le 1,\ \forall (i,j)\in E \end{aligned} \end{aligned}$$
(5)

The constant W is a bound of the optimal objective, and the variables \(x_i\in \{0,1\}\) indicates whether each node is selected into the independent set.

To generate the dataset, random graph instances are sampled from the Erdős–Rényi model G(n, p) [7]. The model contains two parameters: the number of nodes n, and the existence probability p of an edge between every pair of nodes. We set \(p=0.5\) while generating the dataset, which corresponds to the case where all possible graphs on n nodes are chosen with equal probability.

4.2 Implementation and Training

In order to examine the model’s capability to predict the satisfiability of PB problem, we implement the model in Python, and several experiments are designed to train the model and evaluate its performance on different datasets for different purposes. All the experiments are running on a personal computer with Intel Core i7-8700 CPU (3.20 GHz) and NVIDIA GeForce RTX 2080Ti GPU.

For reproducibility, we would like to give the setting of hyper-parameters as follows. In our configuration, The dimension of node embedding vectors \(d=128\), and the time step of message passing T is set to 5 for 0–1KP and 50 for WIS. Our model learns from the training sets in batches, with each batch containing 12 K nodes. The learning rate is set to \(2\times 10^{-5}\).

4.3 Experimental Results

Classification Accuracy. As previously noted, the most direct and important target of the model is to classify the satisfiability of PB problems. So we examine it as the first step. There are 7 groups of experiments in total with different settings. For 0–1KP, we set up 3 groups of experiments with different sizes, where n is uniformly distributed in range [3, 10], [11, 40] and [41, 100] respectively. For WIS, we set up 4 groups of experiments with different sizes, where n is uniformly distributed in range [3, 10], [11, 20], [21, 30] and [31, 40] respectively. The reason for lacking of the results in \(n > 40\) is that for each instance the number of constraints is proportional to \(n^2\), so the graph is too hard to be fully trained in no more than 1,000 epochs. The complete experimental configuration and classification accuracy on the validation and testing sets are shown in Table 1. The first part is the description of datasets, which includes the number of variables, the average number and length of constraints. The constraint length means the number of variables with coefficients other than 0 in a constraint. The number of epochs required for training to convergence is different from each other, and we list the actual spent epochs. Finally, the classification accuracy on the validation and testing sets are shown respectively.

Table 1. The experimental configuration and the classification accuracy results for training our model on different PB problems and scales.
Full size table

The experimental results show that our model can effectively accomplish the classification task on unknown problems with similar distributions. In each group of \(n \le 40\), the model can converge and obtain more than 85% accuracy both on the validation set and the testing set. When n is expanded to 100 items in 0–1KP, the accuracy is still up to 79%. From the results, our model is believed to have learned some features related to the satisfiability of problems. Furthermore, it is worth noting that the generated PB instances under these problems have very different distributions, whether in terms of the average number or length of constraints. Therefore, it indicates that the model has wide availability to work on different PB problems without changing the structure. This confirms one of the main advantage of our model: general modeling capability.

Comparison with Other Approaches. As far as we know, the proposed model is the first end-to-end GNN model to solve the satisfiability of PB problem. However, because of the close relationship between PB and SAT, we are interested in the comparison between our model (denoted as PB-GNN) and NeuroSAT, a GNN-based model that predicts the satisfiability of SAT formulas. We train these two models on the same problems respectively, each for 200 epochs. To transform PB constraints into SAT clauses of equal satisfiability, we call Minisat+Footnote 1, a high-performance PB solver that achieves excellent ranks in the PB competitionFootnote 2. The accuracy results on the validation sets are shown in Table 2. Due to the inevitable introduction of new variables and clauses in the transformation process, the effect of NeuroSAT is limited by the growth of problem scales. For 0–1KP, the training accuracy on NeuroSAT with the transformed SAT formulas is significantly lower than that of the original problems on PB-GNN. And for WIS, when training on the original problems where \(n \ge 10\), it is almost impossible to converge within 200 epochs. Besides, the accuracy results of NeuroSAT when \(n=40\) are not available, because each epoch takes more than 2 h, which makes the overall training time unacceptable. The results indicate that PB-GNN has achieved better performance on general PB problems with numerical constraints. It is worth mentioning that when dealing with SAT instances, we can easily transform SAT clauses into PB constraints. For example, a clause \(l_1 \vee l_2 \vee \dots \vee l_k\) is equivalent to the constraint \(\sum _{i=1}^{k}{l_i} \ge 1\). In this case, the message passing process of PB-GNN is almost the same as that of NeuroSAT. To confirm this, we train the two models for 200 epochs on two datasets SR(3, 10) and SR(10, 40) respectively as defined in [22]. It can be found that the accuracy of PB-GNN and NeuroSAT is very close, which means the performance of our model is also comparable with the state-of-the-art model on SAT instances.

Another point of concern is the time spent for solving. The average time costs taken by PB-GNN and CPLEX to solve per instance from the testing sets are counted. Table 2 demonstrates the results in milliseconds. It can be seen that compared with the classic CSP solver CPLEX, our model only takes less than 10% of time to return the prediction of satisfiability. In addition to the lower computational amount of the model, another reason is that the problem instances can be input in batches, and the solving process is accelerated with parallelization. This is not to suggest that our model beats the classic solver in time. After all CPLEX is able to work without any pre-training. As a matter of fact, the results inspire us a promising scenario of the model when a large number of similar instances need to be solved with high frequency.

Table 2. Comparison of the classification accuracy and the average solving time between our model (PB-GNN) and other approaches.
Full size table

Generalization to Larger Scales. We are also interested in whether the model trained on smaller-scale data can work on larger-scale data. We examine two models, one has been trained for 400 epochs on 0–1KP and the other for 600 epochs on WIS, both of which are on the datasets where \(n \in [11, 40]\). For each model, we set up 15 groups of data with \(n \in [10, 80]\) in steps of 5. Within each group, 5 testing sets are generated with different offset \(\delta =\{\pm 1, \pm 2, \pm 5, \pm 8, \pm 10\}\) as described in Sect. 4.1. The other configuration of data generation is the same as that of validation sets. Such testing data can show more clearly the learning effect and generalization ability of our model on the instances of varying complexity.

Fig. 2.
figure 2

The change in accuracy of the model when predicting the satisfiability of larger-scale instances than those appeared in the training sets.

Full size image

Figure 2 shows the change in accuracy when testing our model on the above datasets. On one hand, it is easy to find that the generalization ability is related to the problem structure. For 0–1KP, since the structures of different scales are similar, the accuracy can be maintained relatively well even if the problem instances become larger. But for WIS, a larger-scale instance leads to a more complicated graph. The accuracy drops rapidly outside the training set, because the features learned in low dimensions are more likely to lose effectiveness. On the other hand, the model also achieves different accuracy on the instances generated under different offsets. When \(\delta =\pm 10\), the accuracy greater than 80% can be kept to \(n=65\) for 0–1KP and \(n=50\) for WIS. However, the model fails to learn effective features even on the training sets when \(\delta =\pm 1\) on both problems. Eventually, when the number of variables continuously increases, the accuracy is reduced to about 50%, which means it almost becomes a purely random model. To conclude, the experimental results indicate that the generalization performance of the model is affected by both the structure and difficulty of the problem.

5 Conclusion and Future Work

In this paper, we investigate whether a deep learning model based on GNN can solve a general class of CSPs with numerical constraints: the Pseudo-Boolean problem. More specially, the target is to correctly classify whether a decision PB problem is satisfiable. We present an extensible architecture that accepts a set of PB constraints with different lengths and forms as input. First, a weighted bipartite graph representation is established on the normalized constraints. After that, an iterative message passing process is executed. Finally, the satisfiability is calculated and returned through a readout phase. Experiments on two representative PB problems, 0–1 knapsack and weighted independent set, show that our model PB-GNN can successfully learn some features related to the structure of specific problem within 600 epochs, and achieves high-quality classification results on different distributions. Our model is shown to have several advantages over the previous works. In the aspect of network structure, it integrates the edge weights into the updating function of node embeddings, so that the parameter space is relatively small, making our model easier to converge. Regarding the accuracy of prediction, PB-GNN outperforms NeuroSAT, a foundational model in this field, on PB benchmarks with numerical coefficients, and is still comparable with it when applied to SAT instances.

We hope the model can provide a basis for a series of future works on learning to solve different CSPs with numerical constraints. There are also several perspectives for further work. On one hand, it needs to be acknowledged that the scale of learnable benchmarks by the current model is relatively small, and it should be improved to learn larger-scale instances, even those benchmarks that are difficult for the state-of-the-art solvers. On the other hand, we will try to decode the assignment of variables from the trained model, so that it can be called a real “solver”. There are reasons to believe that the development of graph representation learning will help the model to obtain more accurate features related to the problem structures, thereby reducing the heavy manual work of designing specific heuristic algorithms.