Abstract
In this chapter, we will cover known classifiers that can be used in X-ray testing. Several examples will be presented using Python. The reader can easily modify the proposed implementations in order to test different classification strategies. We will then present how to estimate the accuracy of a classifier using hold-out, cross-validation and leave-one-out. Finally, we will present an example that involves all steps of a pattern recognition problem, i.e., feature extraction, feature selection, classifier’s design, and evaluation. We will thus propose a general framework to design a computer vision system in order to select—automatically—from a large set of features and a bank of classifiers, those features and classifiers that can achieve the highest performance.
Ideal detection of a handgun superimposed onto a laptop (X-ray image \(\mathtt{B0019\_0001}\) colored with ‘sinmap’).
Access provided by Autonomous University of Puebla. Download chapter PDF

6.1 Introduction
Considerable research efforts in computer vision applied to industrial applications have been developed in recent decades. Many of them have been concentrated on using or developing tailored methods based on visual features that are able to solve a specific task. Nevertheless, today’s computer capabilities are giving us new ways to solve complex computer vision problems. In particular, a new paradigm on machine learning techniques has emerged posing the task of recognizing visual patterns as a search problem based on training data and a hypothesis space composed of visual features and suitable classifiers. Furthermore, now we are able to extract, process, and test in the same time more image features and classifiers than before. In our book, we propose a general framework that designs a computer vision system automatically, i.e., it finds—without human interaction—the features and the classifiers for a given application avoiding the classical trial and error framework commonly used by human designers. The key idea of the proposed framework is to design a computer vision system as shown in Fig. 6.1 in order to select—automatically—from a large set of features and a bank of classifiers, those features and classifiers that achieve the highest performance.
Whereas Chap. 5 covered feature extraction and selection, the focus of this chapter will be the classification. Once the proper features are selected, a classifier can be designed. Typically, the classifier assigns a feature vector \(\mathbf{x}\) with n features \((x_1 \dots x_n)\) to one class. In case of defects detection, for example, there are two classes: flaws or no-flaws. In case of baggage screening, there can be more classes: knives, handguns, razor blades, etc. In pattern recognition, classification can be performed using the concept of similarity: patterns that are similar are assigned to the same class [12]. Although this approach is very simple, a good metric defining the similarity must be established. Using representative samples, we can make a supervised classification finding a discriminant function \(h(\mathbf{x})\) that provides us information on how similar a feature vector \(\mathbf{x}\) is to a class representation.
In this chapter, we will cover many known classifiers (such as linear discriminant analysis, Bayes, support vector machines, neural networks among others). Several examples will be presented using Python. The reader can easily modify the proposed implementations in order to test different classification strategies. Afterwards, we present how to estimate the accuracy of a classifier using hold-out, cross-validation, and leave-one-out. The well-known confusion matrix and receiver-operation-characteristic curve will be outlined as well. We will explain by detailing the advantages and disadvantages of each one. Finally, we will present an example that involves all steps of a pattern recognition problem, i.e., feature extraction, feature selection, classifier’s design, and evaluation.
6.2 Classifiers
In this section, the most relevant classifiers are explained with several examples. Before we start with the explanation of the classifiers, let us review the syntax of some basic functions of pyxvis Library. The implementation of this functions is based on sklearn library.
 Python Example 6.1 The basic syntax of how to use classification algorithms in pyxvis Library is given in this code. Examples that use these commands are shown in this section (e.g., see Example 6.2).
Python Example 6.1 The basic syntax of how to use classification algorithms in pyxvis Library is given in this code. Examples that use these commands are shown in this section (e.g., see Example 6.2).

The training and testing stages of a classification process is given in following four steps (see Fig. 6.18):
-
1.
We load in
 the name and the parameters of the classifier using function
the name and the parameters of the classifier using function  with the string
with the string  Footnote 1
Footnote 1
-
2.
We define a classifier using function
 with the name and parameters of the model
with the name and parameters of the model  . The defined classifier is stored in
. The defined classifier is stored in  .
. -
3.
Classifier
 is trained using training data (
is trained using training data ( ) with function
) with function  . The defined classifier is stored in
. The defined classifier is stored in  .
. -
4.
Trained classifier
 is tested on testing data (
is tested on testing data ( ) using function
) using function  . The classification, i.e., labels of the testing samples, are stored in vector
. The classification, i.e., labels of the testing samples, are stored in vector  . To evaluate the effectiveness of the classifier, we can count the number of coincidences between
. To evaluate the effectiveness of the classifier, we can count the number of coincidences between  (real labels of testing data) and
(real labels of testing data) and  (classification using trained classifier).Footnote 2 \(\square \)
(classification using trained classifier).Footnote 2 \(\square \)
6.2.1 Minimal Distance
The simplest classifier is probably based on the concept of ‘minimal distance’. In this classifier, each class is represented by its center of mass that can be viewed as a template [10]. Thus, a mean value \({\bar{\mathbf{x }}}_k\) of each class is calculated on the training data:
where \(\mathbf{x}_{jk}\) is the jth sample of class \(\omega _k\) of the training data, and \(N_k\) is the number of samples of the kth class. A test sample \(\mathbf{x}\) is assigned to class \(\omega _k\) if the Euclidean distance \(\parallel \mathbf{x} - {\bar{\mathbf{x }}}_k \parallel \) is minimal. Formerly,

A useful formulation is defining the distance function  . Thus, we can write (6.2) as
. Thus, we can write (6.2) as

This formulation based on minimal distances will be used in the following sections. In pyxvis Library, this classifier is implemented using function  with parameter
with parameter  .
.
 Python Example 6.2 In this example, we show how to train and test a classifier based on Euclidean minimal distance. We use data that was simulated using a mixture of Gaussian distributions. The data consists of 800 samples for training and 400 samples for testing purposes. Each sample has two features \(x_1\) and \(x_2\) and it belongs to class \(\omega _1\) or \(\omega _0\). Figure 6.2 shows the feature spaces for training and testing.
Python Example 6.2 In this example, we show how to train and test a classifier based on Euclidean minimal distance. We use data that was simulated using a mixture of Gaussian distributions. The data consists of 800 samples for training and 400 samples for testing purposes. Each sample has two features \(x_1\) and \(x_2\) and it belongs to class \(\omega _1\) or \(\omega _0\). Figure 6.2 shows the feature spaces for training and testing.

The output of this code is shown in Fig. 6.5. In this case, the accuracy, defined as the ratio of samples correctly classified, is 85.50% in the testing dataset. The low performance of this classifier is because the decision line is a straight line. The reader can imagine that the decision line can be computed in three steps: (i) Compute the centers of mass of each class distribution in the training set as \({\bar{\mathbf{x}}}_1\) and \({\bar{\mathbf{x}}}_0\) according to (6.1). (ii) Compute \(\ell _C\) the straight line that contains both centers of mass. (iii) Compute the decision line \(\ell \) as the line that is perpendicular to \(\ell _C\) and equidistant to \({\bar{\mathbf{x}}}_1\) and \({\bar{\mathbf{x}}}_0\). The decision line is shown in Fig. 6.5. Obviously, the straight line is not able to separate these curved distributions.
The syntax of the use of the classification functions in pyxvis Libraryis explained in Listing 6.1. \(\square \)
6.2.2 Mahalanobis Distance
The Mahalanobis classifier employs the same concept as minimal distance (see Sect. 6.2.1), however, it uses a distance metric based on the ‘Mahalanobis distance’, in which, by means of the covariance matrix, the features to be evaluated are weighted according to their variances. A test sample \(\mathbf{x}\) is assigned to class \(\omega _k\) if the Mahalanobis distance of \(\mathbf{x}\) to class \(\omega _k\), denoted as  , is minimal. The Mahalanobis distance is defined as
, is minimal. The Mahalanobis distance is defined as

where \(\mathbf{C}_k\) is the covariance matrix of the kth class. It can be estimated as
where \(\mathbf{x}_{jk}\) is the jth sample of class \(\omega _k\) of the training data, and \(N_k\) is the number of samples of the kth class. Some examples are illustrated in Fig. 6.3. Formerly,

where distance  is defined in (6.4). In pyxvis Library, this classifier is implemented using function
is defined in (6.4). In pyxvis Library, this classifier is implemented using function  with parameter
with parameter  . An example of this classifier is presented in Example 6.4.
. An example of this classifier is presented in Example 6.4.
6.2.3 Bayes
In Bayes classifier the idea is to assign the test sample \(\mathbf{x}\) to the most probable class. For this purpose, we use the conditional probability \(p(\omega _k|\mathbf{x})\), that gives the probability of class \(\omega _k\) occurs given sample \(\mathbf{x}\). Thus, if \(p(\omega _k|\mathbf{x})\) is maximal the \(\mathbf{x}\) is assigned to class \(\omega _k\):

Using Bayes theorem we can write the conditional probability as
where \(p(\omega _k|\mathbf{x})\) is known as ‘posterior’, \(p(\omega _k)\) as ‘prior’, \(p(\mathbf{x}|\omega _k)\) as ‘likelihood’ and \({p(\mathbf{x})}\) as ‘evidence’. Since \(p(\mathbf{x})\) is the same by evaluating \(p(\omega _k|\mathbf{x})\) for all k we can re-write (6.7) as follows:

In order to evaluate (6.9) properly, we need good estimations for \(p(\mathbf{x}|\omega _k)\) and \(p(\omega _k)\). There are several known approaches to estimate these, some of which will be covered in the following sections under the assumption of Gaussian distributions of the classes (see Sects. 6.2.4 and 6.2.5).
In Naïve Bayes approach, each feature \(x_i\) is assumed to make an independent and equal contribution to our output. Obviously, this assumption is not correct in real world, however, in many practical cases it works well enough. Using this assumption, Eq. (6.8) can be formulated as
and the classification rule for this case is

The prior \(p(\omega _k)\) can be estimated by the number of available samples in the training dataset of each class. Thus, \(p(\omega _k) = N_k/N\), where \(N_k\) is the number of samples that belong to class \(\omega _k\) and \(N=\sum _k N_k\) the total number of samples. Nevertheless, in many cases of X-ray testing the available samples are not balanced, e.g., in defect detection problems there are a reduced number of flaws in comparison with the large number of non-flaws [7]. If we use the estimation \(p(\omega _k) = N_k/N\) then the most important class to be detected will have a very low prior, and it will be very difficult to detect. In such cases, the prior must be considerably increased in order to be the more probable.
In order to estimate \(p(\mathbf{x}|\omega _k)\), we can use an approach based on Kernel Density Estimation (KDE) [22]:
where K is a kernel function such as a Gaussian, that has a mean zero and variance of one, \(\Delta \) is the bandwidth, and \(\alpha _k\) is a normalization factor equal to \(1/(N_k \Delta )\). Since \(K(\mathbf{x}/\Delta )\) integrates to \(\Delta \), with this normalization factor we ensure that \({\hat{p}}(\mathbf{x}|\omega _k)\) integrates to one. Example of KDE can be found in Fig. 5.21 that were estimated using the training data of Fig. 5.23. In pyxvis Library, this classifier is implemented using function  with parameter
with parameter  (for KDE implementation) or
(for KDE implementation) or  (for a naive estimation of the probability density function, where each variable is considered to be statistically independent) (Fig. 6.4).
(for a naive estimation of the probability density function, where each variable is considered to be statistically independent) (Fig. 6.4).
Classification using Bayes and dmin. [ \(\rightarrow \) Example 6.3
 ]
]
 Python Example 6.3 In this example, we show how to train and test a Bayes classifier using Kernel Density Estimation and Naive Bayes Estimation. We use the same simulated data addressed in Example 6.2 and illustrated in Fig. 6.2.
Python Example 6.3 In this example, we show how to train and test a Bayes classifier using Kernel Density Estimation and Naive Bayes Estimation. We use the same simulated data addressed in Example 6.2 and illustrated in Fig. 6.2.

The output of this code is shown in Fig. 6.5. In this case, the accuracy, defined as the ratio of samples correctly classified, is 93.00% and 90.75% for Naive–Bayes and KDE-Bayes respectively. The reader can compare this result with the accuracy obtained by classifier of Example 6.2. \(\square \)
6.2.4 Linear Discriminant Analysis
For Gaussian distributions with \(\mathbf{x} \in \mathbb {R}^n\) :
where a good estimation for center of mass \(\mu _k\) and covariance \(\Sigma _k\) of class \(\omega _k\) can be taken from (6.1) and (6.5) respectively. Since the logarithm is a monotonically increasing function  . Thus, (6.9) can be written as
. Thus, (6.9) can be written as

Using some manipulation,

It is clear, that we do not need to evaluate  because this term is constant and the location of the maximum does not change.
because this term is constant and the location of the maximum does not change.
In Linear Discriminant Analysis (LDA) [11], we assume \(\Sigma _k = \Sigma \) (constant) for all k, i.e., term  in (6.16) is constant as well, and it is not necessary to be evaluated. Consequently,
in (6.16) is constant as well, and it is not necessary to be evaluated. Consequently,

where constant C corresponds to terms  . Covariance matrix \(\Sigma \) can be computed from training data. A good estimation is the average of the individual covariance matrices \(\Sigma = \frac{1}{K}\sum _k \mathbf{C}_k\). Formerly, the LDA classifier is defined as follows:
. Covariance matrix \(\Sigma \) can be computed from training data. A good estimation is the average of the individual covariance matrices \(\Sigma = \frac{1}{K}\sum _k \mathbf{C}_k\). Formerly, the LDA classifier is defined as follows:

where  is defined in (6.17). In pyxvis Library, the LDA classifier is implemented using function
is defined in (6.17). In pyxvis Library, the LDA classifier is implemented using function  with parameter
with parameter  . An example of this classifier is presented in Example 6.4.
. An example of this classifier is presented in Example 6.4.
A variant of Mahalanobis classifier is obtained by assuming that not only \(\Sigma _k\) is constant, but also \(p(\omega _k)\) is constant.Footnote 3 Thus, \(\Sigma _k = \Sigma \) and \(p(\omega _k) = p_c\) for all k. That means that in (6.16) terms  is constant as well:
is constant as well:

where constant C corresponds to terms  . The classification is performed by (6.6) where
. The classification is performed by (6.6) where  is defined in (6.19). The reader can observe that if we assume that \({\Sigma } = \mathbf{I}\) we obtain the Minimal Distance classifier (6.3).
is defined in (6.19). The reader can observe that if we assume that \({\Sigma } = \mathbf{I}\) we obtain the Minimal Distance classifier (6.3).
6.2.5 Quadratic Discriminant Analysis
In Quadratic Discriminant Analysis (QDA) [11], we assume that \(\Sigma _k\) and \(p(\omega _k)\) are not constant for all k, i.e., in (6.16) only term  is constant:
is constant:

where constant C corresponds to terms  . Formerly,
. Formerly,

where  is defined in (6.20). In pyxvis Library, QDA classifier is implemented using function
is defined in (6.20). In pyxvis Library, QDA classifier is implemented using function  with parameter
with parameter  .
.
 Python Example 6.4 In this example, we show how to train and test three different classifiers: Mahalanobis (see Sect. 6.2.2), LDA (see Sect. 6.2.4) and QDA (see Sect. 6.2.5). We use the same simulated data addressed in Example 6.2 and illustrated in Fig. 6.2.
Python Example 6.4 In this example, we show how to train and test three different classifiers: Mahalanobis (see Sect. 6.2.2), LDA (see Sect. 6.2.4) and QDA (see Sect. 6.2.5). We use the same simulated data addressed in Example 6.2 and illustrated in Fig. 6.2.
Classification using LDA, QDA and Mahalanobis. [ \(\rightarrow \) Example 6.4
 ]
]

The output of this code is shown in Fig. 6.6. In these cases on the testing data, we obtain 85.25%, 84.25%, 86.75%, and 89.00% for LDA, QDA, Mahalanobis and Mahalanobis-0 respectively. It is clear that Mahalanobis and QDA achieve a better performance than LDA and Mahalanobis-0 because they can model the curved distributions. \(\square \)
6.2.6 K-Nearest Neighbors
K-Nearest Neighbors (KNN) is a non-parametric approach, in which the K most similar training samples to a given test feature vector \(\mathbf{x}\) are determined [11]. The assigned class is the most frequent class from those K samples [8]. In other words, we find—in the training set—the K nearest neighbors of \(\mathbf{x}\) and we evaluate the majority vote of their classes:

where \(\{ \mathbf{x}^i \}_{i=1}^K\) are the K nearest neighbors of \(\mathbf{x}\), and \(y(\mathbf{x}^i)\) the labeled class of \((\mathbf{x}^i)\).
KNN can be implemented (avoiding the exhaustive search of all samples of the training set) by a search using a \(k-\)d tree structure [2] to search the nearest neighbors. In pyxvis Library, KNN classifier is implemented with function  with parameter
with parameter  K
K  where K is the number of neighbors to consider.
where K is the number of neighbors to consider.
 Python Example 6.5 In this example, we show how to train and test a Bayes classifier using Kernel Density Estimation. We use the same simulated data addressed in Example 6.2 and illustrated in Fig. 6.2.
Python Example 6.5 In this example, we show how to train and test a Bayes classifier using Kernel Density Estimation. We use the same simulated data addressed in Example 6.2 and illustrated in Fig. 6.2.

The output of this code is Fig. 6.7 for different number of neighbors. In this case, we obtain 90.75%, 93.50%, 94.25%, and 93.75% for 1, 3, 7, and 15 neighbors respectively. It is clear that KNN classifier can properly model any distribution. The hyper-parameter K, i.e., the number of neighbors is to be estimated for the best performance on the testing dataset. \(\square \)
Classification using KNN. [ \(\rightarrow \) Example 6.5
 ]
]
6.2.7 Neural Networks
Artificial neuronal networks are mathematical tools derived from what is known about the mechanisms and physical structure of biological learning, based on the function of a neuron. They are parallel structures for the distributed processing of information [3]. A neural networks consists of artificial neurons connected in a network that is able to classify a test feature vector \(\mathbf{x}\) evaluating a linear weighted sum of non-linear functions as illustrated in Fig. 6.8. The weights, the functions, and the connections are estimated in a training phase by minimizing the classification error [3, 4]. In this section, we only mention that neural networks have been established as one of the best classification approaches in pattern recognition. The basic structure of the neural networks and the learning strategies developed for training neural networks are the basis of deep learning models. Nowadays, it is well known that deep learning has been successfully used in image and video recognition. For these reasons, we decided to dedicate in this book an entire chapter to deep learning (see Chap. 7), and in Sect. 7.2 of this chapter, we address the theory of neural networks and give some examples.
 Python Example 6.6 In this example, we show how to train and test a Neural Network. We use the same simulated data addressed in Example 6.2 and illustrated in Fig. 6.2. In pyxvis Library, neural networks are implemented with function
Python Example 6.6 In this example, we show how to train and test a Neural Network. We use the same simulated data addressed in Example 6.2 and illustrated in Fig. 6.2. In pyxvis Library, neural networks are implemented with function  with parameter
with parameter  \((n_1,\cdots ,n_p)\)
\((n_1,\cdots ,n_p)\)  where \(n_i\) is the number of nodes of hidden layer for an architecture of p hidden layers.
where \(n_i\) is the number of nodes of hidden layer for an architecture of p hidden layers.

The output of this code is Fig. 6.9 for different configurations of hidden layers:  means one hidden layer with 10 nodes, whereas
means one hidden layer with 10 nodes, whereas  means two hidden layers with 12 and 6 nodes respectively.Footnote 4 In this case, we obtain 94.50% and 93.25% respectively. The reader can compare this result with the accuracy obtained by classifier of Examples 6.2, 6.3, 6.4, and 6.5. It is clear that classifiers based on neural networks can properly model the curved distributions. \(\square \)
means two hidden layers with 12 and 6 nodes respectively.Footnote 4 In this case, we obtain 94.50% and 93.25% respectively. The reader can compare this result with the accuracy obtained by classifier of Examples 6.2, 6.3, 6.4, and 6.5. It is clear that classifiers based on neural networks can properly model the curved distributions. \(\square \)
Classification using Neural Networks (NN). [ \(\rightarrow \) Example 6.6
 ]
]
6.2.8 Support Vector Machines
Key idea of support vector machine: a Given a two-class problem, find a decision line \(\ell \). b There are many possible decision lines that can separate both classes. c In SVM, we search decision line  so that the margin b is maximized. The support vectors are defined as those samples that belong to the margin lines
so that the margin b is maximized. The support vectors are defined as those samples that belong to the margin lines
The original Support Vector Machines (SVM) find a decision line that separate two classes (\(\omega _1\) and \(\omega _0\)) as illustrate in Fig. 6.10a. In this example, we can see that there are many possible decision lines like \(\ell _1\), \(\ell _2\), and \(\ell _3\) among others (see Fig. 6.10b). A relevant question arises: which decision line \(\ell \) can separate both classes at ‘best’? In SVM strategy, we define the ‘margins’ \(b_1\) and \(b_0\) as the minimal distance from the decision line to a sample of class \(\omega _1\) and \(\omega _0\) respectively. After SVM criterion, the ‘best’ separation line  is one that (i) it is in the middle, i.e., \(b_1 = b_0 = b\), and (ii) its margin is maximal, i.e., \(b=b_{\max }\). Thus, decision line
is one that (i) it is in the middle, i.e., \(b_1 = b_0 = b\), and (ii) its margin is maximal, i.e., \(b=b_{\max }\). Thus, decision line  is equidistant to the margin lines and the margin is maximal.
is equidistant to the margin lines and the margin is maximal.
In \(\mathbb {R}^2\) we have a decision line, however, in general, in \(\mathbb {R}^n\), we have a hyperplane that is defined as

where \(\mathbf{x} = [x_1 \dots x_n]^\mathsf{T}\) is our feature vector and \(\mathbf{a} = [a_1 \dots a_n]^\mathsf{T}\) and \(a_0\) are the linear parameters to be estimated. The solution for \(\left\{ a_j \right\} _{i=0}^n\) can be found following an optimization approach [21]. In the solution, \(\left\{ a_j \right\} _{i=0}^n\) depends only on the support vectors, i.e., the samples of both classes that belong to the margin lines as shown in Fig. 6.10c. The solution of this optimization problem consists of parameter values \(\lambda _i\) corresponding to ith support vector:
for m support vectors, where \(z_i = \pm 1\) if \(\mathbf{x}_i\) belongs to \(\omega _1\) and \(\omega _0\) respectively. In addition, \(a_0\) can be calculated from any support vector as \(a_0 = z_i-\mathbf{a}^\mathsf{T}{} \mathbf{x}_i\) [11]. In SVM, the classification of a test sample \(\mathbf{x}\) can be formulated as follows:

In practice, however, there is some overlapping between the classes as shown in Fig. 6.11a. If we have a decision line that separates the feature space, we will have misclassified samples. In SVM strategy, we consider only the misclassified samples as illustrated in Fig. 6.11b. They will be the support vectors. The ith support vector has a distance \(e_i\) to the decision line that corresponds to an error (see Fig. 6.11c). After SVM criterion, the ‘best’ decision line  is one that minimizes the total error \(e=\sum _i e_i\). Again, the solution for \(\left\{ a_i \right\} _{i=0}^n\) depends only on the support vectors, and they can be estimated using an optimization approach [21]. The classification is performed according to (6.25).
is one that minimizes the total error \(e=\sum _i e_i\). Again, the solution for \(\left\{ a_i \right\} _{i=0}^n\) depends only on the support vectors, and they can be estimated using an optimization approach [21]. The classification is performed according to (6.25).
Key idea of support vector machine with overlapping: a Given a two-class problem with overlapping, find a decision line  . b By choosing a decision line
. b By choosing a decision line  there will be misclassified samples. c The misclassified samples are the support vectors. Each of them has an error \(e_i\) defined as the perpendicular distance to the decision line
there will be misclassified samples. c The misclassified samples are the support vectors. Each of them has an error \(e_i\) defined as the perpendicular distance to the decision line  . In SVM, we search decision line
. In SVM, we search decision line  so that the total error \(\sum e_i\) is minimized
so that the total error \(\sum e_i\) is minimized
The kernel trick: the original 2D space is transformed into a 3D space where the separation of the classes is linear (this case can be found in Example 6.7 using dataset ‘P2’)
The previous approach estimates a straight line decision boundary in feature space. In many cases, however, it is convenient to find a curve that separates the classes as illustrated in Fig. 6.12a. In order to use SVM linear classification, the feature space can be transformed into a new enlarged feature space (Fig. 6.12b) where the classification boundary can be linear. Thus, as shown in Fig. 6.12c, a simple linear classification (6.25) can be designed in the transformed feature space in order to separate both classes [21].
The original feature space is transformed using a function \(f(\mathbf{x})\). Thus, according to (6.23) and (6.24) we obtain:
where \(\langle f(\mathbf{x}_i),f(\mathbf{x})\rangle \) is the inner product \([f(\mathbf{x}_i)]^\mathsf{T}f(\mathbf{x})\). In (6.26), we can observe that for the classification, only the kernel function \(\langle f(\mathbf{x}_i),f(\mathbf{x})\rangle = K(\mathbf{x}_i,\mathbf{x})\) that computes inner products in the transformed space is required. Consequently, using (6.26) we can write (6.25) in general as

Table 6.1 shows typical kernel functions that are used by SVM classifiers. They should be a symmetric positive (semi-) definite function [11]. In pyxvis Library, SVM classifier is implemented with function  with parameter
with parameter  ,
,  ,
,  ,
,  for the four kernels of Table 6.1.
for the four kernels of Table 6.1.
 Python Example 6.7 In this example, we show how to train and test SVM classifiers. We use the same simulated data addressed in Example 6.2 and illustrated in Fig. 6.2.
Python Example 6.7 In this example, we show how to train and test SVM classifiers. We use the same simulated data addressed in Example 6.2 and illustrated in Fig. 6.2.

The output of this code is Fig. 6.13 (for the donut example) and Fig. 6.14 (for the general example). In this case, we obtain 86.75%, 91.50%, 93.50%, and 91.25% for SVM-LIN, SVM-RBF (gamma=0.1, C=0.05), SVM-RBF (gamma=0.03, C=1), and SVM-POL (gamma=0.1, C=0.5, degree=2).Footnote 5 The reader can compare this result with the accuracy obtained by classifier of Examples 6.2, 6.3, 6.4, 6.5, and 6.6. It is clear that (no-linear) SVM classifiers can properly model the curved distributions. \(\square \)
Classification using SVM. [ \(\rightarrow \) Example 6.7
 ]
]
 Python Example 6.8 In this example, we show how easy is to compare many classifiers in pyxvis Library. The idea of this example is to train and test a list of 30 classifiers given in variable
Python Example 6.8 In this example, we show how easy is to compare many classifiers in pyxvis Library. The idea of this example is to train and test a list of 30 classifiers given in variable  . We use now a dataset of 3 classes and 2 features as illustrated in Fig. 6.15.
. We use now a dataset of 3 classes and 2 features as illustrated in Fig. 6.15.

The output of this code is the evaluation of the accuracy on training and testing subsets of the 30 classifiers as follows:

In addition, Fig. 6.15 shows the classifier that achieves the best accuracy on testing subset. In this case, the best classifier is #19 –  with an accuracy of 94.50%. \(\square \)
with an accuracy of 94.50%. \(\square \)
6.2.9 Classification Using Sparse Representations
In this kind of classifier, the strategy is to use sparse representations of the original data to perform the classification. Thus, the features are first transformed into a sparse representation (see Sect. 5.5) and afterwards, the sparse representation is used by the classifier.
According to Eq. (5.38) it is possible to learn the dictionary \(\mathbf{D}\) and estimate the most important constitutive components \(\mathbf{Z} = \{ \mathbf{z}_i\}_{i=1}^N\) of the representative signals \(\mathbf{X} = \{ \mathbf{x}_i\}_{i=1}^N\). In a supervised problem—with labeled data \((\mathbf{x}_i,d_i)\), where \(d_i\) is the class of sample \(\mathbf{x}_i\)—, naturally the classification problem can be stated as follows [1]: given training data \((\mathbf{x}_i,d_i)\), design a classifier h—with parameters \({\theta }\)—which maps the transformed samples \(\mathbf{z}_i\) to its classification label \(d_i\), thus, \(h(\mathbf{z}_i,\theta )\) should be \(d_i\). In order to classify a new sample data \(\mathbf{x}\), it is transformed into \(\mathbf{z}\) using dictionary \(\mathbf{D}\) and then it is classified as \(d=h(\mathbf{z},\theta )\). Nevertheless, since \(\mathbf{Z}\) is estimated to represent the original data efficiently, there is no reason to accept as true that this new representation can ensure an optimal separation of the classes. Another classification strategy uses one dictionary \(\mathbf{D}_k\) per class [15], that is learned using the set \(\mathbf{X}_k\),Footnote 6 that contains only the samples of class \(\omega _k\) of the training data: \(\mathbf{X}_k = \{ \mathbf{x}_i | d_i=k \}\). With this strategy, using (5.39) a test sample \(\mathbf{x}\) is codified by \(\mathbf{z} = \mathbf{z}_k\) with dictionary \(\mathbf{D} = \mathbf{D}_k\) for all classes \(k=1 \dots K\), and a reconstruction error is computed as \(e_k = ||\mathbf{x} - \mathbf{D}_k\mathbf{z}_k||\). Finally, sample \(\mathbf{x}\) is assigned to the class with the smallest reconstruction error:

This test strategy, however, does not scale well for a large number of classes. For these reasons, new strategies have been developed in order to learn at the same time reconstructive and discriminative dictionaries (for robustness to noise and for efficient classification respectively) [24]. This can be achieved by adding a new discrimination term in the objective function that includes the representation that is also the most different from the one of signals in other data classes:

The discrimination term \(J(\mathbf{D},\mathbf{Z},\mathbf{c},\theta )\) depends on the dictionary, the coefficient vectors, the labels of the samples \(\mathbf{d}\), and the parameters \(\theta \) of the model used for classification. Parameter \(\gamma \) weights the trade-off between approximation and classification performance. This strategy with a common dictionary has the advantage of sharing some atoms of the dictionary when representing samples of different classes. Equation (6.29) can be solved efficiently by fixed-point continuation methods when the classifier is based on logistic regression methods [16].
Another approach that can be used to classify samples in X-ray testing is based on sparse representations of random patches. This approach, called Adaptive Sparse Representation of Random Patches (ASR+), has been successfully used in other recognition problems [17, 18]. The method consists of two stages (see Fig. 6.16): In the training stage, random patches are extracted from representative images of each class (e.g., in baggage screening we can have handguns, razor blades, etc.) in order to construct representative dictionaries. A stop list is used to remove very common words from the dictionaries [23]. In the testing stage, random test patches of the query image are extracted, and for each non-stopped test patch a dictionary is built concatenating the ‘best’ representative dictionary of each class. Using this adapted dictionary, each non-stopped test patch is classified following the Sparse Representation Classification (SRC) methodology [26] by minimizing the reconstruction error. Finally, the query image is classified by patch voting. Thus, this approach is able to learn a model for each recognition task dealing with a larger degree of variability in contrast, pose, expression, occlusion, object size, and distance from the X-ray detector.
Overview of the proposed method. The figure illustrates the recognition of three different objects. The shown classes are three: clips, razor blades, and springs. There are two stages: Learning and Testing. The stop list is used to filter out patches that are not discriminating for these classes. The stopped patches are not considered in the dictionaries of each class and in the testing stage
This method was tested in the recognition of five classes in baggage screening: handguns, shuriken, razor blades, clips, and background (see some samples in Fig. 6.17). In our experiments, there are 100 images per class. All images were resized to 128 \(\times \) 128 pixels. The evaluation is performed using leave-one-out (see Sect. 6.3.3). The obtained accuracy was \(\eta = 97.17\%\).
6.3 Performance Evaluation
In this section, we will see how to evaluate the performance of a classifier and how to build the datasets ‘training data’ and ‘testing data’. In general, there is a set \(\mathbb {D}\) that contains all available data, that is the features of representative samples and their corresponding labels. Sometimes, from set \(\mathbb {D}\) a subset \(\mathbb {X} \subset \mathbb {D}\) is chosen, however, in most cases \({\mathbb {X}} = {\mathbb {D}}\). We call subset \(\mathbb {X}\) the ‘used data’ because it is used to evaluate the performance of a classifier as illustrated in Fig. 6.18. Set \(\mathbb {X}\) consists of (i) a matrix \(\mathbf{X}\) of size \(N \times p\), for N samples and p features; and (ii) a vector \(\mathbf{d}\) of N elements with the labels (one label per sample).
In order to estimate the accuracy of a classifier, we can follow this general strategy:
-
1.
From \(\mathbb {X}\), select training data \((\mathbf{X}_{\hbox {train}}, \mathbf{d}_{\hbox {train}})\) and testing data \((\mathbf{X}_{\hbox {test}}, \mathbf{d}_{\hbox {test}})\):
$$\begin{aligned} (\mathbf{X}_{\hbox {train}}, \mathbf{d}_{\hbox {train}},\mathbf{X}_{\text{ test }}, \mathbf{d}_{\hbox {test}}) = \hbox {DataSelection}(\mathbb {X}) \end{aligned}$$(6.30)Typically, a given percentage S of \(\mathbb {X}\) is used for training and the rest (100-S) for testing. That means, we have \(N_{\hbox {train}} = N \times S/100\) samples for training and \(N_{\hbox {test}} = N - N_{\hbox {train}}\) for training. There are many ways to perform the data selection:
-
Random (yes/no): we can choose randomly \(N_{\hbox {train}}\) of \(\mathbb {X}\) or, for example, the first \(N_{\hbox {train}}\) samples of \(\mathbb {X}\).
-
Stratified (yes/no): in stratified case, we select the same S percentage of each class (so the relative number of samples for each class is the same in original dataset and selected dataset), whereas in unstratified cases we select S percentage of \(\mathbb {X}\) (so the relative number of samples for each class is not necessarily the same in original dataset and selected dataset).
-
Replacement (with/without): Data selection without replacement means that once a sample has been selected, it may not be selected again. In data selection with replacement a sample of \({\mathbb {X}}\) is allowed to be replicated. It must be ensured that samples in the training data are not in the testing data and viceversa.
-
-
2.
Using training data \((\mathbf{X}_{\hbox {train}}, \mathbf{d}_{\hbox {train}})\) train a classifier:
$$\begin{aligned} \theta = \hbox {ClassifierTrain}(\mathbf{X}_{\hbox {train}}, \mathbf{d}_{\hbox {train}}), \end{aligned}$$(6.31)where \(\theta \) is a vector that contains all parameters of the classifier that was trained. For instance, in a simple classifier like Euclidean minimal distance (see Sect. 6.2.1) we store in \(\theta \) only the centers of mass of each class in the training set.
-
3.
Using the features of the testing data \(\mathbf{X}_{\hbox {test}}\), the classifier and its parameters \(\theta \), we predict the labels of each testing sample and store them in vector \(\mathbf{d}_s\) of \(N_{\hbox {test}}\) elements:
$$\begin{aligned} \mathbf{d}_s = \hbox {Classify}(\mathbf{X}_{\hbox {test}}, \theta ). \end{aligned}$$(6.32)It is worth mentioning that in this step it is not allowed to use the labels of the testing data \(\mathbf{d}_{\hbox {test}}\).
-
4.
Now, we can compute the accuracy of the testing data defined as
$$\begin{aligned} \eta _i = \frac{\#\hbox { test samples correctly predicted}}{N_{\hbox {test}}}. \end{aligned}$$(6.33) -
5.
In (6.33), we use index i because the procedure from steps 1 to 4 can be repeated n times, for \(i=1 \dots n\). Thus, we can compute the final estimation of the accuracy as
$$\begin{aligned} \eta = \frac{1}{n}\sum _{i=1}^n \eta _i. \end{aligned}$$(6.34)
In the following section, we will explain typical strategies used in the literature.
6.3.1 Hold-Out
In hold-out, we take a percentage S of \(\mathbb {X}\) for training and the rest for testing as shown in 6.19. In our general methodology, this strategy corresponds to \(n = 1\) in (6.34). This is the simplest way how to evaluate the accuracy. It is recommended just in case the computational time is so enormous that the cost of training a classifier several times is prohibitive. Hold-out can be a good starting point to test if the features and classifier that we are designing are suitable for the recognition task. Nevertheless, the standard deviation of the accuracy estimation can be very high as we will see in next example. An example that evaluates 30 classifiers using hold-out methodology has already been shown in Example 6.8. Additionally, in this section we show a very simple example that evaluates only one classifier.
Estimation of the accuracy of a classifier using hold-out. The figure follows the color representation of Fig. 6.18 for training and testing data
 Python Example 6.9 In this example, we show how to evaluate a classifier using hold-out strategy. We use the same simulated data addressed in Example 6.2 and illustrated in Fig. 6.2.
Python Example 6.9 In this example, we show how to evaluate a classifier using hold-out strategy. We use the same simulated data addressed in Example 6.2 and illustrated in Fig. 6.2.

The output of this code is the value of the estimated accuracy. This number should be around 93%. This method is implemented in function  in pyxvis Library. If we repeat this experiment 1000 times, the mean of the accuracy is 0.9287, the standard deviation is 0.0152, the maximal value is 0.9708 and the minimal value is 0.8792, i.e., the estimation is not very accurate because there is a variation of 9.2% between maximal and minimal value! \(\square \)
in pyxvis Library. If we repeat this experiment 1000 times, the mean of the accuracy is 0.9287, the standard deviation is 0.0152, the maximal value is 0.9708 and the minimal value is 0.8792, i.e., the estimation is not very accurate because there is a variation of 9.2% between maximal and minimal value! \(\square \)
Estimation of the accuracy of a classifier using cross-validation with v folds. The figure follows the color representation of Fig. 6.18 for training and testing data
6.3.2 Cross-Validation
Cross-validation is widely used in machine learning problems [13]. In cross-validation, the data is divided into v folds. A portion \(s=(v-1)/v\) of the whole data is used to train and the rest (1/v) for test. This experiment is repeated v times rotating train and test data to evaluate the stability of the classifier as shown in Fig. 6.20. Then, when training is performed, the samples that were initially removed can be used to test the performance of the classifier on these test data. Thus, one can evaluate the generalization capabilities of the classifier by testing how well the method will classify samples that have not already been examined. The estimated performance, \(\eta \), is calculated as the mean of the v percentages of the true classifications are tabulated in each case, i.e., \(n=v\) (6.34). In our experiments, we use \(v=10\) folds.Footnote 7 Confidence intervals, where the classification performance \(\eta \) expects to fall, are obtained from the test sets. These are determined by the cross-validation technique, according to a t—Student test [20]. Thus, the performance and also the confidence can be assessed.
 Python Example 6.10 In this example, we show how to evaluate 30 classifiers using cross-validation strategy with 10 folds. We use the same simulated data addressed in Example 6.8 with three classes and two features as illustrated in Fig. 6.15.
Python Example 6.10 In this example, we show how to evaluate 30 classifiers using cross-validation strategy with 10 folds. We use the same simulated data addressed in Example 6.8 with three classes and two features as illustrated in Fig. 6.15.

The output of this code is the estimated accuracy of each classifier. They are presented as follows:

The best result has been achieved by classifier KNN with 15 neighbors. The reader can compare these results with the accuracies presented in Example 6.8. This method is implemented in function  in pyxvis Library. In order to compare Hold-Out with Cross-Validation variations we can repeat the cross-validation 1000 times for classifier KNN with 15 neighbors. The results are: mean of the accuracy is 93.80%, the standard deviation is 1.65%, the maximal value is 94.28%, and the minimal value is 93.11%, i.e., the estimation is more accurate because there is a variation of 1.2% between maximal and minimal. In hold-out the variation for a similar classifier was 9.2%. \(\square \)
in pyxvis Library. In order to compare Hold-Out with Cross-Validation variations we can repeat the cross-validation 1000 times for classifier KNN with 15 neighbors. The results are: mean of the accuracy is 93.80%, the standard deviation is 1.65%, the maximal value is 94.28%, and the minimal value is 93.11%, i.e., the estimation is more accurate because there is a variation of 1.2% between maximal and minimal. In hold-out the variation for a similar classifier was 9.2%. \(\square \)
Estimation of the accuracy of a classifier using leave-one-out. The figure follows the color representation of Fig. 6.18 for training and testing data
6.3.3 Leave-One-Out
In leave-one-out strategy, we perform the cross-validation technique with N folds (the number of samples of \(\mathbb {X}\)). That means, we leave one sample out for testing and we train with the rest (\(N-1\) samples). The operation is repeated for each sample as illustrated in 6.21. The estimated accuracy is the average over the N estimations.
This method is implemented in function  in pyxvis Library. In order to illustrate the estimation accuracy using leave-one-out, we can change—in Example 6.10—the line dedicated to cross-validation by the following line:
in pyxvis Library. In order to illustrate the estimation accuracy using leave-one-out, we can change—in Example 6.10—the line dedicated to cross-validation by the following line:

The results are given as follows:

In this example, the best accuracy was achieved by classifier  with an accuracy of 94.00%. The reader can compare these results with the accuracies presented in Examples 6.8 and 6.10. It is not necessary to repeat it, because Leave-one-out always obtains the same result. That means, there is no variation of the computed performance, however, leave-one-out is very time-consuming because the number of trainings and testings is very large.
with an accuracy of 94.00%. The reader can compare these results with the accuracies presented in Examples 6.8 and 6.10. It is not necessary to repeat it, because Leave-one-out always obtains the same result. That means, there is no variation of the computed performance, however, leave-one-out is very time-consuming because the number of trainings and testings is very large.
6.3.4 Confusion Matrix
The confusion matrix, \(\mathbf{T}\), is a \(K \times K\) matrix, where K is the number of classes of our data. The element T(i, j) of the confusion matrix is defined as the number of samples that belong to class \(\omega _i\) and were classified as \(\omega _j\). A perfect classification means that T(i, i) is \(N_i\) and \(T(i,j) = 0\) for \(i\ne j\), where \(N_i\) is the number of samples of class \(\omega _i\).
 Python Example 6.11 In this example, we show how to compute the confusion matrix for two classifiers DMIN and SVM-RBF. We use the same simulated data addressed in Example 6.2 and illustrated in Fig. 6.2.
Python Example 6.11 In this example, we show how to compute the confusion matrix for two classifiers DMIN and SVM-RBF. We use the same simulated data addressed in Example 6.2 and illustrated in Fig. 6.2.

The output of this code is two confusion matrices that are illustrated in Fig. 6.22. This method is implemented in function  in pyxvis Library that calls function
in pyxvis Library that calls function  of sklearn library. \(\square \)
of sklearn library. \(\square \)
Visualization of confusion matrix of LDA and SVM-RBF. [ \(\rightarrow \) Example 6.11
 ]
]
Typically, in X-ray testing, there are two classes: \(\omega _1\) known as the target or object of interest, and \(\omega _0\) known as the no-target or background. In this two-class recognition problem (known as ‘detection’), we are interested in detecting the target correctly. It is very helpful to build a 2 \(\times \) 2 confusion matrix as shown in Table 6.2. We distinguish
-
True Positive (TP): number of targets correctly classified.
-
True Negative (TN): number of non-targets correctly classified.
-
False Positive (FP): number of non-targets classified as targets. The false positives are known as ‘false alarms’ and ‘Type I error’.
-
False Positive (FN): number of targets classified as no-targets. The false negatives are known as ‘Type II error’.
From these statistics, we can obtain following definitions (see Fig. 6.23):
Positive instances:
Negative instances:
Detections:
True positive rate, known as Sensitivity or Recall:
Precision or Positive Predictive Value:
True negative rate, known as Specificity:
False positive rate, known as 1-Specificity:
False negative rate, known as Miss Rate:
Accuracy:
F1-score:
Ideally, a perfect detection means all existing targets are correctly detected without any false alarms, i.e., \(TP=P\) and \(FP=0\). It is equivalent to: (i) \(TPR=1\) and \(FPR=0\), or (ii) \(Pr=1\) and \(Re=1\), or (ii) \(FN=FP=0\).
Performance curves for a detection problem (see Fig. 6.23). Left) ROC curve. Right) Precision/Recall curve
ROC curves (right) for different class distributions (left). The area under the curve (AUC) gives a good measure of the performance of the detection. The obtained points \((x_i,y_i)\) are used to fit the ROC curve to \(y=(1-a^{\gamma x^b})/(1-a^{\gamma })\). In each ROC curve, the ‘best operation point’ is shown as spscolorred *. This point is defined as the closest point to ideal operation point (0,1)
6.3.5 ROC and Precision-Recall Curves
It is clear, that the performance of a detector depends on some parameters, e.g., the value of a threshold \(\theta \) when segmenting a defect in an X-ray image (see Fig. 6.23). An example to see this phenomenon is shown in Fig. 6.24: increasing the sensitivity of the method the target will be 100% detected, however, the false positives will be increased as well. Typically, there is a trade-off between increasing the true positives and decreasing the false positives, because by increasing the first, the second increases as well. In a detector, i.e., a binary classification task, we can analyze the performance of the detector by variating its parameter \(\theta \).
As a measure of the performance of a detector, two curves can be plotted:
ROC curve: We can analyze the values TPR and FPR as defined in (6.38) and (6.41) respectively (see Fig. 6.24). In this case, we obtain \(TPR(\theta )\) and \(FPR(\theta )\) because the values of these variables depend on parameter \(\theta \).
The receiver operation characteristic (ROC) curve is a plot of \(TPR(\theta )\) versus \(FPR(\theta )\). Thus, we choose different values \(\left\{ \theta _i \right\} _{i=1}^{n}\) and for each value \(\theta _i\) we plot the corresponding point \((x_i,y_i)\), where \(x_i=FPR(\theta _i)\) and \(y_i=TPR(\theta _i)\). An example is illustrated in Fig. 6.25. A measure of performance of the detector is the area under the curve (AUC) [6].
Precision/Recall curve: We can analyze the values Pr and Re as defined in (6.41) and (6.38) respectively (see Fig. 6.24). In this case, we obtain \(Pr(\theta )\) and \(Re(\theta )\) because the values of these variables depend on parameter \(\theta \). As in ROC curve, we choose different values \(\left\{ \theta _i \right\} _{i=1}^{n}\) and for each value \(\theta _i\) we plot the corresponding point \((x_i,y_i)\), where \(x_i=Re(\theta _i)\) and \(y_i=Pr(\theta _i)\). A measure of performance of the detector is the area under the curve, called average precision (PA) [5].
It is worthwhile to mention that the precision and recall values do not depend on the true negatives, like the false positive rate in ROC curve. This is a great advantage when the negative class can be immensely large, e.g., in defect detection, the number of positive instances is limited (there are usually few cases available), and the number of negative instances can be very large. In those cases, FPR will be extremely low, and erroneously we could think that the number of false positives is very low. This is a typical mistake when using ROC curves. In this kind of computer vision problem, typically the precision/recall curve is used.
In object detection, for example, [14], it is very important how to give a measure of the performance of a detector. For this end, there is a set of images with objects to detect, and for each one a bounding box that encloses it has been annotated by a group of human operators. For simplicity, the annotation consists of drawing rectangles (instead of marking every single pixel of the objects). A very established metric in the computer vision community is the ‘intersection over union’ (IoU) and the PASCAL criterion [9]. For this metric, we need to define two bounding boxes according to Fig. 6.26: GT, the bounding box of the ground truth, i.e., a rectangle that encloses the target region (P), and DT, the bounding box of the detection, i.e., a rectangle that encloses the detection (D). The PASCAL criterion considers a detected object if the normalized area of overlap ‘A’ between the detected bounding box DT and the ground truth bounding box GT exceeds 0.5, where A is defined as follows:
with \(\mathsf{GT} \cap \mathsf{DT}\) the intersection of the detected and ground truth bounding boxes and \(\mathsf{GT} \cup \mathsf{DT}\) their union. An example in the detection of defects in aluminum castings is illustrated in Fig. 6.27.
With PASCAL criterion, the statistics of true positives and negatives, and false positives and negatives are measured, and the precision/recall values are computed in different scenarios. The mean average precision (mPA) is typically used to compare the performance of different object detection algorithms (see details in [14]).
Detection on a single image. A detection is considered as true positive is the normalized area of overlap (6.45) is greater than 50%. In this example, the true positives are shown in green, the false positives in red, and the ground truth in yellow
 Python Example 6.12 In this example, we show how to compute the ROC curves and Precision/Recall curves for three classifiers based on neural networks in the classification of a two-class problem with two features. We use the same simulated data addressed in Example 6.2 and illustrated in Fig. 6.2.
Python Example 6.12 In this example, we show how to compute the ROC curves and Precision/Recall curves for three classifiers based on neural networks in the classification of a two-class problem with two features. We use the same simulated data addressed in Example 6.2 and illustrated in Fig. 6.2.

The output of this code are the curves of Fig. 6.28. Variable  must be set to
must be set to  or
or  for ROC curve or Precision/Recall curve respectively. This method is implemented with functions
for ROC curve or Precision/Recall curve respectively. This method is implemented with functions  ,
,  ,
,  , and
, and  of sklearn library and functions
of sklearn library and functions  and
and  of pyxvis Library. \(\square \)
of pyxvis Library. \(\square \)
6.4 Classifier Selection
In order to select the best classifier, we explain in this section a methodology using two examples. Our examples are implemented using powerful functions of pyxvis Library. With these functions, easily, we can (i) extract features, (ii) select features and (iii) select a classifier. Thus, the user can: choose the feature groups that will be extracted, choose the feature selection algorithms to be used, the maximal number of features to be selected, and choose the classifiers that will be evaluated and the number of folds of the cross-validation technique. Using these simple functions, it is possible to design the computer vision system automatically according to the general computer vision framework explained in these three chapters (image processing, image representation and classification, and summarized in Fig. 5.28).
Using this methodology, with a representative set of X-ray images and their labels, we can know which features and which classifier can be used to obtain the best performance. The idea is to find a classification strategy (feature extraction, features selection, and classification as shown in Fig. 6.1) that maximizes the accuracy in this dataset. The proposed methodology (based on [19]) evaluates a set of combinations of features (selected by may feature selection algorithms) and trains and tests a set of classifiers to find best strategy, i.e., the highest accuracy.

In order to show this methodology, we show two examples, Example 6.13 for the detection of fishbones (that uses intensity features), and Example 6.14 for the classification of three threat objects (that uses geometric features extracted after a segmentation of the threat objects).
In order to find the best classification strategy, we use an exhaustive search (Algorithm 1) as follows: we define q classifiers, n feature selection algorithms, and m different numbers of selected features. That means, we valuate the performance of the q classifiers on the \(m \times n\) subsets of selected features. For instance, we could have: \(q =\) 3 classifiers (LDA, KNN with 3 neighbors, and SVM with RBF), \(m=2\) feature selection algorithms (SFS with Fisher criterion and SFS with QDA criterion) with 5, 10, 15, and 20 selected features (\(n=4\)). The accuracy is measured on the training dataset using cross-validation, and on the testing dataset using hold-out. According to Algorithm 1, the highest achieved accuracy on training datase (searching in all \(q \times m \times n\)) is computed as \(\hat{\eta }\). In case a maximal value for \(\hat{\eta }\), the accuracy on testing dataset is evaluated as \(\hat{\eta }_t\). This algorithm is implemented in function  of pyxvis Library.
of pyxvis Library.
 Python Example 6.13 In this example, we can see the whole process of Algorithm 1: (i) feature extraction, (ii) feature selection, and (ii) classifier selection. pyxvis Library provides a suite of helpful commands that can be used in this process. The idea is to design a classifier that can be used to detect fish bones in X-ray images of salmon filets (see details of the dataset in Example 5.9). In this code, we show how to automatically design a computer vision system for this application. For this example, (i) we extract basic intensity, Gabor, LBP, Haralick with distance of 2 pixels, Fourier and HOG features; (ii) we evaluate four different feature selection algorithms based on Fisher, QDA, SVM-LIN and SVM-RBF with 3, 5, 10, 12, and 15 features to be selected; and (iii) we train and test 8 different classifiers: Mahalanobis, Bayes-KDE, SVM-LIN, SVM-RBF, QDA, LDA, KNN-3, KNN-7, and a Neural Network.
Python Example 6.13 In this example, we can see the whole process of Algorithm 1: (i) feature extraction, (ii) feature selection, and (ii) classifier selection. pyxvis Library provides a suite of helpful commands that can be used in this process. The idea is to design a classifier that can be used to detect fish bones in X-ray images of salmon filets (see details of the dataset in Example 5.9). In this code, we show how to automatically design a computer vision system for this application. For this example, (i) we extract basic intensity, Gabor, LBP, Haralick with distance of 2 pixels, Fourier and HOG features; (ii) we evaluate four different feature selection algorithms based on Fisher, QDA, SVM-LIN and SVM-RBF with 3, 5, 10, 12, and 15 features to be selected; and (iii) we train and test 8 different classifiers: Mahalanobis, Bayes-KDE, SVM-LIN, SVM-RBF, QDA, LDA, KNN-3, KNN-7, and a Neural Network.

The result of this algorithm is illustrated in Fig. 6.29-Top. We can see that the best performance was achieved by classifier SVM-RBF using 10 features that were selected using SFS algorithm with Fisher criterion. The accuracy on testing dataset is in this case 97.50%. The indices of the selected features are shown in following output:

\(\square \)
 Python Example 6.14 In this example, we can see the whole process of Algorithm 1 using geometric features: (i) feature extraction, (ii) feature selection, and (ii) classifier selection using pyxvis Library. The idea is to design a classifier that can be used to recognize threat objects in X-ray images (see details of the dataset in Example 5.10). In this code, we show how to automatically design a computer vision system for this application. For this example, (i) we extract basic geometric features, Hu, Flusser and Gupta moments, and Fourier descriptors (the features extracted from the segmented image, for this end we use function
Python Example 6.14 In this example, we can see the whole process of Algorithm 1 using geometric features: (i) feature extraction, (ii) feature selection, and (ii) classifier selection using pyxvis Library. The idea is to design a classifier that can be used to recognize threat objects in X-ray images (see details of the dataset in Example 5.10). In this code, we show how to automatically design a computer vision system for this application. For this example, (i) we extract basic geometric features, Hu, Flusser and Gupta moments, and Fourier descriptors (the features extracted from the segmented image, for this end we use function  of pyxvis Library as explained in Sect. 4.5.1); (ii) we evaluate four different feature selection algorithms based on Fisher, QDA, SVM-LIN, and SVM-RBF with 2, 3, 5, 10, 15, and 20 features to be selected; and (iii) we train and test 8 different classifiers: Mahalanobis, Bayes-KDE, SVM-LIN, SVM-RBF, QDA, LDA, KNN-3, KNN-7, and a Neural Network.
of pyxvis Library as explained in Sect. 4.5.1); (ii) we evaluate four different feature selection algorithms based on Fisher, QDA, SVM-LIN, and SVM-RBF with 2, 3, 5, 10, 15, and 20 features to be selected; and (iii) we train and test 8 different classifiers: Mahalanobis, Bayes-KDE, SVM-LIN, SVM-RBF, QDA, LDA, KNN-3, KNN-7, and a Neural Network.

The result of this algorithm is illustrated in Fig. 6.29-Bottom. We can see that the best performance was achieved by classifier KNN-3 using 5 features selected using QDA criterion. The accuracy on testing dataset is in this case 97.67%. The indices of the selected features are shown in following output:

\(\square \)
6.5 Summary
In this chapter, we covered the following classifiers:
-
Minimal distance (using Euclidean and Mahalanobis distance)
-
Bayes
-
Linear and quadratic discriminant analysis
-
K-nearest neighbors
-
Neural networks
-
Support vector machines
-
Classifiers using sparse representations
In addition, several simple examples were presented using simulated data and real data. The reader can easily modify the proposed implementations in order to test different classification strategies or real data.
Afterwards, we presented how to estimate the accuracy of a classifier using hold-out, cross-validation, and leave-one-out. We covered the well-known confusion matrix and receiver-operation-characteristic curve will be outlined as well.
Finally, we presented an example that involves all steps of a pattern recognition problem, i.e., feature extraction, feature selection, classifier’s design, and evaluation. All steps can be designed automatically using a simple code program of a couple of lines.
Notes
- 1.
The available names of models are:
 (logistic regression),
(logistic regression),  (Minimal Distance),
(Minimal Distance), 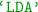 (linear discriminant analysis),
(linear discriminant analysis), 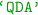 (quadratic discriminant analysis),
(quadratic discriminant analysis), 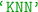 (nearest neighbors),
(nearest neighbors),  (random forest),
(random forest), 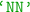 (neural network),
(neural network),  (AdaBoost),
(AdaBoost), 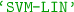 (SVM classifier with linear kernel),
(SVM classifier with linear kernel), 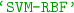 (SVM classifier with RBF kernel).
(SVM classifier with RBF kernel). - 2.
Usually, for this end we can use the accuracy metric explained in Sect. 6.3.
- 3.
In pyxvis Library, this classifier is implemented using function
 with parameter
with parameter 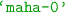 .
. - 4.
For the configuration of Fig. 6.8 is
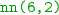 .
. - 5.
In sklearn library, ‘gamma’ defines the influence of the single training examples, ‘C’ is like a regularization parameter in the optimization, and ‘degree’ is the the degree of the polynomial for SVM-POL. See https://scikit-learn.org/stable/auto_examples/svm/plot_rbf_parameters.html for further details.
- 6.
There are some approaches that define the dictionary as the original samples (see Sparse Representation Classification (SRC) [26]), where \(\mathbf{D}_k = \mathbf{X}_k\).
- 7.
The number of folds v can be another number, for instance 5-fold or 20-fold cross-validation estimate offers very similar performances. In our experiments, we use 10-fold cross-validation because it has become the standard method in practical terms [25].
References
Bar, L., Sapiro, G.: Hierarchical dictionary learning for invariant classification. In: 2010 IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP), pp. 3578–3581 (2010)
Bentley, J.: Multidimensional binary search trees used for associative searching. Commun. ACM 18(9), 509–517 (1975)
Bishop, C.: Neural Networks for Pattern Recognition. Oxford University Press, Oxford (2005)
Bishop, C.: Pattern Recognition and Machine Learning. Springer, Berlin (2006)
Boyd, K., Eng, K.H., Page, C.D.: Area under the precision-recall curve: point estimates and confidence intervals. In: Joint European Conference on Machine Learning and Knowledge Discovery in Databases, pp. 451–466. Springer, Berlin (2013)
Bradley, A.P.: The use of the area under the roc curve in the evaluation of machine learning algorithms. Patt. Recogn. 30(7), 1145–1159 (1997)
Carvajal, K., Chacón, M., Mery, D., Acuna, G.: Neural network method for failure detection with skewed class distribution. Insight 46(7), 399–402 (2004)
Duda, R., Hart, P., Stork, D.: Pattern Classification, 2nd edn. Wiley, New York (2001)
Everingham, M., Gool, L.V., Williams, C.K.I., Winn, J., Zisserman, A.: The pascal visual object classes (voc) challenge. Int. J. Comput. Vis. 88(2), 303–338 (2010)
Fukunaga, K.: Introduction to Statistical Pattern Recognition, 2nd edn. Academic Press Inc., San Diego (1990)
Hastie, T., Tibshirani, R., Friedman, J.: The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd edn. Springer, Berlin (2009)
Jain, A., Duin, R., Mao, J.: Statistical pattern recognition: a review. IEEE Trans. Patt. Anal. Mach. Intell. 22(1), 4–37 (2000)
Kohavi, R.: A study of cross-validation and bootstrap for accuracy estimation and model selection. In: International Joint Conference on Artificial Intelligence, vol. 14, pp. 1137–1145. Citeseer (1995)
Lin, T.Y., Maire, M., Belongie, S., Hays, J., Perona, P., Ramanan, D., Dollár, P., Zitnick, C.L.: Microsoft COCO: common objects in context. In: European Conference on Computer Vision, pp. 740–755. Springer, Berlin (2014)
Mairal, J., Bach, F., Ponce, J., Sapiro, G., Zisserman, A.: Discriminative learned dictionaries for local image analysis. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2008)
Mairal, J., Bach, F., Ponce, J., Sapiro, G., Zisserman, A.: Supervised dictionary learning. Tech. Rep. 6652, INRIA (2008)
Mery, D., Bowyer, K.: Face recognition via adaptive sparse representations of random patches. In: IEEE Workshop on Information Forensics and Security (WIFS 2014) (2014)
Mery, D., Bowyer, K.: Recognition of facial attributes using adaptive sparse representations of random patches. In: 1st International Workshop on SoftBiometrics, in Conjunction with European Conference on Computer Vision (ECCV 2014) (2014)
Mery, D., Pedreschi, F., Soto, A.: Automated design of a computer vision system for visual food quality evaluation. Food Bioprocess Technol. 6(8), 2093–2108 (2013)
Mitchell, T.: Machine Learning. McGraw-Hill, Boston (1997)
Shawe-Taylor, J., Cristianini, N.: Kernel Methods for Pattern Analysis. Cambridge University Press, Cambridge (2004)
Silverman, B.W.: Density Estimation for Statistics and Data Analysis, vol. 26. CRC Press, Boca Raton (2003)
Sivic, J., Zisserman, A.: Video Google: a text retrieval approach to object matching in videos. In: International Conference on Computer Vision (ICCV 2003), pp. 1470–1477 (2003)
Tosic, I., Frossard, P.: Dictionary learning. Signal Process. Mag. IEEE 28(2), 27–38 (2011)
Witten, I., Frank, E.: Data Mining: Practical Machine Learning Tools and Techniques, 2nd edn. Morgan Kaufmann, Burlington (2005)
Wright, J., Yang, A.Y., Ganesh, A., Sastry, S.S., Ma, Y.: Robust face recognition via sparse representation. IEEE Trans. Patt. Anal. Mach. Intell. 31(2), 210–227 (2009)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Mery, D., Pieringer, C. (2021). Classification in X-Ray Testing. In: Computer Vision for X-Ray Testing. Springer, Cham. https://doi.org/10.1007/978-3-030-56769-9_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-56769-9_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56768-2
Online ISBN: 978-3-030-56769-9
eBook Packages: Computer ScienceComputer Science (R0)



 the name and the parameters of the classifier using function
the name and the parameters of the classifier using function  with the string
with the string 
 with the name and parameters of the model
with the name and parameters of the model  . The defined classifier is stored in
. The defined classifier is stored in  .
. is trained using training data (
is trained using training data ( ) with function
) with function  . The defined classifier is stored in
. The defined classifier is stored in  .
. is tested on testing data (
is tested on testing data ( ) using function
) using function  . The classification, i.e., labels of the testing samples, are stored in vector
. The classification, i.e., labels of the testing samples, are stored in vector  . To evaluate the effectiveness of the classifier, we can count the number of coincidences between
. To evaluate the effectiveness of the classifier, we can count the number of coincidences between  (real labels of testing data) and
(real labels of testing data) and  (classification using trained classifier).
(classification using trained classifier).
 ]
]

 ]
]










 ]
]












 ]
]
 ] [
] [  ]
] (logistic regression),
(logistic regression),  (Minimal Distance),
(Minimal Distance), 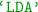 (linear discriminant analysis),
(linear discriminant analysis), 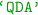 (quadratic discriminant analysis),
(quadratic discriminant analysis), 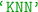 (nearest neighbors),
(nearest neighbors),  (random forest),
(random forest), 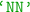 (neural network),
(neural network),  (AdaBoost),
(AdaBoost), 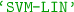 (SVM classifier with linear kernel),
(SVM classifier with linear kernel), 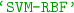 (SVM classifier with RBF kernel).
(SVM classifier with RBF kernel). with parameter
with parameter 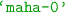 .
.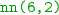 .
.