Monochromatic Random Waves for General Riemannian Manifolds

Abstract

This is a survey article on some of the recent developments on monochromatic random waves defined for general Riemannian manifolds. We discuss the conditions needed for the waves to have a universal scaling limit, we review statistics for the size of their zero set and the number of their critical points, and we discuss the structure of their zero set as described by the diffeomorphism types and the nesting configurations of its components.

1 Introduction

This is a survey article on the recent developments on monochromatic random waves for general Riemannian manifolds obtained in [7,8,9,10, 30]. Let (M, g) be a compact, smooth, Riemannian manifold without boundary of dimension n ≥ 2, and write Δ_g for the corresponding positive definite Laplace–Beltrami operator. Consider an orthonormal basis ${\{\varphi _{{ }_{\lambda _j}}\}}_{j=1}^\infty$ of L ²(M, g) consisting of real-valued eigenfunctions

$$\displaystyle \begin{aligned}\Delta_g \varphi_{{}_{\lambda_j}} = \lambda_j^2 \varphi_{{}_{\lambda_j}},\end{aligned}$$

with eigenvalues , normalized so that $\|\varphi _{{ }_{\lambda _j}}\|{ }_{{ }_{L^2}}=1$.

Laplace eigenfunctions have been a common object of study for the mathematical physics community since they encode how heat and waves propagate across M. From a quantum mechanics point of view, $|\varphi _{{ }_{\lambda _j}}(x)|{ }^2$ is the probability density for finding a quantum particle of energy $\lambda _j^2$ at the point x. It is therefore a natural problem to try to understand how $\varphi _{{ }_{\lambda _j}}$ behaves. For example, one would like to understand how many minimums and maximums $\varphi _{{ }_{\lambda _j}}$ has, as they are the most likely places for the quantum particles to be found at. See Figure 1. Similarly, understanding the geometry of the zero set of $\varphi _{{ }_{\lambda _j}}$ would yield information on the structure of the least likely places for the quantum particles. See Figure 2.

Fig. 1

Zeros and critical points for an eigenfunction on a torus. The function takes positive values on the shaded black areas, and negative values on the white areas. The maximums for the function are attained at the red points, while the minimums occur at the blue points. This picture was created by E. Vouga

Fig. 2

Nodal domains of a monochromatic random wave on the round sphere. Picture created by D. Beliaev

However, it is often the case that studying such questions for $\varphi _{{ }_{\lambda _j}}$ defined on a general manifold is quite hard, as eigenfunctions cannot be computed explicitly. Even more so, for high energies, numerical methods cannot approximate the eigenfunctions in an efficient way that would keep track of features such as the structure of their zero set. It is then natural to randomize the problem and to study how the eigenfunctions behave on average.

It is then natural to work with monochromatic random waves of frequency λ. These are random fields on M defined by

$$\displaystyle \begin{aligned} \phi_\lambda:=\frac{1}{{ \sqrt{\dim H_{\eta,\lambda}}}}\sum_{\lambda_j\in [\lambda, \lambda+\eta(\lambda)]} a_j \varphi_{{}_{\lambda_j}},{} \end{aligned} $$

(1)

where the coefficients a _j ∼ N(0, 1) are real valued, i.i.d, standard Gaussian random variables, η = η _λ = η(λ) is a non-negative function satisfying η(λ) = o(λ) as λ →∞, and

$$\displaystyle \begin{aligned}H_{\eta,\lambda}:=~\bigoplus_{\lambda_j\in [\lambda, \lambda+\eta_\lambda]}\ker(\Delta_g-\lambda_j^2\text{Id}).\end{aligned}$$

We write

$$\displaystyle \begin{aligned}\phi_\lambda\in \operatorname{\mathrm{RW}}_\lambda(M,g, \eta)\end{aligned}$$

for short. The ensembles ϕ _λ are Gaussian models for eigenfunctions of the Laplacian with eigenvalue approximately equal to λ ² on a compact Riemannian manifold (M, g). In the setting of a general smooth manifold, the ensembles $\operatorname {\mathrm {RW}}_\lambda$ were first defined by Zelditch in [36]. Zelditch was inspired in large part by the influential work of Berry [3], which proposes that random planar waves on Euclidean space and flat tori are good semiclassical models for high frequency eigenfunctions in quantum systems whose classical dynamics are chaotic. As we will see in Section 2, when properly scaled, the waves $\phi _\lambda \in \operatorname {\mathrm {RW}}_\lambda (M,g,\eta )$ behave like random planar waves. Random planar waves are Laplace eigenfunctions with eigenvalue 1, and since their frequency is fixed to be 1 they are said to be monochromatic. The fact that the scaled ϕ _λ behave like random planar waves as λ →∞ is the reason why waves in $\operatorname {\mathrm {RW}}_\lambda (M,g, \eta )$ are said to be monochromatic.

On round spheres and flat tori the Laplace eigenvalues occur with large multiplicity. Indeed, $\dim H_{0, \lambda }$ grows like λ ⁿ⁻¹ when λ is an eigenvalue. Therefore, in these cases, one typically takes η ≡ 0 so that $\phi _\lambda \in \operatorname {\mathrm {RW}}_\lambda (M,g,0)$ is an exact eigenfunction and λ ∈{λ _j}. However, for a generic metric on any smooth compact manifold M, the eigenvalues $\lambda _j^2$ are simple. It is then natural to take η so that $\dim H_{\eta ,\lambda }$ has the same rate of growth in powers of λ as the dimension of the eigenspaces for a round sphere. In particular, it is known [7] that if (M, g) has at least one non self-focal point (that is, there exists x ∈ M so that $|\mathcal L_{x,x}|=0$, see (11)), then for every c > 0 there exists C > 0 such that $\dim H_{c,\lambda }$ grows like Cλ ⁿ⁻¹ as λ →∞. Since the existence of a non self-focal point is a very weak condition, it is customary to work with random waves in $\operatorname {\mathrm {RW}}_\lambda (M,g,c)$ for some c > 0.

This survey article focuses on the results of [7,8,9,10, 30]. The results in [7, 9] were the first ones to allow for the treatment of monochromatic random waves to take place on general manifolds by establishing that, when properly rescaled, the waves have a universal behavior. Prior to these results, monochromatic random waves had only been studied for the torus or the sphere. The article [8] is the first one in the literature pertaining statistics of the size of zero set and of the numbers of critical points for monochromatic random waves on general Riemannian manifolds. The results in [10, 30] deal with the study of the diffeomorphism types of the components of the zero sets of the monochromatic random waves, and of the nesting configurations of the components. These results build on the ground breaking work of Nazarov–Sodin [31].

In this article we discuss the following aspects of $\phi _\lambda \in \operatorname {\mathrm {RW}}_\lambda (M,g,\eta )$.

• Section 2 : Universal behavior of ϕ _λ.

• Section 3 : Number of critical points and size of the zero set of ϕ _λ.

• Section 4 : Structure of the zero set of ϕ _λ.

The literature about random waves is extensive and rapidly evolving. This survey by no means attempts to give an overall account of every known result. There are numerous works directly related to the topics of this survey, including [4,5,6, 11, 14,15,16, 19,20,21,22, 25,26,27,28,29, 31, 33, 34].

2 Universal Behavior of ϕ _λ

By the Kolmogorov Consistency Theorem, the law of $\phi _\lambda \in \operatorname {\mathrm {RW}}_\lambda (M,g, \eta ),$ which is a centered smooth Gaussian field, is completely characterized by its covariance kernel

$$\displaystyle \begin{aligned} \Pi_{\eta,\lambda}(x,y) :=\operatorname{\mathrm{Cov}}\left(\phi_\lambda(x),\phi_\lambda(y) \right)=\frac{1}{\dim H_{\eta,\lambda}}\sum_{\lambda_j\in [\lambda, \lambda+\eta_\lambda]}\varphi_{{}_{\lambda_j}}(x)\varphi_{{}_{\lambda_j}}(y),\end{aligned} $$

where x, y ∈ M. The function Π_η,λ(x, y) is the Schwartz kernel for the orthogonal projection operator Π_η,λ : L ²(M, g)→H _η,λ, normalized to have unit trace. The study of local quantities, such as the size of the zero set of ϕ _λ, or the number of critical points of ϕ _λ, hinges on understanding the statistics of ϕ _λ, as λ→∞, restricted to “wavelength balls” of radius ≈ λ ⁻¹ around a fixed point x ∈ M. After rescaling by 1∕λ, the function ϕ _λ has frequency approximately equal to 1 on such balls in the sense that it solves the approximate local eigenvalue equation

$$\displaystyle \begin{aligned} \Delta_{{}_{T_xM}} \phi_\lambda(x+\tfrac{u}{\lambda})\approx \phi_\lambda(x+ \tfrac{u}{\lambda}),\end{aligned} $$

(2)

where $\Delta _{{ }_{T_xM}}$ denotes the flat Laplacian on the tangent space at x, T _xM. One could therefore expect, after the scaling, for the Gaussian random wave $u \mapsto \phi _\lambda (x+\tfrac {u}{\lambda })$ to behave like a Gaussian random wave ϕ _∞ on ${\mathbb R}^n\cong T_xM$ satisfying

$$\displaystyle \begin{aligned}\Delta_{{}_{{\mathbb R}^n}}\phi_\infty =\phi_\infty.\end{aligned} $$

The latter is called a random planar wave, and we discuss them in Section 2.1. Moreover, we shall see in Section 2.2, that for a generic Riemannian metric on M, the rescaled covariance kernel Π_η,λ of $\phi _\lambda \in \operatorname {\mathrm {RW}}_\lambda (M,g, \eta )$ converges in the C ^∞ topology to that of a random planar wave ϕ _∞ on ${\mathbb R}^n\cong T_xM$.

2.1 Random Planar Waves

Let $\sigma _{{ }_{S^{n-1}}}$ be the Haar measure on the round sphere S ⁿ⁻¹, normalized so that $\sigma _{{ }_{S^{n-1}}}(S^{n-1})=1$. Using that the transformation ξ↦ − ξ preserves S ⁿ⁻¹, choose a real-valued orthonormal basis $\{\psi _j\}_{j=1}^\infty$ of $L^2( S^{n-1}, \sigma _{{ }_{S^{n-1}}})$ satisfying

$$\displaystyle \begin{aligned} \psi_j(-\xi)= (-1)^{\epsilon_j} \psi_j(\xi), \qquad \quad \epsilon_j \in \{0,1\}. \end{aligned} $$

(3)

A random planar wave is defined to be the random real-valued function ϕ _∞ on ${\mathbb R}^n$ given by

$$\displaystyle \begin{aligned} \phi_\infty(u)=\sum_{j=1}^\infty b_j\, i^{\eta_j}\, \widehat {\psi_j}(u), \end{aligned} $$

(4)

where

$$\displaystyle \begin{aligned} \widehat {\psi_j}(u)= \int_{{\mathbb R}^n} \psi_j(\xi) e^{- i \langle u, \xi\rangle} d \sigma_{{}_{S^{n-1}}}(\xi), \end{aligned} $$

(5)

and the b _j’s are i.i.d, real valued, standard Gaussian random variables. We write

$$\displaystyle \begin{aligned}\phi_\infty \in \operatorname{\mathrm{RW}}_1({\mathbb R}^n, g_{{}_{{\mathbb R}^n}}),\end{aligned}$$

for short, where $g_{{ }_{{\mathbb R}^n}}$ is the Euclidean metric. We note that the fields in $\operatorname {\mathrm {RW}}_1({\mathbb R}^n, g_{{ }_{{\mathbb R}^n}})$ do not depend on the choice of the orthonormal basis {ψ _j}. In addition, since the Euclidean Laplacian is $\Delta _{g_{{\mathbb R}^n}}=-\sum _{k=1}^n \partial _{u_k}^2$, and $\Delta _{g_{{\mathbb R}^n}}e^{- i \langle u, \xi \rangle } = e^{- i \langle u, \xi \rangle }\sum _{k=1}^n \xi _k^2$, it is immediate that

$$\displaystyle \begin{aligned}\Delta_{g_{{\mathbb R}^n}} \phi_\infty=\phi_\infty.\end{aligned}$$

As explained in the introduction, random planar waves are often called monochromatic random waves because their frequency (the square root of their eigenvalue) is equal to 1.

Next, note that the distributional identity $\sum _{j=1}^\infty \phi _j(\xi ) \phi _j(\eta )=\delta (\xi -\eta )$ on S ⁿ⁻¹ together with (3) lead to the explicit expression for the covariance function:

$$\displaystyle \begin{aligned} \Pi_\infty(u,v):= \text{Cov}(\phi_\infty(u),\phi_\infty(v))=\int_{{\mathbb R}^n} e^{i \langle u-v , \xi \rangle} d\sigma_{{}_{S^{n-1}}}(\xi), \end{aligned} $$

(6)

where $u,v \in {\mathbb R}^n$. From (4) it follows that almost all ϕ _∞’s are analytic in u [1]. It is also known that

$$\displaystyle \begin{aligned} \Pi_\infty(u,v)=\frac{1}{(2\pi)^{\frac{n}{2}}}\frac{J_{\nu}(|u-v|)}{ |u-v|{}^{\nu}}, \end{aligned} $$

(7)

where J _ν is the Bessel function of index $\nu :=\frac {n-2}{2}.$

There is a natural choice of a basis for $L^2(S^{n-1},d\sigma _{S^{n-1}})$ given by spherical harmonics. Let $\{Y^\ell _m\}_{m=1}^{d_{\ell ,n}}$ be a real-valued basis for the space of spherical harmonics $\mathcal E_\ell (S^{n-1})$ of eigenvalue ℓ(ℓ + n − 2), where $d_{\ell ,n}=\dim \mathcal E_\ell (S^{n-1})$. In [10, Corollary 2.2] we prove that the monochromatic Gaussian ensembles ϕ _∞’s take the form

$$\displaystyle \begin{aligned} \phi_\infty(u)=(2\pi)^{\frac{n}{2}} \sum_{\ell=0}^\infty \sum_{m=1}^{d_{\ell,n}} b_{\ell,m} \, Y^\ell_m \left(\frac{u}{|u|}\right) \frac{J_{\ell + \nu}(|u|)}{|u|{}^{\nu}}, \end{aligned}$$

where the b _ℓ,m’s are i.i.d standard Gaussian variables.

2.2 Points of Isotropic Scaling

The discussion around (2) shows that it is natural to study ϕ _λ by fixing x ∈ M and considering the rescaled pullback of ϕ _λ to the tangent space T _xM. We denote this pullback by

$$\displaystyle \begin{aligned} \phi_\lambda^{x}(u):=\phi_\lambda{\left(\exp_{x}{\left(\frac{u}{\lambda} \right)} \right)}, \end{aligned} $$

(8)

where exp_x : T _xM → M is the exponential map. The dilated functions $\phi _\lambda ^x$ are centered Gaussian fields on T _xM, and we denote their scaled covariance kernel by

$$\displaystyle \begin{aligned} \Pi_{\eta,\lambda}^{x}(u,v):=\operatorname{\mathrm{Cov}}(\phi_\lambda^{x}(u) ,\phi_\lambda^{x}(v))=\Pi_{\eta,\lambda}{\left(\exp_{x}{\left(\frac{u}{\lambda} \right)},~\exp_{x}\left(\frac{v}{\lambda} \right) \right)}.\end{aligned}$$

When x is a point of isotropic scaling (see Definition 1 below), we shall see that the kernels $\Pi _{\eta , \lambda }^x$ converge to the covariance kernel of a random planar wave

$$\displaystyle \begin{aligned}\phi_\infty^x \in \operatorname{\mathrm{RW}}_1(T_{x}M, g_{x}).\end{aligned}$$

Here, g _x denotes the constant coefficient metric obtained by freezing g at x. By the Kolmogorov Extension Theorem, together with (6), the random wave $\phi _\infty ^x$ is completely characterized by its two point correlation function kernel

$$\displaystyle \begin{aligned} \Pi_\infty^{x}(u,v)={\left(2\pi \right)}^{\frac{n}{2}}\frac{J_{\tfrac{n-2}{2}}\big(\left\lVert u-v\right\rVert_{g_{x}}\big)} {\left\lVert u-v\right\rVert_{g_{x}}^{\tfrac{n-2}{2}}}=\int_{S_{x}M} e^{i{\left\langle u-v,\xi\right\rangle}_{g_{x}}}d\sigma_{{}_{S_{x}M}}(\xi). \end{aligned} $$

(9)

Here J _ν denotes a Bessel function of the first kind with index ν, S _xM is the unit sphere in T _xM with respect to g _x, and $d\sigma _{{ }_{S_{x}M}}$ is the hypersurface measure on S _xM.

Definition 1

A point x ∈ M is a point of isotropic scaling, denoted $x \in \mathcal {I}\mathcal {S}(M,g,\eta ),$ if for every non-negative function r _λ satisfying r _λ = o(λ) as λ→∞, and all $\alpha , \beta \in \mathbb N^n$, we have

$$\displaystyle \begin{aligned} \sup_{u, v \in B_{r_\lambda}} \left | \partial_u^\alpha \partial_v^\beta \,\left[\Pi_{\eta,\lambda}^{x}(u,v)- \Pi_\infty^{x}(u,v) \right]\big. \right|=o_{\alpha,\beta}(1) \end{aligned} $$

(10)

as λ→∞, where the rate of convergence depends on α, β and B _r denotes a ball of radius r centered at 0 ∈ T _xM. We also say that M is a manifold of isotropic scaling if

$$\displaystyle \begin{aligned}M=\mathcal{I}\mathcal{S}(M,g, \eta)\end{aligned}$$

and if the convergence in (10) is uniform over x ∈ M for each $\alpha , \beta \in \mathbb N^n.$

Verifying that x ∈ M belongs to $\mathcal IS(M,g, \eta )$ is difficult to do directly, except on simple examples such as the flat torus. We briefly recall several settings in which $\mathcal {I}\mathcal {S}(M,g,\eta )$ is known to be large.

• Let S ⁿ be the n-sphere equipped with the round metric $g_{{ }_{S^n}}$. The Mehler–Heine asymptotics [24] imply that

  $$\displaystyle \begin{aligned}\mathcal{I}\mathcal{S}(S^n, g_{{}_{S^n}},0)=S^n,\end{aligned}$$

  when the limit in (10) is taken along the sequence of eigenvalues λ _j →∞ for the sphere. In this case, the ϕ _λ’s are known as random spherical harmonics.

• Let $\mathbb T^n$ be the n-dimensional torus equipped with the flat metric $g_{{ }_{\mathbb T^n}}$. When n ≥ 5 we have that $\mathcal {I}\mathcal {S}(\mathbb T^n, g_{{ }_{\mathbb T^n}},0)=\mathbb T^n.$ For 2 ≤ n ≤ 4, the asymptotics (10) hold at every $x \in \mathbb T^n$ but only for a density one subsequence of eigenvalues [13]. In this case, the ϕ _λ’s are known as random trigonometric polynomials.

• The pointwise Weyl law [17] implies that if lim_λ→∞η _λ = ∞, then $\mathcal {I}\mathcal {S}(M,g,\eta )=M$.

In addition, it is very likely that if (M, g) has no conjugate points, then the condition

$$\displaystyle \begin{aligned}\lim_{\lambda{\rightarrow} \infty}\log(\lambda)\cdot \eta_\lambda=\infty\end{aligned}$$

implies $\mathcal {I}\mathcal {S}(M,g, \eta )=M.$ This was proved by B. Keeler in [18], but with the convergence in (10) only holding for α = β = 0. Note that if (M, g) has negative sectional curvature everywhere, then it has no conjugate points and all points are non self-focal. In contrast, there exist smooth perturbations of the round metric on S ² for which $\mathcal {I}\mathcal {S}(S^2,g,1)\subsetneq S^2$ (see [23, 35]).

For x, y ∈ M let

$$\displaystyle \begin{aligned} \mathcal L_{x,y}=\{\xi \in S_{x}M:\; \exists t>0 \text{ s.t. }\exp_{x}(t\xi )=y\} \end{aligned} $$

(11)

be the set of directions that generate geodesic arcs from x to y. The set $\mathcal L_{x,y}$ is contained in S _xM and S _xM is endowed with the Liouville measure. The corresponding volume of $\mathcal L_{x,y}$ is denoted by $|\mathcal L_{x,y}|$.

The main result of this section is the following, and it was proved in [7, 9].

Theorem 1

Let (M, g) be a compact, smooth, Riemannian manifold, with no boundary. Let η be a non-negative function with liminf_λ→∞η _λ > 0. Let x ∈ M be so that ${\left | \mathcal L_{x,x} \right |}=0$. Then,

$$\displaystyle \begin{aligned} x\in \mathcal{I}\mathcal{S}(M,g,\eta). \end{aligned} $$

(12)

By [32, Lem 6.1], the condition that ${\left | \mathcal L_{x,x} \right |}=0$ for all x ∈ M is generic in the space of Riemannian metrics on a fixed compact smooth manifold M.

Definition 1 gives that if $x\in \mathcal {I}\mathcal {S}(M,g,\eta )$, then the scaling limit of waves in $\operatorname {\mathrm {RW}}_\lambda (M, g,\eta )$ around x is universal in the sense that it depends only on the dimension of M. In the language of Nazarov–Sodin [31] the asymptotics (10) imply that if $M=\mathcal {I}\mathcal {S}(M,g,\eta ),$ then the ensembles $\operatorname {\mathrm {RW}}_\lambda (M,g,\eta )$ have translation invariant local limits.

3 Number of Critical Points and Size of the Zero Set

Define the measures of integration over the zero set {ϕ _λ = 0} and the set of critical points {dϕ _λ = 0} by

$$\displaystyle \begin{aligned}Z_\lambda(\psi):= \int_{\phi_\lambda^{-1}(0)}\psi(x) d\sigma_{{}_{Z_\lambda}}(x)\qquad \text{and} \qquad \operatorname{\mathrm{{Crit}}}_\lambda(\psi):=\sum_{d\phi_\lambda(x)=0}\psi(x),\end{aligned}$$

where $\psi :M{\rightarrow }{\mathbb R}$ and $\sigma _{{ }_{Z_\lambda }}$ is the (n − 1)-dimensional Hausdorff measure over {ϕ _λ = 0}. This section is divided into two parts. In Section 3.1 we give asymptotics for ${\mathbb E}\left [Z_\lambda \right ]$ and ${\mathbb E}\left [ \operatorname {\mathrm {{Crit}}}_\lambda \right ]$, and bounds for their variances. The results in Section 3.1 rely heavily on a careful analysis of what happens for the scaled random waves $\phi ^x_\lambda$. The results for the localized waves are discussed in Section 3.2.

Previous results on the Hausdorff measure of the zero sets focus primarily on exactly solvable examples. On round spheres, for instance, Bérard [2] proved (14) (example (1) on p.3). Later, in the same setting, Neuheisel [25] and Wigman [33] obtained upper bounds for the variance that are of polynomial order in λ. Further, on S ², Wigman [34] found that the variance actually grows like $\lambda ^{-2}\log \lambda$ as λ →∞. On flat tori $\mathbb T^n$ (for exact eigenfunctions) Rudnick and Wigman [29] computed the expected value of the total Hausdorff measure of the zero set and gave an upper bound of the form $\lambda ^2(\dim (H_{0,\lambda }))^{-1/2}$ on its variance. Subsequently, on $\mathbb T^2$, Krishnapur, Kurlberg, and Wigman [19] found that the variance is asymptotic to a constant, while Marinucci, Peccati, Rossi, and Wigman proved that the size of the zero set converges to a limiting distribution that is not Gaussian and depends on the angular distribution of lattice points on circles [22].

The behavior of the number of critical points has been studied in detail on S ². Nicolaescu [26] studied the expected value of the number of critical points, obtaining (15). The variance was studied by Cammarota, Marinucci, and Wigman [6]. They obtain a polynomial upper bound. This upper bound was later improved by Cammarota and Wigman [5] who proved that the variance grows like $\lambda ^2 \log \lambda$ (as opposed to our λ ^7∕2 estimate) as λ →∞. Finally, for smooth domain in ${\mathbb R}^2,$ Nourdin–Peccati–Rossi [27] prove that both for real and complex random waves, the Hausdorff measure of the nodal set is asymptotically normal in the high frequency limit.

3.1 Global Statistics

The main result in this section gives asymptotics for the expected value, and estimates for the variance, of the linear statistics of Z _λ, Crit_λ that are valid for generic Riemannian metrics on M. For the estimates about the means of $Z_\lambda (\psi ), \operatorname {\mathrm {{Crit}}}_\lambda (\psi )$ one needs to ask that (M, g) be a manifold of isotropic scaling (see Definition 1). This is true for any manifold with negative curvature, or with no conjugate points. The variance estimates are more delicate, so one needs to ask in addition that the restrictions of ϕ _λ to small balls centered at different points become asymptotically uncorrelated. This is the following definition.

Definition 2

The random waves $\phi _\lambda \in \operatorname {\mathrm {RW}}_\lambda (M,g, \eta )$ are said to have short-range correlations if for each ε > 0 and every $\alpha , \beta \in \mathbb N$

$$\displaystyle \begin{aligned} \sup_{\{x,y: \, d_g(x,y) \geq \lambda^{-1+\varepsilon}\}} {\left| \nabla_x^\alpha\nabla_y^\beta \Pi_{\eta,\lambda}(x,y) \right|}=o_{\varepsilon}(\lambda^{\alpha + \beta}), \end{aligned} $$

(13)

as λ →∞, where ∇_x, ∇_y are covariant derivatives.

This condition is again generic in the space of Riemannian metrics on (M, g) and is satisfied for example if for any pair of points x, y ∈ M the measure of geodesic arcs joining them is zero. That is, if ${\left | \mathcal L_{x,y} \right |}=0$ for all x, y ∈ M, then the random waves in $\operatorname {\mathrm {RW}}_\lambda (M,g,\eta )$ have short-range correlations.

The condition that ${\left | \mathcal L_{x,y} \right |}=0$ for all x, y ∈ M is known to happen on manifolds of negative curvature, or more generally, with no conjugate points (see [8, Section 1.5]). It is likely that a similar argument would show that ${\left | \mathcal L_{x,y} \right |}=0$ for all x, y ∈ M is also generic but have not checked the details. It is known, however, that ${\left | \mathcal L_{x,y} \right |}=0$ holds for all x, y ∈ M if (M, g) is negatively curved or, more generally, has no conjugate points.

We are ready to state the main theorem of this section. This result was proved in [8].

Theorem 2

Let (M, g) be a smooth, compact, Riemannian manifold of dimension n ≥ 2 with no boundary. Let η = η(λ) be a non-negative function satisfying η(λ) = o(λ) as λ →∞. Let $\phi _\lambda \in \operatorname {\mathrm {RW}}_\lambda (M,g,\eta )$ and suppose that M is a manifold of isotropic scaling (Definition 1). Then, for any bounded measurable function $\psi :M{\rightarrow } {\mathbb R}$,

$$\displaystyle \begin{aligned} \lim_{\lambda{\rightarrow} \infty}\mathbb E \left[ \lambda^{-1} Z_\lambda(\psi) \right] = \frac{1}{\sqrt{\pi n}} \frac{\Gamma \left(\frac{n+1}{2} \right)}{\Gamma \left(\frac{n}{2} \right)} \int_M \psi(x) dv_g(x) \end{aligned} $$

(14)

and

$$\displaystyle \begin{aligned} \lim_{\lambda {\rightarrow} \infty}\mathbb E \left[ \lambda^{-n}\operatorname{\mathrm{Crit}}_\lambda(\psi) \right] = C_n\int_M \psi(x) dv_g(x), \end{aligned} $$

(15)

where C _n is a positive constant that depends only on n. Suppose further that ϕ _λ has short-range correlations in the sense of (13). Then,

$$\displaystyle \begin{aligned} \operatorname{\mathrm{Var}} \left[\lambda^{-1} Z_\lambda(\psi)\right] = O(\lambda^{-\frac{n-1}{2}}) \end{aligned} $$

(16)

and

$$\displaystyle \begin{aligned} \operatorname{\mathrm{Var}} \left[ \lambda^{-n}\operatorname{\mathrm{Crit}}_\lambda(\psi)\right]= O{\left(\lambda^{-\frac{n-1}{2}} \right)}, \end{aligned} $$

(17)

as λ→∞.

Theorem 2 is the first result with a non-trivial variance estimate for the Hausdorff measure of the nodal set of random waves for a generic smooth Riemannian manifold (for real analytic (M, g) a weaker estimate was given in [36, Cor. 2]). A version of (14) was also stated, with a heuristic proof, in [36, Prop. 2.3] for both Zoll and aperiodic manifolds.

We also note that the test function ψ in Theorem 2 can be replaced by a function ψ(x) = ψ(x, ϕ _λ(x), D ²ϕ _λ(x), …) depending on the jets of ϕ _λ provided $\psi :{\mathbb R}^n{\times } C^0({\mathbb R}^n, {\mathbb R}^k){\rightarrow } {\mathbb R}$ is bounded and continuous when $C^0({\mathbb R}^n,{\mathbb R}^k)$ is equipped with the topology of uniform convergence on compact sets. Hence, for example, we could study the distribution of critical values by taking $\psi (u, \phi _\lambda ) = \mathbf 1_{\{\phi _\lambda ^x\geq \alpha \}}(u)$, for $\alpha \in {\mathbb R}.$

In addition, the proof of Theorem 2 actually shows that (14) holds as soon as almost every point is a point of isotropic scaling. That is, it holds provided

$$\displaystyle \begin{aligned}\operatorname{\mathrm{vol}}_g(M\backslash \mathcal{I}\mathcal{S}(M,g,\eta))=0,\end{aligned}$$

(see Definition 1).

Furthermore, by the Borel–Cantelli Lemma, if n ≥ 4 and ϕ _j are independent frequency $j\in \mathbb N$ random waves on (M, g), then (16) shows that the total nodal set measure $j^{-1}Z_{j}(\psi )-{\mathbb E}\left [j^{-1}Z_{j}(\psi )\right ]$ converges almost surely to 0.

Finally, when n = 2 we have $C_2 = {\mathbb E}\left [ \operatorname {\mathrm {{Crit}}}_{\infty ,1}\right ]=\frac {1}{4\pi \sqrt {6}}$ where C ₂ is the dimensional constant in (15), see (25).

Theorem 2 hinges on a careful study of the statistics of ϕ _λ when restricted to “wavelength balls” of radius ≈ λ ⁻¹ around a fixed point x ∈ M of isotropic scaling. The results that describe the behavior of Z _λ or Crit_λ restricted to these shrinking balls are described in Sections 3.2.1 and 3.2.2, respectively. The results are “glued” to obtain Theorem 2. Glueing variance estimates is a delicate matter. It is instrumental to the proof that the waves have short-range correlations.

3.2 Local Statistics

In this section we discuss the behavior of the zero sets and of the critical points for the scaled waves $\phi _\lambda ^x$. When x is a point of isotropic scaling the behavior of the scaled random wave $\phi _\lambda ^x$ converges to that of the random planar wave $\phi _\infty ^x\in \operatorname {\mathrm {RW}}_1(T_{x}M, g_{x})$. One can therefore prove much stronger results on statistics for $\phi _\lambda ^x$ than ϕ _λ.

3.2.1 Local Universality of Zeros

Consider the rescaled random wave $\phi _\lambda ^{x}$ for $x\in \mathcal IS(M,g,\eta )$ and denote by $Z_\lambda ^{x}$ its Riemannian hypersurface (i.e. Hausdorff) measure:

$$\displaystyle \begin{aligned}Z_\lambda^x(A): = \sigma_{{}_{Z_\lambda}}\!\!{\left({\left(\phi_\lambda^{x} \right)}^{-1}(0)\,\cap\, A \right)},\qquad \forall A\subseteq T_{x}M\text{ measurable}.\end{aligned}$$

The main result concerns the restriction of $Z_{\lambda }^{x}$ to various balls B _r of radius r centered at 0 ∈ T _xM. We set

$$\displaystyle \begin{aligned} Z_{\lambda, r}^{x}:= \frac{\mathbf 1_{B_r} \cdot Z_\lambda^x}{\text{vol}( B_r)} \qquad \text{and}\qquad Z_{\infty, r}^x:=\frac{\mathbf 1_{B_r}\cdot Z_\infty^{x}}{\text{vol}( B_r)}. \end{aligned} $$

(18)

We have denoted by $\mathbf 1_{B_r}$ the characteristic function of the ball B _r and by $Z_\infty ^{x}$ the hypersurface measure on $(\phi _\infty ^{x})^{-1}(0)$ for $\phi _\infty ^{x}\in \operatorname {\mathrm {RW}}_1(T_{x}M, g_{x}).$ Again, for various measures μ, we write μ(ψ) for integration of a measurable function ψ against μ. In particular,

$$\displaystyle \begin{aligned}Z_{\lambda, r}^{x}(1)= \frac{\mathcal H^{n-1}{\left({\left(\phi_\lambda^{x} \right)}^{-1}(0)\,\cap\, B_r \right)}}{\text{vol}( B_r) }.\end{aligned}$$

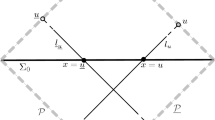
The following result is proved in [8]. See Figure 3 for a depiction of the statement.

Fig. 3

Depiction of the universal behavior displayed by monochromatic random waves. The zero set measure for the monochromatic random wave on the sphere (left) converges to the zero set measure for the random planar wave (right)

Theorem 3 (Weak Convergence of Zero Set Measures)

Let (M, g) be a smooth, compact, Riemannian manifold of dimension n ≥ 2 with no boundary. Let η = η(λ) be a non-negative function satisfying η(λ) = o(λ) as λ →∞. Fix a non-negative function r _λ that satisfies r _λ = o(λ) as λ→∞. Let $\phi _\lambda \in \operatorname {\mathrm {RW}}_\lambda (M,g,\eta )$ and $x \in \mathcal {I}\mathcal {S}(M,g,\eta )$. Suppose lim_λ→∞r _λ exists and equals r _∞∈ (0, ∞].

Case 1(r _∞ < ∞): :

The measures $Z_{\lambda , r_\lambda }^{x}$ converge to $Z_{\infty , r_\infty }^x$ weakly in distribution. That is, for any bounded, measurable function $\psi :T_{x}M{\rightarrow } {\mathbb R}$

$$\displaystyle \begin{aligned} Z_{\lambda, r_\lambda}^x(\psi)\quad \stackrel{d}{\longrightarrow} \quad Z_{\infty, r_\infty}^x(\psi) \end{aligned} $$

(19)

as λ →∞, where $\stackrel {d}{\longrightarrow }$ denotes convergence in distribution.

Case 2(r _∞ = ∞): :

We have the following convergence in probability to a constant:

$$\displaystyle \begin{aligned} Z_{\lambda, r_\lambda}^x(1) \quad \stackrel{p}{\longrightarrow} \quad \frac{1}{\sqrt{\pi n}} \frac{\Gamma \left(\frac{n+1}{2} \right)}{\Gamma \left(\frac{n}{2} \right)}, \end{aligned} $$

(20)

as λ→∞. In particular,

$$\displaystyle \begin{aligned} \lim_{\lambda{\rightarrow} \infty}\operatorname{\mathrm{Var}}\left[Z_{\lambda, r_\lambda}^x(1)\right]=0. \end{aligned} $$

(21)

The function ψ in (19) can be allowed to depend on the jets D ^jϕ _λ, j ≥ 1. More precisely, ψ(u) can be replaced by ψ(u, W(u)), where W is a random field so that $u\mapsto (\phi _\lambda ^x(u), W(u))$ is a continuous Gaussian field with values in ${\mathbb R}^{1 + k}$ and $\psi :{\mathbb R}^n{\times } C^0({\mathbb R}^n, {\mathbb R}^k){\rightarrow } {\mathbb R}$ is bounded and continuous when $C^0({\mathbb R}^n, {\mathbb R}^k)$ is equipped with the topology of uniform convergence on compact sets. Since $(\phi _\lambda ^x(u), D\phi _\lambda ^x(u), D^2\phi _\lambda ^x(u),\ldots )$ is a smooth Gaussian field, we may take $W(u)={\left (D^j\phi _\lambda (u),\,j\geq 1 \right )}.$ Similarly, in (20) and (21), the function 1 = 1(u) can be replaced by ψ(W(u)) where again $\psi :C^0({\mathbb R}^n,{\mathbb R}^k){\rightarrow } {\mathbb R}$ is bounded and continuous in the topology of uniform convergence on compact sets. The only difference is that (20) then reads

$$\displaystyle \begin{aligned}Z_{\lambda, r_\lambda}^x(\psi) -{\mathbb E}\left[Z_{\infty,r_\lambda}^x(\psi)\right] \quad \stackrel{p}{\longrightarrow} \quad 0. \end{aligned}$$

The relations (20) and (21) hold even if the balls $B_{r_\lambda }$ in the definition of $Z_{\lambda , r_\lambda }^{x}$ are replaced by any λ −dependent sets $A_{\lambda ,r_\lambda }$ for which the diameter is bounded above and below by constant times r _λ, and whose volume tends to infinity when r _λ→∞.

The rates of convergence in (19)–(21) - even after the generalizations indicated above- are uniform as x varies over a compact set $S\subset \mathcal {I}\mathcal {S}(M,g,\eta )$ as long as the convergence in (10) is uniform over S.

3.2.2 Local Universality of Critical Points

Let x ∈ M and for each r > 0 define the normalized counting measure

$$\displaystyle \begin{aligned} \operatorname{\mathrm{{Crit}}}_{\lambda,r}^x:=\frac{1}{\operatorname{\mathrm{vol}}(B_r)}\sum_{\substack{d\phi_\lambda^x(u)=0\\ u \in B_r}} \delta_u {} \end{aligned} $$

(22)

of critical points in a ball of radius r. We define $\operatorname {\mathrm {{Crit}}}_{\infty , r}^{x}$ in the same way as $\operatorname {\mathrm {{Crit}}}_{\lambda , r}^{x}$ but with $\phi _\lambda ^{x}$ replaced by $\phi _\infty ^{x}\in \operatorname {\mathrm {RW}}_1(T_{x}M, g_{x}),$ and continue to write μ(ψ) for the pairing of a measure μ with a function ψ. For example,

$$\displaystyle \begin{aligned}\operatorname{\mathrm{{Crit}}}_{\lambda,r}^x(1)=\frac{\#\{ u \in B_r: \; d\phi_\lambda^{x}(u)=0 \}}{\operatorname{\mathrm{vol}}(B_r)}.\end{aligned}$$

Theorem 4

Let (M, g) be a smooth, compact, Riemannian manifold of dimension n ≥ 2 with no boundary. Let η = η(λ) be a non-negative function satisfying η(λ) = o(λ) as λ →∞. Fix a non-negative function r _λ that satisfies r _λ = o(λ) as λ→∞. Let $\phi _\lambda \in \operatorname {\mathrm {RW}}_\lambda (M,g,\eta )$ and $x \in \mathcal {I}\mathcal {S}(M,g,\eta )$. Suppose that lim_λ→∞r _λ exists and equals r _∞∈ (0, ∞].

Case 1. (r _∞ < ∞): :

For k = 1, 2 and each bounded measurable function $\psi :T_xM\to {\mathbb R}$

$$\displaystyle \begin{aligned} \lim_{\lambda \to \infty}{\mathbb E}\left[\operatorname{\mathrm{{Crit}}}_{\lambda, r_\lambda}^{x}(\psi)^k\right]= {\mathbb E}\left[\operatorname{\mathrm{{Crit}}}_{\infty,r_\infty}^{x}(\psi)^k\right]. \end{aligned} $$

(23)

Case 2. (r _∞ = ∞): :

We have

$$\displaystyle \begin{aligned} \lim_{\lambda{\rightarrow} \infty}\operatorname{\mathrm{Var}}[\operatorname{\mathrm{{Crit}}}_{\lambda, r_\lambda}^{x}(1)]={\mathbb E}\left[\operatorname{\mathrm{{Crit}}}_{\infty,1}^{x}(1)\right]. \end{aligned} $$

(24)

This limit is the expected number of critical points in a ball of radius 1 for frequency 1 random waves on ${\mathbb R}^n,$ which is independent of x.

The moments ${\mathbb E}\left [( \operatorname {\mathrm {{Crit}}}_{\infty , r_\infty }^{x}(\psi ))^k\right ]$ are finite for k = 1, 2. In particular, if $\dim (M)=2,$ then for every x ∈ M

$$\displaystyle \begin{aligned} {\mathbb E}\left[ \operatorname{\mathrm{{Crit}}}_{\infty,1}^x(1)\right]=\frac{1}{4\pi \sqrt{6}}. \end{aligned} $$

(25)

The balls $B_{r_\lambda }$ in (24) can be replaced by any λ −dependent sets $A_{\lambda ,r_\lambda }$ for which the diameter is bounded above and below by a constant times r _λ and whose volume tends to infinity with r _λ.

Both ψ in (23) and the function 1 being integrated against $\operatorname {\mathrm {{Crit}}}_{\lambda , r_\lambda }^x$ in (24) can be replaced by a bounded continuous function of the jets of ϕ _λ, giving information for instance about critical points filtered by critical value.

Also, the rates of convergence in (23) and (24) are uniform over $x\in S\subset \mathcal {I}\mathcal {S}(M,g, \eta )$ if (10) is uniform over S.

On the n-dimensional flat torus, Nicolaescu [26] obtained several results related to Theorem 4 in the r _∞ < ∞ case.

4 Structure of the Zero Set

Let (M, g) be a Riemannian manifold, and let ϕ be an eigenfunction for the Laplace operator. The zero set ϕ ⁻¹(0) = {x ∈ M :  ϕ(x) = 0} decomposes into a collection of connected components which we denote by $\mathcal C(\phi )$. See Figure 4. Our interest is in the diffeomorphism types of the components in $\mathcal C(\phi )$. For generic ϕ the components of $\mathcal C(\phi )$ are smooth (n − 1)-dimensional manifolds. The connected components of M∖ϕ ⁻¹(0) are the nodal domains of ϕ and our interest is in their nesting properties, again for generic ϕ.

Fig. 4

Zero set of a random planar wave in ${ \mathbb R}^3$. Picture created by A. Barnett

The results presented in this section build on the ground breaking work of Nazarov–Sodin [31]. They studied the number of nodal domains for monochromatic random waves on manifolds with isotropic scaling. They proved that there exists a positive constant C so that the mean number of nodal domains for ϕ _λ grows like Cλ ⁿ. The approach of [10, 30] to study the diffeomorphism types of the zero set components is very similar in spirit to the work [31] as the rationale is that one is counting components of the zero set with a given diffeomorphism type. A similar argument is carried to deal with the nesting configurations.

The argument developed by Nazarov–Sodin hinges on the fact that most zero set components lie within a ball of radius R∕λ for R > 0 large enough. One can therefore count the number of components of $\phi _\lambda ^x$ within the ball B(0, R) ⊂ T _xM. The latter is done using the universal behavior of $\phi _\lambda ^x$ guaranteed by the fact that M is a manifold of isotropic scaling.

The works of Gayet–Welshinger [14,15,16] are also very related to the results described in this section, only that they are not applicable to monochromatic random waves.

4.1 Diffeomorphism Types

Let $\mathcal D_{n-1}$ denote the (countable and discrete) set of diffeomorphism classes of compact connected smooth (n − 1)-dimensional manifolds that can be embedded in ${\mathbb R}^n$. The compact components c in $\mathcal C(\phi )$ give rise to elements D(c) in $\mathcal D_{n-1}$ (here we are assuming that ϕ is generic with respect to a Gaussian measure so that ϕ ⁻¹(0) is smooth).

Let $\phi _\lambda \in \operatorname {\mathrm {RW}}(M,g,\eta )$. The diffeomorphism types exhibited by the components of $\phi _\lambda ^{-1}(0)$ are described by the probability measure $\mu _{{ }_{\mathcal {D}(\phi _\lambda )}}$ on $\mathcal D_{n-1}$ given by

$$\displaystyle \begin{aligned}\mu_{{}_{\mathcal{D}(\phi_\lambda)}}:= \frac{1}{|\mathcal C(\phi_\lambda)|} \sum_{c \in \mathcal C(\phi_\lambda)} \delta_{{}_{D(c)}},\end{aligned}$$

where $\delta _{{ }_{D}}$ is a point mass at $D\in \mathcal {D}_{n-1}$. The following is part of the main theorem in [30, Theorem 1.1].

Theorem 5

There exists a probability measure $\mu _{{ }_{\mathcal {D}}}$ supported on $\mathcal D_{n-1}$ such that the following holds. Let (M, g) be a smooth, compact, Riemannian manifold of dimension n ≥ 2 with no boundary. Let η = η(λ) be a non-negative function satisfying η(λ) = o(λ) as λ →∞. Suppose that M is a manifold of isotropic scaling. Then, for any given $D \in \mathcal D_{n-1}$ and ε > 0,

$$\displaystyle \begin{aligned}\lim_{\lambda \to \infty}{\mathbb P}\Big(\phi_\lambda\in \operatorname{\mathrm{RW}}_\lambda(M,g, \eta):\,|\mu_{{}_{\mathcal{D}(\phi_\lambda)}}(D)- \mu_{{}_{\mathcal{D}}}(D)|>\varepsilon\Big)=0.\end{aligned}$$

The theorem asserts that there exists a probability measure $\mu _{{ }_{\mathcal {D}}}$ on $\mathcal D_{n-1}$ to which $\mu _{\mathcal D(\phi )}$ approaches as λ →∞, for almost all ϕ. The probability measure $\mu _{{ }_{\mathcal {D}}}$ is universal in that it only depends on the dimension n of M.

For n ≥ 4, little is known about the space $\mathcal D_{n-1}$. In particular, there is no classification for the diffeomorphism types of (n − 1)-dimensional smooth manifolds. This makes it difficult to study the support of $\mu _{{ }_{\mathcal {D}}}$. Remarkably, it is possible to prove that the support of $\mu _{{ }_{\mathcal {D}}}$ is all of $\mathcal D_{n-1}$. This result is proved in [10].

Theorem 6

Every atom of $\mathcal D_{n-1}$ is positively charged by $\mu _{{ }_{\mathcal {D}}}$ . That is,

$$\displaystyle \begin{aligned}\operatorname{\mathrm{supp}}(\mu_{{}_{\mathcal{D}}})=\mathcal D_{n-1}.\end{aligned}$$

Theorem 6 asserts that every diffeomorphism type that can occur will do so with a positive probability for the universal distribution of topological types of random monochromatic waves in [30].

The proof of Theorem 6 relies on the fact that for a manifold of isotropic scaling the statistics of $\phi _\lambda ^x$ converge to those of $\phi _\infty ^x$ for every x ∈ M. Indeed, the proof reduces to establishing the following result.

Theorem 7

Given $D \in \mathcal D_{n-1}$ there exists $\phi \in \ker (\Delta _{{\mathbb R}^n}-\mathit{\text{Id}})$ and $c\in \mathcal C(\phi )$ for which D(c) = D.

Theorem 7 is of basic interest in the understanding of the possible shapes of nodal sets and domains of eigenfunctions in ${\mathbb R}^n$ (it applies equally well to any eigenfunction with eigenvalue λ ² > 0 instead of 1). To prove Theorem 7 one applies Whitney’s approximation Theorem to realize c as an embedded real analytic submanifold of ${\mathbb R}^n$. Then, following some techniques in [12] one can find suitable approximations of $\phi \in \ker (\Delta _{g_{{\mathbb R}^n}}-1)$ and whose zero set contains a diffeomorphic copy of c. The construction of ϕ hinges on the Lax–Malgrange Theorem and Thom’s Isotopy Theorem.

The reduction from Theorem 7 to Theorem 6 is abstract and is based on the “soft” techniques in [30, 31]. In particular, it offers us no lower bounds for these probabilities. Developing such lower bounds is an interesting problem.

4.2 Nesting Configurations

Let ϕ be a Laplace eigenfunction for a Riemannian manifold (M, g). The connected components of M∖ϕ ⁻¹(0) are the nodal domains of ϕ and our interest is in their nesting properties, again for generic ϕ. Let ${\mathcal {U}}$ be a coordinate patch for M. The components of $\mathcal C(\phi )$ that are contained in $\mathcal U$ are denoted by $\mathcal C_{{ }_{\mathcal U}}(\phi )$. To each compact $c \in \mathcal C_{{ }_{\mathcal U}}(\phi )$ we associate a finite connected rooted tree as follows. By the Jordan–Brouwer separation Theorem each component $c \in \mathcal C(\phi )$ has an exterior and interior. We choose the interior to be the end that is contained within $\mathcal U$. The nodal domains of ϕ, which are in the interior of c, are taken to be the vertices of a graph. Two vertices share an edge if the respective nodal domains have a common boundary component (unique if there is one). This gives a finite connected rooted tree denoted T(c); the root being the domain adjacent to c (see Figure 5).

Fig. 5

This picture shows a nodal domain configuration, where positive nodal domains are depicted in orange and negative nodal domains are green. The corresponding rooted tree is shown

The reason for working in a coordinate patch $\mathcal U$ for M is that for general (M, g) there is no global way to define a tree that describes the nesting configuration of the zero set in all of M, for all c ∈ C(ϕ). The reason is that a zero set component may not divide M into two different regions. It is important to note that in a coordinate patch this is always the case. However, according to [31] almost all c’s localize to small coordinate patches. This inconvenience is the reason why [10] is written for M = S ⁿ the round sphere. By the Jordan–Brouwer separation Theorem, on S ⁿ every component of the zero set separates S ⁿ into two distinct components. This gives that the nesting graph for the zero sets is a rooted tree well defined without the need for a coordinate patch.

Let $\mathcal T$ be the collection (countable and discrete) of finite connected rooted trees. The distribution of nested ends of nodal domains of ϕ that lie within $\mathcal U$ is described by the measure $\mu _{{ }_{\mathcal T(\phi ),\mathcal U}}$ on $\mathcal T$ given by

$$\displaystyle \begin{aligned}\mu_{{}_{\mathcal T(\phi),\mathcal U}}:= \frac{1}{|\mathcal C_{{}_{\mathcal U}}(\phi)|} \sum_{c \in \mathcal C_{{}_{\mathcal U}}(\phi)} \delta_{{}_{T(\phi)}},\end{aligned}$$

where $\delta _{{ }_{T}}$ is the point mass at $T \in \mathcal T$.

The following is part of the main theorem in [30, Theorem 1.1]. Also, see [10, Remark 2].

Theorem 8

There exists a probability measure $\mu _{{ }_{\mathcal T}}$ supported on $\mathcal T$ such that the following holds. Let (M, g) be a smooth, compact, Riemannian manifold of dimension n ≥ 2 with no boundary. Let η = η(λ) be a non-negative function satisfying η(λ) = o(λ) as λ →∞. Suppose that M is a manifold of isotropic scaling and let $\mathcal U$ be a coordinate patch for M. Then, for any given $T \in \mathcal T$ and ε > 0,

$$\displaystyle \begin{aligned}\lim_{\lambda \to \infty}{\mathbb P}\Big(\phi_\lambda\in \operatorname{\mathrm{RW}}_\lambda(M,g, \eta):\,|\mu_{{}_{\mathcal T(\phi),\mathcal U}}(T)- \mu_{{}_{\mathcal T}}(T)|>\varepsilon\Big)=0.\end{aligned}$$

Theorem in [30] asserts that there exists a probability measure $\mu _{{ }_{\mathcal T}}$ on $\mathcal T$ to which $\mu _{{ }_{\mathcal T(\phi ),\mathcal U}}$ approaches as λ →∞, for almost all ϕ provided M is a manifold of isotropic scaling.

The probability measure $\mu _{\mathcal T}$ is universal in that it only depends on the dimension n of M. The following result is part of theorem in [10] and deals with the support of $\mu _{{ }_{\mathcal T}}$.

Theorem 9

Every atom of $\mathcal T$ is positively charged by $\mu _{\mathcal T}$ . That is,

$$\displaystyle \begin{aligned}\operatorname{\mathrm{supp}}(\mu_{{}_{\mathcal T}})=\mathcal T.\end{aligned}$$

The proof of Theorem 9 hinges on the fact that any rooted tree can be realized by elements of $\ker (\Delta _{{\mathbb R}^n}-I)$ as described by the following result.

Theorem 10

Given $T \in \mathcal T$ there exists $\phi \in \ker (\Delta _{{\mathbb R}^n}-\mathit{\text{Id}})$ and $c \in \mathcal C(\phi )$ for which T(c) = T.

As far as Theorem 10, the case n = 2 is resolved in [30] using a deformation of $\sin {}(\pi x)\sin {}(\pi y)$ and a combinatorial chess board type argument. This is described in Figure 6. In higher dimensions, for example n = 3, one proceeds by deforming

$$\displaystyle \begin{aligned} \psi(x,y,z)=\sin{}(\pi x)\sin (\pi y)\sin (\pi z). \end{aligned}$$

This ψ has enough complexity to produce all elements in $\mathcal T$ after deformation. However, it is much more difficult to study than the 2-dimensional case. Unlike $\sin {}(\pi x)\sin {}(\pi y)$, the zero set ψ ⁻¹(0) has point and 1-dimensional edge singularities. The analysis of its resolution under deformation requires a lot of care, especially as far as engineering elements of $\mathcal T$. The pay off as we noted is that it is rich enough to prove Theorem 10.

Fig. 6

This picture shows how to perturb the zero set of $\psi (x,y)=\sin {}(x)\sin {}(y)$ by adding $h \in \ker (\Delta _{{ }_{{ \mathbb R}^n}} -I)$ that we prescribe on the singularities of ψ that lie in its zero set so that the zero set of ϕ = ψ + εh, for ε > 0 small, has the correct nesting configuration