Keywords

1 Introduction

In data classification tasks, the data instances that are uncertain to be classified form the main cause of prediction error [2, 9, 23]. Certain classification methods strictly assign a class label to each instance, which may produce farfetched classification results for uncertain instances. Uncertain classification methods aim to measure the uncertainty of data instances and accordingly reject uncertain cases [3, 10, 15]. The methodology of uncertain classification is helpful to reduce the decision risk and involve domain knowledge in classification process [21, 22, 24]. For instance, in decision support for cancer diagnosis, filtering out uncertain cases for further cautious identification, may allow us to avoid serious misdiagnosis [1].

Due to their very good performance, deep neural networks have been widely used in the classification of complex data [14, 17], such as various kinds of medical images. However, most existing deep neural networks lack a strategy to handle uncertain data and may produce serious classification mistakes. For example, classifying CT images using convolutional neural networks without considering uncertainty may lead to overconfident decisions.

Trying to implement uncertain data classification based on deep neural networks, Geifman and El-Yaniv propose a selective classification method with deep neural networks, in which a selection function is constructed to quantify the reliability of predictions [8, 11]. The method relies on the quality of the selection function. If the quantification of reliability is not accurate, the identification of uncertain data cannot be guaranteed. Dempster-Shafer (D-S) evidence theory [5] is also used to measure the uncertainty in machine learning models [6, 7, 20]. Sensoy, Kaplan and Kandemir formulate the uncertainty in deep neural networks from the view of evidence theory [18]. Moreover, evidential neural networks have been constructed and applied for the uncertain classification of medical images [13, 19]. However, if the decision costs of different classes are imbalanced, evidential neural networks are not effective to classify the uncertain data instances of the risky class.

To address these problems, we construct a novel evidential deep neural network model and propose an uncertain data classification method. We formalize the uncertainty of the prediction output with evidence theory. A strategy to adjust the uncertainty in classification is also designed to improve the identification of certain and uncertain data instances in the risky class. The contributions of this paper are summarized as follows:

  • Propose a novel evidential deep neural networks with the loss objective of both prediction error and evidence adjustment;

  • An uncertain data classification method based on evidential deep neural networks (EviNet-UC) is proposed and applied to medical image diagnosis.

The rest of this paper is organized as follows. Section 2 presents the uncertain data classification method with evidential deep neural networks, which includes the model description and the strategy for uncertain data identification. In Sect. 3, we apply the proposed uncertain classification method to medical image data sets and show that the proposed method is effective to reduce the decision costs. Conclusions are given in Sect. 4.

2 Uncertain Data Classification with Evidential Deep Neural Networks

Given a dataset \(\mathcal {D}=\left\{ x_{i}, y_{i}\right\} _{i=1}^{N}\) of N labeled data instances where \(y_{i}\) is the class label of the instance \(x_{i}\), the loss of data classification with the evidential deep neural networks consists of the prediction error term \(L_{i}^{p}\) and the evidence adjustment term \(L_{i}^{e}\) as

$$\begin{aligned} L=\frac{1}{N} \sum _{i=1}^{N}\left( L_{i}^{p}+\lambda * L_{i}^{e}\right) , \end{aligned}$$
(1)

where \(\lambda =\min (1.0, t/10)\) is the annealing coefficient to balance the two terms, t is the index of the current training epoch. At the beginning of model training, \(\lambda <1\) makes the network focus on reducing the prediction error. When \(t \ge 10\) the two terms play equal roles in the loss.

2.1 Prediction Error

For the binary classification of \(x_{i}\), we define the model output \(e_{i}^{+}, e_{i}^{-}\) as the evidence collected by the deep neural network for the positive and negative classes. The sum of the total evidence is \(E=e_{i}^{+}+e_{i}^{-}+2\). According to the evidence, we define the belief values of \(x_{i}\) belonging to positive and negative classes as \(b_{i}^{+}=e_{i}^{+}/E, b_{i}^{-}=e_{i}^{-}/E\), the uncertainty of classification is defined as \(u_{i}=1-b_{i}^{+}-b_{i}^{-}\). Similar to the model proposed in [13], we adopt Beta distribution to formulate the distribution of the prediction with the evidences \(e_{i}^{+}, e_{i}^{-}\). Suppose \(p_{i}\) is the prediction of the instance \(x_{i}\) belonging to the positive class, the probability density function of the prediction is

$$\begin{aligned} f\left( p_{i}; \alpha _{i}, \beta _{i}\right) =\frac{\varGamma \left( \alpha _{i}+\beta _{i}\right) }{\varGamma \left( \alpha _{i}\right) \varGamma \left( \beta _{i}\right) } p_{i}^{\alpha _{i}-1}\left( 1-p_{i}\right) ^{\beta _{i}-1} d p_{i}, \end{aligned}$$
(2)

where the parameters of Beta distribution are \(\alpha _{i}=e_{i}^{+}+1, \beta _{i}=e_{i}^{-}+1\) and \(\varGamma (\cdot )\) is the gamma function. The prediction of the positive class can be obtained by \(p_{i}=\alpha _{i}/E\) and \(1-p_{i}=\beta _{i}/E\) denotes the prediction of negative class.

Based on the probability density of the prediction, we construct the prediction error term for each data instance \(x_{i}\) as the following expectation of squared error,

$$\begin{aligned} L_{i}^{p}&=\int \left\| p_{i}-y_{i}\right\| ^{2} f\left( p_{i}; \alpha _{i}, \beta _{i}\right) d p_{i} \end{aligned}$$
(3)
$$\begin{aligned}&=\int \left\| p_{i}-y_{i}\right\| ^{2} \frac{\varGamma \left( \alpha _{i}+\beta _{i}\right) }{\varGamma \left( \alpha _{i}\right) \varGamma \left( \beta _{i}\right) } p_{i}^{\alpha _{i}-1}\left( 1-p_{i}\right) ^{\beta _{i}-1} d p_{i}. \end{aligned}$$
(4)

Referring to the properties of the expectation and variance of Beta distribution, the formula (4) can be derived as

$$\begin{aligned} L_{i}^{p}&=\int \left\| p_{i}-y_{i}\right\| ^{2} \frac{\varGamma \left( \alpha _{i}+\beta _{i}\right) }{\varGamma \left( \alpha _{i}\right) \varGamma \left( \beta _{i}\right) } p_{i}^{\alpha _{i}-1}\left( 1-p_{i}\right) ^{\beta _{i}-1} d p_{i} \end{aligned}$$
(5)
$$\begin{aligned}&=E\left( \left\| p_{i}-y_{i}\right\| ^{2}\right) \end{aligned}$$
(6)
$$\begin{aligned}&=E\left( p_{i}\right) ^{2}-2 y_{i} E\left( p_{i}\right) +y_{i}^{2}+{\text {var}}\left( p_{i}\right) \end{aligned}$$
(7)
$$\begin{aligned}&=\left( E\left( p_{i}\right) -y_{i}\right) ^{2}+{\text {var}}\left( p_{i}\right) \end{aligned}$$
(8)
$$\begin{aligned}&=\left( y_{i}-\frac{\alpha _{i}}{\alpha _{i}+\beta _{i}}\right) ^{2}+\left( 1-y_{i}-\frac{\beta _{i}}{\alpha _{i}+\beta _{i}}\right) ^{2}+\frac{\alpha _{i} \beta _{i}}{\left( \alpha _{i}+\beta _{i}\right) ^{2}\left( \alpha _{i}+\beta _{i}+1\right) }. \end{aligned}$$
(9)

2.2 Evidence Adjustment

Besides the prediction error, the uncertain cases in the classification should also be considered in real application scenarios. Identifying uncertain data instances for abstaining from classification is helpful to reduce the decision risk. In [13], a regularization term is integrated into the objective of neural network to reduce the evidences of uncertain instances. But this strategy ignores the difference of the risks of uncertain instances from different classes. To find out the uncertain instances of risky class effectively, we expect to rescale the data uncertainty u through adjusting the evidence and add an evidence adjustment term into the loss objective. The evidence adjustment term is constructed by the Kullback-Leibler divergence between the distributions of prediction with original and adjusted evidences. We also adopt the Beta distribution for the prediction with adjusted evidences and define \(\lambda >1\) as the evidence adjustment factor. The evidence adjustment term is expressed as

$$\begin{aligned} L_{i}^{e}=K L\left( f\left( p_{i} ; \tilde{\alpha }_{i}, \tilde{\beta }_{i}\right) | f\left( p_{i} ; 1, \tilde{\lambda }\right) \right) ,\end{aligned}$$
(10)

where \((1, \tilde{\lambda })=\left( 1, y_{i} \lambda +\left( 1-y_{i}\right) \right) \), \(\left( \tilde{\alpha }_{i}, \tilde{\beta }_{i}\right) =\left( \left( 1-y_{i}\right) \alpha _{i}+y_{i}, y_{i} \beta _{i}+\left( 1-y_{i}\right) \right) \) are the parameters of the Beta distributions of the prediction \(p_{i}\) with adjusted and original evidences.

Let ‘1’ denote the positive class and ‘0’ denote the negative class. When the instance \(x_{i}\) belongs to positive class, \(y_{i}=1,(1, \tilde{\lambda })=(1, \lambda )\) and \(\left( \tilde{\alpha }_{i}, \tilde{\beta }_{i}\right) =\left( 1, \beta _{i}\right) \). If \(x_{i}\) belongs to negative class, \(y_{i}=0,(1, \tilde{\lambda })=(1,1)\) and \(\left( \tilde{\alpha }_{i}, \tilde{\beta }_{i}\right) =\left( \alpha _{i}, 1\right) \). For a negative-class instance, the adjustment term guides the parameter \(\alpha _{i}\) to 1 and thereby reduce the evidence of positive class to 0. For a positive-class instance, the adjustment term guides the parameter \(\beta _{i}\) to \(\lambda \). This will force the neural networks to promote the positive-class evidence for certain positive instances to reduce the prediction error.

According to the definition of KL divergence, the evidence adjustment term can be further simplified as

$$\begin{aligned} L_{i}^{e}&=\int f\left( p_{i} ; \tilde{\alpha }_{i}, \tilde{\beta }_{i}\right) \log \frac{f\left( p_{i} ; \tilde{\alpha }_{i}, \tilde{\beta }_{i}\right) }{f\left( p_{i} ; 1, \tilde{\lambda }\right) } d p_{i} \end{aligned}$$
(11)
$$\begin{aligned}&=\int f\left( p_{i} ; \tilde{\alpha }_{i}, \tilde{\beta }_{i}\right) \log f\left( p_{i} ; \tilde{\alpha }_{i}, \tilde{\beta }_{i}\right) d p_{i}-\int f\left( p_{i} ; \tilde{\alpha }_{i}, \tilde{\beta }_{i}\right) \log f\left( p_{i} ; 1, \tilde{\lambda }\right) d p_{i} \end{aligned}$$
(12)
$$\begin{aligned}&=E\left( \log f\left( p_{i} ; \tilde{\alpha }_{i}, \tilde{\beta }_{i}\right) \right) -E_{B\left( \tilde{\alpha }_{i} \tilde{\beta }_{i}\right) }\left( \log f\left( p_{i} ; 1, \tilde{\lambda }\right) \right) . \end{aligned}$$
(13)

Referring to the properties of Beta distribution, the expectations in (13) can be further derived for computation as

$$\begin{aligned}&E\left( \log f\left( p_{i} ; \tilde{\alpha }_{i}, \tilde{\beta }_{i}\right) \right) \end{aligned}$$
(14)
$$\begin{aligned} =&E\left( \log \frac{\varGamma \left( \tilde{\alpha }_{i}+\tilde{\beta }_{i}\right) }{\varGamma \left( \tilde{\alpha }_{i}\right) \varGamma \left( \tilde{\beta }_{i}\right) } p_{i}^{\tilde{\alpha }_{i}-1}\left( 1-p_{i}\right) ^{\tilde{\beta }_{i}-1}\right) \end{aligned}$$
(15)
$$\begin{aligned} =&E\left( \log \frac{\varGamma \left( \tilde{\alpha }_{i}+\tilde{\beta }_{i}\right) }{\varGamma \left( \tilde{\alpha }_{i}\right) \varGamma \left( \tilde{\beta }_{i}\right) }+\left( \tilde{\alpha }_{i}-1\right) \log p_{i}+\left( \tilde{\beta }_{i}-1\right) \log \left( 1-p_{i}\right) \right) \end{aligned}$$
(16)
$$\begin{aligned} =&\log \frac{\varGamma \left( \tilde{\alpha }_{i}+\tilde{\beta }_{i}\right) }{\varGamma \left( \tilde{\alpha }_{i}\right) \varGamma \left( \tilde{\beta }_{i}\right) }+\left( \tilde{\alpha }_{i}-1\right) E\left( \log p_{i}\right) +\left( \tilde{\beta }_{i}-1\right) E\left( \log \left( 1-p_{i}\right) \right) \end{aligned}$$
(17)
$$\begin{aligned} =&\log \frac{\varGamma \left( \tilde{\alpha }_{i}+\tilde{\beta }_{i}\right) }{\varGamma \left( \tilde{\alpha }_{i}\right) \varGamma \left( \tilde{\beta }_{i}\right) }+\left( 2-\tilde{\alpha }_{i}-\tilde{\beta }_{i}\right) \psi \left( \tilde{\alpha }_{i}+\tilde{\beta }_{i}\right) +\left( \tilde{\alpha }_{i}-1\right) \psi \left( \tilde{\alpha }_{i}\right) +\left( \tilde{\beta }_{i}-1\right) \psi \left( \tilde{\beta }_{i}\right) , \end{aligned}$$
(18)

and

$$\begin{aligned}&E_{B\left( \tilde{\alpha }_{i}, \tilde{\beta }_{i}\right) }\left( \log f\left( p_{i} ; 1, \tilde{\lambda }\right) \right) \end{aligned}$$
(19)
$$\begin{aligned} =&E_{B\left( \tilde{\alpha }_{i}, \tilde{\beta }_{i}\right) }\left( \log \frac{\varGamma (1+\tilde{\lambda })}{\varGamma (1) \varGamma (\tilde{\lambda })} p_{i}^{1-1}\left( 1-p_{i}\right) ^{\tilde{\lambda }-1}\right) \end{aligned}$$
(20)
$$\begin{aligned} =&E_{B\left( \tilde{\alpha }_{i}, \tilde{\beta }_{i}\right) }\left( \log \frac{\varGamma (1+\tilde{\lambda })}{\varGamma (1) \varGamma (\tilde{\lambda })}+(\tilde{\lambda }-1) \log \left( 1-p_{i}\right) \right) \end{aligned}$$
(21)
$$\begin{aligned} =&\log \frac{\varGamma (1+\tilde{\lambda })}{\varGamma (1) \varGamma (\tilde{\lambda })}+(\tilde{\lambda }-1) E_{B\left( \tilde{a}_{i}, \tilde{\beta }_{i}\right) }\left( \log \left( 1-p_{i}\right) \right) \end{aligned}$$
(22)
$$\begin{aligned} =&\log \frac{\varGamma (1+\tilde{\lambda })}{\varGamma (1) \varGamma (\tilde{\lambda })}+(\tilde{\lambda }-1)\left( \psi \left( \tilde{\beta }_{i}\right) -\psi \left( \tilde{\alpha }_{i}+\tilde{\beta }_{i}\right) \right) , \end{aligned}$$
(23)

in which \(\psi (\cdot )\) denotes the digamma function.

2.3 Classification of Uncertain Data

As explained above, based on the belief values of \(x_{i}\) belonging to positive and negative classes \(b_{i}^{+}=e_{i}^{+}/E, b_{i}^{-}=e_{i}^{-}/E\), we can measure the classification uncertainty of \(x_{i}\) by \(u_{i}=1-b_{i}^{+}-b_{i}^{-}\). With this uncertainty measure, applying the evidential neural networks to classify data, we can not only assign class labels to instances but also identify the uncertain ones. Through sorting the classified instances according to their uncertainty in ascending order, we select the top k uncertain instances for classification rejection to reduce the prediction risk.

Fig. 1.
figure 1

Evidence distribution of positive-class instances with different rejection rates. (a) rejection rate = 0%, (b) rejection rate = 10%, (c) rejection rate = 20%, (d) rejection rate = 30%.

Full size image

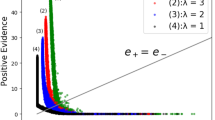
Applying the proposed evidential neural network to the Breast IDC dataset (see the Sect. 3), Fig. 1(a) shows the evidence distribution of all the instances of positive class for multiple values of \(\lambda \). We can see that the factor \(\lambda \) adjusts the evidences of instances and the evidences of certain positive instances are promoted. The data instances with low-level evidences for both classes have high uncertainty in classification. Thus the instances located in the bottom-left corner indicate uncertain cases. Figure 1(b–d) display the evidence distribution of data instances after filtering out 10%, 20%, 30% uncertain instances, respectively. Based on the uncertain data identification strategy, we implement the uncertain data classification method with an evidential neural network (EviNet-UC). The effectiveness of the proposed method will be demonstrated in the following section.

3 Experimental Results

To show that the uncertain classification method with evidential neural network is effective to reduce decision costs, we tested the proposed method on the medical datasets Breast IDC [4] and Chest Xray [16]. The Breast IDC dataset consists of the pathological images of patients with infiltrating ductal carcinoma of the breast. The training set has 155314 images and the test set has 36904 images. We set the cancer case as positive class and the normal case as negative class. The Chest Xray dataset has 2838 chest radiographs, in which 427 images are chosen as the test data and the rest are set as the training data. The pneumonia and normal cases are set as positive class and negative class, respectively. For the algorithm implementation, we constructed the evidential deep neural networks based on the resnet18 architecture  [14] and we modified the activation function of the output layer to the ReLU function.

To achieve the overall evaluation of the classification methods, we adopt the measures of accuracy, F1 score, precision, recall rate and decision cost. Suppose the number of the instances of negative class is N and the number of positive-class instances is P, TP and FP denote the numbers of true positive and false positive instances, TN and FN denote the true negative and false negative instances respectively. The measures are defined as

$$\begin{array}{c} { accuracy }\,=\,(TP+TN) /(P+N), \\ { F1\,score }\,=\,(2 * TP) /(2 * TP+FN+FP), \\ { precision }\,=\,TP /(TP+FP), \\ { recall }\,=\,TP /(TP+FN). \end{array}$$

Assuming correct classification to have zero cost, \({\text {cost}}_{N P}, \cos t_{P N}\) denote the costs of false-positive classification and false-negative classification, respectively. The average decision cost of classification can be calculated as

$$decision cost ={\text {cost}}_{NP} \cdot \frac{FP}{P+N}+\cos t_{PN} \cdot \frac{FN}{P+N}.$$

Based on the measures above, we carried out two experiments to evaluate the performance of the proposed uncertain classification method with evidential neural network (EviNet-UC). The first experiment aims to verify the superiority of the classification of the proposed method. Specifically, we compared the EviNet-UC method with other four uncertain classification methods based on deep neural networks: EvidentialNet  [13], SelectiveNet  [12], Resnet-pd and Resnet-md  [19]. For fair comparison, we implemented all the methods above based on the resnet18 architecture.

We set rejection rate = 0 (no rejection), \({\text {cost}}_{P N}=5, \cos t_{N P=1}\) and applied all the classification methods to the Breast IDC dataset. The comparative experimental results are presented in Fig. 2 and Table 1. We can find that the proposed EviNet-UC method achieves the highest recall rate and the lowest decision cost among all the comparative methods. This means that the proposed method is effective to reduce the misclassification of the risky class (cancer case). Moreover, we changed the rejection rate from 0 to 0.5 to further compare the classification methods. Figure 3 presents the recall rates and the decision costs of different methods with different rejection rates. We can see that the EviNet-UC method achieves the best performance for all rejection rates. Compared to other methods, the proposed method is more effective to reduce the classification risk.

Fig. 2.
figure 2

Comparative experimental results on Breast IDC dataset.

Full size image
Table 1. Comparative experimental results on Breast IDC dataset.
Full size table
Fig. 3.
figure 3

(a) Recall rates of different classification methods with varying rejection rates, (b) decision costs with rejection rates.

Full size image

The second experiment aims to show that the proposed method is effective to identify uncertain data. Varying the rejection rate in [0, 1] and applying EviNet-UC on the Chest Xray dataset, we obtained the classification results for different numbers of rejected uncertain radiographs. Figure 4 illustrates the evaluation of the classification based on EviNet-UC with varying rejection rates. It can be seen that accuracy, precision, recall rate and F1 score increase as the rejection rate increases. This indicates that the rejected data instances have uncertainty for classification and the EviNet-UC method can improve the classification results through filtering out the uncertain instances.

Fig. 4.
figure 4

Classification evaluation of EviNet-UC with varying rejection rates.

Full size image
Fig. 5.
figure 5

(a) certain negative-class instance (normal case), (b) certain positive-class instance (pneumonia), (c) uncertain normal case, (d) uncertain pneumonia case.

Full size image

When rejection rate = 10%, Fig. 5 presents the certain and uncertain instances identified by EviNet-UC. Figure 5 (a) shows a certain negative-class instance of normal radiograph, in which the lung area is very clear. EviNet-UC produces high negative probability \(p^{-}\) = 0.95 and low uncertainty u = 0.09 to indicate the confident classification. In contrast, Fig. 5 (b) shows a certain positive-class instance of pneumonia radiograph, in which there exist heavy shadows. Correspondingly, EviNet-UC produces high positive probability \(p^{+}\) = 0.95 and low uncertainty u = 0.1.

Figure 5 (c) displays an uncertain normal case. In general, the lung area is clear but there exists a dense area of nodule in the right part (marked in red circle). EviNet-UC produces high uncertainty u = 0.44 to indicate the judgement is not confident. Figure 5 (d) shows another uncertain case of pneumonia. In the radiograph, there exists a shadow area in the right lung but the symptom is not prominent, which leads to the uncertainty u = 0.35 for pneumonia identification. The uncertain radiographs will be rejected for cautious examination to further reduce the cost of misclassification.

4 Conclusions

Certain classification methods with deep neural networks strictly assign a class label to each data instance, which may produce overconfident classification results for uncertain cases. In this paper, we propose an uncertain classification method with evidential neural networks which measures the uncertainty of the data instances with evidence theory. Experiments on medical images validate the effectiveness of the proposed method for uncertain data identification and decision cost reduction. Our method currently focuses on only binary classification problem and the relationship between the decision cost and the evidence adjustment factor also requires theoretical analysis. Exploring the evidence adjustment factor in multi-class classification problems and constructing the precise uncertainty measurement for reducing decision risk will be future works.